Как научиться ментальной арифметике самостоятельно
Основа ментальной арифметики — обучение технике устного быстрого счета с помощью абакуса. Абакус — это стародавние японские счеты, очень похожие на те, что знакомы нам с детства. Отличие в том, что числа в абакусе обозначаются определенным их положением на спице, а не только количеством косточек на ней. Чтобы разобраться, как научиться ментальной арифметике и в каком возрасте лучше всего ей заниматься, мы подготовили эту статью.
Что нужно для обучения ментальной арифметике?
Чтобы знать, как научиться ментальной арифметике, для начала нужно понять, что необходимо для процесса обучения. Обучаться ментальной арифметике лучше всего не дома, а в специальных развивающих центрах, потому что это довольно специфическая и сложная методика, которой не так просто научиться самим родителям. Будет лучше, если вашему ребёнку основы данной программы расскажут квалифицированные педагоги. К тому же, в свободном доступе почти нет специальных материалов, методических пособий и учебников, которые необходимы для обучения ментальной арифметике. Кроме обучающих книг нужно иметь специальные счёты – абакус (или соробан).
Как научиться ментальной арифметике?
- Сначала дети учатся считать на абакусе физически и в работе со счетами задействуются обе руки. Это начальный этап по тренировке обоих полушарий головного мозга.
- Следующий этап — представление образа абакуса в уме и тренировка перекидывания косточек в своем воображении.
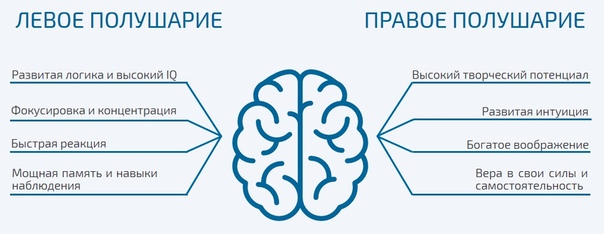
Именно в момент процесса вычислений на воображаемом абакусе начинают укрепляться нейронные связи между двумя полушариями мозга, правое и левое полушария начинают работать одновременно. Образ абакуса хранится у ребенка в правом полушарии (которое отвечает за образное мышление), а в левом хранятся числа, которые ребенок считает (левое полушарие отвечает за точность и логику).
Простое сложение
Главное правило счёта на соробане: «Считать нужно слева направо», что не соответствует привычному нам способу вычисления.
Начинать вычисления стоит с чисел, сумма и разность которых даёт не более 9 при сложении и не менее 1 при вычитании.
Примеры вроде 1+6, 2+7, 12+24 или 123+432 подойдут на первых порах.
- Начнём со сложения единиц: для примера 1+2 поднимите на крайней правой спице 1 костяшку вверх, а затем добавьте к ней ещё 2.
- Для примера:12+32. Откладываем в колонке десятков — 1 косточку, в единицах — 2. Затем к 1 костяшке придвигаем 3, к 2 костяшкам единиц ещё 2.
Простое вычитание
Изучать вычитание также стоит с простых примеров:
- Рассмотрим вычитание на единицах. Простой пример: 4 — 2 = 2. Из четырёх поднятых костяшек убираем 2 и получаем результат.
- Простой пример с десятками: 24 — 13 = 11. Из столбца десятков убираем 1 костяшку остаётся 1. Переходим к единицам: от 4 костяшек отнимаем 3, у нас остаётся 1 костяшка. Результат готов.
Сложное сложение
Пример: 4 + 8 = 12
Как решать?
- Установите 4 костяшки в столбце единиц.
- Для 8 костяшек места уже не найдётся.
- Вспоминаем принцип дополнительных чисел: число 10 даёт наша 8 и цифра 2.
- Вычтите дополнительную цифру 2 из 4.
- Добавьте единицу в столбик десятков.
- Результат — 12.
Сложное вычитание
Пример: 12 — 7 = 5.
Как решать?
- Установите 1 костяшку на столбец с десятками, добавьте 2 к единицам.
- Вспомните, что 7 — это 10 и 3.
- Уберите 1 костяшку из столбца десятков.
- Прибавьте в столбце единиц к 2 костяшкам дополнительные 3. Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».

Умножение
Есть несколько возможных способов умножения на соробане, мы рассмотрим один из самых распространённых.
Обратите внимание: чтобы умножать на соробане, нужно хорошо знать таблицу умножения.
Также необходимо запомнить следующие термины, которые мы рассмотрим на примере a x b = c, где:
a — это множимое;
b — это множитель;
с — произведение.
Пример: 43 x 8 = 344.
Шаг 1
В первом столбце слева устанавливаем множитель — 8, отступаем один столбец и откладываем множимое — 43. Отступаем 2 столбца — с этого столбца начнём записывать результат.
Шаг 2
Умножаем 3 на 8. Результат 24 записываем в 7 и 8 столбцах. Завершая операцию, убираем цифру 3 с доски, сдвинув костяшки вверх.
Шаг 3
Умножьте 4 на 8. Результат 32 запишите следующим образом: 3 в 6 столбец — перед прошлым результатом, а 2 сложите с результатом в 7 столбце, то есть с 2. Три цифры в результате дают ответ — 344.
Деление
Для деления мы также используем стандартные математические термины a ÷ b = c, где:
a — делимое;
b — делитель;
c — частное.
Делимое набирается на спицах в правом конце соробана, делитель — в левом конце. Результат записывается посередине.
Между делимым и делителем рекомендуют оставить минимум 4 пустых столбца для записи результата.
Также существуют правила размещения первой цифры частного:
- Если количество цифр в делителе меньше (или равно) количеству цифр в делимом, расположите первую цифру частного, отступив 2 столбца слева от делимого.
- Если количество цифр в делителе больше, нежели в делимом, начните располагать частное, отступив 1 столбец слева от делимого.
Пример: 72 ÷ 2
- Помещаем делитель 2 в левую часть счёт, делимое — 72 — в правую.
- Делим первое число 7 на 2. Цифра 2 помещается в 7 полностью три раза — поднимаем 3 костяшки в соответствии с правилом №1, отступив 2 столбца влево от делимого.

- Умножим полученное число 3 на делитель — 2. Результат — 6 — вычтем из первой цифры делимого — 7. Убираем лишние костяшки, остаётся единица.
- Остаток от делимого — 12 делим на делитель — 2. Полученный результат — 6 помещаем в следующий свободный столбец для записи результата. Получаем в итоге — 36.
Где можно обучиться ментальной арифметике?
Научиться ментальной арифметике самостоятельно можно, но сложно. Для этого нужно будет сначала родителям пройти длительный курс обучения. К тому же в общем доступе почти невозможно достать нужные методические пособия и дидактические материалы. Поэтому мы советуем отдать ребенка в специализированный центр, где его будут обучать профессиональные квалифицированные педагоги с большим опытом работы и специальным образованием.
Ментальная арифметика в AMAKids
Многие спрашивают, где научиться ментальной арифметике. Наш совет – в «Академии развития интеллекта AMAKids». Наиболее результативный возраст для обучения — от 5 до 16 лет, некоторые методики ограничиваются возрастом 6–11 лет. Методика «Амакидса» эффективно работает со всеми возрастными группами, начиная с 5-летнего возраста и заканчивая взрослыми людьми в возрасте старше 60 лет (главное, чтобы малыши умели считать до 10, а у взрослых было желание и мотивация). При этом, если заниматься регулярно, развитие умственных способностей младших школьников, а также учеников средней школы идет максимально возможными темпами. Наш развивающий центр приглашает всех желающих посетить первое пробное занятие бесплатно!
Единственный способ понять, как научиться ментальной математике, чтобы это дало серьезные результаты (улучшение работы памяти, концентрации внимания и т. д.) — это регулярные тренировки. Если заниматься раз в неделю в группе по ментальной арифметике, а затем выполнять ежедневно домашние задания в течение 15–30 минут, эффективность не заставит себя ждать. Особенно важно, чтобы тренировки проходили не только в учебниках и тетрадях, а с помощью онлайн-платформы, на которой можно выставить разные режимы выполнения заданий и скорости появления цепочек примеров на экране.
Ментальная арифметика дает возможность развиваться и в точных науках, и в творчестве. И происходит это именно за счет улучшения межполушарного взаимодействия мозга. Ребенок начинает понимать, что обучение — это не только обычная ежедневная рутина, но и увлекательный творческий процесс, и занимается с удовольствием. А если есть мотивация, то и эффективность обучения возрастает — ребенок становится успешным в самых разных сферах своей деятельности.
Академия развития интеллекта AMAKids для детей от 5 до 16 лет
ЗАПИСЬ НА БЕСПЛАТНЫЙ УРОК
Введите телефон, и мы Вам перезвоним для уточнения деталей
Выберите городМоскваСанкт-ПетербургАбаканАбинскАгинскоеАзовАксайАлуштаАнапаАнгарскАннаАпрелевкаАпшеронскАрмавирАрхангельскАстраханьАфипскийАхтубинскАчинскБарнаулБатайскБахчисарайБелая ХолуницаБелгородБелореченскБерезовскийБлаговещенскБратскБрянскВеликий НовгородВерхняя ПышмаВерхняя СалдаВидноеВихоревкаВладивостокВладикавказВладимирВолгоградВолжскийВологдаВолоколамскВоронежВоскресенскВсеволожскВыксаВятские ПоляныГатчинаГорно-АлтайскГорячий КлючГригорьевскГрозныйГрязовецГубкинГудермесГусиноозерскДжанкойДзержинскДзержинскийДивногорскДимитровградДинскаяДмитровДолгопрудныйДомодедовоДрожжиноДрокиноДятьковоЕвпаторияЕйскЕкатеринбургЕлизовоЕмельяновоЕссентукиЖелезногорск (Красноярский край)Железногорск (Курская область)Железногорск –ИлимскийЖелезнодорожныйЖигулевскЖирновскЖуковскийЗабайкальскЗавьяловоЗарайскЗаречныйЗвенигородЗеленогорскЗеленоградЗерноградЗлатоустЗональная СтанцияИвановоИвантеевкаИволгинскИжевскИловля ИркутскИстра Йошкар-ОлаКабанскКазаньКалач-на-ДонуКалачинскКалининградКалугаКаменск-УральскийКамышинКанашКанскКарабашКаслиКаспийскКемеровоКерчьКиржачКировКирово-ЧепецкКировскКисловодскКовровКолаКоломнаКольчугиноКомсомольск-на-АмуреКопейскКореновскКоролёвКостромаКотельникиКотельничКотовоКрасногорскКраснодарКраснокаменскКрасноуфимскКрасноярскКропоткинКстовоКулешовка КурганКурганинск КурскКурчатовКызылКыренКяхтаЛениногорскЛуховицыЛыткариноЛьговЛюберцыМагаданМагнитогорскМайкопМалоярославецМарковаМарксМахачкалаМедведевоМиассМинеральные ВодыМинусинскМисайлово МихайловкаМихайловскМичуринскМогойтуйМожайскМосковскийМурманскМуромМытищиНабережные ЧелныНаро-ФоминскНахабиноНевинномысскНемчиновкаНефтеюганскНижнекамскНижний НовгородНижний ТагилНижняя СалдаНовоаннинскНововоронежНовокузнецк НовокуйбышевскНовомосковскНовороссийскНовосибирскНовочебоксарскНовочеркасскНовый УренгойНогинскНоябрьскОбнинскОдинцовоОктябрьский ОмскОмутнинскОрелОренбургОрехово-ЗуевоОсташковОтрадноеОтрадныйПГТ КировскоеПавлиноПензаПервоуральскПермьПетровск-ЗабайкальскийПетрозаводскПетропавловск-КамчатскийПоведникиПодольскПолевскойПоселение СосенскоеПротвиноПсковПушкиноРайсеменовскоеРеутовРостов-на-ДонуРубцовскРыбинскРыльскРязаньСаган-НурСакиСамараСаранскСаратовСаяногорскСевастопольСеверобайкальскСеверодвинскСеверскСегежаСергиев ПосадСеровСерпуховСимферопольСлавянск на КубаниСлободскойСмоленскСоветскСоколСолнечногорскСосново-ОзёрскоеСосновоборскСочиСреднеуральскСтарый КрымСтарый ОсколСтерлитамакСтупиноСудакСургутСуровикиноСухой ЛогСыктывкарСысертьТазовскийТаманьТамбовТаруса ТверьТемрюкТимашевскТихвинТольяттиТомскТроицкТуапсеТулаТулунТурунтаевоТырныаузТюменьУлан-УдэУльяновскУржумУрус-МартанУрюпинскУссурийскУсть — Лабинск Усть — ОрдынскийУсть-КутУфаФеодосияФроловоФрязиноХабаровскХанты-МансийскХимкиХотьковоЧайковскийЧалтырьЧебоксарыЧелябинскЧеркесскЧерногорскЧеховЧистопольЧитаШадринскШалиШаховскаяШелеховЩёлковоЭлектростальЭлистаЭнгельсЭнемЮжно-СахалинскЮрьяЯкутскЯлтаЯранскЯрославльЯсногорскд.
Выберите адрес
Нажимая на кнопку ПЕРЕЗВОНИТЬ МНЕ, Вы даете согласие на обработку своих персональных данных и получение важных уведомлений, информационно-рекламных сообщений о новых методиках и акциях компании.перезвоните мне
Спасибо!
Ваша заявка зафиксирована!
С Вами свяжутся в ближайшее время
Академия развития интеллекта AMAKids для детей от 5 до 16 лет
ЗАПИСЬ НА БЕСПЛАТНЫЙ УРОК
Введите телефон, и мы Вам перезвоним для уточнения деталей
Выберите городМоскваСанкт-ПетербургАбаканАбинскАгинскоеАзовАксайАлуштаАнапаАнгарскАннаАпрелевкаАпшеронскАрмавирАрхангельскАстраханьАфипскийАхтубинскАчинскБарнаулБатайскБахчисарайБелая ХолуницаБелгородБелореченскБерезовскийБлаговещенскБратскБрянскВеликий НовгородВерхняя ПышмаВерхняя СалдаВидноеВихоревкаВладивостокВладикавказВладимирВолгоградВолжскийВологдаВолоколамскВоронежВоскресенскВсеволожскВыксаВятские ПоляныГатчинаГорно-АлтайскГорячий КлючГригорьевскГрозныйГрязовецГубкинГудермесГусиноозерскДжанкойДзержинскДзержинскийДивногорскДимитровградДинскаяДмитровДолгопрудныйДомодедовоДрожжиноДрокиноДятьковоЕвпаторияЕйскЕкатеринбургЕлизовоЕмельяновоЕссентукиЖелезногорск (Красноярский край)Железногорск (Курская область)Железногорск –ИлимскийЖелезнодорожныйЖигулевскЖирновскЖуковскийЗабайкальскЗавьяловоЗарайскЗаречныйЗвенигородЗеленогорскЗеленоградЗерноградЗлатоустЗональная СтанцияИвановоИвантеевкаИволгинскИжевскИловля ИркутскИстра Йошкар-ОлаКабанскКазаньКалач-на-ДонуКалачинскКалининградКалугаКаменск-УральскийКамышинКанашКанскКарабашКаслиКаспийскКемеровоКерчьКиржачКировКирово-ЧепецкКировскКисловодскКовровКолаКоломнаКольчугиноКомсомольск-на-АмуреКопейскКореновскКоролёвКостромаКотельникиКотельничКотовоКрасногорскКраснодарКраснокаменскКрасноуфимскКрасноярскКропоткинКстовоКулешовка КурганКурганинск КурскКурчатовКызылКыренКяхтаЛениногорскЛуховицыЛыткариноЛьговЛюберцыМагаданМагнитогорскМайкопМалоярославецМарковаМарксМахачкалаМедведевоМиассМинеральные ВодыМинусинскМисайлово МихайловкаМихайловскМичуринскМогойтуйМожайскМосковскийМурманскМуромМытищиНабережные ЧелныНаро-ФоминскНахабиноНевинномысскНемчиновкаНефтеюганскНижнекамскНижний НовгородНижний ТагилНижняя СалдаНовоаннинскНововоронежНовокузнецк НовокуйбышевскНовомосковскНовороссийскНовосибирскНовочебоксарскНовочеркасскНовый УренгойНогинскНоябрьскОбнинскОдинцовоОктябрьский ОмскОмутнинскОрелОренбургОрехово-ЗуевоОсташковОтрадноеОтрадныйПГТ КировскоеПавлиноПензаПервоуральскПермьПетровск-ЗабайкальскийПетрозаводскПетропавловск-КамчатскийПоведникиПодольскПолевскойПоселение СосенскоеПротвиноПсковПушкиноРайсеменовскоеРеутовРостов-на-ДонуРубцовскРыбинскРыльскРязаньСаган-НурСакиСамараСаранскСаратовСаяногорскСевастопольСеверобайкальскСеверодвинскСеверскСегежаСергиев ПосадСеровСерпуховСимферопольСлавянск на КубаниСлободскойСмоленскСоветскСоколСолнечногорскСосново-ОзёрскоеСосновоборскСочиСреднеуральскСтарый КрымСтарый ОсколСтерлитамакСтупиноСудакСургутСуровикиноСухой ЛогСыктывкарСысертьТазовскийТаманьТамбовТаруса ТверьТемрюкТимашевскТихвинТольяттиТомскТроицкТуапсеТулаТулунТурунтаевоТырныаузТюменьУлан-УдэУльяновскУржумУрус-МартанУрюпинскУссурийскУсть — Лабинск Усть — ОрдынскийУсть-КутУфаФеодосияФроловоФрязиноХабаровскХанты-МансийскХимкиХотьковоЧайковскийЧалтырьЧебоксарыЧелябинскЧеркесскЧерногорскЧеховЧистопольЧитаШадринскШалиШаховскаяШелеховЩёлковоЭлектростальЭлистаЭнгельсЭнемЮжно-СахалинскЮрьяЯкутскЯлтаЯранскЯрославльЯсногорскд. Стараядеревня Бутовоп. Артип. Новоомскийп. Яблоновскийп.Сеннойпгт Красногвардейскоепгт. Свободныйс. Мошенскоес. Нижний Саянтуйс. Учкекенс. Ширастаница Каневскаястаница Полтавская
Стараядеревня Бутовоп. Артип. Новоомскийп. Яблоновскийп.Сеннойпгт Красногвардейскоепгт. Свободныйс. Мошенскоес. Нижний Саянтуйс. Учкекенс. Ширастаница Каневскаястаница Полтавская
Выберите адрес
Нажимая на кнопку ПЕРЕЗВОНИТЬ МНЕ, Вы даете согласие на обработку своих персональных данных и получение важных уведомлений, информационно-рекламных сообщений о новых методиках и акциях компании.перезвоните мне
Спасибо!
Ваша заявка зафиксирована!
С Вами свяжутся в ближайшее время
Академия развития интеллекта AMAKids для детей от 5 до 16 лет
ЗАПИСЬ НА БЕСПЛАТНЫЙ УРОК
Введите телефон, и мы Вам перезвоним для уточнения деталей
Выберите городМоскваСанкт-ПетербургАбаканАбинскАгинскоеАзовАксайАлуштаАнапаАнгарскАннаАпрелевкаАпшеронскАрмавирАрхангельскАстраханьАфипскийАхтубинскАчинскБарнаулБатайскБахчисарайБелая ХолуницаБелгородБелореченскБерезовскийБлаговещенскБратскБрянскВеликий НовгородВерхняя ПышмаВерхняя СалдаВидноеВихоревкаВладивостокВладикавказВладимирВолгоградВолжскийВологдаВолоколамскВоронежВоскресенскВсеволожскВыксаВятские ПоляныГатчинаГорно-АлтайскГорячий КлючГригорьевскГрозныйГрязовецГубкинГудермесГусиноозерскДжанкойДзержинскДзержинскийДивногорскДимитровградДинскаяДмитровДолгопрудныйДомодедовоДрожжиноДрокиноДятьковоЕвпаторияЕйскЕкатеринбургЕлизовоЕмельяновоЕссентукиЖелезногорск (Красноярский край)Железногорск (Курская область)Железногорск –ИлимскийЖелезнодорожныйЖигулевскЖирновскЖуковскийЗабайкальскЗавьяловоЗарайскЗаречныйЗвенигородЗеленогорскЗеленоградЗерноградЗлатоустЗональная СтанцияИвановоИвантеевкаИволгинскИжевскИловля ИркутскИстра Йошкар-ОлаКабанскКазаньКалач-на-ДонуКалачинскКалининградКалугаКаменск-УральскийКамышинКанашКанскКарабашКаслиКаспийскКемеровоКерчьКиржачКировКирово-ЧепецкКировскКисловодскКовровКолаКоломнаКольчугиноКомсомольск-на-АмуреКопейскКореновскКоролёвКостромаКотельникиКотельничКотовоКрасногорскКраснодарКраснокаменскКрасноуфимскКрасноярскКропоткинКстовоКулешовка КурганКурганинск КурскКурчатовКызылКыренКяхтаЛениногорскЛуховицыЛыткариноЛьговЛюберцыМагаданМагнитогорскМайкопМалоярославецМарковаМарксМахачкалаМедведевоМиассМинеральные ВодыМинусинскМисайлово МихайловкаМихайловскМичуринскМогойтуйМожайскМосковскийМурманскМуромМытищиНабережные ЧелныНаро-ФоминскНахабиноНевинномысскНемчиновкаНефтеюганскНижнекамскНижний НовгородНижний ТагилНижняя СалдаНовоаннинскНововоронежНовокузнецк НовокуйбышевскНовомосковскНовороссийскНовосибирскНовочебоксарскНовочеркасскНовый УренгойНогинскНоябрьскОбнинскОдинцовоОктябрьский ОмскОмутнинскОрелОренбургОрехово-ЗуевоОсташковОтрадноеОтрадныйПГТ КировскоеПавлиноПензаПервоуральскПермьПетровск-ЗабайкальскийПетрозаводскПетропавловск-КамчатскийПоведникиПодольскПолевскойПоселение СосенскоеПротвиноПсковПушкиноРайсеменовскоеРеутовРостов-на-ДонуРубцовскРыбинскРыльскРязаньСаган-НурСакиСамараСаранскСаратовСаяногорскСевастопольСеверобайкальскСеверодвинскСеверскСегежаСергиев ПосадСеровСерпуховСимферопольСлавянск на КубаниСлободскойСмоленскСоветскСоколСолнечногорскСосново-ОзёрскоеСосновоборскСочиСреднеуральскСтарый КрымСтарый ОсколСтерлитамакСтупиноСудакСургутСуровикиноСухой ЛогСыктывкарСысертьТазовскийТаманьТамбовТаруса ТверьТемрюкТимашевскТихвинТольяттиТомскТроицкТуапсеТулаТулунТурунтаевоТырныаузТюменьУлан-УдэУльяновскУржумУрус-МартанУрюпинскУссурийскУсть — Лабинск Усть — ОрдынскийУсть-КутУфаФеодосияФроловоФрязиноХабаровскХанты-МансийскХимкиХотьковоЧайковскийЧалтырьЧебоксарыЧелябинскЧеркесскЧерногорскЧеховЧистопольЧитаШадринскШалиШаховскаяШелеховЩёлковоЭлектростальЭлистаЭнгельсЭнемЮжно-СахалинскЮрьяЯкутскЯлтаЯранскЯрославльЯсногорскд. Стараядеревня Бутовоп. Артип. Новоомскийп. Яблоновскийп.Сеннойпгт Красногвардейскоепгт. Свободныйс. Мошенскоес. Нижний Саянтуйс. Учкекенс. Ширастаница Каневскаястаница Полтавская
Стараядеревня Бутовоп. Артип. Новоомскийп. Яблоновскийп.Сеннойпгт Красногвардейскоепгт. Свободныйс. Мошенскоес. Нижний Саянтуйс. Учкекенс. Ширастаница Каневскаястаница Полтавская
Выберите адрес
Нажимая на кнопку ПЕРЕЗВОНИТЬ МНЕ, Вы даете согласие на обработку своих персональных данных и получение важных уведомлений, информационно-рекламных сообщений о новых методиках и акциях компании.перезвоните мне
Спасибо!
Ваша заявка зафиксирована!
С Вами свяжутся в ближайшее время
Ментальная арифметика для детей обучить самому дома
- Главная /
- Полезное
Можно ли освоить ментальную математику, занимаясь с ребенком дома? Обучить самому, без серьезных денежных затрат? Да, можно!
На этой странице нашего сайта мы собрали все необходимое для мини-уроков в домашних условиях. От вас — желание заняться чем-то полезным с ребенком, 10-20 минут свободного времени, от нас — полезные видео, бесплатные тетради, книги и многое другое. Забирайте, скачивайте, сохраняйте себе!
Для занятий дома вам понадобятся
- Видеоуроки. Азы ментальной арифметики в наших коротких обучающих видео. Смотрите с ребенком и сами — знакомьтесь с методикой!
- Тренажер по ментальной арифметике онлайн. Освоить ментальный счет и начать решать примеры поможет наш тренажер. Занимайтесь онлайн, это весело, легко и интересно!
- Книги и пособия по ментальной арифметике. Прямо сейчас вы можете скачать бесплатно полезные книги и самоучитель. Они помогут вам верно выстроить обучение на дому.

- Задания по ментальной арифметике. Детские уроки — это минимум скучной теории и максимум интересной практики. Скачайте бесплатно красочные, веселые задания для детей и упражняйтесь в счете и примерах!
- Рабочие тетради. Легкий способ научить ребенка сложению и вычитанию — заниматься дома по этим тетрадям. Скачайте их бесплатно, распечатайте и погружайтесь в увлекательный мир математики!
- Программы обучения. Как самостоятельно организовать занятия и все предусмотреть? Какой режим выбрать? Узнайте подробности в этих программах и занимайтесь дома с пользой!
- Игры по ментальной арифметике. Как сделать обучение интересным и не напрягать ребенка теорией? Занимайтесь, играя! Научить легче тогда, когда в ежедневные занятия вносится элемент игры.
- Генератор примеров по ментальной арифметике. Чем больше занимаетесь, тем лучше результаты! Используйте наш генератор примеров, чтобы тренировать память ребенка и скорость решения задач.
- Флеш-карты. Скачайте и распечатайте бесплатно наши полезные флеш-карты для домашних занятий. Вооружитесь всем необходимым, занимайтесь регулярно, последовательно и результаты вас порадуют!
Заниматься дома по нашим материалам — это простой секрет того, как вырастить умного ребенка!
Внимание: Акция на бесплатные материалы ограничена! Подробности и сроки действия уточняйте у менеджеров в нашем магазине Abakus Store.
Полезные видео
КАК НАУЧИТЬСЯ МЕНТАЛЬНОЙ АРИФМЕТИКЕ? | АКАДЕМИЯ AMAKids
Основа ментальной арифметики — обучение технике устного быстрого счета с помощью абакуса. Абакус — это стародавние японские счеты, очень похожие на те, что знакомы нам с детства. Отличие в том, что числа в абакусе обозначаются определенным их положением на спице, а не только количеством косточек на ней. Чтобы разобраться, как научиться ментальной арифметике и в каком возрасте лучше всего ей заниматься, мы подготовили эту статью.
ЧТО НУЖНО ДЛЯ ОБУЧЕНИЯ МЕНТАЛЬНОЙ АРИФМЕТИКЕ?Чтобы знать, как научиться ментальной арифметике, для начала нужно понять, что необходимо для процесса обучения. Обучаться ментальной арифметике лучше всего не дома, а в специальных развивающих центрах, потому что это довольно специфическая и сложная методика, которой не так просто научиться самим родителям. Будет лучше, если вашему ребёнку основы данной программы расскажут квалифицированные педагоги. К тому же, в свободном доступе почти нет специальных материалов, методических пособий и учебников, которые необходимы для обучения ментальной арифметике. Кроме обучающих книг нужно иметь специальные счёты – абакус (или соробан).
КАК НАУЧИТЬСЯ МЕНТАЛЬНОЙ АРИФМЕТИКЕ?- Сначала дети учатся считать на абакусе физически и в работе со счетами задействуются обе руки. Это начальный этап по тренировке обоих полушарий головного мозга.
- Следующий этап — представление образа абакуса в уме и тренировка перекидывания косточек в своем воображении.
Именно в момент процесса вычислений на воображаемом абакусе начинают укрепляться нейронные связи между двумя полушариями мозга, правое и левое полушария начинают работать одновременно. Образ абакуса хранится у ребенка в правом полушарии (которое отвечает за образное мышление), а в левом хранятся числа, которые ребенок считает (левое полушарие отвечает за точность и логику).
Главное правило счёта на соробане: «Считать нужно слева направо», что не соответствует привычному нам способу вычисления.
Начинать вычисления стоит с чисел, сумма и разность которых даёт не более 9 при сложении и не менее 1 при вычитании.
Примеры вроде 1+6, 2+7, 12+24 или 123+432 подойдут на первых порах.
- Начнём со сложения единиц: для примера 1+2 поднимите на крайней правой спице 1 костяшку вверх, а затем добавьте к ней ещё 2.
- Для примера:12+32. Откладываем в колонке десятков — 1 косточку, в единицах — 2. Затем к 1 костяшке придвигаем 3, к 2 костяшкам единиц ещё 2.
Изучать вычитание также стоит с простых примеров:
- Рассмотрим вычитание на единицах. Простой пример: 4 — 2 = 2. Из четырёх поднятых костяшек убираем 2 и получаем результат.
- Простой пример с десятками: 24 — 13 = 11. Из столбца десятков убираем 1 костяшку остаётся 1. Переходим к единицам: от 4 костяшек отнимаем 3, у нас остаётся 1 костяшка. Результат готов.
- По тому же принципу работаем с сотнями: 432 — 322 = 110. Из столбца сотен от 4 отнимем 3, из 3 вычтем 2 останется 1, из 2 вычтем 2 — все костяшки из столбца единиц возвращаются в нулевую позицию.
Пример: 4 + 8 = 12
Как решать?
- Установите 4 костяшки в столбце единиц.
- Для 8 костяшек места уже не найдётся.
- Вспоминаем принцип дополнительных чисел: число 10 даёт наша 8 и цифра 2.
- Вычтите дополнительную цифру 2 из 4.
- Добавьте единицу в столбик десятков.
- Результат — 12.
Пример: 12 — 7 = 5.
Как решать?
- Установите 1 костяшку на столбец с десятками, добавьте 2 к единицам.
- Вспомните, что 7 — это 10 и 3.
- Уберите 1 костяшку из столбца десятков.
- Прибавьте в столбце единиц к 2 костяшкам дополнительные 3. Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».

Есть несколько возможных способов умножения на соробане, мы рассмотрим один из самых распространённых.
Обратите внимание: чтобы умножать на соробане, нужно хорошо знать таблицу умножения.
Также необходимо запомнить следующие термины, которые мы рассмотрим на примере a x b = c, где:
a — это множимое;
b — это множитель;
с — произведение.
Пример: 43 x 8 = 344.
Шаг 1
В первом столбце слева устанавливаем множитель — 8, отступаем один столбец и откладываем множимое — 43. Отступаем 2 столбца — с этого столбца начнём записывать результат.
Шаг 2
Умножаем 3 на 8. Результат 24 записываем в 7 и 8 столбцах. Завершая операцию, убираем цифру 3 с доски, сдвинув костяшки вверх.
Шаг 3
Умножьте 4 на 8. Результат 32 запишите следующим образом: 3 в 6 столбец — перед прошлым результатом, а 2 сложите с результатом в 7 столбце, то есть с 2. Три цифры в результате дают ответ — 344.
ДЕЛЕНИЕДля деления мы также используем стандартные математические термины a ÷ b = c, где:
a — делимое;
b — делитель;
c — частное.
Делимое набирается на спицах в правом конце соробана, делитель — в левом конце. Результат записывается посередине.
Между делимым и делителем рекомендуют оставить минимум 4 пустых столбца для записи результата.
Также существуют правила размещения первой цифры частного:
- Если количество цифр в делителе меньше (или равно) количеству цифр в делимом, расположите первую цифру частного, отступив 2 столбца слева от делимого.
- Если количество цифр в делителе больше, нежели в делимом, начните располагать частное, отступив 1 столбец слева от делимого.
Пример: 72 ÷ 2
- Помещаем делитель 2 в левую часть счёт, делимое — 72 — в правую.
- Делим первое число 7 на 2. Цифра 2 помещается в 7 полностью три раза — поднимаем 3 костяшки в соответствии с правилом №1, отступив 2 столбца влево от делимого.

- Умножим полученное число 3 на делитель — 2. Результат — 6 — вычтем из первой цифры делимого — 7. Убираем лишние костяшки, остаётся единица.
- Остаток от делимого — 12 делим на делитель — 2. Полученный результат — 6 помещаем в следующий свободный столбец для записи результата. Получаем в итоге — 36.
Научиться ментальной арифметике самостоятельно можно, но сложно. Для этого нужно будет сначала родителям пройти длительный курс обучения. К тому же в общем доступе почти невозможно достать нужные методические пособия и дидактические материалы. Поэтому мы советуем отдать ребенка в специализированный центр, где его будут обучать профессиональные квалифицированные педагоги с большим опытом работы и специальным образованием.
МЕНТАЛЬНАЯ АРИФМЕТИКА В AMAKIDSМногие спрашивают, где научиться ментальной арифметике. Наш совет – в «Академии развития интеллекта AMAKids». Наиболее результативный возраст для обучения — от 5 до 16 лет, некоторые методики ограничиваются возрастом 6–11 лет. Методика «Амакидса» эффективно работает со всеми возрастными группами, начиная с 5-летнего возраста и заканчивая взрослыми людьми в возрасте старше 60 лет (главное, чтобы малыши умели считать до 10, а у взрослых было желание и мотивация). При этом, если заниматься регулярно, развитие умственных способностей младших школьников, а также учеников средней школы идет максимально возможными темпами. Наш развивающий центр приглашает всех желающих посетить первое пробное занятие бесплатно!
Единственный способ понять, как научиться ментальной математике, чтобы это дало серьезные результаты (улучшение работы памяти, концентрации внимания и т. д.) — это регулярные тренировки. Если заниматься раз в неделю в группе по ментальной арифметике, а затем выполнять ежедневно домашние задания в течение 15–30 минут, эффективность не заставит себя ждать. Особенно важно, чтобы тренировки проходили не только в учебниках и тетрадях, а с помощью онлайн-платформы, на которой можно выставить разные режимы выполнения заданий и скорости появления цепочек примеров на экране.
Ментальная арифметика дает возможность развиваться и в точных науках, и в творчестве. И происходит это именно за счет улучшения межполушарного взаимодействия мозга. Ребенок начинает понимать, что обучение — это не только обычная ежедневная рутина, но и увлекательный творческий процесс, и занимается с удовольствием. А если есть мотивация, то и эффективность обучения возрастает — ребенок становится успешным в самых разных сферах своей деятельности.
Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения
Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения
Ментальная арифметика – популярная методика гармоничного и равного развития обоих полушарий мозга. Методика одинаково подходит для детей и взрослых и заключается в обучении быстрому устному счету с применением специального инструмента, который называют абакусом или соробаном.
Научить детей ментальной арифметике в домашних условиях помогут видео уроки на сайте ВСЕ КУРСЫ ОНЛАЙН.
Строение и функции абакуса (соробана)
Абакус – древние китайские счеты. Состоит из рамки, перекладины, спиц и косточек. Перекладина делит косточки горизонтально на 2 части. Нижние получили название «земных» (смотрят всегда вниз), верхние – «небесных» (смотрят вверх). Косточки играют роль единиц, десятков и сотен. Сначала ученики осваивают простые арифметические действия (сложение и вычитание), затем сложные (умножение и деление). Следующий этап – счет без использования инструмента, в уме. Ученик двигает пальцами, представляя абакус, и решает примеры с многозначными числами. Инструмент можно запросто сделать самостоятельно, переконструировав обычные советские счеты.
Основные принципы
- Считать правильно двумя руками, используя указательные и большие пальцы.
- Поднимают кости всегда большим пальцем, опускают и двигают «небесные» косточки указательным.
- Абакус нужно придерживать левой рукой.

- В правой руке всегда находится ручка для заметок и записей, обхваченная мизинцем, безымянным и средним пальцами.
- Сброс косточек в исходное положение делают, обхватив перекладину двумя рабочими пальцами и двигаясь справа налево.
Набор чисел
Крайний правый столбец предназначен для набора единиц, второй для десятков, третий для сотен, следующие для тысяч и так далее. Исходное положение означает ноль. Поднятые нижние бусины – единицы от 1 до 4, десятки от 10 до 40 и аналогичные сотни, тысячи в зависимости от столбца. Верхние опущенные бусины обозначают числа, кратные пяти: 5, 50, 500, 5000 и т.д. по мере удаления столбцов. Цифра 7 – это 5+2. Значит нужно опустить небесную косточку и поднять две земных. Все остальные числа набирают по аналогичному принципу. Для тренировки хорошо использовать онлайн-тренажеры в Google или установить специальное приложение.
Правила
Правила имеют условные названия, которые образно иллюстрируют действия. Выполняются всегда в строгой последовательности.
- «Просто» — поднятие нужного количества земных косточек, опускание небесной или то и другое одновременно.
- «Брат» — когда первый пункт не работает и сумма выдает 5.
- «Друг» — два числа, дающие 10.
- «Друг + Брат» — совмещает два предыдущих правила, выполняется двумя руками.
Сложение (простое и с переходом на 10)
Самое простое действие, с которого начинают обучение. Начинать первое знакомство можно в детском саду, начальной школе. Сначала следует научиться считать до 10. Затем решать примеры до 3. Следующий этап — сложение всех чисел без перехода на десятки. В качестве закрепляющих заданий эффективно использовать карточки с изображениями разных комбинаций на счетах. Например, найти правильный ответ на заданный пример. При сложении за пределами десятка суммы необходимо разложить на простые составляющие. Состав десяти может иметь несколько комбинаций (1+9, 2+8, 3+7, 4+6, 5+5).
Состав десяти может иметь несколько комбинаций (1+9, 2+8, 3+7, 4+6, 5+5).
Вычитание
Разницу считают подобно сумме, по правилам «просто», «брат», «друг», «друг+брат». Существует масса онлайн тренажеров и конструкторов заданий для закрепления арифметических навыков. Современные ученики обожают работать на компьютере, поэтому заставлять тренироваться даже не придется. Будущие математики сами с удовольствием будут выполнять нужные упражнения.
Умножение
Умножение (многократное сложение) можно выполнять несколькими различными методами. Самый простой и безошибочный был предложен Японским Комитетом по абакусу. Принцип напоминает умножение в столбик на бумаге, так же последовательно. Чтобы работать с двузначными числами (45*56), нужно учесть: ответ получится четырехзначным, и нужно будет уметь его прочитать.
Деление
Деление производят по принципу многократного вычитания. Конечно, без выученной «на зубок» таблицы умножения приступать к действию не имеет смысла. Самый удобный метод разработан Такаши Койима в книге об использовании и теории японского абакуса. Главный плюс — использование привычной школьной терминологии: делимое, делитель, частное. Делимое находится правее центра, делитель левее, разделенные тремя-четырьмя свободными линейками.
Положительное влияние счета на абакусе
В Азии предмет входит в обязательную программу почти во всех учебных заведениях. С помощью простого девайса дети учатся умножать и делить многозначные числа без калькулятора. Существуют и другие сопутствующие бонусы.
- Развивается зрительная и слуховая память, повышается внимание и сосредоточенность.
- Активируется интуиция, сообразительность, смекалка.
- Возникает нестандартное мышление, самостоятельность, уверенность в принятии решений.
- Усиливаются творческие способности и предрасположенность к изучению иностранных языков.

Тренировочные упражнения
Благодаря японской методике родители имеют прекрасную возможность одновременно учить детишек счету и прокачивать ум и интеллект в целом. Европейцы подхватили идею и дополнили интерактивными технологиями: компьютерным тренажером (анзаном), флеш-картами и другими программами. Важно заниматься каждый день в течение двух-трех лет , начиная с четырех-шестилетнего возраста.
В результате регулярных занятий повышается успеваемость в школе за счет улучшения памяти и повышения концентрации внимания. Ребенок легче запоминает новые слова, исторические даты и факты, теоремы и формулы. Одновременно развивается воображение и творческое мышление, способность нестандартно подходить к решению задач.
Ментальная арифметика | SkillsYouNeed
Ментальная арифметика — это бесценный математический навык, позволяющий производить вычисления в уме без использования каких-либо инструментов, таких как калькулятор, ручка, бумага или пальцы! Он может пригодиться в бесчисленных повседневных ситуациях, от разработки лучшей сделки с несколькими покупками в супермаркете до расчета, как долго вам нужно будет ждать следующего поезда.
Люди, которым необходимо использовать математику в своей работе, будь то бухгалтерский учет, розничная торговля или инженерное дело, например, часто делают довольно сложные и быстрые оценки в своей голове, чтобы иметь хорошее представление о том, какой будет ответ, прежде чем они приступят к пора сделать более сложный расчет.
Ментальная арифметика также помогает развить настоящее понимание математических методов арифметики, а не просто выполнять вычисления посредством запоминания.
Практика ментальной арифметики может показаться тяжелой работой, а некоторым людям, которые находят сложную математику, это даже может показаться пугающей перспективой. Но, как и во всем, чем больше вы это делаете, тем легче становится.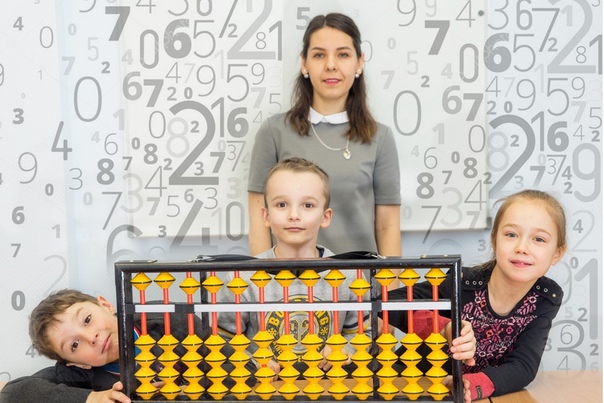 Эта страница дает вам несколько полезных советов, которые сделают процесс быстрее, проще и намного менее пугающим.
Эта страница дает вам несколько полезных советов, которые сделают процесс быстрее, проще и намного менее пугающим.
Каждый может научиться ментальной математике! Они не только для математиков.
Умножение чисел на 10, 100 и 1000 и их кратные
Чтобы выполнить простое умножение, вам необходимо иметь базовое представление о разряде . Подробнее об этом читайте на нашей странице Numbers . Здесь следует помнить две вещи:
- Важны нули
- Десятичные точки всегда отделяют целые числа от «битов».
Чтобы мысленно умножить любое число на 10:
Оставьте десятичную точку на месте. В уме переместите все цифры на одну позицию влево и при необходимости добавьте в конец ноль.
24 × 10 = 24,0 × 10 = 240
175 × 10 = 175,0 × 10 = 1750
3,56 × 10 = 35,6
Вы можете перемещать десятичную точку вместо цифр, но только то или другое!
Некоторым людям легче думать о перемещении десятичной точки, чем о перемещении цифр.В приведенном выше примере десятичная точка остается на том же месте, а все цифры сдвигаются влево.
Это то же самое, что и перемещение десятичной точки вправо !
24 × 10 = 24,0 × 10 = 240
175 × 10 = 175,0 × 10 = 1750
3,56 × 10 = 35,6
Чтобы умножить любое число на 100:
Либо
Оставьте десятичную точку на месте. Переместите цифры на два места влево , добавляя при необходимости нули в конце:
845 × 100 = 845.00 × 100 = 84500
37,64 × 100 = 3764
OR
Переместите десятичную запятую на два разряда вправо:
56,734 × 100 = 5673,4
Чтобы умножить любое число на 1000:
Используйте любой из двух методов, как и раньше, и переместите на три позиции :
Переместите цифры влево:
23,476 × 1000 = 23476
Или переместите десятичную точку вправо:
8,45692 × 1000 = 8456,92
Умножение на десятки, сотни и тысячи или более:
Основная идея: если вам нужно умножить число на 200, сначала умножьте на 2, а затем переместите цифры. Вы можете сделать это с любым количеством. Например, если вам нужно что-то умножить на 5000, сначала умножьте свое число на 5, а затем переместите три десятичных разряда.
Вы можете сделать это с любым количеством. Например, если вам нужно что-то умножить на 5000, сначала умножьте свое число на 5, а затем переместите три десятичных разряда.
Количество перемещаемых мест всегда равно количеству нулей.
Например, умножьте 25 на 5000. Это довольно сложно сделать в уме, но весь фокус в том, чтобы разбить это на простые вычисления.
Сначала умножьте 25 на 5:
25 × 5 = 125
Затем переместите цифры на три позиции влево (или десятичную точку на три позиции вправо):
125 × 1000 = 125000.
Деление на 10, 100, 1000 и кратное
Этот процесс точно такой же, как и при умножении, но в обратном порядке.
Чтобы разделить на 10, вы либо
оставьте десятичную точку на месте и переместите цифры на одну позицию вправо,
или
переместите десятичную запятую на одну позицию влево.
За 100 вы перемещаетесь на два места.
За 1000 вы перемещаетесь на три позиции и так далее.
785 ÷ 100 = 7,85
56 ÷ 1000 = 0,056
Помните, что слева от десятичной точки всегда должен стоять ноль, если ваш ответ меньше 1,0
450 ÷ 1000 = 0,450 = 0,45
Вы можете удалить любые нули справа от чисел после десятичной точки. Однако вы НЕ МОЖЕТЕ сделать это , если нули стоят перед десятичной точкой или между десятичной точкой и другими числами.
Погружения, кратные десяткам, сотням или тысячам (или более):
Основная идея: если вам нужно разделить на 7000, сначала разделите на 7, а затем переместите цифры на три пробела.
Например, 56 ÷ 7000:
56 ÷ 7 = 8
8 ÷ 1000 = 0,008
Ваш ответ соответствует ожиданиям?
Если вы беспокоитесь, что не помните, двигаете ли вы свои цифры влево или вправо, взгляните на свой ответ.
Если вы умножаете исходное число на число больше 1, вы ожидаете, что ваш ответ будет больше, чем число, с которого вы начали.
Аналогично, если вы делите на число больше 1, ваш ответ будет меньше. Если это не так, то вы знаете, что ошиблись!
Сложение и вычитание в уме
Так же, как вы это делали с умножением и делением в уме, вы можете изучить некоторые приемы, которые упростят умственное сложение и вычитание.
Как и раньше, эти уловки не связаны с математическим волшебством, это просто случай разбивки задачи на более мелкие части, которые легче решить в уме.
Лучше всего это сделать с помощью нескольких примеров.
Пример 1:Разделение вычитания на сотни, десятки и единицы (или более).
Посчитайте 352 — 13 в уме.
Разделите это на два более простых вычитания: отнять 13 — это то же самое, что отнять 10, а затем отнять 3.
352 — 10 = 342
342 — 3 = 339
Пример 2:
Вы можете применить тот же принцип, что и в примере 1, к более сложному вычитанию:
Посчитайте 4583 — 333 в уме.
Сначала уберите 300, затем 30, затем 3:
4583-300 = 4283
4283-30 = 4253
4253-3 = 4250
Пример 3:
Работа с неудобными числами, близкими к 10:
Посчитайте 77 — 9 в уме.
Убрать 9 — это то же самое, что убрать 10, а затем добавить 1.
77 — 10 = 67
67 + 1 = 68
Пример 4:
Работа с неудобными числами, близкими к 100:
Посчитайте 737 + 96 в уме.
Добавление 96 аналогично сложению 100 с последующим вычитанием 4.
737 + 100 = 837
837 — 4 = 833
Пример 5:
Работа с неудобными числами, близкими к 1000 (или даже больше):
Посчитайте 5372 — 985 в уме.
Этот выглядит даже сложнее, чем другие, но независимо от того, насколько велики задействованные числа, вы все равно можете разбить расчет на простые части.
Вычитание 985 аналогично вычитанию 1000 с последующим добавлением 15 (поскольку 1000–985 = 15).Вы даже можете добавить 15 поэтапно, добавляя 10 и затем 5.
5372 — 1000 = 4372
4372 + 10 = 4382
4382 + 5 = 4387
Сложение и умножение в голове
Иногда у вас в голове возникает действительно сложный расчет, и это кажется невозможным. Однако, если вы посмотрите на то, как его можно разделить, используя навыки, полученные в примерах выше, что-то действительно сложное может стать намного проще.
Например, посчитайте 97 × 7 в своей голове .
Есть два способа справиться с этим, и вы можете найти один способ проще, чем другой:
Метод 1:
97 совпадает с (100-3), поэтому вы можете думать о вычислении как
7 × (100-3)
Это то же самое, что
(7 × 100) — (7 × 3)
Теперь вы заменили сложное умножение двумя простыми умножениями и вычитанием:
7 × 100 = 700
7 × 3 = 21
700 — 21 = 700 — 20 — 1 = 679
Следовательно, 97 × 7 = 679
Метод 2:
97 — это почти 100, поэтому вы можете начать с вычисления 7 × 100 = 700.
Следующий шаг — учесть разницу между 97 и 100, которая составляет 3.
Итак, 7 лотов из 3 — это 21.
700 — 21 = 679
Применение навыков умственной математики к деньгам и процентам
Как вы узнали из приведенных выше примеров, умственная математика заключается в том, чтобы разбить задачу на числа, с которыми легко справиться в уме. Иногда нам нужно перевернуть расчет и подумать о нем по-другому.
Два примера, когда вам могут понадобиться ваши умственные математические навыки, — это когда вы имеете дело с деньгами или когда вам нужно вычислить процент, оба из которых часто возникают, когда вы ходите по магазинам.
При работе с деньгами можно округлить сумму до ближайшего целого фунта, а затем обработать пенни отдельно. Вы часто видите цены, отмеченные таким образом, чтобы заставить вас думать, что они дешевле, чем они есть на самом деле. Например, 24,99 фунтов стерлингов — это всего лишь один пенни от 25 фунтов стерлингов, но продавец хочет, чтобы вы подумали, что это ближе к 24 фунтам стерлингов.Когда вы делаете мысленные математические вычисления, иметь дело с 25 фунтами стерлингов намного проще, чем с 24,99 фунтами стерлингов.
Полезный мысленный прием для вычисления процентов — это помнить, что они обратимы, поэтому 16% от 25 равно 25% от 16. Неизменно одно из них будет намного легче вычислить в уме… попробуйте!
Заключение
Ментальная арифметика может показаться довольно пугающей, но со временем вы сможете использовать эти приемы ментальной математики, чтобы разбить сложную задачу на более мелкие части, над которыми легче думать.Здесь нет никакого волшебства, просто нужно взглянуть на проблему по-другому.
Дополнительная литература по навыкам, которые вам нужны
Основы счета
Часть необходимых навыков Руководство по счету
Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами. Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
6 ментальных математических стратегий | Советы и рекомендации для студентов
Когда у них нет под рукой манипуляторов или рабочих документов, учащиеся должны чувствовать себя комфортно, выполняя основную математику в уме.
К счастью, может сделать любой ребенок, если он знает правильные советы и рекомендации .
Вот шесть умственных математических стратегий, которым можно научить ваших учеников.Вы дадите им уверенность, что они отложат калькулятор и начнут решать проблемы самостоятельно!
Округление до десяти
Работа с партиями по 10 значительно упрощает сложение и вычитание, потому что не требуется заимствование или перенос. Студенты могут максимально использовать это, округляя суммы в сумме до ближайших 10.
Уловка состоит в том, чтобы сохранить «лишние» числа, использованные для округления, а затем вычесть их в конце. Смоделируйте это своим ученикам с помощью числовой речи.Например, если сумма 57 + 48, ваш мыслительный процесс может быть:
- Я округлю эти числа до 60 + 50, потому что их легче сложить.
- Но я должен иметь в виду, что я дал себе дополнительные 5 для округления (3, чтобы превратить 57 в 60, и дополнительные 2, чтобы превратить 48 в 50). Когда я доберусь, мне придется вычесть эти 5 из своего окончательного ответа.
- Моя округленная сумма: 60 + 40 = 110.
- Минус 5 = 105.
Работать слева направо
На бумаге мы учим студентов решать многозначные суммы справа налево, начиная с единиц и заимствуя / перегруппировывая по мере необходимости.
Но если они делают это мысленно, они могут работать наоборот и не беспокоиться о том, чтобы отслеживать заимствования и перегруппировку. Возьмем для примера 34 + 17:
- Сначала мы складываем 3 и 4 в столбце десятков, получая 40.
- Теперь мы складываем 4 и 7 в столбце единиц, что дает нам 11.
- Добавьте 11 к 40, и мы получим 51.
Используйте хаки умножения
Запоминание таблиц умножения является серьезным математическим препятствием для большинства учащихся начальной школы, но становится намного проще, если они запоминают следующие «уловки»:
- Любое количество умноженное на 1 остается неизменным.

- В конце любого числа, умноженного на 10, добавляется ноль.
- Любое число до 9 умноженное на 11 — это одна и та же цифра, повторяемая дважды (например, 99).
Вместе эти приемы мгновенно дают учащимся 60 фактов умножения, которые могут быть вычислены автоматически — без запоминания.
Поднимите десятичную дробь, чтобы легко найти процент
Вычислить 10% чаевых в ресторане — одна из самых цитируемых задач по математике. К счастью, для этого есть чит, который легко запомнить.
Все, что нужно студентам, — это переместить десятичную запятую на одну позицию назад, в результате чего получится ровно 10% от исходной суммы. Таким образом, 25 долларов превращаются в 2,50 доллара, а 7,50 доллара в 75 центов.
Как только они овладеют навыками, учащиеся могут использовать много 10%, чтобы быстро вычислить и другие проценты. Им нужно только удвоить его, чтобы получить 20%, или уменьшить вдвое, чтобы получить 5%. Сложите эти два вместе, и у них будет 25%.
Розничная терапия внезапно становится намного проще!
Сделайте предположения
В повседневной жизни математические вычисления в уме редко должны быть точными на 100%.Если это так, мы все равно тянемся за калькулятором или листом бумаги.
Скажите своим ученикам, что можно подойти к более сложной математической задаче, «угадывая» ответ.
Это может означать, что нужно просто работать с высшими разрядами в сумме и использовать это для вычисления, что ответ будет «около» определенного числа. Затем они могут проверить ответ с помощью тренировки.
Разбери проблему
Глядя на некоторые из этих математических стратегий в уме, вы можете задаться вопросом, почему они, кажется, используют гораздо больше шагов, чем подход из учебника.Разве это не сбивает с толку, когда ученики размышляют над этим в уме?
На самом деле наоборот . Вместо того, чтобы сразу переходить к окончательному решению, учащиеся добьются гораздо большего успеха, если они разделят большую проблему на ряд более мелких, а затем будут систематически их решать.
Вместо того, чтобы сразу переходить к окончательному решению, учащиеся добьются гораздо большего успеха, если они разделят большую проблему на ряд более мелких, а затем будут систематически их решать.
Помните, маловероятно, что этот процесс будет происходить естественным образом для всех. Лучший способ научить этому — моделировать числовую речь, когда вы сами решаете проблему.Подумайте вслух и четко обратите внимание на каждый шаг, который вы делаете, чтобы прийти к окончательному решению.
Совет: потренируйтесь в этом сами перед тем, как стать моделью в классе. Многие мыслительные движения, которые вы делаете, могут быть настолько интуитивными и быстрыми (в конце концов, вы же учитель математики), что вы даже не узнаете их, пока не замедлитесь и не начнете делать заметки!
Нужна дополнительная помощь, чтобы отточить умственную математику ваших учеников?
Наш ассортимент онлайн-программ обучения математике был разработан с педагогической точки зрения , чтобы отточить умственную математику и беглость фактов с помощью увлекательных мероприятий, таких как живые соревнования и динамичные игры.Подпишитесь на бесплатную пробную версию и узнайте, почему любят 5 миллионов студентов по всему миру.
Оттачивайте умственную математику своих учеников с помощью наших программ онлайн-обучения
Изучите программы12 методов улучшения умственной математики + загружаемый список
Психологическая математика не входит в состав большинства учебных программ, но учеников, которые не могут быстро или автоматически решать относительно простые уравнения в своей голове, скорее всего, будут бороться с более сложным содержанием. Но прежде чем ответить на вопрос: «Как я могу улучшить свою умственную математику?», Полезно знать определение (определения) умственной математики. Что такое ментальная математика? Ассоциация учителей математики Манитобы определяет ментальную математику как:Комбинация когнитивных стратегий, которая улучшает гибкое мышление и чувство чисел. Он производит мысленные вычисления без использования внешних запоминающих устройств. Он улучшает скорость вычислений за счет повышения эффективности, точности и гибкости.Или, с точки зрения учащихся, это:
- Математика, сделанная в уме
- Математика, которая выполняется в уме, быстро и эффективно
- Разогрев головы математикой
- Чтобы выполнить математику мгновенно, без вложенных усилий операций и процессов
- Математика, которую вы понимаете настолько хорошо, что вам не нужно ничего записывать, чтобы проводить вычисления / найти ответ
[Существует] значительная положительная корреляция между мысленными вычислениями и математическими рассуждениями. Примечательно, что вместо того, чтобы подвергать учащихся знакомым классическим задачам, учащиеся должны иметь возможность решать исключительные / нестандартные проблемы, и особенно детей младшего возраста следует поощрять к умственному вычислению для развития обоих навыков.Исследователи Duke опубликовали в журнале Clinical Psychological Science исследование о ментальной математике — с точки зрения здоровья.После сканирования мозга 186 студентов, результаты показали, что вовлечение префронтальной коры головного мозга во время мысленных математических упражнений связано с улучшением эмоционального здоровья. К счастью, вы уже помогаете студентам развить основные умственные математические навыки, когда учите округлять, оценивать и беглость фактов — развивая чувство числа, а также то, как они запоминают и воспроизводят шаги и решения.
Пора практиковаться в мысленной математике!
Чтобы улучшить то, как ваши ученики развивают и практикуют эти умственные математические навыки, попробуйте следующие 12 стратегий. Используйте те, которые лучше всего подходят для вас, и храните загружаемый список у себя на столе для быстрой справки. 1. Представьте мнемонические устройства Учащиеся, которые борются с беглостью базовых фактов, могут улучшить их, используя мнемонические приемы — такие подсказки, как рифмы и акронимы, чтобы помочь вспомнить информацию. В ее магистерской диссертации Обучение через мнемонику в элементарных Школьные классы , Арианна Уэйт-Макгоф обнаружила, что учителя понимают положительное влияние этого устройства на учеников в классной комнате и «за ее пределами».Текущее исследование показывает, что пение, движение и общее удовольствие от предмета улучшают процесс обучения и долгосрочное запоминание материала. Все эти требования присутствуют при использовании мнемоники в классе. Мои исследования подтвердили аналогичные результаты. Все учителя, которых я опрашивал, отметили более высокий уровень обучения, вовлеченности и веселья во время пения песен на основе основного материала.В качестве примера возьмем этот мнемонический прием для умножения: Мне должно быть 16 лет, чтобы водить пикап с колесной формулой 4×4. Поскольку их должно быть легко запоминать, полезно, если в них задействованы:
- Рифмы
- Материальные объекты или сценарии
- Быстрые истории, извлекающие большие объемы информации
 Скорее всего, им будет легче запоминать создаваемые ими мнемонические устройства. 2. Читайте книги по математике Есть много книг по математике, которые эффективно контекстуализируют процессы, лежащие в основе решения уравнений, помогая учащимся запомнить их. В зависимости от возраста ученика, учтите:
Скорее всего, им будет легче запоминать создаваемые ими мнемонические устройства. 2. Читайте книги по математике Есть много книг по математике, которые эффективно контекстуализируют процессы, лежащие в основе решения уравнений, помогая учащимся запомнить их. В зависимости от возраста ученика, учтите: - У каждого апельсина было 8 ломтиков — В этой книге основное внимание уделяется счету и сложению, излагая задачи в простых для обработки предложениях. Он устанавливает новую сцену, полную вопросов, с каждым поворотом страницы.
- Виноград математики — Эта книга, содержащая основные задачи умножения, представляет собой серию иллюстрированных загадок.Каждая загадка предлагает подсказки и секреты решения определенного уравнения, помогая учащимся улучшить понимание прочитанного наряду с математическими навыками.
- Sir Cumference — Эта серия книг, созданная во времена средневековья, посвящена измерениям и геометрии. С помощью своего сына и жены, Радиуса и леди Ди из Аматера, рыцарь сэр Кумферент должен решать математические задачи, которые представляют угрозу для его семьи и королевства.
- Секреты ментальной математики — В отличие от детской книги, это руководство обещает «мгновенно заставить вас думать как математический гений» с помощью «математика» Артура Бенджамина.Поскольку в нем более 200 страниц, вы можете добиться большего успеха в выборе ключевых отрывков и чтении — и применении — умственных математических уловок со своими учениками. Есть также предисловие Билла Ная, ученого парня!
 После того, как они поделятся своими ответами, читайте дальше, чтобы узнать ответ. 3. Обеспечьте соответствующие текстовые задачи Многие студенты будут более восприимчивы к математическим упражнениям и практике, если материал будет интересным. Дэвид Кембер, профессор методики учебной программы и педагогики, и его команда опубликовали статью в Активное обучение в высшем образовании о мотивах обучения студентов. Проведя собеседование с 36 студентами бакалавриата, Кембер пришел к выводу:
После того, как они поделятся своими ответами, читайте дальше, чтобы узнать ответ. 3. Обеспечьте соответствующие текстовые задачи Многие студенты будут более восприимчивы к математическим упражнениям и практике, если материал будет интересным. Дэвид Кембер, профессор методики учебной программы и педагогики, и его команда опубликовали статью в Активное обучение в высшем образовании о мотивах обучения студентов. Проведя собеседование с 36 студентами бакалавриата, Кембер пришел к выводу:Само преподавание абстрактной теории демотивирует. Актуальность может быть установлена посредством: демонстрации того, как теория может быть применена на практике, установления релевантности к местным случаям, соотнесения материала с повседневными приложениями или поиска приложений в актуальных новостных проблемах.Другими словами, если учащиеся не сочтут ваш урок математикой релевантным, их мотивация к обучению значительно снизится. Простой, но эффективный способ оживить содержание — это придумывать математические словесные задачи. Это потому, что вы можете адаптировать вопросы к ученикам. Например, вы можете:
- Задайте актуальные вопросы — Задачи со словами, основанные на текущих событиях или проблемах, могут заинтересовать учащихся, предоставляя четкие, осязаемые способы применения знаний. Студенты не только найдут ваши уроки более интересными, но и сочтут, что их стоит знать.
- Включите имена учащихся — Назовите символы вопроса в честь учащихся — это простой способ сделать его понятным, мотивируя класс к решению проблемы.

S найдите слово «проблема» T преобразовать слова в уравнение A Ответить на проблему R Ознакомьтесь с решением
4.Играйте в оценочные игры в классе Оценочные игры — это увлекательные математические задания, которые побуждают учащихся развивать навыки и методы, которые они могут использовать для упрощения уравнений в уме. В популярной во многих классах оценочной игре, которую легко запустить, но сложно играть, нужно всего два кубика и лист бумаги, разделенный на две колонки. В одном столбце перечислены значения на каждой грани игральных костей, а в другом — числа по вашему выбору. Например:| Сторона игральной кости | Число |
| 1 | 189 |
| 2 | 345 |
| 5 | 878 |
| 6 | 777 |
 Интересные варианты для классов с 1-го по 8-й включают:
Интересные варианты для классов с 1-го по 8-й включают: - Математические факты Бинго — Создавайте карточки бинго, содержащие ответы на различные уравнения. Затем раздайте их студентам. Вместо того, чтобы набирать числа, сформулируйте уравнения типа 8 x 7.Определив, что продукт — 56, они могут отметить число, указанное на их карточках.
- Встань, сядь — Выберите число и поделитесь им со студентами. Затем прочитайте уравнения вслух. Сидя в круге, ученики должны встать, если ответ совпадает с выбранным вами числом. Если они неправильно встают или остаются на своих местах, устраняйте их, пока не останется один ученик.
- 101 и Out — Как следует из названия, цель состоит в том, чтобы набрать как можно ближе к 101 очку, не превышая его.Начните с разделения класса на группы, дайте каждой кубик, бумагу и карандаш. Группы по очереди бросают кубик, решая, лучше ли посчитать число по номиналу или умножить его на 10. После каждого броска число добавляется к общей сумме группы. Игра заканчивается, когда группа набирает 101 очко или выходит из строя — в зависимости от того, что наступит раньше.
- Prodigy Game — Бесплатная и согласованная с учебными планами англоязычного мира, Prodigy автоматически дифференцирует контент и дает адаптивную обратную связь для каждого ученика.
 Учителя также могут выполнять внутриигровые задания по доставке нестандартного контента, что делает его любимым более чем миллиона преподавателей.
Учителя также могут выполнять внутриигровые задания по доставке нестандартного контента, что делает его любимым более чем миллиона преподавателей.
- NRICH — На этом веб-сайте, осуществляемом в рамках текущего проекта Кембриджского университета, представлены математические игры, статьи и задачи. Он разделяет ресурсы по ключевым этапам в Соединенном Королевстве и уровням обучения в США, что позволяет вашим учащимся легко получить доступ к нужному контенту.
- Математика — это развлечение — Этот веб-сайт содержит контент, подходящий для младших школьников, с использованием кратких предложений и мультипликационных персонажей.Помимо упражнений, охватывающих основные математические навыки, есть игры и головоломки.
 Им просто нужно уменьшить вдвое четное число и удвоить другое число. Они останавливают этот процесс, когда четное целое число не может быть уменьшено вдвое или когда уравнение становится управляемым. Используя 33 x 48 в качестве примера, вот процесс:
Им просто нужно уменьшить вдвое четное число и удвоить другое число. Они останавливают этот процесс, когда четное целое число не может быть уменьшено вдвое или когда уравнение становится управляемым. Используя 33 x 48 в качестве примера, вот процесс: - 33 x 48
- 66 x 24
- 132 x 12
- 264 x 6
- 528 x 3
- 1,584
- Создание математического информационного бюллетеня — Разделите лист на два столбца и запишите около 10 математических фактов, относящихся к одному и тому же навыку, в левом столбце. Включите числа, предложения и ответы. В правом столбце напишите «Ответы.”Раздайте копии листов студентам.
- Выполнение упражнения — Цель учащихся — изучить математические факты в левом столбце, правильно воспроизведя их в столбце «Ответы». Для этого дайте им время изучить факты. Затем они складывают бумагу, чтобы закрыть левую колонку, записывая — по памяти — первый факт в колонке «Ответы». Если все правильно, студент может перейти к следующему факту. В случае ошибки ученик пытается снова, пока не воспроизведет математический факт должным образом.
- Запись освоенных навыков — После того, как учащийся заполнил определенное количество листов, относящихся к общему навыку, вы можете наградить его или ее значком, обозначающим овладение навыками. Эта стратегия геймификации может сделать упражнение более увлекательным.
 10. Используйте подход с записанными проблемами Полезная стратегия активного обучения, подход с записанными проблемами — это один из наиболее эффективных способов для учащихся повысить беглость фактов, указывает на исследование 2004 года, которое впервые использовало эту стратегию.Во-первых, получите или сделайте аудиозапись основных математических задач с короткими паузами между постановкой задачи и ответом. Во-вторых, раздайте каждому ученику карандаш и бумагу. Пока вы проигрываете запись, ученики должны записать каждое уравнение и попытаться решить его, прежде чем будет дан ответ. Если ученик не может решить вопрос, он или она записывает правильный ответ. Если учащийся получает неправильный ответ, он или она вычеркивает его и записывает правильный ответ.Вы можете удлинить паузы, чтобы учащиеся не зависели от ответов, а вы можете сократить их, чтобы стимулировать автоматизацию. 11. Строительные блоки Хотите знать, как улучшить скорость умственной математики в вашем классе? Ознакомьте учащихся со стандартными блоками, такими как таблицы умножения или дроби, десятичные дроби и их эквиваленты в процентах. Кредит: Fact Monster [/ caption]
Чем больше ваши ученики узнают, как выглядят таблицы умножения или их эквиваленты, тем быстрее они смогут распознавать и решать проблемы в классе и за его пределами.В исследовании, опубликованном в журнале Journal of Neuroscience под названием «Почему ментальная арифметика имеет значение: активация мозга во время однозначной арифметики предсказывает математические оценки в средней школе», 33 старшеклассника проверили способность решать уравнения сложения и вычитания. , что коррелировало с их математическими показателями PSAT. Интересно, как отметила нейробиолог доктор Сьюзан Барри:
10. Используйте подход с записанными проблемами Полезная стратегия активного обучения, подход с записанными проблемами — это один из наиболее эффективных способов для учащихся повысить беглость фактов, указывает на исследование 2004 года, которое впервые использовало эту стратегию.Во-первых, получите или сделайте аудиозапись основных математических задач с короткими паузами между постановкой задачи и ответом. Во-вторых, раздайте каждому ученику карандаш и бумагу. Пока вы проигрываете запись, ученики должны записать каждое уравнение и попытаться решить его, прежде чем будет дан ответ. Если ученик не может решить вопрос, он или она записывает правильный ответ. Если учащийся получает неправильный ответ, он или она вычеркивает его и записывает правильный ответ.Вы можете удлинить паузы, чтобы учащиеся не зависели от ответов, а вы можете сократить их, чтобы стимулировать автоматизацию. 11. Строительные блоки Хотите знать, как улучшить скорость умственной математики в вашем классе? Ознакомьте учащихся со стандартными блоками, такими как таблицы умножения или дроби, десятичные дроби и их эквиваленты в процентах. Кредит: Fact Monster [/ caption]
Чем больше ваши ученики узнают, как выглядят таблицы умножения или их эквиваленты, тем быстрее они смогут распознавать и решать проблемы в классе и за его пределами.В исследовании, опубликованном в журнале Journal of Neuroscience под названием «Почему ментальная арифметика имеет значение: активация мозга во время однозначной арифметики предсказывает математические оценки в средней школе», 33 старшеклассника проверили способность решать уравнения сложения и вычитания. , что коррелировало с их математическими показателями PSAT. Интересно, как отметила нейробиолог доктор Сьюзан Барри:Студенты с более высокими показателями PSAT по математике задействовали части мозга, левую надмаргинальную извилину и двустороннюю переднюю поясную извилину, которые были связаны с арифметическим извлечением фактов.12. Number talk Рут Паркер, генеральный директор организации Mathematics Education Collaborative, и Кэти Ричардсон, одна из ведущих национальных преподавателей элементарной математики, разработали эту ментальную математическую практику.Для начала поставьте абстрактную математическую задачу. Возьмите пример задачи 18 x 5 и попросите своих учеников попытаться решить ее в уме. Естественно, в классе более 20 учеников вы, вероятно, обнаружите, что они ответили правильно, но по-другому.Напротив, студенты с более низкими показателями PSAT по математике задействовали правую внутри теменную борозду, область, участвующую в обработке числовых величин. При выполнении теста в сканере учеников с более высокими баллами PSAT по математике больше полагались на свою память об арифметических фактах ().
| Пять способов решения 18 x 5 | ||||
| 20 x 5 = 1002 x 5 = 10100 — 10 = 90 | 10 x 5 = 508 x 5 = 4050 + 40 = 90 | 18 x 5 = 9 x 109 x 10 = 90 | 18 x 2 = 362 x 36 = 7218 + 72 = 90 | 9 x 5 = 4545 x 2 = 90 |
Исследования показывают, что лучшие классы математики — это те, в которых студенты изучают числовые факты и чувство чисел посредством увлекательных занятий, которые сосредоточены на математическом понимании, а не на механическом запоминании.Итак, мы надеемся, что эти упражнения помогут вашим ученикам практиковать мысленную математику в этом учебном году и в дальнейшем. Загружаемый список практик мысленной математики Щелкните здесь , чтобы загрузить и распечатать упрощенный список из 12 практик мысленной математики, который будет всегда у вас на столе.
 Готовы поделиться этими математическими секретами в уме? Ладно, это не совсем секреты. Но использование этих методов мысленной математики должно помочь вашим ученикам развить навыки округления, оценки и владения фактами, что позволит им легко и автоматически решать многие уравнения, подготовив их к работе с более сложным содержанием.Вооружившись повышенной уверенностью, вы можете заметить всплеск вовлеченности и мотивации студентов. Эти преимущества сами по себе являются убедительным аргументом в пользу практики мысленной математики.
Готовы поделиться этими математическими секретами в уме? Ладно, это не совсем секреты. Но использование этих методов мысленной математики должно помочь вашим ученикам развить навыки округления, оценки и владения фактами, что позволит им легко и автоматически решать многие уравнения, подготовив их к работе с более сложным содержанием.Вооружившись повышенной уверенностью, вы можете заметить всплеск вовлеченности и мотивации студентов. Эти преимущества сами по себе являются убедительным аргументом в пользу практики мысленной математики.>> Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной платформе, которая помогает учащимся развивать умственные математические навыки, практикуясь в увлекательной игровой среде обучения. Он соответствует учебным планам англоязычных стран, его любят более миллиона учителей и 50 миллионов студентов.
Ментальная математика | Уловки | Проблемы
Содержание
20 января 2021 г.
Время чтения: 5 минут
ВведениеБывают моменты, когда нам нужно производить мгновенные арифметические вычисления. Например, предположим, что вы идете в магазин, чтобы купить футболку, которая предлагает вам 10% скидку. Очевидно, у вас не будет ручки и бумаги для арифметических расчетов окончательной цены, которую вы должны заплатить.
Это времена, когда нужно быстро рассчитывать, и это тоже без каких-либо ресурсов. В такие моменты вам может помочь только ваш мозг. Поэтому очень важно, чтобы каждый разработал определенные приемы для умственной математики в такие моменты.
Кроме того, один из фактов ментальной математики состоит в том, что существует положительная корреляция между ментальным расчетом и математическим рассуждением. Итак, если вы увеличите свои умственные математические способности, ваши математические и логические навыки рассуждений увеличатся автоматически.
Также читайте:
Загрузить PDF
Вот несколько дополнительных моментов, касающихся навыков умственной математики. Чтобы просмотреть их, нажмите кнопку «Загрузить».
| 📥 | Ментальная математика: как ее улучшить? | Загрузить |
Что такое ментальная математика?
Как следует из названия, ментальная математика относится к группе навыков, которые позволяют людям выполнять арифметические вычисления «в уме» без использования калькуляторов или других ресурсов.Ментальная математика полезна в повседневной жизни, чтобы ответить на различные вопросы, например:
Какова окончательная цена продажи конкретного товара?
Какое правильное количество сдачи я должен получить от кассира?
В какое время уехать, чтобы вовремя добраться до того или иного места?
Важность развития умственных математических навыков
В детстве легко понять и развить уловки для умственной математики.Их важно развивать, потому что:
Это помогает учащимся лучше понять основные математические концепции и концепции более высокого уровня.
Регулярное использование и решение задач по математике помогает ребенку улучшить его / ее чувство чисел. Например, что лучше? Покупка коробки из 12 шоколада за 100 рупий или покупка плитки индивидуального шоколада за 100 рупий. 10.
Это помогает студентам решать задачи более высокого уровня с большей скоростью.
Стимулирует мозг и делает его острее. Это развивает у учащихся воображение, визуализацию и творческие способности.
Повышает уверенность в себе и самооценку студента.
Это похоже на упражнение для мозга, которое поддерживает его здоровье.
Имеет множество практических применений.
Регулярные попытки пройти тесты по математике подготовят вас к академическим и конкурсным экзаменам.
Глядя на вышеупомянутые причины, становится ясно, что очень важно развивать эти умственные математические уловки. Эти навыки не врожденные. Существуют различные методы и техники улучшения навыков, которые подводят нас к следующему вопросу.
Как улучшить умственную математику?
Вот некоторые из способов улучшения умственных математических способностей детей: —
Один из самых основных и важных математических фактов заключается в том, что вы изучаете математические понятия на практике.Все мы начинаем медленно, но очень важно поставить перед собой задачу быстрее выполнять арифметические вычисления без использования документов или калькуляторов.
Это возможно только в том случае, если мы регулярно практикуем эти вычисления в нашем мозгу, используя наши умственные способности.
Даже если вам нужно время, чтобы что-то посчитать, рекомендуется использовать ручку и бумагу вместо калькулятора. Это помогает в развитии умственных способностей ученика. Вы заметите, что ваш мозг начинает медленно и неуклонно развивать эти навыки, и вам даже не потребуется ручка и бумага.
Студенты достигли возраста обучения. Поэтому очень важно, как старейшинам, поддерживать их на каждом этапе. Они могут потерять уверенность в своих силах. Поэтому очень важно поддерживать их на каждом шагу.
Мысленные вычисления включают в себя построение техник решения конкретных проблем, а не запоминание ответов. Существуют различные инструменты и игры для развития этих умственных стратегий, такие как карточки, онлайн-видео, математические головоломки и т. Д.
Математика — практический предмет.Это можно сделать проще, если учащиеся разовьют привычку сравнивать уравнения и визуализировать их с примерами из реальной жизни.
Узнайте, как выполнять мысленную математику. Каждый ученик начинает с ручки и бумаги. Затем они должны перейти к вычислениям на пальцах, и со временем у них разовьется привычка считать в уме.
Обучение бесполезно, если оно не делается искренне. Поэтому важно, чтобы это было весело и увлекательно. Это помогает ребенку не сдаваться и преодолевать неудачи.
Вы также можете использовать приложения / веб-сайты, которые содержат множество ресурсов по ментальной математике, а также тесты по ментальной математике, которые помогут вам отточить свои умственные навыки.
Как выполнять умственные математические трюки?
Некоторые математические приемы в уме объясняются с помощью простых математических задач следующим образом: —
Уловка чисел, близких к кратным 10
Выполните вычисления, кратные 10, а затем сложите / вычтите требования.
Например,
Чтобы прибавить 9 к любому числу, сначала прибавьте 10, а затем вычтите 1. Примерно 9 + 7 = 10 + 7 — 1 = 16.
76 + 99 можно изменить на 75 + 100.
Еще один пример: 107 + 105 = 100 + 100 + 12 = 212
Уловка удвоения плюс один
Преобразуйте разные числа в одно и то же, а затем добавьте / вычтите требование. Например, 5 + 6 на единицу больше, чем 5 + 5 +1 = 11, или 9 + 8 равно 9 + 9-1 или 8 + 8 +1 = 17.
Выполните сложение, разбив числа по разрядам
Например, предположим, что у нас есть следующий вопрос: 220 + 364 + 44 + 18 = ??
200 + 300 = 500
20 + 60 +40 +10 = 130
4 + 4 +8 = 16
Повторите процесс:
500 + 100 = 600
30 + 10 = 40
А на месте единицы имеем 6.
Теперь выполняем, 600 + 40 + 6 = 646
Вычтем прибавив
Это немного сложно, но регулярная практика упрощает все.Например, если вас просят найти, что такое 87–46, представьте это как «46 плюс какое число равно 87?» Другими словами, подумайте о 46 + ___ = 87. Ответ на вычитание будет таким же, как и на произведенное сложение, т.е. 41.
Отличный трюк
Чтобы найти 5 раз любое число, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 58 можно найти, умножив 10 × 58 = 580 и взяв половину, т.е.е. 290. Мы можем использовать эту стратегию для создания других комбинаций, но для этого сначала нужно очень крепко владеть этими базовыми концепциями ментальной математики.
Четыре и восемь чисел
Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 72? Сначала найдите 72 x 2 = 144. Затем удвойте это, 144 x 2 = 288. Точно так же восемь умноженное на число просто означает удвоение трижды. Продолжая наш пример, если нам нужно найти 8 × 72, нам просто нужно снова удвоить 288, что приведет к 576.
Умножение по частям
Это довольно простая стратегия. Предположим, мы должны мысленно найти 3 × 74. Мы можем разбить его на части, например, 3 × 70 и 3 × 4, а затем сложить результаты. Получим 210 + 12 = 222.
Заключение
Регулярное использование и решение задач по математике в уме помогает ребенку улучшить его / ее чувство чисел и лучше понять основные математические концепции и концепции более высокого уровня.
Умственные математические навыки одинаково полезны как в повседневной, так и в академической жизни.Вы можете следовать вышеупомянутым советам, чтобы улучшить это. Вы даже можете продемонстрировать свои навыки быстрого расчета перед друзьями!
О компании Cuemath
Cuemath, удобная для учащихся платформа по математике и кодированию, проводит регулярные онлайн-классы для учебы и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков. структуру Cuemath Fee и подпишитесь на бесплатную пробную версию.
Часто задаваемые вопросы (FAQ)
Что такое ментальная математика?
Под умственной математикой понимается группа навыков, которая позволяет людям выполнять арифметические вычисления «в уме» без использования калькуляторов или других ресурсов. t помогает учащимся лучше понять основы математики и концепции более высокого уровня
Как улучшить умственные математические навыки?
Регулярная практика и расчеты без использования калькуляторов помогут вам улучшить умственные математические навыки.Продолжайте заставлять себя выполнять сложные вычисления в уме. Существуют различные инструменты и игры для развития этих умственных стратегий, такие как карточки, онлайн-видео, математические головоломки и т. Д.
Внешние ссылки
Чтобы узнать больше о ментальной математике, посетите эти блоги:
4 забавных способа улучшить навыки умственной математики вашего ребенка
Понимание простых математических фактов может дать учащимся огромное преимущество в школе. Мысленно решая базовые задачи на сложение и вычитание, ребенок может повысить беглость математики, что позволит ему легче продвигаться к математике более высокого уровня.
Игра в простые, но увлекательные математические игры — это фантастический способ не только развить умственные математические способности вашего ребенка, но и идеальный способ улучшить числовые факты. Вот несколько наших любимых занятий.
Война умножения
С этой веселой карточной игрой ваш ребенок быстро овладеет фактами умножения! Перетасуйте колоду карт и раздайте их рубашкой вверх, давая каждому игроку равное количество карт. Присвойте карточкам с картинками значение 10, а тузам — значение 11.Каждый игрок переворачивает две карты лицом вверх, читает числовое предложение и дает ответ. Например, если ваш ребенок рисует 7 и 8, он говорит, что 7 × 8 = 56. Если вы возьмете 6 и 4, вы скажете, что 6 × 4 = 24. Поскольку его продукт больше, он выигрывает четыре карты и кладет их в конец своей стопки. Продолжайте игру, пока у одного игрока не закончатся карты.
Ментальная тайна
Попросите ребенка отсчитать пять маленьких предметов, таких как пенни, шарики или конфеты, и попросить его закрыть глаза.Затем спрячьте некоторые из пяти предметов, оставив остальные открытыми. Попросите ребенка подсчитать, сколько предметов он видит и сколько предметов закрыто. Практикуйте это задание, пока ваш ребенок не сможет быстро решить эти простые уравнения. Добавьте один дополнительный объект, как только ваш ребенок освоит этот уровень, чтобы увеличить сложность. Для детей постарше начните с 10-20 предметов.
101 и выход
Для игры вам понадобятся лист бумаги, карандаш и один кубик. Цель игры состоит в том, чтобы набрать как можно больше очков, не превышая 101.Игроки по очереди бросают кости. Во время броска вы можете принять число либо за единицу, либо за десятку. Например, если вы выбрасываете 5, это может быть равно 5 или 50. Игроки ведут текущий учет своего общего количества во время игры. Эта игра — отличный способ построить умственные математические стратегии, поскольку дети часто критически думают о том, какое число им нужно бросить следующим.
Математическая опасность
Дайте ребенку лист бумаги и назовите число. Дайте им одну минуту, чтобы найти как можно больше способов составить число, используя сложение, вычитание, умножение и деление.
Изучение базовых, но полезных математических стратегий может значительно повысить уверенность вашего ребенка в себе.
IWTL Как стать намного быстрее в мысленной математике: IWantToLearn
Woot, я кое-что знаю, так как занимаюсь мысленной математикой. Я был ужасен в алгебре и геометрии, пока мой учитель в 11 классе не дал мне книгу по ментальной математике … что-то в ней заставило ВСЕ щелкнуть в моей голове … и теперь у меня нет проблем даже с триггером и калькулятором.
Выучите таблицу умножения до 100, а также убедитесь, что вы можете без проблем перевернуть ее (разделить).(Не потому, что он действительно чрезвычайно полезен для разума 20×20, а потому, что он заставит вас изучить закономерности и закономерности, а также умственную математику, управляющую памятью.) www.cut-the-knot.org/arithmetic/rapid/rapid.shtml
http://math.about.com/library/bldivide.htm
http://www.angelfire.com/me/marmalade/ mathtips.html
http://mathtricks.org/
Там намного больше, у меня была книга, но сейчас я не могу вспомнить ее название… Отредактирую, если найду. Большинство из них находятся в Google на разных сайтах, просто нужно продолжать поиск. Изменить: не тот, который у меня был, но просматривал его, это ssdd. http://www.reddit.com/r/IWantToLearn/comments/162xaz/iwtl_how_to_get_much_faster_at_mental_math/c7s97d9
3) Изучите ярлыки и уловки для разбивки. 10% — это процентное соотношение, которое легко вычислить, обычно вы просто меняете десятичный разряд. 142,65 доллара = 14,265 доллара = 14,27 доллара. Поэтому, если вы хотите 15%, рассчитайте это как 10% + (половина от 10%), а не как 15%. Для округления сложения / вычитания до хороших четных чисел затем вычтите / сложите меньшие биты в конце, например 14729 + 6984 = (14700 + 7000) + (29-16) = 21700 + 13 = 21713.. Намного легче отслеживать два числа (одно большое, красиво круглое, одно маленькое), чем значащие цифры, а также перенос и заимствование больших чисел.
4) Практика. Упражняться. Упражняться. Упражняться. Упражняться. Упражняться.
Когда вы получаете счет в ресторане, просчитайте все чаевые от 5% до 15% в уме. Затем вычислите их процент, если округлить их до ближайшего приращения в 5 долларов. Поработайте над своей памятью для чисел … посчитайте все автомобили ч / б и первичного / вторичного цветового круга, которые вы видите по дороге на работу / в школу.Держите итоги в голове на ходу. Запишите их по прибытии и посмотрите, сможете ли вы вспомнить их в конце дня. Выучите пи до как можно большего числа значащих цифр, просто для дерьма и хихиканья … отлично подходит для числовой памяти. Повторяйте, пока не сможете. Также может помочь поиск шаблонов в телефонных номерах, пинах, паролях, научиться связывать сложные числа с фигурами на цифровой клавиатуре и т.д. Удачи!
7 практических советов по ментальной математике (которые может использовать ЛЮБОЙ!)
Скорее всего, вы слышали о ментальной математике — способности производить вычисления в уме — и о том, как важно для детей ее выучить.Но почему это важно? Потому что ментальная математика связана с ЧУМСТВОМ ЧИСЛА: способность манипулировать числами в голове различными способами для выполнения вычислений. В свою очередь было доказано, что чувство числа предсказывает успехи студента в алгебре. По сути, то, что мы делаем с переменными в алгебре, аналогично тому, что учащиеся могут научиться делать с числами в младших классах.
Люди с пониманием чисел гибко используют числа . Они могут разбирать их и складывать различными способами для проведения расчетов.Это очень похоже на умение «ИГРАТЬ» словами, чтобы составлять интересные предложения, или умение играть с аккордами и мелодиями, чтобы сочинять песни.
Но ментальная математика / числовое чутье не только для «математических гениев» — как раз наоборот! Выучить основы этого сможет КАЖДЫЙ, и это значительно упростит изучение математики и алгебры! Мы ожидаем, что наши дети выучат много английских слов и смогут складывать эти слова разными способами в предложения, так почему бы не ожидать, что они сделают то же самое с числами? И они могут, если им показывают основы и показывают примеры того, как это происходит.Итак, давайте перейдем к практической части этого письма: математические стратегии для ВСЕХ.
- «Девятка».
Чтобы прибавить 9 к любому числу, сначала прибавьте 10, а затем вычтите 1. В моих книгах по Math Mammoth я рассказываю детям эту сюжетную линию, где девять очень сильно хотят равняться 10… поэтому он спрашивает это другое число в качестве «единицы». Другое число становится на единицу меньше. Например, мы меняем сложение 9 + 7 на 10 + 6, что намного проще решить.
Но эта «хитрость» расширяется.Можете ли вы придумать простой способ сложить 76 + 99? Измените его на 75 + 100. Как насчет 385 + 999?
Как бы вы сложили в голове 39 + 28? Пусть 39 станет 40… что уменьшает 28 до 27. Теперь сложение составляет 40 + 27. Еще один способ — подумать о компенсации: 39 — это на единицу меньше 40, а 28 — на два меньше, чем 30. Итак, их сумма на три меньше чем 70.
- двухместных + 1.
Поощряйте детей запоминать двойные числа от 1 + 1 до 9 + 9. После этого у них под рукой появляется множество других фактов сложения: те, которые мы можем назвать «двойные плюс еще один».Например, 5 + 6 на единицу больше, чем 5 + 5, или 9 + 8 просто на единицу больше, чем 8 + 8.
- Используйте факты сложения при сложении больших чисел.
Как только вы узнаете, что 7 + 8 = 15, вы также сможете делать все эти сложения в уме:
- 70 + 80 это 15 десятков, или 150
- 700 + 800 это 15 соток, или 1500
- 27 + 8 — это 20 и 15, то есть 35. Или подумайте так: поскольку 7 + 8 на пять больше, чем десять, то 27 + 8 на пять больше, чем следующие десять.
- Вычесть сложением.
Это очень важный принцип, основанный на связи между сложением и вычитанием. Детям действительно не нужно запоминать факты вычитания как таковые, если они могут использовать этот принцип. Например, чтобы найти 8-6, подумайте: «Шесть плюс какое число дает 8?» Другими словами, подумайте о сложении отсутствующего числа 6 + ___ = 8. Ответ на это также является ответом на 8 — 6.
Этот принцип особенно удобен с вычитаниями, такими как 13-7, 17-8, 16-9 и другими основными фактами вычитания, где уменьшаемое значение находится между 10 и 20.Но вы также можете использовать его во множестве других ситуаций. Например, число 63–52 легче решить сложением: 52 + 11 дает 63, поэтому ответ на 63–52 — 11.
- Пять умноженное на число.
Теперь обратим внимание на умножение. Вот изящный трюк, о котором вы, возможно, не знали. Чтобы найти любое число в 5 раз, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 48 можно найти, умножив 10 × 48 = 480 и взяв половину результата, что дает нам 240.Конечно, вы также можете использовать эту стратегию для таких фактов умножения, как 5 × 7 или 5 × 9.
- Четыре и восемь чисел.
Если вы умеете удваивать числа, значит, это у вас уже есть! Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 59? Сначала найдите удвоение 59, что составляет 118. Затем удвойте это, и вы получите 236.
- «Девятка».

