Какие бывают модели в информатике: Информационные модели — урок. Информатика, 6 класс.

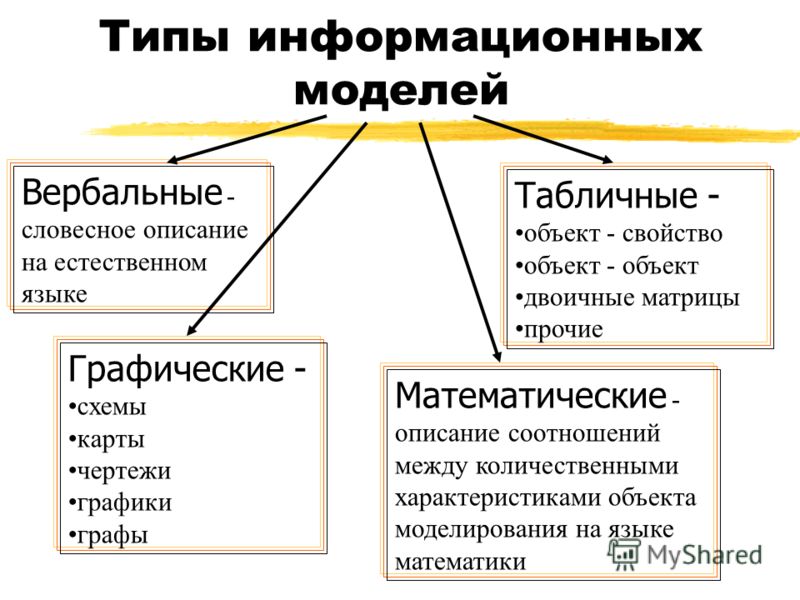
Знаковые модели. Словесные модели

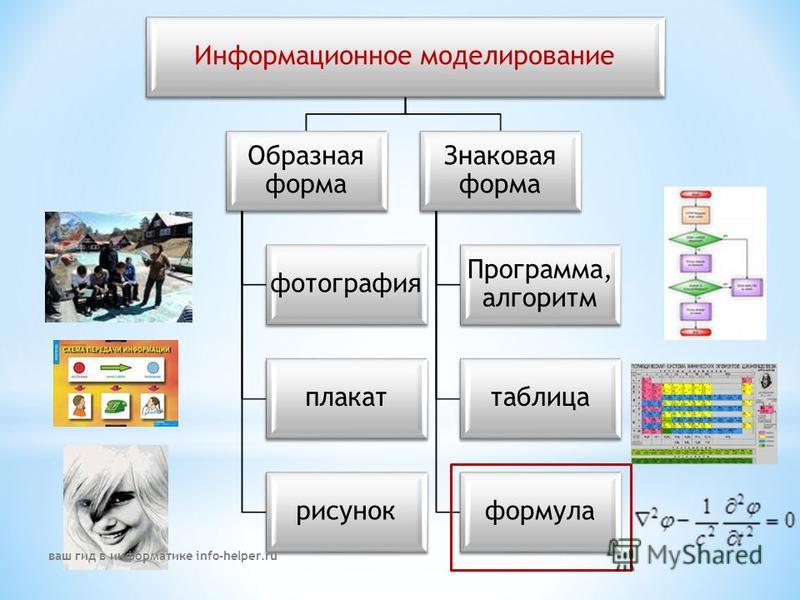
К видам информационных моделей по способу представления относятся: образные модели, знаковые модели и смешанные модели. Образные

модели – это зрительные образы объектов, которые зафиксированы на каком-либо носителе. Примерами образных моделей являются рисунки в учебниках, фотографии, чертежи и так далее. Знаковые модели – это модели, которые представлены в виде текста, формул или программ на специальном языке программирования. К знаковым моделям относятся словесные описания, формулы в учебниках математики, физики и прочие. Смешанные модели – это модели, в которых одновременно используются образные и знаковые модели. Смешанные модели включают в себя таблицы, графики, диаграммы и так далее.

Сегодня мы рассмотрим словесные модели. Словесные модели – это описания предметов, явлений, событий, процессов на естественных языках.

Естественный язык – это язык, предназначенный для общения людей. Важно, чтобы этот язык понимали все люди, участвующие в общении.

Существуют разнообразные стили словесных описаний. Различают разговорный и книжный стили. Разговорный стиль чаще всего используется в общении для передачи своих мыслей, эмоций, чувств, всего, что нас окружает (например, отдых на выходных с родителями или друзьями). Это происходит на одном из естественных языков (русский, английский и так далее). Таким образом, разговорный стиль служит для общения между людьми.

Книжный стиль можно разделить на подкатегории:

·      научный;

·      официально-деловой;

·      публицистический;

·      художественный.

Сегодня на уроке мы более подробно рассмотрим художественный стиль

. Он используется в произведениях художественной литературы. С помощью этого стиля автор воздействует на чувства и воображение читателя, передаёт свои чувства, мысли, использует все богатство лексики. После прочтения, человек анализирует литературное произведение, выделяет в нем объекты и их свойства, отношения между героями, связи между событиями и так далее.

Например «Какая прекрасная пора — зима! Закружило, завьюжило. Морозы сковали водоёмы. Застыли берёзы в белоснежной бахроме, поблёскивают мохнатые шапки на соснах, искрятся припорошённые снегом шишки на ветвях елей. Кругом студёная тишь. Кусается морозный воздух. Снежный покров надёжно укрыл землю. Выходишь из елового сумрака — дух захватывает: такое сияние снега, неба, солнца! Просто чудо!».

В данном тексте мы можем видеть, как автор старается передать все свои

эмоции и чувства по отношению к этой поре года.

Или же ещё один пример:

·      Ты красива, как фотомодель!

·      Ты ленивый словно тюлень!

·      Ты покраснела как рак!

·      По небу плыли белые, как сахарная вата, облака.

·      Этот холм будто дворец, возведённый самой природой.

В данных высказываниях используются сравнения.

Третий пример основывается на использовании инверсий. Инверсия – это использование обратного порядка слов для усиления тех или иных фрагментов и придания словам особой стилистической окраски.

·      Боязнь потери к темной стороне привести может.

·      Решать сам буду, кого в обучение брать.

·      Если раз ступишь на тёмную тропу, навсегда она твою судьбу определит.

Как говорилось ранее, словесные модели – это описания предметов, явлений, событий, процессов на естественных языках.

Сам же естественный язык, предназначенный, прежде всего, для повседневного общения, имеет целый ряд своеобразных черт:

·      Многозначность – почти все слова имеют не одно, а несколько значений;

·      Использование слов в прямом и переносном смысле;

·      Использование синонимов, омонимов и пр. ..

Это всё придаёт общению выразительность, но вместе с тем мешает при создании многих информационных моделей, где нужна точность и однозначность.

Важно запомнить:

·      Знаковые модели – это модели, которые представлены в виде текста, формул или программ на специальном языке программирования.

·     

Словесные модели – это описания предметов, явлений, событий, процессов на естественных языках.

·      Естественный язык – это язык, предназначенный для общения людей.

Классификация математических моделей — Информатика, информационные технологии

В качестве основного классификационного признака для ММ целесообразно использовать свойства операторов моделирования исхода операции и оценивания показателя ее эффективности [12, 35].

Оператор моделирования исхода Н может быть функциональным (т. е. заданным системой аналитических функций) или алгоритмическим (т. е. содержать математические, логические и логико-лингвистические операции, не приводимые к последовательности аналитических функций). Кроме того, он может быть детерминированным (когда каждому элементу множества U ´ ? соответствует детерминированное подмножество значений выходных характеристик модели Y или стохастическим (когда каждому значению множества U ´ ? соответствует случайное подмножество ).

Оператор, оценивания показатель эффективности ?, может задавать либо точечно-точечное преобразование (когда каждой точке множества выходных характеристик Y ставится в соответствие единственное значение показателя эффективности W), либо множественно-точечное преобразование (когда показатель эффективности задается на всем множестве полученных в результате моделирования значений выходных характеристик модели).

В зависимости от свойств названных операторов все ММ делятся на три основных класса: аналитические, статистические, имитационные.

Для аналитических моделей характерна детерминированная функциональная связь между элементами множеств U, ?, Y, а значение показателя эффективности W определяется с помощью точечно-точечного отображения. Аналитические модели имеют весьма широкое распространение. Они хорошо описывают качественный характер (основные тенденции) поведения исследуемых систем. В силу простоты их реализации на ЭВМ и высокой оперативности получения результатов такие модели часто применяются при решении задач синтеза систем, а также при оптимизации вариантов применения в различных операциях.

К статистическим относят ММ систем, у которых связь между элементами множеств U, ?, Y задается функциональным оператором Н, а оператор ?является множественно-точечным отображением, содержащим алгоритмы статистической обработки. Такие модели применяются в тех случаях, когда результат операции является случайным, а конечные функциональные зависимости, связывающие статистические характеристики учитываемых в модели случайных факторов с характеристиками исхода операции, отсутствуют. Причинами случайности исхода операции могут быть случайные внешние воздействия; случайные характеристики внутренних процессов; случайный характер реализации стратегий управления. В статистических моделях сначала формируется представительная выборка значений выходных характеристик модели, а затем производится ее статистическая обработка с целью получения значения скалярного или векторного показателя эффективности.

Имитационными называются ММ систем, у которых оператор моделирования исхода операции задается алгоритмически. Когда этот оператор является стохастическим, а оператор оценивания показателя эффективности задается множественно-точечным отображением, имеем классическую имитационную модель, которую более подробно рассмотрим в гл. 9. Если оператор H является детерминированным, а оператор ? задает точечно-точечное отображение, можно говорить об определенным образом вырожденной имитационной модели.

На рис. 8.2 представлена классификация наиболее часто встречающихся математических моделей по рассмотренному признаку.

Важно отметить, что при создании аналитических и статистических моделей широко используются их гомоморфные свойства (способность одних и тех же ММ описывать различные по физической природе процессы и явления). Для имитационных моделей в наибольшей степени характерен изоморфизм процессов и структур, т. е. взаимно однозначное соответствие элементов структур и процессов реальной системы элементам ее математического описания и соответственно модели.

Согласно [53], изоморфизм — соответствие (отношение) между объектами, выражающее тождество их структуры (строения). Именно таким образом организовано большее число классических имитационных моделей. Названное свойство имитационных моделей проиллюстрировано рис. 8.3.

Имитационные модели являются наиболее общими ММ. В силу этого иногда все модели называют имитационными [55]:

• аналитические модели, «имитирующие» только физические законы, на которых основано функционирование реальной системы, можно рассматривать как имитационные модели I уровня;
• статистические модели, в которых, кроме того, «имитируются» случайные факторы, можно называть имитационными моделями II уровня;
• собственно имитационные модели, в которых еще имитируется и функционирование системы во времени, называют имитационными моделями III уровня.

Классификацию ММ можно провести и по другим признакам [53].

На рис. 8.4 представлена классификация моделей (прежде всего аналитических и статистических) по зависимости переменных и параметров от времени. Динамические модели, в которых учитывается изменение времени, делятся на стационарные (в которых от времени зависят только входные и выходные характеристики) и нестационарные (в которых от времени могут зависеть либо параметры модели, либо ее структура, либо и то, и другое). На рис. 8.5 показана классификация ММ еще по трем основаниям: по характеру изменения переменных; особенностям используемого математического аппарата; способу учета проявления случайностей. Названия типов (видов) моделей в каждом классе достаточно понятны. Укажем лишь, что в сигнально-стохастических моделях случайными являются только внешние воздействия на систему. Имитационные модели, как правило, можно отнести к типам:

• по характеру изменения переменных — к дискретно-непрерывным моделям;
• математическому аппарату — к моделям смешанного типа;
• способу учета случайности — к стохастическим моделям общего вида.

Статьи к прочтению:

Математическое моделирование. Выбор модели. Грунтовое основание. Модель Винклера и Пастернака.

Похожие статьи:

Информационное моделирование — тест с ответами

Информатика в настоящее время является стремительно развивающийся наукой. Многие студенты постают в технические университеты, чтобы в будущем связать свою деятельность с IT или приближенными областями. Для проверки знаний по теме Информационное моделирование предлагаем пройти тестирование на этой странице. Обращаем ваше внимание, что в тесте правильные ответы выделены символом [+].

Что такое прототип:

[+] а) исходный объект

[-] б) повторяющийся объект

[-] в) объект-заменитель

Что такое модель:

[-] а) объект в единственном экземпляре

[+] б) объект-заменитель

[-] в) исходный объект

Какие бывают модели:

[-] а) истинные

[-] б) правдивые

[+] в) натурные

Существует ли информационная модель:

[+] а) да

[-] б) нет

[-] в) не всегда

Что является примером материальной модели:

[-] а) прогноз погоды

[-] б) земной шар

[+] в) макет дома

Какие бывают модели:

[-] а) правильные

[+] б) информационные

[-] в) неполные

Метод воспроизведения и исследования определённого фрагмента действительности (предмета, явления, процесса, ситуации) или управления им, основанный на представлении объекта с помощью модели:

[-] а) изображение

[-] б) образ

[+] в) моделирование

Один из примеров натуральной модели:

[+] а) муляж ананаса

[-] б) рисунок

[-] в) план местности

Один из примеров натуральной модели:

[-] а) рисунок

[-] б) фотография

[+] в) манекен

Один из примеров натуральной модели:

[-] а) фотография

[+] б) макет здания

[-] в) план местности

Один из примеров натуральной модели:

[+] а) глобус

[-] б) физическая формула

[-] в) математическая формула

Набор признаков, содержащий всю необходимую информацию об исследуемом объекте или процессе, называют:

[-] а) практической моделью

[+] б) информационной моделью

[-] в) фактической моделью

Соотнесите модель и вид модели:

Формула:

[+] а) смешанная информационная модель

[-] б) знаковая информационная модель

[-] в) образная информационная модель

Соотнесите модель и вид модели:

Таблица:

[-] а) смешанная информационная модель

[-] б) образная информационная модель

[+] в) знаковая информационная модель

Соотнесите модель и вид модели:

Фотография:

[+] а) образная информационная модель

[-] б) знаковая информационная модель

[-] в) смешанная информационная модель

Необходимо закончить предложение: «Модель, по сравнению с объектом-оригиналом, содержит …»:

[-] а) больше информации

[+] б) меньше информации

[-] в) столько же информации

Необходимо выбрать пропущенное слово: «Словесное описание горного ландшафта является примером … модели»:

[-] а) образной

[-] б) смешанной

[+] в) знаковой

Выберите пару объектов, о которой можно сказать, что она находится в отношении «объект – модель»:

[-] а) компьютер – процессор

[+] б) город – путеводитель по городу

[-] в) апельсин – кожура апельсина

Каково общее название моделей, которые представляют собой совокупность полезной и нужной информации об объекте:

[-] а) материальные

[-] б) словесные

[+] в) информационные

Что будет информационной моделью организации дня ребенка в детском саду:

[-] а) меню приема пищи

[+] б) распорядок дня

[-] в) список группы

Что является материальной моделью:

[+] а) глобус

[-] б) график

[-] в) карта мира

Любой объект может:

[-] а) иметь только одну модель

[+] б) иметь множество моделей

[-] в) для каждого объекта – только фиксированное количество моделей

Что воспроизводит модель:

[-] а) только внешние данные объекта

[-] б) все характеристики объекта

[+] в) наиболее существенные для исследования характеристики объекта

Чем является схема пожарной сигнализации:

[-] а) словесной моделью

[+] б) графической моделью

[-] в) табличной моделью

Чем является график квадратичной функции является:

[-] а) натуральной моделью

[-] б) табличной моделью

[+] в) графической моделью

Информационная модель объекта автомобиль-это:

[-] а) объект-оригинал

[+] б) схема внутреннего устройства

[-] в) поэтическое описание

Выберите натурную модель:

[+] а) радиоуправляемая модель моторной лодки

[-] б) описание маршрута

[-] в) карточка из библиотечного каталога

Выберите модель, которая может использоваться для управления движением транспорта:

[-] а) физическая карта

[-] б) муляж транспортного средства

[+] в) расписание движения

Выберите информационную модель:

[+] а) график

[-] б) формула

[-] в) рисунок

Натуральная модель объекта человек-это:

[-] а) рисунок строения тела

[+] б) макет скелета

[-] в) объект-оригинал

2.

Общие признаки и свойства моделей.

 

2. Общие признаки и свойства моделей.

Общие признаки моделей

1. Модель представляет собой «четырехместную конструкцию», компонентами которой являются субъект; задача, решаемая субъектом; объект-оригинал и язык описания или способ воспроизведения модели. Особую роль в структуре обобщенной модели играет решаемая субъектом задача. Вне контекста задачи или класса задач понятие модели не имеет смысла.

2. Каждому материальному объекту соответствует бесчисленное множество в равной мере адекватных, но различных по существу моделей, связанных с разными задачами.

3. Паре задача-объект соответствует множество моделей, содержащих в принципе одну и ту же информацию, но различающихся формами ее представления или воспроизведения.

4. Модель всегда является лишь относительным, приближенным подобием объекта-оригинала и в информационном отношении принципиально беднее последнего.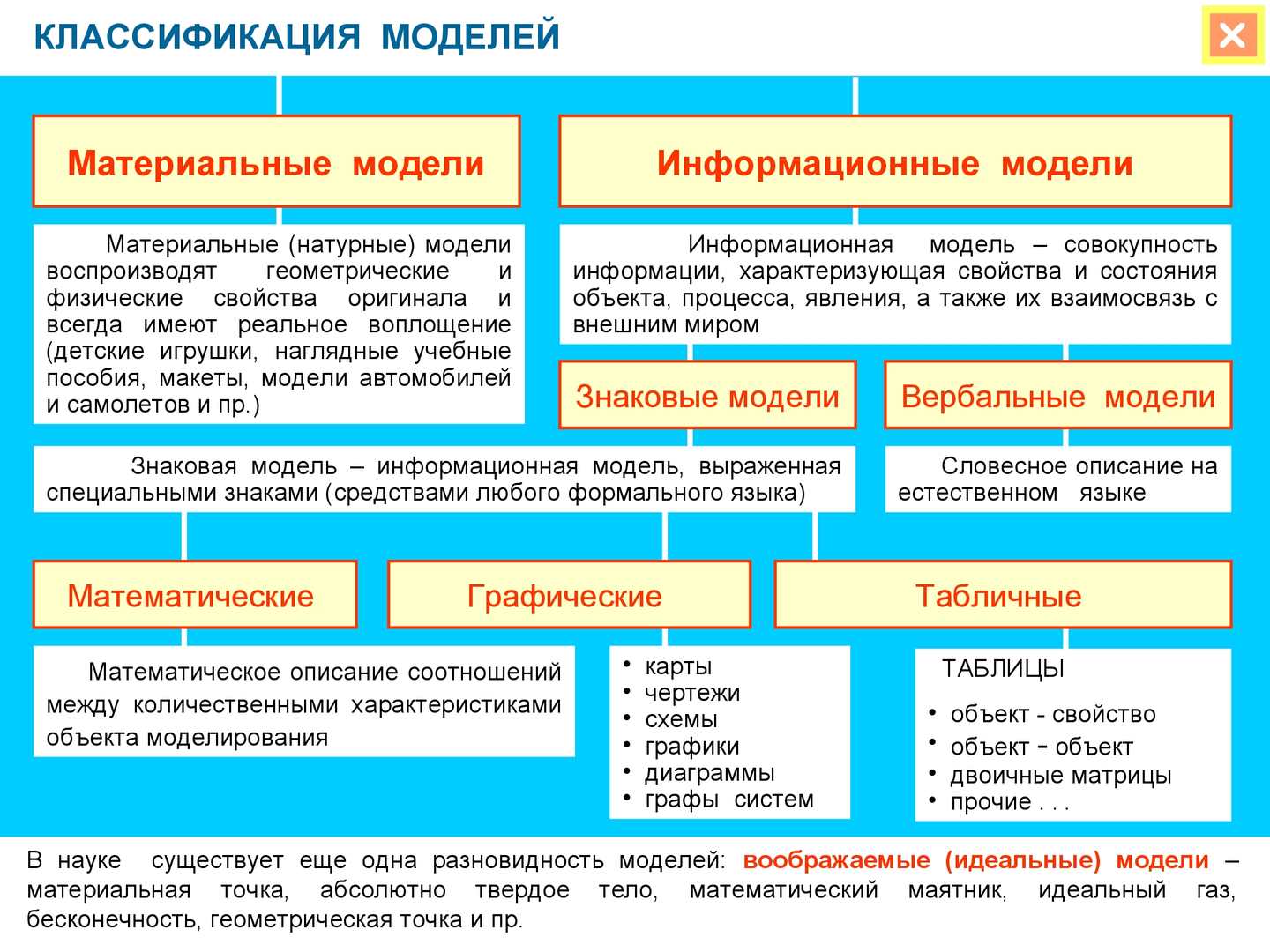

5. Произвольная природа объекта-оригинала, фигурирующая в принятом определении, означает, что этот объект может быть материально-вещественным, может носить чисто информационный характер и, наконец, может представлять собой комплекс разнородных материальных и информационных компонентов. Однако независимо от природы объекта, характера решаемой задачи и способа реализации модель представляет собой информационное образование.

6. В частном случае роль объекта моделирования в исследовательской или прикладной задаче играет не фрагмент реального мира, рассматриваемый непосредственно, а некая идеальная конструкция, т.е. по сути дела другая модель, созданная ранее и практически достоверная.

СВОЙСТВА МОДЕЛЕЙ

1) конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;

2) упрощенность: модель отображает только существенные стороны объекта;

3) приблизительность: действительность отображается моделью приблизительно;

4)·адекватность: степень успешности описания моделью объекта моделирования;

5) информативность: модель должна содержать достаточную информацию о системе – в рамках гипотез, принятых при построении модели.

 

 

< Предыдущая		Следующая >

Моделирование и симуляция: информатика иллюзий

От редакции Предисловие.

Предисловие.

Глава 1. Основные концепции и инструменты.

1.1. Моделирование и симуляция: что это такое ?.

1.2. Валидность, достоверность, сговорчивость и проверка.

1.3. Состояние системы и причинные системы.

1.4. Классификация динамических систем.

1.5. Дискретное и непрерывное моделирование.

1.6. Развитие программного обеспечения для моделирования.

Глава 2. Непрерывное моделирование.

2.1. Вступление.

2.2 Обыкновенные дифференциальные уравнения и модели систем с сосредоточенными параметрами.

2.3. Непрерывное моделирование с помощью аналоговых компьютеров.

2.4. Численные методы решения обыкновенных дифференциальных уравнений (ОДУ).

2.5. Графики прохождения сигналов.

2.6. Графики облигаций.

2.7. Альтернативные инструменты моделирования и динамической неопределенности.

2.8. Системы с распределенными параметрами.

2.9. Системная динамика.

2.10. Галактическое моделирование и проблема N тел.

Глава 3. Дискретное и комбинированное моделирование — пример реализации PASION.

3.1. Действительны ли дискретные модели ?.

3.2. Система моделирования PASION.

3.3. Генератор модели массового обслуживания QMG.

3.4. Комплексный системный симулятор PASION.

Глава 4. Дифференциальные включения в моделировании и симуляции.

4.1. Дифференциальные включения.

4.2. Возможные приложения.

4.3. Решатель дифференциального включения.

4.4. Применение в обработке неопределенности.

4.5. Неопределенное будущее и дифференциальные включения.

4.6. Выводы и дальнейшие исследования.

Глава 5. Гидродинамика — моделирование колеблющегося потока газа.

5.1. Вычислительная гидродинамика.

5.2. Численные задачи.

5.3. Инструмент моделирования.

5.4. Примеры.

5.5. Колеблющийся газовый поток.

5.6. Двумерные гидродинамические модели недействительны.

5.7. Выводы.

Глава 6. Моделирование явлений общей теории относительности.

6.1. Некоторые основные понятия.

6.3. Инструмент моделирования и модельное время.

6.4. Имитационные эксперименты.

Глава 7. Взаимодействие враждебных иерархических структур: моделирование борьбы террористических и антитеррористических организаций .

7.1. Вступление.

7.2. Модель.

7.3. Структуры.

7.4. Инструмент и реализация модели.

7,5. Имитационные эксперименты.

7.6. Выводы.

Глава 8. О метрической структуре в пространстве моделей динамических систем.

8. 1. DEVS.

8.2. Определения.

8.3. Расстояние между моделями.

8.4. Примеры.

8.5. Выводы.

Глава 9. Оптимизация моделирования: пример параллельного алгоритма оптимизации.

9.1. Вступление.

9.2. Постановка задачи.

9.3. Имитационный эксперимент.

9.4. Выводы.

Список литературы.

Индекс.

Концепции, методы и модели компьютерного программирования

Сводка

Преподавание науки и технологий программирования как единой дисциплины, демонстрирующей глубокую взаимосвязь между парадигмами программирования.

Этот новаторский текст представляет компьютерное программирование как единую дисциплину, причем как с практической, так и с научной точки зрения. Книга фокусируется на методах, имеющих непреходящую ценность, и объясняет их в терминах простой абстрактной машины. В книге представлены все основные парадигмы программирования в единой структуре, которая показывает их глубокие отношения, а также то, как и где их использовать вместе. После введения в концепции программирования в книге представлены как хорошо известные, так и малоизвестные модели вычислений («парадигмы программирования»).Каждая модель имеет свой собственный набор методов, и каждая из них включается в зависимости от практической применимости. Общие модели включают декларативное программирование, декларативный параллелизм, параллелизм передачи сообщений, явное состояние, объектно-ориентированное программирование, параллелизм с общим состоянием и реляционное программирование. Специализированные модели включают программирование графического пользовательского интерфейса, распределенное программирование и программирование в ограничениях. Каждая модель основана на своем языке ядра — простом базовом языке, состоящем из небольшого числа элементов, значимых для программиста.Языки ядра вводятся постепенно, добавляя концепции одну за другой, тем самым показывая глубокие взаимосвязи между различными моделями. Языки ядра определены в терминах простой абстрактной машины. Поскольку большое количество языков и парадигм программирования можно смоделировать с помощью небольшого набора тесно связанных языков ядра, этот подход позволяет программисту и студенту понять лежащее в основе единство программирования. В книге есть множество программных фрагментов и упражнений, все из которых могут выполняться в системе программирования Mozart, программном пакете с открытым исходным кодом, который включает интерактивную среду инкрементной разработки.

Твердая обложка

105,00 долларов США Икс ISBN: 9780262220699 936 с. | 8 дюймов x 10 дюймов 249 илл. Февраль 2004 г.

Не продается на Индийском субконтиненте.

Авторы

Питер Ван Рой

Питер Ван Рой — профессор кафедры вычислительной техники и инженерии Католического университета Лувена в Лувен-ла-Нев, Бельгия.

Сейф Хариди

Сейф Хариди — профессор компьютерных систем на факультете микроэлектроники и информационных технологий Королевского технологического института Швеции и главный научный советник Шведского института компьютерных наук.

Описательная модель

— обзор

16.2 Методы интеллектуального анализа данных Oracle

Проблемы интеллектуального анализа данных можно разделить на две категории. В некоторых ситуациях вы имеете некоторое представление о том, что ищете — например, вас интересуют клиенты, которые, вероятно, купят цифровую камеру.Это известно как управляемое или управляемое обучение . В других случаях вы предоставляете процессу добычи полезных ископаемых найти что-то интересное — например, высокий уровень аварий на определенном перекрестке. Это называется неориентированным или неконтролируемым обучением. При обучении без учителя алгоритмы интеллектуального анализа данных описывают некоторые внутренние свойства или структуру данных и поэтому иногда называются описательными моделями . С другой стороны, методы контролируемого обучения обычно используют модель для прогнозирования значения или поведения некоторой величины и поэтому называются моделями прогнозирования .

Oracle Data Mining поддерживает различные методы интеллектуального анализа данных, каждый из которых относится к одной из этих двух категорий.

1.

Описательные модели / обучение без учителя:

▪

Правила ассоциации или анализ корзины

▪

02 Кластеризация

9179

2.

Прогностические модели / контролируемое обучение:

▪

Классификация

▪

Регрессия

▪

Важность каждого из этих атрибутов

мы рассмотрим

некоторая деталь.Oracle Data Mining также предоставляет специальные алгоритмы для интеллектуального анализа текста и приложений для медико-биологических наук, которые мы не будем обсуждать в этой книге.

16.2.1 Правила ассоциации

Все мы знакомы с функцией Amazon.com — «Привет, Джейн! У нас есть для вас новые рекомендации ». Этот тип персонализации веб-сайта использует метод интеллектуального анализа данных, известный как правила ассоциации. Интеллектуальный анализ с использованием ассоциативных правил находит элементы, которые часто встречаются вместе. Например, правила ассоциации могут обнаружить, что большой процент пользователей, купивших книгу «Властелин колец », также купили книгу «Хоббит». Итак, если вы покупаете Властелин колец , он может порекомендовать вам также прочитать Хоббит.

Интеллектуальный анализ данных с использованием ассоциативных правил также известен как «анализ рыночной корзины». Когда вы посетите местный продуктовый магазин, вы можете обнаружить, что в отделе морепродуктов есть лимоны или соус тартар рядом с рыбой. Это связано с тем, что, как выяснилось, 80 процентов людей, покупающих рыбу, также покупают лимоны, чтобы пойти с ней. Большинство из этих магазинов предлагают своего рода карточки постоянных покупателей — подсчитывая, какие комбинации товаров были куплены одним и тем же человеком, они могут организовать свои полки более подходящим образом и даже отправить вам купоны на те же или похожие товары для следующего визит.

Интеллектуальный анализ с использованием ассоциативных правил включает подсчет того, сколько раз определенная группа элементов встречается вместе. В этом случае вам не обязательно знать, какую комбинацию искать заранее — следовательно, это относится к категории неконтролируемого или ненаправленного обучения. Алгоритм ассоциации предлагает правила типа «A подразумевает B.» Пользователя этого алгоритма интересуют две величины: поддержка и уверенность.

▪

Поддержка сообщает нам процент транзакций, в которых комбинация элементов A и B происходит вместе.Это помогает определить комбинации, которые достаточно часты, чтобы представлять интерес (например, покупка рыбы отдельно или покупка рыбы и лимонов вместе).

▪

Доверие сообщает нам, какой процент транзакций, имеющих товар A, также имеет товар B (например, в скольких транзакциях с рыбой есть и лимоны).

Чтобы использовать правила ассоциации, пользователь должен обеспечить требуемый уровень поддержки и уверенности, чтобы правило считалось интересным.Например, предположим, что мы указываем, что для того, чтобы правило было интересным, оно должно иметь поддержку 20 процентов и достоверность 70 процентов. Если выяснится, что на самом деле 40 процентов всех транзакций связаны с комбинацией рыбы и лимонов, тогда комбинация «рыба, лимоны» превышает минимальную поддержку в 20 процентов. Теперь, если мы обнаружили, что 50 процентов всех транзакций связаны с рыбой, тогда комбинация «рыба, лимоны» имеет достоверность (40/50) * 100 = 80 процентов, поэтому она также соответствует критерию минимальной достоверности.Следовательно, «рыба подразумевает лимоны» будет указано как правило ассоциации.

Для принятия значимых бизнес-решений важны как поддержка, так и доверие. Рассмотрим этот альтернативный пример района, где рыба не очень популярна из-за высокого содержания ртути. Может быть, только 5 процентов сделок связано с рыбой. Товар «рыба» не пользуется достаточной поддержкой, и, следовательно, правило «рыба подразумевает лимоны» не окажет существенного влияния на наши продажи.

На рисунке 16.1 показан типичный результат анализа интеллектуального анализа данных с использованием ассоциативных правил, проанализированный с помощью такого инструмента, как Oracle Discoverer.Первые два правила гласят, что люди часто покупают ВИНО или ЛИМОНЫ к РЫБЕ.

Рисунок 16.1. Правила связывания

Алгоритм, используемый Oracle Data Mining для правил связывания, априори называется . Пользователь обеспечивает минимальную желаемую поддержку и уверенность. Алгоритм сначала находит единичные элементы, которые встречаются часто и имеют минимальную поддержку, например, рыба. Затем он находит пары элементов, которые имеют минимальную поддержку, так что хотя бы один элемент в паре часто встречается, например рыба и лимоны.Он повторяет этот процесс, чтобы придумывать все более крупные комбинации предметов, пока больше не сможет найти. После того, как он обнаружил все «часто встречающиеся наборы элементов», он затем находит те, которые удовлетворяют минимальному требованию доверия со стороны пользователя. Они сообщаются как правила ассоциации. Oracle Database 10 g имеет реализацию этого алгоритма на основе SQL.

16.2.2 Кластеризация

Кластеризация — это метод, используемый для разделения большого набора данных со многими атрибутами на небольшое количество «плотно упакованных» групп.Такие группы нелегко заметить человеческому глазу из-за большого количества задействованных атрибутов. Например, предположим, что у вас есть данные переписи населения, включая несколько атрибутов, таких как возраст, род занятий, частота заболеваний и т. Д. Сгруппировав эти данные, можно обнаружить, что есть несколько очагов, где преобладает определенное заболевание, что, возможно, указывает на загрязненное водоснабжение в этих регионах. Поскольку у нас нет определенного представления о том, что мы можем найти, это еще один пример обучения без учителя.

Группы, созданные с помощью хорошего алгоритма кластеризации, таковы, что все элементы в одной группе в некоторых отношениях очень похожи друг на друга и очень не похожи на элементы в других группах.

Рисунок 16.2 иллюстрирует концепцию кластеров в данных. На этом рисунке два атрибута данных нанесены на диаграмму рассеяния для выделения кластеров. Для всех элементов в каждом кластере значения двух атрибутов имеют большее сходство по сравнению с элементами в разных кластерах. Это пример, когда кластеры в данных были очевидны при простом построении графика.На практике визуализировать кластеры таким образом не всегда возможно, поскольку у нас может быть более двух или трех измерений! Например, в приложениях биоинформатики вы можете иметь тысячи измерений! В этих ситуациях мы используем математические алгоритмы кластеризации для идентификации кластеров.

Рисунок 16.2. Кластеризация

Одним из приложений, где используется кластеризация, является сегментация рынка. Предположим, вы являетесь крупным розничным продавцом, продающим широкий ассортимент товаров от мыла до музыкальных автоматов.С помощью кластеризации вы можете сегментировать свою клиентскую базу на группы на основе демографических данных или прошлых покупательских привычек. Это позволяет настраивать рекламную стратегию для каждого сегмента и лучше обслуживать более прибыльные сегменты.

Кластеризация выполняется путем сначала анализа небольшого участка данных для определения кластеров. После определения кластеров оставшиеся данные затем анализируются, чтобы с определенной вероятностью отнести каждый отдельный элемент к кластеру.

Алгоритмы кластеризации

Интеллектуальный анализ данных Oracle поддерживает два алгоритма кластеризации:

▪

Расширенные k-средства

▪

O-Cluster

Алгоритм кластеризации k-средних значений является алгоритмом кластеризации. группирует данные в указанное количество k кластеров.Он группирует элементы в кластеры на основе их относительного «расстояния» друг от друга. Таким образом, все точки в одном кластере «ближе» друг к другу, чем к точкам в других кластерах. Расширенный алгоритм k-средних является разновидностью алгоритма k-средних, который формирует кластеры иерархическим образом. Он начинается с того, что все данные находятся в одном кластере, а затем последовательно разбивает их на более мелкие кластеры, пока не будет получено желаемое количество кластеров. Он очень эффективен по сравнению с традиционными k-средними, поскольку требует только одного прохода через данные и, следовательно, может обрабатывать большие наборы данных.Он хорошо работает даже для наборов данных с менее чем 10 атрибутами. Метрическое «расстояние», используемое k-means, может быть определено только для числовых атрибутов; следовательно, если у вас есть дискретные значения (например, цвет = красный, черный, синий), то k-средние нельзя использовать.

Алгоритм O-Cluster определяет кластеры, используя диапазоны значений атрибутов. Пользователю не нужно указывать количество кластеров для создания. Этот алгоритм можно использовать для нечисловых атрибутов, которые имеют дискретный набор значений.

16.2.3 Извлечение признаков

Извлечение признаков — это процесс, который идентифицирует важные особенности или атрибуты данных. Некоторыми примерами этого метода являются распознавание образов и определение общих тем в большой коллекции документов. Если данные имеют много измерений (например, ключевые слова в документе), то можно использовать извлечение признаков для получения более краткого описания данных.

Один из примеров извлечения функций, с которым все мы можем иметь дело, — это программное обеспечение для обнаружения спама.Если бы у нас была большая коллекция электронных писем и ключевые слова, содержащиеся в этих письмах, то процесс извлечения функций мог бы найти корреляции между различными ключевыми словами. Например, может показаться, что слова Буш и выборы коррелируют. Таким образом, набор электронных писем теперь можно описать с помощью гораздо меньшего количества словосочетаний, чем то, с чего мы начали. Например, вы можете сказать, является ли электронное письмо текущим новостным сообщением о президентских выборах в США или предлагает вам незапрошенный ипотечный продукт или новое диетическое решение.Как только мы это сделаем, мы сможем связать определенные комбинации слов или фраз как спам и автоматически отфильтровать эти электронные письма. Конечно, это очень упрощенное описание любого реального алгоритма, но, надеюсь, оно помогло вам понять концепцию извлечения признаков.

Извлечение признаков может быть полезно для уменьшения количества атрибутов, описывающих данные. Это может ускорить интеллектуальный анализ данных с использованием методов контролируемого обучения, таких как классификация, о которых мы вскоре поговорим.

Oracle Data Mining использует различные методы для извлечения признаков, такие как неотрицательная матричная факторизация (NMF). Подробности этой техники выходят за рамки этой книги.

16.2.4 Классификация

Предположим, вы хотите настроить таргетинг на рекламу новой цифровой камеры и хотите знать, кто из ваших клиентов, скорее всего, купит камеру. Классификация — это метод интеллектуального анализа данных, который полезен для этого приложения. Классификация делит данные на два или более четко определенных класса.В отличие от кластеризации, где вы не знаете, какие группы будут сгенерированы, в классификации вы точно знаете, что представляет каждая группа. В предыдущем примере это две группы: клиенты, которые, скорее всего, купят камеру, и клиенты, которые , а не , скорее всего, купят камеру. Это пример обучения с учителем.

При классификации вы сначала анализируете небольшую часть ваших данных, чтобы построить модель . Например, вы можете проанализировать реальные данные людей, которые купили цифровые фотоаппараты, и людей, которые не покупали цифровые фотоаппараты, за определенный период времени. Данные, используемые для построения модели, известны как данные построения . Модель будет построена с учетом различных факторов, таких как возраст, доход и род занятий, которые, как известно, влияют на покупательские привычки людей. Эти факторы известны как атрибуты предиктора . Прогнозируемый результат называется целевым атрибутом , а его значения (независимо от того, купит ли человек камеру или нет) известны как категории , или классы . После того, как модель была сгенерирована, ее можно применить к другим данным, чтобы сделать прогноз.Это известно как применение модели , оценка или . В нашем примере вы могли бы использовать модель, чтобы предсказать, купит ли определенный покупатель цифровую камеру.

В предыдущем примере целевой атрибут имеет два значения: будет покупать цифровую камеру и не покупать цифровую камеру. Вы также можете использовать классификацию для прогнозирования атрибутов с более чем двумя значениями — например, низкий, средний или высокий риск невыполнения платежа лицом.

Классификация часто используется для создания профилей клиентов.Например, как только вы определили, кто из ваших клиентов, скорее всего, купит цифровую камеру, вы можете профилировать их по роду занятий, как показано на рисунке 16.3. Из этого графика вы теперь знаете, что наиболее вероятными покупателями являются инженеры или руководители. Таким образом, теперь вы можете более точно нацеливать свои рекламные акции на этих клиентов и сократить свои расходы.

Рисунок 16.3. Классификация

Чтобы классификация работала правильно, данные сборки должны содержать достаточное количество образцов для каждой целевой категории; в противном случае это может быть неточно.Другими словами, ваши данные о сборке должны включать достаточное количество людей, которые покупали цифровые фотоаппараты в прошлом, и достаточное количество тех, кто этого не делал.

Тестирование модели классификации

Интеллектуальный анализ данных с использованием классификации обычно включает этап тестирования, чтобы проверить, насколько хороша модель. Для этого проверяются данные, результат которых известен, чтобы увидеть, насколько хорошо ему соответствуют прогнозы модели. Например, вы можете взять данные о клиентах, которые покупали цифровую камеру в прошлом, и сравнить их с прогнозами, данными моделью.

Тестирование модели включает вычисление структуры, известной как матрица неточностей . Матрица неточностей сообщает вам, сколько раз прогноз модели соответствовал фактическим данным, а сколько — нет. Столбцы соответствуют прогнозируемым значениям, а строки — фактическим значениям. Например, на рис. 16.4 модель верна 555 + 45 = 600 раз и неверна 12 + 8 = 20 раз. Это говорит о том, что эта модель довольно хороша.

Рисунок 16.4. Матрица неточностей

Вычислительный подъемник

Другой показатель, используемый для определения эффективности модели, — это подъемник . Чтобы понять, что такое подъемник, рассмотрим следующий пример. Предположим, у нас есть клиентская база из 100 000 домашних хозяйств, и в среднем около 2,5% (2 500 клиентов) откликаются на любое конкретное продвижение. Мы хотим стать умнее и ориентироваться только на тех клиентов, которые с наибольшей вероятностью откликнутся. При наличии хорошей модели классификации мы должны быть в состоянии идентифицировать большинство из 2500 вероятных респондентов, ориентируясь на гораздо меньшее, чем 100 000 домохозяйств. Учитывая определенный процент целевых клиентов, рост — это отношение количества респондентов, полученных с помощью модели, к количеству, полученному без модели.

Подъем рассчитывается следующим образом. Модель классификации применяется к фактическому набору данных о клиентах, из которого мы знаем, кто отреагировал на прошлую рекламную акцию, а кто нет. Затем клиенты сортируются по вероятности ответа в соответствии с прогнозом модели, причем сначала наиболее вероятные респонденты. Этот отсортированный список затем делится на 10 равных групп, известных как децилей. Для каждого дециля подсчитывается количество клиентов в наборе данных, которые фактически ответили на рекламную акцию. Если модель хороша, то большинство респондентов должно происходить из нескольких верхних децилей, поскольку они были предсказаны как наиболее вероятные респонденты.

Если вы нарисуете график с децилями от 1 до 10 по оси X и количеством фактических респондентов по оси Y, вы обычно получите кривую, показанную на рисунке 16.5. Эта кривая говорит вам, что вам нужно ориентироваться только на клиентов в первых трех децилях (30 процентов домохозяйств), чтобы получить 70 процентов тех, кто с большой вероятностью откликнется. С другой стороны, прямая линия на этом рисунке соответствует случайному продвижению по службе, при котором все, по прогнозам, ответят с одинаковой вероятностью.Без модели, которая будет вам руководить, если вы нацеливаетесь на 30 процентов домохозяйств, вы получите только 30 процентов вероятных респондентов. Чтобы получить 70 процентов вероятных респондентов, вам нужно будет охватить 70 процентов домохозяйств! Чем выше изогнутая линия от прямой линии для первых одного или двух децилей, тем лучше подъемная сила модели.

Рисунок 16.5. Использование анализа роста для целевых рекламных акций

Матрица неточностей и рост — широко используемые методы для определения точности моделей классификации.Oracle Data Mining предоставляет API, которые позволят вам вычислить эти количества.

Классификационные алгоритмы

Oracle предлагает три алгоритма для классификации:

▪

Наивный байесовский алгоритм

▪

Адаптивный алгоритм байесовской сети

▪

9000 машин с поддержкой векторов Алгоритм Байеса (NB) основан на теореме вероятности, известной как теорема Байеса, и предполагает, что каждый атрибут не зависит от другого.Интересным свойством алгоритма NB является то, что вы можете строить и перекрестно проверять модель, используя одни и те же данные. Этот алгоритм лучше всего работает с небольшим количеством атрибутов предиктора (менее 200).

Алгоритм адаптивной байесовской сети (ABN) в его наиболее интуитивно понятной форме (известный как построение с одной функцией) создает модель в виде дерева решений, показанного на рисунке 16. 6. Из этого дерева решений вы можете видеть, что мужчины в возрасте от 15 до 35 лет и женщины старше 26 лет, скорее всего, купят фотоаппарат.Поскольку модель, созданная ABN, представлена ​​в удобочитаемой форме, бизнес-аналитику или руководителю будет удобнее использовать ее для принятия бизнес-решений. Алгоритм ABN обычно более точен, чем NB, но для построения модели требуется больше времени.

Рисунок 16.6. Адаптивное дерево решений байесовской сети

Oracle также предоставляет два других режима для модели адаптивной байесовской сети, называемые сокращенным, наивным байесовским и усиленным, которые концептуально позволяют описывать данные с использованием нескольких деревьев решений; однако эти режимы не обеспечивают удобочитаемых правил.

Машины опорных векторов (SVM) — это метод классификации, основанный на теории машинного обучения (искусственного интеллекта). В этом методе математические функции, называемые ядрами , используются для преобразования данных, что позволяет более четко дифференцировать данные по различным категориям. Это метод прогнозирования, поскольку машина (алгоритм) сначала обучается с использованием некоторых исходных обучающих данных, а затем учится правильно классифицировать новые данные. SVM используется во многих реальных приложениях, таких как распознавание рукописного ввода и классификация изображений.

16.2.5 Регрессия

Регрессия — это метод прогнозного моделирования, который позволяет описать взаимосвязь между двумя переменными с помощью линии или кривой. Если значение одной переменной (называемой независимой переменной ) известно, линия или кривая затем могут использоваться для прогнозирования значения другой переменной (называемой зависимой переменной ). Наиболее распространенный метод — это линейная регрессия , при которой вы находите прямую линию, которая соответствует данным.В главе 6 мы увидели некоторые встроенные функции SQL для анализа линейной регрессии. Например, линейная регрессия может использоваться, чтобы определить, имеет ли цена количества какое-либо отношение к его общим продажам.

Важно отметить разницу между классификацией и регрессией: классификация позволяет классифицировать данные, когда целевой атрибут является дискретным, тогда как регрессия позволяет классифицировать данные, когда целевой атрибут является непрерывным или числовым.

Машину опорных векторов, используемую для классификации, также можно использовать для создания регрессионных моделей для данных.

16.2.6 Стандарт PMML

Язык разметки для прогнозного моделирования (PMML) — это развивающийся стандарт на основе XML для определения моделей интеллектуального анализа данных. PMML предоставляет независимый от производителя метод определения моделей, так что моделями можно обмениваться между различными приложениями. Таким образом, одно приложение может создавать модель, а другое может применять модель к набору данных. Oracle Data Mining поддерживает импорт и экспорт правил связывания и наивных байесовских моделей.

9780125980517: Вероятностные модели для информатики — AbeBooks

С задней стороны обложки :

Роль вероятности в информатике растет, и вместо специальной книги многие профессионалы используют множество похожих, но не совсем применимых альтернатив. Чтобы удовлетворить потребности компьютерных ученых, мудрец теории вероятностей и статистики Шелдон Росс разработал главный вероятностный титул для компьютерных ученых, занимающихся компьютерным моделированием и моделированием.

Четкое понимание природы вероятностного моделирования является важной задачей при разработке компьютерных систем и программного обеспечения.

Математика точная и понятная. Как и в других своих бестселлерах, Росс дает очень четкие объяснения концепций и охватывает те вероятностные модели, которые наиболее востребованы и применимы к компьютерным наукам (и связанным с ними) темам.

Ключевой особенностью этой книги является множество интересных примеров и упражнений, которые были выбраны для освещения представленных техник. Например, есть примеры, относящиеся к упаковке контейнеров, алгоритмам сортировки, алгоритму поиска, случайным графам, задачам самоорганизующихся списков, антицепям, минимальным и максимальным разрезам в графах, случайным перестановкам, проблеме максимального взвешенного независимого множества, хешированию, вероятностной проверке. , задача max SAT, сети массового обслуживания, модели распределенных рабочих нагрузок и многое другое.

Об авторе :

Доктор Шелдон М. Росс — профессор кафедры промышленной и системной инженерии Университета Южной Калифорнии.Он получил докторскую степень по статистике в Стэнфордском университете в 1968 году. Он опубликовал множество технических статей и учебников в области статистики и прикладной вероятности. Среди его текстов — «Первый курс вероятности», «Введение в вероятностные модели», «Стохастические процессы» и «Вводная статистика». Профессор Росс является соучредителем и постоянным редактором журнала «Вероятность в области инженерии и информационных наук». Он является научным сотрудником Института математической статистики, научным сотрудником ИНФОРМС и лауреатом Премии Гумбольдта в США для старших ученых.

«Об этом заголовке» может принадлежать другой редакции этого заголовка.

Компьютерные модели и философия

Использование компьютеров для моделирования сложных явлений — особенно эволюционных, социальных и психологических явлений — открывает важные новые области в философии науки, а также влияет на существующую теорию научных моделей.Такие модели также предоставляют новые и захватывающие возможности для изучения глубоких и увлекательных тем, которые сами по себе представляют философский интерес, посредством компьютерных экспериментов с мыслями. С этим связано использование компьютерных моделей для облегчения понимания или в качестве «насосов интуиции». Даже если компьютерные модели имеют сомнительный реализм, они могут служить потенциально ценной цели в качестве доказательств существования или контрпримеров к общим утверждениям. Все эти виды использования относительно бесспорны, но на другом конце спектра находятся предположения о возможности искусственной жизни.

Компьютерные модели в физических науках

Компьютерные модели обычно используются в физических науках, что обусловлено огромным объемом требуемых вычислений и часто сложными связями между теорией и наблюдением. Традиционно компьютер имел тенденцию быть обработчиком чисел, решая наборы уравнений, которые моделируют рассматриваемые явления на высоком уровне абстракции (как, например, в статистической механике). Однако в последнее время невероятный рост мощности компьютеров позволил реализовать модели, которые представляют большое количество сущностей по отдельности, а не только вместе, как в The Millennium Simulation Project, который смоделировал более 10 миллиардов частиц. Это позволяет моделировать явления, которые нельзя адекватно обрабатывать статистически, потому что поведение отдельных сущностей — даже внутри большого коллектива — оказывает несоразмерное влияние. Хороший пример в человеческом масштабе дает моделирование транспортного потока, как в этом апплете Traffic Simulator, созданном Каем Хорстманном (Государственный университет Сан-Хосе).

Агентные модели

Еще один шаг в том же направлении — моделирование отдельных сущностей, которые обладают потенциалом для своего собственного отличительного поведения.Каждая сущность или «агент» хранится как «объект» в программе, каждый со своим индивидуальным «состоянием» (обычно определяемым значениями, заданными диапазону целочисленных переменных). Опять же, это стало возможным только благодаря быстрому развитию компьютеров, которые теперь достаточно большие и быстрые, чтобы можно было разыграть модели такого типа с тысячами агентов, каждый из которых взаимодействует с другими последовательно, возможно, миллионы раз (например, либо случайным образом). или в зависимости от их географического положения и перемещений).Использование объектно-ориентированных языков программирования (таких как C ++, Delphi и Java) значительно упростило их реализацию. А в последнее время такое моделирование на основе агентов стало практичным для программистов-неспециалистов благодаря разработке таких инструментов, как NetLogo, которые позволяют им относительно легко разрабатывать модели мощности, которые были бы немыслимы даже для опытных программистов. десятилетия назад.

Компьютерные модели в биологических науках

Биологические науки характеризуются сложными взаимодействиями между системами, которые сами по себе очень сложны.Некоторые из этих взаимодействий — между белками, клетками, органами и т. Д. — происходят внутри отдельных животных или растений, их изучение относится к быстро развивающейся области системной биологии, которая была преобразована с помощью компьютерных моделей. Между тем взаимодействия между организмами — как при изучении эволюции или поведенческой экологии — теперь широко исследуются с использованием агентно-ориентированных моделей. Один из самых известных из них, «Бойды» Крейга Рейнольдса, изображен выше. Это служило демонстрацией того, что «стайное» поведение можно прекрасно объяснить на основе гипотезы о том, что птицы действуют без какой-либо центральной координации, в соответствии с тремя простыми и применяемыми на местном уровне правилами.Таким образом, он предоставил важное доказательство существования потенциального типа объяснения и открыл новую линию эмпирических исследований.

Компьютерные модели в поведенческих науках

Агентно-ориентированные модели

также предоставляют очень естественную среду для исследования крупномасштабных взаимодействий между людьми, как в социальных науках и экономике. Было заметно, что такие исследования составляют новую парадигму генеративной науки, согласно которой модели подтверждаются не успешным предсказанием , а вместо этого успешным поколением уже наблюдаемых явлений на простых (и правдоподобных) основаниях.

Междисциплинарная область, представляющая особый интерес для философов, — это Эволюция сотрудничества, которая может иметь большое значение для моральной философии, а также для всех наук о поведении.

научных моделей: определение и примеры — видео и стенограмма урока

Визуальные модели

Визуальные модели — это блок-схемы, изображения и диаграммы, которые помогают нам обучать друг друга. Это те, с кем не-ученые имеют наибольший опыт.В офисе вы можете создать блок-схему, описывающую выполняемую вами работу. Возможно, заказы поступают по телефону, и эта информация передается как на склад, так и в отдел членства. Если вы включите все входные и выходные данные, эта блок-схема является примером визуальной модели.

В науке визуальные модели часто используются в качестве образовательных инструментов, например, в классе или при передаче от ученого коллеге. Например, визуальная модель может показать основные процессы, влияющие на то, из чего состоит атмосфера.Независимо от того, насколько вы умны и образованы, диаграммы чрезвычайно полезны для объяснения того, как устроен мир. Они могут описывать абстрактные концепции и показывать вещи, которые были бы слишком крошечными или слишком гигантскими, чтобы увидеть их собственными глазами.

Математические / компьютерные модели

Научные модели — это часто математические модели , в которых вы используете математику для описания конкретного явления. Например, вы могли заметить, что сила тяжести на объекте равна его массе, умноженной на силу гравитационного поля.Когда вы соединяете все свои уравнения гравитации, вы получаете общую модель гравитации, которую впервые создал Ньютон.

Но у людей есть свои пределы. Те математические уравнения, которые придумал Ньютон, могут сбивать с толку. Это нормально, когда вы изучаете простые ситуации в научной лаборатории, но как насчет реального мира? Использовать законы Ньютона для объяснения течения реки над сушей сложнее, чем вы думаете.

Вам необходимо принять во внимание типы камней и почвы, их трение и соленость, а также то, как вода течет вокруг растений и различных камней произвольной формы.Это, конечно, непросто, поэтому для полного объяснения вы можете использовать компьютерные модели , которые способны выполнять сложные вычисления и анимацию. Ввод в компьютер всего, что мы знаем о гравитации и силах, позволяет ему выяснить, что произойдет, гораздо быстрее, чем это мог бы сделать любой человек.

Математические и компьютерные модели используются для предсказания самых разных вещей. Например, как может развиваться изменение климата или что может произойти, если астероид упадет на Землю. Они также используются для моделирования автокатастроф или для моделирования огня и дыма для исследований безопасности или даже для голливудских фильмов.

Пересмотр моделей

Модель несовершенна по определению. Он лишь представляет что-то в мире таким образом, чтобы мы могли делать прогнозы. Но реальный мир иногда показывает нам, что нам есть чему поучиться. Научные модели постоянно меняются или обновляются, когда мы получаем новые данные. Если мы обнаружим данные, которые не соответствуют нашим предыдущим моделям, тогда кто-то должен выяснить, что пошло не так, и внести улучшения.

Иногда старая модель не ошибочна, она просто неполная. Например, когда Альберт Эйнштейн придумал свои теории относительности, они были более точной заменой законов движения и гравитации Ньютона. Означает ли это, что Ньютон ошибался? Ну не совсем. Законы Ньютона делают фантастическую работу по предсказанию поведения движущихся объектов и предсказанию силы тяжести. Проблема в том, что они работают только тогда, когда объекты движутся относительно медленно, и не объясняют, почему и как работает гравитация.

Эйнштейн расширил эти теории, создав свою собственную модель движения и гравитации, которая не только работала как законы Ньютона для медленно движущихся объектов, но также работала для объектов, приближающихся к скорости света.Старая модель не ошибалась, просто она работала только при определенных обстоятельствах.

Наука направлена ​​на улучшение наших знаний о мире, и это постепенный процесс. Это случается с множеством фальстартов и упрощений. Это одна из сильных сторон науки: она позволяет нам узнавать больше каждый день и постепенно со временем улучшать наше понимание мира.

Резюме урока

Научная модель — это когда ученые представляют что-то в реальном мире таким образом, чтобы его было легче понять или сделать прогнозы.Это может быть просто, например, диаграмма, физическая модель или изображение, или сложное, например, набор вычислительных уравнений или компьютерная программа.

Основными видами научных моделей являются визуальные, математические и компьютерные модели. Визуальные модели — это блок-схемы, изображения и диаграммы, которые помогают нам обучать друг друга. Математические модели включают научные уравнения, которые аппроксимируют и объясняют, как устроен мир, что позволяет нам делать расчеты и прогнозы. Компьютерные модели могут выполнять сложные вычисления, на которые у человека уйдет очень много времени.Мы используем компьютеры, чтобы предсказать, как вещи могут вести себя в мире, и помочь нам найти ответы на наши научные вопросы.

Три основных типа научных моделей

Визуальный	Математическая	Компьютер
* Часто используется в качестве учебных пособий * Включите диаграммы, изображения и диаграммы	* Когда математика используется для описания конкретного явления * Использует вычисления для прогнозирования	* Возможность сложных вычислений и анимации * Может использоваться для моделирования событий на основе математики и данных

Результаты обучения

К концу урока вы должны быть уверены в следующем:

• Вспомните цель научной модели
• Назовите и опишите три типа научных моделей

COMP_SCI 372, 472: Проектирование и построение моделей с многоагентными языками | Компьютерные науки

COMP_SCI 472 требует записи в аспирантуру.

Этот курс посвящен исследованию, построению и анализу многоагентных моделей. Изучаются и анализируются образцы моделей из различных областей контента. Представлены пространственные и сетевые топологии. Рассмотрены известные агентные структуры, а также методология репликации, проверки и валидации агентных моделей. Мы используем современные инструменты ABM и науки о сложности. Этот курс может помочь удовлетворить требования к курсу проекта и области искусственного интеллекта для специализаций CS и CIS, а также удовлетворить требования в области искусственного интеллекта для Ph.D. студенты в CS. Он также удовлетворяет требованиям курса дизайна для аспирантов Learning Sciences, засчитывается в специализацию Cognitive Science и как дополнительный факультатив для специализации Cognitive Science.

• Соединение с COMP_SCI 472 . См. Описание для COMP_SCI 342 .
• Этот курс удовлетворяет требованиям AI Breadth Requirement
• Этот курс включен в перекрестный список LRN_SCI 372/472 (весна 2021 г. ).

КООРДИНАТОР КУРСА: Проф. Ури Виленский

НЕОБХОДИМЫЕ УЧЕБНИКИ: Введение в агентное моделирование: моделирование природных, социальных и инженерных сложных систем с помощью NetLogo — Ури Виленски, MIT Press

ЦЕЛЬ КУРСА: Построение и анализ многоагентных моделей как в пространственной, так и в сетевой топологии

ПОДРОБНЫЕ ТЕМЫ КУРСА:

• Что такое агент?
• Агрегаты стационарные и передвижные
• Взаимодействие между агентами
• Топологии агентов
• Свойства сетей
• Приложения ABM
• Искусственная жизнь
• Сравнение с моделями системной динамики
• Интеграция машинного обучения
• Эволюционные вычисления
• Систематическое исследование пространства параметров модели
• Проверка спецификации модели
• Тиражирование моделей
• Проверка моделей
• Подключение ABM к физическим устройствам
• Датчики и двигатели
• Объединение людей и виртуальных агентов
• Совместное моделирование

КЛАССЫ:

• В этом классе нет экзаменов
• 20% Участие
• 30% Домашнее задание
• 50% Окончательный проект

ЦЕЛИ КУРСА ДЛЯ СТУДЕНТОВ:

По окончании этого курса студент должен уметь:

• Определение основных механизмов новых агентных моделей
• Определение компромиссов при разработке и использовании топологий агентов
• Создание оригинальных многоагентных моделей
• Использование инструментов анализа поведения и анализа для анализа пространства параметров модели
• Проверка и проверка моделей на основе агентов
• Применяйте агентное моделирование как к научным, так и к повседневным явлениям

.