Двухфакторные производственные функции. Производственная функция Кобба-Дугласа. Предельная норма замены труда капиталом
Лабораторная работа N1. Двухфакторные производственные функции. Часть 1. Производственная функция Кобба-Дугласа.
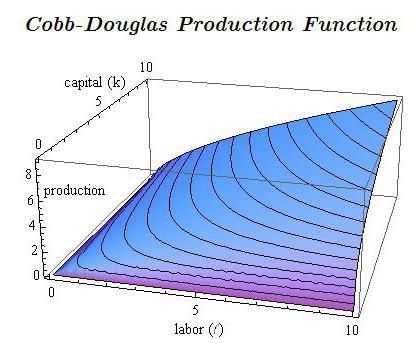
Производственная функция (ПФ) описывает зависимость объема выпускаемой продукции от затрачиваемых или используемых ресурсов. В данной лабораторной работе мы будем рассматривать двухфакторную производственную функцию Кобба-Дугласа, описывающую зависимость выпуска продукции Q от вложенного капитала K и затраченного труда L в следующем виде
(1), где A, a, b — положительные параметры; a < 1, b < 1, величина A зависит от выбранных единиц измерения и эффективности производственного процесса.
График
ПФ двух переменных, очевидно, представляет собой поверхность в трехмерном
пространстве. Линия уровня ПФ, т.е. линия, в каждой точке которой объем выпуска
при разных значениях K, L один и тот
же, называется изоквантой или кривой безразличия производства. Изокванты не
пересекаются, причем большему объему производства отвечают изокванты, более
удаленные от начала координат.
линия, в каждой точке которой объем выпуска
при разных значениях K, L один и тот
же, называется изоквантой или кривой безразличия производства. Изокванты не
пересекаются, причем большему объему производства отвечают изокванты, более
удаленные от начала координат.
При исследовании свойств ПФ используются предельные величины. Предельным продуктом капитала (труда) называется частная производная ПФ по переменной K (L) соответственно:
. (2)
Легко показать, что предельные продукты капитала и труда для ПФ Кобба-Дугласа равны:
. (3)
Еще одной важной характеристикой ПФ является предельная норма замены труда капиталом, определяемая отношением соответствующих предельных продуктов и для функции Кобба-Дугласа имеющая вид:
. (4)
Задание к лабораторной работе
1. $C$30).
Используя маркер автозаполнения скопируйте данную формулу в диапазон B2:Z26.
$C$30).
Используя маркер автозаполнения скопируйте данную формулу в диапазон B2:Z26.
На основании расчетных значений ПФ Кобба-Дугласа постройте график (Вставка – Диаграмма, выберите тип Поверхность, в списке вид укажите стандартную поверхность. В следующем окне диалога на вкладке Диапазон данных выберите Ряды в столбцах, в поле Диапазон введите A1:Z26).
После построения поверхности вы можете менять ее ориентацию в пространстве. Для этого выделите диаграмму, выполните команду Диаграмма – объемный вид и в диалоговом окне Формат трехмерной проекции найдите и используйте кнопки, осуществляющие поворот диаграммы.
2. Построение изоквант функции Кобба – Дугласа
Скопируйте полученную диаграмму в область по соседству с областью исходной диаграммы (при этом должна быть нажата клавиша Ctrl). Выделите дочернюю диаграмму и выполните последовательность действий
 Далее для типа Поверхностная выберите вид Контурная диаграмма.
Полученные в результате кривые представляют изокванты ПФ. При желании вы можете
изменить расстояние по вертикали (шаг по z) между секущими
плоскостями. Для этого щелкните два раза по области легенды и в появившемся
окне диалога на вкладке Шкала установите новую цену основных и
промежуточных делений (соответствующий флажок должен быть убран). Озаглавьте
рабочий лист (например, Функция Кобба-Дугласа). Измените значения параметров a, b и понаблюдайте за
изменениями расчетных графиков. Сумма данных постоянных может быть как равна
единице, так и быть меньше или больше единицы.
Далее для типа Поверхностная выберите вид Контурная диаграмма.
Полученные в результате кривые представляют изокванты ПФ. При желании вы можете
изменить расстояние по вертикали (шаг по z) между секущими
плоскостями. Для этого щелкните два раза по области легенды и в появившемся
окне диалога на вкладке Шкала установите новую цену основных и
промежуточных делений (соответствующий флажок должен быть убран). Озаглавьте
рабочий лист (например, Функция Кобба-Дугласа). Измените значения параметров a, b и понаблюдайте за
изменениями расчетных графиков. Сумма данных постоянных может быть как равна
единице, так и быть меньше или больше единицы. 3. Построение поверхностей предельного продукта капитала и труда
Расчет данных функций будем проводить по формулам (3). Вначале рассчитаем предельный продукт капитала.
Скопируйте
рабочий лист с рассчитанной функцией Кобба-Дугласа. Для этого достаточно
щелкнуть правой кнопкой мыши на ярлычке рабочего листа, выбрать в контекстном
меню опцию переместить/скопировать и установить флажок создавать
копию. $C$30)/B$1 и провести копирование в диапазон B2:Z26. Постройте диаграмму.
$C$30)/B$1 и провести копирование в диапазон B2:Z26. Постройте диаграмму.
4. Построение поверхности предельной нормы замены труда капиталом.
Постройте расчетную сетку точек аналогично предыдущим случаям. В ячейки A30 и B30 введите значения параметров a, b (в нашем случае 0,3 и 0,7). В ячейку B2 введите формулу = ($B$30/$A$30)*($A2/B$1) и скопируйте формулу в диапазон ячеек B2:Z26. Постройте диаграмму.
Алешин Толбей. Математические модели в экономике pdfauthor=Ярославский государственный университет имени П.Г.Демидова
%PDF-1.6 % 946 0 obj > endobj 948 0 obj >stream application/pdf
 40.18FalseThis is MiKTeX-pdfTeX 2.9.6499 (1.40.18)uuid:17f568dc-7d45-420a-8858-4df9b2e8f503uuid:5d4825b2-d7e6-4652-a40d-7dff50fd237a
endstream
endobj
945 0 obj
>
endobj
2 0 obj
>
endobj
871 0 obj
>
endobj
869 0 obj
>
endobj
870 0 obj
>
endobj
485 0 obj
>
endobj
540 0 obj
>
endobj
606 0 obj
>
endobj
673 0 obj
>
endobj
734 0 obj
>
endobj
780 0 obj
>
endobj
776 0 obj
>
endobj
782 0 obj
>
endobj
783 0 obj
>stream
xڍU0+\ZG!m$@r ԃXx-KpHw|r{ƼD YBh jK!}Pb_ v[_FivP^vҐ%{(Qh\p&sFv(=DBWg9Q`חx)QGV\?/ RkLSd`kjܘpŖ)
40.18FalseThis is MiKTeX-pdfTeX 2.9.6499 (1.40.18)uuid:17f568dc-7d45-420a-8858-4df9b2e8f503uuid:5d4825b2-d7e6-4652-a40d-7dff50fd237a
endstream
endobj
945 0 obj
>
endobj
2 0 obj
>
endobj
871 0 obj
>
endobj
869 0 obj
>
endobj
870 0 obj
>
endobj
485 0 obj
>
endobj
540 0 obj
>
endobj
606 0 obj
>
endobj
673 0 obj
>
endobj
734 0 obj
>
endobj
780 0 obj
>
endobj
776 0 obj
>
endobj
782 0 obj
>
endobj
783 0 obj
>stream
xڍU0+\ZG!m$@r ԃXx-KpHw|r{ƼD YBh jK!}Pb_ v[_FivP^vҐ%{(Qh\p&sFv(=DBWg9Q`חx)QGV\?/ RkLSd`kjܘpŖ) Как была получена функция Кобба-Дугласа?
В экономике и эконометрике производственная функция Кобба-Дугласа — это особая функциональная форма производственной функции, широко используемая для представления технологической взаимосвязи между количеством двух или более затрат (особенно физического капитала и труда) и объемом выпуска, который может производиться этими входами. {1-a}$? Как мы это получаем$K$ должен быть повышен до некоторого коэффициента «$a$»и это нужно умножить на $L$ повышен некоторым фактором «$1-a$«? Какое доказательство этой формулы? Я не могу найти ответ на этот вопрос, я много ищу.
{1-a}$? Как мы это получаем$K$ должен быть повышен до некоторого коэффициента «$a$»и это нужно умножить на $L$ повышен некоторым фактором «$1-a$«? Какое доказательство этой формулы? Я не могу найти ответ на этот вопрос, я много ищу.
Обновить. Я нашел статью, в которой показано, как это сделать, но я не понимаю некоторых шагов. Может ли кто-нибудь мне помочь? Вот ссылка:
https://www.studocu.com/en-gb/document/kings-college-london/mathemtics-for-economists/lecture-notes/cobb-douglas-revision/4229598/view
В этих терминах предположения, сделанные Коббом и Дугласом, можно сформулировать следующим образом:
- Если исчезнут труд или капитал, исчезнет и производство.
- Предельная производительность труда пропорциональна количеству продукции на единицу труда.
- Предельная производительность капитала пропорциональна количеству продукции на единицу капитала.
Решение. Поскольку производство на единицу труда равно$\frac{P}L$ предположение 2 говорит, что:
$$\frac{∂P}{∂L} = α\frac{P}L $$
для некоторой постоянной α. α$$ где $C_1(K_0)$ — постоянная интегрирования, и мы запишем ее как функцию $K_0$ поскольку это может зависеть от стоимости $K_0$.
α$$ где $C_1(K_0)$ — постоянная интегрирования, и мы запишем ее как функцию $K_0$ поскольку это может зависеть от стоимости $K_0$.
3.4. Виробнича функція Кобба—Дугласа
Перше формалізоване подання. Серед субституційних функцій виробництва з частковою заміщеністю ресурсів широко відома функція Кобба—Дугласа, названа так по іменах професорів Чиказького університету.Економіст Поль Дуглас зібрав статистичні дані за період 1899—1922 рр. щодо обробної промисловості США й у 1927 р. звернувся до математика Чарльза Кобба з проханням формалізувати за допомогою математичної моделі виявлені закономірності впливу праці та капіталу на випуск продукції.
У 1928 р. ними було запропоновано степеневу виробничу функцію такого вигляду:
де Q — обчислений або очікуваний індекс виробництва продукції обробної промисловості за деякий характерний інтервал часу;
L — індекс зайнятості в обробній промисловості;
K — індекс постійного капіталу;
A, α — позитивне постійне число, що характеризує технологію виробництва.
Використовуючи статистичні дані за зазначений період, Ч. Кобб і П. Дуглас одержали таку виробничу функцію для обробної промисловості США [21, с. 4, 33, 35 та ін.]:
Тут R2 — коефіцієнт множинної детермінації, що показує, яка частина змін залежної змінної (у даному випадку — Q) обумовлена змінами незалежних змінних (L, K). Його значення говорить про те, що зміни Q на 94 % обумовлені змінами L і K. Зауважимо, що значення показників ступеня за незалежних змінних у сумі дорівнює одиниці.Щоб оцінити внесок кожного фактора в кінцевий продукт, Ч. Кобб і П. Дуглас за допомогою диференціального числення, використовуючи часткові похідні, розрахували граничний продукт праці та капіталу:
Отже, у функції (3.15), отриманій Коббом і Дугласом, збільшення обсягу трудовитрат на 1 % веде до збільшення випуску на 0,75 %, а збільшення капіталу на 1 % збільшує випуск на 0,25 %. Оскільки значення EQ,L та EQ,K менше одиниці, випуск продукції відносно нееластичний і за працею, і за капіталом.
Поширення та модифікації. Після опублікування основної праці Ч. Кобба і П. Дугласа численними дослідниками були отримані виробничі функції аналогічного типу для різних видів виробництв, секторів економіки, географічних районів США і навіть для різних країн (табл. 3.3).
Оцінки виробничих функцій, наведені в табл. 3.3, отримано на основі узагальнення емпіричних даних з використанням функції Кобба—Дугласа такого вигляду:
У другій половині XX ст. степеневі функції почали застосовувати не тільки для аналізу виробничих процесів із відчутними результатами, а й для аналізу різних явищ суспільно-політичного життя. Так, у 1975 р. було розроблено степеневу виробничу функцію для поліції Лос-Анджелеса, що пов’язує кількість арештів за кримінальні злочини з такими змінними факторами, як кількість груп поліцейських-мотоциклістів, кількість поліцейських усередині помешкань, кількість осіб, які недавно звільнені і проживають у місті тощо [24, с. 366].
Виробничу функцію Кобба—Дугласа типу (3. 13) часто подають у логарифмічному вигляді:
13) часто подають у логарифмічному вигляді:
lgY=lgA+algL+(1-a)lgK
У СРСР Б. М. Михайлевським і Ю. П. Соловйовим на основі опрацювання статистичних даних за 1951—1963 рр. по народному господарству в цілому було отримано таку виробничу функцію [21, с. 456]:
lgYt=-0.524+1.11(0.541lgLt+0.334lgKt+0.1251lgRt+0.00518
де Yt — отриманий національний дохід;
Lt — кількість відпрацьованих людино-годин;
Kt — вартість капітальних благ;Rt — оцінка сільськогосподарських земель;
t — рік.
Приклади виробничих функцій розглянутого типу, отриманих для галузей, видів виробництв, підприємств, можна продовжити. Дослідниками було встановлено, що сума коефіцієнтів при змінних може дорівнювати одиниці, але може бути і більше, і менше одиниці; еластичність випуску за змінними факторами була пов’язана з еластичністю масштабу; для багатьох виробництв були визначені мінімально ефективні розміри випуску і т. д. Нами розглядатимуться ці питання в наступних темах.
На теперішній час підходи П. Дугласа і Ч. Кобба розвиваються за такими напрямами:
Дугласа і Ч. Кобба розвиваються за такими напрямами:
урахування невизначеності;
урахування лагів запізнення випуску стосовно часу здійснення витрат;
повніше відображення технічного прогресу та якості праці;
поєднання кореляційного (кількісного) аналізу з дисперсійним (якісним) для повнішого врахування впливу факторів на ефективність виробництва тощо [21, с. 458, 459].
Ключові положення
Ізокванта — геометричне місце точок у просторі факторів виробництва, для яких характерний однаковий обсяг випуску продукції.
Ізоквантна варіація показує, як можна комбінувати фактори виробництва, щоб забезпечити визначений обсяг випуску продукції.
Ізокванти можуть бути побудовані на основі даних виробничої сітки або шляхом розрізу “пагорба випуску” горизонтальною площиною, рівнобіжною площині факторів виробництва OKL (див. рис. 1.2).
Сукупність ізоквант, кожна з яких відбиває максимально можливий випуск за різних комбінацій факторів виробництва, називається картою ізоквант.
Ізокванти мають такі властивості: вони не перетинаються, опуклі до початку координат; мають негативний нахил; чим далі розміщені від початку координат, тим більший обсяг випуску характеризують.
Виробничі фактори мають властивості заміщеності і доповнюваності. Показником заміщення виступає MRTS — гранична норма технологічного заміщення одного фактора іншим — та кількість ресурсу і-го виду, що може бути вивільнена в обмін на збільшення застосування ресурсу j-го виду на одиницю так, щоб загальний обсяг продукції залишився незмінним. Кількісні значення MRTS варіюють від 0 (відсутність взаємозамінності факторів) до ∞ (абсолютна, ідеальна взаємозамінність факторів).
Доповнюваність факторів вимірюють коефіцієнтом доповнюваності, що його кількісні значення, як і MRTS, варіюють від 0 до ∞. При цьому зі збільшенням доповнюваності рівень заміщеності знижується, і навпаки.
Ізокванти можуть мати різну конфігурацію, яка визначається особливостями технологічного процесу і, насамперед, ступенем заміщеності та доповнюваності виробничих факторів. У мікроекономічній теорії виробництва найчастіше фігурують лінійна і неперервна ізокванти.
У мікроекономічній теорії виробництва найчастіше фігурують лінійна і неперервна ізокванти.
Геометричне місце точок у просторі факторів виробництва, для яких характерний однаковий розмір граничної норми технічного заміщення між факторами, називається ізокліной. Ізокліни можуть бути як прямими, так і кривими, як з позитивним, так і з негативним нахилом до осі абсцис.
Ізокліни у вигляді променів, що виходять із початку координат, характеризують для однорідних виробничих функцій технічно можливі шляхи збільшення обсягів випуску продукції, тобто переходу з нижчої ізокванти на вищу.
Виробнича функція Кобба—Дугласа зв’язує випуск (або іншій кінцевий результат) із розміром виробничих факторів у вигляді добутку обсягів застосування факторів із визначеними степеневими коефіцієнтами. Дослідження показали, що багато явищ виробничого і соціального життя суспільства досить добре апроксимуются залежностями такого типу.
Дослідження показали, що багато явищ виробничого і соціального життя суспільства досить добре апроксимуются залежностями такого типу.
Кобб obb — Справочник химика 21
Функция Кобба-Дугласа устанавливает предельную норму замещения труда капиталом в размере [c.557]Для промышленного производства наиболее важной характеристикой эмульсии является ее устойчивость. Основные требования к эмульгаторам сформулированы Коббом (1946). Эмульгаторы должны 1) уменьшать поверхностное натяжение до 5 дин/см для эмульсий, которые приготавливают перемешиванием, и до 0,5 дин/см для эмульсий, не требующих интенсивного перемешивания 2) достаточно [c.19]
Скорость пропитки приведена для различных ее стадий, характеризующихся глубиной проникновения жидкости в толщу бумаги и выражаемой в процентах от полного поглощения. Обращает на себя внимание, что наиболее эффективно использование интенсификатора И1 для ускорения пропитки бумаги-основы водным раствором нитрита натрия, который определяет скорость пропитки бумаги-основы водным раствором ингибитора УНИ при низкой впитывающей способности бумаги-основы (15—30 г/м по Коббу).

Для иллюстрации возьмем производственную функцию Кобба-Дугласа в ее простом статическом варианте [c.556]
Расчет /Св по формализму, вытекающему из функции Кобба-Дугласа, затруднен неустойчивостью параметра п. Все же, более или менее достоверным представляется значение 0,2583. Если принять его, то по формуле (13.37) получается [c.562]
Д. Коббом и X. Винтером. Отличие ее от установки последнего из названных авторов состоит в применении термостата для поддержания постоянной температуры холодных спаев термопары и использования вместо гальванометра со [c.59]
Д. Коббом и X. Винтером. Особенно это касается кривых нагревания, полученных последним из них. [c.59]
Казалось бы, оба способа симметричны, и поэтому при неизменных условиях способ растворения в воде будет давать эмульсии М/В, в способ растворения в масле — эмульсии В/М. Это справедливо, если условия действительно неизменны, а число ГЛБ эмульгаторов одинаково. Обычно эмульсии М/В требуются чаще. Было найдено (Кобб, 1946), что в большинстве случаев способ растворения в масле дает лучшие эмульсии, чем способ растворения в воде, причем капли оказываются достаточно малыми и одинаковыми по размеру. [c.21]
Обычно эмульсии М/В требуются чаще. Было найдено (Кобб, 1946), что в большинстве случаев способ растворения в масле дает лучшие эмульсии, чем способ растворения в воде, причем капли оказываются достаточно малыми и одинаковыми по размеру. [c.21]
Холлингс и Кобб нагревали в трубке до 800° смесь водорода и метана. При этой температуре в течение минуты разлагалось только 2% метана. При 1 100° к концу 47-й секунды разложение достигало уже 65%. Опыты проведенные Уайтекером и Александером прп 1400°, вполне подтвердили предыдущие результаты, [c.236]
Приведем вкратце наиболее интересные работы по этому вопросу, а, именно Бона. Т1 Коварда, Холлингса и Кобба, В. Гарднера. [c.238]
Бон и Ковар д, работа которых была затем подтверждена Холлингсом и Коббом, заставляли этан циркулировать в трубке, нагретой до 675°. [c.238]
Дефтон и Кобб= пропускали пары бензина или толуола в присутствии азота или водорода через кокс, помещенный в нагреваемую электричеством трубку. [c.344]
[c.344]
Саундерс [298 а] не смогли повторить синтеза, Коббу [297 а] также не удалось выделить лактон. Описанный Саксом [299] лактон, полученный им обработкой трифенилкарбинол-о-сульфометил-амида соляной или серной кислотой, в действительности представляет собой производное сахарина [297 б]. [c.394]
Впитываемость водного раствора ингибитора системой макрокапилляров может быть охарактеризована показателем впитьшаемости по Коббу, впитываемость микрокапиллярами клеточной стенки волокна — только по сорбционной способности волокна по отношению к конкретному ингибитору. Высокая впитываемость по Коббу в условиях интенсивной сушки не является достаточным условием, предотвращающим появление налета солей ингибитора на поверхности бумаги. Это становится очевидным, если рассмотреть процесс появления налета ингибитора на поверхности бумаги с позиции тепло-и массообмена в процессе сушки. В сушку поступает бумага с ка-пиллярноудержанной влагой, и период постоянной скорости сушки заключается в выходе воды из макрокапилляров и ее испарении на поверхности бумаги.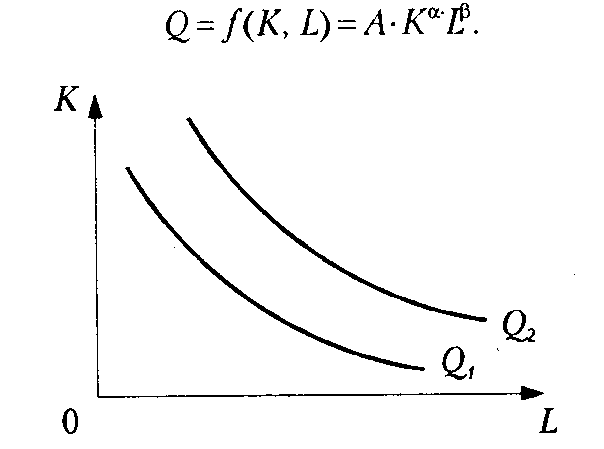 Это происходит до тех пор, пока влажность на поверхности бумаги выше гигроскопической. [c.155]
Это происходит до тех пор, пока влажность на поверхности бумаги выше гигроскопической. [c.155]
Формулы удовлетворительно согласуются с опытными данными Бевиера [770] и Кобба [794]. [c.128]
Возможность химического взаимодействия твердых веществ друг с другом была впервые выявлена в России в работах П. П. Аносова, Н. Н. Бекетова и Д. И. Чернова — известных русских ученых-металловедов. После работ Ф. М. Флавицкого (1902— 1907), Д. Кобба (1909) и И. Хедвала (1911—1914) было начато систематическое исследование механизма твердофазовых реакций и условий их протекания. Наиболее масштабные и результативные исследования, выполненные в 20-е и 30-е годы, принадлежат И. Хедвалу, Г. Тамману и К. Вагнеру, усилиями которых был заложен тот научный фундамент, на котором в основном базируется современное учение о твердофазовом взаимодействии. [c.290]
Наиболее значительными среди ранних работ являются исследования Адамса и Кобба [5], а также Джадда [38]. Однако только в последние годы возникла более ясная картина. Особый интерес представляют исследования Канэко [357], Такасаки [649] и Сем-мельрофа [597, 598]. [c.324]
Однако только в последние годы возникла более ясная картина. Особый интерес представляют исследования Канэко [357], Такасаки [649] и Сем-мельрофа [597, 598]. [c.324]
Пытаясь описать свои экспериментальные результаты, Канэко вывел формулу для показателя светлоты, основанную на формуле Адамса и Кобба [5] и модифицированную Джаддом [325]. Формула Канэко объединяет два уравнения [c.325]
Но в этом ответственном пункте обнаруживается слабость производственной функции (13.33). Попытки определения параметра п на основе структурных и динамических рядов У, К, L выявили неустойчивость его значений на одном и том же статистическом материале. У разных авторов величина и меняется от 0,15 до 0,75. Это обусловлено не столько дефектами информационного обеспечения, сколько концептуальной неадекватностью форм взаимосвязи У с Ки L, постулируемых структурой производственной функции (13.33). Практическая ненадежность оценок функции Кобба-Дугласа и других ( ES, функций Солоу, Сато) определяется нереальностью лежащих в их основе гипотез [c. 557]
557]
Фактически этот процесс базируется на устойчивой закономерности в соотнощении капитальных затрат на автоматизацию и обусловленного ею прироста капиталовооруженности труда. Поэтому полезно сравнить оценки необходимых инвестиций в высвобождение одного работника по функции Кобба-Дугласа и по фактически наблюдаемым отногиениям. [c.557]
Несмотря на то, что термография как метод физикохимического анализа использовалась при исследованиях еще в XIX в., для изучения термической деструкции твердых топлив она впервые применена в 1914 г. Голлингсом и Д. Коббом [51—53]. [c.52]
Несколько позже (1926 г.) были опубликованы результаты термографического исследования углей, проведенные X. Винтером [60]. Хотя в сущности им был использован метод X. Гол-лингса и Д. Кобба, условия проведения опытов несколько отличались от предыдущих. Общий вид установки по Винтеру представлен на рис. 36. Для исследования применяли уголь в виде брикетов массой 10—15 г. [c.55]
[c.55]
В общем, оценивая достоинство экспериментов X. Гол-лингса, Д. Кобба и X. Винтера, следует отметить, что несмотря на несовершенство методик их проведения и са- [c.57]
Реакция между свободной кремнекислотой и карбонатом кальция впервые была тщательно изучена Коб-вом , особенно в случае взаимодействия при нагревании осажденного карбоната кальция с кварцем при атмосферном [давлении. Взаимодействие начинается в твердой фазе при температуре около 800 С, которая немного ииже температуры диссоциации карбоната, независимо от количественных соотнощений компонентов. После нагревания в течение нескольких часов карбонат уже не обнаруживается. Если в смеси имеется избыток извести, то, согласно Коббу, в результате образуется двукальциевый силикат но если имеется избыток кремнезема, то возникает метасиликат кальция. [c.586]
Кобб (см. С. I, 94) наблюдал, что реакция в твердых смесях, состоящих из кварца и карбоната кальция , протекает с заметной скоростью при. температурах около 700—i800° Яндер подтвердил это. Процесс взаимодействия карбоната бария с кремнеземом также подтвердился опытами Таммана и Кальсинга кремнезем обычно начинает вступать в реакцию при температуре около 750—775°С, когда в нем начинается процесс внутреннего обмена местами. Реакции между твердыми карбонатом кальция и кремнеземом начинаются примерно при той же температуре, как и реакция карбоната бария с кремнеземом, хотя давление диссоциации ВаСОз при этой температуре все еще остается намного ниже. [c.710]
температурах около 700—i800° Яндер подтвердил это. Процесс взаимодействия карбоната бария с кремнеземом также подтвердился опытами Таммана и Кальсинга кремнезем обычно начинает вступать в реакцию при температуре около 750—775°С, когда в нем начинается процесс внутреннего обмена местами. Реакции между твердыми карбонатом кальция и кремнеземом начинаются примерно при той же температуре, как и реакция карбоната бария с кремнеземом, хотя давление диссоциации ВаСОз при этой температуре все еще остается намного ниже. [c.710]
Физико-химические основы реакций в сырьевых смесях впервые рассматривались Энделлом при исследовании процесса спекания. Агломерация при спекании объяснялась образованием небольшого количества расплава в преобладающей кристаллической смеси клинкерных минералов . Для клинкеров типично сосуществование расплавленной фазы (которая при охлаждении превращается в стекловидную цементирующую массу) с включенными в нее кристаллами, так же, как в керамических изделиях муллит заюлючен в стеклофазе. При обжиге сырья и его превращении в клинкер образуются основные силикаты и алюминаты кальция. Эти реакции были впервые исследованы Коббом (см. О. I, 59) в системе окись кальция — кремнезем — двуокись угле рода. Наккен» также изучил реакции, предшествующие спеканию, и особенно подчеркнул увеличение реакционной способности за счет уменьшения размера зерен. [c.770]
При обжиге сырья и его превращении в клинкер образуются основные силикаты и алюминаты кальция. Эти реакции были впервые исследованы Коббом (см. О. I, 59) в системе окись кальция — кремнезем — двуокись угле рода. Наккен» также изучил реакции, предшествующие спеканию, и особенно подчеркнул увеличение реакционной способности за счет уменьшения размера зерен. [c.770]
Одна из таблиц форм соединений минеральных веществ угля, установленных на основании составных частей золы, была представлена Мерсоном и Коббом [6]. На эту таблицу часто ссылаются, и мы приводим ее здесь (см. табл. 1). [c.53]
Оригинальное устройство для пиролиза полимеров пред.пожили Г. Джиа-коббо и В. Симон [125]. Эти авторы наносили исследуемый образец полимера на ферромагнитную проволоку (0,5Х 20 мм) и в потоке газа-носителя пол ещали ее в стеклянный капилляр. Ферромагнитная проволока с помощью высокочастотной печн нагревалась в течение 2-10 с до точки Кюри.
 В течение всего процесса пиролиза температура ферромагнитной проволоки оставалась постоянной. При использовании различных ферромагнетиков можно изменять температуру пиролиза. [c.99]
В течение всего процесса пиролиза температура ферромагнитной проволоки оставалась постоянной. При использовании различных ферромагнетиков можно изменять температуру пиролиза. [c.99]Для импульсного пиролиза твердых образцов Стернберг и Литтл [18] применяли слаботочный высоковольтный разряд. Такой метод дает хорошо воспроизводимые результаты. Пирограмма полиэтилена, полученная этим методом, была совершенно аналогична той, которую получили Кобб и др. [24, 25] при помощи обычной ячейки с нагреваемой нитью. Пиролиз твердых и жидких образцов, под действием высоковольтного разряда проводили также Джонс и Моррис [19]. [c.79]
Сульфаты родия (III) могут реагировать с сульфатами щелочных металлов, давая соли типа квасцов MeRh(S04)2 пНзО. Такие соли были получены Бунзеном [28], Зейбертом и Коббе [29], Пичини и Марино [30] и др. Их готовят смешиванием растворов сернокислого родия(1И) и соответствующего сульфата. При концентрировании растворов выделяются кристаллы двойных солей. Вместо солей ро-дия(1П) применяют также растворы гидрата окиси родия(П1) в серной кислоте. [c.54]
Вместо солей ро-дия(1П) применяют также растворы гидрата окиси родия(П1) в серной кислоте. [c.54]
Исследовавшие это соединение Зейберт и Коббе [29] считали, что родий в нем двухвалентен и соединение отвечает формуле 4 RhSOs- [c.55]
Производственная функция Кобба-Дугласа контрольная по экономико-математическому моделированию
Кафедра «» по курсу «» 00 1EВыполнил: студент гр. БО Ковчегин И. А. Преподаватель: Москва 2016:49:042004-12-15T19:39:00Z Возникновение теории производственных функций принято относить к 1927 г., когда Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на F 06 1 процентов, а увеличение затрат труда на 1% приведет к росту выпуска на F 0 6 2 процентов. Можно предположить, что обе величины F 06 1 и F 0 6 2 находятся между нулем и единицей. Они должны быть положительными, так как увеличение затрат производственных факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, так как разумно предположить, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными. Если F 06 1 и F 0 6 2 в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства (y увеличивается в меньшей пропорции, чем К и L). В соответствии с допущением о конкурентности рынков факторов производства и F 06 2 имеют дальнейшую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда. Если рынок труда имеет конкурентный характер, то ставка заработной платы (w) будет равна предельному продукту труда (dy/dL): . Следовательно, общая сумма заработной платы (wL) будет равна F 06 2y, а доля труда в общем выпуске продукции (wL/Y) составит постоянную величину F 06 2. Аналогичным образом норма прибыли выражается через dy/dK: , и, следовательно, общая прибыль ( F 07 2К) будет равна F 0 6 1y, а доля прибыли будет постоянной величиной F 06 1.
Если F 06 1 и F 0 6 2 в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства (y увеличивается в меньшей пропорции, чем К и L). В соответствии с допущением о конкурентности рынков факторов производства и F 06 2 имеют дальнейшую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда. Если рынок труда имеет конкурентный характер, то ставка заработной платы (w) будет равна предельному продукту труда (dy/dL): . Следовательно, общая сумма заработной платы (wL) будет равна F 06 2y, а доля труда в общем выпуске продукции (wL/Y) составит постоянную величину F 06 2. Аналогичным образом норма прибыли выражается через dy/dK: , и, следовательно, общая прибыль ( F 07 2К) будет равна F 0 6 1y, а доля прибыли будет постоянной величиной F 06 1. Существует ряд проблем по применению такой функции, особенно в тех случаях, когда она используется для экономики в целом. В частности, даже в тех случаях, когда между выпуском продукции, производственным оборудованием и трудом в производственном процессе существует технологическая зависимость, то совершенно необязательно, что 0 0 1 Fподобная зависимость существует тогда, когда ука занные факторы комбинируются в масштабах экономики в целом. Во-вторых, даже если такая зависимость для экономики в целом существует, то нет никаких оснований считать, что она будет иметь простую форму. 5 При построении производственной функции Кобба–Дугласа параметры A, F 06 1, F 0 6 2 можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов (МНК): 1) Производственную функцию Кобба–Дугласа приводят к линейному виду путем логарифмирования 2) При применении МНК цель заключается в минимизации суммы квадратичных отклонений (SSD) между наблюдаемыми величинами ln(yi), (i=1…N; N – количество наблюдений) и соответствующими оценками .
Существует ряд проблем по применению такой функции, особенно в тех случаях, когда она используется для экономики в целом. В частности, даже в тех случаях, когда между выпуском продукции, производственным оборудованием и трудом в производственном процессе существует технологическая зависимость, то совершенно необязательно, что 0 0 1 Fподобная зависимость существует тогда, когда ука занные факторы комбинируются в масштабах экономики в целом. Во-вторых, даже если такая зависимость для экономики в целом существует, то нет никаких оснований считать, что она будет иметь простую форму. 5 При построении производственной функции Кобба–Дугласа параметры A, F 06 1, F 0 6 2 можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов (МНК): 1) Производственную функцию Кобба–Дугласа приводят к линейному виду путем логарифмирования 2) При применении МНК цель заключается в минимизации суммы квадратичных отклонений (SSD) между наблюдаемыми величинами ln(yi), (i=1…N; N – количество наблюдений) и соответствующими оценками . 3) Введем векторы ; ; ; и матрицу Тогда критерий можно записать в виде . Дифференцируя SSD по вектору Х и приравнивая производную к нулю систему уравнений МНК или . 4) Для оценки критерия значимости выборочных коэффициентов регрессии оценивают дисперсию выборочных коэффициентов , где cii – элементы главной диагонали матрицы . F 0 7 3 2 – дисперсия погрешности измерений. Оценка F 07 32 определяется по формуле Рассчитывается значение t – параметра 6 Если полученное значение t больше, чем табличное t F 0 6 1 при (N-3-1) степеней свободы, тогда Xi существенно отлично от нуля при уровне F 06 1. Доверительные границы для определяются по формуле Тогда вероятность того, что величина Xi действительно находится в этих пределах, составит 1– F 06 1. 5) Для оценки адекватности регрессивной модели наблюдаемым величинам объема выпуска y рассчитывается коэффициент множественной детерминации: , где . При малом объеме выборки используется скорректированный коэффициент множественной детерминации Чем меньше отличается от единицы, тем более обосновано решение о том, что выборочные коэффициенты регрессии могут быть полезны для изучения производственного процесса.
3) Введем векторы ; ; ; и матрицу Тогда критерий можно записать в виде . Дифференцируя SSD по вектору Х и приравнивая производную к нулю систему уравнений МНК или . 4) Для оценки критерия значимости выборочных коэффициентов регрессии оценивают дисперсию выборочных коэффициентов , где cii – элементы главной диагонали матрицы . F 0 7 3 2 – дисперсия погрешности измерений. Оценка F 07 32 определяется по формуле Рассчитывается значение t – параметра 6 Если полученное значение t больше, чем табличное t F 0 6 1 при (N-3-1) степеней свободы, тогда Xi существенно отлично от нуля при уровне F 06 1. Доверительные границы для определяются по формуле Тогда вероятность того, что величина Xi действительно находится в этих пределах, составит 1– F 06 1. 5) Для оценки адекватности регрессивной модели наблюдаемым величинам объема выпуска y рассчитывается коэффициент множественной детерминации: , где . При малом объеме выборки используется скорректированный коэффициент множественной детерминации Чем меньше отличается от единицы, тем более обосновано решение о том, что выборочные коэффициенты регрессии могут быть полезны для изучения производственного процесса. Мы имеем данные по ВВП Мексики за 20 лет (таблица 1) относительно рабочей силы (L) и капитала (K). Эти точки не будут лежать на 1 прямой, так как между экономическими величинами не существует строгой взаимосвязи, потому что на ВВП кроме рабочей силы и капитала могут влиять и другие факторы. Поэтому экономическая спецификация эконометрической модели имеет вид: , где K – число производственного капитала L – число производственных трудовых часов или, другими словами, число производственных единиц гуманного капитала Или в линейном виде: Таблица 1 Мексика, 1955-1974 гг. Реальный ВВП (миллионы песо, выраженные в песо 1960г.) Численность рабочих (тысяч человек) 7 где N – число наблюдений (20), P – число объясняющих переменных (2). Число степеней свободы (df) определяется следующим образом: для регрессии df=M–1=3–1=2, для остатка df=N–M=20–3=17, итоговый df=N–M=20–1=19, где M – число оцениваемых параметров регрессии, N – число наблюдений. Сумма квадратов отклонений определяется следующим образом.
Мы имеем данные по ВВП Мексики за 20 лет (таблица 1) относительно рабочей силы (L) и капитала (K). Эти точки не будут лежать на 1 прямой, так как между экономическими величинами не существует строгой взаимосвязи, потому что на ВВП кроме рабочей силы и капитала могут влиять и другие факторы. Поэтому экономическая спецификация эконометрической модели имеет вид: , где K – число производственного капитала L – число производственных трудовых часов или, другими словами, число производственных единиц гуманного капитала Или в линейном виде: Таблица 1 Мексика, 1955-1974 гг. Реальный ВВП (миллионы песо, выраженные в песо 1960г.) Численность рабочих (тысяч человек) 7 где N – число наблюдений (20), P – число объясняющих переменных (2). Число степеней свободы (df) определяется следующим образом: для регрессии df=M–1=3–1=2, для остатка df=N–M=20–3=17, итоговый df=N–M=20–1=19, где M – число оцениваемых параметров регрессии, N – число наблюдений. Сумма квадратов отклонений определяется следующим образом. Сумма квадратов, обусловленная регрессией (RSS): , где – условная (групповая) средняя переменной y Остаточная сумма квадратов, характеризующая влияние неучтенных факторов (ESS): . Общая сумма квадратов отклонений зависимой переменной от средней (TSS): . Средние квадраты (MS) представляют собой несмещенные оценки дисперсий зависимости переменной, обусловленных соответственно регрессией и воздействием неучтенных случайных факторов ошибок: F-критерий значимости уравнения регрессии определяется: F=1719,231 больше табличного значения критерия Фишера-Снедекора F0,05;2;17=3,59, то есть уравнение регрессии значимо, следовательно исследуемая зависимая переменная y очень близко описывается включенными в регрессионную модель переменными ln(K) и ln(L). 10 Стандартная ошибка – это оценка стандартного отклонения распределения коэффициента регрессии вокруг его истинного значения. t-статистика – оценка коэффициента, деленная на его стандартную ошибку. На основании полученных данных можно вывести функцию Кобба-Дугласа для вышеописанной ситуации: На основании полученной модели можно вывести производственную функцию Кобба- Дугласа путем экспонирования: Полученная модель может быть использована для прогнозирования будущих значений ВВП на основе известных или ожидаемых уровнях капитала и рабочей силы.
Сумма квадратов, обусловленная регрессией (RSS): , где – условная (групповая) средняя переменной y Остаточная сумма квадратов, характеризующая влияние неучтенных факторов (ESS): . Общая сумма квадратов отклонений зависимой переменной от средней (TSS): . Средние квадраты (MS) представляют собой несмещенные оценки дисперсий зависимости переменной, обусловленных соответственно регрессией и воздействием неучтенных случайных факторов ошибок: F-критерий значимости уравнения регрессии определяется: F=1719,231 больше табличного значения критерия Фишера-Снедекора F0,05;2;17=3,59, то есть уравнение регрессии значимо, следовательно исследуемая зависимая переменная y очень близко описывается включенными в регрессионную модель переменными ln(K) и ln(L). 10 Стандартная ошибка – это оценка стандартного отклонения распределения коэффициента регрессии вокруг его истинного значения. t-статистика – оценка коэффициента, деленная на его стандартную ошибку. На основании полученных данных можно вывести функцию Кобба-Дугласа для вышеописанной ситуации: На основании полученной модели можно вывести производственную функцию Кобба- Дугласа путем экспонирования: Полученная модель может быть использована для прогнозирования будущих значений ВВП на основе известных или ожидаемых уровнях капитала и рабочей силы. Наглядно полученная зависимость прироста ВВП от изменения рабочей силы (L) и капитала (K) изображен на рисунке 2 с помощью MathCAD 2000. 11 Рисунок . Зависимость прироста ВВП от изменения капитала (K) и рабочей силы (L) В полученной модели наблюдается возрастающий эффект от масштаба, так как сумма F 0 6 1 и F 0 6 2 превышает 1 (равна 1,185729). Это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции. Для примера определим объем ВВП в среднем при ожидаемом уровне капитала 50.000 млн. песо и уровне рабочей силы 15.000 тысяч человек. 12
Наглядно полученная зависимость прироста ВВП от изменения рабочей силы (L) и капитала (K) изображен на рисунке 2 с помощью MathCAD 2000. 11 Рисунок . Зависимость прироста ВВП от изменения капитала (K) и рабочей силы (L) В полученной модели наблюдается возрастающий эффект от масштаба, так как сумма F 0 6 1 и F 0 6 2 превышает 1 (равна 1,185729). Это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции. Для примера определим объем ВВП в среднем при ожидаемом уровне капитала 50.000 млн. песо и уровне рабочей силы 15.000 тысяч человек. 12
Производственная функция Кобба-Дугласа – обзор
2.1 Модель 3GR
Во многих источниках используется производственная функция Кобба-Дугласа для анализа взаимосвязи между потреблением энергии и экономическим ростом [14,16–18]. Производственная функция Кобба-Дугласа показала, что уровень производства объясняется капиталом, трудом и другими детерминантами экономического роста [19]. Хотя многие тесты причинно-следственной связи показывают, что причинно-следственная связь между экономическим ростом и потреблением энергии является двунаправленной [11,20,21]. Чтобы прояснить эту взаимосвязь, мы использовали модель 3GR, которая объясняет трехсторонние отношения между потреблением энергии, энергоемкостью и объемом производства, а также их парные корреляции с точки зрения темпов роста.
Чтобы прояснить эту взаимосвязь, мы использовали модель 3GR, которая объясняет трехсторонние отношения между потреблением энергии, энергоемкостью и объемом производства, а также их парные корреляции с точки зрения темпов роста.
Фундаментальная формула модели 3GR выводится из количественного определения энергоемкости (отношение энергии к валовому внутреннему продукту), представленного в виде уравнения. (1) [15].
(1)(GRECi+1)=(GREOi+1)(GREIi+1).
где, GREC GREO GREO I GREI I — темпы роста потребления энергии, экономический выпуск и энергоемкость в I и года соответственно; они безразмерны.
Темпы роста объема производства, потребления энергии, энергоемкости рассчитываются по уравнению. (2) [15],
(2)GRi=(xi−xi−1)/xi−1.
Где, x i – значение экономической продукции или потребления энергии или энергоемкости в i м году. GR i — скорость роста соответствующего значения, например, GREI , GREO и GREC .
GR i — скорость роста соответствующего значения, например, GREI , GREO и GREC .
Эквивалентное значение GREI , GREO и GREC в исследовательский период определяется по уравнению.(3) [15],
(3)EVGR=∏1n(GRj+1)n−1−1.
Где EV GR эквивалентно значению GREC , GREO и GREI ; они безразмерны. Субиндекс 1 относится к первому году (1996 г.) периода исследования. n – период исследования, равный восемнадцати годам.
На основании уравнения. (1) и некоторые гипотезы, уравнение. (4), уравнение (5) и уравнение (6) можно было получить. Согласно уравнению (3), можно рассчитать эквивалентное значение GREO в исследовательский период.И разумно предположить, что (1+ GREO i ) в уравнении. (1) равно эквивалентному значению GREO плюс один. Таким образом, существует линейная зависимость между GREC и GREI , а наклон линии определяется GREO , как показано в уравнении. (4) [15],
(4) [15],
(4)GRECi=k1GREIi+(k1-1)
Аналогичным образом можно рассчитать эквивалентное значение GREI и GREC в исследовательский период, уравнение.(5) и уравнение (6) можно было получить [15],
(5)GRECi=k2GREOi+(k2−1).
(6)GREOi=k3/(GREIi+1)−1.
На основании уравнения. (3), существует отношение множественного умножения, как уравнение. (7) показано [15],
(7)∏1i(GRECj+1)=∏1i(GREOj+1)×∏1i(GREIj+1).
Где k 1 , k 2 и k 3 — некоторые константы, равные эквивалентному значению GREO , GREI и GREC плюс один соответственно. Символ ‘∏’ означает умножение по одному.Чтобы проанализировать влияние каждого фактора на потребление энергии, эквивалентное значение потребления энергии определяется как уравнение. (8),
(8)EVEC=(EC1−EC0)+(EC2−EC0)2+⋯+(ECi−EC0)i+⋯+(ECn−EC0)nn
Где, EV EC представляет собой эквивалент годового потребления энергии; EC i – годовое потребление энергии в i ом году. Их единица измерения – тонны SCE .
Их единица измерения – тонны SCE .
Как объем производства, так и энергоемкость играют важную роль в потреблении энергии.Чтобы отразить их влияние на потребление энергии, формула. (9) и уравнение (10) введены,
(9)EVEC-EO=(EO1-EO0)×EI0+(EO2-EO0)×EI0+EI122+⋯+(EOi-EO0)×EI0+EI1+⋯+EIi-1ii+⋯+( EOn−EO0)×EI0+EI1+⋯+EIn−1nnn
(10)EVEC−EI=(EI1−EI0)×EO0+(EI2−EI0)×EO0+EO122+⋯+(EIi−EI0)×EO0+EO1+⋯ +EOi-1ii+⋯+(EIn-EI0)×EO0+EO1+⋯+EOn-1nnn
Где EV EC-EO и EV EC-EI эквивалентно значению потребление энергии, вызванное эффектом EO и эффектом EI (сокращенные термины в разделе 3.4.1) соответственно. Их единица измерения – тонны SCE. EO i – годовой объем производства в i th году. Его единица $. EI i – годовая энергоемкость в i ом году. Его единицей являются тонны SCE за доллар.
Кроме того, взаимосвязь между эффектом EO и эффектом EI также повлияет на общее потребление энергии. Это интерактивное влияние на потребление энергии является неизвестной функцией, поэтому тождество выводится как уравнение.(11) показывает. где -EI ) — неизвестная функция, которая представляет собой интерактивное влияние на потребление энергии. EV EC-EO , EV , EV-EI, и F ( EV EC-EO , EV EC-EI ) быть положительным или отрицательным, EV EC является продуктом их действия, взаимоотменяющего друг друга.Чтобы напрямую сравнить эффект EO и эффект EI на потребление энергии, их абсолютная доля в потреблении энергии рассчитывается по уравнению. (12), уравнение (13) и уравнение (14),
(12)P(EVEC-EO)=|EVEC-EO||EVEC-EO|+|EVEC-EI|+|f(EVEC-EO,EVEC-EI)|×100%
(13)P(EVEC-EI)=|EVEC-EI||EVEC-EO|+|EVEC-EI|+|f(EVEC-EO,EVEC-EI)|×100%
(14)P(f (EVEC-EO,EVEC-EI))=|f(EVEC-EO,EVEC-EI)||EVEC-EO|+|EVEC-EI|+|f(EVEC-EO,EVEC-EI)|×100%
Где, P ( EV EC-EO ), P ( EV EC-EI ) и P ( F ( EV EC -EO , EV EC-EI )) — абсолютная доля эффекта EO , эффекта EI и их интерактивного эффекта в энергопотреблении соответственно; их единицей является %. | EV EC-EO |, | EV EC-EI | и | f ( EV EC-EO , EV EC-EI )| Абсолютное значение EV EC-EO , EV EV-EI и F ( EV EC-EO , EV EC-EI ), их единица измерения — тонны SCE .
| EV EC-EO |, | EV EC-EI | и | f ( EV EC-EO , EV EC-EI )| Абсолютное значение EV EC-EO , EV EV-EI и F ( EV EC-EO , EV EC-EI ), их единица измерения — тонны SCE .
Производственная функция Кобба-Дугласа – обзор
8.2.2 Технологии в МС
МС используют смесь эндогенных и экзогенных подходов к представлению технологий и включают технологии в ряд моделей, составляющих человеческое развитие, социально-экономические изменения и группировки биофизических проблем в IF, а не рассматривать их как дискретную и отдельную модель.
В модели здравоохранения технология влияет на смертность через экзогенную спецификацию, связанную со временем, основанную на работе и параметризации, выполненной Всемирной организацией здравоохранения (см. Раздел 5.2.4.2). МС не представляют собой технологические изменения в образовании, где они могут повлиять на затраты на одного учащегося и/или качество результатов. Тем не менее, МФ построили общий индекс развития общества знаний, который опирается на пять вспомогательных индексов, которые в совокупности реагируют на грамотность, высшее образование, НИОКР, распространение ИКТ (для которых МФ также рассчитывает индекс) и международную экономическую интеграцию. .
Раздел 5.2.4.2). МС не представляют собой технологические изменения в образовании, где они могут повлиять на затраты на одного учащегося и/или качество результатов. Тем не менее, МФ построили общий индекс развития общества знаний, который опирается на пять вспомогательных индексов, которые в совокупности реагируют на грамотность, высшее образование, НИОКР, распространение ИКТ (для которых МФ также рассчитывает индекс) и международную экономическую интеграцию. .
В экономической модели представление технологии (в более общем смысле, многофакторной производительности или МФП) обширно и сложно (см. раздел 6.1.4.1). Он начинается с основной спецификации прогресса в зависимости от времени в ведущей стране мира и конвергенции других стран на основе ВВП на душу населения по паритету покупательной способности. Множественные факторы в категориях человеческого, социального, физического капитала и капитала знаний вызывают аддитивные или вычитающие корректировки основных ставок. Конечным продуктом является чистое годовое изменение MFP, отражающее то, что Джиллингем и др. (2007, стр. 8) характеризуют как неоклассический подход роста к эндогенной производительности.
(2007, стр. 8) характеризуют как неоклассический подход роста к эндогенной производительности.
Подход MFP, однако, применяется только к четырем из шести экономических секторов в IF, а именно к тем, в которых производственные функции Кобба-Дугласа непосредственно определяют добавленную стоимость в денежном выражении от капитала, труда и производительности (четыре – это сырье, производство, услуги и информационно-коммуникационные технологии). Два других сектора, сельское хозяйство и энергетика, являются физическими моделями в IF, в которых повышение производительности влияет на соответствующие физические переменные производства до того, как они будут преобразованы в валюту и включены в более широкую экономическую модель.В сельском хозяйстве цены на сельскохозяйственные культуры вызывают связанные с производительностью изменения базовых темпов роста урожайности, в противном случае зависящих от времени (первоначально привязанных к историческим закономерностям), при условии также допущения о насыщении и экзогенных сценариях. В энергетике цены аналогичным образом изменяют скорость изменения физической производительности основного капитала в зависимости от типа энергии, которая имеет первоначальную основу в исторических закономерностях, но со временем модифицируется как снижением производительности с истощением ископаемых ресурсов, так и экзогенными предположениями относительно технического прогресса.Что касается спроса, то повышение энергоэффективности имеет основные экзогенные, зависящие от времени характеристики, которые также подвержены изменениям, вызванным ценой.
В энергетике цены аналогичным образом изменяют скорость изменения физической производительности основного капитала в зависимости от типа энергии, которая имеет первоначальную основу в исторических закономерностях, но со временем модифицируется как снижением производительности с истощением ископаемых ресурсов, так и экзогенными предположениями относительно технического прогресса.Что касается спроса, то повышение энергоэффективности имеет основные экзогенные, зависящие от времени характеристики, которые также подвержены изменениям, вызванным ценой.
В водной модели экзогенные параметры могут управлять эффективностью каждой категории спроса. Они дополняют изменяющуюся интенсивность водопользования в тех же категориях с ценой.
На основе сценария пользователи модели могут вносить экзогенные изменения в технологический прогресс в различных представлениях в IF. Например, можно параметрически представить длинные волны экономического прогресса Кондратьева (Кондратьев, 1926).Сценарии могут в более общем плане представлять прерывистые и разрушительные стороны технологии. В исследованиях с IF, посвященных возможности очень быстрого и значительного продления жизни (Hughes et al., 2015), а также экономическим выгодам и рискам кибертехнологий и их уязвимости (Hughes et al., 2016; Zurich Insurance Group, 2015), в рамках проекта были предприняты некоторые важные шаги по изучению последствий технологических разрывов.
В исследованиях с IF, посвященных возможности очень быстрого и значительного продления жизни (Hughes et al., 2015), а также экономическим выгодам и рискам кибертехнологий и их уязвимости (Hughes et al., 2016; Zurich Insurance Group, 2015), в рамках проекта были предприняты некоторые важные шаги по изучению последствий технологических разрывов.
Что касается последнего, то в этом столетии весьма вероятно крупномасштабное разрушительное воздействие искусственного интеллекта (ИИ) и робототехники, что указывает на необходимость дальнейшего расширения горизонтов проекта.С этой целью команда IFs приступила к количественной оценке и представлению возможного прогресса ИИ в вариациях от узких (например, Siri, Alexa и другие ранние персональные помощники) до общих (приложения, использующие рассуждение и творчество) и сверхразума (интеллектуальные способности, бросающие вызов или превосходящие другие). у человека) (см. Scott et al., 2017). Даже если подрыв ИИ проявится только в абсолютно положительном видении Шумпетера (1942) творческого разрушения существующих экономических и социальных моделей, он повлияет на огромное количество рабочих мест и жизней во время перехода. Например, Winick (2018) обобщил 18 различных оценок воздействия автоматизации на рабочую силу. Среди них особенно часто цитируется отчет McKinsey (Manyika et al., 2017), в котором оценивается, что к 2030 году во всем мире можно будет автоматизировать 400–800 миллионов рабочих мест. Сила такой автоматизации может работать синергетически с появлением крупных сетевых эффектов, которые поддерживать рост и олигопольную или даже монополистическую власть огромных новых технологических компаний. Среди возможных взаимосвязанных последствий — увеличение доли ВВП, приходящейся на компании по сравнению с работниками, замедление роста заработной платы и либо опустошение рынка труда по мере автоматизации средних навыков, либо более масштабная потеря рабочих мест ниже самых высококвалифицированных. уровень.Все такие эффекты будут усиливать неравенство внутри страны, что будет иметь серьезные последствия для человеческого и социального развития. Подобно последствиям изменения окружающей среды, такой технологический прорыв очень заслуживает внимания в глобальных моделях.
Например, Winick (2018) обобщил 18 различных оценок воздействия автоматизации на рабочую силу. Среди них особенно часто цитируется отчет McKinsey (Manyika et al., 2017), в котором оценивается, что к 2030 году во всем мире можно будет автоматизировать 400–800 миллионов рабочих мест. Сила такой автоматизации может работать синергетически с появлением крупных сетевых эффектов, которые поддерживать рост и олигопольную или даже монополистическую власть огромных новых технологических компаний. Среди возможных взаимосвязанных последствий — увеличение доли ВВП, приходящейся на компании по сравнению с работниками, замедление роста заработной платы и либо опустошение рынка труда по мере автоматизации средних навыков, либо более масштабная потеря рабочих мест ниже самых высококвалифицированных. уровень.Все такие эффекты будут усиливать неравенство внутри страны, что будет иметь серьезные последствия для человеческого и социального развития. Подобно последствиям изменения окружающей среды, такой технологический прорыв очень заслуживает внимания в глобальных моделях.
Затраты-выпускные отношения для производственной функции Кобба-Дугласа
Затратные-выпускные отношения для производственной функции Кобба-ДугласаВзаимоотношения «затраты-выпуск» для производства Кобба-Дугласа функция
Производственная формула : Q = BoL BL K BK , где Q=выпуск, L=труд, K=капитал, а Bo, BL и BK равны положительные параметры.
1. Эластичность выпуска для коэффициента Кобба-Дугласа
производственная функция: показатель степени по каждому фактору производства = эластичность
выпуска (Q) по отношению к этому фактору.
Итак, для функции здесь B L = %DQ/%DL = e Q,L и B K = %DQ/%DK = e Q,K .
| Доказательство: рассмотрим e Q,L и вспомним формулу
для оценки точечной эластичности, которая в данном случае будет равна: дк л Расчет dQ/дл: дК
BL BoL BL K BK BL Q Вырезав средние члены для суммирования результатов, мы имеем: dQ BL Q Затем мы можем умножить обе части на L/Q, чтобы выделить термин BL: dQ L |
2. Возврат к шкале Кобба-Дугласа производственная функция: сумма показателей факторов производства = эластичность выпуска (Q) по отношению к масштабу производства.
| Доказательство: Поскольку каждый показатель степени представляет собой эластичность выпуска
по отношению к родственному фактору производства имеем: B L = %DQ/%DL, что => %DQ = B L %DL, и B K = %DQ/%DK, что => %DQ = B K %DK.  Итак, когда оба L и К изменить, %DQ = B L %DL + B K %DK. Для изменения масштаба %DL = %DK = %DScale, поэтому %DQ
= B L %DScale + B K %DScale => |
Какова формула производственной функции Кобба-Дугласа? – Greedhead.net
Какова формула производственной функции Кобба-Дугласа?
Формула для этой формы: Q = f(L, K), в которой труд и капитал являются двумя факторами производства, оказывающими наибольшее влияние на количество выпускаемой продукции.
Что такое производственная функция Производственная функция Кобба-Дугласа?
В экономике и эконометрике производственная функция Кобба-Дугласа представляет собой особую функциональную форму производственной функции, широко используемую для представления технологической взаимосвязи между количеством двух или более ресурсов (в частности, физического капитала и труда) и объемом выпуска, который может быть произведен …
Как рассчитать общую факторную производительность по Коббу-Дугласу?
TFP рассчитывается путем деления объема производства на средневзвешенное геометрическое значение затрат труда и капитала со стандартным взвешиванием, равным 0. гамма) = f(L,K,M).
гамма) = f(L,K,M).
Что означает Альфа у Кобба Дугласа?
Альфа — это просто процент капитала, который я использую в своем производственном процессе, тогда как бета — это процент используемого труда.
Как рассчитать производительность?
Вы можете измерить производительность труда с помощью уравнения производительности труда: общий объем производства / общий объем затрат. Предположим, ваша компания произвела товаров или услуг на сумму 80 000 долларов (выход), используя 1500 рабочих часов (вход). Чтобы рассчитать производительность труда вашей компании, вы должны разделить 80 000 на 1 500, что равно 53.
Что такое производственная функция с примерами?
Одним из очень простых примеров производственной функции может быть Q=K+L, где Q — количество продукции, K — количество капитала, а L — количество труда, используемого в производстве. Например, фирма с пятью работниками будет производить пять единиц продукции, если у нее есть по крайней мере пять единиц капитала.
Какие существуют виды производственной функции?
3 типа производственных функций: Производственная функция Кобба Дугласа.Леонтьевская производственная функция. Производственная функция CES.
Какие факторы не учитываются в общей факторной производительности?
Остаток Солоу — это часть роста выпуска экономики, которая не может быть объяснена накоплением капитала и труда, факторов производства.
Что означают А и Б в Коббе Дугласе?
Функция Кобба-Дугласа имеет вид Q=KαLβ, где Q=выход, K=капитал, L=труд, а альфа и бета используются для представления долей входа капитала и труда соответственно.Альфа — это просто процент капитала, который я использую в своем производственном процессе, а бета — это процент используемого труда.
Что означает предпочтение Кобба Дугласа?
предпочтения хорошего поведения
предпочтений Кобба-Дугласа — одно из простейших алгебраических представлений предпочтений хорошего поведения. 2. Предпочтения Кобба-Дугласа. Предположим, что функция полезности потребителя определяется как: u x1,x2.
2. Предпочтения Кобба-Дугласа. Предположим, что функция полезности потребителя определяется как: u x1,x2.
Каково ограничение производственной функции Кобба-Дугласа?
Ограничения производственной функции Кобба Дугласа Невозможно объединить различные факторы из-за дефицита факторов и из-за их неделимости.2) Ни один производитель не увеличивает объем производства ради получения постоянной прибыли. Производитель стремится не к постоянной отдаче, а к достижению возрастающей отдачи.
Что такое планировщик производительности?
Планировщик производительности — это журнал, в котором отслеживается ваше расписание, выполненная вами работа и (конечно) ваша продуктивность. Хотя это можно сравнить с обычным журналом или дневником, мы заверяем вас, что они существенно отличаются.
Производственная функция Кобба-Дугласа
В экономике производственная функция представляет собой отношение между выпуском и комбинацией факторов или ресурсов, использованных для его получения.
Q=f(L,K)
Где:
— Q — количество продуктов
— L количество труда, затраченного на производство Q, например, часов труда в месяц.
— K часы капитала, использованные для производства Q, например, часы, в течение которых машина работала для производства Q.
Могут быть и другие входы, K и L являются просто примерами.
Производственная функция Кобба-Дугласа представляет собой особую форму производственной функции. Он широко используется, потому что имеет много привлекательных характеристик , как мы увидим ниже.
Основная форма производственной функции Кобба-Дугласа выглядит следующим образом:
Q(L,K) = A L β K α
Где:
— Q — количество продукции.
— L — количество труда.
— К — количество капитала.
— A — положительная константа.
— β и α являются константами от 0 до 1.
Графически:
Предельный продукт
Предельный продукт – это изменение общего объема производства при бесконечно малом изменении вводимых ресурсов . Предельный продукт – это первая производная производственной функции по вводимым ресурсам.
Предельный продукт – это первая производная производственной функции по вводимым ресурсам.
∂Q/∂L
В случае производственной функции Кобба-Дугласа:
∂Q/∂L = Aβ L (β-1) K α
Мы видим, что если L или K увеличивается, общий выпуск будет увеличиваться, то есть предельный продукт положителен .
Как видно из следующих графиков, предельный продукт убывает.
Эластичность выпуска — это временное изменение выпуска в ответ на изменение уровня труда или капитала.
(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)
Если эластичность выпуска больше 1, производственная функция эластична, и наоборот. В случае производственной функции Кобба-Дугласа эластичность выпуска можно довольно легко измерить:
(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)
= [ Aβ L (β-1) K α ] / [AL β K α / L ]
= [ Aβ L (β-1) K α ] . (β-1) K α ]
(β-1) K α ]
= β
Эластичность выпуска по отношению к труду постоянна и равна β.Если β равно 0,2, а труд увеличивается на 10%, выпуск увеличится на 2%.
α и β представляют собой эластичности выпуска капитала и труда и являются постоянными.
Возврат к масштабу
Возврат к масштабу измеряет, какой дополнительный результат будет получен при пропорциональном изменении всех факторов. Если выпуск увеличивается более чем пропорционально, мы говорим, что имеем возрастающую отдачу от масштаба. Если объем производства увеличивается менее чем пропорционально, мы говорим, что отдача от масштаба уменьшается.
В случае производственной функции Кобба-Дугласа, чтобы проверить, насколько увеличится выпуск при пропорциональном увеличении всех факторов, мы умножаем все входы на постоянный коэффициент c. Y’ представляет новый выходной уровень .
y ‘= A (Cl) β (CK) α
= A C β L β C α L α
= C β C α AL β K α
= c (β+α) Y
Как мы видим, если все входы меняются в c раз, выпуск увеличивается на c (β+α) .
Тогда:
Если β+α=1 , производственная функция имеет постоянную отдачу от масштаба.
Если β+α > 1, производственная функция имеет возрастающую отдачу от масштаба.
Если β+α < 1, производственная функция имеет убывающую отдачу от масштаба.
Как записать производственную функцию Кобба-Дугласа? – СидмартинБио
Как записать производственную функцию Кобба-Дугласа?
Формула для этой формы: Q = f(L, K), в которой труд и капитал являются двумя факторами производства, оказывающими наибольшее влияние на количество выпускаемой продукции.
Как вы интерпретируете производственную функцию Кобба-Дугласа?
Производственная функция Кобба-Дугласа выражается следующим образом: A, a и β — положительные параметры, где = a > O, β > O. Уравнение говорит о том, что выпуск напрямую зависит от L и C, и та часть выпуска, которая не может быть объяснена с помощью L, а С объясняется с помощью А, который является «остаточным», часто называемым техническим изменением.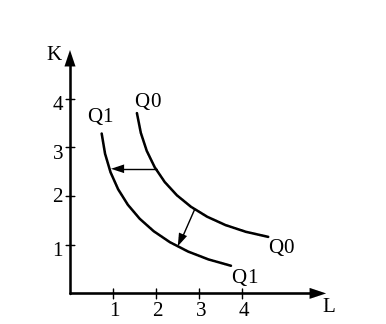
Что такое модель Кобба-Дугласа?
Производственная функция Кобба-Дугласа моделирует взаимосвязь между выпуском продукции и производственными затратами (факторами).Он используется для расчета соотношения ресурсов друг к другу для эффективного производства и для оценки технологических изменений в методах производства.
Что такое функция Кобба-Дугласа в экономике?
В экономике и эконометрике производственная функция Кобба-Дугласа представляет собой особую функциональную форму производственной функции, широко используемую для представления технологической взаимосвязи между количеством двух или более ресурсов (в частности, физического капитала и труда) и объемом выпуска, который может быть произведен …
Для чего используется производственная функция Кобба-Дугласа?
Какова общая форма производственной функции Кобба-Дугласа?
Общая форма производственной функции Кобба-Дугласа для набора n входных данных: Y = f (x 1, x 2,…, xn) = γ ∏ i = 1 nxi α i, где Y обозначает выпуск, xi — вход i, а γ и α i — параметры, определяющие общую эффективность производства и реакцию выпуска на изменения количества вводимых ресурсов.
Какова формула производственной функции?
Другая форма производственной функции сводит затраты только к труду и физическому капиталу. Формула для этой формы: Q = f (L, K), в которой труд и капитал являются двумя факторами производства, оказывающими наибольшее влияние на количество выпускаемой продукции. Произошла ошибка при попытке загрузить это видео.
Какие единицы используются в производственной функции CD?
Производственная функция C-D, показывающая постоянную отдачу от масштаба, изображена на рисунке 20.Затраты труда отложены по горизонтальной оси, а капитал по вертикальной оси. Для производства 100 единиц продукции используются ОС, единицы капитала и OL единицы труда.
Как узнать, возвращается ли производственная функция к масштабу?
Как мы видим, если все входы меняются в c раз, выпуск увеличивается в c (β+α). Если β+α=1, производственная функция имеет постоянную отдачу от масштаба.
Как рассчитать производственную функцию Кобба-Дугласа? – СидмартинБио
Как рассчитать производственную функцию Кобба-Дугласа?
Формула производственной функции Кобба-Дугласа для одного товара с двумя факторами производства выражается следующим образом: Y = A * Lᵝ * Kᵅ, это уравнение производственной функции является основой нашего калькулятора производственной функции Кобба-Дугласа, где: Y равно общий объем производства или выпуска товаров.
Как найти альфа и бета в производственной функции Кобба-Дугласа?
Функция Кобба-Дугласа имеет вид Q=KαLβ, где Q=выход, K=капитал, L=труд, а альфа и бета используются для представления долей входа капитала и труда соответственно.
Как рассчитать производственную функцию?
Производственная функция представляет собой математическое уравнение, которое вычисляет максимальный выпуск, которого может достичь фирма при выбранном количестве вводимых ресурсов (капитал, труд и земля).Производственную функцию можно рассчитать по формуле: Q = f (капитал, земля, труд), где затраты являются функцией выпуска.
Как найти MPL и MPK из производственной функции?
MPL = Δ TP / Δ L Минимальные издержки производства возникают, когда предельный продукт труда, деленный на стоимость одной единицы труда, равен MPK, деленному на стоимость одной единицы капитала.
Что такое производственная функция Производственная функция Кобба-Дугласа?
В экономике и эконометрике производственная функция Кобба-Дугласа представляет собой особую функциональную форму производственной функции, широко используемую для представления технологической взаимосвязи между количеством двух или более ресурсов (в частности, физического капитала и труда) и объемом выпуска, который может быть произведен …
Что такое производственная функция Кобба-Дугласа и ее свойства?
Производственная функция Кобба-Дугласа моделирует взаимосвязь между выпуском продукции и производственными затратами (факторами).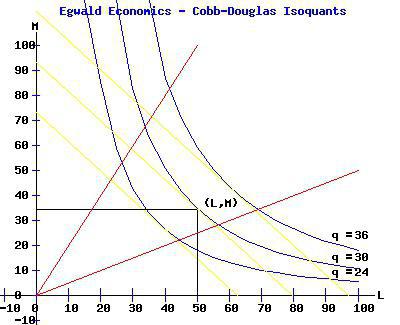 Он используется для расчета соотношения ресурсов друг к другу для эффективного производства и для оценки технологических изменений в методах производства.
Он используется для расчета соотношения ресурсов друг к другу для эффективного производства и для оценки технологических изменений в методах производства.
Как рассчитать выходной MPL?
Он находится путем умножения предельного продукта труда (MPL) — количества дополнительной продукции, которую может произвести один дополнительный рабочий, — на цену продукции. Если сотрудник колл-центра службы поддержки может принять восемь звонков в час (MPL), и каждый звонок приносит компании 3 доллара, то MRPL составляет 24 доллара.
Что такое APL и MPL?
Средний продукт труда (APL) равен Q/L, а предельный продукт труда (MPL) равен дополнительному выпуску, полученному за счет найма еще одной единицы труда. Кривые расположены справа и выглядят так из-за закона убывающей отдачи. MPL = наклон кривой TP.
Каковы входы производственной функции Кобба-Дугласа?
Могут быть и другие входы, K и L это только примеры. Производственная функция Кобба-Дугласа представляет собой особую форму производственной функции. Он широко используется, потому что имеет много привлекательных характеристик, как мы увидим ниже. Основная форма производственной функции Кобба-Дугласа выглядит следующим образом: Q(L,K) = A L β K α.
Он широко используется, потому что имеет много привлекательных характеристик, как мы увидим ниже. Основная форма производственной функции Кобба-Дугласа выглядит следующим образом: Q(L,K) = A L β K α.
Что такое модель Кобба-Дугласа?
В 1928 году Чарльз Кобб и Пол Дуглас представили точку зрения, согласно которой объем производства является результатом количества вложенного труда и физического капитала. Этот анализ привел к расчету, который используется до сих пор, в основном из-за его точности.
Какова формула производственной функции?
Другая форма производственной функции сводит затраты только к труду и физическому капиталу.Формула для этой формы: Q = f (L, K), в которой труд и капитал являются двумя факторами производства, оказывающими наибольшее влияние на количество выпускаемой продукции. Произошла ошибка при попытке загрузить это видео.
Как узнать, возвращается ли производственная функция к масштабу?
Как мы видим, если все входы меняются в c раз, выпуск увеличивается в c (β+α).