Масштаб как измеряется: Понятие масштаба. Измерение расстояний на местности и на карте

Понятие масштаба. Измерение расстояний на местности и на карте

Самарский областной центр технического творчества учащихся

Самарская городская общественная организация
«Детско-молодежный спортивно-технический клуб Контур»

Абрамов А.В.

Самара, 2000 г.

1 часть

Пособие для учащихся учреждений дополнительного образования и для занятий спортивной радиопеленгацией в семье

1.4. Понятие масштаба. Измерение расстояний на местности и на карте.

Вспомним материал параграфа 2. Там говорилось о важнейших свойствах карты. Одно из них гласило: все объекты на карте уменьшены по сравнению с соответствующими объектами местности в одинаковое количество раз. А во сколько же раз карта уменьшена по сравнению с местностью? Наверное, разные карты уменьшены по-разному. Величина, характеризующая степень уменьшения карты, называется масштабом.

Масштаб карты — это дробь, в числителе которой стоит единица, а в знаменателе – величина, показывающая, во сколько раз уменьшены объекты карты по сравнению с соответствующими объектами местности.

Масштаб карты указывается в зарамочном оформлении. Знание масштаба позволяет нам измерять расстояния по карте и переводить их в расстояния на местности. В примере, рассмотренном в предыдущем параграфе, мы, двигаясь к лесному озеру, не знали, сколько нам до него идти. Вдруг мы отклонились от азимута и озеро давно уже позади? Такого вопроса не возникло, если бы мы, измерив расстояние от домика лесника до озера по карте, рассчитали это расстояние на местности.

Пусть масштаб карты составляет 1:15000. Это означает, что все расстояния местности уменьшены при нанесении на карту в 15000 раз. Следовательно, расстояния, измеренные по карте, при переносе на местность должны быть увеличены в 15000 раз. Каждый сантиметр карты составляет 15000 сантиметров на местности или 150 метров. Таким образом, для карты масштаба 1:15000,  1 см на карте соответствует 150 метрам на местности, а 1 мм – 15 метрам.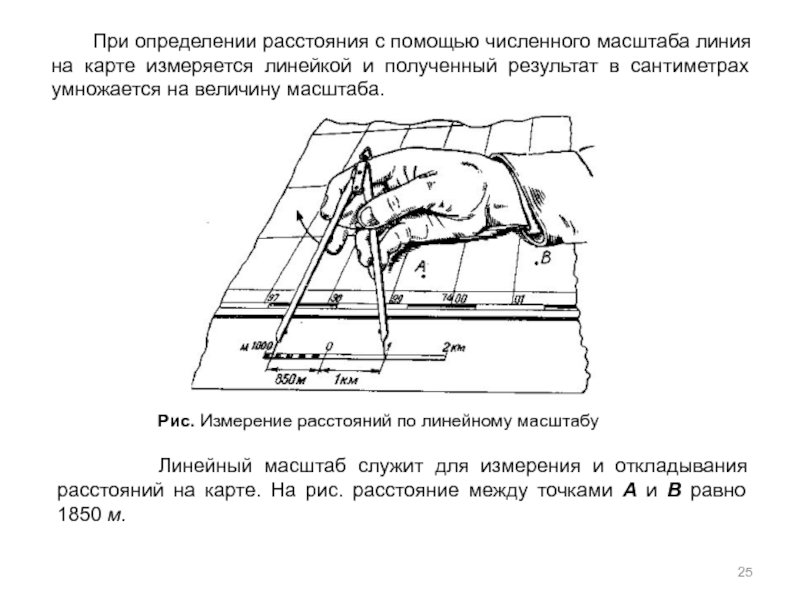

Как перевести расстояние, измеренное по карте, в расстояние на местности? Очень просто. Нужно расстояние в миллиметрах умножить на 15 (вспомните, ведь 1 мм это 15 м). И тогда мы получим расстояние в метрах.

Обратите внимание, что в значении масштаба не указана единица измерения (1:15000). Это не случайно. Дело в том, что нет никакой разницы в каких единицах вести измерения. Хоть в попугаях и слоненках, как это делалось в известном мультфильме. Выражение масштаба показывает, что 1 единица на карте, будь то миллиметр, сантиметр, попугай, соответствует 15000 таких же единиц на местности (миллиметров, сантиметров, попугаев).

Для удобства работы условимся измерять расстояния на карте в миллиметрах, а на местности в метрах. Тогда для перевода единиц карты в единицы местности можно воспользоваться таким соотношением:

Чтобы найти расстояние между двумя объектами местности в метрах, нужно на карте измерить это расстояние в миллиметрах, умножить на знаменатель масштаба и перевести полученный результат в метры, то есть разделить на тысячу.

Запишем соотношение в виде формулы:

 

где – F(m) – расстояние на местности в метрах,

K(mm) – расстояние по карте в миллиметрах, M – знаменатель масштаба.

Задания для самостоятельной работы.

• Определите расстояния между КП по картам различных масштабов.
• Выберите на карте перегон заданной длины.
• Вдоль тропы установлены КП с номерами. На карточке нарисован отрезок и указан масштаб. Добежать до «своего» КП.
• Добежать до заданного КП. Нарисовать отрезок в разных масштабах.
• Даны направления (азимуты) и расстояния. Найти КП на местности.
• Идти от КП к КП (с точки каждого КП видны другие) и рисовать маршрут в виде ломаной линии при заданном масштабе.

Какие вида масштаба существуют? Приведите пример численного масштаба . Переведите его в именованый масштаб

Масшта́б (нем. Maßstab, букв. «мерная палка»:  Maß «мера»,  Stab «палка») — в общем случае отношение двух линейных размеров. Во многих практических областях применения масштабом называют отношение размера изображения к размеру изображаемого объекта.

То есть, на картах, планах, аэро- или космических снимках это отношение длины отрезка к его действительной длине на местности. Принято, на картах принимать за единицу измерения — 1 сантиметр, а на местности измерять расстояние в метрах.

Виды указания масштабов

Существует три вида указания масштаба:

• численный;
• именованный;
• линейный.

Численный масштаб (самый распространенный и удобный) — масштаб дробного вида, где числитель — единица, а знаменатель — число, показывающее во сколько раз уменьшено данное изображение територии (пример: 1:100 000; 1:15 000). Обе цифры указаны в сантиметрах, что делает невозможным ошибку в переводе, конвертации одних единиц измерения в другие. Но на практике использование такого масштаба не является удобным. Поэтому, при роботе непосредственно на местности, численный масштаб чаще всего переводят в именованный.

Именованный (или словесный) масштаб — словесное указание того, какое расстояние на местности соответствует 1 сантиметру на карте (пример: в 1 см 5 км или 1 см = 500 метров). Такой вид масштаба понятен человеческому уму, но будет сложно производить расчеты и очень легко сделать ошибку.

Существует так же и третий вид указания масштаба. Это линейный масштаб.

Линейный масштаб — вспомогательная мерная линейка на картах для быстрого измерения расстояний, без расчетов.

Масштаб карт всегда одинаков во всех ее точках.

Стандарты топографических карт и планов

В России приняты стандартные численные масштабы:

1:1 000 000
1:500 000 
1:200 000
1:100 000
1:50 000
1:25 000
1:10 000.

*Для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000. 

Точность масштаба

Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0,01 см.

Точность масштаба имеет большое значение, когда в задании нам нужно указать возможную погрешность измерения.
Поэтому, для ее определения следует знаменатель численного масштаба разделить на 10 000 (1 м содержит 10 000 отрезков по 0,01 см). Так, для карты масштаба 1:25 000 точность масштаба равна 2,5 м.

Перевод численного масштаба в именованный

Так как длины линий на местности принято измерять в метрах, а на картах и планах — в сантиметрах, то масштабы удобней всего выражать в словесной форме, например:

в одном сантиметре 100 метров. Это соответствует численному масштабу 1:10 000. Поскольку 1 метр равняется 100 сантиметрам, то число метров на местности, содержащееся в 1 см на карте, легко определяется путем деления знаменателя численного масштаба на 100. Или на 100 000 — для перевода в км.

Примеры:
1:1000 — в 1 см 10 метров
1:500 000 — в 1 см 5 км.

Задание:
перевести в именованный масштаб.
1:5 000 —
1:12 500 —
1:1000 000 —
1: 200 —

География — 10

ПРОВЕРЬТЕ

ИЗУЧЕННОЕ

1. Расположите карты данных территорий, составленных на бумаге с одинаковыми размерами, по увеличению проведенной на них генерализации: 1.
   Карта Азербайджана. 2. Карта города Баку. 3. Карта мира. 4. Карта Каспийского мира. 5. Карта Африки.
2. Перечертите таблицу в тетрадь и заполните.

   Положительные особенности генерализации	Отрицательные особенности генерализации

*3.

Сколько см² займет на картах масштабами 1: 5 000 000 и 1:15 000 000 территория на Земле, площадь которой 90 000 км²? Сравните ответы и определите, на какой карте генерализация больше. Обоснуйте свой ответ.

11

МАСШТАБ И ИСКАЖЕНИЯ. ПРАКТИЧЕСКИЙ УРОК

Известно, что на каждой карте обозначается масштаб, на основании чего вычисляются расстояние и площадь. На всех картах есть искажения. Только ввиду того, что карта считается математически правильным изображением, на ней возможно провести точные математические вычисления.

Вспомните длины дуг меридиан и параллелей и выполните следующие задания.

Вычислите расстояние между A и B по меридиану в градусах и километрах.

Вычислите расстояние по параллели 40° с.ш. между Баку (50° в.д.) и Анкарой (33° в.д.) в градусах и километрах (на 40° широты 1° = 85,4 км).

Расстояние на карте возможно измерять с точностью при помощи главного и специального масштабов. Масштаб, обозначенный у края карты, — главный. На основании главного масштаба точное расстояние можно измерять только на линии нулевых искажений. На других частях карты, где имеются искажения, для измерения расстояний пользуются специальным масштабом. Специальный масштаб определяется способом деления действительных длин меридианов и параллелей на их длину на карте.

Определение расстояния по карте при помощи масштаба и градусной сетки

Карта — это основной инструмент географа и путешественника.

Это статья превратит карту из неопознанного объекта, которого ты боялся, в твоего помощника.

Вначале работы с картой или планом могут возникнуть вопросы как определить направление север — юг, как пользоваться масштабом и как правильно определить расстояние.

Пункт 1: направления

На плане направления (стороны света) могут быть указаны двумя способами:

1. Направление север — юг показано стрелкой

2. Если нет стрелки, то по умолчанию север — вверху, юг — внизу.

На карте направления определяют с помощью градусной сетки (cети параеллелей и меридианов).

Пункт 2: масштаб

Ключевым компонентом карты или плана является масштаб.

Масштаб показывает на сколько линия на карте меньше линии в действительности.

Например, масштаб географической карты 1:1000000. Это значит что в 1 см карты 1 000 000 см на местности.

Масштаб на планах и картах изображают в трех видах: численном, именованном, линейном.

Численный масштаб записывают как отношение чисел 1:100, 1:500, 1:100 000. Первое число — расстояние на изображении, а второе число — реальное расстояние на местности в тех же единицах измерения

Пример: масштаб 1:1000, 1 см на карте соответсвует 1000 см (1000 см = 10 м ) на местности

Именованный масштаб — масштаб, выраженный словами

Пример: «в 1 сантиметре 1 километр»

Линейный масштаб — это прямая линия разделенная на равные отрезки (они еще называются основанием масштаба и обычно равны 1 см) . Основание масштаба соответсвует определенному расстоянию на местности.

Пункт 3: измерение расстояний на крупномасштабной карте или плане

Измерять расстояние можно с помощью масштаба.

. Пошаговый план:

1. Чертим прямую линию между двумя точками

2. С помощью линейки измеряем расстояние в сантиметрах

3. Умножаем полученное число на величину маштаба

Пример: мы имеем карту с численным маштабом 1:1000, измеренное расстояние между точками равно 5 см. Рассчитываем расстояние на местности 5 см *1000 см = 5000 см или 50 м.

Навыки измерения расстояние с помощью масштаба понадобится нам в решении 9 задания ОГЭ.

Пункт 4: измерение расстояний с помощью градусной сети

Для расчета расстояний на мелкомасштабных картах или глобусах удобней расчитывать расстояние по 1 градусу дуги меридиана и 1 градусу дуги экватора.

Так как все меридианы имеют одинаковую длину (40009 км) можно вычислить длину дуги одного градуса.

Длина дуги одного градуса меридиана (или одного градуса на экваторе) равна 111 км.

Как определить расстояние между двумя пунктами, лежащими на одном меридиане:

1. Посчитать разницу между ними в градусах (из широты одного пункта вычесть широту другого пункта)

2. Далее необходимо число градусов умножить на 111 км.

Пример: С корабля, находящегося в точке с координатами 13 с.ш.73 з.д., поступило радиосообщение о неисправности двигателя. Какое расстояние до неисправного судна пройдёт ремонтный корабль из порта Риоача (11 с.ш. 73з.д.), если известно, что корабль будет идти строго по меридиану, а неисправное судно останется в той же точке, откуда было передано сообщение?

Действуем по алгоритму:

1.  Находим разницу между кораблями в градусах: 13 — 11 = 2

2. В одном градусе 111 км, следовательно в 2 градусах 2*111 = 222 км

Ответ: 222 км

Как определить расстояние между двумя пунктами, лежащими на экваторе:

1. Определяем расстояние между ними в градусах (из долготы одного пункта вычитаем долготу другого пункта)

2. Далее необходимо число градусов умножить на 111 км.

Чтобы определить расстояние между двумя точками, расположенными на одной параллели, необходимо знать число километров, соответствующее длине 1 градуса дуги конкретной параллели (так как обхват планеты сужается к полюсам и длины пареллелй соответственно уменьшаются).

Навыки измерения расстояние по карте понадобятся нам в решение 30 задание ЕГЭ

Масштаб (определение, обозначение, измерение) | Природоведение. Реферат, доклад, сообщение, краткое содержание, конспект, сочинение, ГДЗ, тест, книга

Чтобы на листе бумаги разместить изображение местности, его дают в очень уменьшенном виде.

Что такое масштаб. На местности расстояния указывают в метрах или километрах. Например, расстояние от Киева до Харькова составляет 480 км. Такое расстояние показать на бумаге невозможно. Поэтому на планах и картах расстояния даны в уменьшенном виде — в сантиметрах и миллиметрах. Чтобы перевести большие расстояния на мест­ности в небольшие на карте, используют масштаб.

Вычислим, каким будет расстояние от Киева в Харькова, например, на настенной карте. Условимся, что на бумаге все расстояния будем изо­бражать в 1 млн раз меньше, чем в действительности. Тогда 1 см на карте будет соответствовать 1 000 000 см на местности. Следовательно, наш масштаб 1 : 1 000 000 (читается: одна миллионная). Масштаб указывает, во сколько раз расстояние на местности уменьшено на карте. Тогда расстояние от Киева до Харькова, на местности равное 480 км, на карте данного масштаба определяем так:

480 км переводим в сантиметры — 48 000 000 см;

48 000 000 см : 1 000 000 см (масштаб) = 48 см.

Следовательно, расстояние от Киева до Харько­ва на карте составляет 48 см.

Масштаб — это мера уменьшения расстояний на местности при изображении их на глобусе, карте или плане.

Рис. 103. Изображение масштаба на карте

Как обозначают масштаб. На карте масштаб записывают в виде нецелого числа, например — 1 : 100 000 (чита­ется: одна стотысячная) (рис. 103). Число 1 — это расстояние на карте, которое соответствует 100 000 таких расстояний на местности (то есть 1 см на карте равен 100 000 см на местно­сти). Важно помнить, что в масшта­бе обе цифры всегда представлены в сантиметрах. Обычно рядом с числом масштаба приводится его объясне­ние. Например, в 1 см 1 км (то есть 100 000 см для удобства переводят в километры). Это также означает, что 1 см на карте соответствует 1 км на местности.

Глобусы, как и карты, имеют масштаб. Он показывает, во сколько раз глобус меньше действительных размеров Земли. В отличие от карт на глобусах уменьшение земной поверхности значительное. Например, на глобусе с масшта­бом 1 : 30 000 000 в одном сантиметре уложились 30 млн сантиметров (или 300 км) земное поверхности. То есть все земные объекты на таком глобусе уменьшены в 30 млн раз.

Запись масштаба

Чем больше уменьшение на глобусе и карте, тем большую по площади территорию можно изобразить. Но чем больше уменьшение, тем меньше и менее выразительными будут объекты на карте.

Как измеряют расстояния и длины на карте и глобусе. Расстояние между двумя объектами на карте измеряют по прямой линии обычной линейкой. Иногда необходимо измерить расстояние не по прямой, а по кривым линиям (например, длину извилистой реки). В этом случае можно использовать обыкновенную нитку. Нить прикладывают к кривой линии на карте, повторяя её изгибы. Затем выпрямив нитку, измеряют её длину линейкой. Материал с сайта //iEssay.ru

Расстояния на глобусе удобно измерять гибкой линейкой или с помощью полоски бумаги либо нитки (рис. 104). Далее, используя масштаб, определяют расстояние или длину на местности.

Рис. 104. Измерение расстояния: а — на карте; б — на глобусе

Масштабирование документа

Быстрое увеличение и уменьшение масштаба

1. В панели состояния Приложение Office щелкните ползунок масштаба. 

2. Передвиньте ползунок к нужному процентному значению масштаба. Нажмите кнопку —или +, чтобы постепенно увеличивать масштаб.

Примечание: В Outlook масштабе ползунок масштаба увеличивает только содержимое области чтения.

Щелкните заголовки ниже, чтобы получить дополнительные сведения.

Выбор конкретного масштаба

Примечание: Эта процедура недоступна вExcel в Интернете. В качестве обходного решения можно открыть файл в Excel Desktop, чтобы изменить этот параметр. 

Вы можете указать, какая часть документа, презентации или листа будет представлена на экране.

В Word

Выполните одно из следующих действий:

• На вкладке Вид в группе Масштаб выберите элемент Масштаб 100%. Это возвращает масштаб 100 %.

• На вкладке Вид в группе Масштаб нажмите кнопку Одна страница,Несколько страницили Ширина страницы.

• На вкладке Вид в группе Масштаб выберите элемент Масштаб и введите процентное значение или выберите другие нужные параметры.

В PowerPoint

Выполните одно из следующих действий:

• На вкладке Вид в группе Масштаб нажмите кнопку Вписать в окно ,чтобы изменить размер текущего слайда PowerPoint окна.

  Примечание: Рядом с ползуноком масштаба в панели состояния также есть кнопка Вписать в окно.

• На вкладке Вид в группе Масштаб выберите элемент Масштаб и введите процентное значение или выберите другие нужные параметры.

В Excel

Выполните одно из следующих действий:

• На вкладке Вид в группе Масштаб выберите элемент Масштаб 100%.

• На вкладке Вид в группе Масштаб нажмите кнопку Увеличить до выделения ,чтобы развернуть представление выбранных ячеек.

• На вкладке Вид в группе Масштаб выберите элемент Масштаб и введите процентное значение или выберите другие нужные параметры.

В Outlook

В главном Outlook масштаб ползунок — единственный способ увеличить или уменьшить масштаб. Когда вы читаете или редактируете сообщение, увеличьтесь с ленты:

1. В открытом сообщении на вкладке Сообщение в группе Масштаб нажмите кнопку Масштаб.

2. В диалоговом окне Масштаб введите процентное соотношение или выберите другие нужные параметры.

Сохранение масштаба в PowerPoint или Excel

Примечания: 

• Word не сохраняет параметры масштаба в документах. Вместо этого документ открывается на последнем использованном вами масштабе.

• Excel в Интернете не поддерживает сохранение масштаба, так как на вкладке Вид нет группы Масштаб, поэтому для изменения масштаба необходимо использовать ее в панели состояния. В качестве обходного решения можно открыть файл в Excel Desktop, чтобы сохранить масштаб с помощью следующей процедуры:

1. Откройте презентацию или лист, который нужно сохранить вместе с заданным масштабом.

2. На вкладке Вид в группе Масштаб выберите элемент Масштаб.

3. Выберите нужный параметр.

4. Нажмите кнопку Сохранить.

   Сочетания клавиш: CTRL+S

Масштаб карты.

Определение расстояний — презентация онлайн

1. Урок 7. Масштаб карты. Определение расстояний

Карта – это уменьшенное
изображение участка местности.
А это дом друга
Во сколько раз уменьшенное?
А это школа
В два?
В три?
Или в 10?
А может в 100 или в миллион?
Масштаб показывает во сколько
раз уменьшена карта по
сравнению с местностью, на ней
изображенной.
Это мой дом
Тут магазин

2. Масштаб карты

Масштаб выражается
соотношением чисел.
Первое число – всегда один
сантиметр.
Второе число может быть любым
количеством сантиметров.
Если карта меньше участка
местности в два раза, то ее
масштаб 1:2
Если она меньше в 20 раз, то ее
масштаб 1:20
А если меньше в 20 тысяч раз, то
масштаб ее 1:20 000
Масштаб 1: 1000
В одном сантиметре
карты содержится
1000 см местности.
Или в 1 см 10 метров
Масштаб 1: 10 000
В одном сантиметре
карты содержится 10
тысяч см местности.
Или в 1 см 1000
метров, то есть 1
километр

3. Масштаб карты

Давайте запомним!

4. Масштаб карты

Масштаб — это дробное число
1 см
на плане
1000 см
на местности
Надо знать!
В 1 метре — 100 сантиметров
В 1 километре – 1000 метров – 1000 00
сантиметров
Переведем численный масштаб в
именованный
1 см
1000 см
1:100
в 1 см 10 м

5. Масштаб карты

Если длина вашего класса
составляет 10 метров, то на карте
масштабом 1:1000 его длина будет
всего 1 сантиметр.
Вот если вы возьмете лист бумаги
шириной в 20 сантиметров, то по
короткой стороне его уместится
целых 20 ваших классов.
Масштаб 1:1000

6. Расстояние

Расстояние от школы до дома.
Как его измерить?
Линейкой на карте или шагами на
улице?
Это моя школа
Курвиметр – прибор для
измерения расстояний. Это та же
линейка только колесная.
Курвиметр может кататься по
карте как угодно, описывая любые
фигуры.
Это мой дом
Масштаб 1:1000

7. Расстояние

Длина пути по карте масштаба
1:1000 составила 10 сантиметров.
Значит весь путь составит 100
метров.
А если 75 сантиметров при том же
масштабе?
Поход из дома
в школу
15 см
25 см
Тогда получаем 75:75000.
Делим последнюю цифру на 100 и
получаем 750 метров.
5 см
15 см
Именно такой путь нам и придется
преодолеть
15 см
Масштаб 1:1000

8. Расстояние

Длина нашего пути может быть
измерена шагами.
Для этого нам вначале узнать
сколько шагов мы должны сделать,
чтобы пройти расстояние в 10
метров.
Отмеряем 10 метров и считаем
наши шаги.
Чтобы считать было легче, можно
вести счет только под одну ногу.
Тогда наш счет будет идти в парах
шагов.
10 метров отмеряем рулеткой
Идем, считая шаг под одну ногу
Сколько вышло пар шагов?
Варианты ответов:
А) 9
Б) 3
В) 4
Г) 5
Д) 6
Допустим в 10 метрах у вас получилось 6
пар шагов.
А вам надо пройти 185 метров. Сколько пар
шагов вам надо сделать? 185 метров
множим на 6 и делим на 10.
Получаем 111 пар шагов

9. Расстояние

Если измерять расстояния в собственной квартире, где особенно не
разбежишься, то считать путь надо не парами шагов, а ступнями.
10 метров отмеряем рулеткой
1 метр
Ставим ступню к ступне и считаем каждую. Но можно считать и под оду ногу парами, если расстояние будет
большое.
Красным цветом обозначена ступня правой ноги, а зеленым цветом – ступня левой ноги.
Сколько вышло ступней на этом отрезке?
А сколько пар ступней на нем уложилось?

10. Кладоискатели

Игроков двое или больше.
Прячем клад так, чтобы его было
видно с расстояния 30 см.
Размер «клада» с наперсток, если
игра происходит в квартире.
Если играем на улице, то «клад»
можно зарыть в землю, а
обозначить место воткнутой в
землю спичкой.
Старт
ложный «клад»
ложный «клад»
ложный «клад»
«клад»
На пути движения надо устроить
несколько ложных «кладов»,
обозначив их также, как
обозначен и настоящий.
ложный «клад»
Финиш

11. Советы

Почаще тренируйтесь измерять расстояния. Чем чаще это делать, тем
легче считать дистанцию. При этом хорошо развивается глазомер.
Если из содержания урока осталось что-то непонятно, то задавайте
вопросы, отвечу подробно.

Типы данных и шкалы измерения

Данные являются ценным активом настолько, что это самый ценный ресурс в мире. Это делает понимание различных типов данных и роль специалиста по обработке и анализу данных более важными, чем когда-либо. В деловом мире все больше компаний пытаются понять большие числа и то, что они могут с ними сделать. Экспертиза данных пользуется большим спросом. Определение правильных данных и шкал измерения позволяет компаниям организовывать, идентифицировать, анализировать и, в конечном счете, использовать данные для обоснования стратегий, которые позволят им оказывать реальное влияние.

Данные высшего уровня: качественные и количественные

Что такое данные? Короче говоря, это совокупность измерений или наблюдений, разделенных на два разных типа: качественные и количественные.

Качественные данные относятся к информации о качествах или к информации, которую невозможно измерить. Как правило, описательный и текстовый. Примеры включают цвет глаз человека или тип автомобиля, на котором он ездит. В опросах он часто используется для классификации ответов «да» или «нет».

Количественные данные являются числовыми. Он используется для определения информации, которую можно подсчитать. Некоторые примеры количественных данных включают расстояние, скорость, рост, длину и вес. Легко запомнить разницу между качественными и количественными данными, поскольку одни относятся к качествам, а другие — к количествам.

Книжная полка, например, может иметь 100 книг на полках и иметь высоту 100 сантиметров. Это количественные точки данных. Цвет книжной полки — красный — является качественной точкой данных.

Что такое количественные (числовые) данные?

Количественные или числовые данные можно разделить на два типа: дискретные и непрерывные.

Дискретные данные

Дискретные данные — это целое число, которое нельзя разделить или разбить на отдельные части, дроби или десятичные дроби. Примеры дискретных данных включают количество домашних животных у кого-то — можно иметь двух собак, но не двух с половиной собак. Количество побед чьей-либо любимой команды также является формой дискретных данных, потому что у команды не может быть полувыигрыша — это либо победа, либо поражение, либо ничья.

Непрерывные данные

Непрерывные данные описывают значения, которые можно разбить на разные части, единицы, дроби и десятичные дроби. Можно измерять непрерывные точки данных, такие как рост и вес. Время также можно разбить – на полсекунды или на полчаса. Температура — еще один пример непрерывных данных.

Дискретный и непрерывный

Существует простой способ запомнить разницу между двумя типами количественных данных: данные считаются дискретными, если их можно сосчитать, и непрерывными, если их можно измерить. Кто-то может считать студентов, купленные билеты и книги, а кто-то измеряет рост, расстояние и температуру.

Что такое качественные (категориальные) данные?

Качественные данные описывают качество точек данных и не являются числовыми. Он используется для определения информации, а также может быть дополнительно разбит на подкатегории по четырем шкалам измерения.

Свойства и шкалы измерения

Шкалы измерения — это то, как переменные определяются и классифицируются.Психолог Стэнли Стивенс разработал четыре общепринятые шкалы измерения: номинальное , порядковое , интервальное и отношение . Каждая шкала измерения имеет свойства, которые определяют, как правильно анализировать данные. Оцениваются следующие свойства: идентичность , величина , равные интервалы и минимальное значение, равное нулю .

Свойства измерения

• Идентичность: Идентичность относится к каждому значению, имеющему уникальное значение.

• Величина: Величина означает, что значения имеют упорядоченное отношение друг к другу, поэтому переменные имеют определенный порядок.

• Равные интервалы: Равные интервалы означают, что точки данных вдоль шкалы равны, поэтому разница между точками данных 1 и 2 будет такой же, как разница между точками данных 5 и 6.

• Минимальное значение нуля: Минимальное значение нуля означает, что весы имеют истинную нулевую точку.Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.

Четыре шкалы измерения

Понимая масштаб измерения своих данных, специалисты по данным могут определить тип статистического теста для выполнения.

1. Номинальная шкала измерения

Номинальная шкала измерения определяет свойство идентичности данных. Эта шкала имеет определенные характеристики, но не имеет числового значения.Данные могут быть помещены в категории, но не могут быть умножены, разделены, добавлены или вычтены друг из друга. Также невозможно измерить разницу между точками данных.

Примеры номинальных данных включают цвет глаз и страну рождения. Номинальные данные можно снова разбить на три категории:

• Номинал с заказом: Некоторые номинальные данные могут быть разбиты на подкатегории по порядку, например, «холодный, теплый, горячий и очень горячий».

• Номинальные без порядка: Номинальные данные также могут быть подразделены на номинальные без порядка, например, мужские и женские.

• Дихотомические: Дихотомические данные определяются наличием только двух категорий или уровней, таких как «да» и «нет».

2. Порядковая шкала измерения

Порядковая шкала определяет данные, расположенные в определенном порядке. Хотя каждое значение ранжировано, нет информации, которая бы указывала, что отличает категории друг от друга. К этим значениям нельзя ни добавить, ни вычесть.

Примером такого рода данных могут быть точки данных об удовлетворенности в опросе, где «один = счастлив, два = нейтрально и три = несчастен».Когда кто-то финишировал в гонке, также описываются порядковые данные. Хотя первое, второе или третье место показывает, в каком порядке финишировали бегуны, оно не указывает, насколько далеко финишер, занявший первое место, был впереди бегуна, занявшего второе место.

3. Интервальная шкала измерения

Шкала интервалов содержит свойства номинальных и упорядоченных данных, но разницу между точками данных можно определить количественно. Этот тип данных показывает как порядок переменных, так и точные различия между переменными.Их можно складывать или вычитать друг из друга, но нельзя умножать или делить. Например, 40 градусов — это не 20 градусов, умноженных на два.

Эта шкала также характеризуется тем, что число ноль является существующей переменной. В порядковой шкале ноль означает, что данные не существуют. В интервальной шкале ноль имеет значение — например, если вы измеряете градусы, ноль имеет значение температуры.

Точки данных на шкале интервалов имеют одинаковую разницу между собой.Разница на шкале между 10 и 20 градусами такая же, как и между 20 и 30 градусами. Эта шкала используется для количественной оценки различий между переменными, тогда как две другие шкалы используются только для описания качественных значений. Другие примеры интервальных шкал включают год выпуска автомобиля или месяцы года.

4. Шкала отношений

Шкалы измерения отношений включают свойства всех четырех шкал измерения. Данные являются номинальными и определяются тождеством, могут быть классифицированы по порядку, содержат интервалы и могут быть разбиты на точные значения.Вес, рост и расстояние — все это примеры переменных отношений. Данные в шкале отношений можно складывать, вычитать, делить и умножать.

Шкалы отношений также отличаются от шкал интервалов тем, что шкала имеет «истинный нуль». Число ноль означает, что данные не имеют точки значения. Примером этого является рост или вес, поскольку кто-то не может быть ростом ноль сантиметров или весить ноль килограммов, или иметь отрицательные сантиметры или отрицательные килограммы. Примерами использования этой шкалы являются расчет акций или продаж.Из всех типов данных на шкалах измерения специалисты по данным могут больше всего сделать с точками данных отношения.

Подводя итог, можно сказать, что номинальные весы используются для маркировки или описания значений. Порядковые шкалы используются для предоставления информации о конкретном порядке точек данных, что в основном наблюдается при использовании опросов удовлетворенности. Шкала интервалов используется для понимания порядка и различий между ними. Шкалы отношений дают больше информации об идентичности, порядке и различиях, а также разбивку числовых деталей в каждой точке данных.

Использование количественных и качественных данных в статистике

После того, как специалисты по обработке данных получат окончательный набор данных из своей выборки, они смогут начать использовать эту информацию для создания описаний и выводов. Для этого они могут использовать как описательную, так и логическую статистику.

Описательная статистика

Описательная статистика помогает продемонстрировать, представить, проанализировать и обобщить результаты, содержащиеся в образце. Они представляют данные в простой для понимания и презентабельной форме, например, в виде таблицы или графика.Без описания данные были бы в необработанном виде без пояснений.

Подсчет частоты

Специалисты по данным могут описать статистику с помощью подсчета частоты или статистики частоты, которая описывает, сколько раз переменная присутствует в наборе данных. Например, количество людей с голубыми глазами или количество людей с водительскими правами в выборке можно подсчитать по частоте. Другие примеры включают квалификацию образования, такую ​​как аттестат о среднем образовании, университетский диплом или докторскую степень, а также категории семейного положения, такие как холост, женат или разведен.

Частотные данные представляют собой форму дискретных данных, так как части значений не могут быть разбиты на части. Вместо этого для расчета непрерывных точек данных, таких как возраст, специалисты по данным могут использовать центральную статистику тенденций. Для этого они находят среднее или среднее значение точки данных. Используя пример возраста, это может сказать им средний возраст участников в выборке.

Хотя специалисты по обработке и анализу данных могут делать выводы на основе описательной статистики и представлять их в понятной форме, они не всегда могут делать выводы.Вот тут и приходит на помощь статистика выводов.

Логическая статистика

Логическая статистика используется для разработки гипотезы на основе набора данных. Было бы невозможно получить данные от всего населения, поэтому специалисты по данным могут использовать логическую статистику для экстраполяции своих результатов. Используя эту статистику, они могут делать обобщения и прогнозы в отношении более широкой выборки, даже если они не опросили их всех.

Примером использования логической статистики являются выборы. Еще до того, как вся страна проголосовала, специалисты по данным могут использовать подобную статистику, чтобы делать предположения относительно того, кто может победить на основе меньшего размера выборки.

Использование визуализации данных для обмена идеями

Визуализация данных описывает методы, используемые для создания графического представления образца данных путем кодирования его с помощью визуальных фрагментов информации. Это помогает передавать данные зрителям четким и эффективным способом.

Характеристики эффективных графических дисплеев

Эффективная визуализация может помочь людям анализировать сложные значения данных и делать выводы.Целью этого процесса является максимально четкое изложение результатов. Графический дисплей с эффективным обменом сообщениями будет четко отображать данные и позволит зрителю получить представление и тенденции из набора данных и выявить различные результаты между данными.

Примеры визуализации данных

Наилучшее визуальное представление набора данных определяется отношениями, которые специалисты по данным хотят передать между точками данных. Они хотят представить распределение с выбросами? Они хотят сравнить несколько переменных или проанализировать одну переменную во времени? Представляют ли они тенденции в вашем наборе данных? Вот некоторые из ключевых примеров визуализации данных.

• Гистограмма используется для сравнения двух или более значений в категории и того, как несколько фрагментов данных соотносятся друг с другом.

• Линейная диаграмма используется для визуального представления тенденций, шаблонов и колебаний в наборе данных. Линейные графики обычно используются для прогнозирования информации.

• Точечная диаграмма используется для отображения взаимосвязи между точками данных в компактной визуальной форме.

• Круговая диаграмма используется для сравнения частей целого.

• Воронкообразная диаграмма используется для представления того, как данные перемещаются по различным шагам или стадиям процесса.

• Гистограмма используется для представления данных за определенный период времени или интервал.

Количественные сообщения

Количественные сообщения описывают отношения данных.В зависимости от выборки существуют разные способы передачи количественных данных.

• Номинальное сравнение: Подкатегории сравниваются по отдельности в произвольном порядке.

• Временной ряд: Индивидуальная переменная отслеживается в течение периода времени, обычно представленного в виде линейной диаграммы.

• Ранжирование: Подкатегории ранжируются по порядку, обычно представленному в виде гистограммы.

• Часть к целому: Подкатегории представлены в виде соотношения по сравнению с целым, обычно представленным в виде гистограммы или круговой диаграммы.

• Отклонение: Подкатегории сравниваются с контрольной точкой, обычно представленной в виде гистограммы.

• Частотное распределение: Подкатегории подсчитываются в интервалах, обычно представленных в виде гистограммы.

• Корреляция: Два набора мер сравниваются, чтобы определить, движутся ли они в одном и том же или противоположном направлении, обычно представленном на диаграмме рассеивания.

Расширьте свои знания в области обработки данных

Поскольку наука о данных становится все более востребованным навыком, сейчас самое подходящее время, чтобы расширить свои знания о самом ценном ресурсе в мире: данных.Степень в области науки о данных позволит вам выявлять, анализировать и представлять сложные и переплетенные сети данных. Затем вы можете использовать эти идеи для прогнозирования и создания стратегий, особенно в бизнес-среде. Магистр наук о данных UNSW может дать вам навыки, необходимые для того, чтобы раскрыть всю мощь данных и помочь компаниям принимать более эффективные решения, позволяя им добиваться значительных изменений и результатов.

измерительная шкала | статистический анализ

шкала измерения , в статистическом анализе, тип информации, представленной числами.Каждая из четырех шкал (т. е. номинальная, порядковая, интервальная и относительная) предоставляет различный тип информации. Измерение относится к осмысленному присвоению чисел, и понимание шкал измерения важно для интерпретации чисел, присвоенных людям, объектам и событиям.

Номинальные весы

В номинальных весах числа, такие как номера водительских прав и серийные номера продуктов, используются для обозначения или идентификации людей, объектов или событий. Пол является примером номинального измерения, в котором число (т.g., 1) используется для обозначения одного пола, например мужского, а другое число (например, 2) используется для другого пола, женского. Цифры не означают, что один пол лучше или хуже другого; они просто используются для классификации людей. На самом деле можно использовать любые другие числа, потому что они не представляют количество или качество. Невозможно использовать названия слов с некоторыми статистическими методами, но в системах кодирования можно использовать числительные. Например, пожарные могут захотеть изучить взаимосвязь между полом (где мужчина = 1, женщина = 2) и результатами тестов на физические способности (с числовыми баллами, указывающими способности).

Порядковые шкалы

В порядковых шкалах числа представляют ранговый порядок и указывают порядок качества или количества, но они не указывают количество количества или степень качества. Обычно цифра 1 означает, что человек (или предмет, или событие) лучше, чем человек, отмеченный цифрой 2; человек 2 лучше, чем человек 3, и так далее — например, ранжировать людей с точки зрения потенциала продвижения по службе, при этом человек с рейтингом 1 имеет больший потенциал, чем человек с рейтингом 2.Однако такая порядковая шкала не показывает, насколько больше потенциал лидера по сравнению с человеком, которому присвоен рейтинг 2, и здесь может быть очень небольшая разница между 1 и 2. При использовании порядкового измерения (а не интервального измерения) применимы определенные статистические методы (например, ранговая корреляция Спирмена).

Интервальная шкала

В интервальных шкалах числа образуют континуум и предоставляют информацию о величине разницы, но в шкале отсутствует истинный нуль.Различия между соседними числами равны или известны. Если используется ноль, то он просто служит точкой отсчета на шкале, но не указывает на полное отсутствие измеряемой характеристики. Температурные шкалы Фаренгейта и Цельсия являются примерами измерения интервалов. В этих шкалах 0 ° F и 0 ° C не указывают на отсутствие температуры.

Весы для пропорций

Шкалы отношений обладают всеми характеристиками интервальных шкал, а также истинным нулем, что означает полное отсутствие измеряемой характеристики.Физические характеристики людей и объектов могут быть измерены с помощью весов отношений, и, таким образом, рост и вес являются примерами измерения отношений. Оценка 0 означает полное отсутствие роста или веса. Рост человека 1,2 метра (4 фута) составляет две трети роста человека ростом 1,8 метра (6 футов). Точно так же человек весом 45,4 кг (100 фунтов) на две трети тяжелее человека весом 68 кг (150 фунтов).

Джо Энн Ли

закон больших чисел | статистика

закон больших чисел , в статистике, теорема о том, что по мере увеличения числа одинаково распределенных случайно сгенерированных величин их выборочное среднее (среднее) приближается к теоретическому среднему.

Закон больших чисел впервые доказал швейцарский математик Якоб Бернулли в 1713 году. Он и его современники разрабатывали формальную теорию вероятностей с целью анализа азартных игр. Бернулли предусмотрел бесконечную последовательность повторений игры на чистой случайности только с двумя исходами: победой или поражением. Обозначив вероятность выигрыша как 90 293 p 90 294 , Бернулли рассмотрел долю раз, когда такая игра будет выиграна при большом числе повторений. Принято считать, что эта дробь в конечном итоге должна быть близка к p . Именно это точно доказал Бернулли, показав, что при неограниченном возрастании числа повторений вероятность того, что эта дробь окажется на любом заданном расстоянии от p , приближается к 1,

.

Британская викторина

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Существует и более общая версия закона больших чисел для средних, доказанная более века спустя русским математиком Пафнутием Чебышевым.

Закон больших чисел тесно связан с тем, что обычно называют законом средних чисел. При подбрасывании монеты закон больших чисел гласит, что доля выпавших орлов в конце концов будет близка к ¹ / ₂ . Следовательно, если первые 10 бросков дают только 3 орла, кажется, что какая-то мистическая сила должна каким-то образом увеличить вероятность выпадения орла, возвращая долю орла к ее конечному пределу ¹ / ₂ .Однако закон больших чисел не требует такой мистической силы. Действительно, доле головок может потребоваться очень много времени, чтобы приблизиться к ¹ / ₂ ( см. рисунок ). Например, чтобы получить 95-процентную вероятность того, что доля выпадения орла находится в диапазоне от 0,47 до 0,53, количество подбрасываний должно превышать 1000. Другими словами, после 1000 бросков первоначальный недобор всего в 3 орла из 10 бросков компенсируется результатами оставшихся 990 бросков.

Ричард Рутледж

кластерный анализ | статистика | Британика

кластерный анализ , в статистике набор инструментов и алгоритмов, который используется для классификации различных объектов по группам таким образом, чтобы сходство между двумя объектами было максимальным, если они принадлежат к одной группе, и минимальным в противном случае. В биологии кластерный анализ является важным инструментом таксономии (классификации живых и вымерших организмов). В клинической медицине его можно использовать для выявления пациентов с заболеваниями общей причины, пациентов, которые должны получать одинаковое лечение, или пациентов, у которых должен быть одинаковый уровень ответа на лечение. В эпидемиологии кластерный анализ имеет множество применений, например, для поиска значимых конгломератов регионов, сообществ или районов с аналогичными эпидемиологическими профилями, когда задействовано много переменных и не существует естественных группировок.В общем, всякий раз, когда нужно классифицировать большие объемы информации по небольшому количеству значимых категорий, может быть полезен кластерный анализ.

Исследователи часто сталкиваются с задачей сортировки наблюдаемых данных в осмысленные структуры. Кластерный анализ представляет собой индуктивный исследовательский метод в том смысле, что он раскрывает структуры, не объясняя причин их существования. Это метод генерации гипотез, а не проверки гипотез. В отличие от дискриминантного анализа, когда объекты распределяются по уже существующим группам на основе статистических правил распределения, кластерный анализ создает группы или обнаруживает скрытую структуру групп в данных.

Классификация методов

В первом широком подходе методы кластерного анализа могут быть классифицированы как иерархические, если результирующая группировка имеет возрастающее число вложенных классов, напоминающих филогенетическую классификацию, или неиерархические, если результаты выражаются в виде уникального раздела всего набора объекты.

Иерархические алгоритмы могут быть разделительными или агломеративными. Разделительный метод начинается со всех случаев в одном кластере. Этот кластер постепенно разбивается на все более мелкие кластеры.Агломеративные методы обычно начинаются с одночленных кластеров, которые последовательно сливаются до тех пор, пока не образуется один большой кластер. На начальном этапе два объекта с наименьшим расстоянием (или наибольшим сходством) объединяются в кластер. На следующем этапе идентифицируется и изучается объект с наименьшим расстоянием до любого из первых двух. Если он ближе к четвертому объекту, чем к любому из первых двух, третий и четвертый объекты становятся вторым кластером из двух случаев; в противном случае третий объект включается в первый кластер.Процесс повторяется, добавляя наблюдения к существующим кластерам, создавая новые кластеры или объединяя уже возникшие до тех пор, пока каждый объект не будет исследован и не выделен в один кластер или не станет отдельным кластером сам по себе. На каждом этапе процесса формируется другой раздел, вложенный в раздел, созданный на следующем этапе. Обычно исследователь выбирает тот раздел, который оказывается наиболее значимым для конкретного приложения.

Расстояние и сходство являются ключевыми понятиями в контексте кластерного анализа.Большинство алгоритмов, особенно те, которые дают иерархические разбиения, начинаются с матрицы расстояния или подобия. Записи ячеек этой матрицы представляют собой расстояния или сходства между парами объектов. Существует много типов расстояний, из которых наиболее распространенным является евклидово расстояние. Евклидово расстояние между любыми двумя объектами — это квадратный корень из суммы квадратов разностей всех координат векторов, определяющих каждый объект. Его можно использовать для переменных, измеряемых на интервальной шкале.Когда для расчета расстояния используются две или более переменных, доминирует переменная с большей величиной. Чтобы избежать этого, принято сначала стандартизировать все переменные.

Выбор типа расстояния имеет решающее значение для всех алгоритмов иерархической кластеризации и зависит от характера переменных и ожидаемой формы кластеров. Например, евклидово расстояние имеет тенденцию давать сферические кластеры. К другим часто используемым расстояниям относятся манхэттенское расстояние, расстояние Чебышева, расстояние степени и процентное расхождение.Манхэттенское расстояние определяется как среднее расстояние между переменными. В большинстве случаев он дает результаты, аналогичные простому евклидову расстоянию. Однако влияние одиночных больших разностей (выбросов) ослабляется (поскольку они не возведены в квадрат). Расстояние Чебышева может быть уместно, когда объекты, отличающиеся только одной переменной, следует считать разными. Дистанция степени используется, когда важно увеличить или уменьшить прогрессивный вес, который присваивается переменным, по которым соответствующие объекты сильно различаются.Дистанция мощности управляется двумя определяемыми пользователем параметрами, r и p . Параметр p управляет прогрессивным весом, который присваивается различиям отдельных переменных, а параметр r управляет прогрессивным весом, который присваивается большим различиям между объектами. Если r и p равны 2, то это расстояние равно евклидову расстоянию. Процент расхождений можно использовать, когда данные состоят из категориальных переменных.

Правила связывания

Когда кластеры состоят из одного объекта, расстояние между ними можно рассчитать с помощью любого из вышеупомянутых расстояний. Однако когда кластеры формируются двумя или более объектами, необходимо определить правила для расчета этих расстояний.

Расстояние между двумя кластерами может быть определено как расстояние между двумя ближайшими объектами в двух кластерах. Этот подход, известный как правило ближайшего соседа, связывает объекты вместе и имеет тенденцию формировать цепные кластеры.

Другими популярными правилами связывания являются среднее значение пары-группы и центроид пары-группы. Первое из этих правил определяется как среднее расстояние между всеми парами объектов в двух разных кластерах. Этот метод имеет тенденцию формировать естественные отчетливые группы объектов. Центроид парной группы — это расстояние между центроидами или центрами тяжести кластеров.

Наиболее часто используемым методом неиерархической кластеризации является алгоритм k -средних, основанный на принципах дисперсионного анализа.На самом деле его можно рассматривать как дисперсионный анализ в обратном направлении. Если число кластеров зафиксировано как k , алгоритм начнет с k случайных кластеров, а затем переместит объекты между ними с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами.

Хорхе Бакаллао Галлестей Редакторы Британской энциклопедии

Шкалы измерения / Уровень измерения

Четыре шкалы измерения

Посмотрите видео с обзором четырех шкал измерения.

Видео не видно? Кликните сюда.

Данные можно классифицировать по одной из четырех шкал: номинальной, порядковой, интервальной или относительной. Каждый уровень измерения имеет некоторые важные свойства, которые полезно знать. Например, только шкала отношений имеет значащие нули.

На круговой диаграмме отображаются группы номинальных переменных (т. е. категории).

1. Номинальная шкала. Номинальные переменные (также называемые категориальными переменными) могут быть помещены в категории. Они не имеют числового значения , поэтому их нельзя складывать, вычитать, делить или умножать. У них тоже нет порядка; если кажется, что они имеют порядок, то у вас, вероятно, вместо этого есть порядковые переменные.

Порядковая шкала классифицирует по рангу.

2. Порядковая шкала. Порядковая шкала содержит вещи, которые можно расположить по порядку. Например, от самого горячего к самому холодному, от легкого к самому тяжелому, от самого богатого к самому бедному. По сути, если вы можете ранжировать данные по 1-му, 2-му, 3-му месту (и так далее), то у вас есть данные в порядковой шкале.

3. Интервальная шкала. Интервальная шкала имеет упорядоченные числа со значимыми делениями. Температура находится на интервальной шкале: разница в 10 градусов между 90 и 100 означает то же самое, что и 10 градусов между 150 и 160. Сравните это с рейтингом средней школы (который является порядковым), где разница между 1-м и 2-м может быть 0,01. и между 10 и 11 .5. Если у вас есть значимые деления, у вас есть что-то на шкале интервалов.

Вес измеряется на шкале соотношений.

4. Шкала соотношений. Шкала отношений точно такая же, как и шкала интервалов, с одним важным отличием: ноль имеет смысл. Например, высота, равная нулю, имеет смысл (это означает, что вы не существуете). Сравните это с нулевой температурой, которая, пока существует, ничего особенного не значит (хотя, надо признать, по шкале Цельсия это точка замерзания воды).

Ссылки

Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Додж, Ю. (2008). Краткая энциклопедия статистики. Спрингер.
Эверитт, Б.С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .

7 типов шкал измерения данных в исследованиях

Шкалы измерения в исследованиях и статистике — это различные способы определения переменных и группировки их в разные категории. Иногда называемый уровнем измерения, он описывает характер значений, присвоенных переменным в наборе данных.

Термин «шкала измерения» происходит от двух ключевых слов в статистике, а именно; измерение и масштаб. Измерение — это процесс записи наблюдений, собранных в рамках исследования.

Масштабирование, с другой стороны, представляет собой присвоение объектам чисел или семантики. Эти два слова, объединенные вместе, относятся к взаимосвязи между назначенными объектами и записанными наблюдениями.

Что такое шкала измерения?

Шкала измерения используется для квалификации или количественного определения переменных данных в статистике. Он определяет тип методов, которые будут использоваться для статистического анализа.

Существуют различные виды шкал измерения, и тип собираемых данных определяет вид шкалы измерения, которая будет использоваться для статистических измерений.Этих шкал измерения четыре, а именно; номинальная шкала, порядковая шкала, интервальная шкала и шкала отношений.

Измерительные весы используются для измерения качественных и количественных данных. Номинальная и порядковая шкалы используются для измерения качественных данных, а шкалы интервалов и отношений используются для измерения количественных данных.

Характеристики шкалы измерения

Идентичность

Идентичность определяется как присвоение чисел значениям каждой переменной в наборе данных.Рассмотрим вопросник, в котором запрашивается пол респондента, например, с вариантами «Мужской» и «Женский». Значения 1 и 2 могут быть присвоены мужчинам и женщинам соответственно.

Над этими значениями нельзя выполнять арифметические операции, поскольку они предназначены только для целей идентификации. Это характеристика номинальной шкалы.

Величина

Величина определяется как размер шкалы измерения, где числа (тождество) имеют неотъемлемый порядок от наименьшего к наибольшему.Обычно они представлены на шкале в порядке возрастания или убывания. Позиция в гонке, например, располагается от 1-го, 2-го, 3-го до наименьшего.

Этот пример измеряется в порядковой шкале, потому что он имеет как идентичность, так и величину.

Равные интервалы

Равные интервалы определяются как шкала со стандартным порядком. То есть разница между каждым уровнем на шкале одинакова. Это не относится к приведенному выше примеру с порядковой шкалой.

Каждая позиция не имеет одинаковой разницы интервалов. В гонке 1-е место может завершить гонку за 20 секунд, 2-е место — за 20,8 секунды, а 3-е место — за 30 секунд.

Переменная, которая имеет идентичность, величину и равный интервал, измеряется по шкале интервалов.

Абсолютный ноль

Абсолютный ноль определяется как характеристика, уникальная для шкалы отношений. Это означает наличие нуля на шкале и определяется отсутствием измеряемой переменной (т.г. без квалификации, без денег, без указания пола и т. д.

Уровни измерения данных  

Уровень измерения данного набора данных определяется отношением между значениями, присвоенными атрибутам переменной данных . Например, отношение между значениями (1 и 2), присвоенными атрибутам (мужской и женский) переменной (Пол), является «идентичностью». Это через. пример номинальной шкалы.

Зная различные уровни измерения данных, исследователи могут выбрать лучший метод статистического анализа.Существуют различные уровни измерения данных: номинальная, порядковая, интервальная шкала и шкала отношений

Номинальная шкала

Номинальная шкала — это шкала измерения, которая используется для целей идентификации. Это самый холодный и самый слабый уровень измерения данных среди четырех.

Иногда называемая категориальной шкалой, атрибутам присваиваются номера для облегчения идентификации. Однако эти числа не являются качественными по своей природе и действуют только как ярлыки.

Единственным статистическим анализом, который может быть выполнен на номинальной шкале, является подсчет процентов или частоты.Его можно проанализировать графически, используя гистограмму и круговую диаграмму.

Пример номинальной шкалы

В приведенном ниже примере популярность политической партии измеряется по номинальной шкале.

К какой политической партии вы относитесь?

• Независимый
• Республиканский
• Демократический

Обозначение независимого как «1», республиканца как «2» и демократа как «3» никоим образом не означает, что какой-либо из атрибутов лучше, чем другой.Они просто используются в качестве идентификатора для удобного анализа данных.

Порядковая шкала

Порядковая шкала включает ранжирование или упорядочение атрибутов в зависимости от масштабируемой переменной. Элементы этой шкалы классифицируются в соответствии со степенью встречаемости рассматриваемой переменной.

Атрибуты в порядковой шкале обычно располагаются в порядке возрастания или убывания. Он измеряет степень появления переменной.

Порядковая шкала может использоваться в исследованиях рынка, рекламе и опросах удовлетворенности клиентов.Он использует квалификаторы, такие как очень, очень, больше, меньше и т. д., чтобы описать степень.

Мы можем выполнять статистический анализ, например, медиану и моду, используя порядковую шкалу, но не среднее значение. Однако существуют и другие статистические альтернативы среднему, которые можно измерить с помощью порядковой шкалы.

Пример порядковой шкалы

Например: Компании-разработчику программного обеспечения может понадобиться спросить своих пользователей:

Как бы вы оценили наше приложение?

• Отлично
• Очень хорошо
• Хорошо
• Плохо
• Плохо

Атрибуты в этом примере перечислены в порядке убывания.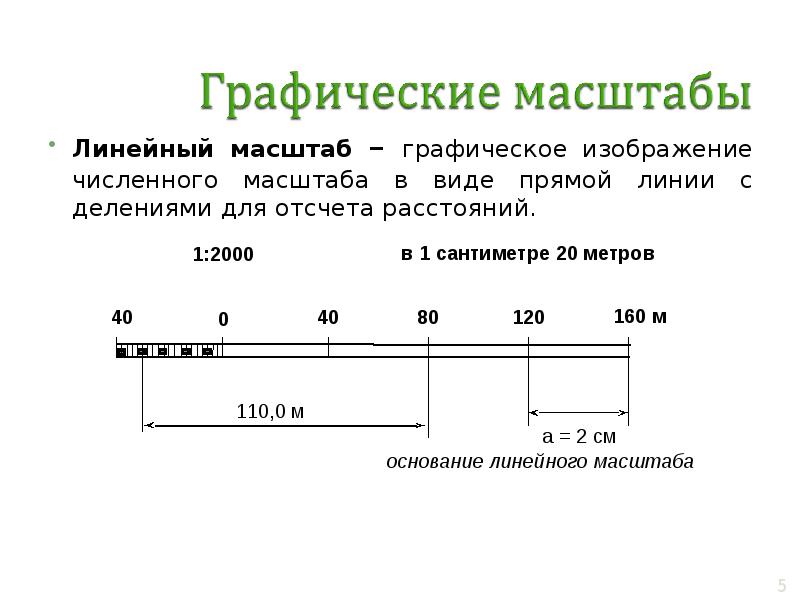

Интервальная шкала

Интервальная шкала измерения данных представляет собой шкалу, в которой уровни упорядочены и каждые численно равные расстояния на шкале имеют одинаковую интервальную разность. Если это расширение порядковой шкалы, с основным отличием в наличии равных интервалов.

С помощью шкалы интервалов вы не только знаете, что данный атрибут A больше, чем другой атрибут B, но также и степень, в которой A больше, чем B.Также, в отличие от порядковой и номинальной шкалы, арифметические операции могут выполняться на интервальной шкале.

Шкала времени с 5-минутным интервалом

Используется в различных секторах, таких как образование, медицина, инженерия и т. д. Некоторые из этих применений включают расчет CGPA учащегося, измерение температуры пациента и т. д. 

Пример интервальной шкалы

Типичным примером является измерение температуры по шкале Фаренгейта. Его можно использовать для расчета среднего значения, медианы, режима, диапазона и стандартного отклонения.

Шкала отношений

Шкала отношений — это пиковый уровень измерения данных. Это расширение шкалы интервалов, поэтому оно удовлетворяет четырем характеристикам шкалы измерения; идентичность, величина, равный интервал и свойство абсолютного нуля.

Этот уровень измерения данных позволяет исследователю сравнивать как различия, так и относительную величину чисел. Некоторые примеры шкал отношений включают длину, вес, время и т. Д.

Что касается исследования рынка, примерами шкалы общих отношений являются цена, количество клиентов, конкуренты и т. д. Она широко используется в маркетинге, рекламе и коммерческих продажах.

Шкала отношений измерения данных совместима со всеми методами статистического анализа, такими как меры центральной тенденции (среднее, медиана, мода и т. д.) и меры дисперсии (диапазон, стандартное отклонение и т. д.).

Пример шкалы отношений

Например: Опрос, который собирает веса респондентов.

К какой из следующих категорий вы относитесь? Весят

• более 100 кг
• 81 — 100 кгс
• 81 — 100 кгс
• 61 — 80 кг
• 40 — 60 кг
• 40 — 60 кг
• менее 40 кг
• , менее 40 кг

Как собрать номинальные, порядковые, интервальные и соотношения данных с Formplus  

Formplus — лучший инструмент для сбора номинальных, порядковых, интервальных и относительных данных. Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные.Выполните следующие шаги, чтобы собрать данные о Formplus

Шаг 1 — выберите функцию

Мы будем использовать вопросы с несколькими вариантами ответов для сбора данных о конструкторе форм Formplus.

• Зарегистрируйтесь или войдите в свою учетную запись на https://www. formpl.us/
• Перейдите на вкладку «Параметры выбора» в меню конструктора форм.
• Нажмите на переключатель.

Шаг 2 — Редактировать форму

Номинальные данные

• Нажмите кнопку редактирования, чтобы отредактировать форму.
• Отредактируйте вопрос и варианты выбора.
• Нажмите кнопку «Сохранить», чтобы сохранить изменения.

Порядковые данные

• Повторить Шаг 1 .
• Нажмите кнопку редактирования, чтобы изменить форму.
• Изменить вопрос и варианты выбора
• Присвоить значения вариантам выбора.
• Нажмите кнопку «Сохранить», чтобы сохранить изменения.

Интервальные данные

• Нажмите на знак «+» внизу, чтобы добавить новую страницу.

• Повторить Шаг 1 .
• Нажмите кнопку редактирования, чтобы изменить форму.
• Отредактируйте вопрос и варианты выбора.
• Нажмите кнопку «Сохранить», чтобы сохранить изменения.

Примечание : параметры интервальных данных не имеют нулевого значения.

Данные соотношения

• Повторить Шаг 1 .
• Нажмите кнопку редактирования, чтобы изменить форму.
• Отредактируйте вопрос и варианты выбора.
• Нажмите кнопку «Сохранить», чтобы сохранить изменения.
• Нажмите кнопку «Сохранить» в правом верхнем углу, чтобы сохранить форму.

Примечание: пример данных отношения имеет нулевое значение, что отличает его от интервальной шкалы.

Шаг 3. Настройка и предварительный просмотр формы

Типы шкал измерения

Существует два основных типа шкал измерения, а именно; сравнительные шкалы и несравнительные шкалы.

Сравнительные шкалы 

При сравнительной шкале респондентов просят сравнить один объект с другим. При использовании в маркетинговых исследованиях клиентов просят оценить один продукт в прямом сравнении с другими. Сравнительные шкалы можно дополнительно разделить на парное сравнение, ранговый порядок, постоянную сумму и шкалы q-сортировки.

Шкала парного сравнения — это метод шкалы, который представляет респондентам одновременно два объекта и предлагает им выбрать один в соответствии с заранее определенным критерием.Исследователи продуктов используют его в сравнительных исследованиях продуктов, предлагая покупателям выбрать наиболее предпочтительный для них продукт из двух тесно связанных продуктов.

Например, в последней версии программного продукта появилось 3 новых функции. Но компания планирует удалить одну из этих функций в новой версии. Поэтому исследователи продукта проводят сравнительный анализ наиболее и наименее предпочтительной функции.

1. Какая функция из следующих пар наиболее предпочтительна для вас?

• Фильтр — Диктофон
• Фильтр — Видеомагнитофон
• Диктофон — Видеомагнитофон
• Шкала ранжирования:

При ранжировании респондентам одновременно предоставляется техника масштабирования. в порядке приоритета на основе заранее определенного критерия.Он в основном используется в маркетинге для измерения предпочтения бренда, продукта или функции.

При использовании в конкурентном анализе респондента могут попросить ранжировать группу брендов с точки зрения личных предпочтений, качества продукции, обслуживания клиентов и т. д. Результаты сбора этих данных обычно получают в ходе совместного анализа, поскольку клиентов, чтобы различать варианты.

Шкала ранжирования является типом порядковой шкалы, поскольку она упорядочивает атрибуты от наиболее предпочтительных к наименее предпочтительным, но не имеет определенного расстояния между атрибутами.

Например:

Расположите следующие бренды от наиболее предпочтительных до наименее предпочтительных.

• Coca-Cola
• Pepsi Cola
• Dr перец
• Mountain Dew
• Шкала постоянной суммы

Шкала постоянной суммы — это тип шкалы измерения, где как очки, доллары, фишки или жетоны среди объектов-стимулов по какому-то заданному критерию.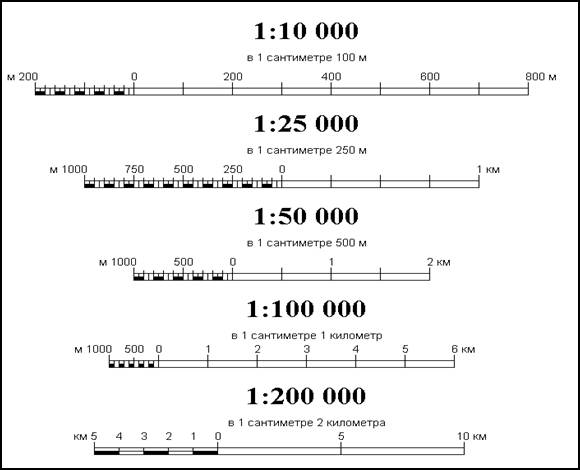 Шкала с постоянной суммой присваивает каждому атрибуту фиксированное количество единиц, отражая важность, которую респондент придает ему.

Этот тип шкалы измерения можно использовать для определения факторов, влияющих на решение покупателя при выборе продукта для покупки. Например, вы можете определить, насколько важны цена, размер, аромат и упаковка для покупателя при выборе марки духов для покупки.

Некоторые из основных недостатков этого метода заключаются в том, что респонденты могут быть сбиты с толку и в конечном итоге присвоить больше или меньше баллов, чем указано.Исследователям остается иметь дело с группой данных, которые неоднородны и могут быть трудны для анализа.

Избегайте этого с помощью функции логики в Formplus. Эта функция позволяет добавить ограничение, запрещающее респонденту добавлять больше или меньше баллов, чем указано в вашей форме.

Шкала Q-сортировки — это тип шкалы измерений, использующий технику ранжирования для сортировки сходных объектов по некоторому критерию. Респонденты сортируют количество утверждений или установок в стопки, обычно по 11.

Масштабирование Q-Sort помогает присваивать ранги разным объектам в одной группе, и различия между группами (стопками) четко видны. Это быстрый способ облегчить различение среди относительно большого набора атрибутов.

Например, новый ресторан, который только готовит свое меню, может захотеть собрать некоторую информацию о том, что нравится потенциальным клиентам:

Предоставленный документ содержит список из 50 блюд. Пожалуйста, выберите 10 блюд, которые вам нравятся, 30 блюд, к которым вы относитесь нейтрально (ни нравится, ни не нравится) и 10 блюд, которые вам не нравятся.

Несравнительные шкалы  

При несравнительной шкале клиентов просят оценить только один объект. Эта оценка совершенно не зависит от других исследуемых объектов. Иногда называемая монадической или метрической шкалой, несравнительная шкала может быть далее разделена на непрерывную и детализированную шкалы оценок. критерий к другому переменному критерию.Также называемая графической оценочной шкалой, она дает респонденту возможность поставить оценку в любом месте в зависимости от личных предпочтений.

После получения оценок исследователь делит строку на несколько категорий, а затем присваивает баллы в зависимости от категории, к которой относятся оценки. Этот рейтинг можно визуализировать как в горизонтальном, так и в вертикальном виде.

Несмотря на простоту построения, непрерывная рейтинговая шкала имеет ряд существенных недостатков, что ограничивает ее использование в маркетинговых исследованиях.

Детализированная рейтинговая шкала — это разновидность порядковой шкалы, в которой каждому атрибуту присваиваются номера. Респондентов обычно просят выбрать атрибут, который лучше всего описывает их чувства по заранее определенному критерию.

Детализированная рейтинговая шкала далее делится на 2, а именно; Шкала Лайкерта, шкала Стапеля и семантическая шкала.

Шкала Лайкерта — это порядковая шкала с пятью категориями ответов, которая используется для упорядочивания списка атрибутов от лучшего к наименьшему. В этой шкале используются наречия степени, такие как очень сильно, сильно и т. Д., Для обозначения разных уровней.

Это шкала с 10 категориями, обычно от -5 до 5 без нуля. Это вертикальная шкала с 3 столбцами, где атрибуты расположены посередине, а наименьшее (-5) и максимальное (5) — в 1-м и 3-м столбцах соответственно.

• Семантическая дифференциальная шкала

Это семибалльная рейтинговая шкала с конечными точками, связанными с биполярными метками (например,г. хороший или плохой, счастливый и т. д.). Его можно использовать для маркетинга, рекламы и на разных этапах разработки продукта.

Если по своей сути исследуется более одного элемента, его можно визуализировать в таблице с более чем 3 столбцами.

Заключение  

В двух словах, шкалы измерения относятся к различным мерам, используемым для количественной оценки переменных, которые исследователи используют при проведении анализа данных. Они являются важным аспектом исследований и статистики, поскольку именно уровень измерения данных определяет используемый метод анализа данных.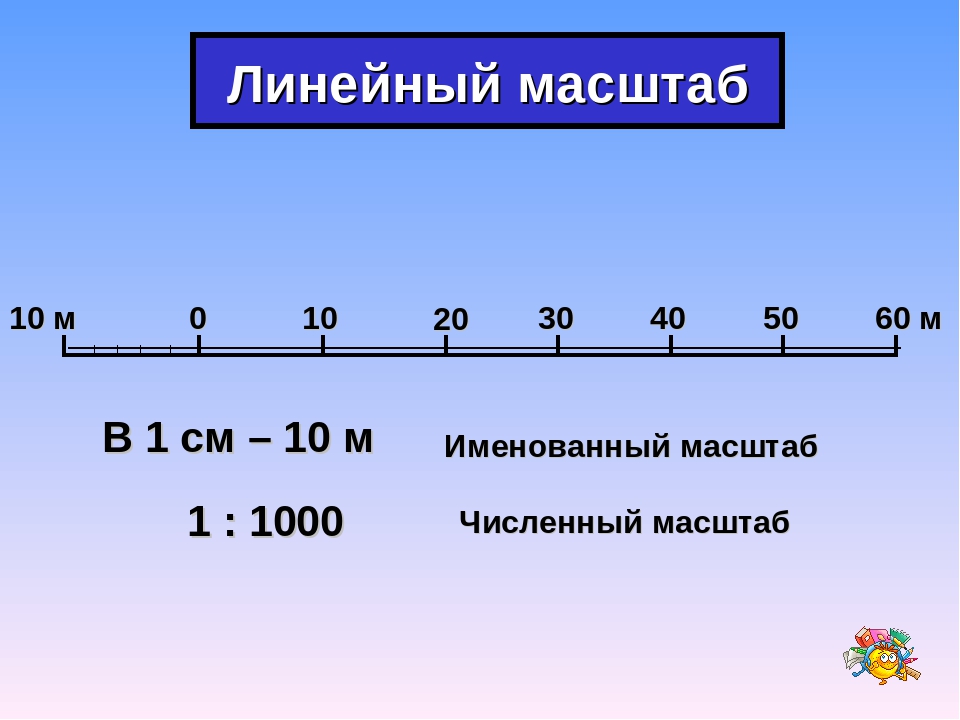

Понимание концепции шкал измерений является необходимым условием для работы с данными и выполнения статистического анализа. Различные шкалы измерения имеют некоторые схожие свойства, и поэтому важно правильно проанализировать данные, чтобы определить их шкалу измерения, прежде чем выбирать метод для анализа.

Существует несколько методов масштабирования для измерения одной и той же шкалы измерений. Поэтому не существует единого способа выбора метода масштабирования для исследовательских целей.

Шкалы измерений и типы данных

 

В статистическом анализе важно знать о различных шкалах измерения, а именно:

• ИНТЕРВАЛ
  Шкала с фиксированным и определенным интервалом, например. температура или время.
• НОМЕР
  Шкала для упорядочивания наблюдений от низкого к высокому с любыми связями, связанными с недостаточной чувствительностью измерения e. г. балл из анкеты.
• НОМИНАЛ при заказе
  Шкала для группировки по категориям с порядком напр. легкой, средней или тяжелой степени. Это может быть трудно отделить от порядкового номера.
• НОМИНАЛ без заказа
  Шкала для группировки по уникальным категориям, например. цвет глаз.
• ДИХОТОМИЧЕСКИЙ
  Как для номинального, но только две категории e.г. мужской женский.
  

 

В дополнение к классификации шкал измерений для описания типов данных используются другие родственные термины:

 

• КАТЕГОРИЧЕСКАЯ и ЧИСЛОВАЯ (количественная или качественная)
  Данные, представляющие категории, такие как дихотомические (две категории) и номинальные (более двух категорий) наблюдения, в совокупности называются категориальными (качественными).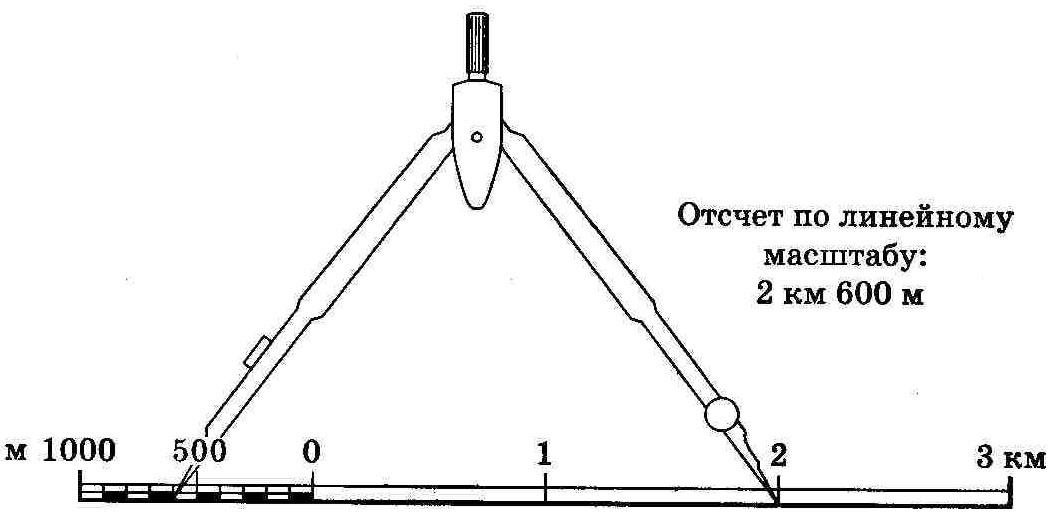 Данные, которые подсчитываются или измеряются численно определенным методом, называются числовыми (количественными).
• ДИСКРЕТНЫЙ и ПОРЯДОЧНЫЙ КАТЕГОРИЧЕСКИЙ
  Дискретные данные получаются из наблюдений, которые могут принимать только определенные числовые значения, обычно подсчеты, такие как количество детей или количество пациентов, посещающих клинику за год. Упорядоченные категориальные данные иногда обрабатываются как дискретные данные, это неправильно. Например, используя классификацию социального класса Генерального регистратора, было бы неправильно говорить, что класс I в пять раз превышает социально-экономический статус класса V, поскольку между этими категориями нет строгой числовой зависимости.Из этого следует, что средний социальный класс является бессмысленной статистикой. Таким образом, упорядоченные категориальные данные не следует рассматривать как дискретные данные для статистического анализа. Дискретные данные можно рассматривать как упорядоченные категориальные данные в статистическом анализе, но при этом теряется некоторая информация.
• НЕПРЕРЫВНЫЙ
  Непрерывные данные — это числовые данные, которые теоретически могут быть измерены в бесконечно малых единицах. Например, кровяное давление обычно измеряется с точностью до 2 мм рт. ст., но оно может быть измерено с гораздо большим разрешением разницы.Шкала интервальных измерений предназначена для непрерывных данных. Иногда непрерывным данным при определенных пороговых значениях присваиваются дискретные значения, например, возраст последнего дня рождения является дискретным значением, но сам возраст является непрерывной величиной; в этих ситуациях разумно рассматривать дискретные значения как непрерывные. Помните, что информация теряется, когда непрерывные данные записываются только в диапазонах (упорядоченных категориях), а статистический анализ непрерывных данных является более мощным, чем анализ категорийных данных.
• ПРОЦЕНТЫ и ОТНОШЕНИЯ
  Проценты или отношения обобщают две части информации, а именно составляющие их значения числителя и знаменателя. Простые соотношения (от 0 до 1, т. е. знаменатель — это максимально возможное значение, которое может принимать числитель) можно рассматривать как непрерывные данные. Более сложные для анализа данные возникают, когда отношение представляет собой изменение, и значение может быть отрицательным. Отношения наблюдений по сравнению с эталонными значениями, т.е.г. рост по отношению к среднему значению референтной популяции для данного пола и возраста трудно обрабатывать, поскольку значения могут падать в обе стороны от 1 (100%).

 

Многие статистические методы подходят только для данных определенных шкал измерения. При выборе статистического метода важно понимать, как были измерены данные для анализа. Лучшей стадией исследования для обдумывания шкал измерений является стадия проектирования, на которой статистические ограничения, накладываемые определенными шкалами измерений, могут повлиять на ваш выбор наблюдений и методов измерения.

 

Обратите внимание, что преобразование данных изменяет их шкалу измерения.