ООО «СТАММ» Счеты первоклассника (АБАК) — «Хороший тренажер для обучения ребенка счету в пределах 20-ти! С выдвигающимися полосками и кружками другого цвета! Можно наглядно все объяснить и показать ребенку как на одной строке, так и на двух! ФОТО + принципы работы!»
Увидела такой абак в книжном магазине, решила купить ребенку. Ему, конечно, до школьной математики еще далеко, еще дошкольный возраст.., но он уже очень любит все считать по порядку, знает цифры и фигуры.

Абак в сложенном виде
В качестве счетного материала абак ему очень понравился. С ним можно примитивно поиграть, выдвигая и задвигая назад эти две полосочки. А также этим же способом — учиться считать. Например, можно объяснять элементарные примеры: 2+1= — выдвинули на верхней строке полоску на 2 белых кружка (проговариваем: «Два»), выдвигаем на нижнем ряду полоску на один кружок (выдвигая полоски, мы видим, что кружочки становятся белыми, а не красными) -( проговариваем: «плюс один, равно…») Предлагаем ребенку посчитать (если умеет) или считаем вместе, сколько получилось: «один, два, три». И проговариваем пример полностью, с ответом: «Два плюс один равно три».

Абак в процессе вычислений
Аналогично можно работать с вычитанием.
С абаком можно осваивать счет в пределах 20-ти.
Кружочки расположены в два ряда, в каждом ряду 10 кружков. При этом десяток можно увидеть не только горизонтально (в один ряд), но и в два ряда, но по 5 кружков. За счет того, что пятерки тоже отделены, можно учить считать пятерками. А также, в дальнейшем, думаю, можно азам умножения на абаке обучить: 5Х2= (Возьмем 5 раз по 2 кружка, получим….(выдвигаем одновременно обе полоски на одно деление пять раз) или 2Х5= (возьмем 2 раза по 5 кружков, получим….(выдвигаем сначала одну полоску на 5 кружочков, а затем — другую). В итоге, считали немного по-разному, но результат один (10).
Так можно объяснить, что от перемены мест слагаемых (множителей) сумма (произведение) не меняется.
В математическом плане очень хорошо использовать, поможет освоить сложение, вычитание и даже умножение в пределах 20-ти. Также на самом абаке по краю еще есть линейка. А на обратной стороне некоторая информация из сферы математики, геометрии.

Обратная сторона абака
Очень полезная штука! Поможет в освоении математики!
irecommend.ru
Абакус (Что это, Зачем и Как Обучаться)
Абакус (лат. abacus доска) счетная доска начала использоваться для арифметических вычислений с V века до н.э. в Древнем Риме и Греции.
Изначально абак представлял собой доску, разделенную линиями на полосы, а счет осуществлялся с помощью камушек или похожих предметов.
Примером современного абакуса послужил найденный 2200 лет назад на Дальнем Востоке абак, состоящий из рамки с прутьями, нанизанными на них деревянными бусинками.
Казалось бы, простой на вид предмет древности, ставший неотъемлемым предметом для счета в древности и неотъемлемой частью культуры Дальнего Востока, по своей сути является конкурентом современному компьютеру.
В XV веке абакус перекочевал в Японию, получив еще одно название — Соробан, и активно используется по сегодняшний день в системе образования младших классов для обучения счета вместо калькулятора.
Рамка — Держит все спицы, бусинки и разделительную линейку ва месте.
Спица — Это палочки, которые держат бусинки. Они двигаются вверх иди вниз по спине
Бусинки — Представляют числа на абакусе. Они двигаются по спице и прикасаются к разделительной линейке или рамке. Когда бусинки прикасаются к рамке, что значит ваш абакус обнулен.
Разделительная линейка — Линейка (обычно белая) которая пересекает все спины и разделяет их на «Братья» и «Друзья» бусинки. Только когда бусинки прикасаются к разделительной линейке, у них есть какое-то значение.
Единичная точка — Может быть использована как десятичная точка. Может быть использована как занятая, которая разделяет числа на тысячи.
Например: 102,387,555 = Сто два миллиона, триста восемьдесят семь тысяч, пятьсот пятьдесят пять
Бусинки — братья — Над разделительной линейкой есть только одна бусинка «брат» на каждой спице, бусинка «брат»
Бусинки — друзья — Есть четыре бусинки-друга под разделительной линейкой на каждой спице. Каждая бусинка-друг равна » 1 »
Обнуление абакуса Традиционный способ
ШАГ 1: Поместите аоакус на столе.
ШЛГ 3: Осторожно поместите абакус назад на стол, не двигая нижние бусинки.
ШАГ 4; Затем, положите палец между верхней бусинкой и разделительнрой линейкой с левой стороны абакуса.
ШАГ 5: Проведите пальцем вдоль разделительной линейки пока не достигнете другого конца рамки.
Забавный способ; наездиочищение или паровоз
ШАГ 1: Соедините большой и указательный
ШАГ 2: Поместите пальцы с правой стороны разделитель нон линейки абакуса так, чтобы линейка была между пальцами и вы держите линейку.
ШАГ 3: Теперь поддерживайте абакус левой рукой так, чтобы он не двигался.
ШАГ 4: Затем, плавно проведите пальцами вдоль разделительной линии не разжимая с правой стороны рамки до левого края рамки.
Слева направо: Когда работаете c двузначными числами: всегда прибавлявляйте и отнимайте сначала десятичные цифры, а за тем работаете с единичными числами
Урок 1 . Бусинки- Друзья.
Значение бусинки-друга=1
Есть четыре бусинки-друга на каждой спице.
Используйте свой большой палец для того, чтоб подвинуть бусинки-друга вверх (прибавляя) гак, пок она не коснется разделительной линейки. Используйте свой указательный палец тля топ чтобы подвинуть бусинку-друга вниз (вычитая). Всегда обнуляйте абакус, вычищая все бусинки с разделительной линейки перед тем, как начать новы с чет. Установление цифр па абакусе:
— Номера десятичных чисел возвращаются к десятичной спице;
— Единичные числа возвращаются к единичной спице.
Урок 2. Введение. Бусинки-братья.
1. Значение бусинки-брата — 5
2. Есть только I бусикка-брат над разделительной линейкой на каждой спице.
3. Используйте свой указательный п*лдсц для того. чтобы подвинул. бусинку-брата вниз (прибавляя) лак. пока она не коснел ся разделительной линейки.
4. Используйте свой указательный пален для того, чтобы подвинуть бусинку-брата вверх (вычитая) так. пока она не коснется рамки.
5. Всегда обнуляйте абакус, вычищая нее бусинки от разделительной линейки перед тем. как начать новый счет.
6. Установление цифр на абакусе:
— Номера десятичных чисел возвращаются к десятичной спице;
— Единичные числа возвращаются к единичной спице.
mentalar.ru
Рабдологический абак Клода Перро / ua-hosting.company corporate blog / Habr
Французский ученый и архитектор Клод Перро, брат знаменитого сказочника Шарля Перро, изобрел оригинальное счетное устройство — рабдологический абак. Суммирующая машина стала ценным дополнением XVII –XVIII веков, периода, достаточно богатого на изобретения счетных приборов.
Клод Перро (1613-1688)
Перро дал своему изобретению наименование в духе древних времен, когда абаком называли небольшую доску, на которой писали цифры. И поскольку машина выполняла арифметические операции с помощью маленьких палочек с цифрами, то посчиталась рабдологической.

римский абак
Впервые устройство упоминалось в книге «Сборник большого числа машин собственного сочинения» (1700 год) Клода Перро, изданной посмертно. В сборнике находились описания практически всех изобретений автора («маятниковые часы», «машина для поднятия тяжести», «машина для увеличения эффекта огнестрельного оружия» и т.д). Рабдологический абак значился под номером десять.
Это была компактная и простая вычислительная машина, отметившаяся в истории благодаря существенному отличию от других изобретенных устройств своей области. Вместо привычных зубчатых колес Паскаля, в рабдологическом абаке использовались зубчатые рейки (кремальеры).
Счетная машина была в виде пластины с палец толщиной, высота достигала примерно 30 см., а ширина — 14 см. На лицевой стороне устройства было вырезано два окошка, где отображались результаты. В верхнем окошке демонстрировался результат вычитания, а в нижнем – сложения. В нижней части лицевой стороны была выгравирована таблица умножения.

Кроме того на лицевой стороне было прорезано семь пазов, вдоль которых размещались шкалы с делениями 1, 2, 3, 4, 5, 6, 7, 8, 9. В пазах находились линейки. С помощью штифта с заостренным кончиком, они передвигались вверх и опускались вниз к основанию устройства.
Глубокие риски разделяли каждую линейку на 26 частей. В риски вставлялось острие штифта, что позволяло с легкостью и необходимой точностью перемещать линейки. В верхних одиннадцати делениях линейки находилась возрастающая последовательность (0,1,2,3,4,5,6,7,8,9,0) для вычитания. В нижних одиннадцати делениях размещалась последовательность, которая убывала (0,9,8,7,6,5,4,3,2,1,0). Соответственно, она использовалась для сложения. Цифры этих последовательностей показывались в окошках результата. В нижнем окошке они были искомой величиной сложения, а в верхнем окошке — искомой величиной вычитания.
Последовательности, нанесенные на линейки, отделялись друг от друга четырьмя пустыми делениями.
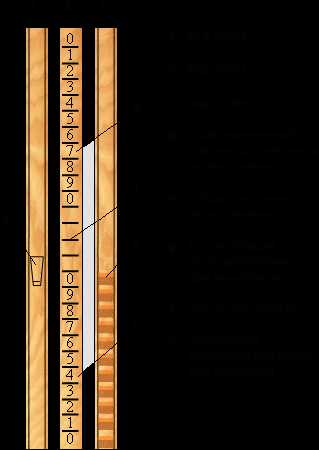
В суме устройство использовало семь линеек, которые были отделены друг от друга тонкими пластинками. В линейках соблюдалась последовательность по возрастанию. Крайняя правая символизировала разряд единиц, следующая за ней линейка представляла разряд десятков, далее — сотен и так вплоть до разряда миллионов.
В каждой пластинке, отделяющей линейки друг от друга, имелось отверстие. Оно использовалось для переноса переполнения из младшего разряда в старший и находилось у основания линейки, придвинутой к самому верху устройства. Размером отверстие достигало трех делений линейки.
У каждой линейки возле основания правой стороны располагалось 11 зубцов — по одному на деление. С другой стороны линейки (если считать снизу — под 11 и 12 делением) находился подпружиненный крючок. Зубцы и крючок использовались для переноса переполнения из младшего разряда в старший.

Перенос из младшего разряда в старший происходил следующим образом. Когда планка младшего разряда находилась в верхней части устройства (то есть в окошках результата сложения и вычитания находились нули), подпружиненный крючок был скрыт в теле линейки, упираясь в пластинку, располагающуюся слева от нее. По мере продвижения линейки вниз, подпружиненный крючок приближался к отверстию в пластинке. Когда в окошке результата сложения появлялась принадлежащая передвигаемой линейке цифра 7, подпружиненный крючок начинал выдвигаться в отверстие планки, и в момент, когда в окошке результата появлялась цифра 9, входил в зацепление с зубцами линейки старшего разряда. В дальнейшем передвижение линейки младшего разряда перемещало линейки старшего разряда. В итоге, когда в окошке результатов сложения появлялась цифра 0 линейки младшего разряда, следующая за цифрой 9, линейка старшего разряда передвигалась ровно на одно деление вниз за счет сцепления крючка с зубцами.

Пример операции сложения 127+65
Шаг 1. Сперва все разряды рабдологического абака устанавливаются на 0. Для этого с помощью штифта линейки передвигаются в крайнее верхнее положение.
Шаг 2. Штифт ставится в паз на риску линейки младшего разряда, находящуюся напротив цифры 7. Линейка сдвигается до тех пор, пока штифт не упрется в нижний торец паза. При этом в окошке результата сложения в младшем разряде отобразится вводимое число 7. Важный момент — в окошке результата вычитания в младшем разряде будет отображаться число, необходимое для дополнения семерки до десяти, то есть цифра 3.
Шаг 3. Аналогичная операция продлевается и с разрядом десяток, только в этом случае паз устанавливается напротив цифры 2.
Шаг 4. Для разряда сотен паз устанавливается напротив цифры 1. Далее паз передвигается вниз до упора, то есть на одно деление. В окошке результата сложения будет отображено число 127.
Шаг 5. Следующее действие — ввод второго слагаемого. Штифт устанавливается в паз на риску линейки младшего разряда, находящуюся напротив цифры 5, линейка сдвигается вниз до упора. При этом штифт остановится напротив цифры 2, так как линейка упрется в нижнюю стенку устройства раньше, чем штифт достигнет нижнего торца паза. В тоже время линейка разряда десяток опустится на одно деление вниз, за счет работы механизма переноса переполнения. В окне результата сложения отобразится цифра 130.
Шаг 6. Для того, чтобы получить верную цифру в разряде единиц — 2, следует, не извлекая штифта из прорези, продвинуть линейку вверх, пока штифт не упрется в торец паза. Таким образом, в окне результата сложения отобразится цифра 132.
Шаг 7. Завершающий этап — вводится разряд десятков второго слагаемого. Для этого штифт устанавливается в паз на риску линейки разряда десятков, находящуюся напротив цифры 6, линейка сдвигается вниз до упора. На этом вычисления заканчиваются, а в окошке результата сложения отображается искомое значение: 192.
Пример операции вычитания 68-23
Шаг 1. Все разряды рабдологического абака устанавливаются в 0. Для этого с помощью штифта, линейки передвигаются в крайнее верхнее положение.
Шаг 2. Вводится младший разряд уменьшаемого. Линейка младшего разряда передвигается так, чтобы в окошке результата вычитания в позиции младшего разряда отобразилась цифра 8. Чтобы этого добиться, необходимо поставить штифт в паз на риску, находящуюся напротив цифры 2, и сдвинуть линейку вниз до тех пор, пока штифт не упрется в торец паза.
Шаг 3. Далее вводится разряд десяток уменьшаемого, для чего соответствующая линейка передвигается так, чтобы в окошке результата вычитания на второй позиции отобразилась цифра 6. Для этого штифт ставится в паз на риску, находящуюся напротив цифры 4, а линейка сдвигается вниз до тех пор, пока штифт не упрется в торец паза. В итоге, окно результата вычитания отобразит число 68.
Шаг 4. Вычитаемое вводится также, как и слагаемое при сложении. Для ввода младшего разряда вычитаемого, штифт устанавливается в паз на риску линейки младшего разряда, напротив цифры 3. Линейка двигается вниз, пока штифт не упрется в торец паза. Далее вводится старший разряд вычитаемого, для чего штифт устанавливается в паз на риску второй слева линейки, напротив цифры 2. Линейка двигается вниз, пока штифт не упрется в торец паза. Разница двух чисел найдена, в окошке результата вычитания отображается искомый результат: 45.
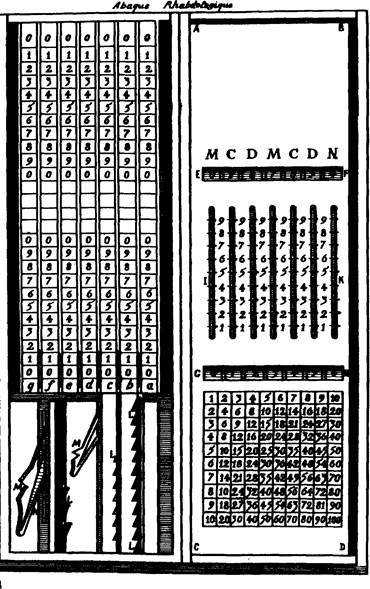
При вычитании с помощью рабдологического абака использовался прием дополнения до десяти, аналогичный способу, используемому в Паскалине.
Как пример, решение уравнения: Y=68-23=45. Используя метод дополнения, число 68 представлено в виде разницы чисел 100 и 32 (68=10-32). В результате, уравнение сводится к следующему виду: Y=68-23=100-32-23=100-(32+23)=27. Подобное преобразование заменяет вычитание на сложение и вычитание результата сложения из 100, что есть преобразование, обратное дополнению. Следовательно, остается решить задачу автоматического дополнения до десяти, для чего на всех линейках нанесено две последовательности цифр, а на крышке рабдологического абака — два окошка вывода результата, расположенных так, что суммы двух чисел, отображенных в окошках и располагающихся друг под другом, всегда равняются десяти.
В своей конструкции Перро использовал элементы, которые впервые применил шотландский математик Джон Непер в простейшем множительном приборе. Он предназначался для умножения, деления, извлечения квадратного корня и был подробно описан Непером в последней публикации при его жизни («Rabdologia seu Numerationis»,1617 год).

палочки Непера
Описание рабдологического абака показывает его отличие от существующих в то время вычислительных машин. И, что важно, устройство было довольно простым в использовании. Однако, должного признания рабдологический абак не получил. Возможно из-за ненадежности устройства подпружиненного крючка (он применялся не только для переноса, но и для фиксации реек в положениях, соответствующих вводимым числам), который при постоянной эксплуатации часто выходил из строя. Но если реализованное изобретение не стало широко использоваться на практике, то идеи Перро, впоследствии нашли применение в других простых и надежных счетных приборах («счислитель Куммера», «Комптатор Ганса Забельного» и т.д.).

«Считатель Куммера» (1846 год)
P.S. Мы проводим акцию специально для читателей Хабра. Пост с подробностями тут.
habr.com
