Аннуитет это денежный поток: что это, текущая и будущая стоимость аннуитета по формуле

Содержание

Аннуитеты в МСФО

В данной статье мы продолжим говорить о дисконтировании денежных потоков и в этот раз речь пойдет об аннуитетных денежных потоках.

Что такое аннуитет?

Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Например, фиксированная сумма зарплата, арендных выплат, платежей банку по кредиту и т.д.

Аннуитеты бывают пренумерандо и постнумерандо. Данные термины обозначают момент платежа. Термин пренумерандоозначает платежи в начале каждого периода, постнумерандо — в конце временного периода.

Формула аннуитета

Аннуитетные денежные потоки также можно дисконтировать, то есть определять их текущую стоимость. Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег.

Дисконтирование аннуитетных платежей

ПРИМЕР 1. Необходимо выбрать наиболее выгодный вариант:

А) получить 40,000 долларов сегодня или

(Б) 5 раз по 10,000 долларов в конце каждого из следующих 5 лет.

Банковская ставка для получения кредита на данный срок составляет 10%.

На первый взгляд вариант (Б) в сумме лучше (5 х 10,000 = 50,000), чем 40,000 долларов. Но действительно ли это так? Ведь мы знаем, что у денег есть еще и «временная» стоимость. Чтобы сравнить эти два варианта между собой, надо привести их к одному моменту времени (к моменту «сейчас»), поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость.

Для начала давайте вспомним, как выглядит формула дисконтирования:

PV = FV х 1/(1+R)ⁿ

где,

Future value (FV) – будущая стоимость Present value (PV) – текущая (дисконтированная/приведенная) стоимость. R – ставка процента (норма доходности, требуемая инвестором), N – число лет от даты в будущем до текущего момента

Коэффициенты дисконтирования, используемые для нашего примера

1/(1+R)ⁿ — это 0.9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:

10,000 х 0,9091 = 9,091
10,000 х 0,8264 = 8,264
10,000 х 0,7513 = 7,513
10,000 х 0,6830 = 6,830
10,000 х 0,6209 = 6,209
Итого: 37,907

Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В итоге, пять платежей по 10,000 долларов в конце каждого года с учетом дисконтирования стоят 37,907 долларов, что немного меньше, чем 40,000 сегодня. Следовательно, при ставке 10%, 40,000 долларов сегодня будет выгоднее, чем предложенный аннуитет 5 лет по 10,000 долларов.

Формулу дисконтированной стоимости аннуитета можно записать следующим образом:

PV = PMT х [1/(1+R)¹ + 1/(1+R)² + 1/(1+R)³ + 1/(1+R)

4 +1/(1+R)⁵] = 10,000 х (0.9091+0.8264+0.7513+0.6830+0.6209) = 10,000 х 3.7907 = 37,907

где PMT (от английского payment) – это сумма аннуитетного платежа.

Как Вы могли заметить, вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз. Результат сложения коэффициентов дисконтирования за 5 лет называется коэффициентом аннуитета. В данном примере коэффициент аннуитета равен 3,7907.

Таким образом, для нахождения текущей стоимости аннуитетов необходимо разовый платеж умножить на коэффициент аннуитета (10,000*3,7907 = 37,907).

Итак, мы разобрали пример с аннуитетными платежами в конце каждого года (постнумерандо) .

ПРИМЕР 2. Давайте немного изменим условия нашего примера. Необходимо выбрать наиболее выгодный вариант:

А) получить 40,000 долларов сегодня или

Б) 5 раз по 10,000 долларов в начале каждого из следующих 5 лет.

Это будет так называемый аннуитет пренумерандо.

В данной ситуации, так как первый платеж производится в начале года, то самый важный нюанс, о котором надо помнить, это то что, первый платеж не надо дисконтировать (т.е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице. Но необходимо дисконтировать остальные 4 платежа, так как они отложены во времени. Для иллюстрации составим следующую таблицу:

10,000 х 1.000 = 10,000
10,000 х 0.9091 = 9,091
10,000 х 0.8264 = 8,264
10,000 х 0.7513 = 7,513
10,000 х 0.6830 = 6,830
Итого: 41,698

Следовательно, предложенный аннуитет 5 лет по 10,000 в начале года будет выгоднее, чем 40,000 сегодня при ставке 10%.

Формула дисконтированной стоимости аннуитета:

PV = PMT + PMT х [1/(1+R)¹ + 1/(1+R)² + 1/(1+R)³ + 1/(1+R)⁴] = 10,000 + 10,000 х (0.9091+0.8264+0.7513+0.6830) = 10,000 + 10,000 х 3.1698 = 41,698

Обратите внимание, что в данном примере мы определили коэффициент аннуитета для четырех отложенных во времени платежей, а не для пяти, а первый платеж не дисконтировали.

Как видно из данных примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.

Все блоги

Аннуитетный и дифференцированный платежи: что это такое и в чем разница — Ипотека

Самые актуальные вопрос для заемщика связаны с погашением кредита: сумма и дата платежа, способы оплаты и многое другое.

Платеж по кредиту состоит из основного долга и процентов. Основной долг — это размер кредита. А проценты — это сумма, которую берет банк за пользование кредитом.

Есть два вида платежей — аннуитетный и дифференцированный. Выясняем, что это такое, и чем они отличаются друг от друга.

Аннуитетный платеж

Аннуитетные платежи одинаковы, но соотношение в них основного долга и процентов — разное. Здесь проценты за пользование начисляются на остаток долга, поэтому в начале кредита — процентов больше, основного долга — меньше. А к концу кредита — наоборот.

Однако есть случаи, когда платежи не будут одинаковыми. При выходе на пенсию в период кредита, график рассчитывается «ступенькой». До пенсии платежи считаются из текущего дохода клиента, а после — из минимального уровня пенсии.

Также аннуитетный платеж может измениться при досрочном погашении кредита.

Размер платежа клиент всегда может посмотреть в графике, который менеджер по ипотеке предоставляет на сделке.

Как погасить аннуитетный платеж

Оплата аннуитетного платежа может только безналичная. Клиент пополняет свой обычный счет, затем деньги, согласно платежному поручению, автоматически поступают на кредитный счет, который называют ссудным.

Клиент может оплатить кредит несколькими способами: через «Сбербанк Онлайн» на сайте или в приложении, через банкоматы, терминалы и в офисах Сбербанка в регионе обслуживания кредита. При себе необходимо иметь документ, удостоверяющий личность.

Дата оплаты кредита может совпадать с датой выдачи, а может и отличаться — на усмотрение заемщика. В платежную дату до 21:00 средства должны быть на счету клиента, указанном в поручении. Лучше перевести деньги накануне.

Важно! Если дата платежа выпадает на выходной или праздничный день, то списание произойдет в этот день, если на счету есть деньги. А если их нет, то пополнить счет можно в первый рабочий день после выходных. И это не будет считаться просрочкой.

Дату платежа можно менять, но не чаще 1 раза в год. Для этого надо написать заявление в отделении банка в городе выдачи кредита. При этом дата последнего кредитного платежа не меняется — она всегда будет соответствовать дню предоставления кредита.

Таким же образом можно поменять и счет списания. В новом поручении вам надо указать несколько счетов и очередность списания. Если сумма платежа больше, чем денег на первом счете, остаток спишется со второго, если и на нем не хватит средств — то с третьего и так далее.

Если по каким-то причинам заемщик не может пополнить счет, то можно погасить кредит со счета другого человека. Такой платеж делается разово, поручение на автосписание оформить нельзя. Если кредит в рублях, то счет может быть любого человека, если в валюте — только поручителя.

Дифференцированный платеж

При дифференцированном платеже ежемесячные платежи становятся меньше, сумма основного долга в платеже всегда будет одной и той же. А вот проценты, начисляемые на остаток основного долга, будут уменьшаться по мере выплаты кредита. Ежемесячная сумма основного долга считается просто — сумма кредита делится на количество платежей.

Здесь нет графика платежей, а есть срочное обязательство, по которому клиент обязуется оплачивать кредит.

Кредиты с дифференцированными платежами выдавались в Сбербанке до 2011 года, а сейчас выдаются только с аннуитетными.

Как погасить дифференцированный платеж

Оплата возможна и наличным, и безналичным способом сразуна ссудный счет. Варианты оплаты такие же, как при аннуитете: через «Сбербанк Онлайн», банкоматы или в офисе банка.

Важно! Погашение кредита не привязано к определенной дате. Клиент должен оплатить кредит не позднее 10 числа месяца, следующего за платежным.

Например, кредит выдан 13 июня 2010 года, соответственно первый платежный месяц — июль, поэтому первый платеж клиент должен осуществить не позднее 10 августа 2010 года.

Сумма платежа здесь меняется ежедневно, т.к. проценты начисляются на остаток по кредиту каждый день. Узнать актуальную сумму можно в дату погашения в офисе банка, в «Сбербанк Онлайн», банкомате и контактном центре.

Сейчас читают

Инструкция: как правильно оформить справку о доходах

Как снять обременение после выплаты ипотеки

Как досрочно погасить ипотеку

Аннуитет — это… Что такое Аннуитет?

Аннуите́т (фр. annuité от лат. annuus — годовой, ежегодный) или финансовая рента — общий термин, описывающий график погашения финансового инструмента (выплаты вознаграждения или уплаты части основного долга и процентов по нему), когда выплаты устанавливаются периодически равными суммами через равные промежутки времени. Аннуитетный график отличается от такого графика погашения, при котором выплата всей причитающейся суммы происходит в конце срока действия инструмента, или графика, при котором на периодической основе выплачиваются только проценты, а вся сумма основного долга подлежит к оплате в конце.

Сумма аннуитетного платежа включает в себя основной долг и вознаграждение.

В широком смысле, аннуитетом может называться как сам финансовый инструмент, так и сумма периодического платежа, вид графика погашения финансового инструмента или другие производные понятия, оттенки значения. Аннуитетом, например, является:

Один из видов срочного государственного займа, по которому ежегодно выплачиваются проценты, и погашается часть суммы.
Равные друг другу денежные платежи, выплачиваемые через определённые промежутки времени в счёт погашения полученного кредита, займа и процентов по нему.
Соглашение или контракт со страховой компанией, по которому физическое лицо приобретает право на регулярно поступающие суммы, начиная с определённого времени, например, выхода на пенсию.
Современная стоимость серии регулярных выплат, производимых с определенной периодичностью в течение срока, установленного договором страхования.

Аннуитетный график также может использоваться для того, чтобы накопить определённую сумму к заданному моменту времени, внося равновеликие вклады на счёт или депозит, по которому начисляется вознаграждение.

Виды аннуитетов

По времени выплаты первого аннуитетного платежа различают:

аннуитет постнумерандо — выплата осуществляется в конце первого периода,
аннуитет пренумерандо — выплата осуществляется в начале первого периода.

Коэффициент аннуитета

Коэффициент аннуитета превращает разовый платёж сегодня в платёжный ряд. С помощью данного коэффициента определяется величина периодических равных выплат по кредиту:

где — процентная ставка за один период (всего периодов n), — количество периодов на протяжении всего действия аннуитета.
(следует учитывать, что данная формула является чисто математической, то есть на практике возможны некоторые девиации, вызванные округлением, а также неодинаковой продолжительностью месяца и года; особенно это касается последнего по сроку платежа).

Предполагается, что выплаты производятся постнумерандо, то есть в конце каждого периода. И тогда величина периодической выплаты A = K·S, где S — величина кредита.

Пример расчёта. Рассчитаем ежемесячную выплату по трехлетнему кредиту суммой $ 12000 по ставке 6 % годовых. Поскольку выплаты будут производиться каждый месяц, необходимо привести процентную ставку из годового значения к месячному: 6 %/12 = 0,5 %, или 0,005 в месяц. Подставляем в указанную выше формулу следующие значения: , мес. Полученный коэффициент умножаем на сумму кредита — 12000. Получаем 365 $/мес.

Обычно погашение долга предусматривает ежемесячные или ежеквартальные выплаты, и задаётся годовая процентная ставка . Если выплаты производятся постнумерандо раз в год в течение лет, то точная формула для коэффициента аннуитета:

или по упрощенной формуле:

где (всегда показатель степени) — количество периодов = n*m.

Будущая стоимость аннуитетных платежей

Будущая стоимость аннуитетных платежей предполагает, что платежи осуществляются на приносящий проценты вклад. Поэтому будущая стоимость аннуитетных платежей является функцией как величины аннуитетных платежей, так и ставки процента по вкладу.

Будущая стоимость серии аннуитетных платежей (FV) вычисляется по формуле (предполагается сложный процент)

где r — ставка процента, n — количество периодов, в которые осуществляются аннуитетные платежи, X — величина аннуитетного платежа.

Аннуитет пренумерандо в рассматриваемом случае начисления процентов по аннуитетным платежам, имеет на один год начисления процентов больше. Поэтому формула для вычисления будущей стоимости аннуитета пренумерандо приобретает следующий вид

В табличных процессорах в состав финансовых функций входит функция для вычисления будущей стоимости аннуитетных платежей. В OpenOffice.org Calc для вычисления будущей стоимости аннуитетных платежей (как постнумерандо, так и пренумерандо) применяется функция FV.

См. также

Ссылки

CFA — Как рассчитывать приведенную стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA

Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.

Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.

Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.

Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.

Расчет текущей стоимости (PV) серии равных денежных потоков.

Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при t = 1).

Всего простой аннуитет включает N платежей с первым взносом при t = 1 и последним при t = N.

Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:

$ \mathbf {PV = {A \over (1 + r)} + {A \over (1 + r) ^ 2} + {A \over (1 + r) ^ 3} + \cdots + {A \over (1 + r)^{N-1}} + {A \over (1 + r)^N}} $ (формула 10)

где:

A = сумма аннуитета,
r = процентная ставка за период, соответствующая частоте выплаты аннуитета (например, годовой, ежеквартальный или ежемесячный),
N = количество аннуитетных платежей.

Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:

$ \mathbf {PV = A \left [1- {1 \over (1 + r)^N} \over r \right]} $ (формула 11)

Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.

Пример расчета текущей (приведенной) стоимости обычного аннуитета.

Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.

Норма прибыли составляет 12% в год.

Сколько вы должны заплатить за этот актив?

Решение:

Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:

A = €1,000
r = 12% = 0.12
N = 5

$ \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \left[ 1-{1\over(1.12)^5} \over 0.12 \right] \end{aligned} } $

= €1,000 * (3.604776)
= €3,604.78

Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.

Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).

При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.

На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.

Авансовый аннуитет в размере $100 за период.

На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:

единовременная сумма в размере $100 на текущую дату (при t = 0) и
обычный аннуитет в размере $100 за период в течение 3-х периодов.

При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.

Существует альтернативный способ расчета текущей стоимости авансового аннуитета.

По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.

Поэтому мы можем модифицировать формулу 11, умножив правую часть уравнения на (1 + r):

PV (Авансовый аннуитет) = $ \mathbf {A \left[ 1-(1+r)^{-N} \over r \right] (1+r) } $

Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.

Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.

Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.

Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:

немедленную единовременную выплату в размере $2 млн. или
аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.

Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.

Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)

Решение:

Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
t = 0 и выбрать наибольшее значение.

Текущая стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.

Второй вариант — аннуитет. Поскольку первый платеж происходит при t = 0, вы можете разделить этот аннуитет на две части:

немедленную выплату $200 000 от текущей даты (t = 0) и
обычный аннуитет в размере $200 000 в год в течение 19 лет.

Чтобы рассчитать этот аннуитет, вам нужно найти текущую стоимость обычного аннуитета, используя формулу 11, а затем добавить к нему 200 000 долларов.

A = $200,000
N = 19
r = 7% = 0.07

$ \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= $200\ 000 \left[ 1-{1\over(1.07)^{19}} \over 0.07 \right] \end{aligned} } $
= $200,000(0.335595)
= $2,067,119.05

19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.

Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.

Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.

Пример расчета прогнозируемой текущей стоимости обычного аннуитета.

Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.

После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.

Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?

Решение:

Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.

При этом, на момент t = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить текущую стоимость (PV) этого аннуитета с помощью формулы 11, а затем посмотреть на нее на временной шкале.

A = €1,000,000
r = 5% = 0.05
N = 30

$ \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \ 000 \left[ 1-{1\over(1.05)^{30}} \over 0.05 \right] \end{aligned} } $
= €1,000,000 * (15.372451)
= €15,372,451.03

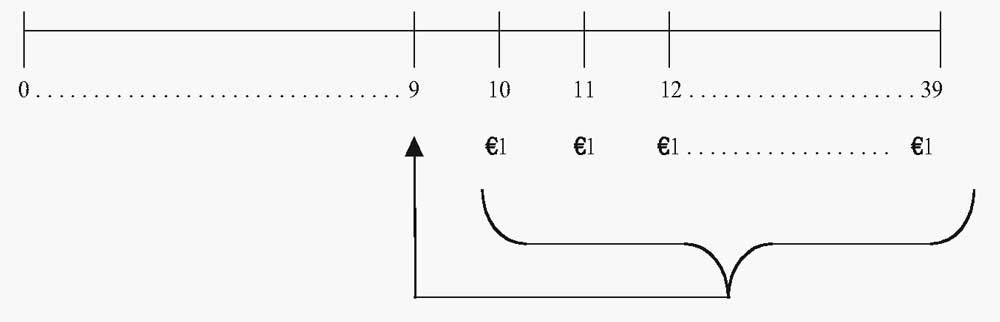Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).

На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.

Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.

Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.

Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).

Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.

Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:

FV_N = €15,372,451.03 (текущая стоимость при t = 9)
N = 9
r = 5% = 0.05

PV = FV_N * (1 + r)^—^N
= €15,372,451.03 * (1.05)^-9
= €15,372,451.03 * (0.644609)
= €9,909,219.00

Приведенная стоимость на текущую дату (при t = 0) пенсионного обязательства составляет €9,909,219.00.

Приведенный пример иллюстрирует три процедуры:

Как вычислять текущую стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?

Рассмотрим случай обычного аннуитета, который продолжается бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).

Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать формулу 10, чтобы учесть бесконечную последовательность денежных потоков:

$ \mathbf {PV = A \sum _{t = 1} ^{\infty} \left[ 1 \over (1 + r)^t \right] } $ (формула 12)

Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:

PV = A / r (формула 13)

Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.

Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)^N приближается к 0, а формула 11 упрощается до формулы 13.

Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.

Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.

При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.

Формула 13 справедлива только для бессрочного аннуитета с равными платежами. В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.

Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.

Пример расчета текущей стоимости (PV) перпетуитета.

Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.

Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?

Решение:

Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:

A = £100
r = 5% = 0.05

PV = A/r
= £100/0.05
= £2,000

Облигация будет стоить £2 000.

Текущая стоимость на момент времени, отличный от текущей даты (t = 0).

На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.

Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим PV₁ = $ 100 / 0,05 = $2 000 при 5%-й ставке. Кроме того, мы можем рассчитать PV на текущую дату как PV₀ = $2,000 / 1.05 = $ 1,904.76.

Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.

По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.

При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года (t = 3) и $29,99 на текущую дату (t = 0).

Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.

Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.

Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.

Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?

Решение:

Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).

1. Находим текущую стоимость перпетуитета при t = 4:

A = £100
r = 5% = 0.05

PV = A/r
= £100/0.05
= £2,000

2. Находим текущую стоимость будущего значения при
t = 4.

С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.

Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:

FV_N = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4

PV = FV_N * (1 + r)^—^N
= £2,000 * (1.05)^-4
= £2,000 * (0.822702)
= £1,645.40

Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.

Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.

В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.

Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.

Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.

Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.

Следующий пример иллюстрирует этот результат.

Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.

С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:

Перпетуитет 1 на £100 в год, начиная с 1-го года (первый платеж при t = 1).
Перпетуитет 2 на £100 в год, начиная с 5-го года (первый платеж при t = 5).

Решение:

Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).

Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:

PV₀ (Перпетуитет 1) = £100 / 0.05 = £2,000
PV₄ (Перпетуитет 2) = £100 / 0.05 = £2,000
PV₀ (Перпетуитет 2) = £2,000 / (1.05)⁴ = £1,645.40

PV₀ (Аннуитет)
= PV₀ (Перпетуитет 1) — PV₀ (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60

Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.

Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?

Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.

Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.

В таблице ниже приведена последовательность денежных потоков с

временными периодами в 1-м столбце,
денежными потоками во 2-м столбце и
текущей стоимостью (PV) каждого денежного потока в 3-м столбце.

В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.

Серия неравных денежных потоков и их приведенная стоимость при ставке 5%.
Период	Денежный поток ($)	PV при t=0
1	1,000	$1,000(1.05)^-1 =	$952.38
2	2,000	$2,000(1.05)^-2 =	$1,814.06
3	4,000	$4,000(1.05)^-3 =	$3,455.35
4	5,000	$5,000(1.05)^-4 =	$4,113.51
5	6,000	$6,000(1.05)^-5 =	$4,701.16
		Сумма =	$15,036.46

Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.

Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.

Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:

PV = $15,036.46
N = 5
r = 5% = 0.05

FVN = PV * (1 + r)^N
= $15,036.46 * (1.05)⁵
= $15,036.46 * (1.276282)
= $19,190.76

CFA — Как рассчитывать будущую стоимость (FV) последовательности денежных потоков (аннуитета)? | программа CFA

При оценке денежных потоков, последовательно осуществляемых в течение многих периодов времени, обычно используются следующие термины:

Аннуитет (англ. ‘annuity’) — это ограниченная последовательность (серия) денежных потоков.
Обычный или простой аннуитет или аннуитет постнумерандо (англ. ‘ordinary annuity’) — это серия денежных потоков, в которой денежные потоки происходят через 1 период, т.е. в начале следующего периода или в конце текущего периода (например, 1-й поток индексируется как t = 1).
Авансовый аннуитет или аннуитет пренумерандо (англ. ‘annuity due’) — это серия денежных потоков, в которой денежные потоки происходят немедленно, т.е. в начале текущего периода (1-й поток индексируется как t = 0).
См. примеры расчета авансового аннуитета.
Бессрочный аннуитет или перпетуитет или вечная рента (англ. ‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
См. пример расчета перпетуитета.

Как вычислять обычный аннуитет, то есть FV равных денежных потоков?

Рассмотрим обычный аннуитет с начислением 5% годовых.

Предположим, что у нас есть 5 отдельных депозитов по $1 000, поступающих с равными интервалами, каждый из которых составляет 1 год, причем 1-й платеж происходит при t = 1.

Наша цель — найти будущую стоимость (FV) этого обычного аннуитета после внесения последнего депозита при t = 5. Поскольку все 5 депозитов вносятся с периодичностью в 1 год, последний платеж осуществляется через 5 лет.

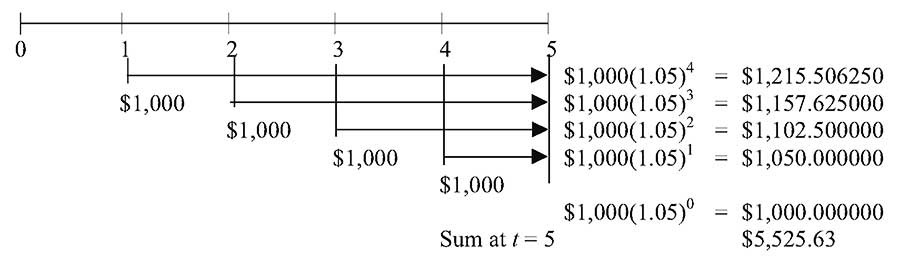Будущая стоимость (FV) пятилетнего обычного аннуитета.

Как показывает временная линия на рисунке выше, мы находим будущую стоимость каждого депозита на сумму $1 000 к моменту времени t = 5, используя для каждого депозита формулу FV (2):

FV_N = PV * (1 + r)^N.

Стрелки на рисунке выше соответствуют дате каждого депозита от даты 1-го платежа до t = 5 и указывают на расчет будущей стоимости FV для соответствующего депозита.

Например, по 1-му депозиту в размере $1 000 (при t = 1) будут начисляться проценты в течение 4-х последующих периодов.

Используя формулу FV, мы вычисляем будущую стоимость 1-го депозита при t = 5, которая составляет:

$1 000 * (1,05)⁴ = $1 215,51.

Для всех других платежей мы вычисляем FV аналогичным образом.

Обратите внимание, что мы находим будущую стоимость при t = 5, поэтому последний (5-й) платеж не важен и не отображается на временной линии.

Теперь, имея все значения FV при t = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е. всей последовательности равных денежных потоков. Эта сумма составляет $5 525,63.

Теперь рассмотрим общую формулу аннуитета, в которой:

A — сумма аннуитета,
N — количество периодов и
r — процентная ставка за период.

Мы можем рассчитать будущую стоимость как

FV_N = A * [(1 + r)^N-1 + (1 + r)^N-2 + (1 + r)^N-3 + … + (1 + r)¹ + (1 + r)⁰],

что можно упростить до следующей формулы:

$$\mathbf { FV_N = A \left[ {(1+r)^N — 1} \over r \right] }$$

FV_N = A * [((1 + r)^N -1) / r] (формула 7)

Выражение в квадратных скобках — это фактор будущей стоимости аннуитета (англ. ‘future value annuity factor’).

Этот коэффициент означает будущую стоимость обычного аннуитета на одну денежную единицу (т.е. на $1 в нашем примере).

Умножение фактора будущей стоимости аннуитета на сумму аннуитета дает будущую стоимость обычного аннуитета.

Для обычного аннуитета, изображенного на рисунке выше, фактор будущей стоимости аннуитета из формулы 7 можно рассчитать как:

[((1.05)⁵ — 1) / 0.05] = 5.525631.

Если сумма аннуитета A = $1 000, то будущая стоимость аннуитета составляет $1,000 * (5.525631) = $5,525.63, что соответствует вычислению, сделанному ранее.

Следующий пример иллюстрирует, как можно рассчитать будущую стоимость обычного аннуитета, используя формулу 7.

Пример расчета будущей стоимости простого аннуитета.

Предположим, что пенсионный план вашей компании с установленными взносами позволяет вам инвестировать до €20 000 в год. Вы планируете инвестировать €20 000 в год в индексный инвестиционный фонд в течение следующих 30 лет.

Исторически сложилось так, что этот фонд в среднем приносил своим инвесторам 9% в год.

Исходя из того, что вы будете зарабатывать 9% в год, сколько пенсионных средств будет на вашем счете после внесения последнего платежа?

Решение:

Используйте формулу 7, чтобы найти будущую стоимость аннуитета:

A = €20,000
r = 9% = 0.09
N = 30

Фактор FV аннуитета = [(1 + r)^N — 1] / r
= [(1.09)³⁰ — 1] / 0.09 = 136.307539.

FV_N = €20,000 * (136.307539) = €2,726,150.77.

Предполагая, что фонд будет зарабатывать в среднем 9% в год, вы получите €2,726,150.77 к моменту выхода на пенсию.

Как вычислять аннуитет при неравных денежных потоках?

Довольно часто последовательность денежных потоков аннуитета неравномерна. То есть, потоки денежных средств не являются одинаковыми платежами, осуществляемыми через равные периоды времени.

Это исключает использование в расчете фактора будущей стоимости аннуитета.

Например, у инвестора может быть план сбережений, который предполагает неравные денежные выплаты в зависимости от месяца года или более низкие сбережения во время запланированного отпуска.

В этом случае будущую стоимость серии неравных денежных потоков можно вычислить, рассчитав и суммировав FV каждого отдельного денежного потока.

Пример расчета аннуитета при неравномерных денежных потоках.

Предположим, что у вас есть 5 денежных потоков, которые описаны в таблице ниже. Платежи пронумерованы относительно текущей даты (t = 0).

Серия неравных денежных потоков и их будущая стоимость при ставке 5%.
Год	Денежный поток, $	Будущая стоимость на 5-й год
t = 1	1,000	$1,000 (1.05)⁴ =	$1,215.51
t = 2	2,000	$2,000(1.05)³ =	$2,315.25
t = 3	4,000	$4,000(1.05)² =	$4,410.00
t = 4	5,000	$5,000(1.05)¹ =	$5,250.00
t = 5	6,000	$6,000(1.05)° =	$6,000.00
		Сумма =	$19,190.76

Все платежи, указанные в таблице выше, отличаются по сумме. Поэтому самый прямой подход к расчету будущей стоимости этих инвестиций при t = 5, — это вычисление FV каждого отдельного платежа при t = 5, а затем суммирование найденных значений FV.

Совокупная FV на 5-й год равна $19,190.76, как показано в третьем столбце таблицы.

Аннуитет :: Инвестиции онлайн — ВАШ Путь в мире бизнеса.

Аннуитет можно рассматривать как особые денежные потоки в финансовом секторе.

Это разновидность инвестиций, которые приносят вкладчику определенный фиксированный доход через равные промежутки времени. Чаще всего этот финансовый инструмент используется в страховых или пенсионных фондах.

Это могут быть периодические выплаты по сберегательным или депозитным сертификатам, облигациям и прочим финансовым инструментам. Периодом времени между аннуитетными платежами называют интервалом платежа. Сроков самого аннуитета называется время от первого платежа до последнего.

Аннуитет наиболее популярен среди современных участников финансового рынка.

При таком виде финансовой ренты можно легко планировать будущие доходы и расходы, а значит таким образом обеспечивается более стабильная и бесперебойная работа финансовог или любого другого учреждения.

Виды аннуитетов:

1. По происхождению плательщиков:

— пенсионные — довольно популярные в последнее время инвестиции в собственную старость. Выплачиваются пенсионным фондом.

— страховые — выплаты страховых компаний.

— финансовые — аннуитетные платежи банков и прочих финучереждений.

— аннуитеты, которые выплачиваются различными юридическими лицами.

2. По времени выплаты первого аннуитетного платежа:

— пренумерандо/авансовый. Здесь выплата осуществляется в начале определенного периода.

— постнумерандо/обыкновенный. Финансовые выплаты осуществляются в конце периода.

3. По моменту поступления средств принято различать:

— срочные аннуитеты. Средства поступают в течении конкретного ограниченного времени равными долями и через равные временные промежутки. Рассчитываются такие аннуитеты как по схеме наращения, так и дисконтирования. Если говорить о конкретных примерах — то для обыкновенного аннуитета это могут быть любые арендные платежи (за квартиру, землю и т.д.). Понять авансовый аннуитет можно на примере ежемесячного пополнения банковского вклада в начале месяца, с целью получения большей суммы процетов.

— бессрочные аннуитеты, также известные как вечная рента — это равные поступления через одинаковые периоды времени напротяжении длительного срока. Примером такого аннуитета может послужить консоль — долгосрочные государственные облигации, действующие более 30 лет. Бессрочный аннуитет также можно разделить на пренумерандо и постнумерандо с дисконтированием.

4. По количеству выплат. Рассмотреть данный вид аннуитетных инвестиций можно на примере банковского вклада и получения процентов по нему:

— выплаты единожды в год;

— срочные — несколько выплат за один год.

5. По количеству начисления процентов напротяжении года:

— ежегодно;

— несколько раз в течении всего года;

— непрерывно.

6. По размеру платежей и учету инфляции:

— фиксированные аннуитетные платежи;

— валютные аннуитеты — привязаны к одной или нескольким стабильным валютам;

— индексируемые — привязанные к инфляционному индексу;

— переменные — величина аннуитета привязана исключительно к индексу доходности отдельных рыночных финансовых инструментов.

Все финансовые инвестиции зависят от реальной стоимости денег.

Естественно, при покупке и окончании аннуитета, эта величина может изменяться. Поэтому следует рассчитать текущую, а также итоговую стоимость аннуитетов согласно формул.

Стоимость аннуитета (FVA и PVA)| КАЛЬКУЛЯТОР

Аннуитет постнумерандо — англ. Ordinary Annuity, представляет собой серию платежей, которые периодически осуществляются в конце каждого периода (например, месяца, квартала, полугодия или года). При этом аннуитет постнумерандо, как правило, выплачивается в течение фиксированного периода времени. Наиболее распространенными примерами такого аннуитета могут служить ипотека с фиксированной процентной ставкой и купонные платежи (англ. Coupon Payment) по облигациям с фиксированной процентной ставкой.

Размер платежа при аннуитете постнумерандо зависит от основной суммы, процентной ставки и периода времени, в течение которого будут осуществляться платежи. В финансовых расчетах используются такие величины как настоящая стоимость (англ. Present Value) и будущая стоимость (англ. Future Value), которые необходимы для оценки целесообразности тех или иных инвестиций.

Будущая стоимость аннуитета постнумерандо рассчитывается по следующей формуле:

где A – размер платежа;
i – процентная ставка за период;
N – количество периодов.

Эта формула может быть применена для определения будущей суммы накоплений инвестора, что удобно рассмотреть на простом примере. Допустим, инвестор решил ежемесячно вносить на депозит по 800 у.е. в течение 5 лет при условии, что процентная ставка останется фиксированной на протяжении всего срока в размере 5% годовых. Чтобы воспользоваться приведенной выше формулой, необходимо привести в соответствие исходные данные.

Размер ежемесячного платежа составит 800 у.е.
Годовую процентную ставку необходимо привести к месячной, которая составит 0,4167% (5%/12).
Количество периодов составит 60 (5 лет по 12 платежей).

Таким образом в распоряжении инвестора через 5 лет будет сумма в размере 54404,87 у.е.

FVA=800*((1+0,004167)60-1)/0,004167=54404,87 у.е.

Настоящая стоимость аннуитета постнумерандо рассчитывается следующим образом:

Например, эта формула может использоваться в практических расчетах для определения размера ежемесячного платежа по ипотеке. В этом случае кредитор предоставляет заемщику сумму, необходимую для покупки объекта недвижимости. При этом заемщик обязуется осуществлять регулярные платежи в пользу кредитора в течение оговоренного периода времени.

Допустим, что банк предоставил заемщику 150000 у.е. для приобретения квартиры на следующих условиях:

срок кредитования 15 лет;
процентная ставка 8% годовых;
погашение ипотеки осуществляется ежемесячно в конце каждого месяца.

Используя формулу настоящей стоимости аннуитета постнумерандо можно рассчитать размер ежемесячного платежа:

Чтобы воспользоваться этой формулой необходимо привести в соответствие исходные данные.

Настоящая стоимость аннуитета составит 150000 у.е.
Годовую процентную ставку необходимо привести к месячной, которая составит 0,6667% (8%/12).
Количество периодов составит 180 (15 лет по 12 платежей).

Таким образом размер ежемесячного платежа составит 1433,48 у.е.

A=(150000*0,006667)/(1-(1+0,006667)-180)=1433,48 у.е.

Следовательно, заемщик обязан в течение 15 лет осуществить в пользу банка 180 платежей по 1433,48 у.е.

В некоторых случаях аннуитет может не иметь фиксированного периода, в течение которого будут осуществляться платежи. Например, в случае пенсионного страхования выплаты будут осуществляться в пользу пенсионера пожизненно. В некоторых случаях таким договором может быть установлен минимальный период времени, в течение которого должны будут осуществляться выплаты, однако максимальный период ограничен только продолжительностью жизни получателя.

Учебное пособие по временной стоимости денег

Представление о том, что доллар сегодня предпочтительнее, чем доллар когда-нибудь в будущем, достаточно интуитивно понятно для большинства людей, чтобы понять без использования моделей и математики. Принципы приведенной стоимости предоставляют больше поддержки для этого. заявление, тем не менее, и позволяет нам точно рассчитать, сколько доллар в будущем будет стоить в сегодняшних долларах и перемещать денежные потоки во времени.Приведенная стоимость — это интуитивно привлекательная концепция, простая для вычисления и имеющая широкий спектр применения. Это полезно при принятии решений, начиная от простых личных решений (покупка дома, экономия для детского образования и оценки дохода на пенсии) до более сложных корпоративных финансовых решений (выбор проектов в которые вкладывать средства, а также правильный набор финансирования для этих проектов).

Линии времени и обозначения

Работа с денежными потоками, которые находятся в разные моменты времени, упрощается с использованием временной шкалы , которая показывает как время, так и сумма каждого денежного потока в потоке.Таким образом, денежный поток в размере 100 долларов в конце каждого из следующих 4 года могут быть изображены на временной шкале, подобной изображенной ниже.

На рисунке 0 означает прямо сейчас. Таким образом, денежный поток, который происходит в момент времени 0, уже имеет приведенную стоимость. сроки и не требует корректировки по временной стоимости. Здесь необходимо проводить различие между периодом времени и момент времени. Часть временной шкалы между 0 и 1 относится к период 1, который в этом примере является первым годом.Денежный поток, который происходит на момент времени 1 относится к денежному потоку, который происходит в конце периода 1. Ставка дисконтирования, которая в этом примере составляет 10%, указывается для каждого периода на временной шкале и может быть разной для каждого периода. Обратите внимание, что в С точки зрения приведенной стоимости, денежный поток, который возникает в конце периода 1, эквивалентен денежному потоку, который происходит в начале периода 2.

Денежные потоки могут быть как положительными, так и отрицательными; положительные денежные потоки называются денежными поступлениями а отрицательные денежные потоки называются оттоком денежных средств.В условных обозначениях используются следующие сокращения используются:

Обозначение	Стенды для
PV	Текущая стоимость
ФВ	Будущая стоимость
Cf _т	Денежный поток на конец периода т
А	Аннуитет: постоянные денежные потоки в течение нескольких периодов
к	Ставка дисконтирования (также часто сокращенно r или i )
г	Ожидаемый темп роста
№	Количество периодов получения или выплаты денежных потоков

Интуитивная основа для текущей стоимости

Есть три причины, по которым денежный поток в будущем стоит меньше, чем аналогичный денежный поток сегодня.

Физические лица предпочитают текущее потребление будущему. Люди бы чтобы отказаться от нынешнего потребления, в будущем нужно предложить больше. Если предпочтение текущего потребления сильное, Людям придется предложить гораздо больше в плане будущего потребления, чтобы отказаться от текущего потребления, что является компромиссом что фиксируется высокой реальной доходностью или ставкой дисконтирования. И наоборот, когда предпочтение отдается потреблению тока слабее, люди будут соглашаться на меньшее с точки зрения будущего потребления и, соответственно, на низкую реальную норму прибыли или учетная ставка.
Когда есть денежная инфляция, стоимость валюты со временем снижается. В чем выше инфляция, тем больше разница в стоимости между денежным потоком сегодня и тем же денежным потоком в будущем.
Обещанный денежный поток может не быть доставлен по ряду причин: должник может не выпустить платежа, обещанного может не быть поблизости, чтобы получить платеж, или могут вмешаться какие-то другие непредвиденные обстоятельства, чтобы предотвратить обещанный платеж от внесения или уменьшить его.Любая неопределенность или риск, связанный с денежный поток в будущем снижает ценность денежного потока сегодня.

Процесс корректировки будущих денежных потоков для отражения этих факторов называется дисконтированием, и Величина этих факторов отражается в ставке дисконтирования. Ставка дисконтирования включает все вышеперечисленное. факторы. Фактически, ставку дисконтирования можно рассматривать как составную часть ожидаемой реальной прибыли (отражающей потребление предпочтения в совокупности по сравнению с инвестирующим населением), ожидаемый уровень инфляции (чтобы зафиксировать ухудшение покупательной способности денежного потока) и неопределенности, связанной с денежным потоком.

Механика временной стоимости

Денежные потоки в разные моменты времени нельзя сравнивать и агрегировать. Все денежные потоки должны быть приведены в один и тот же момент времени, прежде чем можно будет проводить сравнения и агрегирование. Процесс дисконтирования будущих денежных потоков конвертирует их в денежные потоки в выражении дисконтированной стоимости. И наоборот, процесс начисления сложных процентов конвертирует текущие денежные потоки в будущие денежные потоки.

Существует пять типов денежных потоков: простые денежные потоки, аннуитеты, растущие аннуитеты, бессрочные и растущие бессрочные.

A. Простые денежные потоки

Простой денежный поток — это единичный денежный поток (CF) в определенный период времени в будущем t , обычно изображаемый как CF _т . Этот денежный поток может быть дисконтирован до настоящего времени с использованием ставки дисконтирования, отражающей неопределенность. денежного потока. Одновременно с этим можно сложить денежные потоки в настоящем, чтобы получить ожидаемую стоимость будущего денежного потока.

И.Дисконтирование простого денежного потока
Дисконтирование денежного потока преобразует его в доллары приведенной стоимости и позволяет пользователю делать несколько вещей. Первый, Как только денежные потоки конвертируются в доллары с приведенной стоимостью, их можно агрегировать и сравнивать. Во-вторых, если текущая стоимость правильно рассчитанный, пользователю должно быть безразлично между будущим денежным потоком и текущей стоимостью этого денежного потока. В приведенную стоимость денежного потока можно записать следующим образом:

, где CF _t равно денежному потоку на конец периода t , а где k равно учетная ставка.

При прочих равных условиях приведенная стоимость денежного потока будет уменьшаться по мере увеличения ставки дисконтирования. увеличивается и продолжает уменьшаться по мере того, как в будущем происходит денежный поток.

Иллюстрация: дисконтирование денежного потока
Предположим, вы ожидаете получить единовременную выплату в размере 500 000 долларов через десять лет и соответствующую скидку. ставка для этого денежного потока составляет 10%. Приведенная стоимость этого денежного потока может быть оценена как:
Обратите внимание, что приведенная стоимость является убывающей функцией ставки дисконтирования и времени; чем больше скидка ставка или чем дольше период времени, тем меньше текущая стоимость.
II. Составление денежного потока
Текущие денежные потоки можно перенести в будущее за счет сложения денежного потока по соответствующей ставке дисконтирования.

, где CF ₀ соответствует текущему денежному потоку, а k равно ставке дисконтирования.
Этот эффект сложения увеличивается как со ставкой дисконтирования, так и со временем; чем больше ставка дисконтирования или тем дольше период времени, тем больше будущее значение.
III. Частота дисконтирования и начисления процентов
Частота начисления сложных процентов влияет как на будущую, так и на текущую стоимость денежных потоков. В простых примерах наличные Часто предполагается, что потоки дисконтируются и суммируются ежегодно, т. е. процентные платежи и доход рассчитываются в конце каждый год, исходя из баланса на начало года. Однако в некоторых случаях проценты могут рассчитываться чаще, например, ежемесячно или раз в полгода.В этих случаях настоящие и будущие ценности могут сильно отличаться от тех. рассчитывается ежегодно; заявленная процентная ставка на годовой основе может значительно отклоняться от действующей или истинной уровень интереса. Эффективную процентную ставку можно рассчитать следующим образом:

, где n равно количеству периодов начисления сложных процентов в течение года (2 = полугодие; 12 = ежемесячно), а k равняется заявленной годовой процентной ставке.
Когда начисление сложных процентов становится непрерывным, эффективная процентная ставка может быть рассчитана следующим образом:

, где e равно экспоненциальной функции, а k равно заявленной годовой процентной ставке.

В таблице ниже представлены эффективные ставки в зависимости от частоты начисления сложных процентов для номинальной процентной ставки. ставка 10 процентов.

B. Аннуитеты

Аннуитет — это постоянный денежный поток, который происходит через равные промежутки времени в течение фиксированного периода времени.Аннуитет может происходят в конце каждого периода или в начале каждого периода.

I. Приведенная стоимость ренты на конец периода
Приведенную стоимость аннуитета можно рассчитать, взяв каждый денежный поток и дисконтируя его до представить, а затем суммировать текущие значения. В качестве альтернативы при расчетах можно использовать формулу. В случае аннуитета которые происходят в конце каждого периода, эту формулу можно записать как

, где A равно аннуитету (периодический денежный поток), k равно ставке дисконтирования, а n равно количеству периодов (лет).
Иллюстрация: Оценка текущей стоимости аннуитетов
Предположим, у вас есть выбор: купить копировальный аппарат за 10 000 долларов наличными или платить 3 000 долларов в год в течение 5 лет. для того же копировального аппарата. Если альтернативные издержки составляют 12%, что бы вы предпочли?

Приведенная стоимость платежей в рассрочку превышает цену выкупа; поэтому вы хотели бы заплатить 10 000 долларов наличными сейчас.
В качестве альтернативы, приведенная стоимость могла быть оценена путем дисконтирования каждого денежного потока обратно на текущая и совокупная приведенная стоимость, как показано ниже:

Иллюстрация: приведенная стоимость нескольких аннуитетов
Предположим, вы пытаетесь оценить приведенную стоимость ожидаемых пенсионных обязательств фирмы, сумма которых номинальные условия до:

Годовой денежный поток за

лет
1 5 200 миллионов долларов
6 10 300 миллионов долларов
11 20 400 млн. Долл. США

Если ставка дисконтирования составляет 10%, приведенная стоимость этих трех аннуитетов может быть оценена следующим образом:

Приведенная стоимость первого аннуитета = 200 миллионов долларов США x PV (A, 10%, 5) = 758 миллионов долларов США
Текущая стоимость второго аннуитета = 300 миллионов долларов x PV (A, 10%, 5) / 1.10 ⁵ = 706 миллионов долларов
Текущая стоимость третьего аннуитета = 400 миллионов долларов x PV (A, 10%, 10) / 1,10 ¹⁰ = 948 миллионов долларов

Текущая стоимость второго и третьего аннуитетов может быть оценена в два этапа. Во-первых, стандартный подарок Стоимость аннуитета рассчитывается за период получения аннуитета. Во-вторых, приведенная стоимость возвращается к настоящее. Таким образом, для второго аннуитета приведенная стоимость 300 миллионов долларов в год в течение 5 лет рассчитывается как 1 137 миллионов долларов; эта приведенная стоимость действительно на конец пятого года, поэтому ее необходимо дисконтировать еще на 5 лет, чтобы получить сегодняшнее настоящее стоимостью 706 миллионов долларов.Точно так же стоимость третьего аннуитета (2458 миллионов долларов) дисконтируется еще на 10 лет назад до настоящего времени. стоимость 948 долларов.

Сумма накопленной приведенной стоимости = 758 долларов США + 706 долларов США + 948 долларов США = 2 412 миллионов долларов США.

II. Коэффициенты амортизации — аннуитеты с учетом текущей стоимости
В некоторых случаях известна приведенная стоимость денежных потоков, и необходимо оценить размер аннуитета. Это часто бывает с жилищным и автомобильным кредитом, например, когда заемщик получает ссуду сегодня и возвращает ее в равные ежемесячные платежи в течение длительного периода времени.Этот процесс нахождения ренты, когда известна текущая стоимость рассматривается ниже:

Иллюстрация: расчет ежемесячного платежа по кредиту на дом
Предположим, вы пытаетесь занять 200000 долларов, чтобы купить дом по обычной 30-летней ипотеке с ежемесячным платежи. Годовая процентная ставка по кредиту составляет 8%. Ежемесячные выплаты по этому кредиту можно оценить с помощью аннуитета. формула оплаты:
Примечание: Ежемесячная процентная ставка по кредиту = APR / 12 = 0.08/12 = 0,0067
III. Будущая стоимость аннуитетов на конец периода
В некоторых случаях физическое лицо может планировать откладывать фиксированную ренту за каждый период на несколько периодов и захочет знать, сколько он или она будет иметь в конце периода. Будущая стоимость на конец периода аннуитет можно рассчитать следующим образом:

Иллюстрация: Индивидуальные пенсионные счета (IRA)
Индивидуальные пенсионные счета (IRA) позволяют налогоплательщикам делать безналоговые инвестиции в назначенную пенсию учетная запись.Предположим, что человек инвестирует 2000 долларов в конце каждого года, начиная с 25 лет, для ожидаемого выхода на пенсию. в возрасте 65 лет и рассчитывает получать 8% годовых от инвестиций. Ожидаемая стоимость счета на дату вывода из эксплуатации может быть оценивается следующим образом:
IV. Аннуитет с учетом будущей стоимости
Физические или юридические лица, у которых есть фиксированные обязательства или цели, которые необходимо выполнить (с точки зрения экономии) через некоторое время будущим нужно знать, сколько им следует откладывать на каждый период для достижения этой цели.Если вам дана будущая стоимость и ищите аннуитет, можно использовать следующее уравнение:

Иллюстрация: резерв фонда погашения
В любой ссуде с воздушными платежами в течение срока ссуды производятся только процентные платежи, в то время как основная сумма кредита выплачивается в конце периода. Компании, которые занимают деньги, используя ссуды с воздушными платежами или обычные облигации ( те же функции) часто откладывают деньги на погашение средств в течение срока ссуды, чтобы обеспечить их достаточное количество на срок выплаты основной суммы кредита или номинальной стоимости облигаций.Таким образом, компания с долгом номинальной стоимостью 100 миллионов долларов, подлежащих погашению через 10 лет, необходимо будет ежегодно откладывать на следующую сумму (при процентной ставке 8%):

Компания должна будет откладывать 6,9 млн долларов в конце каждого года, чтобы обеспечить достаточное количество средств. (100 миллионов долларов) для погашения долга при наступлении срока погашения.
V. Влияние аннуитетов на начало каждого года
Рассмотренные до сих пор аннуитеты имели денежные потоки на конец периода.И нынешние, и будущие ценности будут будут затронуты, если денежные потоки происходят в начале каждого периода, а не в конце. Чтобы проиллюстрировать этот эффект, рассмотрим аннуитет в размере 100 долларов в конце каждого года в течение следующих 4 лет со ставкой дисконтирования 10%, в отличие от аннуитета с выплаты производятся в начале каждого года.
Поскольку первая из этих аннуитетов происходит прямо сейчас, а оставшиеся денежные потоки принимают форму на конец периода. аннуитета более 3 лет, текущая стоимость этой ренты может быть записана следующим образом:

В целом, приведенная стоимость аннуитета на начало периода за n лет может быть записана следующим образом:

или как:
Обратите внимание, что эта приведенная стоимость будет выше, чем приведенная стоимость эквивалентного аннуитета в конце каждого периода.
Будущую стоимость аннуитета на начало периода обычно можно оценить, допустив одну дополнительную период начисления процентов по каждому денежному потоку:

Эта будущая стоимость будет выше, чем будущая стоимость эквивалентной ренты в конце каждого периода.
Иллюстрация: IRA — сбережения в начале каждого периода, а не в конце
Снова рассмотрим пример человека, который откладывает 2000 долларов в конце каждого года на следующие 40 лет. в учетной записи IRA, зарабатывающей 8%.Будущая стоимость этих вкладов составила 518 113 долларов на конец 40 ^-го года. Если депозиты делались в начале каждого года, а не в конце, будущая стоимость была бы выше:

Как видите, прибыль от осуществления платежей в начале каждого периода может быть значительной.
VI. Влияние денежных потоков, происходящих равномерно в течение года
Денежные потоки не всегда возникают ни в начале, ни в конце каждого периода.Многие фирмы, работающие денежные потоки (например, продажи, расходы) имеют тенденцию происходить более или менее равномерно в течение года. Один из способов справиться с этой ситуацией состоит в том, чтобы рассчитать текущую или будущую стоимость на основе предполагаемых ежедневных денежных потоков и использовать ежедневное начисление сложных процентов, как описано выше. Более простой (хотя и немного менее точный) метод — предположить, что денежные потоки происходят в середине каждого года, а не конец или начало. В этой ситуации можно рассчитать текущую или будущую стоимость, как если бы денежные потоки возникли в конце каждого периода, а затем умножьте результат на квадратный корень из (1 + k).
Иллюстрация: IRA — Инвестирование в течение года, а не в конце
Снова рассмотрим пример человека, который откладывает 2000 долларов в конце каждого года на следующие 40 лет. в учетной записи IRA, зарабатывающей 8%. Будущая стоимость этих вкладов составила 518 113 долларов на конец 40 ^-го года; с выплатами, производимыми в начале каждого года, будущая стоимость составляла 559 562 доллара США. Если бы депозиты были внесены равномерно в течение каждого года будущая стоимость составила бы 538 439 долларов, как рассчитано ниже:

С.Растущие аннуитеты

Растущий аннуитет — это денежный поток, который растет с постоянной скоростью в течение определенного периода времени. Обратите внимание, что квалифицируются как растущая рента, темпы роста в каждый период должны быть такими же, как и в предыдущем периоде.

В большинстве случаев текущую стоимость растущей ренты можно оценить с помощью следующей формулы:

, где г соответствует постоянной скорости роста аннуитета.

Отметим также, что эта формула работает даже тогда, когда темп роста превышает ставку дисконтирования.Настоящее Стоимость растущей ренты может быть оценена во всех случаях, за исключением случаев, когда скорость роста равна ставке дисконтирования. В этом В этом случае приведенная стоимость равна номинальной сумме аннуитетов за период без эффекта роста (т.е. n х А ).

В качестве альтернативы, приведенная стоимость растущей аннуитета может быть найдена с помощью стандартной формулы приведенной стоимости аннуитета, но с использованием скорректированной ставки дисконтирования, которая учитывает темп роста, так что k будет равно: [(1 + k ) / (1 + g )] — 1.

Иллюстрация: стоимость золотого рудника
Предположим, у вас есть права на золотой рудник на следующие 20 лет, в течение которых вы планируете добыть 5000 унций. золота каждый год. Текущая цена за унцию составляет 300 долларов, но ожидается, что она будет увеличиваться на 3% в год. Соответствующая ставка дисконтирования: 10%. Приведенная стоимость золота, которое будет извлечено из этого рудника, может быть оценена следующим образом:

Стандартная приведенная стоимость расчета аннуитета (при k = (1.10 / 1.03) — 1 = 6.8% ) даст то же самое результаты (кроме небольших ошибок округления).

D. Бессрочные права

Бессрочная жизнь — это постоянный денежный поток через равные промежутки времени навсегда. Приведенная стоимость бессрочного капитала может записать как:

, где A — это постоянный денежный поток, а k — ставка дисконтирования. Будущая ценность бессрочного права бесконечно.
Иллюстрация: оценка привилегированных акций
Обычные привилегированные акции не имеют срока погашения и обычно приносят фиксированные дивиденды навсегда. Предположим, у вас есть 100 долларов по привилегированным акциям с номинальной стоимостью выплачивается дивиденд в размере 6% (6 долларов США в год). Стоимость данной акции при ставке дисконтирования 9% составляет:

Стоимость привилегированных акций будет равна их номинальной стоимости только в том случае, если ставка дивидендов равна ставке дисконтирования.

E. Growing Perpetuities

Растущий бессрочный поток — это денежный поток, который, как ожидается, будет постоянно расти с постоянной скоростью. Приведенная стоимость растущую вечность можно записать как:

, где CF ₁ соответствует ожидаемому денежному потоку в следующем году, г соответствует постоянному росту ставка, а k равна ставке дисконтирования.

Хотя у растущего бессрочного дохода и растущего аннуитета есть несколько общих черт, тот факт, что длится вечно, что ограничивает темпы роста.Чтобы эта формула работала, она должна быть меньше ставки дисконтирования.

Иллюстрация: оценка акций со стабильным ростом дивидендов
BellSouth только что выплатила годовые дивиденды (CF ₀) в размере 2,73 доллара на акцию. Его прибыль и дивиденды росли на 6% в год и, как ожидается, будут расти такими же темпами в долгосрочной перспективе. Требуемая норма доходности инвесторами по акциям эквивалентного риска — 12.23%.

В качестве интересного момента предположим, что акция действительно торговалась по 70 долларов за акцию. Эта цена могла быть оправдано более высокими ожидаемыми темпами роста. Чтобы оправдать цену в 70 долларов, темпы роста должны составить приблизительно 8%. Эту скорость роста часто называют предполагаемой скоростью роста.

F. Комбинации и неравномерные денежные потоки

В реальном мире одновременно могут существовать несколько различных типов денежных потоков, включая аннуитеты, простые денежные потоки, а иногда и бессрочные: некоторые примеры обсуждаются ниже.

I. Оценка облигаций
По обычной облигации выплачивается фиксированный купон каждый период в течение всего срока действия облигации и номинальной стоимости облигации. в зрелости. Поскольку купоны фиксированные и выплачиваются через регулярные промежутки времени, они представляют собой аннуитет, а номинальная стоимость облигации представляет собой единый денежный поток, который необходимо дисконтировать отдельно. Тогда стоимость прямой облигации может быть записана следующим образом:

Иллюстрация: стоимость прямой облигации
Допустим, вы пытаетесь оценить обычную облигацию со сроком погашения 15 лет и 10.Ставка купона 75%. Текущий интерес ставка по облигациям данного уровня риска составляет 8,5%. Стоимость облигации определяется как сумма приведенной стоимости аннуитета ( купонные выплаты) и разовая сумма (номинальная стоимость).

Если бы проценты по облигации выплачивались раз в полгода, нам нужно было бы соответствующим образом скорректировать уравнение оценки:

II. Оценка обыкновенных акций
Рассмотрим случай с акциями компании, которая ожидает в ближайшем будущем высокого роста и более низкого и более стабильного роста. рост навсегда после этого.Ожидаемые дивиденды в течение периода высоких темпов роста представляют собой растущую ренту, в то время как дивиденды после этого удовлетворять условиям растущей вечности. Таким образом, стоимость акции может быть записана как сумма двух настоящие ценности.

, где P ₀ равно приведенной стоимости ожидаемых дивидендов, г равно чрезвычайной темп роста за первые n лет ( n = период высокого роста), g _n равняется темпу роста навсегда после года n , D ₀ равно текущим дивидендам на акцию, D _t равно дивидендам на доля в году т , а тыс. равна требуемой норме прибыли (ставке дисконтирования).
Иллюстрация: стоимость быстрорастущих акций
Предположим, что прибыль Eli Lilly на акцию составила 4,50 доллара США, а дивиденды на акцию — 2 доллара США. Аналитики ожидали, что оба расти 9,81% в год в течение следующих 5 лет. Ожидается, что после пятого года темпы роста упадут до 6% в год навсегда, в то время как ожидалось, что коэффициент выплат увеличится до 67,44%. Требуемая доходность акций Eli Lilly составляет 12,78%.
Цену в конце периода высокого роста (P ₅) можно оценить, используя формулу растущего бессрочного дохода:

Приведенная стоимость дивидендов и конечная цена могут быть рассчитаны следующим образом:

Стоимость акций Eli Lilly, исходя из ожидаемых темпов роста и ставки дисконтирования, составляет 52 доллара.74.
Бывают случаи, когда одна рента следует за другой. В этом случае приведенная стоимость будет суммой текущая стоимость двух (или более) аннуитетов. Приведенная стоимость этих двух аннуитетов может быть рассчитана отдельно и накоплена. для получения общей приведенной стоимости. Приведенная стоимость второго аннуитета должна быть дисконтирована до настоящего времени.

Заключение

Текущая стоимость остается одним из самых простых и эффективных методов в финансах, обеспечивающим широкий спектр приложения как в личных, так и в деловых решениях.Денежный поток может быть возвращен к приведенной стоимости путем дисконтирования и перемещения вперед путем сложения. Ставка дисконтирования, по которой производятся дисконтирование и начисление сложных процентов, отражает три фактора: (1) предпочтение для текущего потребления (2) ожидаемая инфляция и (3) неопределенность, связанная с дисконтируемыми денежными потоками.

Вернуться на домашнюю страницу доктора Джессвайн

Последнее обновление этой страницы: Вторник, 17 января 2006 г.

.
Что такое денежный поток?

Наличные деньги — это источник жизненной силы любого бизнеса, и их исчерпание — основная причина неудач малого бизнеса. Даже если вы делаете много продаж, если у вас недостаточно денег в банке, ваш бизнес не сможет оплачивать счета и оставаться открытым.
Вот почему компаниям так важно понимать основы денежного потока и прогнозирования денежных потоков. Вот все, что мы рассмотрим в этом руководстве, чтобы вы могли быстрее узнать о движении денежных средств:
Определение денежного потока
Расчет денежного потока
Разница между деньгами и прибылью
Как анализировать отчет о движении денежных средств
Положительный денежный поток
Отрицательный денежный поток
Денежный расход и взлетно-посадочная полоса
Почему важно прогнозирование денежных потоков
Как спрогнозировать денежный поток
Прямой метод
Косвенный метод
Прогнозирование денежного потока
Как увеличить денежный поток
Дополнительное чтение

Определение денежного потока
Денежный поток измеряет, сколько денег поступает и выводится из вашего бизнеса в течение определенного периода времени.
Компании приносят деньги за счет продаж, возврата инвестиций, а также за счет кредитов и инвестиций — это денежные потоки, поступающие в бизнес.
Компании тратят деньги на товары и услуги, а также на коммунальные услуги, налоги, платежи по кредитам и другие счета — это отток наличности.
Денежный поток измеряется путем сравнения того, сколько денег поступает в бизнес в течение определенного периода времени, с тем, сколько денег уходит из этого бизнеса за тот же период. Обычно денежный поток измеряется в течение месяца или квартала.
Как рассчитать денежный поток
Самая простая формула для расчета денежного потока:
ПОЛУЧЕННЫЕ ДЕНЕЖНЫЕ СРЕДСТВА — ИЗРАЧЕНИЕ ДЕНЕЖНЫХ СРЕДСТВ = ЧИСТЫЙ ДЕНЕЖНЫЙ ПОТОК
Если ваш чистый денежный поток положительный, ваш бизнес имеет положительный денежный поток и накапливает деньги в банке.
Если ваш чистый денежный поток отрицательный, ваш бизнес имеет отрицательный денежный поток, и вы заканчиваете месяц с меньшими деньгами, чем вы начали.
В чем разница между наличными и прибылью?
Вы не поверите, но ваш бизнес может быть прибыльным, но при этом остаться без наличных.Поначалу это может показаться нелогичным, но это потому, что деньги и прибыль — очень разные вещи. Вот почему.
Прибыль может включать продажи, которые вы совершили, но еще не получили оплату.
С другой стороны,
Наличные — это сумма денег, которая у вас есть на вашем банковском счете. Он отражает ликвидность вашего бизнеса и, по сути, если вы не можете использовать его прямо сейчас для оплаты счетов, это не наличные деньги.
Например, если вы делаете много продаж, но выставляете счет своим клиентам, и они платят вам «чистые 30», или в течение 30 дней после получения счета, у вас может быть большой доход на бумаге, но не много наличными. на ваш банковский счет, потому что ваши клиенты еще не заплатили вам.Эти продажи будут отображаться только в вашем отчете о доходах.
Если деньги, которые ваши клиенты должны вам, не поступили на ваш банковский счет, они еще не появятся в вашем отчете о движении денежных средств. На данный момент это фактически недоступно для вашего бизнеса. Это все еще в руках ваших клиентов, даже если вы выставили им за это счет. Вы отслеживаете деньги, которые ваши клиенты должны вам в дебиторской задолженности.
Между тем, вы можете оплачивать счета только наличными на вашем банковском счете. Без этих наличных будет сложно выполнять заказы, получать зарплату и платить за квартиру.Вот почему так важно отслеживать денежные потоки. Чтобы поддерживать бизнес на плаву, вам нужно хорошо понимать, что приходит и что уходит из вашего бизнеса на ежемесячной основе, и делать все возможное, чтобы денежные потоки оставались положительными.
Если вы хотите узнать больше, вы можете ознакомиться с нашим более подробным объяснением разницы между денежным потоком и прибылью.
Как анализировать отчет о движении денежных средств
При анализе отчета о движении денежных средств за прошлые периоды вы смотрите на сумму реальных денежных средств, которые у вас есть в наличии на начало месяца, по сравнению с вашими деньгами на конец месяца.Вы также можете посмотреть свой денежный поток в разные периоды времени — например, ежеквартально, — но хорошее практическое правило — смотреть на свой денежный поток на регулярной основе, чтобы лучше понимать любые изменения в состоянии вашего бизнеса.
Чтобы увидеть наглядный пример того, как это работает в рамках бизнеса, вы можете загрузить этот бесплатный пример денежного потока в формате PDF или Excel.
При проведении анализа движения денежных средств необходимо убедиться, что вы понимаете следующие ключевые термины.
Положительный денежный поток
Положительный денежный поток определяется как наличие более ликвидных денежных средств в конце заданного периода времени по сравнению с тем, что было доступно в начале этого периода.
Допустим, вы начали с 1000 долларов наличными в начале месяца. Вы заплатили 500 долларов по счетам и расходам, а ваши клиенты заплатили вам 2000 долларов за ваши услуги. Хорошие новости: ваш денежный поток положительный, 2500 долларов в месяц.
Если у вас положительный тренд денежного потока, проще:
Оплачивайте счета: Положительный денежный поток гарантирует, что сотрудники получают чеки во время каждого цикла расчета заработной платы. Это также дает лицам, принимающим решения, средства, необходимые для оплаты поставщикам, кредиторам и правительству.
Инвестируйте в новые возможности : Современный деловой мир быстро меняется. Когда наличные деньги легко доступны, владельцы бизнеса могут инвестировать в возможности, которые могут возникнуть в любой момент времени.
Желудок непредсказуемого : Наличие доступа к наличным деньгам означает, что всякий раз, когда оборудование ломается, клиенты не оплачивают счета вовремя, или когда вступают в силу новые правительственные постановления, предприятия могут выжить.
Отрицательный денежный поток
Отрицательный денежный поток — это когда из бизнеса уходит больше, чем поступает.Когда денежный поток отрицательный, сумма наличных на вашем банковском счете сокращается. Это может не быть проблемой, если у вашего бизнеса много денег в банке. Но это действительно означает, что у вашего бизнеса в конечном итоге закончатся деньги, если в какой-то момент он не станет положительным.
Допустим, вы начали с 1000 долларов в банке в начале месяца. Вы заплатили 1500 долларов по счетам и расходам, и, хотя вы проделали много работы и выставили счет своим клиентам за услуги на 3000 долларов, ваши клиенты фактически заплатили вам только 200 долларов.Вы все еще ждете поступления остальных платежей. Ваш денежный поток отрицательный: — 300 долларов в месяц.
Если у вас нет резервов, ваш чек арендной платы может не выпадать. Если у вас уже есть кредитная линия, вы можете рассчитывать на нее для оплаты части своих счетов. Возможно, вы спрогнозировали свой денежный поток и знали, что в этом месяце вам не хватит денег, поэтому вы составили план, чтобы иметь возможность покрыть свои расходы.
Один месяц отрицательного денежного потока не обязательно разрушит ваш бизнес.Но когда вы начинаете видеть тенденцию и ничего не предпринимаете, чтобы обратить ее вспять (или когда вы неприятно удивлены, потому что не отслеживаете свой денежный поток), тогда ваш бизнес оказывается в опасности.
Уровень сжигания наличных денег и взлетно-посадочная полоса
Новые предприятия и стартапы часто имеют отрицательный денежный поток, когда они только начинают работать. У них есть много счетов, которые нужно оплатить, пока они встают и работают, а продаж пока немного. Мы надеемся, что по мере поступления доходов от продаж в бизнес начнут поступать денежные средства, а не просто их отток.Вот почему новые предприятия часто нуждаются в инвестициях и ссудах, чтобы начать работу — им нужны деньги в банке, чтобы покрыть весь отрицательный денежный поток, который происходит в первые дни бизнеса.
При первом запуске важно отслеживать коэффициент сжигания наличных денег, который, по сути, является вашим отрицательным числом денежных потоков — количеством денег, которые вы «сжигаете» каждый месяц. Затем вы можете использовать это число, чтобы выяснить, сколько месяцев у вас осталось наличных — это ваша «взлетно-посадочная полоса». Прочтите наше подробное объяснение скорости сжигания наличных денег и взлетно-посадочной полосы, чтобы узнать больше о том, как найти, измерить и настроить эти показатели.
Отрицательный денежный поток также может произойти, когда бизнес решит инвестировать в новую возможность. Бизнес может делать ставку на то, что инвестиции в новую возможность сейчас окупятся в будущем. Эти инвестиции могут вызвать отрицательный денежный поток в течение некоторого времени, поэтому важно внимательно следить за денежными средствами и иметь надежный прогноз денежного потока, чтобы вы знали, будет ли ваш бизнес оставаться в плюсе.
Почему важно прогнозирование денежных потоков
Вам нужно отслеживать исторический поток денежных средств не реже одного раза в месяц, чтобы вы могли начать отслеживать тенденции в отношении того, что на самом деле происходит с вашим притоком и оттоком денежных средств.
Но это не только измерение прошлого и настоящего, прогнозирование вашего денежного потока также может помочь вам предвидеть, когда у вашего бизнеса может закончиться нехватка денежных средств в будущем. Затем вы можете заранее спланировать и открыть кредитную линию или найти другие займы и инвестиции, которые помогут вам покрыть тот момент в будущем, когда вам понадобится немного дополнительных денег.
Намного легче получить помощь от банка или инвестора, прежде чем вы действительно окажетесь в кризисной ситуации, когда вы не уверены, что сможете оплатить свои счета.Если вы подождете, пока у вас возникнут серьезные проблемы, чтобы принять меры, кредиторы могут посчитать вас слишком рискованным и отклонить ваш запрос.
Прогноз движения денежных средств также может помочь вам спланировать наилучшее время для крупной покупки, например приобретения нового оборудования или служебного автомобиля.
Однако не забывайте учитывать неизвестное. Владельцы бизнеса не могут предсказать будущее, особенно когда речь идет о любых непредвиденных расходах, которые они могут понести (например, преждевременная поломка грузовика и необходимость его замены или утечка данных, приводящая к вынужденному увеличению расходов на ИТ).И они также не могут быть уверены в том, что их клиенты будут платить по счетам вовремя.
Итак, когда вы прогнозируете или просматриваете отчет о движении денежных средств за последний месяц, помните, что наличие некоторого буфера — это хорошо. Вы же не хотите быть в положении, когда вы распределяете каждую копейку до такой степени, что вы не можете покрыть непредвиденные расходы.
Часть анализа вашего денежного потока должна быть связана с риском и влиянием непредвиденных расходов на ваши наличные деньги — и, в конечном итоге, на вашу способность оплачивать счета.
Как спрогнозировать денежный поток и составить отчет о движении денежных средств
Прогноз движения денежных средств — это прогнозирование ваших потребностей в деньгах заранее.
К сожалению, прогнозировать денежный поток немного сложнее, чем прогнозировать другие аспекты вашего бизнеса, такие как продажи и расходы. В отчете о движении денежных средств учитываются ваши прогнозы доходов, прогнозы расходов, а также планы покупки запасов, если ваш бизнес хранит запасы в наличии.
Кроме того, вам необходимо предсказать, когда ваши клиенты будут платить вам — все ли они будут платить вовремя? Или некоторым потребуется больше времени для оплаты?
Такой инструмент, как LivePlan, может значительно упростить прогнозирование денежных потоков, но вы также можете сделать это самостоятельно с помощью электронных таблиц, если хотите.
Существует два метода, которые можно использовать для построения отчета о движении денежных средств: прямой метод и косвенный метод . Хотя оба они приходят к одному и тому же конечному результату и предсказывают, сколько денег у вас будет в банке в будущем, они достигают этой цели по-разному.
Прямой метод прогнозирования денежных потоков
Прямой метод дает очень четкое представление о том, как деньги поступают в бизнес и уходят из него. По сути, вы складываете все денежные средства, полученные вашим бизнесом из различных источников, а затем вычитаете все денежные средства, выплаченные поставщикам, продавцам, сотрудникам и т. Д. Это число будет суммой денежных средств, которую вы либо добавили, либо вычли из ваш банковский счет в течение месяца.
Косвенный метод прогнозирования денежных потоков
Косвенный метод начинается с вашей чистой прибыли из отчета о прибылях и убытках, а затем производится корректировка этого числа для учета неденежных расходов, таких как амортизация.Оттуда вы вносите корректировки, чтобы учесть изменения в запасах, дебиторской и кредиторской задолженности.
Косвенный метод очень распространен для построения отчетов о движении денежных средств за прошлые периоды, поскольку все необходимые числа легко генерируются из вашей системы бухгалтерского учета. Это делает его довольно популярным методом прогнозирования денежных потоков, хотя прямой метод, как правило, проще для людей, которые не так хорошо знакомы с тонкостями бухгалтерского учета.
Прочтите наше руководство, чтобы получить более подробное объяснение двух методов создания отчета о движении денежных средств.
Прогноз движения денежных средств
Если вы прогнозируете денежный поток с помощью таблиц, я рекомендую использовать прямой метод. Это проще и понятнее.
По сути, вы хотите создать будущие оценки того, когда вы будете получать деньги от клиентов и когда будете оплачивать свои счета.
Однако не обязательно прогнозировать каждый отдельный счет и оплату счета. Прогнозирование помогает вам принимать стратегические решения в отношении вашего бизнеса, поэтому делать более широкие оценки в своем прогнозе можно.
Прочтите наше руководство по прогнозированию денежных потоков, чтобы получить подробное объяснение того, как создавать как прямой, так и косвенный прогноз.
Как увеличить денежный поток
Если ваш денежный поток отрицательный или вы просто ищете способы улучшить его в целом, у вас есть множество вариантов. Вот краткий список того, что вы можете сделать:
Убедите своих клиентов платить вам быстрее
Оплачивайте собственные счета немного медленнее
Покупайте меньше запасов и держите меньше запасов под рукой
Рассмотрение проблемных долгов
Открыть кредитную линию или другой вид займа для бизнеса
В зависимости от вашей ситуации, вы можете использовать эти методы или даже рассмотреть более решительные меры, если экономика в целом влияет на вашу способность создавать положительный денежный поток.
Для получения более подробных советов и информации прочтите наши советы экспертов по устранению неполадок, чтобы улучшить ваш денежный поток, и наше руководство по управлению денежным потоком в кризисной ситуации.
Дополнительная литература, которая поможет вам лучше контролировать денежный поток
Денежный поток — это большая тема, и есть много других ресурсов, которые могут вам пригодиться. Вот наш главный список того, что вам следует прочитать дальше:
Как сбалансировать денежный поток в сезонном бизнесе
Сезонные компании сталкиваются с уникальными проблемами, которые необходимо учитывать, включая варианты управления денежными потоками.Ознакомьтесь с этими методами, чтобы эффективно сбалансировать свой денежный поток и избежать сезонных сюрпризов. Читать далее.
Использование факторинга счетов для защиты ваших денежных потоков
Если у вас есть клиенты, которым нужно бесконечно платить, это может вызвать проблемы с движением денежных средств для вашего бизнеса. К счастью, такие решения, как счет-фактура и спотовый факторинг, могут выступать в качестве защиты, помогая защитить ваш денежный поток от будущих бедствий. Читать далее.
Советы по увеличению денежного потока для вашего бизнеса
Надежное управление денежными потоками имеет решающее значение для успеха в бизнесе.Если у вас возникли проблемы с управлением денежным потоком, эти стратегии помогут вам стать лучше. Читать далее.
Как получить помощь по кредитной линии
Каждый бизнес сталкивается с проблемами движения денежных средств. Вместо того, чтобы избегать их, такие меры, как преимущественная кредитная линия, могут помочь вам поддерживать бесперебойную работу. Читать далее.
.
PPT — Глава 5 — Дисконтированные денежные потоки Презентация PowerPoint, скачать бесплатно
Глава 5 — Дисконтированные денежные потоки
Аннуитеты • Элементы: • Множественные денежные потоки • Идентичные (или постоянные) денежные потоки • Конечные ( для фиксированного количества периодов) • Типы аннуитетов • Обычные аннуитеты — Денежные потоки возникают в конце периода • Аннуитеты к оплате — Денежные потоки возникают в начале периода.
Аннуитеты • Мы часто имеем дело с постоянными множественными конечными денежными потоками.• Примеры: • Автокредиты • Ипотека • Целевой фонд pmts
Аннуитеты • Пример: Какова будущая стоимость трехлетнего обычного аннуитета в размере 100 долларов США при 10%? r = 10% 3 1 2 0 $ 100 $ 100 $ 100 $ 100
Аннуитеты 100100100 r = 10% 3 0 2 1 FV =? CF2 (1 + r) 1 CF1 (1 + r) 2
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Конец» • Установите P / Y (платежи в год) на 1 • Очистите регистр • Введите 0, затем нажмите PV • Введите 100, затем нажмите pmt • Введите 10, затем нажмите i • Введите 3, затем нажмите n • Нажмите FV и альт FV = ____331.00 Меню «Временная стоимость денег» n i PV pmt FV
Аннуитеты • Пример: Какова приведенная стоимость 3-летнего обычного аннуитета в размере 100 долларов США при 10%? r = 10% 3 1 2 0 $ 100 $ 100 $ 100 $ 100
Аннуитеты 100 / (1 + i) 100100100 r = 10% 3 0 2 1100 / (1 + i) 1100 / (1 + i ) 2 100 / (1 + i) 3
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Конец» • Установите P / Y (выплаты в год) на 1 • Очистите регистр • Введите 0, затем нажмите FV • Введите 100, затем нажмите pmt • Введите 10, затем нажмите i • Введите 3, затем нажмите n • Нажмите PV и альт PV = ____- $ 248.68 Меню «Временная стоимость денег» ni PV pmt FV
Аннуитеты • Какова будущая стоимость 3-летнего аннуитета в размере 100 долларов под 10% r = 10% 3 0 100 долларов 100 долларов 100 долларов 100 долларов
Аннуитеты 100 100 100 r = 10% 3 0 2 1 FV =? CF2 (1 + r) 1 CF1 (1 + r) 2 CF1 (1 + r) 3
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Начать» • Установите P / Y (платежи на год) до 1 • Очистить регистр • Введите 0, затем нажмите PV • Введите 100, затем нажмите pmt • Введите 10, затем нажмите i • Введите 3, затем нажмите n • Нажмите FV и альт FV = ____- $ 364.10 Меню «Временная стоимость денег» ni PV pmt FV
Аннуитеты • Какова приведенная стоимость 3-летнего аннуитета, подлежащего выплате в размере 100 долларов США под 10% r = 10% 3 0 100 долларов США 100 долларов США 100 долларов США
Аннуитеты 100 / (1 + i) 100 100 100 r = 10% 3 0 2 1 100 / (1 + i) 1 100 / (1 + i) 2
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Начать» • Установите P / Y (выплаты в год) на 1 • Очистить регистр • Введите 0, затем нажмите FV • Введите 100, затем нажмите pmt • Введите 10, затем нажмите i • Введите 3, затем нажмите n • Нажмите PV и альт PV = ____- 273 доллара.55 Меню «Временная стоимость денег» n i PV pmt FV
Аннуитеты • Пример: для выхода на пенсию вам понадобится 1 миллион долларов ровно через 40 лет. Если вы можете зарабатывать 10% в год, сколько вам нужно инвестировать каждый год, если вы сделаете свой первый платеж ровно через год? • Что это за аннуитет?
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Конец» • Установите P / Y (платежи в год) на 1 • Очистите регистр • Введите 0, затем нажмите PV • Введите 1 миллион долларов, затем нажмите FV • Введите 10, затем нажмите i • Введите 40, затем нажмите n • Нажмите pmt и viola pmt = ____- $ 2259.41 Меню «Временная стоимость денег» n i PV pmt FV
Аннуитеты • Пример: сегодня вам нужно 1000 долларов, чтобы купить ПК. ЕСЛИ вы можете получить ссуду под 10% годовых сроком на 3 года, сколько будут составлять ваши ежегодные платежи, если вы сделаете первый платеж в течение одного года? • Что это за аннуитет?
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Конец» • Установите P / Y (выплаты в год) на 1 • Очистите регистр • Введите 1000, затем нажмите PV • Введите 0, затем нажмите FV • Введите 10, затем нажмите i • Введите 3, затем нажмите n • Нажмите pmt и viola pmt = ____- 402 доллара.11 Меню «Временная стоимость денег» ni PV pmt FV
Аннуитеты • Пример: вы платите 864,80 доллара за инвестицию, которая обещает вам 250 долларов в год в течение следующих 4 лет, при этом платежи производятся в конце год. Какую процентную ставку вы получите от этой инвестиции? • Что это за аннуитет?
Аннуитеты Использование финансового калькулятора • Важно: • Установите режим «Конец» • Установите P / Y (выплаты в год) равным 1 • Очистите регистр • Введите — 864 доллара.80, затем нажмите PV • Введите 0, затем нажмите FV • Введите 250 долларов, затем нажмите pmt • Введите 4, затем нажмите n • Нажмите i и альт i = ____ 6.07 Меню «Временная стоимость денег» ni PV pmt FV
Бессрочные платежи • Элементы бессрочного права • Множественные потоки денежных средств • Идентичные (или постоянные) потоки денежных средств • Бесконечные — потоки денежных средств продолжаются вечно
Бессрочные платежи • Пример: какова текущая стоимость (или рыночная цена) каждой акция привилегированных акций, по которой выплачивается 4 доллара в год, если ставка альтернативных издержек составляет 8%?
Perpetuities PV = платеж / процентная ставка = pmt / i
Неравномерные денежные потоки • Платеж (pmt) — обозначает постоянные денежные потоки • Денежный поток (CF) — обозначает денежные потоки в целом, включая неравномерные денежные потоки
Общие уравнения ценообразования: • PV = CF1 [1 / (1 + r) 1] + CF2 [1 / (1 + r) 2] +… + CFn [1 / (1 + r) ) n] • FV = CF1 (1 + r) n-1 + CF2 (1 + r) n-2 +… + CFn (1 + r) n
Неравномерный денежный поток • Пример: Что такое PV этого неравномерного денежного потока? Предполагая, что ставка альтернативных издержек составляет 10%? график: r = 10% 5 0 $ 100 $ 300 $ 300 $ -50 PV = $?
Неравномерный денежный поток • Напишите уравнение для PV, которое вы можете решить с помощью любого калькулятора.• Решение для финансового калькулятора: • Ввод в регистр денежных потоков • CF0 = 0 • CF1 = 100 • CF2 = 300 • CF3 = 300 • CF4 = -50 • Затем введите 10% для процентной ставки и нажмите NPV
Неравномерно Денежный поток • В последнем примере будет ли PV больше или меньше, если бы ставка альтернативных издержек была больше? • Зачем? • Проверьте свой ответ, используя большую альтернативную стоимость, скажем, 20% PV при 20% = ___________
Неравномерный денежный поток • В последнем примере будет ли PV больше или меньше, если бы ставка альтернативных затрат была меньше? • Зачем? • Проверьте свой ответ, используя более высокую альтернативную стоимость, скажем, 5% PV @ 5% = ___________
Осложнения: полугодовые и другие периоды начисления сложных процентов • Пример: рассчитайте FV 100 долларов, инвестированных в течение 2 лет под 8%, если проценты начисляются ежегодно, раз в полгода и ежемесячно.• Ежегодно: r = 8% 1 2 0 $ 100 FV =?
Осложнения: полугодовые и другие периоды начисления сложных процентов На финансовом калькуляторе: n = i = PV = Pmt = FV =
Осложнения: полугодовые и другие периоды начисления сложных процентов • Полугодовые: r = 8% 1 1/2 1 1/2 2 0 $ 100 FV =?
Осложнения: полугодовые и другие периоды начисления сложных процентов В финансовом калькуляторе: n = i = PV = Pmt = FV =
Осложнения: полугодовые и другие периоды начисления сложных процентов • Ежемесячно: n = i = PV = Pmt = FV =
Сложности: полугодовые и другие периоды начисления сложных процентов • Примечание: • Простая (или котируемая) процентная ставка часто указывается в качестве процентной ставки для ссуд, банковских счетов, кредитов. карты и облигации.В последнем примере простая или котируемая процентная ставка составляла 8%. • Эффективная годовая ставка (или ERA) процентная ставка — это годовая ставка, фактически получаемая или выплачиваемая, если рассматривать сложное начисление.
Осложнения: полугодовые и другие периоды начисления сложных процентов Эффективная годовая ставка (EAR) = (1+ (isimple / n) n — 1
Осложнения: полугодовые и другие периоды начисления сложных процентов (n — количество начисленных процентов каждый год) • Каким был EQAR для каждой частоты начисления сложных процентов в последнем примере • Годовой: EAR = • Полугодовой: EAR = • Ежемесячный: EAR =
Дробные периоды времени • Пример : Рассчитайте PV 100 долларов, инвестированных в течение полугода на банковский счет, на который выплачивается EAR в размере 8%
Дробные периоды времени • Пример: Рассчитайте FV 100 долларов, вложенных в течение полугода на банковский счет, который приносит EAR в размере 8%
Дробные периоды времени • Пример. Рассчитайте PV 100 долларов, вложенных в течение 9 месяцев на банковский счет, на который выплачивается EAR в размере 8%
Fractional Time Peri ods • Пример. Рассчитайте справедливую стоимость 100 долларов, инвестированных в течение 9 месяцев на банковский счет, на который выплачивается EAR в размере 8%
Амортизированные ссуды • Это ссуды, которые погашаются серией равных платежей.• Пример: вам нужно 1000 долларов сегодня, чтобы купить ПК. ЕСЛИ вы можете получить ссуду под 10% годовых на 3 года, сколько вы будете платить за год, при условии, что первый платеж будет ровно через год. • Что это за аннуитет?
Амортизированные ссуды • Нарисуйте временную шкалу График погашения ссуд Год BegBal Pmt Int Prin EndBal 1 2 3 Итого
Сравнение различных типов процентных ставок • Простая (или указанная) процентная ставка часто бывает укажите процентную ставку по кредитам, банковским счетам, кредитным картам и облигациям.• Эффективная годовая ставка (или EAR) процентная ставка — это годовая ставка, фактически получаемая или выплачиваемая с учетом начисления сложных процентов. • Периодическая ставка — это ставка, взимаемая или выплачиваемая за каждый период. • Годовая процентная ставка (APR) — это ставка, сообщаемая (в соответствии с требованиями закона) для заемщиков — это периодическая ставка, умноженная на количество периодов в году. Таким образом, фактические эффекты компаундирования не учитываются. (То же, что и простая ставка)
Сравнение различных типов процентных ставок • Периодическая ставка = isimple / n • isimple = Периодическая ставка xn • Эффективная годовая ставка (EAR) = (1+ (isimple / n) n — 1
Сравнение различных типов процентных ставок • Пример. Предположим, что годовая процентная ставка вашей кредитной карты составляет 18%.Какая у вас эффективная годовая процентная ставка? (Проценты начисляются один раз в месяц)
Сравнение различных типов процентных ставок • Пример: Предположим, у вас есть ипотечный кредит под 7,5%. Какая у вас эффективная годовая процентная ставка? (вы платите ежемесячно)
.
PPT — Презентация PowerPoint для оценки дисконтированного денежного потока, скачать бесплатно
Глава Оценка шести дисконтированных денежных потоков
Краткое содержание главы • Будущие и текущие значения множественных денежных потоков • Оценка уровня денежных потоков: аннуитеты и бессрочные выплаты • Сравнение ставок: влияние сложения • Типы ссуд и амортизация ссуд
0 1 2 3 7 000 4 000 4 000 Множественные потоки денежных средств 6.1 — FV Пример 1 • В настоящее время у вас есть 7000 долларов на банковском счете с 8% -ной процентной ставкой.Вы думаете, что сможете внести дополнительные 4000 долларов в конце каждого из следующих трех лет. Сколько у вас будет через три года? 4,000.00
Множественные денежные потоки — пример FV 2 • Предположим, вы инвестируете 500 долларов в паевой инвестиционный фонд сегодня и 600 долларов через год. Если фонд платит 9% годовых, сколько у вас будет через два года? 0 1 2 9% 500 600
Множественные денежные потоки — БС Пример 2 (продолжение) • Используя денежные потоки с предыдущей страницы, сколько у вас будет через 5 лет, если вы больше не будете зарабатывать депозиты? 0 1 2 3 4 5 9% 500 600
Множественные денежные потоки — пример FV 3 • Предположим, вы планируете внести 100 долларов на счет в течение одного года и 300 долларов на счет через три года.Сколько будет на счету через пять лет, если процентная ставка 8%? 0 1 2 3 4 5 8% 100 300
Несколько денежных потоков — пример PV 1 • Вам предлагается инвестиция, которая принесет вам 200 долларов в течение одного года, 400 долларов в следующем году, 600 долларов через год и 800 долларов в конце следующего года. Вы можете заработать 12% на аналогичных инвестициях. Сколько стоит эта инвестиция сегодня? 0 1 2 3 4 12% 200 400 600 800
Неравномерные денежные потоки — использование калькулятора • Другой способ использования финансового калькулятора для неравномерных денежных потоков — использование ключей денежных потоков • HP 10BII • Введите первый денежного потока, используя кнопки +/- для обозначения оттока • Нажмите CF • Введите второй денежный поток • Нажмите CF • Введите процентную ставку как I / Y • Используйте вторую функцию, затем кнопку NPV для вычисления текущего значения • Чтобы очистите эту функцию, используйте вторую функцию, Очистить все
Решения, Решения • Ваш брокер звонит вам и сообщает, что у него есть прекрасная инвестиционная возможность.Если вы вложите 100 долларов сегодня, вы получите 40 долларов через год и 75 долларов через два года. Если вам требуется 15% -ный возврат инвестиций, связанных с этим риском, следует ли вам брать инвестиции? • Используйте ключи CF для вычисления стоимости инвестиций. CF CF CF I / Y 2nd NPV Примечание: NPV (чистая приведенная стоимость) — это добавление или уничтожение богатства, возникающего в результате инвестирования. Если NPV положительный, вы создаете богатство. Если NPV отрицательный, вы уничтожаете богатство. Следовательно, правило принятия решения — принимать только проекты с NPV> 0 Отклонение: NPV <0
Аннуитеты и бессрочные выплаты 6.2 • Аннуитет — конечная серия равных платежей, которые происходят через равные промежутки времени • Если первый платеж происходит в конце периода, он называется обычным аннуитетом • Если первый платеж происходит в начале периода, он называется причитающийся аннуитет • Бессрочный период — бесконечная серия равных платежей
Аннуитеты — Основные формулы • Аннуитеты: где: PV = текущая стоимость FV = будущая стоимость C = равный периодический денежный поток R = процентная ставка или ставка дисконтирования t = количество периодов времени
Обычные аннуитеты по сравнению с аннуитетами к уплате • Обычная аннуитетная — первый платеж происходит в период времени 1 • Аннуитетный платеж — первый платеж происходит в период времени 0
Аннуитеты и калькулятор • Решить любая проблема типа аннуитета с использованием функциональных клавиш, вы должны использовать клавишу PMT • Используйте клавишу PMT только тогда, когда каждый денежный поток имеет точно такой же размер и происходит через равные промежутки времени • Обычный аннуитет по сравнению с причитающимся аннуитетом • Чтобы переключить калькулятор между обычным аннуитетом и аннуитетом к оплате, введите 2-й лв (HP 10BII) • Если вы видите «BGN» или «Начать» на дисплее вашего калькулятора, вы настроили его для выплаты аннуитета • Большинство проблем связаны с обычными аннуитетами.
Аннуитеты — Пример 1 • После тщательного перерасчета бюджета вы определили, что можете позволить себе платить 632 доллара в месяц на новый спортивный автомобиль.Ваш банк будет кредитовать вас под 1% в месяц на 48 месяцев. Сколько можно взять в долг? • Формульный подход • Расчетный подход • PMT • FV • N • I / Y • PV
Аннуитет — Пример лотереи • Предположим, вы выиграли лотерею на сумму 10 миллионов долларов от Информационного центра Publishers. Деньги выплачиваются равными ежегодными взносами в размере 333 333,33 доллара в течение 30 лет. Если подходящая ставка дисконтирования составляет 5%, сколько на самом деле стоит лотерея сегодня? Формула Подход Калькулятор Подход PMT FV N I PV
Поиск платежа • Предположим, вы хотите занять 20 000 долларов на новую машину.Вы можете занимать под 8% годовых, ежемесячно начисляемых (8% / 12 = 0,66667% в месяц). Если вы берете кредит на 4 года, каков ваш ежемесячный платеж? Формульный подход Калькулятор Подход PV FV N I PMT
Определение количества платежей — пример 1 • У вас немного не хватило на февральские каникулы, поэтому вы положили 1000 долларов на свою кредитную карту. Вы можете позволить себе только минимальный платеж в размере 20 долларов в месяц. Процентная ставка по кредитной карте — 1,5% в месяц. Как долго вам нужно будет выплатить 1000 долларов?
Определение количества платежей — пример 1 • Формульный подход • Начните с основной формулы аннуитета и решите для неизвестного показателя t, используя журналы.Подход с помощью калькулятора PV FV PMT I N месяцев
Определение количества платежей — пример 2 • Предположим, вы занимаете 2000 долларов под 5% и собираетесь делать ежегодные платежи в размере 734,42 долларов. Как скоро вы погасите кредит? Подход с помощью калькулятора PV FV PMT I N лет
Определение ставки на финансовом калькуляторе • Предположим, вы одалживаете у родителей 10 000 долларов, чтобы купить машину. Вы соглашаетесь платить 207,58 долларов в месяц в течение 60 месяцев.Какая ежемесячная процентная ставка? Подход с помощью калькулятора PV FV PMT NI% в месяц
Аннуитет — определение ставки без финансового калькулятора • Метод проб и ошибок • Выберите процентную ставку и вычислите PV платежей на основе этой ставки • Сравните вычисленную PV с фактической суммой кредита • Если вычисленная PV> суммы кредита, то процентная ставка слишком низкая (например, r = 0,5% вычисленная PV = 10 738,11 долларов США) • Если вычисленная PV <сумма кредита, то процентная ставка слишком высока (e .грамм. r = 2% вычисленной PV = 7 215,48 долл. США) • Скорректируйте ставку и повторите процесс до тех пор, пока вычисленная PV и сумма займа не станут равными
Будущие значения аннуитетов — Пример 1 • Предположим, вы начинаете откладывать на пенсию, делая депозит 2000 долларов в год в рамках RRSP. Если процентная ставка составляет 7,5%, сколько у вас будет через 40 лет? Формульный подход Калькулятор Подход PMT PV N I FV
Аннуитетный платеж — Пример 1 • Вы экономите на новом доме и вкладываете 10 000 долларов в год на счет, выплачивая 8% годовых.Первый платеж производится сегодня. Сколько у вас будет через 3 года? Формула Подход Калькулятор Подход 2-й BGN PMT PV NI FV
Perpetuity • Perpetuity • Perpetuity: Поток денежных потоков, который продолжается вечно Где: PV = Текущая стоимость C = равный периодический денежный поток, начиная с периода времени 1 r = скидка ставка
Бессрочная передача — Пример 1 • Хоум Банк Канады хочет продать привилегированные акции по цене 100 долларов за акцию.Очень похожий выпуск привилегированных акций, уже находящихся в обращении, имеет цену 40 долларов за акцию и предлагает дивиденды в размере 1 доллара каждый квартал. Какие дивиденды должен предложить Home Bank, если его привилегированные акции будут продаваться?
Perpetuity — продолжение примера 1 • Сначала найдите требуемую доходность для сопоставимого выпуска: • Затем, используя указанную выше требуемую доходность, найдите дивиденд для нового привилегированного выпуска:
Growing Perpetuity • До сих пор обсуждались бессрочные выплаты с постоянными выплатами. • Растущие бессрочные выплаты имеют денежные потоки, которые растут с постоянной скоростью и продолжаются вечно. 3 доллара за акцию в следующем году.Инвесторы ожидают, что годовые дивиденды будут расти на 6% в год навсегда. Требуемая доходность — 11%. Какова цена акций сегодня?
Растущий аннуитет • Растущий аннуитет имеет конечное число денежных потоков, которые растут с постоянной скоростью • Формула растущего аннуитета:
Растущий аннуитет — Пример 1 • Жиль Лебудер только ему предложили работу с оплатой 50 000 долларов в конце первого года обучения. Он ожидает, что его зарплата будет увеличиваться на 5% в год до выхода на пенсию через 40 лет.Какова текущая стоимость его пожизненной зарплаты при процентной ставке 8%?
Эффективная годовая ставка (EAR) 6,3 • Эффективная годовая процентная ставка — это фактическая ставка, выплачиваемая (или получаемая) после учета начисления сложных процентов, происходящего в течение года • Например, 10%, начисленные дважды в год, имеют EAR 10,25%. Это означает, что 10%, начисляемые дважды в год, идентичны 10,25%, начисляемым ежегодно. • Если вы хотите сравнить две альтернативные инвестиции с разными периодами начисления сложных процентов, вам необходимо вычислить EAR для обеих инвестиций, а затем сравнить EAR.
Годовая процентная ставка (номинальная ставка) • Это годовая ставка, установленная законом • По определению, номинальная ставка или годовая процентная ставка = ставка за период, умноженная на количество периодов в году • Следовательно, чтобы получить период Мы изменим формулу годовой процентной ставки: • Ставка за период = годовая процентная ставка / количество периодов в году • НИКОГДА не делите эффективную ставку на количество периодов в году — она НЕ даст вам ставку за период
Расчет годовых ( Номинальная процентная ставка) • Какой будет годовая процентная ставка, если месячная ставка равна.5%? • Какова годовая процентная ставка, если годовая ставка составляет 0,5% • Какова месячная ставка, если годовая процентная ставка составляет 12% с ежемесячным начислением сложных процентов?
Что следует помнить • Вы ВСЕГДА должны убедиться, что период начисления сложных процентов и период выплаты совпадают. • Если выплаты являются годовыми, вы используете годовое начисление сложных процентов. • Если платежи производятся ежемесячно, вы используете ежемесячное сложение
Расчет EAR — Пример 1 • Для расчета EAR используйте следующую формулу: • Например, EAR для 10%: Периоды сложения EAR 2 10.25% 4 10.3813% 12 10.4713% 52 10.5065% 365 10.5156%
Решения, Решения II • Вы сравниваете два сберегательных счета. Один платит 5,25% ежедневно. Другой платит 5,3%, начисляемые раз в полгода. Какую учетную запись вы бы использовали? • Первая учетная запись: • EAR = • Вторая учетная запись: • EAR = • Вы должны выбрать первую учетную запись (учетную запись, которая ежедневно пополняется), потому что вы зарабатываете более высокую эффективную процентную ставку.
Решения, Решения II Продолжение • Давайте проверим выбор.Предположим, вы вкладываете по 100 долларов в каждую учетную запись. Сколько у вас будет на каждой учетной записи через год? • Первый счет: • Дневная ставка = • FV =, OR, • N; I / Y; PV; БС = • Второй счет: • Полугодовая ставка = • БС =, OR, • N; I / Y; PV; CPT FV = • У вас больше денег на первом счете.
Вычисление APR из EAR • Если у вас есть эффективная ставка, как вы можете вычислить APR? Измените уравнение EAR, и вы получите:
APR — Пример 1 • Предположим, вы хотите заработать эффективную ставку в 12%, и вы просматриваете счет, который пополняется на ежемесячной основе.Какой годовой процент они должны платить?
Вычисление платежей с годовой процентной ставкой — Пример 1 • Предположим, вы хотите купить новую компьютерную систему, и магазин разрешает вам делать ежемесячные платежи. Вся компьютерная система стоит 3500 долларов. Срок кредита составляет 2 года, процентная ставка — 16,9% с ежемесячным начислением сложных процентов. Какой у вас ежемесячный платеж? • Формульный подход Калькулятор Подход PV FV N I PMT
Будущие значения с ежемесячным начислением сложных процентов • Предположим, вы вносите 50 долларов в месяц на счет с годовой процентной ставкой 9% на основе ежемесячного начисления сложных процентов.Сколько у вас будет на счету через 35 лет? Формульный подход Калькулятор Подход PMT PV NI FV
Непрерывное начисление процентов • Иногда инвестиции или займы рассчитываются на основе непрерывного начисления сложных процентов • EAR = er — 1 • e — основание натурального логарифма, равное 2,7183 (хотя это на самом деле неокончательная, неповторяющаяся десятичная дробь) • e отображается на большинстве калькуляторов ex • Пример: Какова эффективная годовая ставка 7%, начисляемая непрерывно? • EAR = e.07 — 1 =
.

Аннуитеты в МСФО

Что такое аннуитет?

Формула аннуитета

Дисконтирование аннуитетных платежей

Аннуитетный и дифференцированный платежи: что это такое и в чем разница — Ипотека

Аннуитетный платеж

Как погасить аннуитетный платеж

Дифференцированный платеж

Как погасить дифференцированный платеж

Сейчас читают

Инструкция: как правильно оформить справку о доходах

Как снять обременение после выплаты ипотеки

Как досрочно погасить ипотеку

Аннуитет — это… Что такое Аннуитет?

Виды аннуитетов

Коэффициент аннуитета

Будущая стоимость аннуитетных платежей

См. также

Ссылки

CFA — Как рассчитывать приведенную стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA

Расчет текущей стоимости (PV) серии равных денежных потоков.

Пример расчета текущей (приведенной) стоимости обычного аннуитета.

Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.

Пример расчета прогнозируемой текущей стоимости обычного аннуитета.

Как вычислять текущую стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?

Пример расчета текущей стоимости (PV) перпетуитета.

Текущая стоимость на момент времени, отличный от текущей даты (t = 0).

Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.

Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.

Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?

CFA — Как рассчитывать будущую стоимость (FV) последовательности денежных потоков (аннуитета)? | программа CFA

Как вычислять обычный аннуитет, то есть FV равных денежных потоков?

Пример расчета будущей стоимости простого аннуитета.

Как вычислять аннуитет при неравных денежных потоках?

Пример расчета аннуитета при неравномерных денежных потоках.

Аннуитет :: Инвестиции онлайн — ВАШ Путь в мире бизнеса.

Стоимость аннуитета (FVA и PVA)| КАЛЬКУЛЯТОР

Будущая стоимость аннуитета постнумерандо рассчитывается по следующей формуле:

Настоящая стоимость аннуитета постнумерандо рассчитывается следующим образом:

Используя формулу настоящей стоимости аннуитета постнумерандо можно рассчитать размер ежемесячного платежа:

Учебное пособие по временной стоимости денег

Что такое денежный поток?

Определение денежного потока

Как рассчитать денежный поток

В чем разница между наличными и прибылью?

Как анализировать отчет о движении денежных средств

Положительный денежный поток

Отрицательный денежный поток

Уровень сжигания наличных денег и взлетно-посадочная полоса

Почему важно прогнозирование денежных потоков

Как спрогнозировать денежный поток и составить отчет о движении денежных средств

Прямой метод прогнозирования денежных потоков

Косвенный метод прогнозирования денежных потоков

Прогноз движения денежных средств

Как увеличить денежный поток

Дополнительная литература, которая поможет вам лучше контролировать денежный поток

Как сбалансировать денежный поток в сезонном бизнесе

Использование факторинга счетов для защиты ваших денежных потоков

Советы по увеличению денежного потока для вашего бизнеса

Как получить помощь по кредитной линии

PPT — Глава 5 — Дисконтированные денежные потоки Презентация PowerPoint, скачать бесплатно

PPT — Презентация PowerPoint для оценки дисконтированного денежного потока, скачать бесплатно

Добавить комментарий Отменить ответ