Масса м – Электронные весы – купить весы у производителя МАССА-К

Весы МАССА К электронные торговые весы масса к производства massa k

На сайте MASSATORG.RU вы можете приобрести качественные электронные весы для промышленности, торговли и медицины. Высокое качество и надежность, низкая цена, простота в эксплуатации и сервисном обслуживании — вот основные характеристики, выгодно отличающие электронные весы «МАССА-К».

Наш сайт был создан специально, чтобы вам было удобно:

• Легко ознакомиться с продукцией, МассаК
• Выбрать и сразу приобрести подходящие для вас весы
• Ознакомиться с сертификатами для весов
• Скачать необходимые драйвера и ПО
• Оборудование и системы автоматизации для своего бизнеса
• Подобрать оборудование и системы автоматизации для своего бизнеса

Другими словами, наш сайт – это простая площадка со всей необходимой информацией о весовом оборудовании. Вы можете купить весы, представленные на нашем сайте в один клик.

Мы предлагаем широкий ассортимент продукции Масса К — электронные весы для промышленности, торговли и медицины; весы с печатью этикеток ВПМ, весы торговые, весы настольные, весы товарные, весы промышленные, весы крановые, весы медицинские, весы лабораторные, весовые терминалы.

Cерийный выпуск нового семейства весов с печатью этикеток был запущен в 2008 году.Электронные (настольные) торговые весы с печатью этикеток и фасовочные весы с печатью этикеток серии ВПМ. Товарные весы с печатью этикеток серии TB-S P успешно используются в качестве настольных весов с увеличенной платформой. Товарные весы с печатью этикеток

ТВ-М Р — напольные весы.

Вы можете заказать у нас весы, воспользовавшись формой Заказа на нашем сайте, предварительно ознакомившись с информацией об интересующем товаре. Надеемся, наши весы станут надежным помощником в Вашем бизнесе!

massatorg.ru

Масса | Наука | FANDOM powered by Wikia

https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%81%D1%81%D0%B0

---

Ма́сса (от др.-греч. μάζα, кусок теста) — скалярная неотрицательная релятивистски инвариантная физическая величина, одна из важнейших величин в физике. В нерелятивистском приближении, когда скорости тел много меньше скорости света, определяет их инерционные и гравитационные свойства^[1].

Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства (в частности, вес).

Наличие массы у элементарных частиц объясняется их взаимодействием с полем Хиггса. Чем сильнее это взаимодействие, тем больше масса у элементарной частицы^[2][3].

В современной физике понятие «количество вещества» имеет другой смысл, а масса тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). Масса проявляется в природе несколькими способами.

Гравитационная и инертная массы равны друг другу (с высокой точностью — порядка 10⁻¹³ — экспериментально^[6][7], а в большинстве физических теорий, в том числе всех, подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт не о «новой физике», просто говорят о массе, не уточняя, какую из них имеют в виду.

В классической механике масса системы тел равна сумме масс составляющих её тел. В релятивистской механике масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс компонентов, а включает в себя энергию связи и зависит от характера движения частиц друг относительно друга

[Комм 1].

Прямые обобщения понятия массы включают в себя такие тензорные характеристики как момент инерции, и такие характеристики свойств системы «тело плюс среда», как массовое водоизмещение, присоединённую массу и эффективную массу, используемые в гидростатике, гидродинамике и квантовой теории. В квантовой теории рассматриваются также поля с нестандартными кинетическими членами (например, поле Хиггса), которые можно рассматривать как поля, масса квантов которых зависит от их энергии^{[источник не указан 1862 дня]}.

Международный эталон килограмма, сделан в виде цилиндра, имеющего диаметр и высоту 39,17 мм.
Материал — сплав, содержащий 90 % платины и 10 % иридия.
Эталон хранится в штаб-квартире Международного бюро мер и весов в Севре.

Принцип эквивалентности Править

Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.

Гравитационная масса — характеристика тел в классической механике, являющаяся мерой их гравитационного взаимодействия. Отличается по определению от инертной массы, которая определяет динамические свойства тел.

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.

Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств.

На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10⁻³)^[9]. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (чувствительность к относительной разности инертной и гравитационной масс в лучшем эксперименте на 2009 год равна (0,3±1,8)×10⁻¹³)^[6][7].

Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности». Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки

законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы.
Слабый принцип отличается тем, что слова «законы природы» заменяются в нём словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.

Определение массы Править

Возможные 4-импульсы тел с нулевой и положительной массой покоя. Векторы 4-импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот четырёхимпульс, и различаются энергией и 4-скоростью частицы. Ускорение частицы сводится к движению конца 4-импульса по гиперболе. Векторы четырёхимпульса, построенные от точки пересечения осей до любой точки на синих полупрямых, имеют нулевую длину и могут относиться только к частицам нулевой массы (например, фотонам). Энергия этих частиц (с точностью до коэффициента

c) равна модулю их 3-импульса.

В нерелятивистской классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В специальной теории относительности масса неаддитивная, но тоже инвариантная величина, определяемая, как абсолютная величина 4-вектора энергии-импульса^[10]:

$ m^2 = \frac{E^2}{c^4} — \frac{\mathbf{p}^2}{c^2} $,

где E — полная энергия свободного тела, p — его импульс, c — скорость света.

В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:

$ m^2 = {1 \over c^2} g_{ik}p^i p^k. $

Здесь $ g_{ik} $ — метрический тензор, $ p^i $ — 4-импульс.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то $ m = \tfrac{E_0}{c^2} $ — масса определяется энергией покоя (Эквивалентность массы и энергии).

Особенно просто выглядят эти определения в системе единиц, в которой скорость света принята за 1 (например, в планковской или же в принятой в физике элементарных частиц системе единиц, в которой масса, импульс и энергия измеряются в электронвольтах):

В СТО: $ m = \sqrt{p_i^2} = \sqrt{E^2 — \mathbf{p}^2} $.

В ОТО: $ m = \sqrt{g_{ik}p^i p^k} $.

Следует, однако, отметить, что частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300 000 км/с), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.

О «массе покоя» и «релятивистской массе» Править

В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом параграфе.

В большом количестве источников^[11][12], относящихся к началу и середине XX века, а также в научно-популярных^[8], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса

$ \mathbf{p} = m \mathbf{v}. $

В таком случае $ m = \tfrac{E}{c^2} $ и говорили, что масса тела растёт с увеличением скорости. При таком определении понятие массы было эквивалентно понятию энергии, а также требовало отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён в течение длительного времени^[8], так как позволял провести многочисленные аналогии с классической физикой, однако в современной научной литературе используется редко^[13], так как вносит дополнительную путаницу в терминологию, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц.

Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство

$ P_\mu = m u_\mu, $

где m — инвариантная масса, а u_μ — 4-скорость (производная от 4-координаты по собственному времени частицы $ dr_{\mu}/d\tau $; единичный вектор, направленный вдоль мировой линии частицы).

Также можно записать ковариантный эквивалент второго закона Ньютона:

$ F_\mu = m a_\mu, $

где $ a_\mu = du_{\mu}/d\tau $ — 4-ускорение (кривизна мировой линии частицы).

Масса составных и нестабильных систем Править

Масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния. В частности, для устойчивых систем масса системы всегда меньше суммы масс её элементов на величину, называемую дефектом массы, и равную энергии связи, делённой на квадрат скорости света.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: $ \Delta m c^2 \approx \hbar/\tau $. При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.

Классификация частиц по значению массы Править

Масса известных на сей день частиц является, в общем, неотрицательной величиной, и должна быть равна нулю для тела, движущегося со скоростью света (фотон). Понятие массы особенно важно для физики элементарных частиц, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света) от массивных (скорость которых всегда ниже скорости света). Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения).

Положительная масса Править

К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны (включая нейтрино, которые в первоначальной версии Стандартной модели считались безмассовыми), кварки, W- и Z-бозоны, бозон Хиггса. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: барионы (в том числе протон и нейтрон) и мезоны.

Нулевая масса Править

К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому её называют скоростью света). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.

Следует отметить, что комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.

Отрицательная масса Править

Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира^[14].

Мнимая масса Править

В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.

Единицы измерения массы Править

Тройская унция, золото.

Килограмм является одной из семи основных единиц СИ и равен массе международного прототипа килограмма. Это одна из трёх единиц (наряду с секундой и кельвином), которая определена без ссылок на другие основные единицы.

В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (¹⁄₁₀₀₀ килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс·с²/м (называлась «техническая единица массы» или «инерта»). В атомной физике и химии принято сравнивать [соотносить] массу с относительной атомной массой (а.е.м.), в физике твёрдого тела — с массой электрона (Атомная система единиц), в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрономии единицей для сравнения масс небесных тел служит масса Солнца.

Масса иногда может быть выражена в терминах длины. Масса очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см^-1 ≈ 3,52×10^-41 кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6,73×10²⁴ кг.

Измерение массы Править

Прибор для измерения инертной массы тела человека в невесомости (массметр)

Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.

Этимология и история понятия Править

Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния^[15].

Масса как научный термин была введена Ньютоном как мера количества вещества, до этого естествоиспытатели оперировали с понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон вводит массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе^[16]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведенными точнейшим образом»^[17] (эти опыты Ньютон подробно описал в III томе своих «Начал»).

Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения^[18]. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, и оно подверглось критике ещё в XIX веке как нефизическое и бессодержательное^[19].

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается.

Комментарии Править

1. ↑ Так, например, суммарная масса двух свободных частиц зависит от угла между их импульсами. В частности, масса системы, состоящей из двух фотонов, обладающих энергией Е каждый, равна нулю, если импульсы фотонов сонаправлены, и равна 2E/c², если их импульсы направлены в противоположные стороны^[8].

Источники Править

1. ↑ Окунь Л. Б. Масса // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 50—52. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
2. ↑ Рубаков В. А. Долгожданное открытие: бозон Хиггса // Наука и жизнь. — 2012. — № 10. — С. 20—40. — ISSN 0028-1263. — URL: http://www.nkj.ru/archive/articles/21175/
3. ↑ Садовский М. В. Лекции по квантовой теории поля. — Москва-Ижевск : Институт компьютерных исследований, 2003. — С. 370 — ISBN 5-93972-241-5. — URL: http://eqworld.ipmnet.ru/ru/library/books/Sadovskij2002ru.pdf
4. ↑ Неравенство пассивной гравитационной и инертной масс протяженного тела
5. ↑ Вебер Дж. — Общая теория относительности и гравитационные волны
6. ↑ ^6,06,1Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
7. ↑ ^7,07,1[0712.0607] Test of the Equivalence Principle Using a Rotating Torsion Balance
8. ↑ ^8,08,18,2Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?» // Успехи физических наук. — 2000. — Т. 170. — № 12. — С. 1366—1371.
9. ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5.
10. ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § 9. Энергия и импульс.
11. ↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
12. ↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
13. ↑ Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530.
14. ↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Physical Review, 61, 13, September 1988, pp. 1446—1449
15. ↑ Джеммер, М., 1967, Глава I
16. ↑ Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
17. ↑ И. Ньютон. Математические начала натуральной философии, том I, определение 1.
18. ↑ Тюлина И. А. Об основах ньютоновой механики (к трехсотлетию «Начал» Ньютона) // История и методология естественных наук
    . — М.: 1989. — С. 184-196..
19. ↑ Мах Э. Механика. Историко-критический очерк её развития. Ижевск: НИЦ РХД, 2000, 456 с., ISBN 5-89806-023-5.

В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из-за отсутствия сносок. Вы можете улучшить статью, внеся более точные указания на источники.

• Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
• Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
• Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
• L. B. Okun On the concepts of vacuum and mass and the search for higgs // Modern Physics Letters A. — 2012.
• Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
• Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.

---

---

• Страница 0 — краткая статья
• Страница 1 — энциклопедическая статья
• Разное — на страницах: 2 , 3 , 4 , 5
• Прошу вносить вашу информацию в «Масса 1», чтобы сохранить ее

ru.science.wikia.com

Масса — это… Что такое Масса?

Двухкилограммовая гиря.

Ма́сса (от греч. μάζα) — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя).

В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «массы» можно трактовать несколькими способами:

• Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.
• Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.
• Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.

Гравитационная и инертная массы равны друг другу (с высокой точностью — порядка 10⁻¹³ — экспериментально^[1][2], а в большинстве физических теорий, в том числе всех, подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт не о «новой физике», просто говорят о массе, не уточняя, какую из них имеют в виду.

В классической механике масса системы тел равна сумме масс составляющих её тел. В релятивистской механике масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс компонентов, а включает в себя энергию связи, а также энергию движения частиц друг относительно друга^[3].

Прямые обобщения понятия массы включают в себя тензорные присоединённую массу и эффективную массу — как характеристики инерциальных свойств системы «тело плюс среда» в гидродинамике и квантовой теории. В квантовой теории рассматриваются также поля с нестандартными кинетическими членами, например, поле Хиггса, которые можно рассматривать как поля, масса квантов которых зависит от их энергии.

Принцип эквивалентности

Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.

Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.

Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств.

На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10⁻³)^[4]. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (чувствительность к относительной разности инертной и гравитационной масс в лучшем эксперименте на 2009 год равна (0,3±1,8)·10⁻¹³)^[1][2].

Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности». Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы.
Слабый принцип отличается тем, что слова «законы природы» заменяются в нем словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.

Определение массы

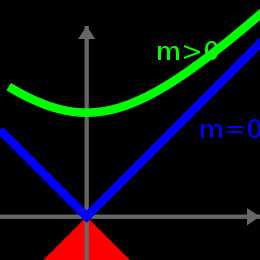Возможные 4-импульсы тел с нулевой и положительной массой покоя. Векторы 4-импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот четырёхимпульс, и различаются энергией и 4-скоростью частицы. Ускорение частицы сводится к движению конца 4-импульса по гиперболе. Векторы четырёхимпульса, построенные от точки пересечения осей до любой точки на синих полупрямых, имеют нулевую длину и могут относиться только к частицам нулевой массы (например, фотонам). Энергия этих частиц (с точностью до коэффициента c) равна модулю их 3-импульса.

В специальной теории относительности под массой понимают модуль 4-вектора импульса^[5]:

,

где E — полная энергия свободного тела, p — его импульс, c — скорость света.

В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:

Здесь  — метрический тензор,  — 4-импульс.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то  — масса определяется энергией покоя.

Особенно просто выглядят эти определения в системе единиц, в которой скорость света принята за 1 (например, в планковской или же в принятой в физике элементарных частиц системе единиц, в которой масса, импульс и энергия измеряются в электронвольтах):

В СТО:

В ОТО:

Следует, однако, отметить, что частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.

В нерелятивистской классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная, но тоже инвариантная величина, определяемая, как абсолютная величина 4-вектора энергии-импульса.

О «массе покоя» и «релятивистской массе»

В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом параграфе.

В большом количестве источников^[6][7], относящихся к началу и середине XX века, а также в научно-популярных^[8], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса

В таком случае и говорили, что масса тела растёт с увеличением скорости. При таком определении понятие массы было эквивалентно понятию энергии, а также требовало отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён в течение длительного времени^[8], так как позволял провести многочисленные аналогии с классической физикой, однако в современной научной литературе используется редко, так как вносит дополнительную путаницу в терминологию, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц.

Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство:

, где m — инвариантная масса, а u_μ — 4-скорость (производная от 4-координаты по собственному времени частицы ; единичный вектор, направленный вдоль мировой линии частицы).

Также можно записать ковариантный эквивалент второго закона Ньютона:

, где  — 4-ускорение (кривизна мировой линии частицы).

Масса составных и нестабильных систем

Масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния. В частности, для устойчивых систем масса системы всегда меньше суммы масс её элементов на величину, называемую дефектом массы, и равную энергии связи, делённой на квадрат скорости света.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: . При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.

Классификация частиц по значению массы

Масса известных на сей день частиц является, в общем, неотрицательной величиной, и должна быть равна нулю для тела, движущегося со скоростью света (фотон). Понятие массы особенно важно для физики элементарных частиц, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света) от массивных (скорость которых всегда ниже скорости света). Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения).

Положительная масса

К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны, кварки, W- и Z-бозоны. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: протон, нейтрон, гипероны и мезоны.

Нулевая масса

Основная статья: Люксон

К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому её называют скоростью света). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.

Следует отметить, что комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.

Отрицательная масса

Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира^[9].

Мнимая масса

В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.

Единицы измерения массы

Килограмм является одной из семи основных единиц СИ; среди них, это одна из трёх единиц (наряду с секундой и Кельвином), которая определена ad hoc, без ссылок на другие базовые единицы и составляющий значение международного прототипа килограмма.

В системе СИ масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (¹⁄₁₀₀₀ килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их число произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс/м•с² (обозначалась как «т. е. м.» или «инерта»). В атомной физике принято сравнивать массу с атомной единицей массы, в физике твёрдого тела — с массой электрона, в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрономии единицей для сравнения масс небесных тел служит масса Солнца.

Масса иногда может быть выражена в терминах длины. Масса очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см^-1 ≈ 3.52×10^-41 кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6.73×10²⁴ кг.

Измерение массы

Этимология и история понятия

Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния^[10].

Масса как научный термин была введена Ньютоном как мера количества вещества, до этого естествоиспытатели оперировали с понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон вводит массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе ^[11]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведенными точнейшим образом»^[12] (эти опыты Ньютон подробно описал в III томе своих «Начал»).

Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, и оно подверглось критике ещё в XIX веке как нефизическое и бессодержательное^[13].

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается.

См. также

Примечания

1. ↑ ^{1 2} Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
2. ↑ ^{1 2} [0712.0607] Test of the Equivalence Principle Using a Rotating Torsion Balance
3. ↑ Таким образом даже безмассовые частицы, например фотоны могут вместе вносить вклад в массу системы, в которую они входят; например, система из двух фотонов с противоположными импульсами, хотя масса каждого нулевая, имеет по определению массы — ненулевую массу, т.к. суммарный импульс такой системы ноль, а энергия не ноль.
4. ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5.
5. ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7, § 9. Энергия и импульс.
6. ↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
7. ↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
8. ↑ ^{1 2} Л. Б. Окунь, Успехи физических наук, 2000, т. 170, с. 1366 [1]
9. ↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Physical Review, 61, 13, September 1988, pp. 1446—1449
10. ↑ Джеммер, М., 1967, Глава I
11. ↑ Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
12. ↑ И. Ньютон. Математические начала натуральной философии, том I, определение 1.
13. ↑ Мах Э. Механика. Историко-критический очерк её развития. Ижевск: НИЦ РХД, 2000, 456 с., ISBN 5-89806-023-5.

Литература

• Джеммер, Макс Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
• Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
• Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
• L. B. Okun On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — DOI:10.1142/S0217732312300418 — arΧiv:1212.1031
• Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
• Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.

Статьи

dal.academic.ru

таблица, объемный вес, вес железобетона

Бетон активно используют в области строительства. Без этого строительного материала невозможно выполнить фундамент, его применяют при строительств оградительных конструкций и массивных промышленных объектов. Но для обеспечения всех эксплуатационных характеристик рассматриваемого изделия очень важно знать такие его параметры, как объемный вес. Остановимся подробнее на этой характеристике, чтобы понять от чего она зависит.

Масса тяжелого бетона

Для изготовления этого строительного материала применяют такие твердые горные породы, как гравий или щебень. Полученные растворы применяют для изготовления несущих конструкций и бетонных оснований. В ходе их производства могут применять определенное долевое соотношение, но оно может меняться. По этой причине точно определить вес 1 м3 бетона не удается. В большинстве случаев масса может принимать значение 1800-2500 кг/м3.

Каковы характеристики бетона в15, указано в данной статье.

Если рассматривать особо тяжелые материалы, то их применяют крайне редко, чаще всего при возведении объектов особого промышленного назначения. При строительстве жилых домов его не задействуют.

Все 1 м3 особо тяжелого бетона зависит от массы бариты или гематита. Эти компоненты применяют в роли наполнителя. Также в составе рассматриваемого строительного материала применяют чугунную дробь и железную руду. Необходимо отметить, что технология получения предполагает использование цементов высоких марок.

Узнать каковы характеристики бетона марки в 25, можно из данной статьи.

Значение объемного веса для особо тяжелого материала будет достигать 2500-3000 кг на м3. Следовательно, стоимость изделий будет намного выше, чем цена тяжелых бетонов.

Вес легких и сверхлегких материалов

Для представленного изделия характерна более пористая структуры. Весит 1 м3 такого материала 500-1800 кг. При изготовлении легких бетонов используют такие наполнители, кактуф, пемза, керамзит. Используют легкие материалы при строительстве перегородок и стен легких построек. 

Для сверхлегкого бетона на 1 м3 составит до 500 кг. Благодаря небольшому весу удается использовать в качестве наполнителя перлит и вермулит. По той причине, что у сверхлегких бетонов низкие показатели прочности, в области строительства их могут задействовать в роли теплоизолятора, например, при заделке стыков и швов.

Каков график набора прочности бетона при электропрогреве бетона, можно узнать из данной статьи.

Отдельно стоит отметить такие виды материала, как пенобетон и газобетон. У них масса не большая по причине наличия ячеистой структуры. Наличие пор в рассматриваемых материалах связано с выделением газов, которое происходит в ходе химической реакции в растворе или же при приготовлении раствора с добавлением пены. Главными достоинствами пенобетона и газобетона остается низкий уровень теплопроводности и высоки коэффициент паропроницаемости.

Какова марка бетона для отмостки, указано в статье.

Марка М200

Эта марка  относится к самой распространенной. Применяют М200 при заливке лестничных перекрытий и оснований, при строительстве дорожек и стяжек пола, в различных строительных конструкциях. Для рассматриваемой маски характерна нагрузка в 200 кг/см3.



При изготовлении бетона применяют следующие компоненты:

• цемент марки 400-500;
• вода;
• просеянный песок;
• гранитный, известковый или гравийный щебень мелких фракций.

Бывают ситуации, когда в ходе производства в состав бетона добавляют разные ингредиенты, благодаря которым удается улучшить эксплуатационные характеристики бетона.

Какова температура прогрева бетона в зимнее время, можно узнать из данной статьи.

М300

Эта марка также часто встречается при строительстве различного рода конструкций. Например, ее используют при возведении аэродромных покрытий, дорожного полотна. Удельная м- бетона М300 будет составлять 18, т/м3.



При изготовлении материала применяют такие ингредиенты:

• цемент марок 400 или 500;
• заполнители;
• просеянный песок;
• вода.

Сколько цемента на 1 куб бетона необходимо, можно узнать из данной статьи.

М400

Применяют эту марку при влагоустойчивой обработке. Для бетона М400 характерны высокие показатели прочности и очень высокая скорость затвердения. При изготовлении материала применяют следующие компоненты:



• цемент;
• песок;
• щебень средних фракций;
• вода.

Удельная масса для М400 будет составлять 2000 кг/м3.

Что собой представляет удельная масса

Такой параметр, как объемный вес зависит от таких показателей, как характер и структуры применяемого сырья при изготовлении. Дома, построенных из легких бетонов, имеют малую стоимость, чем строения, возведение которых осуществлялось с применением тяжелого материала. Плотность раствора находиться в прямой пропорциональности от его м. Если раствор пористый, тем меньшая будет его масса.

О том каков состав огнеупорного бетона можно узнать из данной статьи.

На массу оказывают свое влияние все характеристики его ингредиентов. Самые тяжелее материала изготовляют при применении заполнителей ощутимого веса, например, чугунной дроби. Удельный вес такого смеси составит 2,5-3 т/м3.

На видео – рассказывается о весе бетона в 1м3:

О том сколько весит куб бетона м350, можно узнать в статье.

При использовании наполнителя горной породы привычной плотности можно получить не слишком легкий, но и не сильно тяжелый материал. Сюда стоит отнести гранитный щебень и кварцевый песок. Объемная м- для такого раствора может составить 1,8-2,5 т/м3.

Удельный вес бетона – это физический параметр, который показывает соотношение того, какова масса вещества к объему, который оно занимает. Представленный параметр аналогичен характеристике плотности. Применяют его к цементным изделиям, но здесь стоит важно четко соблюдать пропорцию.

Рассчитать представленную характеристику очень сложно. Чтобы определить вес необходимо раздробить застывший замес и превратить его в мелкую пыль. А сделать это технически очень сложно. По этой причине многие строители пытаются задействовать объемные параметры, ведь рассчитать их гораздо проще.

О том сколько сохнет бетон контакт, указано в статье.

Удельный вес одного м3 смеси будет пропорционален прочности и марке бетона. С учетом рассматриваемой характеристики, конструкции и разделяют на три вида: легкие, тяжелые и особенно тяжелые. Необходимый материал выбирается с учетом того, для каких целей будет возводиться постройка.

На таблице – вес бетона в зависимости от заполнителя:



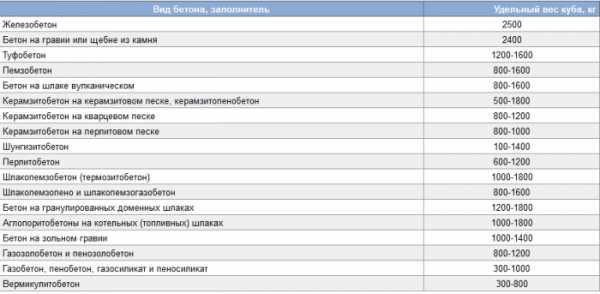
Сравнение с весом железобетона

Железобетон – это строительный материал, который сочетает в себе бетон и сталь, в результате чего обладает уникальными свойствами. Наличие высоких показателей прочности, длительный срок службы позволил этому материалу прочно закрепиться в строительной сфере. 

Так же, как и предыдущий, железобетон подразделяют на 4 группы, для каждой из которых характерен свой удельный вес:

1. Особо тяжелые. Удельная масса составляет 2500 кг/м3. В роли наполнителя здесь выступают бариты, магнетиты, гематиты и металлические скрапы.
2. Тяжелые. Для этих материалов удельная масса составит 1800 – 2500 кг/м3. В качестве наполнителей выступают щебень и гравий.
3. Легкие. Удельный вес составляет 500-1800 кг/м3. Наполнителями выступают песок, перлит, карболит, керамзит. К этой группе материалов можно отнести пенобетон и газобетон.
4. Особо легкие. Удельная масса составит менее 500 кг/м3.

О том сколько щебня нужно на 1 куб бетона, указано здесь.

Если провести аналогию между значения удельной массой для бетона и железобетона, то для двух этих строительных материалов рассматриваемый параметр одинаковый. При выборе бетона всегда внимательно изучайте его характеристики, чтобы не ошибиться в выборе и приобрести качественный материал. Одним из таких параметров остается удельная масса, зная которую вы сможете быть уверенны, что все пропорции для приготовления бетона были соблюдены верно.

resforbuild.ru

Масса определение

МАССА это:

МАССА МАССА
(лат. massa, букв.— глыба, ком, кусок), физ. величина, одна из осн. хар-к материи, определяющая её инерционные и гравитац. св-ва. Понятие «М.» было введено в механику И. Ньютоном в определении импульса (кол-ва движения) тела — импульс р пропорц. скорости свободного движения тела v: p=mv, (1) где коэфф. пропорциональности m — постоянная для данного тела величина, его М. Эквивалентное определение М. получается из ур-ния движения классической механики Ньютона: f=mа. (2) Здесь М.— коэфф. пропорциональности между действующей на тело силой f и вызываемым ею ускорением а. Определённая таким образом М. характеризует св-ва тела, явл. мерой его инерции (чем больше М. тела, тем меньшее ускорение оно приобретает под действием пост. силы) и наз. инерциальной или и н е р т н о й М. В теории гравитации Ньютона М. выступает как источник поля тяготения. Каждое тело создаёт поле тяготения, пропорц. М. тела, и испытывает воздействие поля тяготения, создаваемого др. телами, сила к-рого также пропорц. М. Это поле вызывает притяжение тел с силой, определяемой законом тяготения Ньютона: где r — расстояние между центрами масс тел, G — универсальная гравитационная постоянная, а m1 и m2 — М. притягивающихся тел. Из ф-лы (3) можно получить зависимость между М. тела m и его весом Р в поле тяготения Земли: P=mg, (4) где g=GM/r2 — ускорение свободного падения (М — М. Земли, r»R, где R — радиус Земли). М., определяемая соотношениями (3) и (4), наз. г р а в и т а ц и о н н о й. В принципе ниоткуда не следует, что М., создающая поле тяготения, определяет и инерцию того же тела. Однако опыт показал, что инертная и гравитац. М. пропорц. друг другу (а при обычном выборе ед. измерения численно равны). Этот фундам. закон природы наз. принципом эквивалентности. Экспериментально принцип эквивалентности установлен с очень большой точностью — до 10-12 (1971). Первоначально М. рассматривалась (напр., Ньютоном) как мера кол-ва в-ва. Такое определение имеет вполне определ. смысл только для однородных тел, подчёркивает аддитивность М. и позволяет ввести понятие плотности — М. ед. объёма тела. В классич. физике считалось, что М. тела не изменяется ни в каких процессах (закон сохранения М. (в-ва)). Понятие «М.» приобрело более глубокий смысл в спец. теории относительности А. Эйнштейна (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ), рассматривающей движение тел (или ч-ц) с очень большими скоростями — сравнимыми со скоростью света с»3•1010 см/с. В новой механике, наз. релятивистской, связь между импульсом и скоростью ч-цы даётся соотношением: (при малых скоростях (v т. е. М. ч-цы (тела) растёт с увеличением её скорости. В релятив. механике определения М. из ур-ний (1) и (2) неэквивалентны, т, к. ускорение перестаёт быть параллельным вызвавшей его силе и М. получается зависящий от направления скорости ч-цы. Согласно теории относительности, М. ч-цы связана с её энергией ? соотношением: М. покоя m0 определяет внутр. энергию ч-цы — т. н. энергию покоя ?0=m0c2. Т.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

МАССА

— фундам. физ. величина, определяющая инерционные и гравитац. свойства тел — от макроскопич. объектов до атомов и элементарных частиц — в нерелятивистском приближении, когда их скорости пренебрежимо малы по сравнению со скоростью света с. В этом приближении M. тела служит мерой содержащегося в теле вещества и имеют место законы сохранения и аддитивности M.: масса изолиров. системы тел не меняется со временем и равна сумме M. тел, составляющих эту систему. Нерелятивистское приближение является предельным случаем относительности теории, рассматривающей движение с любыми скоростями вплоть до скорости света.

С точки зрения теории относительности M. т тела характеризует его энергию покоя

, согласно соотношению Эйнштейна:

В теории относительности, как и в нерелятивистской теории, M. изолиров. системы тел со временем не меняется, однако она не равна сумме M. этих тел.

Инерционные (или инерциальные, инертные) свойства M. в нерелятивистской (ньютоновой) механике определяются соотношениями:

и вытекающим из них соотношением

где

— импульс тела,- сила,- ускорение. M. входит также в ф-лу кинетич. энергии тела T:

В ньютоновой теории гравитации M. служит источником силы всемирного тяготения, притягивающей все тела друг к другу. Сила

с к-рой тело с массой mi притягивает тело с массой т ₂, определяется законом тяготения Ньютона:

где

— гравитационная постоянная, а — радиус-вектор, направленный от первого тела ко второму. Из ф-л (4) и (6) следует, что ускорение тела, свободно падающего в гравитац. поле, не зависит ни от его M., ни от свойств вещества, из к-рого тело состоит. Эту закономерность, проверенную на опыте в поле Земли с точностью порядка 10-8 и в поле Солнца с точностью порядка 10-12, обычно наз. равенством инертной и гравитац. (тяготеющей, тяжёлой) M., хотя следует подчеркнуть, что речь идёт не о равенстве двух разных M., а об одной и той же физ. величине — M., определяющей разл. явления. В спец. теории относительности энергия, импульс, скорость и M. связаны между собой соотношениями, отличающимися от соотношений нерелятивистской механики, но переходящими в последние при Важную роль в релятивистской механике играет понятие полной энергии , равной для свободного тела сумме его энергии покоя и кинетич. энергии, По существу всю механику релятивистской свободной частицы описывают два ур-ния:

Отметим, что величина т, входящая в правую часть ур-ния (7), — это та же M., к-рая входит в ур-ния ньютоновой механики. В отличие от энергии и импульса, меняющихся при переходе от одной системы отсчёта к другой, M. остаётся при этом неизменной: она является лоренцевым инвариантом.

Соотношение (3) справедливо и в теории относительности при произвольных значениях

, но соотношения (2) и (4) уже не имеют места. В частности, направление и величина ускорения тела определяются не только силой, но и скоростью, так что при не малых значениях ввести одну величину, к-рая служила бы мерой инертности тела, в этом случае нельзя.

Не является в релятивистском случае M. и источником гравитац. поля, им является тензор энергии-импульса, имеющий в общем случае 10 компонент.

Из ур-ний (7) и (8) следует, что если тело имеет нулевую M., то оно движется всегда со скоростью света и не может находиться в покое, и наоборот, если тело движется со скоростью света, его M. должна равняться нулю. В пределе

из этих ур-ний следует, что
т. е. воспроизводятся соотношение Эйнштейна (1) и норелятивистские выражения (2) и (5) для импульса и кинетич. энергии.

При произвольных значениях

из ур-ний (7) и (8) для тела с можно получить

где

— т. н. лоренц-фактор.

В спец. теории относительности имеют место законы сохранения энергии и импульса. В частности, энергия

(импульс р )системы h свободных частиц равна сумме их энергий (импульсов)

Отсюда и из ф-лы (7) следует, что M. системы не равна сумме M. составляющих её частей. Так, легко проверить, что в простейшем случае двух фотонов с энергией

у каждого их суммарная M. равна нулю, если они летят в одну сторону, и если они летят в противоположные стороны. Этот пример иллюстрирует также и то обстоятельство, что в теории относительности M. системы тел уже не является мерой кол-ва вещества.

Единицей M. в системе СГС служит грамм, в СИ — килограмм. M. атомов и молекул обычно измеряется в атомных единицах массы. M. элементарных частиц принято измерять в

(или, пользуясь системой единиц, в к-рой с = 1,- в МэВ). Напр., M. электрона M. протона M.самой тяжёлой из открытых элементарных частиц —

Известны многочисл. примеры взаимопревращения энергии покоя в кинетич. энергию и наоборот. Так, на встречных электрон-позитронных пучках при столкновении

с энергиямии противоположно направленными импульсами рождается покоящийся Z-бозон. При аннигиляции покоящихся электрона и позитрона вся их энергия покоя превращается в кинетич. энергию фотонов. В результате термоядерных реакций на Солнце происходит превращение двух электронов и четырёх протонов в ядро гелия и два нейтрино и выделяется кинетич. энергия

В этом случае в кинетич. энергию переходит примерно 1% суммы M. частиц, вступающих в реакцию. При делении ядра урана

МэВ, что составляет ~10-3 M. При горении метана
выделяется энергия ~ 10-10 M. В процессе фотосинтеза M. возрастает примерно на такую же величину за счёт поглощения растением кинетич. энергии фотонов.

Если частицы не свободны, как, напр., электроны в металле или кварки в нуклоне, они имеют эффективную массу. Эфф. M. кварка зависит от расстояния, на к-ром она измеряется: чем меньше расстояние, тем меньшем. кварка. Существует принципиальное различие между M. кварка и M. электрона, т. к. кварк, в отличие от электрона, не может находиться в свободном состоянии.

Природа M. элементарных частиц является одним из гл. вопросов физики. На рубеже 19 и 20 вв. предполагали, что M. может иметь эл.-магн. происхождение. В наст, время известно, что эл.-магн. взаимодействие ответственно лишь за малую долю M. электрона. Известно также, что осн. вклад в M. нуклонов даёт сильное взаимодействие, обусловленное глюонами, а не M. входящих в нуклоны кварков. Но не известно, чем обусловлены M. лептонов и кварков. Существует гипотеза, что здесь осн. роль играют фундам. бозоны с нулевым спином — т. н. хиггсовы бозоны (см. Хиггса механизм). Поиски этих частиц — одна из осн. задач физики высоких энергий.

В учебной, научно-популярной и энциклопедической литературе (в частности, в статьях данной энциклопедии, посвящённых релятивистским ускорителям заряж. частиц) ещё широко распространена архаичная терминология, возникшая в нач. 20 в. в процессе создания теории относительности. Исходным пунктом её является использование ф-лы

в области не малых значений где справедлива ф-ла (8). В результате возникли утверждения, что M. тела растёт с увеличением его скорости (энергии), фотон обладает M. и имеется полная эквивалентность между M. и энергией:

Вопреки тому, что писал А. Эйнштейн в статье [1] и книге [2], часто именно эту ф-лу, а не ф-лу (1) называют ф-лой Эйнштейна. Так, определённую M., как правило, обозначают т и называют M., реже — релятивистской M.

или M. движения . При этом обычную M., о к-рой говорилось в этой статье, называют M. покоя или собственной M. и обозначают т ₀. Одной из осн. ф-л теории относительности объявляется ф-ла

Всё это приводит к терминологич. путанице, создаёт искажённые представления об основах теории относительности, создаёт впечатление, что величина

играет роль инертной и гравитац. M. Однако это не соответствует действительности. Напр., если ускоряющая сила параллельна скорости тела, то «мерой инертности» является т. н. «продольная масса», Др. пример — релятивистское обобщение ф-лы (В) на движение лёгкой частицы (электрона или фотона) в гравитац. поле тяжёлого тела массы M (напр., Земли или Солнца). Можно показать (исходя из общей теории относительности), что в этом случае сила, действующая на лёгкую частицу, равна

где

При эта ф-ла переходит в (6). При величина, играющая роль «гравитац. М.», оказывается зависящей не только от энергии частицы, но и от взаимного направления . Если , то «гравитац. М.» равна , а если , то она равна
[для фотона _ T. о., не имеет смысла говорить о «гравитац. М.» фотона, если для вертикально падающего на массивное тело (напр., Землю, Солнце) фотона эта величина в 2 раза меньше, чем для фотона, летящего горизонтально поверхности тела. Именно это является причиной того, что угол отклонения фотона в гравитац. ноле Солнца оказывается в 2 раза больше, чем это следует из интерпретации величины как M.

В целом терминология, использующая понятия «М. покоя», «М. движения», ф-лы (11), (12) и т. п. артефакты, мешает понять сущность теории относительности, затрудняет в дальнейшем знакомство с совр. науч. литературой.

Лит.:1) Einstein А.,Ist die Tragheit eines Korpers von seinem Energieinhalt abhangig?, «Ann. Phys.», 1905, Bd 18, S. 639-41; 2) Эйнштейн А., Сущность теории относительности, пер. с англ., M., 1955, с. 7-44; 3) Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; 4) Тейлор Э., Уилер Д., Физика пространства — времени, пер. с англ., 2 изд., M., 1971. Л. Б. Окунь.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

.

dic.academic.ru>

МАССА это:

МАССА

(от лат, га ass а — глыба, кусок, масса) — одна из осн. физ. хар-к материи, являющаяся мерой её инерц. и гравитац. св-в. В классич. механике Ньютона М. тела равна сумме М. всех малых частей тела (материальных точек) и не зависит от скорости его движения. Инертность тела проявляется в том, что под действием внеш. силы оно изменяет своё движение постепенно, приобретая конечное ускорение. М., входящая в выражение второго закона Ньютона (см. Ньютона законы механики), характеризует инертность тела и наз. его инертной массой. М., входящая в выражение ньютоновского закона тяготения, характеризует гравитац. св-ва тела и наз. его гравитационной (тяжёл ой) массой. При соответствующем выборе гравитационной постоянной можно считать, что для каждого тела гравитац. и инертная М. равны; для определения М. тела можно пользоваться рычажными весами.

В относительности теории М. тела т зависит отскорости v его движения: m = m₀/корень из(1-v2/c2/), где с ~ 3-108 м/с — скорость света в вакууме, то — масса покоя (при v = 0), М. т иногда наз. релятивистской массой тела. При малых скоростях (v < с) т ~ т₀, т. е. в согласии с классич. механикой Ньютона, М. тела практически не зависит от скорости его движения. М. обладают не только частицы в-ва и образованные из них тела, но также и поля (напр., электромагнитное поле). Согласно закону взаимосвязи массы и энергии, полная энергия Е любой системы прямо пропорциональна М. т этой системы: Е = тс2. Из этого соотношения и закона сохранения энергии следует закон сохранения М.: при любых процессах, происходящих в термодинамически изолир. системе (см. Замкнутая система), М. этой системы не изменяется. Единица М. (в СИ) — килограмм (кг).

Большой энциклопедический политехнический словарь. 2004.

dic.academic.ru>

Люди дайте определение по физики «масса тела». ЯПоЖалуйСто Дайте физическое определение что такое масса тела?

Scrall

Принято считать, что масса тела — скалярная величина, характеризующая инертные и гравитационные свойства тела. Массу тела измеряют взвешиванием на весах (используя закон всемирного тяготения Ньютона или второй закон Ньютона) .

Максвел Джеймс Клерк (James Clerk Maxwell) в своей работе «Трактат об электричестве и магнетизме» том 1 («A treatise on electricity and magnetism» Volume 1), Предварительная глава «Об измерении величин», 5.(3) «Масса», выразил единицу массы как производную от длины и времени [X3 T-2].

Кроме этого масса тела M может быть определена как производная второго порядка от объема (размеров) этого тела V по времени:

м = v» ,

где
м — масса тела в естественной системе единиц (ест. с. ед.) ,
v» — ускорение изменения объема тела в ест. с. ед. .
Масса тела может быть измерена по величине ускорения изменения линейных размеров (объема) тела.

Это явление может наблюдаться на уровне элементарных частиц, а также, в ряде случаев, на макротелах. При этом, если эти ускорения изменений объемов частиц или макротел — симметричны относительно своих центров симметрии, то их массы — величины скалярные, а если — асимметричные, то массы — векторные величины. В этом случае формула определения массы тела будет иметь вид частной производной (формула в ест. с. ед.) :

м = sх» ,

где
s — площадь сечения частицы (тела) ,
х — длина частицы (тела) и направление ее массы (вектор) .

Векторы массы м и длины х совпадают.

В окружающем нас мире процессы разбегания в элементарных частицах имеют в общем случае симметричный и равноускоренный характер, поэтому будет справедлива следующая формула для определения массы тела (в ест. с. ед.) :

м = v/т2 .
Размерность единицы измерения величины массы тела может считаться производной от размерностей длины (расстояния) и времени: kg=[Km](m3/s2, где [Km] — размерность коэффициента Km, при этом для сферической системы тел:

Km = 1/G = (1,499)1010 (kg . s2/m3),

где G — гравитационная постоянная.
Для плоских систем тел Кm=4/G . Коэффициент Km возник в результате некогерентности (несогласованности) единиц физических величин (m, s, kg) в SI. Коэффициент Km указывает на неестественность размерностей длины (m), времени (s) и массы (kg). В естественной (когерентной) системе единиц физических величин коэффициент Km будет равен безразмерной единице (к=1). В системе SI:

M = Кm(Х3)» .

где Х — линейные размеры частицы (тела).

Бог от бога

а́сса (от др. -греч. μάζα, кусок теста) — скалярная неотрицательная релятивистски инвариантная физическая величина, одна из важнейших величин в физике. В нерелятивистском приближении, когда скорости тел много меньше скорости света, определяет их инерционные и гравитационные свойства [1].
Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства (в частности, вес).
Наличие массы у элементарных частиц объясняется их взаимодействием с полем Хиггса. Чем сильнее это взаимодействие, тем больше масса у элементарной частицы [2][3].
В современной физике понятие «количество вещества» имеет другой смысл, а масса тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). Масса проявляется в природе несколькими способами.

Определение массы. Что такое масса, напишите определение. И формулу, по возможности)

Mia

МАССА физическая характеристика тела, являющаяся мерой того сопротивления, которое оно оказывает любым изменениям своего состояния покоя или движения, т. е. мера инерции тела. Опытным путем установлено: чтобы сообщить телу ускорение a, к нему следует приложить неуравновешенную силу f, величина которой пропорциональна требуемому ускорению. Это положение, впервые сформулированное И. Ньютоном, называется вторым законом Ньютона. Данный закон выражается формулой где m — постоянная, характеризующая тело, не зависящая ни от f, ни от a, ни от состояния самого тела. Эта постоянная называется массой тела; следует подчеркнуть, что понятие массы определяется лишь эмпирическим соотношением (1). Поскольку величина m служит характеристикой только рассматриваемого объекта, очень просто установить для нее единицу измерения. Первоначально эталон 1 кг был введен законом французского Национального собрания в декабре 1779 и определялся как масса 1 дм3 воды при температуре 4? C, при которой плотность воды максимальна. Преимущество такого определения состоит в легкости, с которой можно приближенно воспроизвести единицу измерения при наличии стандартного литра. Однако трудности точного воспроизведения такой емкости и ее заполнения «до краев» привели к тому, что эта мера была заменена единым прототипом килограмма из сплава платины с иридием, который хранится в Международном бюро мер и весов под Парижем. Остальные страны имеют собственные прототипы единицы массы, предельно точно воспроизводящие международный. Строго говоря, массы следует сравнивать путем измерения сил, которые сообщают им данное ускорение. Однако практические трудности, с которыми приходится сталкиваться на этом пути, столь велики, что обращаются к другому аспекту массы, а именно гравитационному. Закон всемирного тяготения, также связанный с именем Ньютона, утверждает, что между любыми двумя телами действует сила притяжения, пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, т. е. где G — коэффициент, в системе единиц СИ равный (6,670? 0,008)?10-11 м3/кг? с2. Гравитационную силу, действующую на тело со стороны Земли, называют весом тела. Если возникает необходимость сравнить массы двух тел, то сначала их помещают в одно и то же место на поверхности Земли с тем, чтобы расстояния до центра масс Земли были одинаковы в обоих случаях; веса двух масс сравниваются уравновешиванием. Если массы уравновешены, т. е. если их веса равны, то в этом случае равны и сами массы. Следует, однако, подчеркнуть, что логической связи между соотношениями (1) и (2) нет. Если сформировать ряд тел в порядке возрастания их масс в соответствии с формулой (1), то нет причин, по которым этот порядок соответствовал бы формуле (2). То, что значения масс в обоих выражениях очень близки друг другу, впервые было показано Ньютоном, а позднее с большей точностью подтверждено экспериментами, которые проводили с 1891 Л. Этвеш в Венгрии и его продолжатели. Гипотеза тождественности масс послужила отправной точкой общей теории относительности А. Эйнштейна, опубликованной в 1915, однако правильность этой теории пока не получила всеобъемлющего экспериментального подтверждения. Следует подчеркнуть, что «гири», используемые при уравновешивании, представляют собой массы, и процедура «взвешивания» таким методом в действительности эквивалентна сравниванию масс. Если 1кг сахара уравновесить на уровне моря массой весом в 1 кг, а затем сахар и весы поднять на вершину горы, то, хотя сахар и килограммовая гиря немного потеряют в весе, они по-прежнему будут уравновешивать друг друга. То же самое будет, если провести уравновешивание на Луне, где вес составил бы всего 1/6 от веса на уровне земного моря. В общей теории относительности принята гипотеза, что инерционные свойства тел, хотя и в небольшой степени, все же зависят от свойств окружающей среды и поэтому не совсем независимы от условий, в которых находится тело, как это утверждалось выше. В частности, инерция тела, измеренная в направлени

Темнобелос

Надо бы знать 2-ОЙ закон Ньютона: масса равна отношению действующей на тело силы к вызываемому ею ускорению. Или эквивалентный принцип: Инертная масса = гравитационнОЙ .Формула в наших американских имерениях проста : 1 фунт = 16 унций, 7000 гран или 256 драхм, а в вашей метрической системе сикль равен 14,1 грамм).

Читайте также

zna4enie.ru

Атомная единица массы а. е. м. | Формулы и расчеты онлайн

Для характеристики массы атомов и молекул используют понятие атомной массы М.

Атомная масса — относительная величина. Она определяется по отношению к массе атома углерода C, которая принимается равной 12.000 000. Хотя в химии также используют относительные атомные или молекулярные массы А_отн и М_отн, отнесенные к массе атома C, их нельзя считать идентичными атомной массе М, поскольку они относятся к естественной смеси изотопов соответствующего элемента. Таким образом, они определяют среднюю атомную массу элемента. Однако поскольку изотопы одного элемента обладают разными физическими свойствами, в атомной физике принято указывать атомную массу М каждого изотопа.

Для абсолютного определения атомной массы была введена атомная единица массы (а. е. м.).

Атомная единица массы (а. е. м.) равна 1/12 массы атома углерода C.

Отсюда следует, что углерод обладает относительной атомной массой М = 12.000 и абсолютной атомной массой m = 12.000 а. е. м. Атомную единицу массы можно перевести в единицу массы СИ — килограмм.

\[ 1 а. е. м. = \frac{1}{12} m_{C_{12}} = 1.66057 · 10^{-27} кг \] \[ 1 кг = 6.022045 · 10^{26} а. е. м. \]

Отсюда следует для массы атома

\[ m_{а} = M · 1 а. е. м. = M · 1.66057 · 10^{-27} кг \]

Справочная таблица
Массы некоторых элементарных частиц и атомов

Наименование частицы	Обозначение	Число протонов	Число нейтронов	Число электронов	Масса m, а. е. м.
Электрон	e	—	—	1	0.00054858
Протон(ядро атома водорода)	p	1	—	—	1.00727647
Нейтрон	n	—	1	—	1.00866501
Атом водорода	H	1	—	1	1.00782504
Дейтрон (ядро атома дейтерия)	d	1	1	—	2.01354
Атом дейтерия	H	1	1	1	2.01410179
α-частица (ядро атома гелия)	α	2	2	—	4.001488
Атом гелия	He	2	2	2	4.00260327

В помощь студенту

Атомная единица массы а. е. м.	стр. 735

www.fxyz.ru

Формула массы в химии

Определение и формула для расчета массы

Одним из основополагающих законов в химии является закон сохранения массы (масса веществ, вступивших в химическую реакцию, всегда равна массе образовавшихся веществ), который говорит о том, что зная массу веществ, вступивших в реакцию мы легко можем рассчитать массу продуктов этой реакции и наоборот.

Для того, чтобы определить массу вещества используют следующую формулу:

m = n×M,

где n —  количество вещества (моль), а М – молярная масса вещества (г/моль), откуда следует, что единицей измерения массы является [г].

Моль – это количество вещества, которое содержит столько же частиц (молекул, атомов, ионов, электронов), сколько атомов углерода содержится в 12 г изотопа ¹²С.

Масса одного атома ¹²С равна 12 а.е.м., поэтому число атомов в 12 г изотопа ¹²С равно:

N_A = 12 г / 12 × 1,66057×10^-24 г = 1/1,66057×10^-24 = 6,0221×10^-23.

Таким образом, моль вещества содержит 6,0221×10^-23 частиц этого вещества.

Физическую величину N_A называют постоянной Авогадро, она имеет размерность [N_A] = моль^-1. Число 6,0221×10^-23 называют числом Авогадро.

Молярная масса (М) – это масса 1 моль вещества. Легко показать, что численные значения молярной массы М и относительной молекулярной массы M_r равны, однако первая величина имеет размерность [M] = г/моль, а вторая безразмерна:

M = N_A × m (1 молекулы) = N_A × M_r × 1 а.е.м. = (N_A ×1 а.е.м.) × M_r = × M_r.

Это означает, что если масса некоторой молекулы равна, например, 44 а.е.м., то масса одного моля молекул равна 44 г.

Постоянная Авогадро является коэффициентом пропорциональности, обеспечивающим переход от молекулярных отношений к молярным.

Примеры решения задач

ru.solverbook.com