Приемы быстрого счета без калькулятора
Хоть и считается, что математика наводит ужас на значительную часть населения, но деньги считать умеют все. И вот как раз влет это умеют делать люди, далекие от математики.
Помнится, бабушка моего мужа показывала ему на пальцах таблицу умножения на 9. Никакого образования, только огромная практика торговли редиской и клубникой на рынке!
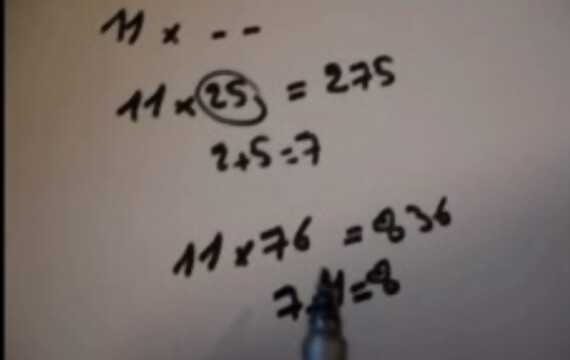
Так вот сегодня я предлагаю вам несколько интересненьких приемов устного счета. Ведь сколько бы замечательных гаджетов (телефоны, смартфоны, айподы и айпады, ай, да чего там…) своя голова она всегда лучше.
Итак, читаем, тут же проверяем и запоминаем приемы вычисления в уме.
1. Умножение на 11
Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583
59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.
85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225
45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.
Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это.
Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
И, как следствие): чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,
34*1,5 = 34+17=51
125*1,5= 125+62,5=187,5
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
16×250 все равно, что:
8×500 все равно, что:
4×1000 = 4,000
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
1000-648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352
И, напоследок, несколько математических трюков:
Интересные результаты:
1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111
9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321
Любимая цифра.
Предложите задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.
Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.
Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.
Угадать возраст.
Умножаем число своих лет на 10, затем любое однозначное число умножить на 9, из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.
Всегда девятка
Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.
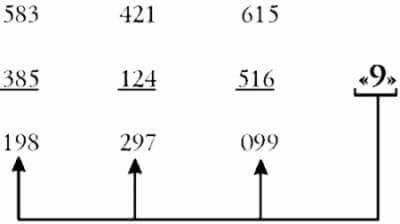
Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.
Загрузка…Как научиться считать на счетах
 Раньше самым необходимым приспособлением у продавцов, бухгалтеров и кассиров были счеты. С их помощью проводятся самые различные вычислительные операции с маленькими и большими числами. Вскоре их вытеснили калькуляторы и другие устройства. Однако несмотря на это научиться считать на счетах полезно и сегодня. Если вы хотите иметь некоторое представление, как это делать, то приступайте к рассмотрению основных счетных операций и общих принципов подсчета.
Раньше самым необходимым приспособлением у продавцов, бухгалтеров и кассиров были счеты. С их помощью проводятся самые различные вычислительные операции с маленькими и большими числами. Вскоре их вытеснили калькуляторы и другие устройства. Однако несмотря на это научиться считать на счетах полезно и сегодня. Если вы хотите иметь некоторое представление, как это делать, то приступайте к рассмотрению основных счетных операций и общих принципов подсчета.
Основные моменты
Для начала рассмотрите счеты. Они могут быть различных размеров. Их костяшки представлены в двух цветах: светлые по краям и темные по середине. Однако могут быть и другие расцветки и расположенность костяшек. Даже сегодня можно приобрести такой прибор.
Изначально все костяшки должны быть выровнены с правой стороны с краю. Такое положение означает, что счеты находятся в нулевом положении. В зависимости от вида счетов, на них может быть 8 или 10 рядов. Каждый из них характеризует определенный класс цифр. Здесь обозначаются не только тысячи и сотни, но и десятки тысяч. При необходимости можно высчитывать довольно весомые значения. При восьми рядах, самый верхний из них будет обозначать десятки тысяч. Тот ряд, который идет вторым означает тысячи, а третий сотни. На четвертом ряду можно посчитать десятки, а на пятом единицы. Дальше на шестом ряду идут четверти, на седьмом – десятые(0,1), а на восьмом сотые(0,01). Это нужно для подсчета самых разных чисел. Продавцы без труда могут посчитать рубли и копейки на таких счетах.
Как работать на счетах
 Для того чтобы набрать на счетах необходимое вам число, понадобятся костяшки, которые будут соответствовать нужному классу цифр. Их необходимо передвигать справа на лево. Чтобы вам было проще разобраться, можно рассмотреть все это на наглядном примере. Так, представьте, что вам нужно набрать 4 733,64. Для этого сначала передвиньте в верхнего ряда 4 костяшки, которые будут означать 4 тысячи. После этого на втором ряду отсчитайте 7 костяшек, что будет равносильно 7 сотням. На третьем ряду отсчитайте 3 костяшки, т.е. десятки. С четвертого ряда передвиньте 3 единицы. Дальше также нужно убрать 6 десятых и 4 сотых.
Для того чтобы набрать на счетах необходимое вам число, понадобятся костяшки, которые будут соответствовать нужному классу цифр. Их необходимо передвигать справа на лево. Чтобы вам было проще разобраться, можно рассмотреть все это на наглядном примере. Так, представьте, что вам нужно набрать 4 733,64. Для этого сначала передвиньте в верхнего ряда 4 костяшки, которые будут означать 4 тысячи. После этого на втором ряду отсчитайте 7 костяшек, что будет равносильно 7 сотням. На третьем ряду отсчитайте 3 костяшки, т.е. десятки. С четвертого ряда передвиньте 3 единицы. Дальше также нужно убрать 6 десятых и 4 сотых.
Если у вас уже есть счеты, попробуйте применить этот метод подсчета на практике. Так вы сможете быстрее освоить эту науку. На самом деле разобраться в этом не сложно. Нужно лишь попрактиковаться.
Арифметические действия на счетах
После того как вы освоите основные положения счет и научитесь правильно отсчитывать костяшки, обозначающие цифры, можете переходить к освоению арифметических действий. Делать это довольно просто. Начните со сложения. Для этого сначала наберите на костяшках одно число, а затем нужно перенести к нему второе число справа на лево. Если числа будут довольно большими, то костяшек может не хватить. В этом случае просто отодвиньте костяшку на один класс выше. Для удобства сложение всегда следует начинать с нижних рядов. Попробуйте произвести действия на своих счетах. Так вы быстрее освоите это.
Если вам нужно провести вычислительные действия, то делать следует тоже самое, но в обратном порядке. Здесь костяшки нужно переносить слева на право. Правильно будет вычитать, начиная с верхних рядов. От большего числа просто отнимите меньшее. В случае если костяшек не хватит, то просто нужно отнять одну из них классом ниже. Хорошо, если кто-нибудь более подробно разъяснит вам, как все это делается и покажет, чтобы вы освоили на личном примере, как это делается.
Если вы хорошо усваиваете арифметические действия на счетах, то можете переходить к более сложным урокам – умножению и делению на счетах.
Умножение на счетах
 Несмотря на то, что умножение на счетах считается одним из сложных действий, освоить его выполнение вполне возможно. Если вы только учитесь этому, то лучше начинать осваивать небольшие значения. Можно рассмотреть несколько несложных вариантов умножения.
Несмотря на то, что умножение на счетах считается одним из сложных действий, освоить его выполнение вполне возможно. Если вы только учитесь этому, то лучше начинать осваивать небольшие значения. Можно рассмотреть несколько несложных вариантов умножения.
Для умножения какого-либо числа на два нужно просто набрать его на счетах, а затем прибавить еще одно такое же число. Если нужно умножить число на три, следует прибавить число еще раз. Чтобы легче было произвести умножение на 4, нужно сначала умножить число на 2, как было описано ранее, а затем снова умножить на 2. Если вы хотите умножить число на 5, то для этого сначала разделите его на 2, а потом умножьте на 10. Это уже не сложно, нужно лишь передвинуть костяшки на уровень выше. Это лишь некоторые операции на умножение, которые вы сможете научиться выполнять на начальном этапе.
Деление на счетах
Делать на счетах деление очень сложно. Справиться с этим могут лишь опытные счетоводы, которые без труда выполняют самые сложные операции. Если вы хотите разделить какое-либо несложное число на 2, то это у вас получиться, но большие примеры лучше посчитать на более современных устройствах или даже в уме.
Осваивайте счеты постепенно. Сначала пробуйте считать самые простые числа, но постепенно переходите к более сложным. На самом деле разобраться с этим вполне легко.
vremya-sovetov.ru
Приемы, облегчающие устный счет и запоминание таблицы умножения
Сколько вам нужно времени, чтобы выполнить довольно простое вычисление: например от 234 отнять 112? Девочки с фото решают от 70 до 90 примеров разной сложности за… 1 минуту.
Приемы быстрого счета: магия, доступная всем
Для того чтобы понять, какую роль в нашей жизни играют цифры, поставьте простой эксперимент. Попробуйте некоторое время обойтись без них. Без цифр, без вычислений, без измерений… Вы окажетесь в странном мире, где почувствуете себя абсолютно беспомощным, связанным по рукам и ногам. Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения — умножением на два. Не верите? А зря. Это — реальность.
«Компьютер» каменного века
Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава «торговой миссии» не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.
С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. «Счетной машиной» неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки — шел искать потерю.
Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: «один», «пара» и «много».
Можно ли считать быстрее компьютера?
Обогнать устройство, выполняющее сотни миллионов операций в секунду? Невозможно… Но тот, кто говорит так, жестоко лукавит, или просто кое-что умышленно упускает из вида. Компьютер — это лишь набор микросхем в пластике, он не считает сам по себе.
Поставим вопрос по-другому: может ли человек, считая в уме, обогнать того, кто выполняет вычисления на компьютере? И здесь ответ — да. Ведь, чтобы получить ответ от «черного чемоданчика», данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему — кроме одного органа. Мозга!
Калькулятор умеет выполнять лишь две операции: сложение и вычитание. Умножение для него — это множественное сложение, а деление — множественное вычитание.
Наш мозг поступает по-другому.
Класс, где учился будущий король математики, Карл Гаусс, как-то получил задание: сложить все числа от 1 до 100. Карл написал на своей доске абсолютно правильный ответ, как только учитель закончил объяснять задание. Он не стал прилежно складывать числа по порядку, как поступил бы любой уважающий себя компьютер. Он применил открытую им самим формулу: 101 х 50 = 5050. И это далеко не единственный прием, ускоряющий вычисления в уме.
Простейшие приемы быстрого счета
Их изучают в школе. Самое простое: если вам нужно прибавить к любому числу 9, прибавляете 10 и вычитаете 1, если 8 (+ 10 — 2), 7 (+ 10 — 3) и т.д.
54 + 9 = 54 + 10 — 1 = 63. Быстро и удобно.
Двухзначные числа складываются так же легко. Если во втором слагаемом последняя цифра больше пяти, число округляется до следующего десятка, а потом «лишнее» вычитается. 22 + 47 = 22 + 50 — 3 = 69. Если ключевая цифра меньше пятерки, то надо сложить сперва десятки, затем единицы: 27 + 51 = 20 + 50 + 7 + 1 = 78.
С трехзначными числами точно так же не возникает никаких трудностей. Складываем их, как читаем, слева на право: 321 + 543 = 300 + 500 + 20 + 40 + 1 + 3 = 864. Гораздо проще, чем в столбик. И гораздо быстрее.
А вычитание? Принцип тот же: вычитаемое округляем до целого и добавляем недостающее: 57 — 8 = 57 — 10 + 2 = 49; 43 — 27 = 43 — 30 + 3 = 16. Быстрее чем на калькуляторе — и никаких претензий от учителя даже во время контрольной!
Нужно ли учить таблицу умножения?
Дети этого, как правило, терпеть не могут. И правильно делают. Ни к чему ее учить! Но не спешите возмущаться. Никто не утверждает, что таблицу не нужно знать.
Ее изобретение приписывают Пифагору, но, скорее всего, великий математик лишь придал законченную, лаконичную форму тому, что уже было известно. На раскопках древней Месопотамии археологи нашли глиняные таблички с сакраментальным: «2 х 2». Люди давно пользуются этой в высшей степени удобной системой вычислений и открыли множество способов, которые помогают постичь внутреннюю логику и красоту таблицы, понять — а не тупо, механически зазубрить.
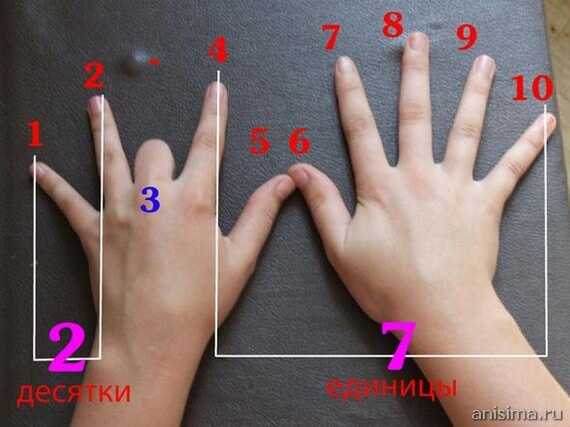
В древнем Китае таблицу начинали учить с умножения на 9. Так проще, и не в последнюю очередь потому, что умножать на 9 можно «на пальцах».
Положите обе руки на стол ладонями вниз. Первый слева палец — 1, второй — 2 и т.д. Допустим, вам нужно решить пример 6 х 9. Поднимите шестой палец. Пальцы слева покажут десятки, справа — единицы. Ответ 54.
«На пальцах» можно посчитать всю таблицу Пифагора, если умеешь умножать на 2, то есть удваивать число, а с этим, как правило, легко справляются даже дети не очень способные к математике.
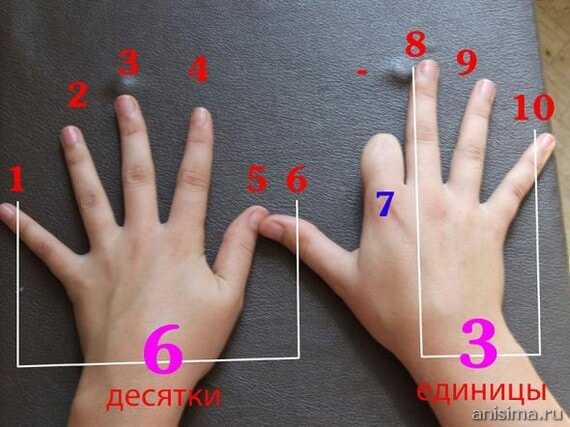
Пример: 8 х 7. Левая рука — первый множитель, правая — второй. На руке пять пальцев, а нам нужно 8 и 7. Загибаем на левой руке три пальца (5 + 3 = 8), на правой 2 (5 + 2 = 7). Загнутых пальцев у нас пять, значит пять десятков. Теперь перемножим оставшиеся: 2 х 3 = 6. Это единицы. Всего 56.
Это лишь один из наипростейших приемов «пальцевого» умножения Их много. «На пальцах» можно оперировать числами до 10 000!
У «пальцевой» системы есть бонус: ребенок воспринимает ее как веселую игру. Занимается охотно, испытывает массу положительных эмоций и в итоге очень скоро начинает проделывать все операции в уме, без помощи пальцев.
Делить так же можно при помощи пальцев, но это немного сложнее. Программисты до сих пор пользуются руками, чтобы перевести числа из десятичной системы в двоичную — это удобнее и гораздо быстрее, чем на компьютере. Но в рамках школьной программы научиться быстро делить можно даже без пальцев, в уме.
Допустим, нужно решить пример 91 : 13. Столбик? Нет нужды пачкать бумагу. Делимое заканчивается на единицу. А делитель — на тройку. Что там в таблице умножения самое первое, где задействована тройка, а заканчивается на единицу? 3 х 7 = 21. Семерка! Вот и все, мы ее поймали. Надо 84 : 14. Вспоминаем таблицу: 6 х 4 = 24. Ответ — 6. Просто? Еще бы!
Волшебство числа
Большинство приемов быстрого счета похоже на фокусы. Взять хотя бы известнейший пример умножения на 11. Чтобы, например, 32 х 11 нужно написать 3 и 2 по краям, а в середину поставить их сумму: 352.
Для умножения двузначного числа на 101 надо просто записать число два раза. 34 х 101 = 3434.
Для умножения числа на 4 нужно два раза умножить его на 2. Для деления — дважды разделить на 2.
Много остроумных и, главное, быстрых приемов помогают возводить число в степень, извлекать квадратный корень. Знаменитые «30 приемов Перельмана» для математически мыслящих людей будут покруче шоу Коперфильда, потому что они еще и ПОНИМАЮТ что происходит, и как оно происходит. Ну а остальные могут просто наслаждаться красивым фокусом. Например, нужно перемножить 45 на 37. Напишем числа на листе и разделим их вертикальной чертой. Левое число делим на 2, отбрасывая остаток, пока не получим единицу. Правое — умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.
«Зарядка» для ума
Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Но мы предпочитаем калькулятор. Почему? Не любим напрягаться. Нам тяжело держать числа, даже двухзначные, в голове. Почему-то не держатся.
Попробуйте выйти на середину комнаты и сесть на шпагат. Почему-то «не сажается», да? А гимнаст делает это совершенно спокойно, не напрягаясь. Тренироваться нужно!
Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100… 98.. 96. Можно считать через три, через восемь — главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами.
calculator888.ru
Приёмы устного счета для быстрого вычисления в уме
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 — это дважды умножить на 2;
-
умножить на 6 — это значит умножить на 2, а потом на 3;
-
умножить на 8 — это трижды умножить на 2;
-
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 — это дважды разделить на 2;
-
разделить на 6 — это сначала разделить на 2, а потом на 3;
-
разделить на 8 — это трижды разделить на 2;
-
разделить на 9 — это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
myintelligentkids.com
Быстрый счёт (Перельман) — Викитека
Материал из Викитеки — свободной библиотеки
Перейти к навигации Перейти к поиску [1]ДОМ ЗАНИМАТЕЛЬНОЙ НАУКИ
БЫСТРЫЙ СЧЕТ Тридцать простых приемов
устного счета Составил
Я. И. ПЕРЕЛЬМАН Ленинград. 1941
[2]От составителя
В настоящее время в продаже нет руководств, содержащих наставления к быстрому выполнению счетных операций в уме. Мы сочли поэтому полезным собрать в краткой брошюре наиболее простые и легко усваиваемые приемы быстрого устного счета. Они рассчитаны на средние способности и имеют в виду не публичные выступления на эстраде, а потребности повседневной жизни. Пользующиеся книжечкой должны помнить, что успешное овладение ее указаниями предполагает не механическое, а вполне сознательное распоряжение приемами и, кроме того, более или менее продолжительную тренировку. Зато, усвоив рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.
Отв. редактор В. А. Камский. Техн. ред. А. Я. Барвиш| М 18609 | 1/4 печ. листа. Тираж 5 000. |
§ 1. Чтобы устно умножить число на однозначный множитель (например, 27 × 8), выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20 × 8 = 160), затем единицы (7 × 8 = 56) и оба результата складывают.
Еще примеры:
34 × 7 = 30 × 7 + 4 × 7 = 210 + 28 = 23847 × 6 = 40 × 6 + 7 × 6 = 240 + 42 = 282
§ 2. Полезно знать на память таблицу умножения до 19 × 9:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 |
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 |
| 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 |
| 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 |
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 |
| 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 |
| 17 | 34 |
ru.wikisource.org
Ментальная Арифметика Умножение
Урок № 4. Ментальная Арифметика Умножение.
Умножение есть не что иное как многократное сложение. Но вместо того, что бы 23 раза прибавлять одно и тоже число, легче выполнить его умножение. Существует особая техника выполнения умножения в окне соробана. Есть несколько различных методов. Здесь приводится метод, который был рекомендован Японским Комитетом по Абакусу. Этот метод считается дающим меньше ошибок и простым в обучении.
Теперь поставим перед собой задачу умножения 23Х47. Число 23 будет называться множимым, а число 47 — множителем. Прежде всего расположим множимое (а это число 23) вблизи центра счетной доски. Пропустив пустую линейку, число 47 (множитель) расположим слева
Между числами пропущены линейки для лучшей наглядности, при не таких маленьких счетах можно пропускать и больше.
Процесс умножения подобен тому, как мы делаем это на бумаге, но отличается последовательностью выполнения действий
Сначала берем правую цифру множимого ( 3) и умножаем на крайнюю левую цифру множимого 3×4=12. Число 12 откладываем слева от множимого (на линейках FG)
затем эту же цифру множимого умножаем на следующую слева направо цифру множителя 3×7=21, получившееся число 21 прибавляем к результату, но уже сдвинув вправо на один разряд (линейки GH ) :
Теперь мы не нуждаемся в цифре 3, так как с ней уже все проделано, очистим эту линейку (E ) для дальнейшей работы
Теперь берем следующее число множимого — в нашем случае это 2. Умножаем его на левую крайнюю цифру множителя. Результат (2×4=08) прибавляем к линейкам EF. Поскольку в общем случае результат занимает 2 разряда, одноразрядный результат надо представлять в виде 08, что бы правильно разместить его на линейках, так получается следующая картина:
В заключение мы должны умножить 2 на оставшуюся цифру множителя 7 и получившийся результат 14 прибавить на линейки FG
К линейке F надо прибавить 1, но она полностью заполнена, поэтому по правилам сложения, прибавляется 1 к следующему разряду (E), а здесь отнимается 9. Затем к линейке G прибавляется 4
получившееся число является результатом действия 23×47=1081
[SWF]http://mentalar.ru/wp-content/uploads/2017/09/000.swf,700,500[/SWF]
Автор публикации
10 Комментарии: 13Публикации: 334Регистрация: 06-06-2017mentalar.ru
Эффективный счёт в уме или разминка для мозга / Habr
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400;
3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
600 : 25 = (600 : 100) x 4 = 6 x 4 = 24;
24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.
Теперь не кажется невозможным умножить в уме 625 на 53:
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 =
= (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
37^2 = 12 x 100 + 13^2 = 1200 + 169 = 1369;
84^2 = 59 x 100 + 34^2 = 5900 + 9 x 100 + 16^2 = 6800 + 256 = 7056;
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
195^2 = (100 + 95)^2 = 10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 70 x 100 + 45^2 = 10000 + (90+5) x 2 x 100 +
+ 7000 + 20 x 100 + 5^2 = 17000 + 19000 + 2000 + 25 = 38025.
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
M = 10m + n, K = 10a + 10 - n.
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
48 x 42 = 2016.
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
99 x 91 = 9009.
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
95 x 95 = 9025.
Тогда предыдущий пример можно вычислить немного проще:
195^2 = (100 + 95)^2 = 10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
habr.com
