Относительная формула – Формулы

Содержание

Использование относительных и абсолютных ссылок

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

По умолчанию используется Относительнаяссылка на ячейку. Например при использовании ссылки на ячейку A2 в ячейке C2, Вы действительно ссылаетесь на ячейки, которая находится двумя столбцами слева (C за вычетом A) и в той же строке (2). Формулы, содержащей относительная ссылка на ячейку изменяется при копировании из одной ячейки в другую. Например при копировании формулы

= A2 + B2 в ячейке C2 до C3, формулы ссылки в ячейке C3 скорректировать вниз на одну строку и становятся = A3 + B3.

Если нужно сохранить исходный ссылку на ячейку при копировании «блокировании» ее, поместив знак доллара ($) перед ссылки на ячейки и столбца. Например, при копировании формулы = $A$ 2 + $B$ 2 от C2 на D2 формулу, должно оставаться точно так же. Это абсолютную ссылку.

В некоторых случаях ссылку можно сделать «смешанной», поставив знак доллара перед указателем столбца или строки для «блокировки» этих элементов (например, $A2 или B$3). Чтобы изменить тип ссылки на ячейку, выполните следующее.

  1. Выделите ячейку со ссылкой на ячейку, которую нужно изменить.

  2. В строка формул щелкните ссылку на ячейку, которую нужно изменить.

  3. Для перемещения между сочетаниями используйте клавиши +T.

    В таблице ниже показано, что происходит при копировании формулы в ячейке A1, содержащей ссылку. Формула копируется в ячейку на две строки ниже и на два столбца правее, т. е. C3.

Ссылка на текущую (описание):

Новая ссылка

$A$1 (абсолютный столбец и абсолютная строка)

$A$1 (абсолютная ссылка)

A$1 (относительный столбец и абсолютная строка)

C$1 (смешанная ссылка)

$A1 (абсолютный столбец и относительная строка)

$A3 (смешанная ссылка)

A1 (относительный столбец и относительная строка)

C3 (относительная ссылка)

См. также

Операторы вычислений и порядок операций

support.office.com

Изменение типа ссылки: относительная, абсолютная, смешанная

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

По умолчанию используется ссылка на ячейку относительная ссылка, которая означает, что ссылка относительно расположение ячейки. Если, например, ссылаться на ячейку A2 в ячейке C2, Вы действительно ссылки на ячейки, которая находится два столбца слева от (C за вычетом A) — в той же строке (2). При копировании формулы, содержащей относительная ссылка на ячейку, который будет изменяться в формуле ссылку.

Например, при копировании формулы = B4 * C4 на ячейку D4 D5, формула в D5 регулирует вправо по одному столбцу и становится = B5 * C5. Если вы хотите сохранить исходный в ссылку на ячейку в этом примере при копировании, внесенные ссылку на ячейку абсолютный перед (B и C) столбцов и строк (2), знак доллара (

$). Затем, при копировании формулы = $B$ 4 * $C$ 4 из D4 для D5 формулу, должно оставаться точно так же.

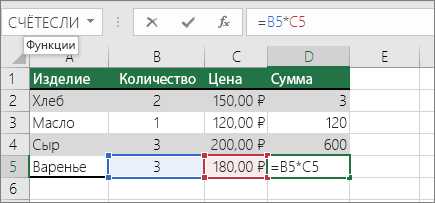
Менее часто нужно смешанного абсолютные и относительные ссылки на ячейки, предшествующего либо значения строку или столбец с знак доллара — исправления, которые столбца или строки (например, $B4 или C$ 4).

Чтобы изменить тип ссылки на ячейку:

  1. Выделите ячейку с формулой.

  2. В строке формул строка формул выделите ссылку, которую нужно изменить.

  3. Для переключения между типами ссылок нажмите клавишу F4.

    В приведенной ниже таблице показано, как изменяется тип ссылки, если формула со ссылкой копируется на две ячейки вниз и на две ячейки вправо.

Копируемая формула

Первоначальная ссылка

Новая ссылка

$A$1 (абсолютный столбец и абсолютная строка)

$A$1 (абсолютная ссылка)

A$1 (относительный столбец и абсолютная строка)

C$1 (смешанная ссылка)

$A1 (абсолютный столбец и относительная строка)

$A3 (смешанная ссылка)

A1 (относительный столбец и относительная строка)

C3 (относительная ссылка)

support.office.com

Полные сведения о формулах в Excel

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

Начните создавать формулы и использовать встроенные функции, чтобы выполнять расчеты и решать задачи.

Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.

Создание формулы, ссылающейся на значения в других ячейках

  1. Выделите ячейку.

  2. Введите знак равенства «=».

    Примечание: Формулы в Excel начинаются со знака равенства.

  3. Выберите ячейку или введите ее адрес в выделенной.

  4. Введите оператор. Например, для вычитания введите знак «минус».

  5. Выберите следующую ячейку или введите ее адрес в выделенной.

  6. Нажмите клавишу ВВОД. В ячейке с формулой отобразится результат вычисления.

Просмотр формулы

  1. При вводе в ячейку формула также отображается в строке формул.

  2. Чтобы просмотреть формулу, выделите ячейку, и она отобразится в строке формул.

Ввод формулы, содержащей встроенную функцию

  1. Выделите пустую ячейку.

  2. Введите знак равенства «=», а затем — функцию. Например, чтобы получить общий объем продаж, нужно ввести «=СУММ».

  3. Введите открывающую круглую скобку «(«.

  4. Выделите диапазон ячеек, а затем введите закрывающую круглую скобку «)».

  5. Нажмите клавишу ВВОД, чтобы получить результат.

Скачивание книги «Учебник по формулам»

Мы подготовили для вас книгу Начало работы с формулами, которая доступна для скачивания. Если вы впервые пользуетесь Excel или даже имеете некоторый опыт работы с этой программой, данный учебник поможет вам ознакомиться с самыми распространенными формулами. Благодаря наглядным примерам вы сможете вычислять сумму, количество, среднее значение и подставлять данные не хуже профессионалов.

Подробные сведения о формулах

Чтобы узнать больше об определенных элементах формулы, просмотрите соответствующие разделы ниже.

Формула также может содержать один или несколько таких элементов, как функции, ссылки, операторы и константы.

Части формулы   

1. Функции. Функция ПИ() возвращает значение числа пи: 3,142…

2. Ссылки. A2 возвращает значение ячейки A2.

3. Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.

4. Операторы. Оператор ^ (крышка) применяется для возведения числа в степень, а * (звездочка) — для умножения.

Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, а не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после редактирования формулы. Обычно лучше помещать такие константы в отдельные ячейки, где их можно будет легко изменить при необходимости, а в формулах использовать ссылки на эти ячейки.

Ссылка указывает на ячейку или диапазон ячеек листа и сообщает Microsoft Excel, где находятся необходимые формуле значения или данные. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.

  • Стиль ссылок A1

    По умолчанию Excel использует стиль ссылок A1, в котором столбцы обозначаются буквами (от A до XFD, не более 16 384 столбцов), а строки — номерами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.

    Ячейка или диапазон

    Использование

    Ячейка на пересечении столбца A и строки 10

    A10

    Диапазон ячеек: столбец А, строки 10-20.

    A10:A20

    Диапазон ячеек: строка 15, столбцы B-E

    B15:E15

    Все ячейки в строке 5

    5:5

    Все ячейки в строках с 5 по 10

    5:10

    Все ячейки в столбце H

    H:H

    Все ячейки в столбцах с H по J

    H:J

    Диапазон ячеек: столбцы А-E, строки 10-20

    A10:E20

  • Создание ссылки на ячейку или диапазон ячеек с другого листа в той же книге

    В приведенном ниже примере функция СРЗНАЧ вычисляет среднее значение в диапазоне B1:B10 на листе «Маркетинг» в той же книге.

    1. Ссылка на лист «Маркетинг».

    2. Ссылка на диапазон ячеек от B1 до B10

    3. Восклицательный знак (!) отделяет ссылку на лист от ссылки на диапазон ячеек.

    Примечание: Если название упоминаемого листа содержит пробелы или цифры, его нужно заключить в апострофы (‘), например так: ‘123’!A1 или =’Прибыль за январь’!A1.

  • Различия между абсолютными, относительными и смешанными ссылками

    1. <c0>Относительные ссылки</c0>.    Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.

      Скопированная формула с относительной ссылкой   

    2. <c0>Абсолютные ссылки</c0>.    Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.

      Скопированная формула с абсолютной ссылкой   

    3. Смешанные ссылки    Смешанная ссылка содержит абсолютный столбец и относительную строку, а также абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет форму $A 1, $B 1 и т. д. Абсолютная ссылка на строку имеет форму $1, B $1 и т. д. При изменении положения ячейки, содержащей формулу, относительная ссылка будет изменена, а абсолютная ссылка не изменится. Если вы копируете или заполните формулу в строках или столбцах, относительная ссылка автоматически корректируется, а абсолютная ссылка не изменяется. Например, при копировании и заполнении смешанной ссылки из ячейки a2 в ячейку B3 она корректируется с = A $1 на = B $1.

      Скопированная формула со смешанной ссылкой   

  • Стиль трехмерных ссылок

    Удобный способ для ссылки на несколько листов    Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. В Microsoft Excel используются все листы, указанные между начальным и конечным именами в ссылке. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.

    • При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.

    • Трехмерные ссылки нельзя использовать в формулах массива.

    • Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.

    <c0>Что происходит при перемещении, копировании, вставке или удалении листов</c0>.    Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.

    • Вставка или копирование.    Если вставить листы между листами 2 и 6, Microsoft Excel прибавит к сумме содержимое ячеек с A2 по A5 на новых листах.

    • <c0>Удаление</c0>.     Если удалить листы между листами 2 и 6, Microsoft Excel не будет использовать их значения в вычислениях.

    • <c0>Перемещение</c0>.    Если листы, находящиеся между листом 2 и листом 6, переместить таким образом, чтобы они оказались перед листом 2 или после листа 6, Microsoft Excel вычтет из суммы содержимое ячеек с перемещенных листов.

    • <c0>Перемещение конечного листа</c0>.    Если переместить лист 2 или 6 в другое место книги, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.

    • <c0>Удаление конечного листа</c0>.    Если удалить лист 2 или 6, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.

  • Стиль ссылок R1C1

    Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. При использовании стиля R1C1 в Microsoft Excel положение ячейки обозначается буквой R, за которой следует номер строки, и буквой C, за которой следует номер столбца.

    Ссылка

    Значение

    R[-2]C

    относительная ссылка на ячейку, расположенную на две строки выше в том же столбце

    R[2]C[2]

    Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее

    R2C2

    Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца

    R[-1]

    Относительная ссылка на строку, расположенную выше текущей ячейки

    R

    Абсолютная ссылка на текущую строку

    При записи макроса в Microsoft Excel для некоторых команд используется стиль ссылок R1C1. Например, если записывается команда щелчка элемента Автосумма для вставки формулы, суммирующей диапазон ячеек, в Microsoft Excel при записи формулы будет использован стиль ссылок R1C1, а не A1.

    Чтобы включить или отключить использование стиля ссылок R1C1, установите или снимите флажок Стиль ссылок R1C1 в разделе Работа с формулами категории Формулы в диалоговом окне Параметры. Чтобы открыть это окно, перейдите на вкладку Файл.

    К началу страницы

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

См. также

Переключение между относительными, абсолютными и смешанными ссылками для функций

Использование операторов вычислений в формулах Excel

Порядок, в котором Excel выполняет операции в формулах

Использование функций и вложенных функций в формулах Excel

Определение и использование имен в формулах

Рекомендации и примеры формул массива

Удаление и удаление формулы

Как избежать неработающих формул

Поиск и исправление ошибок в формулах

Сочетания клавиш и функциональные клавиши в Excel

Функции Excel (по категориям)

support.office.com

Формулы по статистике

~ 7 ~

Тема 1: Группировка статистических данных

Определение числа групп (если группи-ка по непрер. приз-ку или дискрет. со многими знач-ями)

Определение величины равного интервала:

Тема 2: Абсолютные и относительные величины

Относительные величины:

1) относит. вел-на структуры:

2) относит. вел-на планового задания:

3) относит. вел-на выполнения плана:

4) относит. вел-на динамики или темп роста:

5) относит. вел-на сравнения

6) относит. вел-на интенсивности (пример: фондоотдача = объем/стоимость (один год))

Тема 3: Средние величины и показатели вариации

Средняя арифметическая

простая:

взвешенная:

Средняя гармоническая

простая:

взвешенная: , сумма значений признака по группе

Свойства средн. арифметической:

  1. если каждую вари-ту х умен-ть или увел-ть на одно и то же число, то ср. вел-на умен-ется или увел-ется на это же число;

  2. если каждую вари-ту х умен-ть или увел-ть в одно и то же число раз, то ср. вел-на умен-ется или увел-ется в одно и то же число раз;

  3. если каждую частоту f умен-ть или увел-ть в одно и то же число раз, то ср. вел-на не изменится.

Ср. вел-на зависит от вар-ты х и структуры совок-сти, кот. харак-ется долями d.

Ряд распределения имеет 3 центра:

1) ср. аримет-кое;

2) мода – наиболее часто встречающаяся вар-та [M0];

3) медиана – вар-та, стоящая в середине ряда распре-ния. Сначала находят N медианы, кот. равен n/2, если число еди-ц совок-сти n – чётное, или , если число еди-ц совок-сти нечетное [Me].

Осн. пока-ли вариации:

1) размах вариации:

2) ср. линейное отклонение (ср. арифм-кая из абсолют. откл-ний отдел. значений)

Для несгруппир. данных:

Для сгруппир. данных:

3) ср. квадратическое отклонение (хар-ет ср. абсол. откл-ние вар-ты от ср. вел-ны)

Для несгруппир. данных:

Для сгруппир. данных:

4) Дисперсия – квадрат среднеквадр-ного откл-ния

Для несгруппир. данных:

Для сгруппир. данных:

Общая дисперсия: (для сгрупп.) (для несгрупп.)

– ср. вел-на резул. приз-ка в сово-сти, — частота (в совокупности!)

Внутригрупповая дисперсия: — кол-во вариант в группе i

Междугрупповая дисперсия: — кол-во вариант в группе i

Правило сложения дисперсий:

Не имеет еди-ц измерения.

5) Коэффициент вариации хар-ет ср. относит. откл-ние вар-ты от ср. вел-ны.

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом.

В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Выбирается начало отсчета (из х) – условный нуль (A). Обычно как можно ближе к середине распре-ния.

2) Находятся отклонения вариантов от условного нуля ().

4) Если эти отклонения содержат общий множитель (k), то рассчитанные

отклонения делятся на этот множитель.

Способ моментов:

Средняя:

Дисперсия:

Тема 4: Выборочное наблюдение

Обозначения в теории выборки:

N – числи-ль генер. выборки

n – числи-ль генер. выборки

генер. средняя (оценивают)

– выбор. средняя (рассчитывают)

p – генер. доля (оценивают)

w – выбор. доля (рассчитывают)

P(t) – задаваемый уровень веро-сти

Генер. средняя: с задан. уровнем вероя-сти P(t)

– ошибка выборки для ср. вел-ны

, t – критерий надеж-сти, его вел-на зав-т от уровня задан. вероя-сти P(t)

Если 1) P(t) = 0,683, то t=1; 2) P(t) = 0,954, то t=2 ; 3) P(t) = 0,997, то t=3

– среднеквадр. ошибка выборки

– верна для повторного отбора в выборке.

— для бесповторного отбора

Доказано: с задан. уровнем вероя-сти P(t)

– ошибка выборки для доли

, – среднеквадр. ошибка выборки для доли

–для повторного отбора

— для бесповторного отбора

studfiles.net

Относительные величины

Относительные величины бывают четырех видов: интенсивные, экстенсивные, показатели соотношения, показатели наглядности.

Интенсивные показатели — показывают частоту явления в среде. В качестве среды обычно выступает некая совокупность объектов (населения, пациентов, случаев), у части которых происходит какое-то явление. Рассчитывается по следующей формуле:

И.п. = явление/среда*коэффициент.

Коэффициент используется для удобства представления показателя, представляет собой различные степени числа 10 и обычно принимает значения 100, 1000, 10 000, 100 000. Его величина зависит от частоты встречаемости явления: чем реже встречается, тем больше коэффициент. Так, показатели рождаемости, смертности, общей заболеваемости населения обычно рассчитываются на 1000 человек. При расчете материнской смертности, как значительно более редкого события, используется коэффициент 100 000. Наоборот, частота такого распространенного явления, как случай временной утраты трудоспособности, рассчитывается на 100 работающих.

Пример расчета интенсивного показателя:

За год в больнице Н. было выполнено 360 хирургических операций. В 54 случаях в послеоперационном периоде наблюдались различные осложнения. Найти частоту послеоперационных осложнений из расчета на 100 операций.

Решение: Частота послеоперационных осложнений — это интенсивный показатель, который может быть рассчитан как отношение явления к среде. Средой выступает совокупность выполненных операций (360), из числа которых в 54 случаях, как следует из условия задачи, происходило явление — отмечались послеоперационные осложнения. Таким образом:

Частота послеоперационных осложнений = (Число случаев послеоперационных осложнений) / (Число выполненных операций) * 100 = (54 / 360) * 100 = 15.

Значение коэффициента принято равным 100, так как в условии задачи спрашивается частота, рассчитанная на 100 выполненных операций.

Ответ: Частота послеоперационных осложнений в больнице Н. за год составила 15 случаев на 100 выполненных операций.

Экстенсивные показатели — характеризуют структуру явления, измеряются в процентах, реже — в промилле или долях единицы. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по формуле:

Э.п. = часть/целое*100%.

Пример расчета экстенсивного показателя:

В исследовании эффективности лечения пневмонии с использованием нового антибиотика приняли участие 200 пациентов, из них 90 — мужчины. Необходимо определить долю мужчин среди исследуемых, результат выразить в %.

Решение: Пациенты мужского пола представляют собой часть от всей совокупности исследуемых. Следовательно, мы должны воспользоваться формулой для расчета экстенсивных показателей:

Доля пациентов мужского пола среди всех исследуемых = (число мужчин) / (число всех пациентов) * 100% = (90 / 200) * 100% = 45%.

Ответ: Доля пациентов в структуре исследуемых составляет 45%.

Показатели соотношения — характеризуют отношение двух не связанных между собой совокупностей. Данные совокупности могут измеряться в одних величинах, главное условие, что их изменения должны происходить независимо друг от друга. Обычно в таком виде представляются различные индексы, коэффициенты, показатели обеспеченности населения. Рассчитываются по следующей формуле:

П.с. = (первая совокупность) / (вторая совокупность)*коэффициент

Коэффициент обычно принимает значения 1 (для индексов) или 10 000 (для показателей обеспеченности населения).

Пример расчета показателя соотношения:

В одном из районов Республики Татарстан проживает 40 000 населения. В лечебно-профилактических учреждениях данного района развернуты 384 стационарные койки. Какова обеспеченность населения койками в районе?

Решение:Мы имеем две совокупности: население и стационарные койки. Изменения числа населения не зависят от изменений числа стационарных коек и наоборот, в связи с чем делаем вывод о том, что представленные совокупности не связаны между собой. Рассчитаем показатель обеспеченности населения стационарными койками:

Обеспеченность населения койками = (число коек) / (численность населения) *10 000 = (384 / 40 000) * 10 000 = 96.

Ответ: Обеспеченность населения стационарными койками составляет 96 на 10 000 населения.


Презентация на тему «Медицинская статистика. Абсолютные и относительные величины»

Расчетные задачи по теме «Относительные величины»

Онлайн-калькулятор для расчета относительных величин


medstatistic.ru

Урок 7. Относительная молекулярная и относительная формульная массы – HIMI4KA

В уроке 7 «Относительная молекулярная и относительная формульная массы» из курса «Химия для чайников» научимся вычислять относительную молекулярную массу, а также относительную формульную массу веществ; кроме того, выясним что такое массовая доля и приведем формулу для ее вычисления. Напоминаю, что в прошлом уроке «Валентность» мы дадим определение валентности, научились ее определять; рассмотрели элементы с постоянной и переменной валентностью, кроме того научились составлять химические формулы по валентности.

Каждый химический элемент характеризуется определенным значением относительной атомной массы. Состав любого вещества выражается молекулярной или простейшей формулой его структурной единицы. Такая структурная единица состоит из определенного числа атомов химических элементов. Поэтому масса структурной единицы может быть выражена в атомных единицах массы.

Относительная молекулярная масса

Вещества молекулярного строения характеризуются величиной относительной молекулярной массы, которая обозначается Mr.

Относительная молекулярная масса — это физическая величина, равная отношению массы одной молекулы вещества к 1/12 части массы атома углерода.

Эта величина равна сумме относительных атомных масс всех химических элементов с учетом числа их атомов в молекуле. Например, рассчитаем относительную молекулярную массу воды H2O:

Относительная молекулярная масса серной кислоты H2SO4:

Относительные молекулярные массы, как и относительные атомные массы, являются величинами безразмерными. Значение Мr показывает, во сколько раз масса молекулы данного вещества больше атомной единицы массы u. Например, если Mr(H2O) = 18, это значит, что масса молекулы H2O в 18 раз больше 1/12 части массы атома углерода, т. е. в 18 раз больше атомной единицы массы. Соответственно, масса молекулы H2SO4 в 98 раз больше 1/12 части массы атома углерода.

Относительная формульная масса

Вещества немолекулярного строения также характеризуются подобной величиной, которая называется относительной формульной массой. Как и относительная молекулярная масса, она равна сумме относительных атомных масс всех элементов, входящих в состав структурной единицы таких веществ — формульной единицы, и также обозначается Mr. При этом, конечно, необходимо учитывать индексы у символов атомов.

Например, относительная формульная масса вещества CaCO3 равна:

Относительная формульная масса вещества Al2(SO4)3 равна:

Относительная формульная масса показывает, во сколько раз масса формульной единицы данного вещества больше 1/12 части массы атома углерода, или атомной единицы массы u.

Вычисление массовой доли химического элемента по формуле вещества

По формуле вещества можно рассчитать массовую долю атомов каждого химического элемента, который входит в состав этого вещества, т. е. определить, какую часть от общей массы вещества составляет масса атомов данного элемента.

Массовая доля (w) атомов химического элемента в веществе показывает, какая часть относительной молекулярной (формульной) массы вещества приходится на атомы данного элемента.

Массовая доля атомов элемента А в сложном веществе АxBy рассчитывается по формуле:

где w («дубль-вэ») — массовая доля элемента А;
Ar(А) — относительная атомная масса элемента А;
х, у — числа атомов элементов А и В в формуле вещества;
Mr(АхBy) — относительная молекулярная (формульная) масса вещества АхBy.

Массовые доли выражаются в долях единицы или в процентах.

Пример. Определите массовые доли элементов в фосфорной кислоте H3PO4

Спойлер

[свернуть]

Краткие выводы урока:

  1. Относительная молекулярная (формульная) масса вещества — это физическая величина, равная отношению массы молекулы (формульной единицы) вещества к 1/12 части массы атома углерода.
  2. Эта величина равна сумме относительных атомных масс химических элементов, входящих в состав молекулы (формульной единицы) данного вещества, с учетом числа атомов каждого элемента.

Надеюсь урок 7 «Относительная молекулярная и относительная формульная массы» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии.

himi4ka.ru

Относительная формула в Excel — Офис Ассист

Относительные ссылки в Excel позволяют значительно упростить жизнь, даже обычному рядовому пользователю. Используя относительные ссылки в своих вычислениях, Вы можете буквально за несколько секунд выполнить работу, на которую, в противном случае, понадобились бы часы. В данном уроке Вы узнаете все об абсолютных ссылках, а также научитесь применять их при решении задач в Microsoft Excel.

Более подробно об абсолютных ссылках в Excel Вы можете прочитать в данном уроке.

Относительная ссылка — что это?

По умолчанию, все ссылки в Excel являются относительными. При копировании формул, они изменяются на основании относительного расположения строк и столбцов. Например, если Вы скопируете формулу =A1+B1 из строки 1 в строку 2, формула превратится в =A2+B2. Относительные ссылки особенно удобны, когда необходимо продублировать тот же самый расчет по нескольким строкам или столбцам.

Создание и копирование формул с относительными ссылками

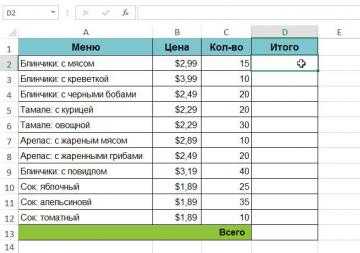
В следующем примере мы создадим выражение, которое будет умножать стоимость каждой позиции в меню на количество. Вместо того чтобы создавать новую формулу для каждой строки, мы можем создать всего одну, а затем скопировать ее в другие строки. Для этого воспользуемся относительными ссылками, чтобы правильно вычислить сумму по каждому элементу.

  1. Выделите ячейку, которая будет содержать формулу. В нашем примере мы выбрали ячейку D2.
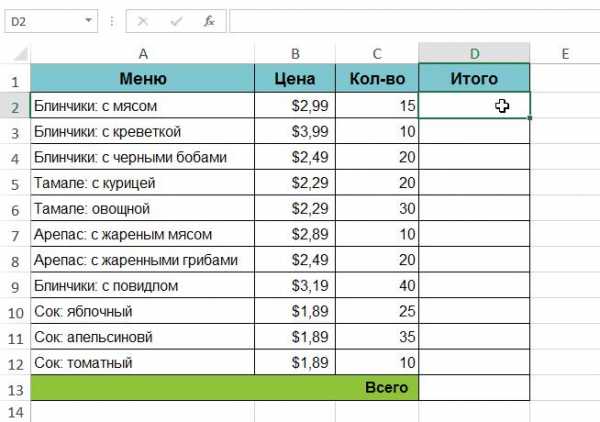
  2. Введите выражение для вычисления необходимого значения. В нашем примере, мы введем =B2*C2.
  3. Нажмите Enter на клавиатуре. Формула будет вычислена, а результат отобразится в ячейке.
  4. Найдите маркер автозаполнения в правом нижнем углу рассматриваемой ячейки. В данном примере мы ищем маркер автозаполнения в ячейке D2.
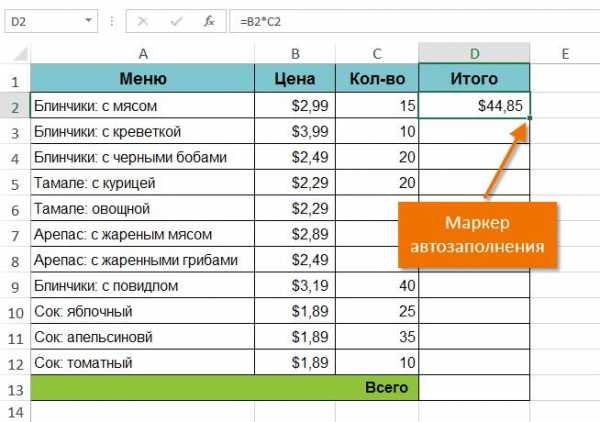
  5. Нажмите и, удерживая левую кнопку мыши, перетащите маркер автозаполнения по необходимым ячейкам. В нашем случае это диапазон D3:D12.
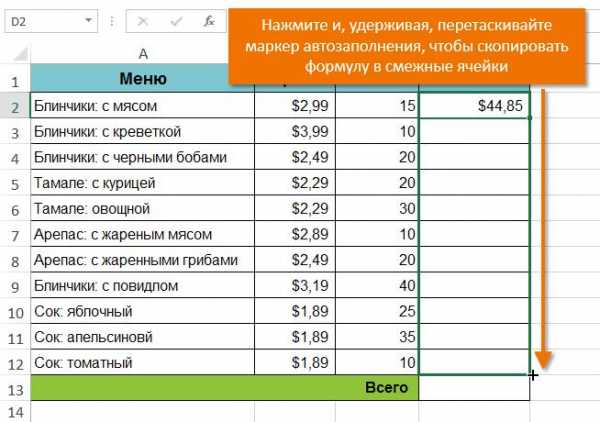
  6. Отпустите кнопку мыши. Формула будет скопирована в выбранные ячейки с относительными ссылками, и в каждой будут вычислены значения.

Вы можете дважды щелкнуть по заполненным ячейкам, чтобы проверить правильность своих формул. Относительные ссылки должны быть разными для каждой ячейки, в зависимости от строки.

В Excel Вы также можете создавать ссылки между листами внутри документа. Более подробно об этом читайте в уроке Ссылки на другие листы в Excel.

officeassist.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *