Теория шести рукопожатий на практике
Теория шести рукопожатий — теория, согласно которой любые два человека на Земле разделены не более чем пятью уровнями общих знакомых (и, соответственно, шестью уровнями связей).Теория была выдвинута в 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом. Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых, в среднем состоящую из пяти человек.
Милгрэм опирался на данные эксперимента в двух американских городах. Жителям одного города было роздано 300 конвертов, которые надо было передать определённому человеку, живущему в другом городе. Конверты можно было передавать только через своих знакомых и родственников. До бостонского адресата дошло 60 конвертов. Произведя подсчеты, Милгрэм определил, что в среднем каждый конверт прошёл через пять человек. Так и родилась теория «шести рукопожатий».
Эксперимент Милгрэма был повторён учеными кафедры социологии Колумбийского университета при помощи электронной почты. Тысячам добровольцев они предложили «достучаться» до 20 засекреченных людей, о которых сообщали имя, фамилию, род занятий, место жительства, образование. Первой успешной попыткой стало определение почтового адреса одного из таких «засекреченных» в Сибири. Доброволец из Австралии нашёл адрес сибирской «цели» при помощи всего четырёх сообщений.
Анализ экспертами Microsoft данных, полученных за месяц общения 242 720 596 пользователей, занял два года. Объём исследуемых данных составил около 4,5 ТБ. На этой базе данных было установлено, что каждый из 240 миллионов пользователей сервиса мог бы «дойти» до другого в среднем за 6,6 «шага». Чем исследователи математически доказали теорию и расхожую шутку о том, что через пять человек каждый из нас знаком с английской королевой.
Миланский университет и социальная сеть Facebook также провели совместное исследование теории шести рукопожатий, взяв за основу данные социального графа Facebook. Было установлено, что двух любых пользователей Facebook отделяет 4,74 уровня связи. Для США количество звеньев составило 4,37.
fishki.net
Теория шести рукопожатий — Википедия
Материал из Википедии — свободной энциклопедии
Теория шести рукопожатий в виде графа. Знакомство между двумя людьми изображено ребром графа, вершины графа — люди.Тео́рия шести́ рукопожа́тий — недоказанная теория, согласно которой любые два человека на Земле разделены не более чем пятью уровнями общих знакомых (и, соответственно, шестью уровнями связей).
Математическая формулировка теории — диаметр графа знакомств не превышает 6.
История возникновения
Теория была выдвинута в 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом (Jeffrey Travers). Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых, в среднем состоящую из пяти человек.
Милгрэм опирался на данные эксперимента в двух американских городах. Жителям одного города было роздано 300 конвертов, которые надо было передать определённому человеку, живущему в другом городе. Конверты можно было передавать только через своих знакомых и родственников. До бостонского адресата дошло 60 конвертов. Произведя подсчеты, Милгрэм определил, что в среднем каждый конверт прошёл через пять человек. Так и родилась теория «шести рукопожатий».
История экспериментальных проверок
Эксперимент Милгрэма был повторён учеными кафедры социологии Колумбийского университета при помощи электронной почты. Тысячам добровольцев они предложили «достучаться» до 20 засекреченных людей, о которых сообщали имя, фамилию, род занятий, место жительства, образование. Первой успешной попыткой стало определение почтового адреса одного из таких «засекреченных» в Сибири. Доброволец из Австралии нашёл адрес сибирской «цели» при помощи всего четырёх сообщений. [1]
Анализ экспертами Microsoft данных, полученных за месяц общения 242 720 596 пользователей, занял два года. Объём исследуемых данных составил около 4,5 ТБ. На этой базе данных было установлено, что каждый из 240 миллионов пользователей сервиса мог бы «дойти» до другого в среднем за 6,6 «шага». Чем исследователи опытным путём подтвердили теорию и расхожую шутку о том, что через пять человек каждый из нас знаком с английской королевой.
Миланский университет и социальная сеть Facebook также провели совместное исследование теории шести рукопожатий, взяв за основу данные социального графа Facebook[2]. Было установлено, что двух любых пользователей Facebook отделяет 4,74 уровня связи. Для США количество звеньев составило 4,37.[3]
Между прочим, на основе теории «тесного мира» возникло и множество популярных в США игр. Например, учёные играют в «Число Эрдёша». Венгерский математик Пал Эрдёш — один из крупных учёных XX века, имеющий огромное число работ, написанных в соавторстве. Нужно найти кратчайшую цепочку от него до другого известного учёного. Если он написал какую-нибудь работу вместе с Эрдёшем, то число Эрдёша у него равно единице. Если в соавторстве с тем, кто, в свою очередь, написал что-нибудь с Палом Эрдёшем, то это число у него равняется двум и т. д. Почти все нобелевские лауреаты имеют небольшие числа Эрдёша.
Использование теории в искусстве
Возможно, правило «шести рукопожатий» появилось в 1929 году в рассказе венгерского фантаста Фридьеша Каринти «Звенья цепи»[4]. Герой его рассказа предлагал экспериментально доказать, «что жители Земли ныне гораздо ближе друг к другу, чем когда-либо прежде». Нужно было выбрать любого человека из 1,5 миллиардов (на тот момент) жителей Земли, и он, используя не более пяти человек, каждый из которых — личный знакомый другого, должен связаться с любым другим человеком на Земле.
В массовой культуре термин «шесть степеней разделения» («six degrees of separation») популяризовал Джон Гуайр в своей пьесе «Шесть степеней разделения» [5]
Также теория проиллюстрирована в фильмах «Реальная любовь» (2003), «Ёлки» (2010), сериале «Друзья» (3 сезон, 16 серия), сериале «Шестеро / Six Degrees».
Примечания
Ссылки
wikipedia.green
Проверка теории шести рукопожатий / Habr

Хочу рассказать о своем эксперименте по проверке «Теории шести рукопожатий». На написание этого материала меня вдохновила статья «Анализ дружеских связей VK с помощью Python» (чтобы избежать повторений, в дальнейшем я буду ссылаться на нее). Так как в целом задача мной была поставлена по-другому, да и использованные методы тоже отличаются, то я решил что это может быть интересно.
Формулировка задачи: визуализировать все связи между двумя пользователями внутри одной социальной сети. При этом связи не должны дублироваться, например если Ваня знает Петю через Олю, то Оля в дальнейших итерациях по поиску общих друзей не участвует. Чтобы попрактиковаться в API, я выбрал “Вконтакте”.
Отталкиваясь от ограничений API и функциональности методов, было решено, что оптимальным количеством «рукопожатий» с позиции времени получения информации будет 3. Так что проверять все-таки будем «Теорию трех рукопожатий», пока что. Таким образом при среднем количестве друзей 200, мы получаем выборку из 8 млн. человек. Например, в масштабах Украины я практически всегда находил связи. Структурно задачу можно разбить на следующие этапы:
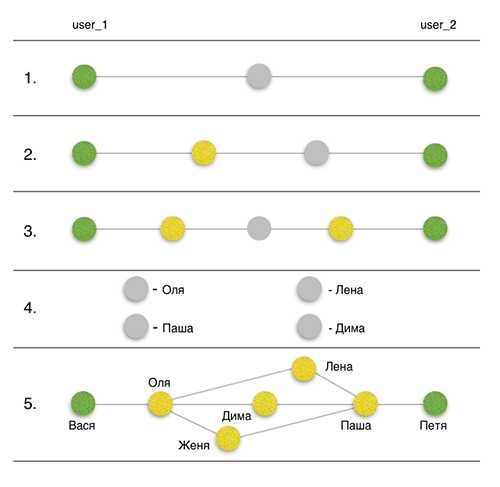
- Поиск общих друзей между исходным пользователем 1 (user_1) и исходным пользователем 2 (user_2).
- Поиск общих друзей между user_2 и друзьями user_1.
- Поиск общих друзей между друзьями user_2 и друзьями user_1.
- Получение детальной информации о найденных связях.
- Визуализация.
Итак, что нам понадобится:
import requests
import time
from threading import Thread
from tokens import *Requests — распространенная HTTP библиотека для Python, описана в статье «Библиотека для упрощения HTTP-запросов».
Time — базовый модуль, название которого говорит само за себя. Будем использовать для введения задержек во времени.
Threading — базовый модуль для работы с потоками. Хорошо описан в статье «Учимся писать многопоточные и многопроцессные приложения на Python».
Tokens — файл tokens.py будет содержать OAuth токены для авторизации в API. Как получить токен описано в исходной статье, а также на странице API «Вконтакте».
Прежде чем приступать к первому этапу, тезисно остановлюсь на функциональности API и некоторых ограничениях:
- Для обращения к методу API используется POST или GET запрос.
- Список использованных мной методов: users.get, friends.get, friends.getMutual, execute.
- Метод execute позволяет запускать до 25 методов одним запросом.
- В секунду можно осуществить не более 3 запросов (используя один токен).
- Ограничение для параметра target_uids метода friends.getMutual — 300. Об этом более подробно остановлюсь ниже.
Таким образом глобально схема сводится к отправке GET запросов на сервер «Вконтакте» и анализу ответов от сервера в формате json. При этом для оптимизации времени мы используем метод execute и многопоточность.
Ремарка к исходной статье, которая меня вдохновила. Автор статьи STLEON использует метод friends.getMutual в режиме “один к одному”, используя параметр target_uid. Я полагаю, что это было вызвано отсутствием параметра target_uids в прошлой версии API. Я же использую этот метод в режиме “один к многим”, что значительно экономит время. Параметр target_uids имеет ограничение на длину строки, о котором я ничего не нашел в документации. Экспериментально было установлено, что максимальная длина составляет порядка 310-330 UID в зависимости от длины каждого идентификатора. Я округлил этот показатель до 300.
Все выше сказанное подытожим объявлением следующих констант:
f_1_max = 300
f_2_max = 24
t = 0.35
Почему f_2_max = 24, а не 25, будет ясно позже.
Этап 1. Поиск общих друзей между user_1 и user_2
Напишем функцию, с помощью которой мы будем общаться с сервером «Вконтакте» посредствам GET запроса:
def vk (method, parameters, token):
return requests.get('https://api.vk.com/method/%s?%s&access_token=%s' % (method, '&'.join(parameters), token)).json()
У этой функции есть три аргумента:
- method — название метода, к которому мы обращаемся через API.
- parameters — параметры этого метода (можно найти в описании каждого метода).
- token — строка, которая авторизирует Вас на сервере. Повторюсь, что получение токена подробно описано здесь и здесь.
Далее для сохранения всей собранной информации мы будем использовать множества. Инициализируем множества для каждого из трех “рукопожатий”.
edges_1, edges_2, edges_3 = set(), set(), set()
Для выполнения условия, чтобы связи не дублировались и Оля не фигурировала как общий друг Пети и Вани во всех трех “рукопожатиях”, а только в первом, необходимо ввести фильтры. Сразу же добавляем в фильтр первого “рукопожатия” исходных пользователей.
filter_1, filter_2 = set(), set()
filter_1.update([user_1, user_2])
Находим друзей user_1 с помощью вызова метода friends.get. После выполнения обращения к методу API, вводим необходимую задержу во времени t = 0.35. Заметьте, что одним из параметров является версия API (v=5.4 в моем случае). Очень важно везде ее указывать, потому что могут появиться несоответствия. Параметры метода order и count — использовать опционально.
friends_1 = set(vk('friends.get', ['user_id=%s' % user_1, 'order=hints', 'count=900', 'v=5.4'], token_1)['response']['items'])
time.sleep(t)
Далее переходим непосредственно к поиску общих друзей между user_1 и user_2 с помощью вызова метода friends.getMutual.
mutual_friends = vk('friends.getMutual', ['source_uid=%s' % user_1, 'order=hints', 'target_uid=%s' % user_2, 'v=5.4'], token_1)['response']
time.sleep(t)
И последний пункт первого этапа — сохранение информации в множество edges_1, обновление filtr_1 и удаление найденных общих друзей из списка друзей user_1, чтобы избежать повторений в будущем.
for user in mutual_friends:
edges_1.update([(user_1, user), (user, user_2)])
friends_1.remove(user)
filter_1.update([user])
Этап 2. Поиск общих друзей между user_2 и друзьями user_1 (friends_1)
Глобально второй этап повторяет первый, вся разница в том, что вместо поиска общих друзей в режиме “один к одному”, мы используем режим “один к многим”, что требует несколько лишних строк кода.
Инициализируем список, в который будем сохранять добытых друзей, а также некоторые переменные, которые нам понадобятся в промежуточных вычислениях.
user_1_mutual_friends, temp_users, j = [], [], 0
Далее, отсчитывая порции (не самое подходящее слово) из друзей user_1 по 300 UID, мы поочередно отправляем запросы к серверу об общих друзьях между user_2 и порцией UID, которые записываются в параметр target_uids метода friends.getMutual.
for i, friend in enumerate(friends_1):
temp_users += [friend]
j += 1
if j == f_1_max:
user_1_mutual_friends += vk('friends.getMutual', ['source_uid=%s' % user_2, 'order=hints', 'target_uids=%s' % str(temp_users)[1:-1], 'v=5.4'], token_1)['response']
temp_users, j = [], 0
time.sleep(t)
if i == len(friends_1) - 1 and len(friends_1) % f_1_max != 0:
user_1_mutual_friends += vk('friends.getMutual', ['source_uid=%s' % user_2, 'order=hints', 'target_uids=%s' % str(temp_users)[1:-1], 'v=5.4'], token_1)['response']
time.sleep(t)
Сохраняем полученную информацию в множество edges_2 и обновляем информацию в фильтре, как было в предыдущем этапе. Здесь могут быть исключения, допустим если UID закрыл доступ к общим друзьям или страница пользователя удалена, поэтому используем конструкцию try-except.
for friend in user_1_mutual_friends:
if friend['id'] != user_2 and friend['id'] not in filter_1:
try:
if friend['common_count'] > 0:
for common_friend in friend['common_friends']:
if common_friend != user_1 and common_friend not in filter_1:
edges_2.update([(user_1, friend['id']), (friend['id'], common_friend), (common_friend, user_2)])
friends_1.remove(friend['id'])
filter_2.update([friend['id'], common_friend])
except:
continue
Этап 3. Поиск общих друзей между друзьями user_2 и друзьями user_1
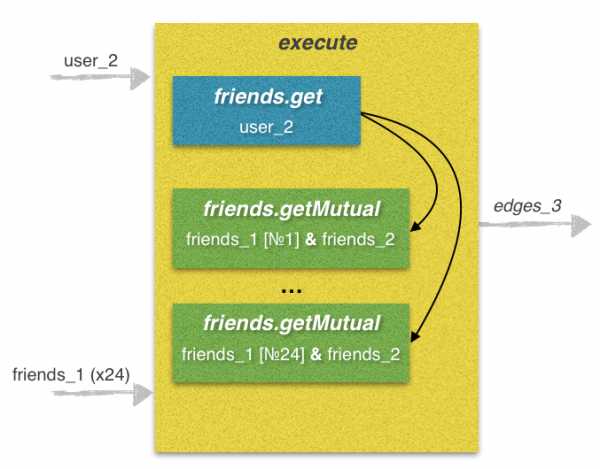
Данный этап является наиболее затратным по времени, так как запросов отправить нужно очень много. Именно здесь невозможно обойтись без использования метода execute. Из практики скажу, что без использования многопоточности, время на выполнение данного этапа по этому алгоритму составляет 50 — 120 секунд, а в некоторых случаях еще больше. С помощью использования нескольких потоков возможно свести время до выполнения одного запроса execute, который обрабатывается от 5 до 12 секунд.
Объявляем filter_3, объединяя множества filter_1 и filter_2. Преобразуем множество друзей user_1 (friends_1) в список.
filter_3 = filter_1.union(filter_2)
friends_1 = list(friends_1)
Далее последует монстрозный блок кода, в котором мы объявляем функцию для поиска общих друзей между друзьями user_1 и друзьями user_2 и сохранения информации в множество edges_3. Здесь опять-таки весь алгоритм такой же, как и в предыдущих этапах, только используется принцип “многие ко многим”, что еще больше усложняет код, тем более в моей имплементации он явно избыточный, так что вам есть над чем поработать. Ниже я приведу некоторые пояснения к этому многобуквию.
def get_edges_3 (friends_1, token):
prefix_code = 'code=var friends = API.friends.get({"v": "5.4", "user_id":"%s", "count":"500", "order": "hints"}).items; ' % user_2
lines, j, k = [], 0, -1
for i, friend in enumerate(friends_1):
lines += ['API.friends.getMutual({"v": "5.4", "source_uid": "%s", "count":"500", "target_uids": friends})' % friend] # Generating string for 'execute' request.
j += 1
if j == f_2_max:
code = prefix_code + 'return [' + ','.join(str(x) for x in lines) + '];'
response = vk('execute', [code, 'v=5.4'], token_1)
for friends in response['response']:
k += 1
if len(edges_3) < max_edges_3:
try:
for one_friend in friends:
if one_friend['common_count'] > 0:
for common_friend in one_friend['common_friends']:
if common_friend not in filter_3 and one_friend['id'] not in filter_3:
edges_3.update([(user_1, friends_1[k]), (friends_1[k], common_friend), (common_friend, one_friend['id']), (one_friend['id'], user_2)])
except:
continue
lines, j = [], 0
time.sleep(t)
if i == len(friends_1) - 1 and len(friends_1) % f_2_max != 0 :
code = prefix_code + 'return [' + ','.join(str(x) for x in lines) + '];'
response = vk('execute', [code, 'v=5.4'], token_1)
for friends in response['response']:
k += 1
if len(edges_3) < max_edges_3:
try:
for one_friend in friends:
if one_friend['common_count'] > 0:
for common_friend in one_friend['common_friends']:
if common_friend not in filter_3 and one_friend['id'] not in filter_3:
edges_3.update([(user_1, friends_1[k]), (friends_1[k], common_friend), (common_friend, one_friend['id']), (one_friend['id'], user_2)])
except:
continue
time.sleep(t)
Сумма строк prefix_code и lines представляет собой код в формате VKScript и является единственным параметром для метода execute. Этот скрипт содержит в себе 25 обращений к методам API.
prefix_code — часть строки, содержащая обращение №1 к методу friends.get. Здесь мы получаем список друзей user_2 и присваиваем его переменной friends.
lines — вторая часть строки, содержащая обращения №№ 2-25 к методу friends.getMutual. Здесь мы получаем список общих друзей между каждым из 24 друзей user_1 и списком друзей user_2. В цикле мы складываем prefix_code и 24 строки lines, таким образом получая строку code, которую используем как параметр к методу execute.
Далее я приведу пример с использованием нескольких потоков, но подробно не буду останавливаться на нем. Всю информацию можно найти в статье «Учимся писать многопоточные и многопроцессные приложения на Python».
t1 = Thread(target=get_edges_3, args=(friends_1[ : len(friends_1) * 1/3], token_1))
t2 = Thread(target=get_edges_3, args=(friends_1[len(friends_1) * 1/3 : len(friends_1) * 2/3], token_2))
t3 = Thread(target=get_edges_3, args=(friends_1[len(friends_1) * 2/3 : ], token_3))
t1.start()
t2.start()
t3.start()
t1.join()
t2.join()
t3.join()
Этап 4. Получение детальной информации о найденных связях
Теперь мы должны сложить все ребра нашего еще непостроенного графа друзей и извлечь из них список вершин. Далее по описанному выше шаблону с помощью метода users.get порциями по 300 UID отправляем запросы на получение данных о фамилии и имени пользователей. На выходе получаем список, в каждой ячейке которого будет UID и словарь с информацией о данном UID. Эти данные в комплексе с множествами ребер в дальнейшем используем для визуализации.
edges = list(edges_1) + list(edges_2) + list(edges_3)
nodes = []
for edge in edges:
nodes += [edge[0], edge[1]]
nodes = list(set(nodes))
nodes_info, temp_nodes, j = [], [], 0
for i, node in enumerate(nodes):
temp_nodes += [node]
j += 1
if j == f_1_max:
nodes_info += vk('users.get', ['user_ids=%s' % str(temp_nodes)[1:-1], 'fields=first_name, last_name', 'v=5.4'], token_1)['response']
temp_nodes, j = [], 0
time.sleep(t)
if i == len(nodes) - 1 and len(nodes) % f_1_max != 0:
nodes_info += vk('users.get', ['user_ids=%s' % str(temp_nodes)[1:-1], 'fields=first_name, last_name', 'v=5.4'], token_1)['response']
time.sleep(t)
for i, node in enumerate(nodes_info):
try:
nodes[i] = (nodes[i], {'first_name': node['first_name'], 'last_name': node['last_name']})
except:
continue
Этап 5. Визуализация
На технической реализации этого этапа я подробно останавливаться не буду. Опишу лишь кратко свой опыт.
Как и в исходной статье, я пробовал использовать библиотеку networkx для построения графа. Изменял диаметр и цвет вершин в зависимости от пола или количества связей, испробовал много методов визуализации, которые доступны в этой библиотеке, но результат мне не нравился. Беспорядочный граф получался не информативным при среднем и большом количестве ребер и вершин. Информация терялась.
Я пришел к выводу, что необходимо какое-то интерактивное решение. Первым, что я нашел, была библиотека D3.js. Но и здесь в формате обычного графа, несмотря на интерактивность, результат был неудовлетворительным. Затем в той же библиотеке был найден пример древовидного построения “Radial Reingold–Tilford Tree”, который мне показался подходящим. При таком построении в центре оказывается user_1, а user_2 — как бы на краю каждой ветви дерева.
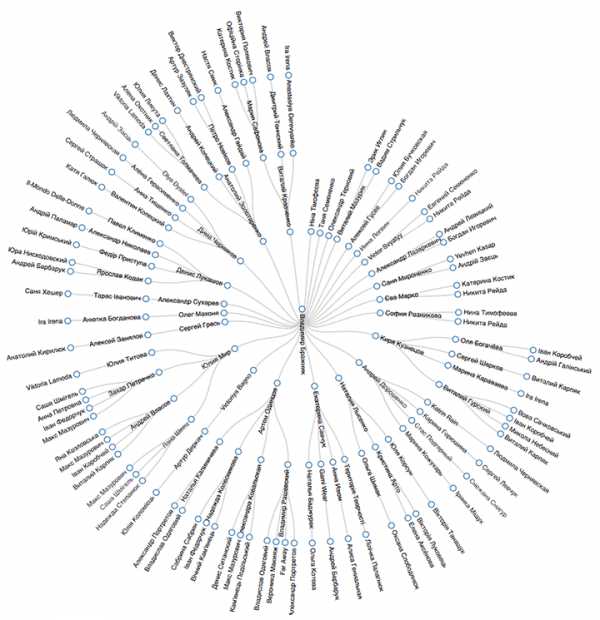
Я смоделировал всю связку с использованием веб-фреймворка СherryPy и результат меня удовлетворил, хотя и пришлось все равно ввести ограничения для отображаемых данных (в зависимости от типа и количества найденных связей). Я намеренно опустил подготовку данных для визуализации, так как эта процедура не представляет интереса и отличается в зависимости от выбранного метода. Мой вариант кода доступен на репозитории GitHub, где также описана подготовка данных для использования с библиотекой D3.js на примере шаблона “Radial Reingold–Tilford Tree”.
Еще было бы интересно отобразить взаимосвязи между списком друзей вот таким образом (см. рисунок ниже), так что можете экспериментировать. Этот пример взят также из D3.js и называется он D3 Dependencies.
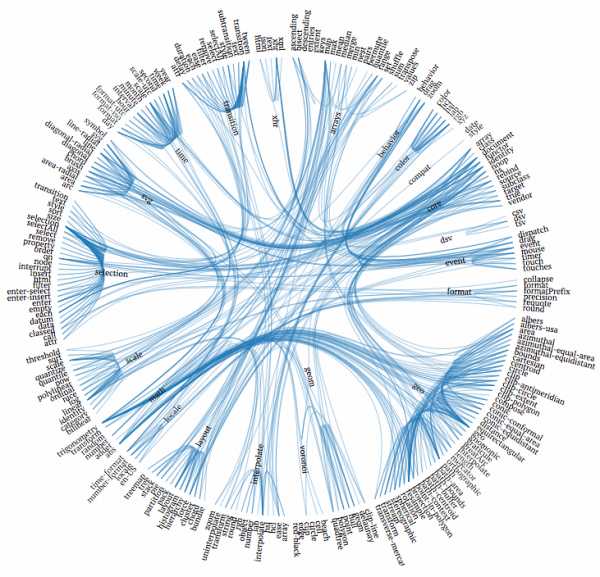
Что касается проверки теории, то в масштабах Украины схема с тремя рукопожатиями работает в 90% случаев. Исключения составляют пользователи с очень маленьким количеством друзей.
Спасибо за внимание.
habr.com
Согласно теории шести рукопожатий, мы все знакомы друг с другом через общих знакомых

Теория шести рукопожатий — теория, согласно которой любые два человека на Земле разделены в среднем лишь пятью уровнями общих знакомых (и, соответственно, шестью уровнями связей).
Теория была выдвинута в 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом. Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через недлинную цепочку общих знакомых. В среднем эта цепочка состоит из шести человек.
Милгрэм опирался на данные эксперимента в двух американских городах. Жителям одного города было роздано 300 конвертов, которые надо было передать определенному человеку, который жил в другом городе. Конверты можно было передавать только через своих знакомых и родственников. До бостонского адресата дошло 60 конвертов. Произведя подсчеты, Милгрэм определил, что в среднем каждый конверт прошел через шесть человек. Так и родилась теория «шести рукопожатий».
Повторили эксперимент Милгрэма при помощи электронной почты ученые кафедры социологии Колумбийского университета. Тысячам добровольцев они предложили «достучаться» до 20 засекреченных человек, о которых сообщали лишь основные характеристики: имя, фамилию, род занятий, место жительства, образование. Первой успешной попыткой стало определение почтового адреса одного из таких «засекреченных» в Сибири. Доброволец из Австралии нашел адрес сибирской «цели» при помощи всего четырех сообщений!
Анализ экспертами Microsoft данных, полученных за месяц общения 242 720 596 пользователей, занял два года. Объем исследуемых данных составил около 4,5 терабайт. На этой базе данных было установлено, что каждый из 240 миллионов пользователей сервиса мог бы «дойти» до другого в среднем за 6,6 «шага». Чем исследователи математически доказали теорию и расхожую шутку о том, что через пять человек каждый из нас знаком с английской королевой.
Между прочим, на основе теории «тесного мира» возникло и множество популярных в США игр. Например, ученые играют в «Число Эрдёша». Венгерский математик Пол Эрдёш — один из крупных учёных ХХ века, имеющий огромное число работ, написанных в соавторстве. Нужно найти кратчайшую цепочку от него до другого известного учёного. Если он написал какую-нибудь работу вместе с Эрдёшом, то число Эрдёша у него равно единице. Если в соавторстве с тем, кто, в свою очередь, написал что-нибудь с Полом Эрдёшом, то это число у него равняется двум и т. д. Почти все нобелевские лауреаты имеют небольшие числа Эрдёша.
Прислал: Артём Вайнштейн
Источник: ru.wikipedia.org
www.factroom.ru
Мир тесен. Теория шести рукопожатий | Нетворкинг 24
автор статьи:
Алексей Бабушкин,
эксперт по нетворкингу,
бизнес-тренер
Наверняка вы слышали выражение «Как тесен мир!» Но, возможно, не представляли насколько тесная связь между людьми. А ведь различными экспериментами доказано, что любые два человека на Земле, в среднем, разделены всего цепочкой из пяти других людей. То есть понадобится не более шести рукопожатий, чтобы познакомиться с абсолютно любым человеком на планете. Поэтому эта концепция получила название «Теория шести рукопожатий».Автором теории шести рукопожатий считается социальный психолог Стенли Милгрэм, который в конце 1960-х годов провел несколько экспериментов, доказывающих это численное значение. Хотя, над вопросом о сетевом взаимодействии в обществе и количестве звеньев между ее объектами ученые и социологи задумывались и ранее.
Предыстория эксперимента
В 1950-х годах ученые Манфред Кохен (Мичиганский университет) и Итиэль де Сола Пул (Массачусетский технологический институт) написали исследовательскую работу «Контакты и влияние». В ней они математически рассчитали законы развития и функционирования социальных сетей. Работа не получила широкой огласки и была напечатана, только спустя 20 лет под названием «Contacts and Influence». Но среди ученых рукопись Кохена и Пула имела довольно хорошую известность. Стенли Милгрэм тоже ознакомился с работой коллег и решил на практике проверить их расчеты.Ход эксперимента Стенли Милгрэма
В конце 60-х годов прошлого века, Стенли Милгрэм провел эксперимент с почтовыми конвертами. Он выбрал два максимально удаленных друг от друга американских города (Омаха и Бостон), чтобы проследить путь, который пройдут письма между двумя незнакомыми между собой адресатами. Случайно выбранным жителям Омахи предложили поучаствовать в исследовании. Участники получили письма, в котором содержалось описание эксперимента и предложение переслать конверт бостонцу, указанному в задании. Если человек знал его лично, то необходимо было выслать письмо непосредственно адресату. Если целевой контакт оказывался неизвестным, то предлагалось выбрать среди своих знакомых тех, кто с большей вероятностью мог быть знаком с персоной в конечном адресе. Когда письмо достигало места назначения осуществлялись подсчеты и делались соответствующие выводы.Результаты эксперимента
После начала эксперимента, в Бостон стали прибывать конверты-путешественники. К сожалению большая часть так и не нашла своих адресатов. Некоторые люди, оказавшиеся промежуточными звеньями цепи, категорически отказались пересылать его дальше. В итоге цели достигли порядка 20% писем. Анализ дошедшей корреспонденции показал, что, в среднем, каждое письмо преодолело путь в шесть человек. Милгрэм назвал свой эксперимент «Теорией тесного мира». Хотя, более широкое распространение получило название «Теория шести рукопожатий».Теория шести рукопожатий в интернете
В 2011 году Корнельский университет проверил теорию шести рукопожатий в интернете. В исследовании были задействованы 721 миллиона аккаунтов Фейсбук. Тогда оказалось, что среднее значение цепи между двумя двумя пользователями — 3,74 звеньев. Через несколько лет Facebook снова провел исследование. На этот раз своими силами. В выборку включили уже 1,6 миллиардов человек, зарегистрированных в соцсети. Результат расчетов получился равный 3,57.Исследования в «Теории тесного мира» проводили и сотрудники Microsoft. В июне 2006 года американцы изучили маршруты 30 миллиардов электронных сообщений. И получили данные, схожие с результатами Милгрэма. Люди, использующие электронную почту, связаны друг с другом в среднем через 6,6 общих знакомых.
Шесть рукопожатий под сомнением
В дальнейшем выводы Милгрэма были предметом постоянных споров. Кто-то их критиковал, кто-то проводил подобные эксперименты. До сих пор нет однозначного вывода о точности длины социальных связей в глобальном мире. Ведь некоторые народы и племена живут до сих пор изолированно от внешнего мира. Но вы можете провести эксперимент «Тесного мира» на себе. Выберите любого человека, с кем бы вам хотелось познакомиться. Попробуйте построить путь до него через своих знакомых и знакомых ваших друзей. Уверен, если вы будете пытливы, то ваш путь не превысит цепочки из 5 человек. У меня получилось!Алексей Бабушкин, эксперт по нетворкингу
networking24.ru
Теория шести рукопожатий — Википедия
Материал из Википедии — свободной энциклопедии
Теория шести рукопожатий в виде графа. Знакомство между двумя людьми изображено ребром графа, вершины графа — люди.Тео́рия шести́ рукопожа́тий — недоказанная теория, согласно которой любые два человека на Земле разделены не более чем пятью уровнями общих знакомых (и, соответственно, шестью уровнями связей).
Математическая формулировка теории — диаметр графа знакомств не превышает 6.
История возникновения
Теория была выдвинута в 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом (Jeffrey Travers). Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых, в среднем состоящую из пяти человек.
Милгрэм опирался на данные эксперимента в двух американских городах. Жителям одного города было роздано 300 конвертов, которые надо было передать определённому человеку, живущему в другом городе. Конверты можно было передавать только через своих знакомых и родственников. До бостонского адресата дошло 60 конвертов. Произведя подсчеты, Милгрэм определил, что в среднем каждый конверт прошёл через пять человек. Так и родилась теория «шести рукопожатий».
Видео по теме
История экспериментальных проверок
Эксперимент Милгрэма был повторён учеными кафедры социологии Колумбийского университета при помощи электронной почты. Тысячам добровольцев они предложили «достучаться» до 20 засекреченных людей, о которых сообщали имя, фамилию, род занятий, место жительства, образование. Первой успешной попыткой стало определение почтового адреса одного из таких «засекреченных» в Сибири. Доброволец из Австралии нашёл адрес сибирской «цели» при помощи всего четырёх сообщений.[1]
Анализ экспертами Microsoft данных, полученных за месяц общения 242 720 596 пользователей, занял два года. Объём исследуемых данных составил около 4,5 ТБ. На этой базе данных было установлено, что каждый из 240 миллионов пользователей сервиса мог бы «дойти» до другого в среднем за 6,6 «шага». Чем исследователи опытным путём подтвердили теорию и расхожую шутку о том, что через пять человек каждый из нас знаком с английской королевой.
Миланский университет и социальная сеть Facebook также провели совместное исследование теории шести рукопожатий, взяв за основу данные социального графа Facebook[2]. Было установлено, что двух любых пользователей Facebook отделяет 4,74 уровня связи. Для США количество звеньев составило 4,37.[3]
Между прочим, на основе теории «тесного мира» возникло и множество популярных в США игр. Например, учёные играют в «Число Эрдёша». Венгерский математик Пал Эрдёш — один из крупных учёных XX века, имеющий огромное число работ, написанных в соавторстве. Нужно найти кратчайшую цепочку от него до другого известного учёного. Если он написал какую-нибудь работу вместе с Эрдёшем, то число Эрдёша у него равно единице. Если в соавторстве с тем, кто, в свою очередь, написал что-нибудь с Палом Эрдёшем, то это число у него равняется двум и т. д. Почти все нобелевские лауреаты имеют небольшие числа Эрдёша.
Использование теории в искусстве
Возможно, правило «шести рукопожатий» появилось в 1929 году в рассказе венгерского фантаста Фридьеша Каринти «Звенья цепи»[4]. Герой его рассказа предлагал экспериментально доказать, «что жители Земли ныне гораздо ближе друг к другу, чем когда-либо прежде». Нужно было выбрать любого человека из 1,5 миллиардов (на тот момент) жителей Земли, и он, используя не более пяти человек, каждый из которых — личный знакомый другого, должен связаться с любым другим человеком на Земле.
В массовой культуре термин «шесть степеней разделения» («six degrees of separation») популяризовал Джон Гуайр в своей пьесе «Шесть степеней разделения»[5]
Также теория проиллюстрирована в фильмах «Реальная любовь» (2003), «Ёлки» (2010), сериале «Друзья» (3 сезон, 16 серия), сериале «Шестеро / Six Degrees».
Примечания
Ссылки
wiki2.red
Теория 6 рукопожатий

Согласно «Теории шести рукопожатий» любые два человека на Земле разделены в среднем лишь пятью уровнями общих знакомых (и, соответственно, шестью уровнями связей). Теория была выдвинута в 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом. Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых, в среднем состоящую из пяти человек. Милгрэм опирался на данные эксперимента в двух американских городах. Жителям одного города было роздано 300 конвертов, которые надо было передать определённому человеку, живущему в другом городе. Конверты можно было передавать только через своих знакомых и родственников. До бостонского адресата дошло 60 конвертов. Произведя подсчеты, Милгрэм определил, что в среднем каждый конверт прошёл через пять человек. Так и родилась теория «шести рукопожатий». Эксперимент Милгрэма был повторён учеными кафедры социологии Колумбийского университета при помощи электронной почты. Тысячам добровольцев они предложили «достучаться» до 20 засекреченных людей, о которых сообщали имя, фамилию, род занятий, место жительства, образование. Первой успешной попыткой стало определение одного из «засекреченных» почтовых адресов в Сибири. Доброволец из Австралии нашёл адрес сибирской «цели» при помощи всего четырёх сообщений. Возможно, правило «шести рукопожатий» появилось в 1929 году в рассказе венгерского фантаста Фридеша Каринти «Звенья цепи». Здесь предлагалось экспериментально доказать, «что жители Земли ныне гораздо ближе друг к другу, чем когда-либо прежде».
Источник: portall.tv
Если вам понравился этот материал, то предлагаем вам подборку самых лучших материалов нашего сайта по мнению наших читателей. Подборку — ТОП интересных фактов и важных новостей со всего мира и о разных важных событиях вы можете найти там, где вам максимально удобно ВКонтакте или В Фейсбуке
Если у вас неправильно отображается страница, не воспроизводится видео или нашли ошибку в тексте, пожалуйста, нажмите сюда.
ecology.md
