Понятие, формула дисконтирования | Таблица дисконтирования
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.
Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов.
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента.
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.
Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210.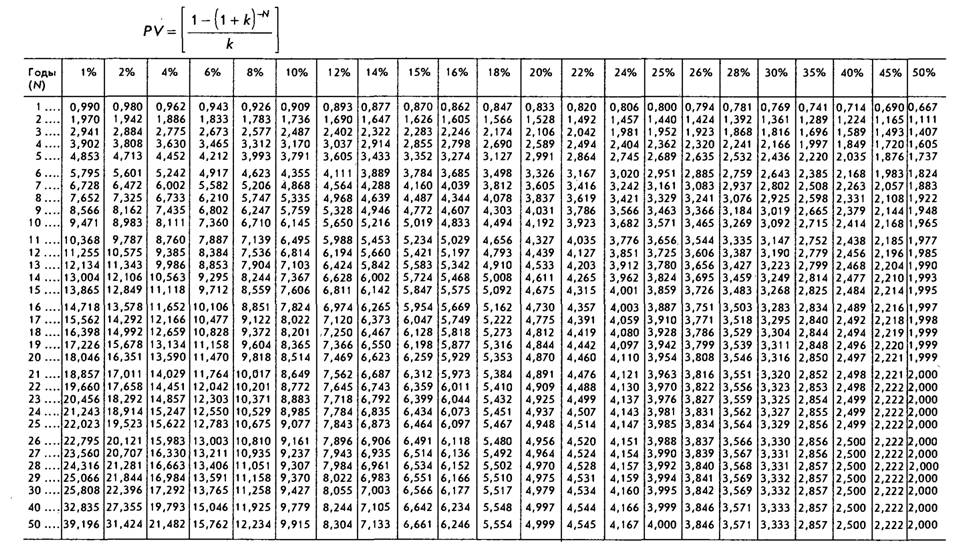 Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)nназывается фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это таблица коэффициентов дисконтирования, которые рассчитываются, как правило, с точностью до четвертого знака после запятой.
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
сегодня | через 5 лет |
62,09 цента | |
X? | 150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)5 = 161,050 долларов. Это более выгодный вариант.
Это более выгодный вариант.
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Самые интересные статьи по теме МСФО и Дипифр:
1. Консолидация — это контроль. МСФО IFRS 10 — это единая концепция контроля для любых объединений бизнеса
2. Как сдать экзамен Дипифр со второго раза?
Перейти на главную страницу
Коэффициент дисконтирования: формула и пример расчета
Важнейший этап на пути к собственному бизнесу – это разработка бизнес-плана. Будучи руководством к действию, направленному на достижение экономической выгоды, бизнес-план в обязательном порядке содержит статью расходов, в которую финансовые менеджеры рекомендуют включать ставку дисконтирования.
Будучи руководством к действию, направленному на достижение экономической выгоды, бизнес-план в обязательном порядке содержит статью расходов, в которую финансовые менеджеры рекомендуют включать ставку дисконтирования.
Но как показывает практика, многие начинающие предприниматели не только избегают использования этого параметра, но и не догадываются о его существовании.
Что такое коэффициент дисконтирования, как рассчитать этот показатель и чем объясняется необходимость его присутствия в бизнес-плане?
Дорогие читатели! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.
Если вы хотите узнать, как решить именно Вашу проблему — обращайтесь в форму онлайн-консультанта справа или звоните по телефону
+7 (804) 333-20-57
Это быстро и бесплатно!
Понятие
Предпринимателям, планирующим развивать бизнес и двигаться по направлению к финансовому благополучию предприятия, стоит освоить понятие «коэффициент дисконтирования».
Что это такое? На языке финансового анализа, таким термином обозначают приведение будущих поступлений фирмы к их стоимости в настоящий момент.
Сам процесс приведения в экономике называют «дисконтированием», а ставку, используемую для расчета показателя – ставкой дисконтирования.
Сегодня применение данному показателю нашли практически в любой сфере экономики и финансов. Его легко можно применить для определения эффективности бизнес-проекта, он способен предугадать финансовый успех конкретной организации.
При разработке строки затрат бизнес-плана сложно обойтись без коэффициента дисконтирования, так как он поможет рассчитать необходимые капиталовложения или выбрать альтернативный вариант, чтобы избежать лишних расходов.
Расчет
Чтобы определить стоимость денежных потоков в будущем, необходимо умножить сумму предполагаемых поступлений на коэффициент дисконтирования. Как найти этот показатель?
Для расчета дисконта применяют следующую формулу:
Kd=1/ (1+i)n;
Где n – время, в течение которого планируется получить прибыль.
Величина i обозначает ставку дисконтирования. Она также известна под названием «норма дисконта». Это переменный показатель, который зависит от множества факторов. Ставкой является процент, выражающий доходность от вкладываемых средств.
Для каждого индивидуального случая предназначена своя процентная ставка. Так, в качестве данной величины может быть использована ставка рефинансирования, процент доходности по вкладу, инфляция, кредитная процентная ставка, предполагаемая доходность проекта и прочее.
В ходе вычислений результат всегда оказывается ниже единицы. Коэффициент дисконтирования показывает, сколько стоит одна единица валюты из определенного периода времени, приведенная на текущую дату.
Ставка дисконтирования
В процессе вычисления коэффициента дисконтирования одной из самых важных задач является расчет нормы дисконта, так как от этого зависит итоговая оценка доходности инвестиционного проекта.
Сама по себе ставка является объектом интереса для инвестора, так как с точки зрения доходности способ капиталовложения с более высокой нормой дисконта должен привлекать его больше, нежели любой другой с аналогичными факторами риска.
Чтобы произвести дисконтирование, необходимо осуществлять расчет по данной формуле коэффициента.
Стоит учитывать и тот факт, что ставка отражает уровень доходности вложений с учетом определенных рисков, а также временных затрат. Что включает в себя норма дисконта:
- рост инфляции;
- показатель, отражающий уровень риска вложений;
- минимальную степень доходности, на которую в любом случае может рассчитывать инвестор.
Как уже было указано, для расчета нормы дисконта используются различные ставки, выбор которых зависит от заданной ситуации. Проценты по депозитам или уровень доходности от облигаций – это лишь основа, «безрисковая ставка» которая берется с поправкой на некоторые риски и временной фактор.
Формула расчета нормы дисконта:
Ставка дисконтирования=безрисковая ставка + риски
В качестве рисков принимаются различные факторы, под воздействием которых вложение денежных средств в конкретный проект становится небезопасным. В данный список можно отнести:
В данный список можно отнести:
Риски неликвидности нового проекта:
- риски, характерные для какой-либо отрасли;
- ошибки персонала;
- проблемы, определяемые конкретно для данной страны.
Чем точнее определяют процентную ставку дисконта, тем больше шансов получить желаемую доходность от проекта.
Пример расчета
Для большей наглядности и лучшего понимания понятия «коэффициент дисконтирования», стоит привести пример расчета показателя по формуле.
Предположим, некий инвестор планирует получить от каких-либо вложений сумму в 100000 долларов через 5 лет. Чему равнозначна эта сумма в пересчете на сегодня?
Чтобы произвести дисконтирование, необходимо осуществлять расчет по формуле Kd=1/ (1+i)n. Если взять за ставку дисконтирование 10%, можно получить следующее значение: Kd=1(1+10%)5=0,6209. Это значит, что один доллар из предполагаемой суммы через пять лет, приведенный на текущую дату, равен 62,09 центам.
Следовательно, 100000 долларов через пять лет – это 62090 долларов сегодня при ставке 10%. Иными словами, 62090 долларов – дисконтированная стоимость суммы в 100000 долларов.
Таблица
Исходя из формулы расчета коэффициента, можно сделать вывод о зависимости его значения от количества периодов и ставки дисконтирования. Чтобы сэкономить время и не производить расчеты дисконта каждый раз, принято пользоваться так называемой таблицей коэффициентов дисконтирования.
Таблица приводит данные с точностью до десятитысячных.
Пользоваться ею достаточно просто – стоит лишь знать исходную ставку дисконтирования и предполагаемый период для расчета. Нужное значение дисконта можно найти на пересечении столбцов этих значений.
Принцип использования таблицы легко усвоить на примере. Предположим, у инвестора появляется необходимость выбора:
- Получить 12000 евро сегодня.
- Получить 15000 евро через 3 года.
Сделать правильный выбор поможет расчет дисконта по таблице. Для этого, необходимо выяснить, чему равна сумма в 15000 евро к получению через 3 года, приведенная на текущую дату. Чтобы произвести вычисления, придется выяснить средний процент по банковским валютным депозитам, оформленным на 3 летний срок.
Для этого, необходимо выяснить, чему равна сумма в 15000 евро к получению через 3 года, приведенная на текущую дату. Чтобы произвести вычисления, придется выяснить средний процент по банковским валютным депозитам, оформленным на 3 летний срок.
Если предположить, что ставка по депозиту равна 10%, можно определить коэффициент дисконтирования:
| Период/ставка | 9% | 10% |
| 3 | 0,7722 | 0,7513 |
| 4 | 0,7084 | 0,6830 |
Итак, на пересечении столбцов «3» и «10%» находится показатель, равный 0,7513. Он означает, что 1 евро спустя 3 года равен 75,13 евроцентам сегодня при депозитной ставке в 10%. Далее следует составить элементарную пропорцию:
| Сегодня | Через 3 года |
| 0,7513 евро | 1 евро |
| Х | 15000 евро |
Х=0,7513*15000/1=11269,5 евро. Эта сумма является дисконтированной стоимостью суммы 15000 евро к получению через 3 года. То есть, 15000 евро, приведенные на текущую дату, дешевле суммы в 12000 евро, взятых сегодня. Соответственно, инвестору из задачи стоит воспользоваться первым предложением.
Эта сумма является дисконтированной стоимостью суммы 15000 евро к получению через 3 года. То есть, 15000 евро, приведенные на текущую дату, дешевле суммы в 12000 евро, взятых сегодня. Соответственно, инвестору из задачи стоит воспользоваться первым предложением.
По аналогии с таблицей дисконта, можно пользоваться таблицей наращения. Она действует прямо противоположно – показывает номинальную стоимость текущих доходов в будущем периоде.
Преимущества и недостатки дисконта
Польза определения коэффициента дисконтирования очевидна: показатель переводит стоимость будущих денежных потоков в настоящий момент и помогает оценить степень рисков.
При этом коэффициент обладает и некоторыми минусами:
- сложность в прогнозировании относительно инвестиционных проектов;
- невозможность учета внешних факторов, таких, как неблагоприятные погодные условия.
Несмотря на выявленные недостатки, коэффициент дисконтирования является незаменимым способом для оценки привлекательности бизнес-идеи.
Фактор дисконтирования — Энциклопедия по экономике
На фактор дисконтирования (г) оказывают влияние следующие факторы [c.95]Этот недостаток снимается методами оценки эффективности, основанными на использовании фактора дисконтирования. [c.98]
Объекты из ядра инерционности могут иметь различные параметры (например, приведенные затраты с учетом фактора дисконтирования или потребность в ресурсах) по исходному и вторичному оптимальным планам. Выше параметры таких объектов определялись по исходному перспективному плану. [c.50]
Значения коэффициентов (факторов) дисконтирования [c.137]
Для облегчения расчетов при начислении сложного процента и при дисконтировании существуют таблицы, в которых для каждого года и для каждой процентной ставки заранее вычислены величины (1 + г)» и (1 + г)-«. Эти величины называются соответственно фактор сложного процента (множитель наращения) и фактор дисконтирования (дисконтный множитель)1.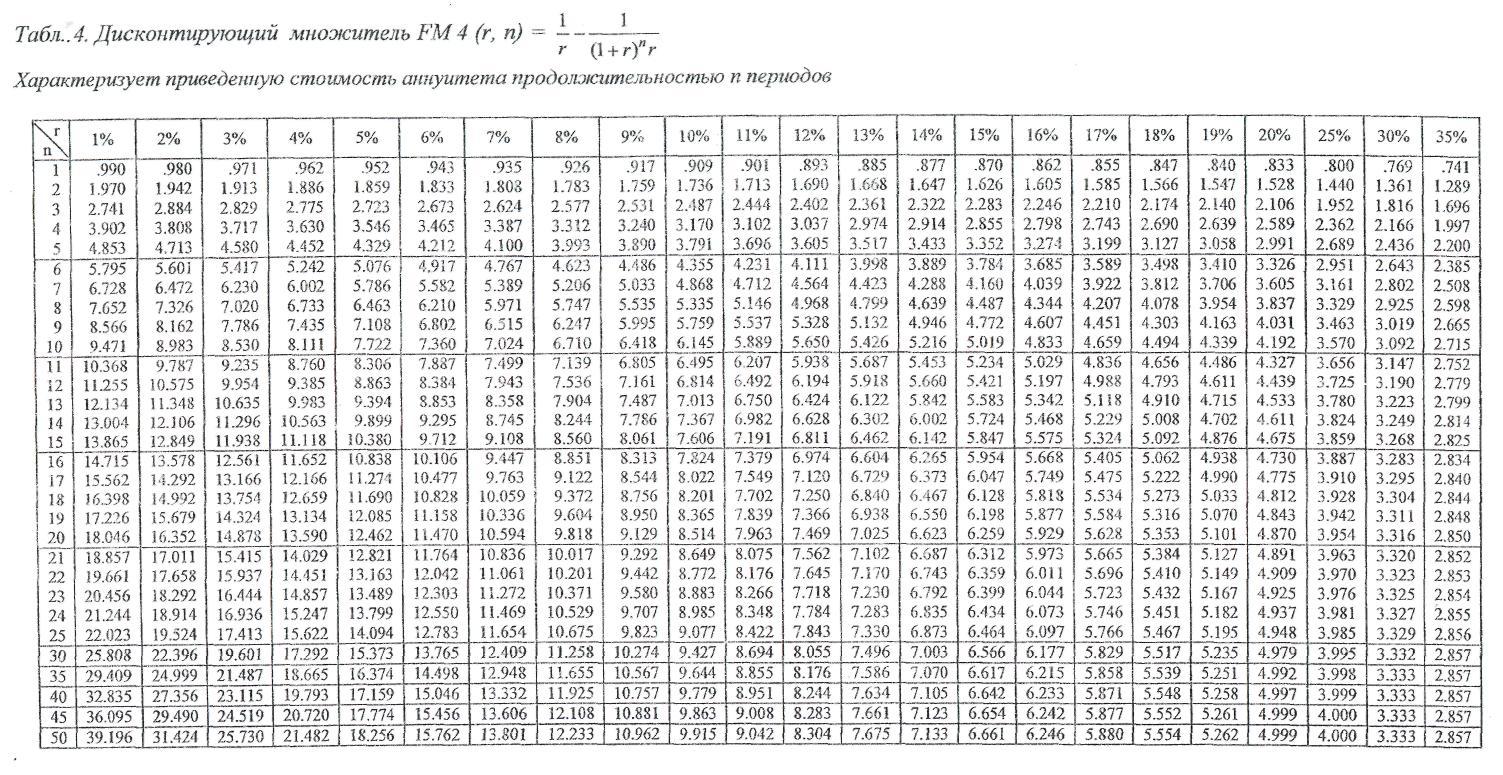 [c.364]
[c.364]
Это величина фактора дисконтирования сразу за 21 год (с 10-го по 30-й), при ставке дисконта 10% (называется текущей стоимостью фактора аннуитета или коэффициентом приведения годовой ренты, берется из специальных таблиц). [c.366]
Год Доход/убыток Фактор дисконтирования Дисконтированный доход/убыток [c.270]
Для каждого интервала планирования (год, квартал) определяются так называемые факторы дисконтирования [c.192]
DFj — фактор дисконтирования для /-го интервала планирования [c.192]
DFn — фактор дисконтирования для последнего интервала планирования. [c.192]
DFm — фактор дисконтирования при сохраненном риске для /-го интервала планирования [c.213]
Номер интервала планирования Чистый поток денежных средств (N F), млн долл. США Фактор дисконтирования, ) Расчет вклада в чистую текущую стоимость от каждого интервала (N F DF), млн долл.США [c.217]
Как уже говорилось, фактор дисконтирования измеряет, сколько стоит 1 доллар в какой-либо будущий период в сравнении с его стоимостью в настоящем. Как правило, О альтернативные издержки времени в один период времени инвестор может использовать 1 доллар, для того чтобы получить (1 + г) долларов в следующем периоде, где г— ставка процента за период. В этом случае мы определяем 5 как
[c.134]
Как правило, О альтернативные издержки времени в один период времени инвестор может использовать 1 доллар, для того чтобы получить (1 + г) долларов в следующем периоде, где г— ставка процента за период. В этом случае мы определяем 5 как
[c.134]
Эффектом, обратным исчезновению отрасли, является рост последней. Допустим, что темпы роста спроса составляют g. Это означает, что при неизменности других факторов в период / + 1 прибыль выше, чем в период /, с коэффициентом 1 + g. Формально это можно представить, предположив постоянство функции прибыли, но с таким фактором дисконтирования, при котором вследствие роста рынка стоимость 1 доллара в следующем периоде превысит стоимость 1 доллара в текущем периоде с коэффициентом 1 + g. Норма дисконтирования в таком случае составит [c.135]
Второе объяснение следует из приведенного выше анализа. Фактор дисконтирования, используемый для определения условий равновесия, включает наряду с временным параметром вероятность выживания. Рассмотрим отрасль с большой сменяемостью фирм, т. е. с высокими.нормами входа и выхода. В этом контексте вероятность того, что какая-то фирма уйдет с рынка в каком-то из периодов, высока и соответственно ее коэффициент дисконтирования невелик. Это в свою очередь означает, что только при нереалистично низкой процентной ставке возникает равновесная ситуация для фирм, устанавливающих монопольные цены. Другими словами, если фирма высоко оценивает вероятность своего ухода с рынка, у нее появляется серьезный стимул уклониться от сговора, поскольку, принимая в расчет его ожидаемые прибыли, она мало что потеряет, если ввяжется в нечестную игру.
[c.136]
е. с высокими.нормами входа и выхода. В этом контексте вероятность того, что какая-то фирма уйдет с рынка в каком-то из периодов, высока и соответственно ее коэффициент дисконтирования невелик. Это в свою очередь означает, что только при нереалистично низкой процентной ставке возникает равновесная ситуация для фирм, устанавливающих монопольные цены. Другими словами, если фирма высоко оценивает вероятность своего ухода с рынка, у нее появляется серьезный стимул уклониться от сговора, поскольку, принимая в расчет его ожидаемые прибыли, она мало что потеряет, если ввяжется в нечестную игру.
[c.136]
Простая модель, которая могла бы объяснить такое поведение, должна иметь в основе какую-либо форму асимметрии фирм. К примеру, допустим, что фактор дисконтирования каждой фирмы начинается с величины 8. Однако с некоторой долей вероятности коэффициент дисконтирования фирмы может опуститься до величины, скажем, 8. Меньшая величина 8 означает, что будущие периоды менее важны для фирмы. Как мы видели в первом параграфе главы, один из элементов, образующих коэффициент дисконтирования фирмы, — это вероятность существования ее в будущем. Фирма, которая находится в затруднительном положении (финансовом или ином), имеет более низкий коэффициент дисконтирования, чем стабильно работающая фирма. Для первой возможность ухода с рынка намного вероятнее.
[c.141]
Фирма, которая находится в затруднительном положении (финансовом или ином), имеет более низкий коэффициент дисконтирования, чем стабильно работающая фирма. Для первой возможность ухода с рынка намного вероятнее.
[c.141]
Теперь рассмотрим случай, когда фирмы конкурируют уже на двух идентичных рынках, каждый из которых имеет те же особенности, что и рынок в предыдущем абзаце. Какова в таком случае наиболее низкая величина фактора дисконтирования, при которой сговор остается устойчивым Теперь действия в обход договоренностей обойдутся дороже это ценовая война на обоих рынках. Но и сами действия стали более выгодными повысится прибыль на обоих рынках. По сути, новое условие устойчивости сговора выражается в [c.144]
Почему это важно Для того чтобы прояснить данную проблему, допустим, что во всех отраслях в выборке наблюдаются одинаковые функции спроса и издержек, отличающиеся только одним аспектом по каким-то экзогенным причинам уровень сговоров в одних отраслях выше, чем в других. Это может быть, к примеру, связано с различными значениями фактора дисконтирования. Кроме того, допустим, что, для того чтобы фирма могла проникнуть на рынок, она должно понести соответствующие издержки F.
[c.161]
Это может быть, к примеру, связано с различными значениями фактора дисконтирования. Кроме того, допустим, что, для того чтобы фирма могла проникнуть на рынок, она должно понести соответствующие издержки F.
[c.161]
Например, на некоторых рынках цены устанавливаются раз в день, на других — раз в неделю. Как следует из параграфа 8.1, этот и другие аспекты определяют различные значения фактора дисконтирования. [c.161]
Оба отличия (частота взаимодействия и реклама как объект инвестиций) соответствуют, если пользоваться терминологией из главы 8, более низкой величине фактора дисконтирования. Другими словами, при прочих равных условиях следует ожидать, что договоренность поддерживать расходы на рекламу на низком уровне соблюсти сложнее, нежели договоренность о сохранении высоких цен. [c.233]
Факторы дисконтирования (приведения) стоимости [c.219]
Поскольку вычисления приведенной стоимости сумм, которые будут получены в отдаленном будущем, более сложны, чем для вложений на год, в этом случае рекомендуется использовать таблицы приведенной стоимости. (Полный набор этих таблиц включен в приложение Б, табл. Б.З в качестве иллюстрации в табл. 5.8 в тексте приведена их часть.) Факторы дисконтирования в таких таблицах представляют собой приведенную стоимость 1 долл., рассчитанную для различных комбинаций периодов и ставок дисконтирования. Например, приведенная стоимость 1 долл., который предполагается получить через год и дисконтированный по ставке 8%, составляет 0,926 долл. На основе этого фактора (0,926) приведенная стоимость 1000 долл., которую предполагается получить через год при ставке 8% дисконта, может быть найдена умножением этого фактора на 1000 долл. Результирующая приведенная стоимость в 926 долл. (0,926 х 1000) соответствует (за ис-
[c.219]
(Полный набор этих таблиц включен в приложение Б, табл. Б.З в качестве иллюстрации в табл. 5.8 в тексте приведена их часть.) Факторы дисконтирования в таких таблицах представляют собой приведенную стоимость 1 долл., рассчитанную для различных комбинаций периодов и ставок дисконтирования. Например, приведенная стоимость 1 долл., который предполагается получить через год и дисконтированный по ставке 8%, составляет 0,926 долл. На основе этого фактора (0,926) приведенная стоимость 1000 долл., которую предполагается получить через год при ставке 8% дисконта, может быть найдена умножением этого фактора на 1000 долл. Результирующая приведенная стоимость в 926 долл. (0,926 х 1000) соответствует (за ис-
[c.219]
Число 0,665 представляет собой фактор дисконтирования или приведения стоимости для 7 периодов и ставки дисконта в 6%. [c.220]
Каждый инвестор должен знать некоторые моменты, связанные с таблицами приведенной стоимости. Во-первых, фактор дисконтирования однократной суммы всегда меньше 1 и только если ставка дисконтирования равна нулю, этот фактор равняется 1. Во-вторых, чем выше ставка дисконтирования для данного года, тем меньше фактор дисконтирования. Другими словами, чем выше альтернативные издержки, тем меньше нужно инвестировать сегодня, чтобы получить данную сумму в будущем. Наконец, чем позднее инвестор собирается получить сумму в будущем, тем меньше она стоит сегодня. Важно также отметить, что при ставке дисконтирования 0% фактор дисконтирования всегда равен 1 и, следовательно, в таком случае будущая стоимость некоторой суммы денег равняется ее приведенной стоимости. [c.220]
Год (1) Доход (в долл.) (2) 9%-й фактор дисконтирования (3) (1) х (2) Приведенная стоимость (в долл.) [c.221]
Приведенная стоимость аннуитета может быть найдена тем же способом, что и приведенная стоимость смешанного потока, но есть и более простой способ. Существуют финансовые таблицы факторов дисконтирования для аннуитетов. (Полный набор таких факторов дисконтирования приведенной стоимости для аннуитетов включен в приложение Б, табл. Б.4 часть ее в качестве примера приведена в табл. 5.11.) Факторы в таких таблицах представляют собой приведенную стоимость аннуитета, равного 1 долл., связанную с различными комбинациями лет и ставок дисконтирования. Например, приведенная стоимость 1 долл., который будет притекать каждый год в течение последующих пяти лет, дисконтированного по ставке 9%, составит [c.221]
ТАБЛИЦА 5.11 Факторы дисконтирования [c.222]
Доходность инвестиций с однократным поступлением денежных средств в будущем можно оценить, используя факторы наращения либо факторы дисконтирования. Мы будем рассчитывать ее на основе факторов дисконтирования, данных в приложении Б, табл. Б.З. Для иллюстрации вычисления полной доходности (IRR) предположим, что инвестор хочет определить доходность инвестиций в 1000 долл., которые, как ожидается, будут стоить 1400 долл. в конце пятилетнего периода владения. Мы можем найти доходность этих инвестиций, решая уравнение, в котором 1400 долл. через 5 лет равны первоначальным инвестициям в 1000 долл., а ставка дисконтирования неизвестна. На первом этапе необходимо разделить приведенную стоимость (1000 долл.) на будущую стоимость (1400 долл.), что дает величину 0,714 (1000 1400). На втором этапе нужно найти в таблице приведенной стоимости фактор дисконтирования для пяти лет, наиболее близкий по ве- [c.227]
Используя полученные значения факторов дисконтирования, можно определить чистую текущую (приведенную) стоимость (NPV, net present value) проекта по следующей формуле [c.192]
DFst — фактор дисконтирования при страховании для 1-го интервала планирования [c.215]
Вторым аспектом, имеющим отношение к рыночной структуре, является симметричность фирм. Как правило, похожим фирмам сохранить сговор проще, чем асимметричным . Чтобы понять почему, рассмотрим дуополистическую ситуацию с ценообразованием, где одна фирма имеет преимущество в издержках. Например, постоянные предельные издержки Фирмы 1 равны с, а постоянные предельные издержки Фирмы 2 — с, последние выше, чем с, но ниже, чем монопольная цена фирмы с низкими издержками. Для Фирмы 1 эффективным будет такой сговор, который позволит ей установить монопольную цену, а для Фирмы 2 — который позволит ей установить более высокую цену и сбыть ноль продукции. Действительно, именно такая цена и такое распределение долей рынка максимизируют величину совокупной прибыли. Тем не менее, такой сговор явно не стабилен, поскольку у Фирмы 2 возникает стимул сбить цену Фирмы ] и извлечь в краткосрочном периоде определенную положительную прибыль. Отметьте справедливость этого аргумента, независимо от величины фактора дисконтирования, поскольку при эффективном решении ситуации Фирма 2 получает нулевую прибыль. Отсюда следует, что никакие штрафные меры не могут удержать Фирму 2 от обходных маневров, поскольку ей нечего терять. [c.142]
Полтева Т.В. Сравнительная характеристика динамических показателей эффективности инвестиционных проектов
Полтева Татьяна Владимировна
Тольяттинский государственный университет
старший преподаватель кафедры «Финансы и кредит»
Polteva Tatiana Vladimirovna
Togliatti State University
assistant professor of the chair «Finance and Credit»
Библиографическая ссылка на статью:
Полтева Т.В. Сравнительная характеристика динамических показателей эффективности инвестиционных проектов // Современные научные исследования и инновации. 2016. № 12 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2016/12/76252 (дата обращения: 13.07.2021).
В системе управления реальными инвестициями предприятия одним из самых ответственных и важных этапов выступает оценка эффективности инвестиционных проектов. От правильности и объективности этой оценки зависят и сроки возврата инвестированного капитала, и способы альтернативного использования капитала, и дополнительно генерируемый денежный поток в предстоящем периоде.
Методы оценки эффективности инвестиционных проектов подразделяются на два типа: простые, или статические, методы и динамические методы, основанные на дисконтировании.
Статические методы не учитывают стоимость денег во времени. Их применяют для оценки эффективности небольших краткосрочных реальных инвестиционных проектов.
Динамические методы стандартизированы на международном уровне и применяются широко с использованием компьютерных технологий. Динамические методы более надежные, они основаны на концепции стоимости денег во времени и сегодня являются преобладающими. Динамические методы основаны на дисконтировании будущих денежных потоков по формуле сложного процента с использованием определенной ставки, которая носит название ставка дисконтирования.
Ставкой дисконтирования называют обычно ежегодную ставку, которая отражает уровень доходности, которую хотел бы получить инвестор от использования вложенного капитала, с учетом уровня риска, присущего проекту. Иначе говоря, это норма доходности проводимой операции, которая компенсирует инвестору временный отказ от альтернативного использования средств, а также риски, связанные с неопределенностью конечного результата. Прежде чем рассчитывать эффективность инвестиционного проекта, инвестору необходимо определить ставку дисконтирования, необходимую для проведения расчетов, то есть ту норму доходности, которую инвестор ожидает от проекта. Это наиважнейший фактор, влияющий на результаты расчета эффективности проекта. Поэтому необходимо понимать, что же следует заложить в ставку дисконтирования для того или иного проекта, от чего она зависит.
В зависимости от различных экономических задач ставка дисконтирования рассчитывается по-разному. Существует несколько методов определения ставки дисконтирования, в большинстве методов ставка дисконтирования включает в себя безрисковую ставку и премию за риск проекта. Чем выше риск проекта, тем выше должна быть ставка дисконтирования.
Итак, к динамическим методам экономической оценки инвестиций относят:
— расчет чистого дисконтированного дохода – NPV;
— расчет индекса доходности – PI;
— расчет внутренней нормы доходности – IRR;
— расчет дисконтированного периода окупаемости – DPP.
Это четыре основных показателя, которые рассчитываются для оценки эффективности инвестиционного проекта. Рассмотрим каждый из показателей более подробно, изучим методику их расчета и способы интерпретации.
Первый показатель – это чистый дисконтированный доход, по-другому его называют чистый приведённый доход, общепринятое обозначение – NPV (Net Present Value). Это один из наиболее популярных и распространенных показателей эффективности инвестиционного проекта.
Чистый дисконтированный доход – это сумма всех положительных и отрицательных дисконтированных денежных потоков проекта. Другими словами, это сумма всех дисконтированных чистых денежных потоков, то есть доходов, за вычетом суммы дисконтированных инвестиций.
Для того чтобы определить чистый дисконтированный доход, необходимо выполнить ряд действий:
— Первое действие – определить сумму инвестиционных вложений в проект. Если инвестиции не единоразовые, то следует продисконтировать инвестиции за каждый период и найти сумму дисконтированных инвестиций.
— Второе действие – произвести расчет текущей стоимости денежных поступлений от проекта. Для этого доходы за каждый период приводятся к текущему моменту времени, то есть дисконтируются (находится PV).
— Третье действие – вычесть из текущей стоимости доходов дисконтированные инвестиционные затраты по проекту. Разница между ними и будет величиной чистого дисконтированного дохода.
Формула для расчета данного показателя представлена ниже.
(1)
где I – инвестиции за i-й период,
P – доход за i-й период,
N – число периодов,
r – ставка дисконтирования.
Для того чтобы проект оказался эффективным, то есть принес как минимум доходность, заложенную в ставке дисконтирования, необходимо, чтобы сумма дисконтированных под эту ставку доходов превысила сумму дисконтированных инвестиций. Поэтому проект будет эффективен, если чистый дисконтированный доход окажется больше нуля. В этом случае проект принесет как минимум ожидаемую доходность, заложенную в ставке дисконтирования. Если чистый дисконтированный доход окажется меньше нуля, то проект необходимо отклонить. Это не означает, что он не принесет никакой доходности. Вполне возможно, проект принесет определенную доходность. Однако она окажется ниже, чем та, которую мы ожидаем и заложили в ставке дисконтирования. И наконец, если чистый дисконтированный доход окажется равным нулю, это будет означать, что реальная доходность проекта, или внутренняя норма доходности, равна той доходности, что мы заложили в ставку дисконтирования. И нам безразлично, принимать проект или нет. Окончательное решение будет зависеть от того, что именно было заложено в ставку дисконтирования.
Расчет чистого дисконтированного дохода инвестиционного проекта – это один из самых простых этапов в оценке проекта. Намного сложнее определить ожидаемые потоки денежных средств от проекта.
Когда мы проводим сравнительную оценку инвестиционных проектов, важно обратить внимание на особенности показателя чистого дисконтированного дохода. Выделим четыре особенности.
1. Чем больший размер инвестиционных затрат в проект и, соответственно, поступлений от проекта, тем большей будет величина NPV при прочих равных условиях, так как показатель чистого дисконтированного дохода является абсолютным.
2. Величина NPV зависит от распределения инвестиционных затрат во времени. Так, если инвестиционные затраты осуществляются только вначале, показатель чистого дисконтированного дохода будет минимальным. Если же инвестиционные затраты распределены во времени, например, предприятие приобрело оборудование в беспроцентную рассрочку, то тогда показатель NPV будет больше. Это связано с тем, что сумма дисконтированных инвестиций будет меньше, а следовательно, показатель чистого дисконтированного дохода – больше.
3. На величину NPV влияет время начала эксплуатационной фазы, когда по проекту начинает поступать приток денежных средств. Так, чем дольше времени проходит от осуществления инвестиционных затрат до начала поступлений по проекту, тем меньшей будет величина чистого дисконтированного дохода при прочих равных условиях. И наоборот. Это связано с тем, что величина инвестиционных затрат за короткий промежуток времени изменится незначительно, так как будет приводиться к сегодняшнему времени под меньшую степень. В то время как величина дохода, поступившего от проекта через несколько лет, будет дисконтироваться уже под большую степень и уменьшится значительно.
4. Значение показателя NPV напрямую зависит от ставки дисконтирования. Очевидно, что чем больше ставка дисконтирования, тем большую доходность от проекта мы ожидаем и тем меньшим будет показатель чистого дисконтированного дохода. Важно при выборе инвестиционного проекта не только сравнивать значения NPV, важен и характер изменения NPV при различных значениях ставки дисконтирования.
Показатель чистого дисконтированного дохода является ключевым в оценке инвестиционной привлекательности проекта в сравнении с его аналогами.
Предположим, мы произвели расчет по двум независимым ординарным инвестиционным проектам, то есть состоящим из исходной инвестиции и последующих притоков денежных средств. Получили следующие значения чистого дисконтированного дохода: у первого проекта NPV оказался равным 1 000 денежных единиц, у второго проекта – 100 денежным единицам.
Как определить, какой из проектов более эффективен? Тот, у кого значение чистого дисконтированного дохода выше? Да, если величина исходных инвестиций была одинаковой для обоих проектов. Сравнительная оценка альтернативных инвестиционных проектов по показателю NPV может дать объективный результат только при их сопоставимых исходных параметрах.
Если представить, что инвестиции в первый проект, NPV которого 1000, составили 1 000 000 денежных единиц, при этом инвестиции во второй проект, NPV которого 100 , составили 500 денежных единиц, тогда становится очевидно, что второй проект в данном случае более рентабелен, так как если рассматривать доход на единицу затрат, то у второго проекта он окажется гораздо выше.
Таким образом, при сравнении эффективности нескольких проектов с различной величиной инвестиционных затрат расчет показателя чистого дисконтированного дохода оказывается недостаточным. Это связано с тем, что NPV является абсолютной величиной.
Для сравнения эффективности проектов с различной величиной инвестиций дополнительно рассчитывают индекс доходности, который является относительной величиной. Рассмотрим данный показатель более подробно.
Итак, индекс доходности, или индекс рентабельности – PI (Profitability Index) – это показатель, который рассчитывается как отношение суммы дисконтированных положительных денежных потоков к сумме дисконтированных инвестиций.
Формула для расчета индекса доходности представлена ниже.
(2)
PI характеризует величину доходов на каждый вложенный рубль с учетом выбранной ставки дисконтирования. То есть характеризует доход проекта на единицу затрат сверх выбранной ставки дисконтирования.
Очевидно, что для того, чтобы проект оказался эффективным, числитель должен превышать знаменатель, а значит, показатель PI должен быть больше единицы. Тогда проект принесет тот минимум, который заложен в ставке дисконтирования. Если PI окажется меньше единицы, то проект следует отклонить, так как он не принесет ожидаемой нормы доходности. Если данный показатель будет равен единице, то внутренняя норма доходности проекта, то есть его настоящая доходность, равна той ставке, под которую мы дисконтировали денежные потоки.
Следует обратить внимание, что показатели чистого дисконтированного дохода и индекса доходности взаимосвязаны. Так, если NPV больше нуля, то PI в любом случае будет больше единицы, так как и в том и в другом случае сумма дисконтированных доходов будет превышать сумму дисконтированных инвестиций. Если чистый дисконтированный доход меньше нуля, то индекс доходности меньше единицы. Если NPV равен нулю, значит сумма дисконтированных доходов равна сумме дисконтированных инвестиций, а значит и PI будет равен единице. Если данная закономерность не соблюдается, значит нужно искать ошибки в расчетах.
Анализируя показатель «индекс доходности», необходимо иметь в виду, что в его основе лежат те же особенности и исходные предпосылки, что и в основе показателя чистого дисконтированного дохода. А значит, на его величину влияют также такие факторы, как распределение инвестиционных затрат во времени, время начала эксплуатационной фазы, величина ставки дисконтирования.
Однако у индекса рентабельности есть одно преимущество, связанное с тем, что он является величиной относительной. А значит, на его размер не оказывает влияния масштаб инвестиционного проекта. Он показывает именно отношение суммы дисконтированных доходов к сумме дисконтированных инвестиций, то есть характеризует доход на единицу затрат. Это преимущество показателя позволяет использовать PI для сравнения эффективности инвестиционных проектов, объем инвестиционных затрат которых различен. Показатель индекса рентабельности очень важен, и именно он используется для формирования портфеля реальных инвестиций в условиях ограниченности инвестиционных ресурсов, когда инвестиционные проекты делимы.
Далее рассмотрим третий показатель – внутреннюю норму доходности, или внутреннюю ставку доходности – IRR (Internal Rate of Return).
По сути, это та доходность, которую приносит проект. Поэтому IRR – это ставка дисконтирования, при которой сумма приведённых доходов равна сумме приведённых инвестиций. То есть это ставка дисконтирования, при которой чистый дисконтированный доход NPV равен нулю, а индекс доходности PI равен единице.
Прямой математической формулы, которая позволяла бы определить показатель IRR, не существует. Для расчёта IRR формулу для расчета чистого дисконтированного дохода приравнивают к нулю, при этом IRR закладывают в качестве ставки дисконтирования. Внутреннюю норму доходности можно найти, только решив данное уравнение. Несложно предположить, что решение подобного рода уравнения может быть крайне затруднительно. Поэтому для расчета данного показателя используют следующие основные способы:
1. Первый способ – это применение специализированных программ и калькуляторов. Так, для расчета внутренней нормы доходности часто используют программу Microsoft Excel. Следует выбрать «функции» – «финансовые» – «ВСД», затем выделить подряд идущие ячейки, которые характеризуют денежные потоки за последовательные равные интервалы времени, и указать предполагаемую величину IRR. И программа рассчитает внутреннюю норму доходности проекта. Значение функции вычисляется программой путем итераций и может показывать или нулевое значение, или несколько значений. Так, при нестандартных денежных потоках, то есть в неординарных проектах, есть возможность получить не одно, а несколько значений внутренней нормы доходности. По сути, внутренняя норма доходности может для проекта и не найтись. Применение Excel сводит сложность процесса расчета показателя IRR к минимуму.
2. Второй способ – метод последовательных итераций, то есть последовательных расчетных действий (рисунок 1).
Рисунок 1 – Нахождение IRR методом последовательных итераций
По сути, это расчет методом подбора. Первая итерация предполагает установление приблизительной IRR, которая может привести к тому, что сумма дисконтированных под эту ставку доходов сравняется с суммой дисконтированных под эту ставку инвестиций. Если по результатам первой итерации окажется, что NPV больше нуля, значит была выбрана слишком маленькая величина IRR и на самом деле она выше. Значит, последующие итерации предполагают использование более высоких значений ставки дисконтирования, пока не будет достигнуто предусмотренное уравнениями равенство. Если же по результатам первой итерации NPV оказался отрицательным, значит была выбрана слишком высокая ставка дисконтирования и показатель IRR на самом деле меньше. Следовательно, последующие итерации предполагают использование более низких значений данного показателя до тех пор, пока не будет выполняться равенство. Конечным результатом всех итераций является нахождение такой ставки дисконтирования, при которой сумма приведённых инвестиций будет равна сумме приведённых затрат. То есть ставка дисконтирования и будет являться искомой IRR.
3. Третий способ – это метод линейной интерполяции. Суть метода линейной интерполяции заключается в следующем. Выбираются две ставки дисконтирования – r1 и r2 –таким образом, чтобы при ставке дисконтирования r1 NPV был положительным, а при r2 – уже отрицательным. Очевидно, что r1 должен быть меньше, чем r2. Затем значения r1 и r2 подставляются в формулу, представленную ниже.
(3)
Точность вычислений обратно пропорциональна длине интервала от ставки r1 до ставки r2. А наилучшая аппроксимация с использованием табулированных значений достигается в том случае, когда длина интервала минимальна, равна примерно 1 %. То есть r1 и r2 должны быть ближайшими друг к другу значениями коэффициента дисконтирования, однако должно соблюдаться изначальное условие. А именно: при ставке дисконтирования r1 NPV должен быть положительным, а при r2 – отрицательным.
IRR определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника. Для определения целесообразности реализации инвестиционного проекта нужно сопоставить IRR с принятой на данном предприятии минимальной нормой прибыли на инвестиции, то есть выбранной ставкой дисконтирования: если IRR больше ожидаемой нормы доходности, то есть ставки дисконтирования, то проект эффективен; если IRR меньше ожидаемой нормы доходности, то есть ставки дисконтирования, то проект неэффективен. Поэтому если показатель NPV положительный, а PI больше единицы, значит IRR проекта больше, чем ставка дисконтирования. Если показатель NPV отрицательный, а PI меньше единицы, значит IRR проекта либо меньше, чем ставка дисконтирования, либо вовсе отсутствует. Если показатель NPV равен нулю, а PI равен единице, значит IRR проекта равна той ставке, что заложена в качестве ставки дисконтирования.
Показатель IRR позволяет сравнивать эффективность вложения в различные по протяженности инвестиционные проекты, в отличие от показателя NPV. Показатель внутренней нормы доходности применяется для сравнительной оценки не только в рамках рассматриваемых проектов, но также и в более широком аспекте. Например, показатель IRR можно использовать в сравнении с коэффициентом рентабельности операционных активов; коэффициентом рентабельности собственного капитала; доходностью по альтернативным видам инвестирования. На предприятии иногда устанавливается целевой норматив показателя IRR, то есть его минимальное значение. Поэтому инвестиционные проекты с более низким значением внутренней нормы доходности автоматически отклоняются как неэффективные.
И четвертый показатель, который рассмотрим, – это дисконтированный период окупаемости – DPP (Discounted Pay-Back Period).
Дисконтированный период окупаемости – это период окупаемости, рассчитанный на основе дисконтированных денежных потоков. Показатель DPP может быть использован больше в качестве вспомогательного показателя при оценке эффективности реальных инвестиционных проектов. Также данный показатель может быть использован в качестве одного из вспомогательных критериальных показателей при формировании инвестиционного портфеля предприятия. В данном случае те проекты, которые будут иметь более высокий DPP при равенстве других показателей, будут отвергаться.
Итак, все рассмотренные показатели для оценки эффективности инвестиционных проектов, а именно – NPV, PI, IRR, DPP – находятся в тесной взаимосвязи между собой. Каждый из показателей позволяет раскрыть какую-либо из сторон инвестиционного проекта. Ввиду этого все эти показатели при оценке эффективности реальных инвестиционных проектов необходимо рассматривать совместно, в комплексе. Если предприятию необходимо выбрать из альтернативных реальных инвестиционных проектов, то ему целесообразно провести соответствующие расчеты по каждому из проектов и занести данные в сравнительную таблицу. Пример сравнительной таблицы представлен ниже (таблица 1).
Таблица 1 – Пример сравнительной таблицы показателей эффективности
Для того чтобы объективно оценить данные по этой таблице, необходимо показатели эффективности по каждому проекту представить в сопоставимых единицах измерения. Ранговая значимость показателей оценки эффективности инвестиционных проектов формируется на регрессионной основе, то есть наименьший ранг – единица – присваивается проекту с наилучшим значением рассматриваемого показателя эффективности. После того как таблица будет заполнена, необходимо оценить и выбрать наиболее подходящий инвестиционный проект.
Сравнительная оценка производится следующим образом:
— во-первых, на основе суммарной ранговой значимости всех показателей: тот проект, у которого сумма рангов оказалась наименьшей, считается лучшим;
— во-вторых, на основе отдельных из рассчитанных показателей, но в том случае, если для предприятия именно эти показатели являются приоритетными.
Количество просмотров публикации: Please wait
Все статьи автора «Полтева Татьяна Владимировна»
Коэффициент дисконтирования — Энциклопедия по машиностроению XXL
Величина D = 1/(1 + Е) называется коэффициентом дисконтирования. [c.450]| Таблица 10.23. Значения сумм коэффициентов дисконтирования |
Внутренняя норма доходности (ВИД) Е равняется коэффициенту дисконтирования, при котором ЧДД равен нулю (на рис. 10.4 ВНД равна 9,4 %). Если значение ВНД данного проекта превышает ставку дисконтирования, значит, инвестор, вложивший в него деньги, получит больший процент, чем в банке. [c.453]
Результаты сравнения вариантов представлены в табл. 10.25. Расчет показателей проведен по формулам для частного случая. Значения сумм коэффициента дисконтирования определены по табл. 10.23. Так, для Тр= 20 лет и Е = ]0 % D = 8,514. [c.455]
При расчете динамических показателей оценки эффективности в прогнозных ценах следует иметь в виду, что коэффициент дисконтирования должен в обязательном порядке учитывать инфляцию (т.е. используется f,,). Поэтому рассмотренные выше показатели чистого дисконтированного дохода и срока окупаемости с приведением затрат к началу периода практически не зависят от того, учитывалась инфляция или нет. [c.459]
Для того, чтобы различать значение д распределения дальновидностей 5от степени коэффициента дисконтирования (д) , в последнем случае будем использовать скобки. [c.1204]
Очевидно, что чем выше значение коэффициента дисконтирования (чем ближе он к единице), тем с большим весом учитываются будущие периоды — в пределе (при 5 = 1) все периоды учитываются одинаково, и наоборот — при стремлении 5 к нулю степень учета будущего уменьшается (у недальновидного игрока коэффициент дисконтирования равен нулю). [c.1204]
Завершив описание результатов, приведенных в [80], отметим, что при решении многих экономических задач полагают, что распределение дальновидности имеет специфический вид 5 (т) = 5 т, где 5 является некоторой константой (так называемым коэффициентом дисконтирования — см. также выше). Оказывается, что в этом случае задача сводится к исходной с помощью замены (у1, ) = 5 Ф (у1, ). Действительно, в каждый момент [c.1204]
В заключение настоящего раздела отметим, что в рассматриваемой задаче считалось, что коэффициент дисконтирования равен единице, то есть будущий доход для центра для него также важен как и доход в настоящем. На практике коэффициент дисконтирования обычно меньше единицы. В этом случае граница для р (см. рисунок 7), начиная с которой оптимальными становятся бесконечно большие действия, сместится вправо. [c.1204]
Соотношение б означает дисконтирование , которое показывает, что любая будущая стоимость может быть дисконтирована до современной стоимости просто путем деления будущей стоимости на коэффициент сложных процентов г для периода в п лет. [c.394]
Пусть в первый момент времени имеется актив, обладающий стоимостью Жо. Тогда, если присутствует инфляция, например, Ь процентов в единицу времени, то стоимость актива в момент времени t > 1 составит1 W(t) = Ж0 (5) t-1, где 5 = 1-р. Если инфляция отсутствует и имеется возможность, например, приобрести ценные бумаги, приносящие доход Ь процентов в месяц2, то W(t) = W0 (5) t-1, где 5 = 1+р. Если рассмотреть обратную задачу — определить текущий эквивалент W0 актива W(t), полученного в периоде t, то получим, что W0 = 5 W(t) (5) -t. Содержательно, в экономике распределение дальновидностей, отражаемое дисконтирующим множителем (коэффициентом дисконтирования) 5 е (0 1], характеризует изменение предпочтений (в большинстве случаев — стоимости активов) во времени3 — чем больше отсрочка в получении некоторого блага, тем меньше его полезность. [c.1204]
FTh2 Если игроки слабо дисконтируют будущее (коэффициенты дисконтирования близки к единице), то для любого вектора выигрышей [c.1204]
Задача №1871 (чистая дисконтированная стоимость и внутренняя норма доходности)
Если чистая дисконтированная стоимость проекта отрицательна, то это означает, что:
- а) внутренняя норма доходности ниже ставки дисконтирования;
- б) внутренняя норма доходности выше ставки дисконтирования;
- в) внутренняя норма доходности равна ставке дисконтирования.
Объясните свой выбор.
Рекомендуемые задачи по дисциплине
Решение задачи:
Внутренняя норма доходности (IRR) – это коэффициент, показывающий максимально допустимый риск по инвестиционному проекту или минимальный приемлемый уровень доходности. Внутренняя норма доходности равна ставке дисконтирования, при которой чистый дисконтированный доход отсутствует, то есть равен нулю.
Данный показатель используется для оценки привлекательности инвестиционного проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r):
| Значение IRR | Вывод |
| IRR больше r | Инвестиционный проект имеет внутреннюю норму доходности выше чем затраты на собственный и заемный капитал. Данный проект следует принять для дальнейшего анализа (при этом чистая дисконтированная стоимость проекта положительная) |
| IRR меньше r | Инвестиционный проект имеет норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него (при этом чистая дисконтированная стоимость проекта отрицательная) |
| IRR=r | Внутренняя доходность проекта равна стоимости капитала, проект находится на минимально допустимом уровне и следует произвести корректировки движения денежных средств и увеличить денежные потоки (при этом чистая дисконтированная стоимость проекта равна нулю) |
Таким образом, если чистая дисконтированная стоимость проекта отрицательна, то это означает, что IRR меньше r, т.е. внутренняя норма доходности ниже ставки дисконтирования. Ответ – а.
Ставка дисконтирования для инвестиционного проекта
Инвестор и заказчик-инициатор инвестиционного проекта как роли всегда находятся в некотором противостоянии. Оно связано с разными целевыми установками исполняемых ролей. Инициатор заинтересован решать производственные задачи и обновлять основной капитал. В глазах инвестора для состоятельности проекта значение имеет результат финансового обоснования экономической эффективности. Начало такого обоснования задает нахождение ставки дисконтирования для инвестиционного проекта. От решения этой непростой задачи зависят успех проекта и достижение целей сторон.
Временная ценность денег для проектного обоснования
Количественное обоснование принимаемых управленческих решений в инвестиционной сфере основывается на двух базисных критериях: стоимости капитала и временной ценности денег. Временной аспект определяет одну из основных граней финансовой эффективности вложений. Дело в том, что любая хозяйственная операция, в том числе и инвестиционная, обладает свойствами динамичности, длительности, начала и конечности. Это не временная «точка» и не статичная категория. Нам для осмысления нужно принять несколько аксиом, чтобы свободнее войти в исследуемое понятийное пространство.
- Каждая операция подлежит рассмотрению с финансовой точки зрения, в общем и конкретно с позиции денежных потоков.
- Денежный поток всегда имеет знак направления движения: поступления (+) и выбытия (-).
- Природа денежных потоков состоит в их оборачиваемости и способности генерировать доход с течением времени.
- События денежного потока несопоставимы, если относятся к разным периодам времени. Для сопоставимости их надлежит преобразовать.
- Преобразование событий денежного потока связаны с процедурами наращения или дисконтирования.
Графическое представление денежных потоков инвестиционного проекта
Графическое представление типовых денежных потоков проекта удобно тем, что образно и наглядно показывает его инвестиционную и эксплуатационную фазы. Взгляните на представленную выше схему. Начальные инвестиционные вложения (Invested Capital, IC) характеризуются компактными во времени, иногда одноактными выбытиями денежных средств (оттоками средств со знаком «-»). Затем, после наступления эксплуатационной фазы, в каждый период формируется операционной Cash Flow (CF) как разница текущих поступлений и выбытий. Подразумевается доминирование притоков денег над их оттоками с итоговым знаком «+». Математически проект хорошо иллюстрируется следующим выражением.
Математическая модель инвестиционного проекта
Основные алгоритмы преобразований событий денежных потоков укладываются в два направления – наращение и дисконтирование. В обоих случаях применяются схемы сложных процентов. В первом случае перерасчет денежных потоков производится от базового момента времени к будущему, а во втором – наоборот. Под базовым моментом следует понимать отправную точку старта инвестиций.
Формулы наращенной и дисконтированной величин денежного потока
Расчет двух вариантов переоценки потоков денежных средств производится по формулам, представленным выше. Дисконтирующий множитель или коэффициент дисконтирования для единичного платежа показывает условно приведенную к базовому моменту цену денежной единицы будущего периода его осуществления. Иными словами, FM позволяет увидеть, насколько обесценится 1 рубль итогового операционного Cash Flow по сравнению с 1 рублем реализованных стартовых инвестиционных вложений.
Практика дисконтирования при инвестициях
Под дисконтированием мы будем понимать процедуру приведения денежного потока к базовому моменту (начальному периоду). В результате данной процедуры текущие потоковые величины умножаются на коэффициент дисконтирования. Ключевым фактором концепции дисконтирования выступает ее ставка. Ставка дисконтирования в литературе также называется нормой дохода, нормативом эффективности, ежегодной ставкой отдачи проекта и т.п.
Расчет системных показателей оценки эффективности проекта тесно связан с правильным выбором нормы дохода. Это касается NPV, внутренней нормы доходности, дисконтированного срока окупаемости инвестиций, рентабельности и других показателей. Благодаря дисконтированию фактор времени прочно интегрируется в значения эффективности и позволяет сделать обоснование проекта более адекватным интересам инвестора.
Скажу откровенно, мне не довелось наблюдать в российской практике тщательно выверенных расчетов ставки отдачи. Как правило, инвестор, руководствуясь личным опытом, своими специфическими соображениями назначает норму дохода без существенного обоснования выбора. Иногда ставка привязывается к ставке рефинансирования плюс некий процент на профит. В некоторых случаях за базис расчета норматива принимается банковский депозит или процент по коммерческому кредиту.
Такую ситуацию считать нормальной, конечно, нельзя. Формирование более высокой методической культуры выбора ставки дисконтирования – задача насущная. Особенно это важно, когда страна нуждается в существенном улучшении инвестиционного климата и многократном увеличении вложений в экономику. Единого подхода к выбору нормы доходности нет. Такой выбор зависит от конкретной ситуации и обусловлен рядом факторов. Методически верно выделить из них две условные группы.
- Факторы, не зависящие от хода реализации проекта (внешние). Эти факторы учитывают политические, экономические риски, инфляцию. В них оцениваются альтернативные инвестиции (в ценные бумаги, банковские депозиты), среднерыночные, безрисковые и отраслевые нормы доходности.
- Факторы, зависящие от структуры проекта (внутренние). Они учитывают структуру источников финансирования, новизну проекта, его риски.
Группа влияющих факторов определяет и методы вычисления ставки дисконтирования. Расчетные схемы, как правило, основываются на оценке стоимости капитала. Методы также делятся по применяемой базе оценки: ожидаемая доходность активов безрискового типа или стоимость финансовых источников инвестиций.
Методы CAPM и кумулятивного построения
Методы первой группы с базой в форме ожидаемой доходности безрисковых активов считаются наиболее распространенными в Западной управленческой школе. К ним относятся две подгруппы методов: методы, основанные на модели капитальных активов (Capital Asset Pricing Model, CAPM), и метод кумулятивного построения. Расчет ставки по модели CAPM выполняется на основе двух ее составляющих: ставки дохода по безрисковым инвестициям и дополнительной ставки, компенсирующей неопределенность вложений в рассматриваемую компанию.
Формула расчета ставки дисконтирования по методу CAPM
Расчет нормы эффективности по модели CAPM производится по формуле, представленной выше. Достоинством метода является фундаментальный принцип, учитывающий связь между доходностью акции и рыночным риском. Среди недочетов модели для российских условий выделяются следующие.
- Модель разработана для западного уровня развития инфраструктуры бизнеса в части высокой конкуренции инвесторов и более совершенного рынка капитала.
- В условиях «плавающего» кризиса и после дефолта 1998 года государственные ценные бумаги не могут восприниматься как безрисковые.
- Непрозрачность и слабость фондового рынка в России не позволяют адекватно рассчитать доходность по безрисковому активу и составить справочники бета-коэффициентов.
- Главный объективный недостаток модели – наличие всего одного учтенного фактора (рыночного риска) для расчета ставки отдачи.
- Трансакционные издержки, налоги и другие дополнительные факторы метод не учитывает.
С развитием модели CAPM возникла модифицированная ее форма, в которой учитывается несистематический риск, именуемый специфическим. Его оценивают экспертно, поскольку средства статистики не дают вывести данный фактор на приемлемый уровень формализации. Расчет ставки дисконтирования производится согласно представленной ниже формуле, рядом с которой размещен пример таблицы поправок на специфический риск.
Формула расчета по методу MCAPM и пример таблицы поправок по экспертным оценкам
К первой группе моделей, позволяющих рассчитать норму дохода в обоснование инвестиций, относится также подход метода кумулятивного построения. Его отличие от CAPM состоит в том, что к величине безрисковой ставки могут быть добавлены многочисленные премии за разнообразные риски, которые можно выявить применительно к конкретному инвестиционному проекту. Приведем некоторые примеры таких рисков:
- риск срывов со стороны участников проекта;
- риск потери потенциальных доходов от инвестиций;
- страховой риск и др.
Если по конкретным страховым случаям капитальные вложения застрахованы, поправка на эти виды рисков не производится. Следует учитывать, что и расходы в данном случае также возрастают на размер платежей по договорам страхования. Рекомендации по размерам премий за различные виды риска можно найти в специализированной литературе. Далее размещена формула метода кумулятивного построения.
Формула по методу кумулятивного построения
Альтернативные методы расчета
Второй методический подход к расчету нормы дисконта для обоснования инвестиций опирается на оценку стоимости источников средств (собственных и привлекаемых). Мы с вами помним, что каждый вид инвестиционных ресурсов имеет свою стоимость. Есть она и у собственного капитала. В практике применяются несколько моделей стоимости собственных источников, среди них выделяются следующие.
- Модель прибыли на акцию.
- Модель установления стоимости привилегированных акций.
- Модель расчета стоимости вновь привлекаемого капитала.
Стоимость инвестиционных ресурсов, определенная на основании одной из указанных выше моделей, рассматривается как номинальная ставка дисконтирования. Ее надлежит откорректировать на риск проекта и плановую инфляцию. Расчет реальной ставки производится с учетом величины премии за риск, которая устанавливается в результате достигнутого соглашения между инвестором и руководством компании. Ниже представлены примеры формул расчета стоимостей собственных и привлеченных ресурсов.
Формулы расчета стоимостей инвестиционных ресурсов по источникам
Редко, когда инвестиционный проект реализуется за счет единственного источника. Как правило, присутствуют и собственные, и привлеченные ресурсы. Поэтому для расчета ставки дисконтирования важно определить общую стоимость задействованного капитала. Для этого используется модель WACC. В ней общая стоимость капитала формируется путем сложения стоимостей отдельных источников, взвешенных по удельным весам их участия в совокупном капитале. Формула расчета нормы дисконта по методу WACC представлена далее.
Формула модели WACC для расчета нормы дисконта
Метод WACC для установления нормы дисконта применим далеко не всегда. Дивиденды акционерам как выражение стоимости собственного капитала могут по различным причинам не соответствовать рыночным уровням доходности. Стоимость заимствований также может вносить искажения в общую картину. Предположим, компания входит в мощную ФПГ, располагающую возможностями льготного кредитования. И ставка по кредиту, оказавшись ниже рыночной, способна нарушить логику расчетов.
Расчеты по модели WACC целесообразно расценивать как ориентир, обозначающий нижний порог при выборе дисконтной ставки. Если же аналитик видит, что структура источников финансирования настолько уникальна, что расчетные значения далеки от рыночных реалий, от данного метода лучше отказаться. В завершение назову еще несколько простых, но иногда действенных методов выбора нормы доходности:
- метод учета инфляции;
- расчет на основе экспертных оценок;
- метод рентабельности собственного капитала ROE;
- метод рыночных мультипликаторов.
Мы рассмотрели основные методы расчета ставки дисконтирования для обоснования и оценки инвестиционных проектов. Специалистам, в чьи обязанности входит такая работа, я бы рекомендовал использовать сразу несколько способов, обязательно включая в них и экспертную оценку, и учет уровня инфляции, и ставки доходности на рынке капитала. Начинать надо с простых вариантов. Далее нужно выбрать один, наиболее подходящий сложный метод, вникнуть в логику расчета, возможно, подкорректировать формулу под реалии бизнеса и осуществить вычисления.
Практика показывает, что многократные итерации расчетов, групповые обсуждения со специалистами финансовой сферы дают приличный результат. Точность планирования возрастает, а усилия окупаются. Ведь даже незначительная ошибка в данном параметре стоит дорого. Как говорится, семь раз отмерь, один раз отрежь!
Коэффициент скидки— Полное руководство по использованию коэффициентов скидки в модели
Что такое коэффициент скидки?
В финансовом моделированииЧто такое финансовое моделирование Финансовое моделирование выполняется в Excel для прогнозирования финансовых показателей компании. Обзор того, что такое финансовое моделирование, как и зачем строить модель. Коэффициент дисконтирования — это десятичное число, умноженное на денежный поток. Бесплатные руководства по оценке, позволяющие изучить наиболее важные концепции в удобном для вас темпе. Эти статьи научат вас передовым методам оценки бизнеса и научат оценивать компанию, используя сопоставимый анализ компании, моделирование дисконтированных денежных потоков (DCF) и прецедентные транзакции, которые используются в инвестиционном банкинге, исследованиях акций, а также стоимость, чтобы дисконтировать ее до ее приведенной стоимости. .Коэффициент увеличивается с течением времени (что означает, что десятичное значение становится меньше), поскольку эффект от увеличения ставки дисконтирования со временем нарастает.
На практике проще использовать функцию XNPV Функция XNPV в Excel Функцию XNPV в Excel следует использовать вместо обычной функции NPV в финансовом моделировании и анализе оценки для обеспечения точности и точности. В формуле XNPV используются конкретные даты, соответствующие каждому дисконтированному денежному потоку в серии. Изучите пошагово в этом руководстве с примерами и снимками в Excel.Однако преимущество ручного расчета коэффициента дисконтирования заключается в том, что вы можете увидеть, какова приведенная стоимость каждого отдельного денежного потока , а не только общая чистая приведенная стоимость.
Скачать бесплатный шаблон
Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон прямо сейчас!
Шаблон коэффициента скидки
Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!Зачем нужен коэффициент скидки?
Некоторые аналитики предпочитают рассчитывать явные коэффициенты дисконтирования в каждый период времени, чтобы они могли более четко видеть эффекты начисления сложных процентов, а также создавать модель дисконтированного денежного потока или модель DCF Бесплатное руководство по обучению DCF-моделиA DCF-модель — это особый тип используемой финансовой модели ценить бизнес.Модель — это просто прогноз неуправляемого свободного денежного потока компании, который легче проверять.
Коэффициент дисконтирования является альтернативой использованию функции XNPV или XIRRXIRR Функция XIRR относится к категории Финансовые функции Excel. Функция рассчитает внутреннюю норму прибыли (IRR) для серии денежных потоков, которые могут быть непериодическими. Если денежные потоки периодические, мы должны использовать функцию IRR. В финансовом моделировании функция XIRR полезна в Excel. Функция XIRR — это функции в Excel.6) = 0,564
Если недисконтированный денежный поток в этот период составляет 120 000 долларов, то, чтобы получить приведенную стоимость этого денежного потока, мы умножаем его на 0,564, чтобы получить 67 736,9 долларов.
Общая чистая приведенная стоимость денежных потоков, показанных в приведенном выше примере, составляет 737 348,1 долларов США, что можно рассчитать путем суммирования отдельных дисконтированных денежных потоков. Мы получаем то же число, что и при использовании функции NPV в Excel.
Приложения в финансовом моделировании
Аналитики будут использовать коэффициенты дисконтирования при выполнении финансового моделирования в Excel, если они хотят получить больше информации о формуле NPV и лучше проиллюстрировать эффект дисконтирования.
Как вы видите в приведенном выше примере, каждый доллар денежного потока, полученного в 10-м году, стоит только 38,6% от каждого доллара денежного потока, полученного сегодня. Когда вы получаете более 15-20 лет, стоимость денежных потоков становится чрезвычайно дисконтированной. Поскольку риск никогда не получить их становится намного выше, альтернативные издержки становятся намного выше.
Коэффициент скидки по сравнению с XNPV
Использование коэффициента скидки позволяет точно указать, сколько дней в каждом периоде.Вы можете сделать это, используя определенные даты в каждом временном периоде и взяв разницу между ними.
Например, с 30 июня 2018 г. по 31 декабря 2018 г. 184 дня, что составляет полгода. Добавляя этот дополнительный уровень в модель, мы можем очень точно определить периоды дисконтирования. Этим достигается тот же эффект, что и при использовании функции XNPV и функции XIRR: XIRR против IRR. Зачем использовать XIRR против IRR. XIRR назначает конкретные даты каждому отдельному денежному потоку, что делает его более точным, чем IRR, при построении финансовой модели в Excel.в Excel.
Дополнительные ресурсы от CFI
Чтобы и дальше развивать свои навыки финансового аналитика мирового класса Аналитическое руководство Trifecta® Окончательное руководство о том, как стать финансовым аналитиком мирового уровня. Вы хотите быть финансовым аналитиком мирового уровня? Вы хотите следовать передовым отраслевым практикам и выделиться из толпы? Наш процесс, который называется The Analyst Trifecta®, состоит из аналитики, презентации и мягких навыков, мы считаем, что следующие ресурсы CFI будут чрезвычайно полезны для вас:
- Формулы и функции Excel Шпаргалка по формулам Excel Шпаргалка по формулам Excel от CFI даст вам все самое лучшее важные формулы для выполнения финансового анализа и моделирования в таблицах Excel.Если вы хотите стать мастером финансового анализа Excel и экспертом по построению финансовых моделей, вы попали в нужное место.
- Руководство по моделированию DCF Бесплатное руководство по обучению модели DCFМодель DCF — это особый тип финансовой модели, используемой для оценки бизнеса. Модель представляет собой просто прогноз свободного денежного потока компании без рычага
- XIRR против IRR XIRR против IRR Зачем использовать XIRR против IRR. XIRR назначает конкретные даты каждому отдельному денежному потоку, что делает его более точным, чем IRR, при построении финансовой модели в Excel.
- Бесплатный курс по формулам Excel
Что такое коэффициент скидки?
В математике коэффициент дисконтирования — это расчет текущей стоимости будущего счастья, или, более конкретно, он используется для измерения того, насколько люди будут заботиться о периоде в будущем по сравнению с сегодняшним днем.
Фактор дисконтирования — это весовой коэффициент, который умножает будущее счастье, доход и убытки, чтобы определить коэффициент, на который следует умножить деньги, чтобы получить чистую приведенную стоимость товара или услуги.
Поскольку стоимость сегодняшнего доллара по сути будет меньше в будущем из-за инфляции и других факторов, часто предполагается, что коэффициент дисконтирования принимает значения от нуля до единицы. Например, с коэффициентом дисконтирования, равным 0,9, действие, которое дало бы 10 единиц полезности, если бы оно было выполнено сегодня, даст, с сегодняшней точки зрения, девять единиц полезности, если оно будет выполнено завтра.
Использование коэффициента дисконтирования для определения чистой приведенной стоимости
В то время как ставка дисконтирования используется для определения приведенной стоимости будущего денежного потока, коэффициент дисконтирования используется для определения чистой приведенной стоимости, которая может использоваться для определения ожидаемой прибыли и убытков на основе будущих платежей — чистой будущей стоимости актива. инвестиции.N, что означает, что коэффициент дисконтирования равен единице, деленной на значение единицы, плюс периодическая процентная ставка в степени количества платежей. Например, если компания имеет шестипроцентную годовую процентную ставку и хочет производить 12 платежей в год, коэффициент дисконтирования будет 0,8357.
Многопериодные и дискретные модели времени
В многопериодной модели агенты могут иметь разные функции полезности для потребления (или другого опыта) в разные периоды времени.Обычно в таких моделях ценят будущий опыт, но в меньшей степени, чем настоящий.
Для простоты коэффициент, с помощью которого они дисконтируют полезность следующего периода, может быть постоянным от нуля до единицы, и если это так, он называется коэффициентом дисконтирования. Фактор дисконтирования можно интерпретировать не как снижение оценки будущих событий, а как субъективную вероятность того, что агент умрет до следующего периода, и поэтому дисконтирует будущий опыт не потому, что он не ценится, а потому, что он не может происходить.
Агенты, ориентированные на настоящее, сильно дисконтируют будущее и поэтому имеют НИЗКИЙ фактор дисконтирования. Противоположная ставка дисконтирования и ориентированность на будущее. В модели с дискретным временем, где агенты дисконтируют будущее с коэффициентом b, обычно принимают b = 1 / (1 + r), где r — ставка дисконтирования.
Как рассчитать коэффициент дисконтирования
Чтобы рассчитать чистую приведенную стоимость инвестиций (NPV), вы должны сначала определить коэффициент дисконтирования. Другими словами, коэффициент дисконтирования измеряет приведенную стоимость будущей стоимости инвестиции.Узнайте, что это означает, как рассчитать коэффициент дисконтирования и как он применяется в финансах ниже.
Какой коэффициент скидки?
Формула коэффициента дисконтирования позволяет рассчитать чистую приведенную стоимость (NPV). Это взвешивающий термин, используемый в математике и экономике, умножение будущих доходов или убытков для определения точного коэффициента, на который умножается стоимость, чтобы получить сегодняшнюю чистую приведенную стоимость. Это может быть применено к товарам, услугам или инвестициям и часто используется при составлении корпоративного бюджета, чтобы определить, добавит ли предложение будущую ценность.
Любое уравнение коэффициента дисконтирования использует предположение, что сегодняшние деньги будут стоить меньше в будущем из-за таких факторов, как инфляция, что дает коэффициенту дисконтирования значение от нуля до единицы.
Коэффициент дисконтирования и чистая приведенная стоимость
Коэффициент дисконтирования и ставка дисконтирования тесно связаны, но, хотя ставка дисконтирования учитывает текущую стоимость будущего денежного потока, коэффициент дисконтирования применяется к чистой приведенной стоимости. Имея в руках эти цифры, вы можете спрогнозировать ожидаемую прибыль или убытки от инвестиций или их чистую будущую стоимость.
Расчеты по формуле коэффициента дисконтирования
Как видно из приведенной выше разбивки, коэффициент дисконтирования можно использовать по-разному:
Для расчета чистой приведенной стоимости
Для помощи в финансовом моделировании
Завершить анализ дисконтированных денежных потоков
В результате эту удобную небольшую формулу может использовать каждый, от страховых компаний до инвесторов.
Общая формула коэффициента дисконтирования:
Коэффициент дисконтирования = 1 / (1 * (1 + Ставка дисконтирования) Номер периода)
Чтобы использовать эту формулу, вам необходимо узнать периодическую процентную ставку или скидку. показатель.Это можно легко определить, разделив годовую процентную ставку фактора дисконтирования на общее количество платежей в год. Вам также необходимо знать общее количество платежей, которые будут произведены.
Как рассчитать коэффициент скидки
Вы можете создать шаблон или таблицу коэффициента скидки в Excel для выполнения этих расчетов, введя приведенную выше формулу со своими собственными цифрами. Например, таблица может выглядеть так:
Б | С | D | E | Ф | |
2 | Период | 1 | 2 | 3 | 4 |
3 | Недисконтированный денежный поток | 100 000 долл. F2) | |||
5 | Коэффициент дисконтирования | 0.93 | 0,86 | 0,79 | 0,74 |
Показывает уменьшение коэффициента дисконтирования с течением времени, будь то годовой коэффициент дисконтирования или более короткие временные рамки для отражения вашего отчетного периода.
Например, чтобы рассчитать коэффициент дисконтирования для денежного потока через год в будущем, вы можете просто разделить 1 на процентную ставку плюс 1. Для процентной ставки 5% коэффициент дисконтирования будет равен 1, деленному на 1.05, или 95%.
После того, как вы рассчитали коэффициент дисконтирования и ставку дисконтирования, вы можете использовать их для определения чистой приведенной стоимости инвестиции. Сложите текущую стоимость всех положительных денежных потоков, вычтя текущую стоимость отрицательных денежных потоков. Применяя процентную ставку, вы получите чистую приведенную стоимость. Есть много калькуляторов коэффициента дисконтирования, которые будут применять эти формулы, или вы можете использовать Excel для анализа.
Преимущества коэффициента дисконтирования
Понимание коэффициента дисконтирования полезно, поскольку оно дает визуальное представление о влиянии начисления сложных процентов с течением времени.Это помогает рассчитать дисконтированный денежный поток. По мере того, как ставка дисконтирования растет с течением времени, денежный поток уменьшается, что позволяет представить временную стоимость денег в десятичном представлении. В целом, инвесторы могут использовать этот тип шаблона коэффициента дисконтирования для перевода будущих доходов от инвестиций в чистую приведенную стоимость.
Мы можем помочь
GoCardless поможет вам автоматизировать сбор платежей, сократив количество администраторов, с которыми ваша команда должна иметь дело при поиске счетов. Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами.
GoCardless используется более чем 55 000 компаний по всему миру. Узнайте больше о том, как вы можете улучшить обработку платежей в своем бизнесе уже сегодня.
Узнать большеЗарегистрироваться
Коэффициент скидки (значение, формула) | Как рассчитать?
Что такое коэффициент скидки?
Коэффициент дисконтирования — это весовой коэффициент, который чаще всего используется для определения приведенной стоимости будущих денежных потоков и рассчитывается путем прибавления ставки дисконтирования к единице, которая затем возводится в отрицательную степень ряда периодов.
Формула коэффициента скидки
Математически это представлено следующим образом:
DF = (1 + (i / n) ) -n * t
где,
- i = Ставка дисконтирования
- t = Количество лет
- n = количество периодов начисления сложных процентов в год
В случае формулы непрерывного начисления сложных процентов Формула непрерывного начисления процентов отображает проценты, полученные при постоянном начислении сложных процентов для бесконечное количество периодов.Для его расчета используются четыре переменные: основная сумма, время, процентная ставка и номер периода начисления сложных процентов. Подробнее, уравнение изменено, как показано ниже,
DF = e -i * t
Расчет (шаг за шагом)
Его можно рассчитать, выполнив следующие действия:
- Во-первых, вычислите ставку дисконтирования для аналогичного вида инвестиций на основе рыночной информации. Ставка дисконтирования — это годовая процентная ставка, обозначаемая как u2018i.u2019
- Теперь определите, как долго деньги будут оставаться инвестированными, то есть срок действия инвестиций в несколько лет. Количество лет обозначено u2018t.u2019
- Теперь вычислите количество периодов начисления сложных процентов ставки дисконтирования в год. Начисление сложных процентов может быть ежеквартальным. Формула начисления сложных процентов отражает общую сумму процентов, которую инвестор может заработать на инвестиции или финансовый продукт, если проценты выплачиваются ежеквартально и реинвестируются в схему.Он учитывает основную сумму, ежеквартальную начисленную процентную ставку и количество периодов для расчета. Подробнее, полугодие, год и т. Д. Количество периодов начисления сложных процентов ставки дисконтирования в год обозначается как u2018 n.u2019 (Этап не требуется для непрерывного компаундирования)
- Наконец, в случае дискретного компаундирования его можно рассчитать по следующей формуле:
DF = (1 + (i / n) u00a0) -n * t
С другой стороны, в случае непрерывного компаундирования его можно рассчитать по следующей формуле:
DF = e -i * t
Примеры (с шаблоном Excel)
Пример # 1
Рассмотрим пример, в котором коэффициент дисконтирования рассчитывается на два года со ставкой дисконтирования 12%.Компаундирование производится:
- Непрерывный
- Ежедневно
- Ежемесячно
- Ежеквартально
- Полугодовой
- Годовой
Дано, i = 12%, t = 2 года
# 1 — Непрерывное смешивание
Формула = e -12% * 2
# 2 — Ежедневное приготовление смеси
с момента ежедневного смешивания, следовательно, n = 365
= (1 + (12% / 365)) -365 * 2
= 0.7867
# 3 — Ежемесячный расчет
С ежемесячного начисления процентов, следовательно, n = 12
Расчет DF выполняется по приведенной выше формуле:
= (1 + (12% / 12)) -12 * 2
= 0,7876
# 4 — Ежеквартальное компаундирование
Так как начисление начисляется за квартал, поэтому n = 4
Расчет DF выполняется по приведенной выше формуле:
= (1 + (12% / 4)) -4 * 2
= 0.7894
# 5 — Полугодовое накопление
С полугодового начисления сложных процентов, поэтому n = 2
= (1 + (12% / 2)) -2 * 2
= 0,7921
# 6 — Годовое накопление
Начиная с годового начисления сложных процентов, следовательно, n = 1,
Расчет DF выполняется по приведенной выше формуле:
= (1 + (12% / 1)) -1 * 2
= 0,7972
Таким образом, коэффициент дисконтирования для различных периодов начисления сложных процентов составит —
.Графическое представление приведенной выше таблицы будет следующим —
Приведенный выше пример показывает, что формула зависит не только от ставки дисконтирования и срока инвестирования, но и от того, сколько раз в течение года происходит начисление сложных процентов.
Пример # 2
Давайте возьмем пример, в котором коэффициент дисконтирования должен быть рассчитан от года 1 до года 5 со ставкой дисконтирования 10%.
Следовательно, расчет DF с 1 по 5 год будет следующим —
- DF для года 1 = (1 + 10%) -1 = 0,9091
- DF для года 2 = (1 + 10%) -2 = 0,8264
- DF для года 3 = ( 1 + 10%) -3 = 0.7513
- DF для года 4 = (1 + 10%) -4 = 0,6830
- DF для года 5 = (1 + 10%) -5 = 0,6209
Следовательно, DF с 1 по 5 год показано на рисунке ниже —
В приведенном выше примере показана зависимость DF от срока владения инвестициями.
Калькулятор коэффициента дисконтирования
| Формула коэффициента дисконтирования = | 1 + ( Ставка дисконтирования / Число периодов начисления процентов ) — Число периодов начисления процентов * Число лет | |
| 1 + (0/0) −0 * 0 = | 0 |
Использование и актуальность
Понимание этого коэффициента дисконтирования очень важно, поскольку он отражает влияние начисления сложных процентов на каждый период времени, что в конечном итоге помогает в расчете дисконтированного денежного потока.Идея состоит в том, что она уменьшается с течением времени по мере нарастания эффекта от увеличения ставки дисконтирования. По сути, это очень важный компонент временной стоимости денег.
Это десятичное представление, используемое для определения временной стоимости денег для денежного потока. Чтобы определить коэффициент дисконтирования для денежного потока, необходимо оценить максимальную процентную ставку, которую можно получить по инвестициям аналогичного характера. Следовательно, инвесторы могут использовать этот фактор для перевода стоимости будущих доходов от инвестиций в приведенную стоимость в долларах.
Коэффициент скидки Видео
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле коэффициента дисконтирования. Здесь мы обсудим, как рассчитать коэффициент скидки, используя практические примеры вместе с загружаемыми шаблонами Excel. Вы можете узнать больше о финансовом анализе из следующих статей —
Определение ставки дисконтирования
Что такое дисконтная ставка?
В зависимости от контекста ставка дисконтирования имеет два разных определения и использования.Во-первых, учетная ставка относится к процентной ставке, взимаемой с коммерческих банков и других финансовых учреждений за ссуды, которые они берут у Федерального резервного банка в рамках процесса ссуды с дисконтным окном. Во-вторых, ставка дисконтирования относится к процентной ставке, используемой в анализе дисконтированных денежных потоков (DCF) для определения приведенной стоимости будущих денежных потоков.
Ключевые выводы
- Термин «ставка дисконтирования» может означать либо процентную ставку, которую Федеральная резервная система взимает с банков за краткосрочные ссуды, либо ставку, используемую для дисконтирования будущих денежных потоков в анализе дисконтированных денежных потоков (DCF).
- В банковском контексте дисконтное кредитование является ключевым инструментом денежно-кредитной политики и частью функции ФРС как кредитора последней инстанции.
- В DCF ставка дисконтирования выражает временную стоимость денег и может определять, является ли инвестиционный проект финансово жизнеспособным или нет.
Дисконтирование со ставкой дисконтирования
Как работает учетная ставка ФРС
Хотя коммерческие банки могут занимать и ссужать капитал друг у друга без необходимости какого-либо обеспечения, используя рыночную межбанковскую ставку, они также могут занимать деньги для своих краткосрочных операционных потребностей в Федеральном резервном банке.Такие ссуды обслуживаются 12 региональными отделениями ФРС, а ссудный капитал используется финансовыми институтами для покрытия дефицита финансирования, предотвращения любых потенциальных проблем с ликвидностью или, в худшем случае, предотвращения банкротства банка. Эта специальная кредитная линия, предлагаемая ФРС, известна как дисконтное окно.
Такие ссуды предоставляются регулирующим органом на ультракороткий период продолжительностью 24 часа или менее, и применимая процентная ставка, взимаемая по этим ссудам, является стандартной ставкой дисконтирования.Эта ставка дисконтирования не является рыночной, а управляется и устанавливается советами Федерального резервного банка и утверждается его Советом управляющих.
Понимание ссуд с дисконтным окном ФРС
Программа дисконтного окна ФРС включает три разных уровня ссуд, и для каждого из них используется отдельная, но взаимосвязанная ставка. Первый уровень, называемый программой первичного кредитования, ориентирован на предложение необходимого капитала «финансово стабильным» банкам, имеющим хорошую кредитную историю.Эта первичная ставка дисконтирования по кредиту обычно устанавливается выше существующих рыночных процентных ставок, которые могут быть доступны в других банках или из других источников аналогичного краткосрочного долга.
Следующий уровень, называемый программой вторичного кредитования, предлагает аналогичные ссуды учреждениям, не имеющим права на получение первичной ставки, и обычно устанавливается на 50 базисных пунктов выше, чем первичная ставка (1 процентный пункт = 100 базисных пунктов). Учреждения этого уровня меньше и могут быть не такими финансово здоровыми, как учреждения первичного уровня, что объясняет более высокую ставку дисконтирования, взимаемую с кредитов, предлагаемых им ФРС.
Третий уровень, называемый сезонной кредитной программой, обслуживает более мелкие финансовые учреждения, у которых более высокая дисперсия денежных потоков, хотя денежные потоки могут быть в значительной степени предсказуемыми.
Например, финансовые институты, связанные с сельским хозяйством или туризмом, могут иметь колебания в своих денежных потоках из-за сезонных колебаний, но, в зависимости от погодных условий, они остаются предсказуемыми. Однако учреждения этого уровня являются наиболее рискованными, и ставки, взимаемые с них, также выше.
Хотя ставки дисконтирования для первых двух уровней определяются ФРС независимо, а процесс определения ставок не принимает во внимание какие-либо рыночные данные, ставка дисконтирования для третьего уровня определяется на основе ставок, преобладающих на рынке. Как правило, при определении ставки дисконтирования для сезонной кредитной программы учитывается среднее значение для выбранного набора рыночных ставок сопоставимых альтернативных механизмов кредитования.
Все три типа ссуд дисконтного окна Федеральной резервной системы обеспечиваются залогом, то есть заемщик должен поддерживать определенное обеспечение или обеспечение по ссуде.
Использование учетной ставки ФРС
Организации-заемщики используют эту возможность экономно, в основном, когда они не могут найти желающих кредиторов на рынке. Предлагаемые ФРС ставки дисконтирования доступны при относительно более высоких процентных ставках по сравнению со ставками межбанковских заимствований, а дисконтные кредиты предназначены для предоставления в качестве экстренного варианта для банков, терпящих бедствие. Заимствования из дисконтного окна ФРС могут даже сигнализировать о слабости для других участников рынка и инвесторов.Пик его использования приходится на периоды финансовых затруднений.
Пример учетной ставки ФРС
Например, использование дисконтного окна ФРС резко возросло в конце 2007 и 2008 годов, когда финансовые условия резко ухудшились, и центральный банк предпринял шаги по вливанию ликвидности в финансовую систему.
В августе 2007 года Совет управляющих снизил первичную учетную ставку с 6,25% до 5,75%, сократив спрэд по ставке по фондам ФРС с 1% до 0,5%. В октябре 2008 года, через месяц после краха Lehman Brothers, размер заимствований в рамках дисконтного окна достиг пика в 403 доллара.5 миллиардов против среднемесячного показателя в 0,7 миллиарда долларов с 1959 по 2006 год. Из-за финансового кризиса совет директоров также продлил период кредитования с ночи до 30 дней, а затем до 90 дней в марте 2008 года. Как только экономика восстановила контроль, эти временные меры были отменены, и учетная ставка была возвращена только к кредитованию овернайт.
В то время как ФРС поддерживает свою собственную учетную ставку в рамках программы дисконтного окна в США, другие центральные банки по всему миру также используют аналогичные меры в различных вариантах.Например, Европейский центральный банк предлагает постоянные механизмы, которые служат в качестве механизмов маржинального кредитования. Финансовые организации могут получить ликвидность овернайт от центрального банка при условии предоставления достаточных приемлемых активов в качестве обеспечения.
Чаще всего ссуды дисконтного окна ФРС выдаются только «овернайт», но в периоды крайних экономических бедствий, таких как кредитный кризис 2008-2009 гг., Период ссуды может быть продлен.
Ставки дисконтирования в анализе дисконтированных денежных потоков (DCF)
Тот же термин, ставка дисконтирования, также используется в анализе дисконтированных денежных потоков.DCF — это широко применяемый метод оценки, используемый для оценки стоимости инвестиции на основе ожидаемых будущих денежных потоков. Основанный на концепции временной стоимости денег, DCF-анализ помогает оценить жизнеспособность проекта или инвестиций путем расчета приведенной стоимости ожидаемых будущих денежных потоков с использованием ставки дисконтирования.
Проще говоря, если проекту требуются определенные инвестиции сейчас (а также в будущие месяцы) и доступны прогнозы относительно будущей прибыли, которую он будет генерировать, то — используя ставку дисконтирования — можно рассчитать текущую стоимость всех таких инвестиций. денежные потоки.Если чистая приведенная стоимость положительна, проект считается жизнеспособным. В противном случае это считается финансово нецелесообразным.
В этом контексте анализа DCF ставка дисконтирования относится к процентной ставке, используемой для определения приведенной стоимости. Например, 100 долларов, вложенных сегодня в схему сбережений, которая предлагает 10% -ную процентную ставку, вырастут до 110 долларов. Другими словами, 110 долларов (будущая стоимость) при дисконтировании по ставке 10% на сегодняшний день равны 100 долларам (приведенная стоимость). Если кто-то знает — или может разумно предсказать — все такие будущие денежные потоки (например, будущая стоимость 110 долларов), то, используя конкретную ставку дисконтирования, можно получить текущую стоимость таких инвестиций.
Особые соображения
Какую ставку дисконтирования следует использовать для инвестиционного или бизнес-проекта? При инвестировании в стандартные активы, такие как казначейские облигации, в качестве ставки дисконтирования часто используется безрисковая норма прибыли. С другой стороны, если бизнес оценивает жизнеспособность потенциального проекта, он может использовать средневзвешенную стоимость капитала (WACC) в качестве ставки дисконтирования, которая представляет собой среднюю стоимость, которую компания платит за капитал за счет заимствования или продажи собственного капитала.В любом случае чистая приведенная стоимость всех денежных потоков должна быть положительной для продолжения инвестирования или реализации проекта.
Часто задаваемые вопросы о ставках скидок
Что означают два значения дисконтной ставки?
Ставка дисконтирования чаще всего используется для процентной ставки, используемой для анализа дисконтированных денежных потоков (DCF) для учета временной стоимости денег. Эта ставка дисконтирования используется для определения текущей стоимости будущих денежных потоков. Второе значение относится к ставке Федерального резерва по кредитованию овернайт для банков, нуждающихся в чрезвычайной ликвидности.Эта ставка будет выше, чем ставка по федеральным фондам.
Какое влияние более высокая ставка дисконтирования оказывает на временную стоимость денег?
Будущие денежные потоки дисконтируются по ставке дисконтирования, поэтому чем выше ставка дисконтирования, тем ниже приведенная стоимость будущих денежных потоков. Точно так же более низкая ставка дисконтирования ведет к более высокой приведенной стоимости. Это означает, что, когда учетная ставка выше, деньги в будущем будут «стоить меньше» или иметь более низкую покупательную способность, чем доллары сегодня.
Как рассчитать дисконтированные денежные потоки?
Расчет DCF инвестиции включает три основных шага. Во-первых, вы прогнозируете ожидаемые денежные потоки от инвестиций. Во-вторых, вы выбираете подходящую ставку дисконтирования. Третий и последний шаг — дисконтировать прогнозируемые денежные потоки до сегодняшнего дня, используя финансовый калькулятор, электронную таблицу или ручной расчет.
Как выбрать подходящую ставку дисконтирования?
Используемая ставка дисконтирования будет зависеть от типа проведенного анализа.Отдельные лица должны использовать альтернативные издержки использования своих денег в другом месте в качестве подходящей ставки дисконтирования — проще говоря, это норма прибыли, которую инвестор может заработать на рынке на вложения сопоставимого размера и риска. Бизнес может использовать ставку дисконтирования, основанную на альтернативных издержках, но также может использовать средневзвешенную стоимость капитала (WACC), или они могут использовать среднюю историческую доходность актива или проекта, аналогичного анализируемому. В некоторых случаях использование безрисковой ставки может быть наиболее целесообразным.
Определение дисконтирования
Что такое дисконтирование?
Дисконтирование — это процесс определения приведенной стоимости платежа или потока платежей, которые должны быть получены в будущем. Учитывая временную стоимость денег, доллар сегодня стоит больше, чем завтра. Дисконтирование — это основной фактор, используемый при оценке будущих денежных потоков.
Дисконтирование со ставкой дисконтирования
Как работает дисконтирование
Например, купонные выплаты по обычной облигации дисконтируются по определенной процентной ставке и суммируются с дисконтированной номинальной стоимостью для определения текущей стоимости облигации.
С точки зрения бизнеса, актив не имеет ценности, если он не может приносить денежные потоки в будущем. По акциям выплачиваются дивиденды. По облигациям выплачиваются проценты, а проекты обеспечивают инвесторам дополнительные будущие денежные потоки. Стоимость этих будущих денежных потоков в сегодняшнем выражении рассчитывается путем применения коэффициента дисконтирования к будущим денежным потокам.
Ключевые выводы
- Дисконтирование — это процесс определения приведенной стоимости будущего платежа или потока платежей.
- Согласно концепции временной стоимости денег, доллар сегодня всегда стоит больше, чем он будет стоить завтра.
- Более высокий дисконт указывает на больший уровень риска, связанного с инвестицией и ее будущими денежными потоками.
Временная стоимость денег и дисконтирование
Когда автомобиль продается со скидкой 10%, это означает скидку к цене автомобиля. Та же концепция дисконтирования используется для оценки финансовых активов.Например, дисконтированная или приведенная стоимость — это стоимость облигации на сегодняшний день. Будущая стоимость — это стоимость облигации в какой-то момент в будущем. Разница в стоимости между будущим и настоящим создается путем дисконтирования будущего обратно в настоящее с использованием коэффициента дисконтирования, который является функцией времени и процентных ставок.
Например, облигация может иметь номинальную стоимость 1000 долларов и иметь скидку 20%, что составляет 800 долларов. Другими словами, инвестор может приобрести облигацию сегодня со скидкой и получить полную номинальную стоимость облигации при наступлении срока погашения.Разница в доходности инвестора.
Чем больше скидка, тем выше доход, который зависит от риска.
Дисконтирование и риск
Как правило, более высокая скидка означает, что существует больший уровень риска, связанного с инвестициями и их будущими денежными потоками. Дисконтирование — это основной фактор, используемый при оценке будущих денежных потоков. Например, денежные потоки прибыли компании дисконтируются по стоимости капитала в модели дисконтированных денежных потоков.Другими словами, будущие денежные потоки дисконтируются обратно по ставке, равной стоимости получения средств, необходимых для финансирования денежных потоков. Более высокая процентная ставка, выплачиваемая по долгу, также означает более высокий уровень риска, который создает более высокий дисконт и снижает приведенную стоимость облигации. Действительно, мусорные облигации продаются с очень большой скидкой. Аналогичным образом, более высокий уровень риска, связанный с конкретной акцией, представленный как бета в модели ценообразования основных средств, означает более высокий дисконт, который снижает приведенную стоимость акции.
Что такое дисконтная ставка?
В финансах ставка дисконтирования имеет два важных определения. Во-первых, ставка дисконтирования является частью расчета приведенной стоимости при проведении анализа дисконтированных денежных потоков, а во-вторых, ставка дисконтирования — это процентная ставка, взимаемая Федеральной резервной системой по кредитам, предоставленным банкам в рамках процесса кредитования дисконтного окна ФРС.
Дисконтированный денежный поток, неопределенность и временная стоимость денег
Первое определение ставки дисконтирования является критическим компонентом расчета дисконтированного денежного потока, уравнения, которое определяет, сколько стоит ряд будущих денежных потоков как единовременная стоимость сегодня.Для инвесторов этот расчет может стать мощным инструментом для оценки бизнеса или других инвестиций с предсказуемой прибылью и денежным потоком.
Например, предположим, что компания ведет бизнес более 100 лет, имеет значительную и стабильную долю рынка в своей отрасли и, несмотря на стабильную прибыльность, не имеет возможности для значительного роста. Компания стабильна, последовательна и предсказуема. Эта компания, как и многие другие акции голубых фишек, является основным кандидатом для анализа дисконтированных денежных потоков.
Если мы можем спрогнозировать прибыль компании в будущем, мы можем использовать дисконтированный денежный поток, чтобы оценить, какой должна быть оценка этой компании сегодня. К сожалению, этот процесс не так прост, как просто сложить числа денежных потоков и получить значение. Вот здесь и появляется ставка дисконтирования.
Денежный поток завтра не стоит так много, как сегодня. Мы можем поблагодарить инфляцию за эту правду. Поскольку цены со временем растут, в будущем на доллар не будет куплено столько товаров, сколько можно купить сегодня.Во-вторых, в любом прогнозе будущего есть неопределенность. Мы просто не знаем, что произойдет, включая непредвиденное снижение доходов компании. У наличных денег сегодня нет такой неопределенности; что есть, то есть. Поскольку денежный поток в будущем несет в себе риск, которого нет у денежных средств сегодня, мы должны дисконтировать будущий денежный поток, чтобы компенсировать нам риск, который мы принимаем в ожидании его получения.
Эти два фактора — временная стоимость денег и риск неопределенности — вместе образуют теоретическую основу для ставки дисконтирования.Более высокая ставка дисконтирования подразумевает большую неопределенность, чем ниже приведенная стоимость нашего будущего денежного потока.
Вычислить, какую ставку дисконтирования использовать при расчете дисконтированного денежного потока, нелегко. Это столько же искусства, сколько и науки. Средневзвешенная стоимость капитала — один из лучших конкретных методов и отличное место для начала, но даже это не даст вам идеальной ставки дисконтирования для каждой ситуации.
Понимая, что наша ставка дисконтирования является обоснованным предположением, а не научной достоверностью, мы все же можем продолжить расчет и получить оценку стоимости этой компании.Если наш анализ показывает, что компания стоит больше, чем акции, торгуемые в настоящее время, это означает, что акции могут быть недооценены и их стоит покупать. Если наша оценка показывает, что акция стоит меньше, чем ее акции в настоящее время торгуются, то она может быть переоценена и является плохой инвестицией.
Дисконтное окно Федеральной резервной системы
Другое важное определение учетной ставки — это процентная ставка, взимаемая с финансовых учреждений, когда они занимают деньги в рамках кредитной линии дисконтного окна Федеральной резервной системы.
Дисконтное окно позволяет банкам занимать деньги для краткосрочных операционных нужд. Эти ссуды обычно продлеваются на 24 часа или меньше. Начисляемая процентная ставка определяется индивидуально каждым из Федеральных резервных банков, но централизованно пересматривается и определяется Советом управляющих Федеральной резервной системы. Как правило, учетная ставка будет одинаковой для всех Федеральных резервных банков, за исключением дней, когда она меняется.
Дисконтное окно фактически предлагает три разные кредитные программы, каждая со своей собственной учетной ставкой.Основная кредитная программа — это основная программа ФРС по кредитованию правомочных банков, находящихся в «в целом хорошем финансовом состоянии». Ставка дисконтирования по этим займам обычно устанавливается выше существующих рыночных процентных ставок, доступных из других источников краткосрочного долга или займа овернайт.
Программа вторичного кредитования доступна финансовым учреждениям, которые не имеют права на участие в программе первичного кредитования, но по-прежнему нуждаются в краткосрочных ссудах для финансирования краткосрочных потребностей или решения серьезных финансовых проблем.Ссуды по вторичной кредитной программе имеют более высокую учетную ставку, чем ссуды по первичной кредитной программе.
Третья программа — это сезонная кредитная программа, доступная небольшим финансовым учреждениям с периодическими колебаниями их денежного потока. Типичным примером являются сельскохозяйственные банки, ссуды и депозиты которых колеблются каждый год в зависимости от сезона роста. Ставка дисконтирования по этим кредитам определяется на основе среднего значения выбранных рыночных ставок сопоставимых альтернативных кредитных линий.
Если вы здесь, потому что хотите узнать больше об акциях, посетите наш Брокерский центр, где мы можем помочь вам начать работу.
Эта статья является частью Центра знаний Motley Fool’s Knowledge Center, который был создан на основе собранной мудрости фантастического сообщества инвесторов. Мы хотели бы услышать ваши вопросы, мысли и мнения о Центре знаний в целом или об этой странице в частности. Ваш вклад поможет нам помочь миру лучше инвестировать! Напишите нам по адресу knowledgecenter @ fool.ком . Спасибо — и продолжайте дурачиться!
.
