Как изобразить линейный масштаб: Виды записи масштаба — урок. География, 5 класс.

3.3.2. Численный и линейный масштаб

Масштаб карты — степень уменьшения линии на карте или плане относительно горизонтального проложения соответствующей линии на местности.

При работе с картой, планами или аэрофотоснимками местности пользуются различными масштабами: численным или линейным.

Численный масштаб — масштаб длин, выраженный отвлеченным числом, в котором числитель — единица, а знаменатель — число, показывающее, во сколько раз уменьшены линейные размеры карты (формула 1):

		d		1
		D		D / d

где d — длина линии на карте;

М — знаменатель масштаба карты;

D — длина горизонтального проложения этой линии на местности.

Масштаб карты или плана определяет подробность изображения на них

элементов местности. Чем больше значение знаменателя численного масштаба М, тем больше степень уменьшения горизонтальных проекций линий местности, тем мельче масштаб плана или карты и менее подробно изображены элементы местности. И наоборот, чем знаменатель М меньше, тем масштаб будет крупнее, тем с большей подробностью и детальностью могут быть показаны на них элементы местности.

Например, численный масштаб 1:50 000 является более мелким, чем масштаб 1:25 000, но более крупным, чем масштаб 1:100 000.

Для удобства знаменатель численного масштаба принимают равным круглому числу: 1:500, 1:1 000, 1:2 000, 1:5 000 и 1:10 000 — для планов,

1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000, 1:1 000 000 — для топографических карт. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены соответственно в 500, 1000, 2000 раз и т. д., то есть отрезку 1 см на плане соответствуют на местности длины: 500 см или 5 м; 1000 см или 10 м; 2000 см или 20 м и т.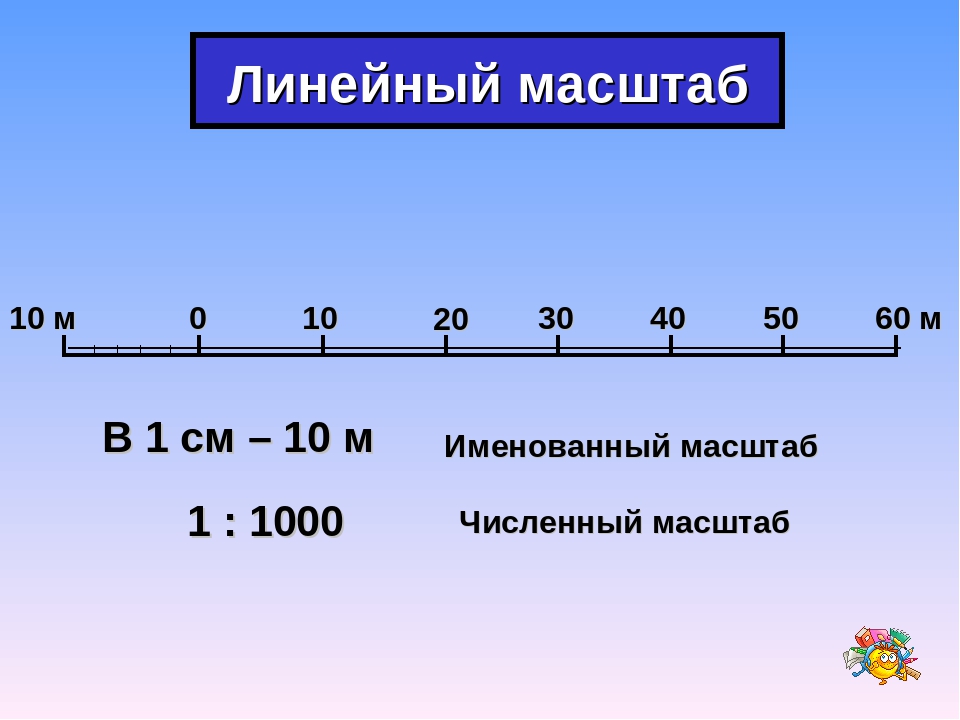

д.

Расстояние на местности в метрах или километрах, соответствующее 1 см карты или плана, называется величиной масштаба. Численный масштаб и величина масштаба размещаются под южной стороной рамки листа карты.

Численный масштаб — безразмерная величина, поэтому им можно пользоваться при измерениях в любых линейных мерах (метрах, милях и т.д.). Величина отношения 1:М сохраняет силу для всех линий плана или карты. Следовательно, масштаб является постоянной величиной.

Непосредственное использование численного масштаба в практической работе связано с вычислениями, которые необходимы для перехода от горизонтальных проекций линий местности к соответствующим линиям плана или карты, и наоборот.

При пользовании численным масштабом расстояния на карте или плане могут быть измерены в сантиметрах линейкой или курвиметром. Полученное при этом число сантиметров умножают на знаменатель масштаба.

Например, линия на карте d = 13,14 см, а масштаб карты 1:100 000. Используя формулу перехода от линий карты (плана) к горизонтальным проекциям соответствующих линий местности D = dM, получим D = 13,14 100 000 = 1314 000 см = 13 140 м = 13,14 км.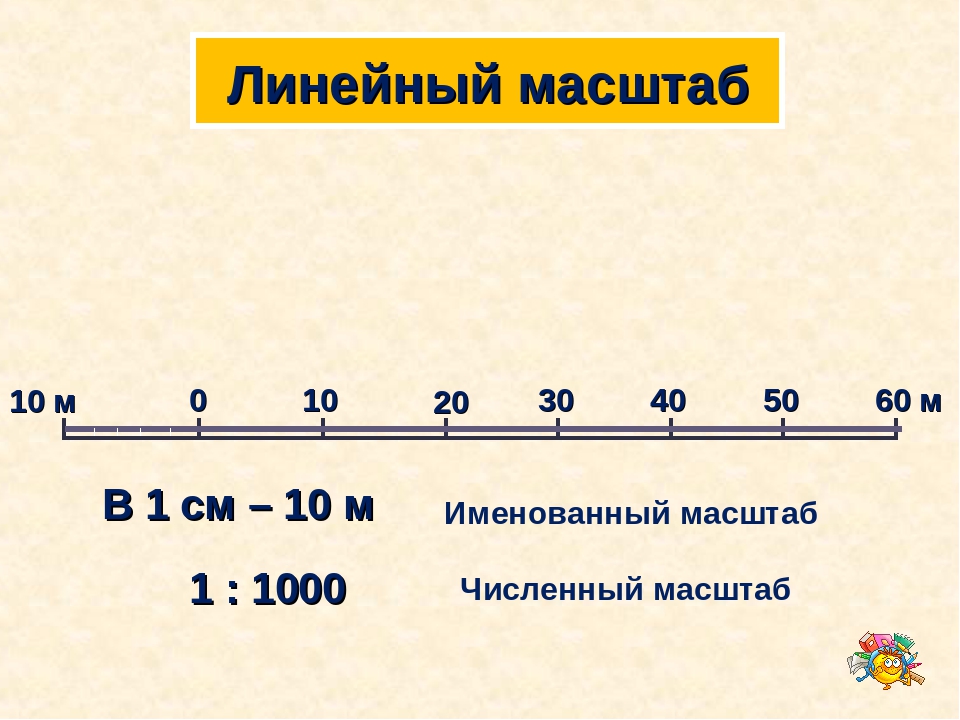

Для нанесения на карту или план линий, измеренных на местности, используют (равенство 2):

	d 	D	(2)
		M
		.
Например, D = 3750м; 1:М = 1:50 000, тогда d = 3750:50 000 = 0,075м
= 7,5см.
		Линейным масштабом называется
	графическое		изображение численного
	масштаба в виде прямой линии с
	делениями для отсчета расстояний. Для
Рис. 40. Линейн6ый масштаб	построения		линейного масштаба на
	прямой линии откладывают ряд отрезков

одинаковой длины, называемой основанием линейного масштаба (рис. 40). Основание масштаба обычно соответствует целому числу километров или сотен метров.

	Для повышения точности измерения первое основание разделено на
более	мелкие	части.	Для	карты	масштаба

1:50 000 наименьшее деление на линейном масштабе будет соответствовать

50 м.

Измерения по линейному масштабу производят циркулем- измерителем. При измерении циркуль следует держать одной рукой, наклоняя от себя так, чтобы были хорошо видны одновременно обе иглы. И определяя с помощью линейного масштаба длину линии, взятой с карты или плана, нужно правую ножку циркуля поставить на одну из черточек справа от нуля с таким расчетом, чтобы вторая его ножка точно совпала с крайним левым основанием масштаба.

Лекция № 5 точность карт и планов масштабы

Лекция № 5

ТОЧНОСТЬ КАРТ И ПЛАНОВ. МАСШТАБЫ

1. Понятие точности измерения и его отображения на карте и плане.

2. Понятие масштаба, виды масштабов.

3. Численный масштаб.

4. Линейный масштаб.

5. Поперечный масштаб

1. Предельная и графическая точности масштабов. При оценке точ­ности нанесения точек на план следует исходить из физиологических возможностей человеческого глаза. Как известно, глаз человека спосо­бен отчетливо различать две точки, если они располагаются под утлом не менее 60″ к наблюдателю. При меньшем угле зрения глаз восприни­мает две точки слившимися в одну.

Расстоянию наилучшего зрения, равному 25 см, углу в 60 » соответствует отрезок, равный 0,1 мм. Таков, например, диаметр кружка от укола остро отточенной иглы. Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линий местности, которым в данном масштабе соответствует отрезок 0,1 мм и более.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм (0,01см) на плане, называется предельной точностью масштаба.

Практически принимается, что длина отрезка на плане или карте может быть оценена с точностью 0,2 мм.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм (0,02 см) на плане, называется графической точностью масштаба.

Значения предельной и графической точностей различных числен­ных масштабов, найденные по формулам (17) и (18), приведены ниже.

Такая точность определения расстояний на плане или карте не мо­жет быть достигнута при использовании линейного масштаба. Поэто­му для повышения точности измерений расстояний на плане или карте применяют поперечный (трансверсальный) масштаб.

2. Масштаб — это отношение длины линии на чертеже, плане, карте l к длине горизонтального проложения, соответствующей линии местности S:

М = l/ S.

При выполнении съемок, составлении геодезических чертежей и при работе с ними приходится пользоваться следующими видами масштабов: численным, пояснительным, линейным, поперечным, переводным.

Численным горизонтальным масштабом называется отношение длины линии, взятой на чертеже, к длине той же линии, взятой на проекции, т.е. на уровенной поверхности или на горизонтальной плоскости.

Иначе говоря, масштаб — это коэффициент подобия, поскольку составление чертежа представляет собой подобное преобразование ортогональной проекции местности, полученной на горизонтальной плоскости.

На профилях различают еще вертикальный численный масштаб, относящийся к высотным элементам проекции.

3. Численный масштаб записывают в виде правильной дроби, у которой числитель единица, а знаменатель показывает степень уменьшения линейных размеров на плане. В метрической системе мер пользуются такими масштабами: 1:500, 1:1000, 1:2000, 1:5000, 1:10 000 и т.д. При сравнении двух или нескольких масштабов между собой надо иметь в виду, что чем больше знаменатель, тем, крупнее масштаб плана, и на таком плане изобразится больше мелких деталей, а измерение линий по нему можно сделать с большей точностью. Следовательно, масштаб 1:5000 крупнее 1:10 000, но мельче 1:2000. Например, численный масштаб 1:1000 показывает, что все горизонтальные проложения линий местности при перенесении их на план уменьшены в 1000 раз, то есть отрезок в 1 см на плане соответствует линии в 1000 см (10 м) на местности

Пример 1: Длина линии на плане масштаба 1:5000 равна 4 см.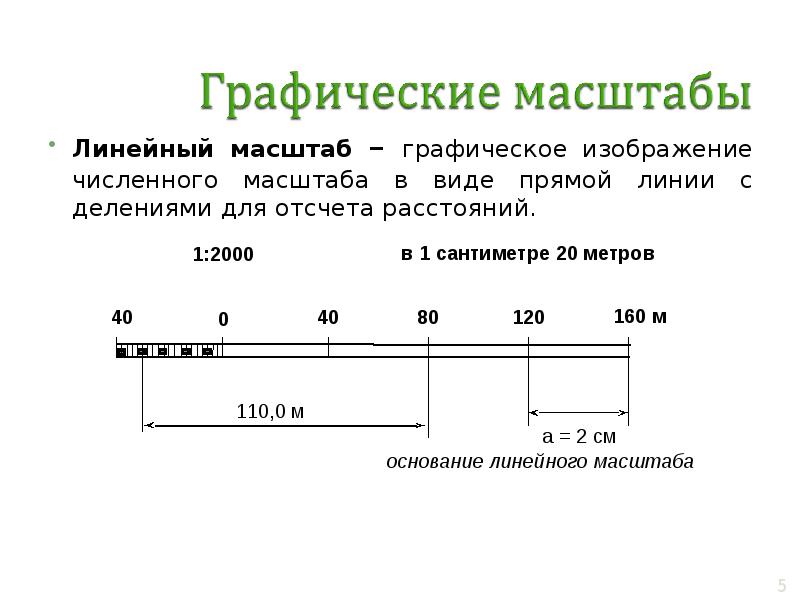 Определить ее длину на местности. Решение: 4х5000=20000 см = 200 м.

Пример 2: Если горизонтальное проложение линии местности равно 283,7 м, масштаб 1:5000, т.е. в сантиметре 50 м, то длина линии на плане будет 283,7:50 = 5,67 см.

4. Линейный масштаб представляет собой шкалу, деления которой подписаны применительно к заданному численному масштабу. Им пользуются при нанесении проекции линий на чертеж, а также при измерении линий на чертеже с целью определения соответствующей им длины на проекции. Применение линейного масштаба избавляет от вычислений, выполняемых при пользовании численным масштабом. Хотя эти вычисления просты, но при большом их количестве становятся утомительными и отнимают много времени.

Рисунок 1 – Линейный масштаб

Для построения метрического линейного масштаба берут прямую линию и откладывают на ней несколько раз (четыре-пять) один и тот же отрезок (1-2 см), называемый основанием масштаба (рис. 1). Первое основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которое на проекции соответствует в заданном масштабе основанию. Вправо от нуля деления масштаба подписывают соответственно расстояниям на местности, выраженным отрезками от нуля до штриха с подписью. В качестве основания для метрических масштабов чаще всего берут отрезок в 2 см. При работе в масштабе 1:1000 и основании, равном 2 см, линейный масштаб подписывают так, как это указано на рис. 1.

При этом масштабе 2 см на бумаге соответствует 2000 см или 20 м на местности, а 1 см — соответственно 1000 см или 10 м.

При пользовании линейным масштабом правую ножку циркуля ставят на нулевое деление или на одно из делений справа от нуля в зависимости от того, меньше или больше одного основания нужно измерить или отложить линию. Левая ножка циркуля располагается либо на делении с нулевой подписью, если длина линии содержит целое число оснований, либо в пределах первого основания, имеющего мелкие деления, с оценкой на глаз десятых долей этих делений.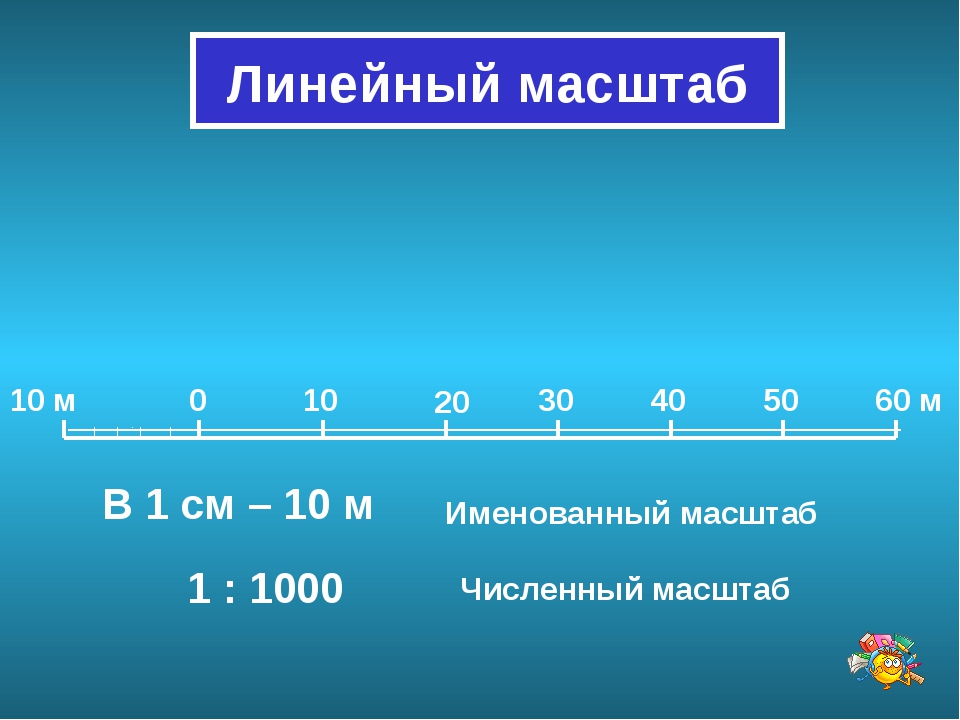 По горизонтальным размерным линиям легко сообразить, где находились ножки циркуля, когда брали тот или иной отрезок. Видно также, что каждый отрезок составляется из двух частей: от нуля до правой ножки циркуля и от нуля до левой ножки его.

При откладывании с помощью измерителя круглых чисел 20, 40 м и т. д. одна ножка измерителя устанавливается на нулевое деление, а вторая — на деление с соответствующей надписью. Каждое деление первого основания слева равно: 20 м : 10 = 2 м. Чтобы отложить, например, 76 м, надо одну ножку измерителя поставить на деление 60, а вторую на восьмое деление от нуля слева (8 х 2 м = 16 м). В итоге получается: 60 м + 16 м = 76 м. Десятые доли метра определяются на глаз (рис. 1).

Применение простого линейного масштаба ограничено вследствие сравнительно небольшой его точности, поэтому для составления точных планов и карт пользуются преимущественно поперечным масштабом.

5. Поперечный масштаб применяют для того, чтобы избежать оценки на глаз долей делений первого основания и в результате повысить точность измерений и построений на чертежах. Обычно пользуются поперечными

Рисунок 2 – Поперечные масштаб

масштабами, награвированными на тонких металлических пластинках или на транспортирах. Поперечный масштаб строится в виде прямоугольника длиной 8-10 см и высотой 2-3 см. В случае надобности поперечный масштаб для заданного численного можно построить (рис.2) следующим образом.

На горизонтальной прямой, как и при построении линейного масштаба, откладывают несколько раз основание (6-10 отрезков, обычно 2 см) и первый отрезок делят на 10 равных частей (обычно в 2 мм). Полученные деления подписывают подобно тому, как это делалось при построении линейного масштаба. Из концов всех оснований проводят вверх вертикальные линии; на крайних линиях откладывают по 10 одинаковых отрезков, например, по 2 мм каждый; полученные в результате этого точки соединяют горизонтальными прямыми. Верхнюю линию первого основания делят на десять равных частей и к ранее нанесенным делениям внизу, на первом основании, проводят косые линии, называемые трансверсалями, как показано на рис.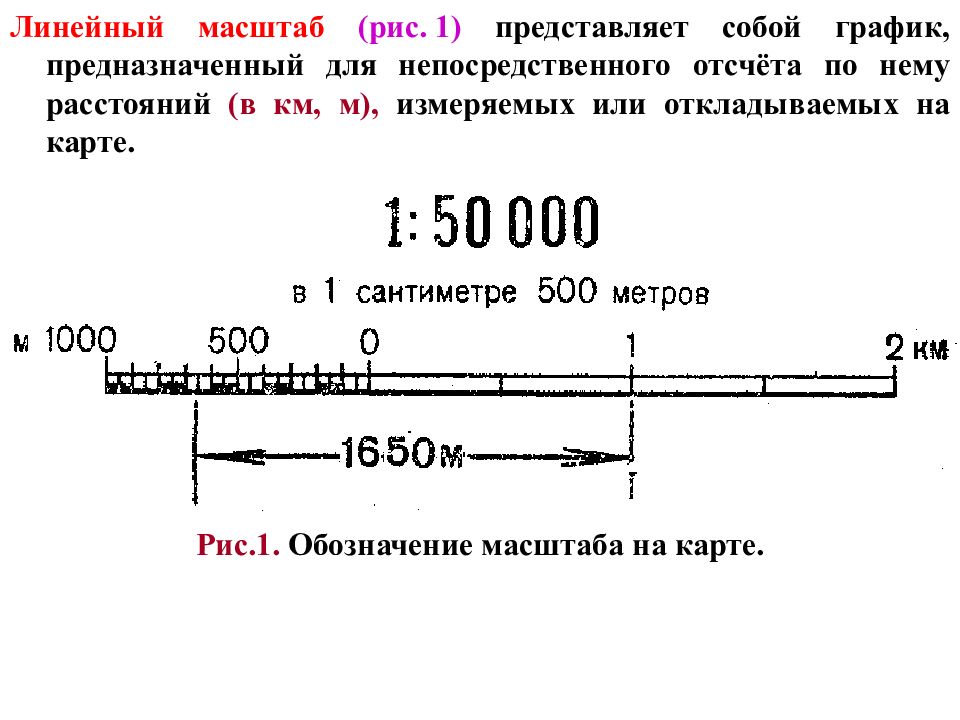 2. Между косыми параллельными линиями заключены горизонтальные отрезки, равные десятой доле основания каждой в отдельности. Между нулевой вертикальной линией и смежной с ней косой линией заключаются отрезки от одной до десяти десятых наименьшего деления основания или от одной до десяти сотых самого основания, т.е. как раз то, что приходится отсчитывать на глаз по линейному масштабу. Значение мелких делений подписано у крайней левой вертикальной линии масштаба, что облегчает пользование им.

Основание самого большого треугольника равно 2 мм. Основание (Х) самого маленького треугольника называется наименьшим делением поперечного масштаба.

Если высоту большого треугольника обозначить буквой Н, а маленького треугольника h, то из соотношения 2/Н=Х/h, получается, что

Х=(2· h)/Н; но h=Н/10,

тогда Х=(2·Н)/(Н·10)=0,2 мм

Каждая от откладываемых по масштабу линий слагается из трех частей:

1) количества целых основания, взятых от нулевой вертикальной линии до правой ножки циркуля;

2) десятых долей основания, взятых между косыми линиями от проходящей через нуль до левой ножки циркуля;

3) сотых долей основания, расположенных между вертикальной и косой линиями, выходящими из нулевой точки масштаба.

Пользуясь поперечным масштабом, нужно следить за тем, чтобы при отложении или измерении отрезка концы обеих ножек циркуля всегда находились на одной и той же горизонтальной линии масштаба.

Масштабы, награвированные на пластинках или на транспортирах, следует разметить соответственно тому численному масштабу, в котором составлен или будет составляться чертеж.

Предельной точностью масштаба называется отрезок на проекции местности, который соответствует наименьшему делению поперечного масштаба, т.е. одной сотой основания его. Наименьшее деление поперечного масштаба равно 0,2 мм или 1/100 основания масштаба.

Половину наименьшего деления основания, равную 0,1 мм, называют графической точностью масштаба.

Поперечный масштаб, в котором наименьшее деление равно 1/100 основания, называется сотенным или нормальным.

Если линейный или поперечный масштаб не построен, а на плане указан только численный масштаб, то для определения предельной точности этого масштаба нужно 0,2 мм умножить на знаменатель его.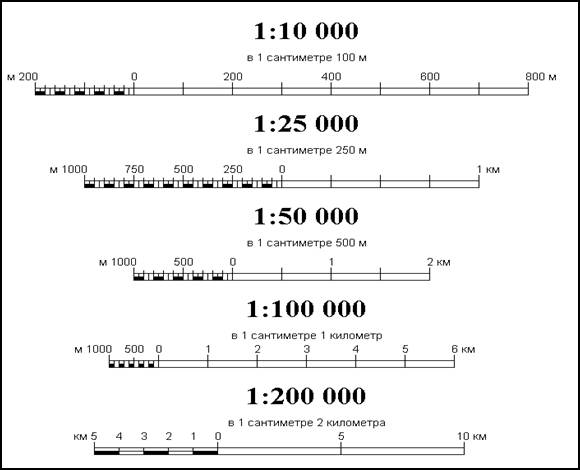 Например, если масштаб 1:1000, 1:2000, 1:5000,1:10 000, то предельная точность его соответственно 0,2, 0,4, 1,0 и 2,0 м.

Чтобы определить расстояния (или отложить отрезки) с помощью поперечного масштаба, необходимо вначале определить, чему равно в принятом масштабе основание, десятая и сотая части основания, а также точность данного масштаба. Например, при масштабе 1: 1000, в 1 см — 10 м, основание 20 м, 1/10 основания -2 м, наименьшее деление -0,2 м, точность масштаба — 0,1 м.

Следовательно, на плане, составленном в масштабе, предельная точность которого равна 1 м, можно измерять или откладывать длину линий с точностью до 1 м. Предмет, имеющий размеры, меньшие предельной точности масштаба, нельзя изобразить на плане.

Для карты масштаба 1:50000 точность масштаба равна 5 м, для карты 1:25000 – 2,5 м и т.п.

Рисунок 3 – Линейный переводный масштаб для численного 1:4200

Если такой предмет по тем или иным соображениям все же надо показать, то его наносят в условном виде с искажением размеров.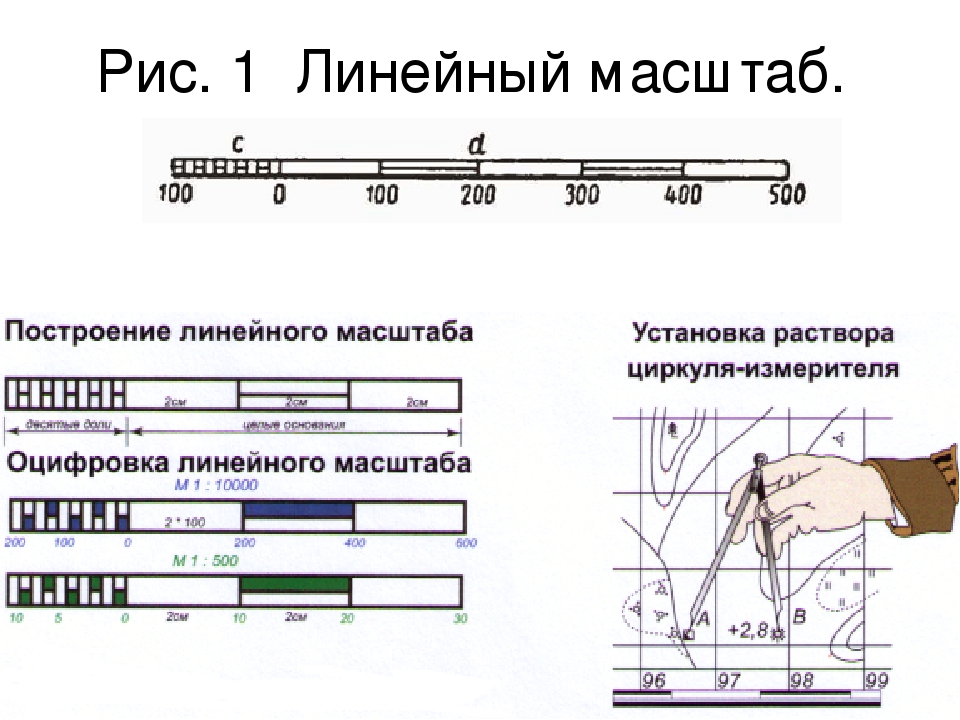

В задании на съемку нужно указывать масштаб, применительно к которому ее следует производить. В некоторых случаях план составляют в более крупном масштабе, чем тот, применительно к которому выполнялась съемка. Делается это для облегчения проектирования. Ясно, что точность такого плана соответствует масштабу съемки, а не масштабу составления чертежа.

Переводный линейный или поперечный масштаб строят в тех случаях, когда заданный численный масштаб связан с единицами измерения не метрического наименования, например, когда длину линий измеряют шагами, саженями, в делениях дальномерной рейки и т.п. На самом же переводном масштабе расстояния должны получаться в метрической системе мер.

Для построения переводного масштаба подбирают такое основание, которое соответствует удобному числу единиц, принятых для измерения на местности – 50, 100, 200 и т.д. Например, если задан численный масштаб 1:4200, то двум сантиметрам соответствует 84 м, а ближайшим круглым числом к 84 будет 100, значит, надо найти отрезок х, соответствующий 100 м на плане масштаба 1:4200, и взять этот отрезок за основание переводного масштаба. Из пропорции 2:84= х:100 получается х =2,38 см. Линейный масштаб для рассмотренного примера показан на рис.3. Если бы на этом рисунке за основание масштаба был взят отрезок, равный 2 см, то получились бы неудобные для измерения деления 84, 168 и т.д. вместо 100, 200 и т.д.т

Например, для того чтобы, в масштабе 1:50000 (рис. 4) отложить длину, равную на местности 1760 м, правую ножку циркуля-измерителя совмещают с точкой 1000 м справа от нуля, а левую с точкой 700 м слева от нуля. Затем изме­ритель поднимают на шесть делений вверх (60 м) и раздвигают до точки, соответ­ствующей 1760 м.

Рисунок 4 – Поперечный масштаб для числового масштаба 1:50000

Чтобы отложить с помощью измерителя 60 м в масштабе 1:1000, достаточно поставить одну ножку измерителя на нуль, а другую на третье основание масштаба (с надписью 60).

Чтобы отложить 68 м, необходимо передвинуть ножку измерителя от нуля на четыре деления влево. Если переместить ножку измерителя на одну горизонтальную линейку вверх, правую — по вертикали, а левую — по наклонной линии, то к величине 68 м прибавится отрезок X₁ = 0,2 м, соответственно на второй линейке добавится 0,4 м, на третьей Х₃ = 0,6 м и т. д. Если расположить измеритель посредине между горизонтальными линейками, например, между 5-ой и 6-ой, то величина отрезка увеличится на 0,1 м. В нашем случае (рис. 5) получается 69,1 м.

Рисунок 5 – Работа с поперечным масштабом

Для определения расстояния с помощью поперечного
масштаба, измеряемый отрезок с плана или карты заключают
в раствор измерителя, который устанавливают таким
образом, чтобы левая игла находилась на одной из
трансверсалей, а правая — на одном из перпендикуляров к
основанию (на рис. 5 установка измерителя отмечена крести­
ком). Тогда измеряемая линия складывается из трех частей:
первая часть равна длине суммы оснований, отложенных
вправо от нуля, вторая — суммарной длине общего количества
малых делений левого основания, третья — отрезку соот­-
ветствующей параллели, заключенному между первой
трансверсалью и секущей линией, проходящей через нулевой
штрих основания поперечного масштаба.

Применительно к рис. 5 определяемое расстояние

L = 4×20 + 5×2 + 7x 0,2 = 91,4 м, в масштабе плана 1:5000 расстояние равнялось бы: L = 4 х 100 + 5×10 + 7×1 = 457 м.

Лекция № 6

УСЛОВНЫЕ ЗНАКИ ПЛАНОВ И КАРТ.

1. Понятие об условных знаках планов карт. Контурные (масштабные) условные знаки.

2. Внемасштабные условные знаки.

4. Условные линейные знаки.

5. Пояснительные условные знаки

1. Важнейшим показателем качества топографических карт и планов наряду с точностью является их наглядность. Она достигается примене­нием условных знаков, с помощью которых на картах и планах изобра­жаются ситуация и рельеф местности. Условные знаки, изображающие ситуацию местности, подразделяются на площадные, внемасштабные, линейные и пояснительные .

Площадные, или масштабные, условные знаки служат для изобра­жения объектов, занимающих значительную площадь и выражающихся в масштабе карты или плана.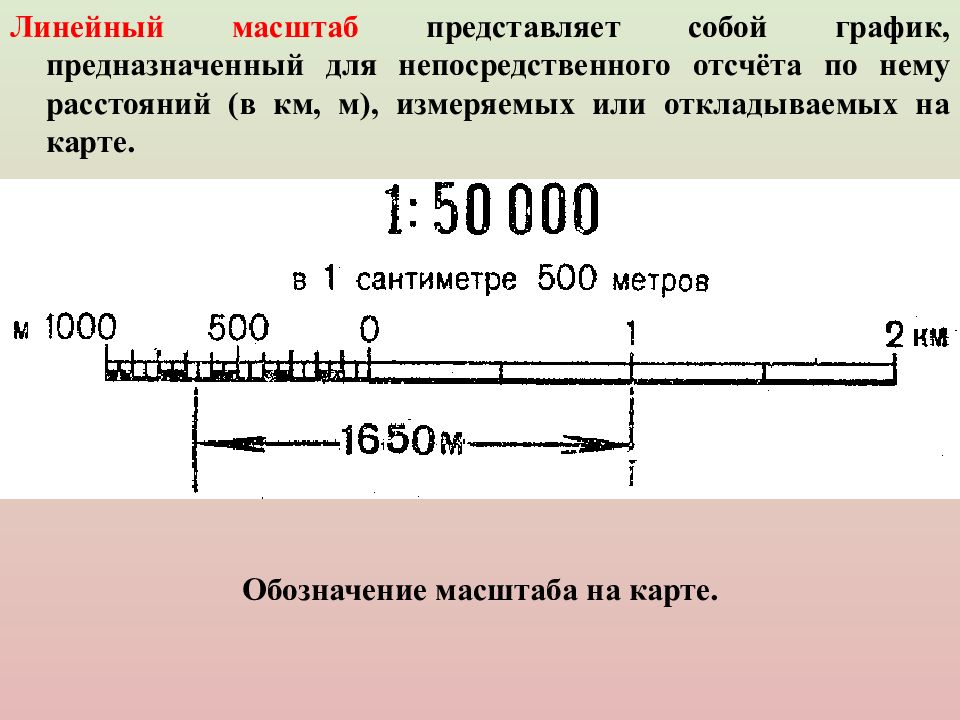 Площадной условный знак состоит из знака границы объекта и заполняющих его знаков или условной окрас­ки. Контур объекта показывается точечным пунктиром (контур леса, луга, болота), сплошной линией (контур водоема, населенного пункта) или условным знаком соответствующей границы (канавы, изгороди). Заполняющие знаки располагаются внутри контура в определенном порядке (произвольно, в шахматном порядке, горизонтальными и вер­тикальными рядами). Площадные условные знаки позволяют не только найти расположение объекта, но и оценить его линейные размеры, площадь и очертания.

2. Внемасштабными называются такие условные знаки, предметы местности изображаются без соблюдения масштаба карты или плана (например, отдельное дерево, километровый столб, колодец и т. д.). Эти знаки не позволяют судить о размерах изображаемых мест­ных предметов. Положению предмета на местности соответствует опре­деленная точка знака (обычно в центре или в вершине прямого угла у основания знака). Следует учесть, что одни и те же местные предметы на картах или планах крупных масштабов могут быть выражены пло­щадными (масштабными) условными знаками, а на картах мелких масштабов — внемасштабными условными знаками.

3. Линейными условными знаками называются знаки, изображающие протяженные объекты на местности, например железные, автогуже­вые дороги, ручьи, границы и другие. Они занимают промежуточное положение между масштабными и внемасштабными условными знака­ми. Длина таких объектов выражается в масштабе карты, а ширина на карте — вне масштаба; обычно она получается больше ширины изоб­ражаемого объекта местности, а его положению соответствует продоль­ная ось условного знака.

4. Пояснительные условные знаки служат для дополнительной харак­теристики изображаемых на карте местных предметов, например: дли­на, ширина и грузоподъемность моста, ширина и характер покрытия дорог, средняя толщина и высота деревьев в лесу, глубина и характер грунта брода и т. д. Различные надписи и собственные названия объек­тов на картах также носят пояснительный характер; каждая из них выполняется установленным шрифтом и буквами определенного раз­мера.

Рельеф местности на топографических планах и картах изображает­ся следующими методами: методами штрихов, отмывки, цветной пла­стики, отметок или горизонталей. На картах крупного масштаба и планах рельеф изображается, как правило, методом горизонталей, имеющим значительные преимущества перед всеми остальными ме­тодами.

Все условные знаки карт и планов должны обладать наглядностью, выразительностью и легко вычерчиваться. Условные знаки для всех масштабов карт и планов устанавливаются нормативными и инструк­тивными документами и являются обязательными для всех организа­ций и ведомств, выполняющих съемочные работы.

Учитывая многообразие сельскохозяйственных угодий и объектов, которое не укладывается в рамки обязательных условных знаков, зем­леустроительные организации издают дополнительные условные зна­ки, отражающие специфику сельскохозяйственного производства.

В зависимости от масштаба карт или плана местные предметы пока­зываются с различной подробностью. Так, например, если на плане масштаба 1:2000 в населенном пункте будут показаны не только отдель­ные дома, но и их форма, то на карте масштаба 1:50 000 — только квар­талы, а на карте масштаба 1:1 000 000 весь город обозначится неболь­шим кружком. Подобное обобщение элементов ситуации и рельефа при переходе от более крупных масштабов к более мелким называется ге­нерализацией карт.

Лекция № 7

ИЗМЕРЕНИЯ И ИХ ПОГРЕШНОСТИ

1. Общие сведения об измерениях

2. Погрешности измерений и их классификация

1. Измерения играют весьма важную роль во всех областях науки и техники; они дают количественную информацию об объектах и явле­ниях, происходящих в природе, позволяют устанавливать происходя­щие в ней закономерности. Основным содержанием геодезических работ является измерение физических величин (горизонтальных и вер­тикальных углов, линий и др.).

В общем смысле физическая величина является характеристикой одного из свойств физического объекта (явления, процесса), общей в качественном отношении для ряда физических объектов, но в количе­ственном выражении индивидуальной для каждого из них.

Измерение физических величин представляет собой познавательный процесс, заключающийся в сравнении данной величины с другой изве­стной величиной, принятой за единицу меры (эталон). В Рекомендаци­ях по межгосударственной стандартизации 29-99 «ГСИ. Метрология. Основные термины и определения» дается следующее определение измерения: «Измерение — совокупность операций по применению тех­нического средства, хранящего единицу физической величины, обеспе­чивающих нахождение соотношения (в явном или неявном виде) измеряе­мой величины с ее единицей и получение значения этой величины».

Измерения любой величины следует рассматривать с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей точность измерений.

Измерения выполняют с помощью технических средств измерений, которые имеют нормированные метрологические характеристики, вос­производящие и (или) хранящие единицу физической величины, раз­мер которой принимают неизменным (в пределах установленной по­грешности) в течение некоторого интервала времени. Измерения производят по определенному алгоритму, называемому методом выпол­нения измерений. После выполнения измерения и получения числового значения (результата измерения) производят оценку погрешности из­мерения.

Различают непосредственные (прямые) и косвенные измерения. При непосредственных измерениях выполняют непосредственное сравнение определяемой величины с единицей меры. Примером может слу­жить изменив длины путем последовательного укладывания мерного прибора (мерной ленты, рулетки) вдоль измеряемой линии. При косвенных измерениях определяемую величину находят путем вычислений по результатам непосредственных измерении одной или нескольких величин, связанных с определяемой величиной математической зависимостью. Примерами являются определения длин линии оптиче­скими дальномерами, параллактическим способом, светодальномерами.

Любое геодезическое измерение выполняется при наличии и взаи­модействии пяти необходимых факторов: объекта измерений, исполнителя, прибора, метода измерения и внешней среды. Под внешней cpедой понимают совокупность всех внешних условий измерений: рельеф, грунт местности, растительный покров, температура, влажность воздуха, освещение, ветер, облачность и др. Конкрет­ное содержание этих факторов в процессе измерения определяет так называемые условия измерения.

С условиями измерений связаны понятия ровноточных и неравноточных измерени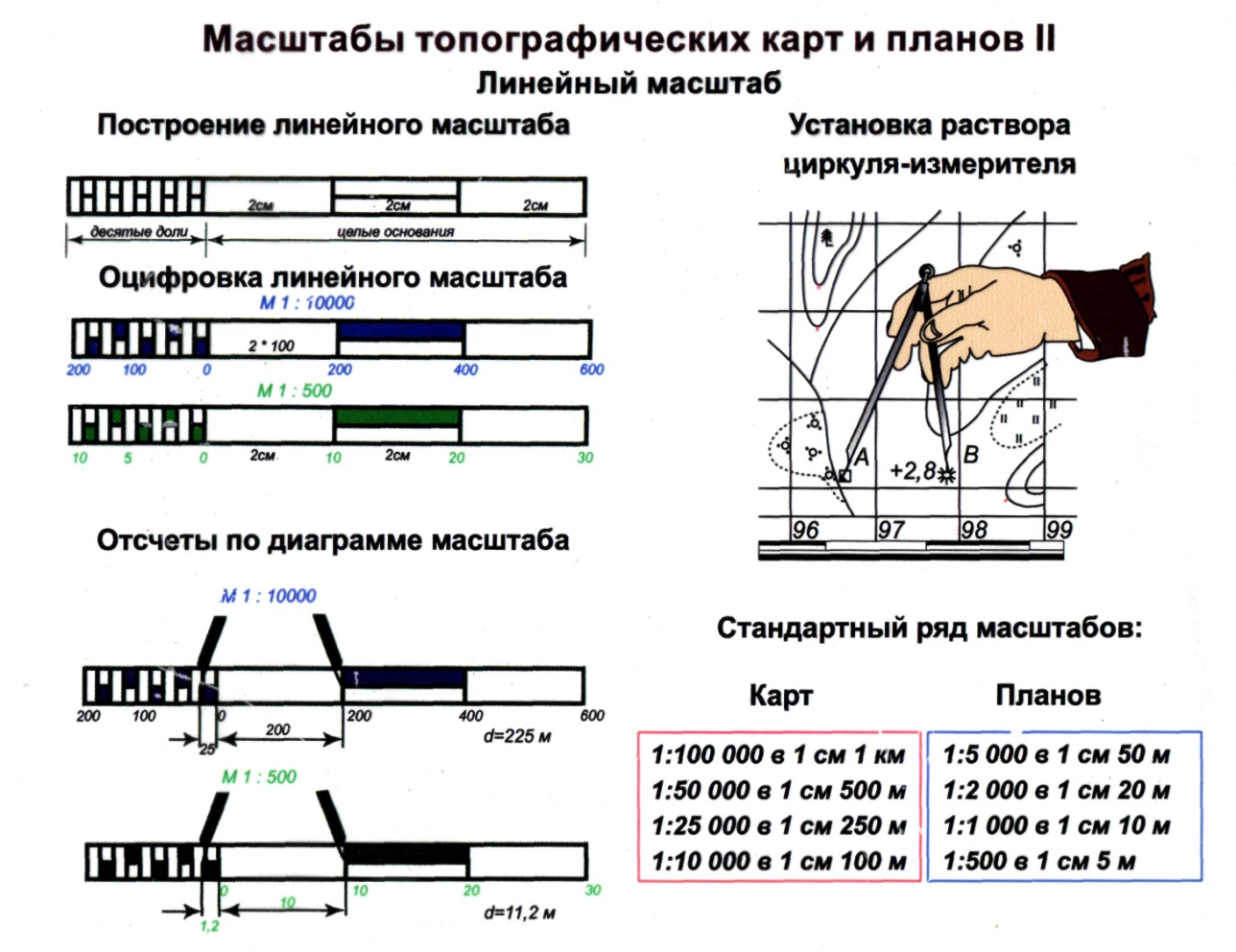й. Измерения, выполняемые при неизменных условиях, позволяющих считать результаты измерении одинаково надежными называют равноточными. Если хотя бы один из факторов, определяющих содержание условий измерений, будет изменяться, то такие измерения называют неравноточными.

Как правило, результаты геодезических измерений непосредствен­но не используются, а предварительно подвергаются математической обработке, которая с помощью вычислительных методов и средств при­водит результаты измерений к виду, удобному для практического использования.

При вычислительной обработке результатов измерений выделяют необходимые и избыточные (добавочные) измерения. Необходимыми называют такие измерения, которые позволяют получить единственный результат прямого или косвенного измерения данной величины. Избыточные измерения позволяют получить два и более значений определяемой величины. Если одна и та же величина измерена п раз, то одно из этих измерений будет необходимым, а остальные (п — 1) из­мерения — избыточные. Например, длина линии местности измерена в прямом и обратном направлениях; в этом случае второе измерение является избыточным. В геодезической практике избыточные измерения являются средством контроля и повышения точности результатов измерений и позволяют судить о качестве измерении.

Внешние условия измерений, методы и средства измерении обуслов­ливают разделение измерений на независимые и зависимые. Независимыми считают измерения, в которых отсутствуют погрешности, одинаково искажающие результаты этих измерений. Геодезические измерения, выполненные разными наблюдателями, приборами, методами в различных внешних условиях являются независимыми.

Поскольку при производстве геодезических измерении наблюдатель, прибор и метод измерений часто остаются неизменными, то полученные результаты будут зависимыми. Однако анализ влияния этих фак­торов показывает, что в пределах необходимой для инженерных работ точности возникающими в этом случае зависимостями можно прене­бречь. Вопросы учета взаимозависимости измеренных величин выхо­дят за рамки излагаемого учебного материала.

2. Любые измерения, как бы тщательно они ни выполнялись, сопро­вождаются неизбежными погрешностями.

Под погрешностью измерения величины понимают отклонение результата измерения от его истинного (действительного) значения, т. е.

А = 1-Х (1)

где А — истинная погрешность измерения; / — результат измерения; X — истинное значение величины.

Согласно РМГ 29-99 под истинным значением физической величины понимается такое значение физической величины, которое идеальным образом характеризует ее в количественном и качественном отноше­ниях. Действительное значение физической величины — это значение величины, полученное в результате ее измерения и настолько близкое к истинному значению, что в поставленной задаче может быть исполь­зовано вместо него. Результат измерения представляет собой прибли­женную оценку истинного значения величины.

Истинное значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершен­ную методику измерений. Лишь в отдельных случаях может быть из­вестно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.

Появление в измерениях погрешностей является следствием непре­рывных изменений указанных ранее факторов, определяющих условия измерений. Каждый из отдельных факторов вызывает появление так называемой элементарной погрешности; общая погрешность измере­ния является алгебраической суммой элементарных погрешностей. Элементарные погрешности могут быть весьма малыми по величине, но их суммарное воздействие способно существенно исказить резуль­тат измерения.

Погрешности измерений можно классифицировать по двум призна­кам: по источнику происхождения; по характеру их действия на резуль­таты измерений и свойствам.

По источнику происхождения различают погрешности средства измерения (приборные), личные (субъективные), внешние и метода из­мерений. Погрешности средства измерения возникают от несовершен­ства применяемых приборов и вследствие невозможности их точной юстировки. Личные погрешности являются следствием физиологиче­ских особенностей наблюдателя. К внешним относятся погрешности, вызываемые воздействием внешних условий измерений (температуры, давления, влажности, скорости ветра, освещенности, рефракции и т. п.) на объект измерения, на измерительный комплекс и на самого наблю­дателя. Погрешности метода измерения вызываются несовершенством принятого метода измерения величины.

По характеру действия погрешностей на результаты измерений их разделяют на грубые, систематические и случайные.

К грубым относят погрешности, сильно искажающие результаты измерения, которые превосходят некоторый допустимый предел, устанавливаемый для данных условий измерений. Грубые погрешности являются следствием промахов и просчетов из-за невнимательности наблюдателя либо его недостаточной квалификации, а также неис­правности применяемых приборов. Грубые погрешности должны быть выявлены и полностью исключены из результатов измерений; это до­стигается путем выполнения избыточных измерений и контрольных вычислений.

Систематическими называют такие погрешности, которые возника­ют от определенного источника погрешностей и всякий раз при данных условиях измерений могут быть одинаковыми по величине и знаку (по­стоянные систематические погрешности), изменяться по определенно­му закону (переменные) либо, изменяясь по величине, сохранять знак (односторонне действующие).

Примерами систематических погрешностей геодезических измере­ний могут служить: погрешность в отсчете по рейке, обусловленная невыполнением главного геометрического условия, предъявляемого к нивелиру; погрешность измерения горизонтального угла при одном положении вертикального круга, вызванная наличием коллимационной погрешности теодолита; погрешность в длине из-за отклонения мерной ленты от створа измеряемой линии и т. п. Влияние переменных систе­матических погрешностей может быть выражено функцией, связыва­ющей результат измерения с каким-либо источником (например, из­менение длины мерного прибора в зависимости от температуры).

В современных высокоточных измерениях систематические погреш­ности являются основным препятствием для существенного повыше­ния точности геодезических определений. Поэтому выявление систе­матических погрешностей, источников их происхождения и выбор мер борьбы с влиянием этих погрешностей являются важнейшей задачей теории погрешностей измерений. Влияние систематических погрешно­стей на результаты геодезических измерений должно быть сведено к минимуму тщательными поверками и юстировками приборов, приме­нением соответствующих методик измерений, а также введением по­правок в измеренные величины.

Случайные погрешности — это неизбежные погрешности, возник­шие из-за несовершенства органов чувств и применяемых приборов, а также изменения внешней среды. Величину, знак и характер влияния случайной погрешности на каждый отдельный результат измерения заранее установить невозможно, поэтому они не могут быть исключе­ны из результатов измерений. Однако эти погрешности при достаточ­но большом числе измерений подчиняются определенным статистическим закономерностям, и изучение их дает возможность получить наиболее надежный результат из совокупности результатов измерений и оценить его точность.

Из вышеизложенного следует, что основными задачами теории погрешностей измерений являются: изучение видов, причин возник­новения погрешностей измерений и их свойств, нахождение по резуль­татам измерений наиболее надежного значения измеряемой величи­ны, установление критериев требуемой точности, оценка точности результатов измерений и функций измеренных величин. Методы ре­шения этих задач позволяют заранее обосновать необходимую и доста­точную точность измерений и с учетом этого произвести выбор соот­ветствующих приборов и методики измерений.

Поскольку грубые и систематические погрешности могут быть об­наружены, изучены и исключены из результатов измерений, в даль­нейшем будем полагать, что на результаты измерений основное влия­ние оказывают случайные погрешности.

Опыт показывает, что случайные погрешности можно рассматри­вать как случайные математические величины, изучением которых занимается теория вероятностей и математическая статистика. Даль­нейшее изложение элементов теории погрешностей приводится с уче­том того, что основы указанных дисциплин изучаются студентами в составе курса высшей математики.

Масштаб плана. Численный, линейный и поперечный масштабы. Точность масштаба

Отношение длины отрезка линии на плане к горизонтальной проекции соответствующего отрезка линии на местности называется масштабом плана. Если масштаб выражается дробью с числителем единица,

При составлении плана необходимо длину каждой линии местности уменьшать в одно и то же число раз; это можно сделать при помощи линейного масштаба. Для построения линейного масштаба на прямой откладывают несколько раз какой-нибудь отрезок, например 1 или 2 см. Откладываемый отрезок называется основанием масштаба. На рис. 6 за основание масштаба взят 1 см. Крайний левый отрезок обычно делят на 10 равных частей. Каждому отрезку на линейном масштабе соответствует определенный отрезок на местности. Отрезки, отложенные от нулевой черточки вправо, в масштабе 1 : 10000, представят на местности 100, 200, 300, 400, 500 м, а влево -10; 20; 30; …; 100 м. Если какой-либо отрезок линии плана оказался на масштабе равным сс1, то ему соответствует на местности 240 м. Наименьший отрезок по такому масштабу соответствует 10 м на местности.

Более мелкие деления можно получить, построив поперечный масштаб. Примем за основание поперечного масштаба отрезок АВ. равный 2 см. и разделим его на 10 равных частей. Это можно сделать так: под произвольным к основанию углом проведем прямую АР, на ней от точки А отложим 10 произвольных, но равных частей.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 ММ на плане, называют ТОЧНОСТЬЮ масштаба. Так, для масштабов 1:500, 1:1000, 1:5000, 1 : 10000, 1 :25 000 точность соответственно равна: 0,05 м, 0,1 м, 0,5 м, 1,0 м, 2,5 м. Это значит, что отрезки, меньшие указанных, уже не будут изображаться на плане данного масштаба. Задаваясь наименьшими длинами линий местности, которые должны быть изображены на плане, можно установить необходимый масштаб плана. Так, например, если наименьший отрезок на местности, который должен изобразиться на плане, равен 0,2 м, то, очевидно, план должен быть составлен в масштабе не мельче 1 :2000. В самом деле, по условию 0,01 см на плане должно соответствовать 0,2 м на местности или 1 см плана — 2000 см на местности, а это значит, что численный масштаб плана должен быть 1 : 2000.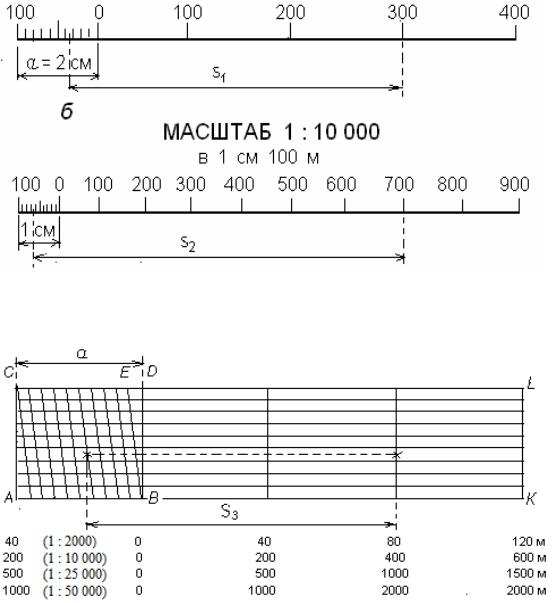

Онлайн урок: Масштаб по предмету Математика 6 класс

Различают три вида масштаба:

• численный
• именованный
• графический

Графический, в свою очередь, делится на линейный и поперечный.

Численный масштаб представляют в виде дроби, где числитель — это единица, а знаменатель показывает степень уменьшения размеров изображения объектов относительно их реальных размеров.

Численный масштаб — это дробь, поэтому числитель и знаменатель выражены в одинаковых единицах измерения.

При обозначении численного масштаба не указывают единицы измерения, указывают только числа (1:2 000, 1:200 000, 1:100 и т. п.).

 

Пример 1

Численный масштаб карты 1:15 000 000, что он показывает?

Данный масштаб показывает, что 1 см на карте соответствует 15 000 000 см в действительности.

Нужно помнить, что чем меньше значение знаменателя в масштабе, тем крупнее масштаб.

 

Пример 2

Масштаб 1:1 000 крупнее, чем 1:15 000, так как знаменатель первого масштаба равен 1 000, а знаменатель второго масштаба 15 000.

1 000 меньше 15 000, следовательно, масштаб 1:1 000 крупнее.

Чем крупнее масштаб, тем больше можно изобразить объектов действительности, карта (план) получается подробней и содержательней.

При большем масштабе хорошо изображать небольшие по площади территории.

Применяется в топографических картах и планах.

На чертежах могут изображаться как уменьшенные изображения реальных объектов, так и увеличенные, если размеры изображаемого объекта слишком малы.

У меня есть дополнительная информация к этой части урока!

Закрыть

Если в записи масштаба знаменатель больше числителя, то такой масштаб называют масштабом уменьшения.

Масштаб 1:m, где m > 1

(например, масштаб 1:4, 1:20, 1:100 и т.п.)

Если в записи масштаба знаменатель меньше числителя, то такой масштаб называют масштабом увеличения

Масштаб m:1, где m > 1

(например, масштаб 4:1, 20:1, 100:1 и т.п.)

Масштаб в натуральную величину:

Масштаб 1:1 (числитель и знаменатель равны единице)

При создании изображений в натуральную величину в информации о чертеже указывают масштаб 1:1

Именованный масштаб—  это, по сути, словесное обозначение численного масштаба.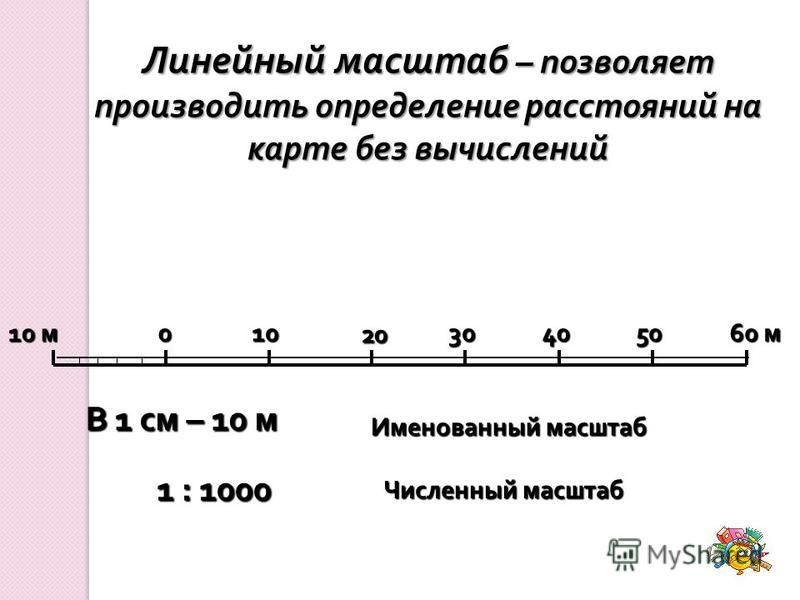

Такой масштаб показывает, сколько одному сантиметру на карте (плане) соответствует метров (километров) на местности.

Расстояние на местности, соответствующее 1 сантиметру на карте (плане), называют величиной масштаба.

 

Пример 3

Дан именованный масштаб: в 1 см — 250 м (в 1 сантиметре 250 метров).

Такой масштаб означает, что 250 м на местности соответствуют 1 см на карте (плане).

Величина этого масштаба равна 250 м.

У меня есть дополнительная информация к этой части урока!

Закрыть

На картах (планах) отмеряют расстояние в сантиметрах, а на местности в метрах или километрах.

Необходимо помнить правила перевода из одной единицы измерения в другую.

1 м = 100 см

1 км = 100 000 см

Рассмотрим правила-помощники для перевода из сантиметров в метры и километры.

Если в значении знаменателя масштаба убрать два последних нуля, то остается число, которое покажет, сколько метров на местности соответствует одному сантиметру на карте (плане), т.е. величину масштаба.

Если в значении знаменателя масштаба убрать пять последних нулей, то остается число, которое покажет, сколько километров на местности соответствует одному сантиметру на карте (плане), т.е. величину масштаба.

Попробуем перевести масштаб из численного в именованный, пользуясь правилами- помощниками

Обратным образом происходит перевод из именованного в численный

Графический масштаб подразделяют на линейный и поперечный.

Линейный масштаб дает возможность определить расстояние и размеры без расчетов и переводов длин из масштабных в реальные, позволяя тем самым ускорить работу с картой.

Линейный масштаб представляет собой отрезок прямой, разделенный на деления (подобно линейке со шкалой).

Эти деления равной длины, но с разным номинальным значением, называют основанием линейного масштаба.

Каждое деление подписано значениями, указывающими размеры соответствующих им отрезков в действительности.

Основание откладывается по всей длине масштабного отрезка (чаще всего с шагом 2 см).

Крайнее левое от нуля основание делят на более мелкие деления — это наименьшее деление линейного масштаба.

Расстояние в действительности, соответствующее номинальному делению масштаба, называют точностью масштаба (т.е. это отрезок на местности, который соответствует одному минимальному значению масштаба).

У меня есть дополнительная информация к этой части урока!

Закрыть

Как правильно пользоваться линейным масштабом

1. Приложить к измеряемому отрезку на карте раствор циркуля, сделать замер
2. Приложить к линейке масштаба полученный раствор циркуля и по делениям отсчитать значение замера

Отсчет берется по двум значениям: правую ножку циркуля необходимо поставить на деление справа от нуля, левая ножка циркуля может выходить за ноль в левое основание.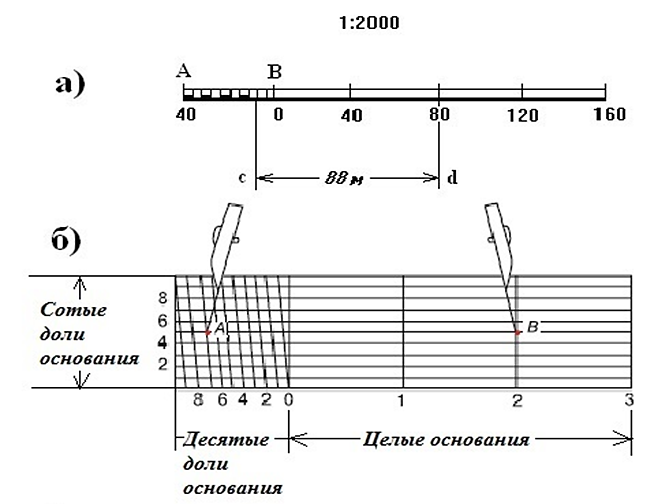 Таким образом, длина замера будет состоять из двух отсчетов: отсчет целого основания и отсчет наименьших делений линейного масштаба левого основания.

Обратите внимание на рисунок линейного масштаба, представленного выше.

Мы можем увидеть, что раствор циркуля укладывается только в одно правое основание линейного масштаба и в два наименьших деления крайнего левого основания.

Сложив все полученные значения, получаем:

измеряемый отрезок на местности = \(\mathbf{200 м + (2 \cdot 20 м) = 240 м}\)

Поперечный масштаб

Поперечный масштаб это улучшенный вариант линейного масштаба, позволяющий делать максимально точные измерения расстояний и размеров.

Выглядит поперечный масштаб, как сетка, состоящая из горизонтальных линий, пересеченных вертикалями и наклонными линиями (трансверсали).

Используют поперечный масштаб подобно линейному, но измерения откладываются по трем основаниям (горизонталям, вертикалям и трансверсалям).

Для фиксирования длины отрезка на карте также используют циркуль.

Чаще всего поперечный масштаб применяют на специализированных картах.

Этот вид масштаба удобен для определения длинны рек, дорог, горных хребтов и других кривых на карте.

Нередко для удобства на картах приводятся все три вида масштабов: численный, именованный, графический (линейный).

Масштабы планов. Численный, линейный и поперечный масштабы

Все мы знаем, что такое масштаб. Это отношение линейных размеров на условном графическом изображении к истинным величинам изображаемого объекта. То есть это соблюдение неких пропорций во время нанесения какого-либо чертежного изображения или редактирования фотографии.

Что такое масштаб, и зачем он нужен

Подобный способ передачи изображения применяется абсолютно во всем, начиная с карт и чертежей и заканчивая обычными фотографиями. Да вот только не всегда нужное изображение можно воспроизвести в натуральную величину. В этом случае на помощь и приходит масштаб. Благодаря ему изображения можно уменьшать или увеличивать, при этом соблюдая необходимые пропорции, которые указываются на чертежах. Что такое масштаб мы уже знаем, так давайте же поговорим о двух его видах.

Масштаб увеличения

Данный вид применяется в том случае, когда изображение в натуральную величину значительно меньше, нежели на чертежах. В этом случае в специальной графе указываются пропорции данного изображения (2:1, 8:1, 16:1, 150:1 и так далее). Пропорции нужно понимать следующим образом: правая цифра обозначает, что весь чертеж необходимо делить на сантиметры (например, 1 сантиметр), а левая — во сколько раз объект уменьшен на 1 сантиметр чертежного изображения. То есть, если мы имеем обозначение 2:1, то это значит, что на 1 сантиметр чертежной линии приходится 0,5 сантиметра объекта.

Масштаб уменьшения

Этот вид применяется в том случае, если объект, который необходимо изобразить, значительно превышает размеры чертежа. В специальной графе пропорций мы указываем, во сколько раз объект превышает изображение (например, 1:2, 1:250, 1:1000 и так далее). Левая цифра обозначает, на сколько сантиметров необходимо делить чертеж (например, на 1 сантиметр), а правая — сколько измерительных единиц приходится на 1 сантиметр. Например, мы имеем карту с обозначением масштаба 1:2000000 см, это значит, что на 1 сантиметр карты приходится 2000000 сантиметров местности (или 20000 метров, или 20 километров на 1 сантиметр).

Как масштабировать фотографии

Очень просто разобраться с составлением карт или чертежей, но вот что такое масштаб фотографий, понять достаточно сложно. Такие изображения имеют другие параметры измерения, а именно разрешение, которое зависит от количества пикселей, находящихся в данном изображении. Масштабируя фотографии, необходимо обращать внимание на количество пикселей, ведь значительно увеличивая с небольшим количеством пикселей, мы ухудшаем его качество и наоборот. Существуют различные программы, с помощью которых можно осуществлять данные операции, при этом качество изображения не становится хуже. Их принцип действия базируется на увеличении числа пикселей в той или иной фотографии, вследствие чего увеличивается разрешение, то есть размер воспроизводимого изображения. Такие программы можно найти в специальных магазинах или скачать из интернета, но лучше всего покупать лицензионные диски, а не скачивать пиратские копии, которые могут ухудшить работу вашего компьютера и сделают невозможной обработку фотографий на нем.

Для того чтобы крупные объекты можно было изобразить и отобразить на бумаге, его вид уменьшают. Примером может стать любая топографическая карта, в которой используется масштаб, необходимый для расчетов размеров и расстояний в реальном виде. Чтобы произвести необходимые измерения, необходимо знать, где и как найти масштаб. Как правило, данный показатель размещается в легенде карты или изображается в зарамочном оформлении. Также иногда для указания масштаба карты используется заголовок и пояснительные надписи в нижней части. В редких случаях популярные карты содержат масштаб в основной части. В случае отсутствия зарамочного оформления или обрезанной карты, зная как определить масштаб, можно самостоятельно произвести все необходимые расчеты.

С помощью чего и как определить масштаб карты?

1. Прежде чем приступить к определению масштаба карты необходимо взять другую карту такой же территории с уже известным масштабом.
2. Далее переходим к поиску одинаковых пар точек местности, отображаемых на обеих картах.
3. С помощью линейки производятся измерения расстояний между выбранными объектами на каждой из карт.
4. Используя полученные измерения, необходимо рассчитать разницу масштаба искомой карты по отношению к масштабу другой.
5. Важно конечное значение масштаба привести в установленный вид, а именно к целому, кратному ста или тысячи значению.
6. При отсутствии возможности использования второй карты, есть другой способ, как определить масштаб карты. В этом вопросе помогут специальные картографические сервисы, найти которые можно в поисковой системе. 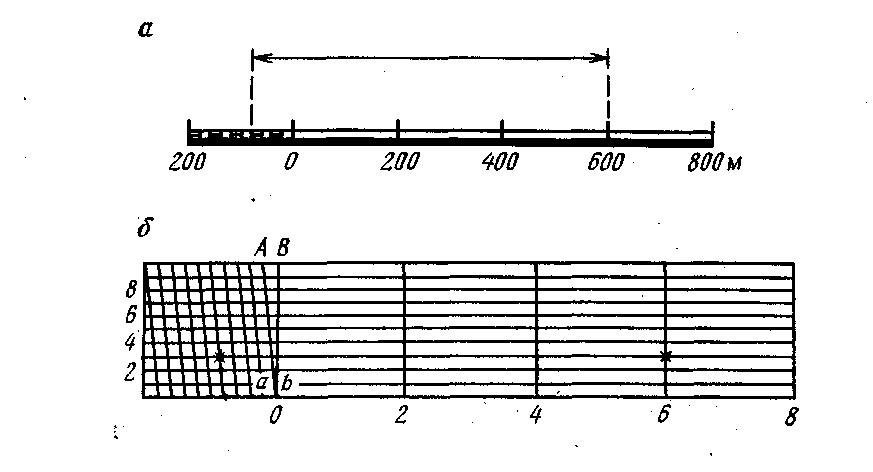Выбрав сервис, необходимо найти ту же территорию, что изображена на карте, и выбранные характерные точки. Далее путем использования инструмента «Линейка» можно легко определить искомое расстояние по выбранным для космоснимков единицам измерения. Последним действием станет определение масштаба карты по известным значениям расстояний на местности и по карте.

Как самостоятельно определить масштаб чертежа.

При отсутствии указания масштаба чертежа в одном из установленных мест есть вариант, как определить масштаб чертежа самостоятельно.

1. Сначала определяется изображенный на чертеже объект с габаритными размерами.
2. Необходимо на чертеже найти вид детали с указанными габаритными размерами. Далее, используя размерную линию какого-либо габаритного размера, путем приложения любого измерительного прибора производится измерение ее длины.
3. После чего для сравнения числового значения размера с полученным результатом необходимо использовать деление результата с числовым значением. Полученное число и будет являться искомым масштабом.

Горизонтальные проекции отрезков при составлении карт и планов изображают на бумаге в уменьшенном виде. Степень такого уменьшения характеризуется масштабом.

Масштаб карты (плана) – это отношение длины линии на карте (плане) к длине горизонтального проложения соответствующей линии местности: .

Масштабы бывают численные, именованные и графические .

Численный масштаб может быть представлен в виде простой дроби – в числителе единица, в знаменателе степень уменьшения m ,например , или М = 1:2000.

Именованный масштаб может быть представлен в виде «в 1 см 20 м». Целесообразность такого соотношения определяется тем, что при изучении местности по карте удобно и привычно оценивать длину отрезков на карте в сантиметрах, а длину горизонтальных проложений на местности представлять в метрах или километрах. Для этого численный масштаб преобразовывают в разнотипные единицы измерения: 1 см карты соответствует такому-то количеству метров (километров) местности.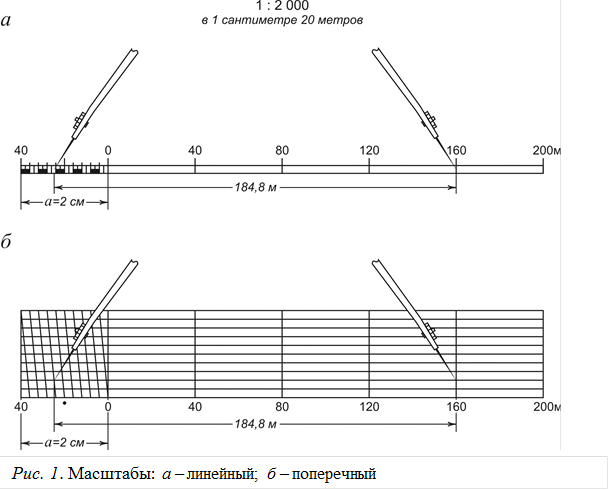

Чтобы избежать вычислений и ускорить работу, пользуются графическими масштабами . Наиболее часто используемыми являются: линейный, клиновый и поперечный.

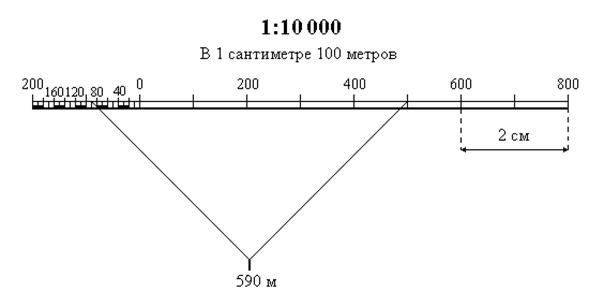
Линейный масштаб строят и используют для удобства пользования картами и планами, он позволяет избежать расчетов при переводе длин линий местности в масштаб карты или плана и наоборот. На топографических картах и планах линейный масштаб вычерчивается под южной рамкой карты или плана.

Рис. 1. Схема компоновки листа топографической карты

Для построения линейного масштабавыбирают исходный отрезок, удобный для данного масштаба. Этот исходный отрезок называется основанием масштаба (рис.2). Основание откладывают на прямой линии необходимое число раз, крайнее левое основание делят на 10 частей. Затем линейный масштаб подписывают, исходя из того численного масштаба, для которого он строится (на рис. 2,а для М = 1:25 000).

Для обеспечения необходимой точности измерений угол между плоскостью карты и каждой ножкой циркуля-измерителя (рис. 2,б )не должен быть менее 60°, и измерение длины отрезка следует произвести не менее двух раз. Расхождение DS (в метрах) между результатами измерений должно быть , где Т — число тысяч в знаменателе численного масштаба. Так, например, при измерении отрезков по карте М и пользовании линейным масштабом, который помещен обычно за южной стороной рамки листа карты, расхождения при двойных измерениях не должны превышать 1,5 ´ 10 = 15 м.

Рис. 2. Линейный масштаб

Если отрезок длиннее построенного линейного масштаба, то его измеряют по частям. В этом случае расхождение между результатами измерения в прямом и обратном направлениях не должно превышать , где п – число установок измерителя при измерении данного отрезка.

Для более точных измерений пользуются поперечным масштабом , имеющим на линейном масштабе дополнительное построение по вертикали (рис. 3).

После того как необходимое количество оснований масштаба отложено (также обычно длиной 2 см, тогда масштаб называется нормальным), восстанавливают перпендикуляры к исходной линии и делят их на равные отрезки (на m частей).

Рис. 3. Поперечный масштаб

Если основание разделено на п частей и точки деления верхнего и нижнего основания соединены наклоннымилиниями (трансверсалями) так, как показано на рис. 3, то отрезок
. Соответственно отрезок ef = 2cd ; рq = 3сd и т. д. Если m = п = 10, то cd = 0,01 основания, т.е. такой поперечный масштаб позволяет определенным образом оценить отрезок с точностью в 0,01 доли основания. Поперечный масштаб, у которого длина основания 2 см и m = п = 10, называют сотенным нормальным.

Поперечный масштаб гравируют на металлических линейках, которые называются масштабными. Перед применением масштабной линейки следует оценить основание и его доли по следующей схеме.

Пусть численный масштаб 1:5000, именованное соотношение будет: в 1 см 50 м. Если поперечный масштаб нормальный, то основание составит 100 м; 0,1 основания – 10 м; 0,01 основания – 1 м. Задача по отложению отрезка заданной длины сводится к определению числа оснований, его десятых и сотых долей. Пусть, например, требуется отложить отрезок d = 173,35 м, т.е. требуется взять в раствор измерителя: 1 основание +7 (0,1 основания) +3 (0,01 основания) и на глаз расположить ножки измерителя между горизонтальными линиями 3 и 4 (рис. 4) так, чтобы линия АБ отсекала 0,35 промежутка между этими линиями (отрезок ДЕ). Обратная задача (определение длины отрезка, взятого в раствор измерителя) соответственно и решается в обратном порядке. Добившись совмещения игл измерителя с соответствующими вертикальной и наклонной линиями так, чтобы обе ножки измерителя находились на одной горизонтальной линии, считываем количество оснований и его долей (d B Г = 235,3 м).

Рис. 4. Определение расстояния с помощью поперечного масштаба

Переходный масштаб. Иногда в практике приходится пользоваться картой или аэроснимком, масштаб которых не является стандартным, например 1:17 500, то есть, 2 см на карте соответствует 350 м на местности; наименьшее деление нормального поперечного сотенного масштаба будет при этом 3,5 м.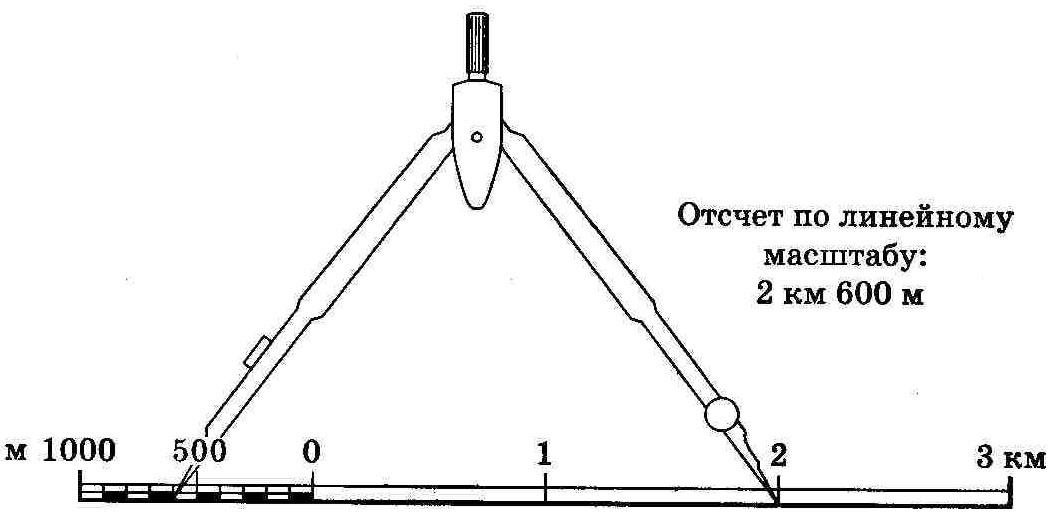 Оцифровка такого масштаба неудобна для практических работ, поэтому поступают следующим образом: основание поперечного масштаба берут не 2 см, а рассчитывают так, чтобы оно соответствовало круглому числу метров, например, 400м. Длина основания в этом случае будет равна 400м/175м=2,28см. Если теперь построить поперечный масштаб с длиной основания 2,28 см, то одно деление левого основания будет соответствовать 40м, а цена наименьшего деления будет равна 4м. поперечный масштаб с дробным основанием называется переходным.

Одним из вариантов переходных масштабов являетсяклиновый (пропорциональный) масштаб. Применяют при работе с разномасштабными аэроснимками и планами. При построении этого масштаба по горизонтали и вертикали откла­дывают одно и то же расстояние, выраженное в разных масшта­бах, концы полученных отрезков соединяют.

Клиновый масштаб (рис. 5) строят при помощи двух катетов прямоугольного треугольника. По горизонтальной линии АВ (основанию) откладывают отрезки по 100м в одном масштабе; по вертикальной линии ВС (справа) откладывают отрезки, равные линии АВ в нужных масштабах, например, 1:12000, 1:15000, 1:17000, 1:24000. Концы соответствующих отрезков по линии ВС затем соединяют с точкой А, лежащей с левой стороны основания масштаба. Клиновый масштаб строится на целлулоиде, алюминии или другом малодеформирующемся материале.

Рис. 5. Клиновый масштаб

На клиновидном масштабе (рис. 5) отложены расстояния: в масштабе 1:12000 линия 1-1″ длиной 340м, в масштабе 1:15000 линия 2-2″ длиной 570м, в масштабе 1:17000 линия 3-3″ длиной 625м, в масштабе 1:24000 линия 4-4″ длиной 890м.

Точность масштаба. Карта или план – это графические документы. Принято считать, что точность графических построений оценивается величиной 0,1 мм. Длина горизонтального проложения линии местности, соответствующего на карте отрезку 0,1 мм называется точностью масштаба (μ). Практический смысл этого понятия заключается в том, что детали местности, имеющие размеры меньше точности масштаба, на карте в масштабе изобразить невозможно, и приходится применять так называемые внемасштабные условные знаки.

Кроме понятия «точность масштаба», существует понятие «точность плана». Точность плана показывает, с какой ошибкой нанесены на план или карту точечные объекты или четкие контуры. Точность плана оценивается в большинстве случаев величиной 0,5 мм, в нее входят ошибки всех процессов создания плана, в том числе и ошибки графических построений.

Масштаб — это отношение длины отрезка на карте, плане или чертеже к соответствующей ему реальной длине на местности.
Масштаб показывает: во сколько раз каждая линия. нанесённая на карту, уменьшена по отношению к её действительным размерам на местности.
Уменьшение изображение — это необходимость, мы редко задумываемся над этим, однако, также редко изображаем предметы в натуральную величину. Как правило для того, чтобы они поместились на листе бумаги, их приходится уменьшать, реже — приходится увеличивать. Особенно актуально это для изображения земной поверхности, ведь изображать её один в один совершенно невозможно.
Любое ли уменьшенное изображение обладает масштабом? Конечно, нет. К рисунку масштаб неприменим, даже если рисунок очень качественный. В любом случае — художник внесёт искажения в изображаемый предмет, а из определения масштаба мы видим, что каждая(!) линия нашего изображения уменьшена по отношению к реальному предмету одинаково. Следовательно, изображение в масштабе может быть выполнено как минимум при наличии измерительных приборов (по крайней мере, линейки). Как максимум — с использованием вычислительной техники.

Масштаб — это отношение. Отношение предполагает процесс деления, значит, масштаб — это математическая дробь, в которой есть числитель и знаменатель. В числителе дроби записывается длина отрезка на изображении, а в знаменателе — длина реального изображаемого отрезка.

Допустим, изображение выполнено (хоть для карты это и невозможно) в масштабе один к одному — длина изображаемого отрезка совпадает с длиной изображённого.
Масштаб записывается как 1:1
Если изображение уменьшено в 3 раза, то масштаб запишется как 1:3
Уменьшение в 100 000 раз записывается как 1:100 000

Если масштаб 1 к 1, значит 1 сантиметру нашего изображения соответствует 1 реальный сантиметр изображаемой поверхности, а если 1:100 000, значит — 1 сантиметру изображения соответствует 100 000 сантиметров.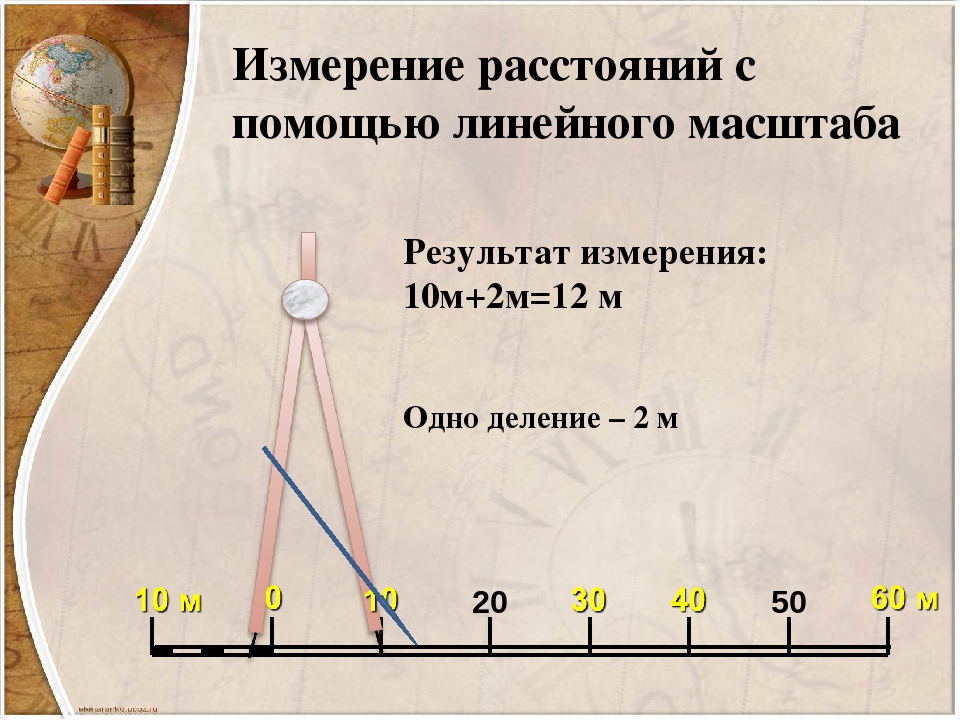 А одному метру изображения? 1 метру тогда будет соответствовать 100 000 метров. Заметим, что какой бы ни была выбранная длина на карте, реальная длина будет больше — в нашем случае в 100 000 раз. Если масштаб 1:1000 — тогда в тысячу; 1:30 000 000 — в тридцать миллионов.

Когда мы скажем, что одному сантиметру карты соответствует тридцать миллионов сантиметров, никто ничего не поймёт. Значит, нужно перевести это астрономическое число во что-то понятное. Мы знаем, что в 1 метре 100 сантиметров. Значит, можно перевести сантиметры в метры. 30 000 000 сантиметров делим на 100 и получаем 300 000 метров. Тоже не слишком удобно, значит, надо переводить дальше. Помним, что в 1 километре 1000 метров. Делим 300 000 метров на 1000. Получилось 300 километров. Значит, в одном сантиметре карты масштаба 1:30 000 000 содержится 300 километров, а это уже можно представить.
Есть простой и надёжный способ перевода сантиметров в километры — в конечном счёте мы делили число на 100 000 (сначала на 100, а затем на 1000), так что можно просто мысленно закрывать 5 нулей и переводить значительно быстрее, однако нужно помнить что это подходит только для перевода сантиметров в километры и только тогда, когда нулей хватает. Для масштаба 1:50 000 нам будет достаточно остановиться на метрах.

Тот масштаб, который пишется в виде дроби через знак «:» называется численным . Примеры численного масштаба: 1:1000 1:1000 000 1:250 000
Регулярно для того чтобы не приходилось всё время выполнять перевод численного масштаба на картах (особенно школьных) указывают именованный масштаб. Он показывает какое расстояние содержится в 1 сантиметре карты и записывается: в 1 см 1 м; в 1 см 10 км; в 1 см 2,5 км соответственно.
Иногда под картой ещё добавляют линейный масштаб в виде мерной линейки. Это удобно, потому что при его наличии можно, воспользовавшись циркулем-измерителем или линейкой измерить расстояние на карте, приложить его к линейному масштабу и получить результат, соответствующий реальному расстоянию.

Ключевой отличительной особенностью карты от рисунка является наличие масштаба. Карта без масштаба — это не карта. Все картографические произведения принято классифицировать согласно масштабу, в котором они выполнены.
– Мелкомасштабные (карты мира или материков – их масштаб мельче 1:1000 000)
– Среднемасштабные (карты стран, крупных островов – от 1:100 000 до 1: 1000 000)
– Крупномасштабные (карты маленьких государств, областей, городов – менее 1: 100 000)
Запомните: чем крупнее масштаб, тем меньше помещается на карту. Дело в том, что масштаб — это дробь, а чем меньше знаменатель дроби, тем она крупнее.

Каждая карта имеет масштаб – число, которое показывает, сколько сантиметров на местности соответствует одному сантиметру на карте.

Масштаб карты обычно указан на ней. Запись 1: 100 000 000 означает, что если расстояние между двумя точками на карте равно 1 см, то расстояние между соответствующими точками её местности равно 100 000 000 см.

Может быть указан в численной форме в виде дроби – численный масштаб (например, 1: 200 000). А может быть обозначен в линейной форме: в виде простой линии или полосы, разделенной на единицы длины (обычно на километры или мили).

Чем крупнее масштаб карты, тем с более детально могут быть изображены на ней элементы ее содержания, и наоборот, чем мельче масштаб, тем более обширное пространство может быть показано на листе карты, но местность на ней изображается с меньшими подробностями.

Масштаб представляет собой дробь, в числителе которой единица. Чтобы определить, какой из масштабов крупнее и во сколько раз, вспомним правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель.

Отношение расстояния на карте (в сантиметрах) к соответствующему расстоянию на местности (в сантиметрах) равно масштабу карты.

Как же эти знания помогут нам при решении задач по математике?

Пример 1.

Рассмотрим две карты. Расстоянию в 900 км между пунктами А и В соответствует на одной карте расстояние в 3 см. Расстоянию в 1 500 км между пунктами С и D соответствует на другой карте расстояние в 5 см. Докажем, что масштабы карт одинаковы.

Решение.

Найдём масштаб каждой карты.

900 км = 90 000 000 см;

масштаб первой карты равен: 3: 90 000 000 = 1: 30 000 000.

1500 км = 150 000 000 см;

масштаб второй карты равен: 5: 150 000 000 = 1: 30 000 000.

Ответ. Масштабы карт одинаковы, т.е. равны 1: 30 000 000.

Пример 2.

Масштаб карты – 1: 1 000 000. Найдём расстояние между точками А и В на местности, если на карте
АВ = 3,42 см ?

Решение.

Составим уравнение: отношение АВ = 3,42 см на карте к неизвестному нам расстоянию х (в сантиметрах) равно отношению между теми же пунктами А и В на местности к масштабу карты:

3,42: х = 1: 1 000 000;

х · 1 = 3,42 · 1 000 000;

х = 3 420 000 см = 34,2 км.

Ответ: расстояние между пунктами А и В на местности равно 34,2 км.

Пример 3

Масштаб карты – 1: 1 000 000. Расстояние между пунктами на местности 38,4 км.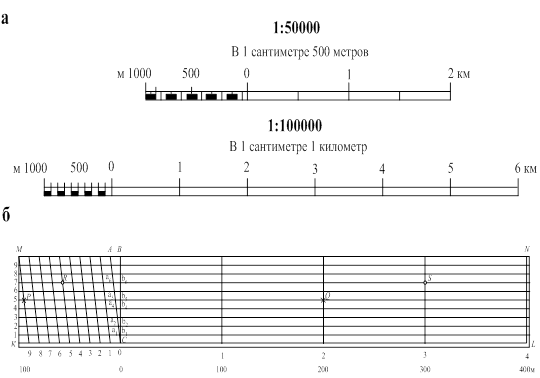 Каково расстояние между этими пунктами на карте?

Решение.

Отношение неизвестного нам расстояния х между пунктами А и В на карте к расстоянию в сантиметрах между теми же пунктами А и В на местности равно масштабу карты.

38,4 км = 3 840 000 см;

х: 3 840 000 = 1: 1 000 000;

х = 3 840 000 · 1: 1 000 000 = 3,84.

Ответ: расстояние между пунктами А и В на карте равно 3,84 см.

Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Масштабы планов и карт. Численный и линейный масштаб, страница 2

Точно таким же путем получим длину отрезка a´b’ (см. рис. 8, в)

затем длины других отрезков между перпендикуляром ОВ₁ и трансверсалью ОС: 6 м,     8 м, 10 м и т. д.

Для удобства пользования поперечным масштабом его подписывают, как показано на рис. 1, в, снизу против перпендикуляров — согласно А В = 200 м: 200, 0, 200, 400, 600 и т. д. и слева против горизонтальных линий — согласно ab = 2 м: 0, 4, 8, 12 и т. д.

По этим подписям отсчитывают расстояние, взятое с плана и отмеченное на рис. 1, в крестиками, при этом одну ножку циркуля ставят на один из перпендикуляров с расчетом, что другая ножка попадет на какую-либо трансверсаль и обе ножки должны стоять на одной горизонтальной линии. Тогда определяемое расстояние между крестиками (концами ножек циркуля-измерителя) будет

Поперечный масштаб при всех его достоинствах не может обеспечить точность выше определенного предела, зависящего от свойств человеческого глаза. Глаз человека в состоянии совмещать острие ножки циркуля с точкой на плане, точку с точкой, штрих со штрихом с точностью около 0,1 мм *, если они находятся на расстоянии 25 см от глаза. Из этого следует, что детали объектов местности (выступы, изгибы), выражающиеся на плане линиями менее 0,1 мм, изобразить нельзя. Поэтому при изображении деталей объектов местности на плане руководствуются точностью масштаба, которая представляет длину горизонтального приложения линии на местности, соответствующую 0,1 мм на плане. Например, точность масштаба 1 : 10 000 равна 1 м, масштаба 1 : 5000 — 0,5 м и др. В соответствии с точностью масштаба при изображении деталей объектов местности на плане и карте неизбежны обобщения (генерализация).

Для определения точности масштаба следует знаменатель численного масштаба М разделить на 10000. Для карты масштаба 1:25000 точность  равна 2,5 м.

ЗАДАНИЕ №3

На условно увеличенном графике нормального поперечногомасштаба утолщенными линиями обозначен раствор циркуля-измерителя, равный расстоянию между двумя точками карты.

В табл. 4 приводятся номера линий и масштабы тех карт, на которых они измерены (рис. 2). Определить длины соответствующих горизонтальных проложений линий местности.

Решение. Основание нормального поперечного масштаба равно 2 см. Влево от нуля оно разделено на 10 частей, следовательно, АВ = 0,1 основания, т. е. АВ = 2 мм, a₁b₁= 0,01 основания =  0,1АВ = 0,2 мм, а₂b₂= 2а₁b₁ . . ., a₉b₉= 9а₁b₁.

Рис. 2 . Номограмма к заданию № 3

Если требуется определить длину отрезка 1 из табл. 3 измеренного на карте масштаба 1 : 10 000, то вначале определяют расстояния на местности, соответствующие 2 см, 2 мм и 0,2 мм на карте в масштабе 1 : 10 000 (2 см — 200 м, 2 мм — 20 м, 0,2 мм — 2 м), затем определяют  длину отрезка 1.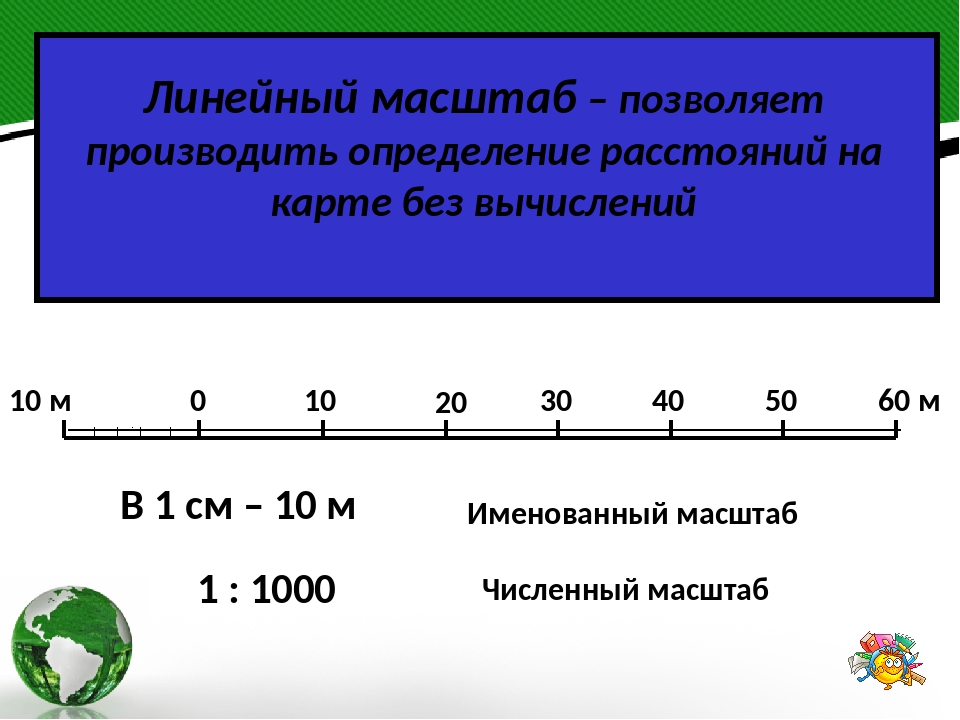 Она равна

2×200 м + 9х2 м + 6х20 м = 538 м.

Таблица  3

ЗАДАНИЕ №4

1. Построить поперечный масштаб с помощью описания, изложенного в задании №2.

2. На топографической карте (выдается преподавателем) определить с помощью двух ниже указанных способов и поперечного масштаба длину объекта (участка дороги, реки и т.п.) или расстояние, указанное преподавателем, представляющих собой:

1)  ломаную линию;

2)  извилистую линию.

Первый способ:

Длину ломаной линии можно определить по сумме ее отрезков. Длину ломаной линии абвг на рис. 2, а  целесообразно измерять способом постепенного наращивания раствора измерителя. Для этого устанавливают его иголки на длину l₁в точки а и б; удерживая иголку в точке б и не изменяя раствора, поворачивают измеритель до продолжения отрезка вб и закрепляют вторую иголку в точке а₁.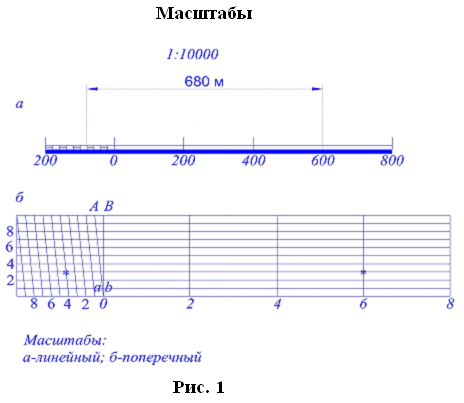 Затем перемещают иголку измерителя из точки б в точку в, получив в растворе измерителя суммарную длину a₁б+,бв=l₁+l₂. Перемещая таким же образом иголку в точку а₂, увеличивают раствор измерителя на величину вг = l₃. Общую длину ломаной линии,        выраженную в метрах местности, определяют по линейному или поперечному масштабу. Для контроля измерение выполняют в обратном направлении; при этом допустимое расхождение двух результате определяют по формуле

ΔS_доп=3·М·10^-4√n , где n – число установок измерителя.

Рис. 2. Два способа измерения длины ломаной и извилистой линий

Длину извилистой линии можно измерить описанным выше способом, разделив ее на приблизительно прямолинейные отрезки.

Второй способ:

Длину извилистой линии можно определить путем многократного откладывания по кривой постоянного раствора измерителя, величину которого называют «шагом» (рис. 2, б) и выбирают в зависимости от извилистости линии порядка 2 — 5 мм. Длину вычисляют умножением величины шага измерителя на число его полных перестановок плюс остаток, измеренный с помощью поперечного масштаба. Контроль осуществляют измерением в обратном направлении.

Масштабы чертежей » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

Масштаб — отношение линейных размеров изображенного на чертеже предмета к его размерам в натуре. Масштаб может быть выражен числом (числовой масштаб) или изображен графически (линейный масштаб).

Числовой масштаб обозначают дробью, которая показывает кратность увеличения или уменьшения размеров изображения на чертеже. При выполнении чертежей в зависимости от их назначения, сложности форм предметов и сооружений, их размеров применяют следующие числовые масштабы (ГОСТ 2.302—68) *:

уменьшения: 1:2; 1 : 2,5; 1:4; 1:5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000;
увеличения: 2:1; 2,5: 1; 4:1; 5:1; 10 : I; 20 : 1; 40 : 1; 50 : 1; 100 : 1;
натуральная величина 1:1.

При проектировании генеральных планов крупных объектов используют масштабы 1 : 2000; 1 : 5000; 1 : 10 000; 1 : 20 000; 1 : 25 000; 1 : 50 000.

В том случае, если чертеж выполнен в одном масштабе, его значение указывают в предназначенной для этого графе основной надписи чертежей по типу 1:1; 1:2; 1 : 100 и т. д. Если же какое-либо изображение на чертеже выполнено в масштабе, отличающемся от указанного в основной надписи, то под соответствующим наименованием изображения указывают масштаб по типу М 1:1; М 1 : 2 и т. д.

Применяя числовой масштаб при выполнении чертежей, приходится делать вычисления, чтобы определить размеры отрезков линий, наносимых на чертеже. Например, чтобы определить длину отрезка на чертеже при длине изображаемого предмета 4000 мм и числовом масштабе 1 :50, нужно 4000 мм разделить на 50 (степень уменьшения) и полученную величину (80 мм) отложить на чертеже.

Для сокращения вычислений пользуются масштабной линейкой или строят соответствующий числовому линейный масштаб, как это показано на рисунке для числового масштаба 1 : 50.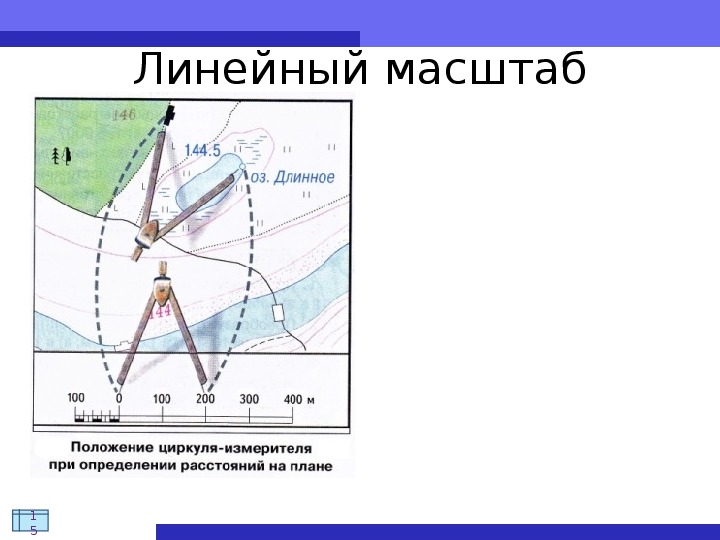

Проводят прямую линию и на ней откладывают несколько раз основание масштаба — величину, которая получается в результате деления принятой единицы измерения (1 м = 1000 мм) на размер уменьшения 1000 : 50 = 20 мм. Первый отрезок с левой стороны делят на несколько равных частей так, чтобы каждое деление соответствовало целому числу. Если этот отрезок разделить на 10 частей, то каждое деление будет соответствовать 0,1 м; если на 5 частей — то 0,2 м. Над точками деления линии на отрезки, равные основанию масштаба, надписывают числовые значения, которые соответствуют натуральным размерам, при этом у первого деления справа всегда ставят нуль. Значение мелких делений от нуля влево также надписывают, как это изображено на рисунке.

Для того чтобы взять, пользуясь построенным линейным масштабом, например, размер 4,65 м (4650 мм), нужно одну ножку циркуля-измерителя поставить на 4 м, а другую — на шестое с половиной дробное деление слева от нуля. Если точность окажется недостаточной, применяют поперечный масштаб.

Поперечный масштаб дает возможность выразить или определить размер с погрешностью до сотых долей основной единицы измерения. Так, на рисунке ниже показано определение размера, равного 4,65 м.

Десятые доли берут на горизонтальном отрезке масштаба, а сотые — на вертикальном.

В тех случаях, когда требуется построить увеличенное или уменьшенное изображение, выполняемое по заданному чертежу, масштаб которого может быть произвольным, применяют угловой (пропорциональный) масштаб.

Угловой масштаб строят в виде прямоугольного треугольника, отношение катетов которого равно кратности изменения масштаба изображения (h:H). С помощью углового масштаба можно изменять масштаб изображения, пользуясь отвлеченными величинами и не вычисляя размеров изображаемого объекта.
Например, требуется изобразить заданный чертеж в увеличенном масштабе. Для этого строим прямоугольный треугольник АВС, у которого вертикальный катет ВС равен отрезку какой- либо прямой, взятой на заданном чертеже, а горизонтальный катет АВ равен длине соответствующего отрезка в масштабе увеличенного чертежа. Таким образом, чтобы увеличить какой-либо отрезок прямой заданного чертежа, например h, надо отложить его параллельно катету ВС углового масштаба (по вертикали) между катетом А В и гипотенузой АС, Тогда увеличенный размер отрезка будет равен размеру Н, взятому (по горизонтали) на стороне АВ углового масштаба.

Можно применить и другой способ. Как и в первом случае, отложим по вертикали какой-либо отрезок заданного чертежа h. Затем в этом же месте отложим длину отрезка h2 с соответствующим увеличением и через полученную точку проведем наклонную прямую AD. Искомые отрезки получим аналогичным образом. Удобно пользоваться измерителем, вычерчивая угловой масштаб на миллиметровой бумаге.
Угловой масштаб может быть использован также и для перевода величин из одного числового масштаба в другой.

На увеличенном чертеже, как и на заданном, необходимо указывать числами действительные размеры, которые имеет изображаемый предмет в натуре, а не на чертеже.

Распечатать

Вконтакте

Facebook

Twitter

Одноклассники

Google+

Практическое использование масштабных коэффициентов — Линейный масштабный коэффициент — 3-й уровень Maths Revision

1ue9nkfb94e.0.0.0.1:0.1.0.$0.$1.$0″> Масштабный коэффициент можно использовать для создания карт и других масштабных диаграмм.

Когда объекты слишком велики для рисования на бумаге, для вычисления меньших пропорциональных размеров используются масштабные коэффициенты.

Планы этажей для проектов домов рисуются в меньшем масштабе. Это поможет дизайнеру увидеть, будут ли вещи хорошо сочетаться друг с другом в каждой комнате дома.

Масштабы на картах и ​​диаграммах обычно изображаются как отношение .

Масштаб, используемый на этом плане (1:100), означает, что каждый 1 см на странице равен 1 м в реальной жизни.

1ue9nkfb94e.0.0.0.1:0.1.0.$0.$2.$0″> Преобразование с использованием масштабного коэффициента

Чтобы преобразовать масштабный чертеж в реальную жизнь, измерьте линию на чертеже и умножьте ее на масштабный коэффициент, чтобы найти реальную длину.

Вопрос

Если на плане этажа указан масштаб \(1 \:\text{см} : 100 \:\text{см}\), а длина кухни на чертеже составляет 4 см, какой длины кухня в реале?

Показать ответ

Реальный размер кухни будет \(4 \times 100 = 400 \:\text{cm}\) (или 4 м) в длину.

1ue9nkfb94e.0.0.0.1:0.1.0.$0.$2.$3″> Чтобы преобразовать реальный чертеж в масштабный, разделите реальный размер на масштабный коэффициент.

Вопрос

Если карта нарисована с использованием масштабного коэффициента, где 2 см соответствует 3,5 км, а расстояние между Бророй и Голспи составляет 8,5 км, то какой длины будет рисунок, показывающий такое же расстояние?

Показать ответ

Длина на чертеже будет \(2 \div 3.5 \times 8.5 = 4.9 \:\text{cm}\) (до 1 dp).

Масштабные линейки — archisoup

Масштаб

Чтобы понять, что такое масштабная линейка и как она помогает в отображении чертежей и карт, мы должны сначала понять, что такое масштаб.

Подробно описано здесь; Масштаб — это метод представления объекта в пропорции, отличной от его реального размера, хотя чаще всего он используется как средство для уменьшения пропорций, его также можно использовать для их увеличения.

Обычно используется для представления крупных объектов и областей, таких как планы зданий и карты. Масштаб уменьшает размеры до приемлемой пропорции, которую можно удобно рассматривать как единое целое, а также легко переносить с помощью традиционных форматов бумаги и методов.

… масштабная линейка — это инструмент, который помогает нам считывать этот масштаб, когда линейка масштаба недоступна и/или чертеж или карта не распечатаны в соответствии с предполагаемым и указанным размером.

Что такое масштабная линейка?

Масштабная линейка представляет собой линейное изображение, разделенное на равные сегменты и используемое для измерения расстояний на чертежах и/или картах, изготовленных в заданном масштабе, но не обязательно напечатанных в одном масштабе.

В частности, в дизайнерских, архитектурных и инженерных профессиях во многих случаях чертежи печатаются с точным размером и поэтому могут быть измерены с помощью масштабной линейки.Однако добавление масштабной линейки означает, что рисунок можно измерить с помощью традиционной линейки и / или с помощью любого другого объекта с правильными пропорциями, такого как кредитная карта или поз.

Что касается карт, то они бывают разных форм и размеров, которые из-за того, что на них показаны большие площади, редко представляют собой традиционный масштаб чертежа, поэтому масштабная линейка является единственным способом точного измерения расстояния.

Почему они важны?

Помимо облегчения чтения карты и чертежа, при наличии линейки масштаба чертеж или карту не обязательно нужно печатать до определенного размера.Это связано с тем, что масштабная линейка, независимо от того, насколько большим или маленьким становится рисунок, сохраняет свою пропорцию по отношению к предмету рисунка.

Это особенно полезно при измерении с помощью цифрового экрана или мобильного устройства, а также когда плоттер недоступен для печати на бумаге требуемого размера.

Типы

Масштабные линейки соответствуют масштабу чертежа или карты, которым они назначены, и могут переноситься с одного чертежа на другой только в том случае, если оба чертежа имеют одинаковое соотношение (масштаб).

Например, масштабная линейка, показывающая имперский масштаб 1:8″, может использоваться только для измерения чертежа в масштабе 1:8″. Если чертеж имеет другой масштаб, для его соответствия требуется другая масштабная линейка.

По этой причине и с точки зрения единиц измерения существует множество вариантов.

Графически, как правило, существует несколько ключевых и стандартных методов представления, как показано ниже, однако в равной степени может быть высокий уровень творчества в том, как отображаются измерительные сегменты и единицы измерения.

Единственный КЛЮЧ и фиксированный фактор в том, что они должны быть прямыми!.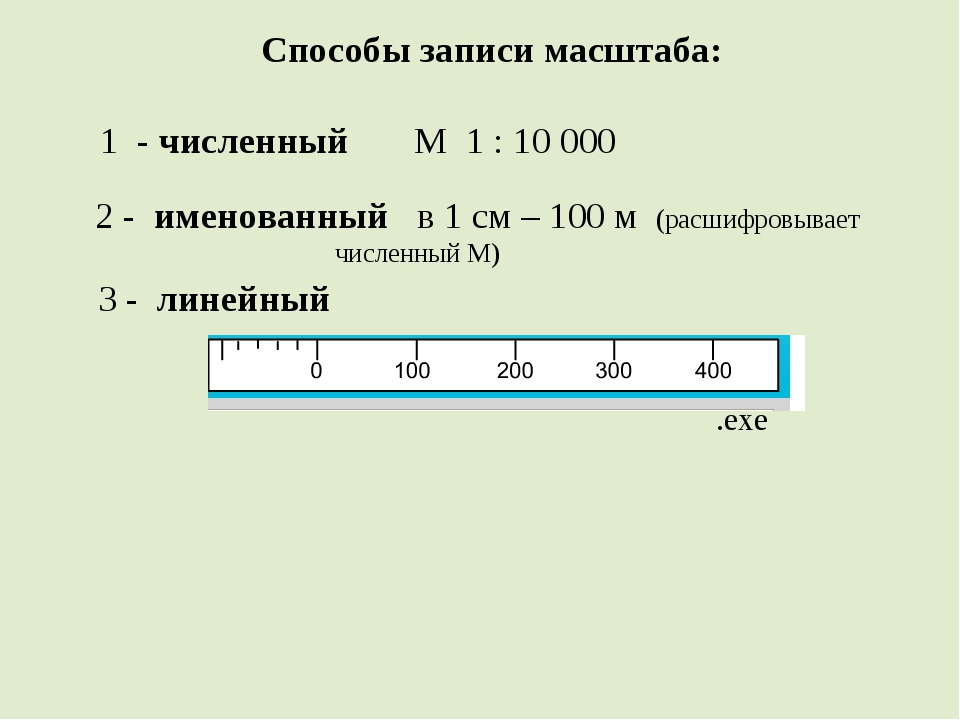

Как они рассчитываются?

Масштабная линейка, если ее часто рассчитывают во время завершения чертежа или карты и до того, как они будут построены (напечатаны) до заданного размера. Если, например, чертеж строится в метрическом масштабе 1:100, а единицы масштабной линейки указаны в метрах, то каждый из его сегментов будет представлять 1 метр и будет в 100 раз меньше реального измерения в 1 метр.

Точно так же масштабные линейки можно рисовать в масштабе 1:1 и, используя относительные единицы измерения для соответствия чертежу, просто наносить на них требуемый размер, соответствующий чертежу.

Как они создаются?

Масштабные линейки можно рисовать в любых имперских или метрических единицах, однако чаще всего это зависит от размера масштабируемого объекта.

Например, план этажа дома чаще всего измеряется в миллиметрах или дюймах, но карта, представляющая гораздо большую территорию, будет измеряться в метрах/футах или милях/километрах, и прилагаемые масштабные линейки будут соответствовать этому .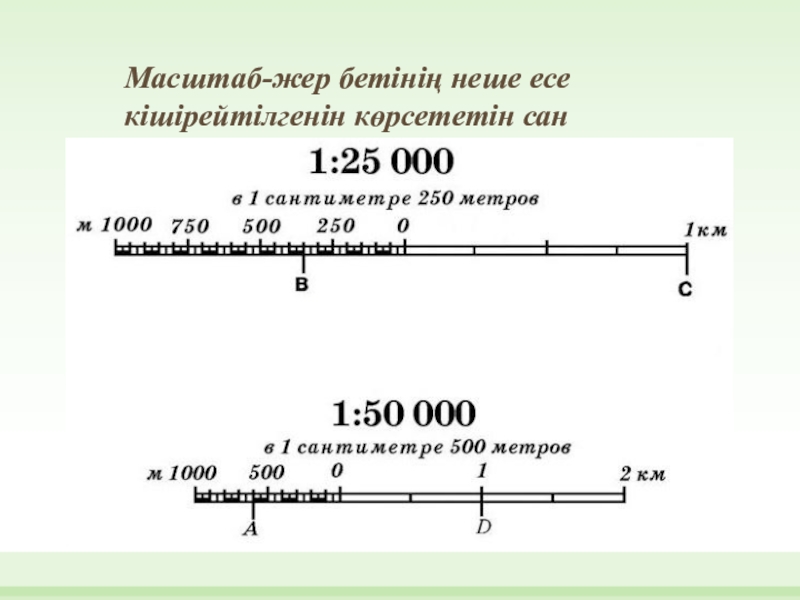

Как они используются?

Масштабная линейка по сути является средством измерения и устройством, и, хотя ее можно использовать независимо, обычно ее используют в сочетании со стандартной линейкой.

Правило используется для выполнения измерений по чертежу и/или карте, а затем измеряется относительно стержня с использованием записанного расстояния.

Chapter2.pmd

%PDF-1.4 % 49 0 объект >>>]/ON[138 0 R]/Порядок[]/RBGroups[]>>/OCGs[75 0 R 138 0 R]>>/Страницы 45 0 R/Тип/Каталог>> эндообъект 74 0 объект >/Шрифт>>>/Поля 79 0 R>> эндообъект 46 0 объект >поток приложение/pdf

dtpcell5

глава 2.пмд

2017-10-24T11:42:03PageMaker 7.02021-07-08T14:29:18+05:302021-07-08T14:29:18+05:30GPL Ghostscript 8.15uuid:0511aadd-7471-4eb6-ab90-1b70df8b64afuuid:5 420a-41e3-8a70-7f6741d11f9a конечный поток эндообъект 45 0 объект > эндообъект 50 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC/ImageI]/XObject>>>/Rotate 0/Type/Page>> эндообъект 1 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 3 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC/ImageI]/XObject>>>/Rotate 0/Type/Page>> эндообъект 7 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 9 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 11 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC/ImageI]/XObject>>>/Rotate 0/Type/Page>> эндообъект 17 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC/ImageI]/XObject>>>/Rotate 0/Type/Page>> эндообъект 24 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 26 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/Повернуть 0/Тип/Страница>> эндообъект 163 0 объект >поток HTk0>6u’ɲF)1 b786I1@»zspoke;c$i;,uDn4IXEDb@=FǙEu’*yb`RG?%\lo=ˢE

Полулогарифмический график (ось x имеет логарифмическую шкалу)

Цвет заливки маркера, заданный как 'auto' , триплет RGB, шестнадцатеричный код цвета, название цвета или краткое название. Параметр 'auto' использует тот же цвет, что и свойство Color родительских осей. Если вы укажете 'auto' и поле графика осей невидимо, цвет заливки маркера цвет фигуры.

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный код цвета.

• Триплет RGB — это трехэлементный вектор-строка, элементы которого указать интенсивность красного, зеленого и синего компоненты цвета.Интенсивность должна быть в диапазон [0,1] ; например, [0,4 0,6 0,7] .

• Шестнадцатеричный код цвета представляет собой вектор символов или строку скаляр, который начинается с символа решетки ( # ) за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться с 0 по F . То значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800' , '#ff8800' , '#F80' и '#f80' эквивалентны.

Кроме того, вы можете указать некоторые распространенные цвета по имени. В этой таблице перечислены названные цвета параметры, эквивалентные триплеты RGB и шестнадцатеричные коды цветов.

'None'

Короткое название	RGB Triblet	Hexadecimal Color Code	Внешний вид
'Red'	R '			[1 0 0]	'# FF0000'
'Green'	'G'	[0 1 0]	'# 00ff00'	9
'Blue'	'B' '9	[0 0 1]	' # 0000FT
'Cyan'	'C'		[0 1 1]	'# 00FFFF
' Magenta '	' M '	[1 0 1]		'# FF00FF'
'Yellow'		'Y'	[1 1 0]	'# FFFF00'
'черный' '	' K ' ' K ' ' K '	[0 0 0]	' # 000000 '
' Белый '	'W'	[1 1]	'#ffffff'
Не применимо	Не применимо	o цвет

Вот триплеты RGB и шестнадцатеричные коды цветов для цветов по умолчанию, которые MATLAB использует во многих типах графиков.

RGB Триплет	Hexadecimal Цветовой код	Внешний вид
[0 0,4470 0,7410]	'# 0072BD'
[ 0.8500 0.3250 0.0980]	'# D95319'
[0,9290 0,6940 0,1250]	'# Edb120'
[0.4940 0,1840 0,5560]	'# 7E2F8E'
[0,4660 0,6740 0,1880]	'# 77AC30'
[0,3010 0,7450 0,9330]	'# 4dbeee'
[0.6350 0,0780 0,1840]	'# A2142F'

Логарифмическая шкала: как ее построить и на самом деле понять

Как интерпретировать логарифмическую шкалу

В линейной шкале, когда мы перемещались на фиксированное расстояние, мы прибавляли или вычитали фиксированный коэффициент к точке.

В логарифмической шкале, когда мы движемся вправо, вместо сложения мы умножаем начальную точку на фиксированный коэффициент. Итак, если мы дважды переместимся на расстояние 10, мы дважды умножим на 10 (я выбрал 10 для простоты):

Изображение автора

Другими словами, по мере нашего движения мы продолжаем умножать или делить на степени 10.

В линейной шкале абсолютное значение расстояния и само расстояние были одинаковыми, а это означало, что если мы переместились на расстояние 2, расстояние добавило два значения.В логарифмическом абсолютное или основное значение расстояния не совпадает с самим расстоянием. Он остается фиксированным, но его значение продолжает увеличиваться в зависимости от расстояния.

Чтобы привить эту мысль, подумайте так. В нашем примере с экзопланетами, чтобы нанести каждую планету на график, нам потребовалось расстояние +1 000 000 единиц, чтобы включить точки более миллиона. Поскольку у нас не так много места, график сжал меньшие значения в одну строку, чтобы соответствовать крайним значениям. Так что расстояние было самой большой проблемой.

Но теперь, если мы используем логарифмическую шкалу для построения экзопланет, мы можем иметь ось с гораздо более коротким расстоянием, которое охватывает значения от 1 до более 1 000 000:

Приведенный выше график не скрывает никаких данных и может легко отображать числа от 1 до 10 миллионов на гораздо более короткой оси, благодаря логарифмам.

Обратите внимание, что я пока не показываю код графиков, потому что не хочу смешивать объяснение кода и логарифмическую шкалу в одном разделе. Мы увидим, как построить график в логарифмическом масштабе подробно в следующем разделе.

Теперь вы можете подумать: «где, черт возьми, все логарифмы?». Что ж, функция логарифмирования вступит в игру, когда мы начнем задавать такие вопросы, как:

• Как изобразить на графике числа, которые не являются степенями 10?
• Как перемещаться между двумя случайными точками на логарифмической прямой?

Представьте, что вы поместили линейку под логарифмической осью так, что 0 см находится прямо под 1.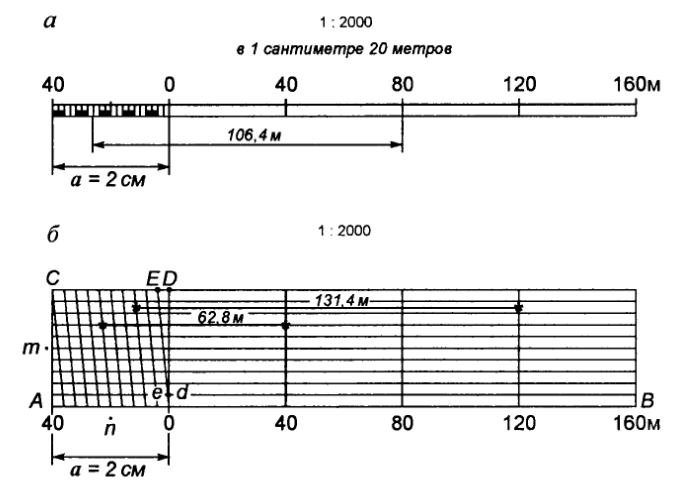 В этом случае расстояние между каждой точкой на логарифмической шкале будет равно 1 см независимо от основания.Например, по основанию 10 1 будет выше 0 см, 10 — выше 1 см, 100 — выше 2 см и так далее.

Если мы изменим основание, сантиметры или точки на линейке не изменятся, изменятся только значения точек выше. Для основания 5 1 по-прежнему будет равно 0 см, 5 будет больше 1 см, 25 больше 2 см и т. д.:

Изображение автора

Теперь мы можем спросить: где я отложу 40 на логарифмической оси основания 6? Другими словами, какая сила у меня есть, чтобы поднять 6, чтобы получить 40? Я думаю, вы знаете, к чему я клоню, но это в основном означает, чему равно log-base-6 of 40?

Изображение автора

Результат — количество сантиметров, которое вам нужно пройти от 0 см.Итак, общая формула для расстояния между 0 см и вашим целевым числом:

Изображение автора

Используя приведенное выше, мы можем вывести формулу для перемещения из любой случайной точки в другую:

Приведенная выше формула находит положение в сантиметрах точка B и вычитает позицию A в сантиметрах, что дает расстояние между двумя точками. Затем вы прибавляете результат к позиции A в сантиметрах. Например, не глядя на саму логарифмическую шкалу, давайте выясним, сколько в сантиметрах нам нужно переместиться от 9 до 146 в логарифмической шкале с основанием 8.Используя формулу:

Результат — сколько в сантиметрах вам нужно переместиться от того места, где 9 расположено вдоль оси бревна.

Подумайте, почему мы всегда начинаем логарифмическую шкалу с 1. Кроме того, можно ли отображать отрицательные значения в логарифмической шкале?

Линейная по сравнению с линейной. Логарифмические шкалы — видео и расшифровка урока

Что такое линейная шкала?

Линейная шкала очень похожа на числовую линейку, описанную выше. Ключом к этому типу шкалы является то, что значение между двумя последовательными точками на линии не меняется независимо от того, насколько высоко или низко вы находитесь на ней.

Например, на числовой прямой расстояние между числами 0 и 1 равно 1 единице. Такое же расстояние в одну единицу находится между числами 100 и 101, или -100 и -101. Как ни посмотри, расстояние между точками постоянно (неизменно) независимо от положения на линии.

Отличный способ визуализировать это — посмотреть на один из старых школьных примеров «Введение в геометрию» или «Промежуточная алгебра» о том, как построить линию. Одно из свойств линии состоит в том, что она является кратчайшим расстоянием между двумя точками.Другое дело, что он имеет постоянный наклон. Наличие постоянного наклона означает, что изменение x и y от одной точки к другой точке на линии не меняется.

Стандартная числовая строка

Что такое логарифмическая шкала?

Логарифмическая шкала сильно отличается. На этой шкале значение между двумя последовательными точками не только изменяется, но и имеет четкую закономерность.

• Логарифмы или «журналы» основаны на показателях степени. 3 = 2 х 2 х 2 = 8.

Представьте, что нам нужно измерить очень большое количество чего-то. Например, минералы в почве, молекулы в воздухе или интенсивность звуковых волн. Иногда нам нужно создать упрощенную шкалу, где каждый шаг представляет собой большое количество единиц, а также увеличивается/уменьшается на определенный коэффициент.

Если ученому нужно измерить миллиарды или даже триллионы молекул, он может просто построить логарифмическую шкалу с каждым числом (т.2 = 100. Числа в логарифмическом масштабе представляют факторное увеличение в реальных единицах.

Отличный способ визуализировать это — посмотреть на график экспоненциальной функции. Одно из свойств, показанных в приведенном ниже примере, заключается в том, что при увеличении x y увеличивается экспоненциально , или на большую величину для каждой дополнительной единицы x.

Эта экспоненциальная линия увеличивается во все большей и большей степени на каждую единицу увеличения x.

Применение и использование

Линейные весы

Линейные весы очень хороши для измерений в реальном мире.Ваша стандартная школьная линейка — прекрасный пример. Ваши 10 сантиметров одинаковы в любой точке мира. Это простое упражнение по основам счета, и в данном случае каждая единица имеет одинаковую длину.

Еще одна линейная шкала — стандартный термометр. Когда вы смотрите на термометр, вы ищете маленькие отметки, каждая из которых соответствует числу, представляющему температуру. Эти метки находятся на одинаковом расстоянии друг от друга, и вы можете просто считать вверх или вниз, чтобы найти точную температуру.Линейные шкалы повсюду в нашем мире, и хотя они не обязательно более полезны, они, безусловно, кажутся более распространенными.

Логарифмические шкалы

Логарифмические шкалы очень хорошо подходят для сведения больших чисел в некоторую управляемую модель. Шкала Рихтера , например, берет силу землетрясения — то, что мы измеряем по магнитуде — и упрощает ее, так что каждый шаг шкалы на самом деле в 10 раз сильнее, чем предыдущий шаг. Таким образом, разница между 1 и 2 по шкале Рихтера на самом деле составляет 10 раз.Или, проще говоря, 2 по шкале в 10 раз больше, чем 1. Точно так же 3 по шкале в 100 раз больше, чем 1.

Как бы сложно это ни звучало, это намного проще, чем объяснять реальную физику. (что требует от вас оценки логарифмической зависимости между амплитудой и магнитудой сейсмических волн). Мы просто знаем, что 10 — это сверхразрушительное воздействие, а 1 — небольшое сотрясение. Спасибо, мистер Рихтер.

Итоги урока

Хорошо, давайте на минутку повторим то, что мы узнали!

Шкала , как обсуждалось в этом уроке, представляет собой выровненный диапазон значений или чисел от самого низкого до самого высокого.На линейной шкале значение между любыми двумя точками никогда не изменится. Логарифм , или логарифм, основан на показателях степени , которые являются верхними индексами рядом с другим базовым числом или переменной и над ним. На логарифмической шкале значение между двумя точками изменяется по определенной схеме.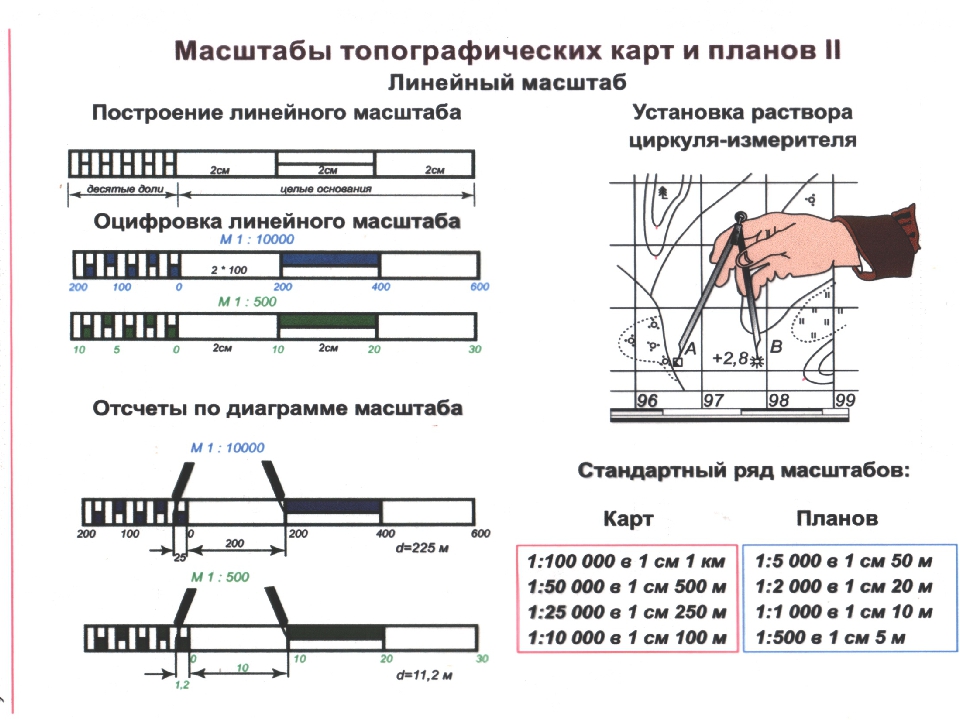 Школьная линейка — отличный пример линейной шкалы, а шкала Рихтера — отличный пример популярной логарифмической шкалы.

Логарифмическая шкала против линейной шкалы: 5 ключевых отличий

Каждый биржевой график содержит две оси — ось X для отображения времени и ось Y для отображения цены.

Существует два основных способа построения графика цены – линейный и логарифмический.

Хотя большинство трейдеров не знают, как устанавливается ценовая шкала, есть несколько ключевых моментов, которые каждый трейдер должен учитывать, когда дело доходит до логарифмической или линейной шкалы.

В этой статье мы обсудим пять ключевых различий между полулогарифмической и линейной шкалой на ценовых графиках.

1. Измерение цены – линейная и логарифмическая шкала

Линейная шкала

<.h4>

Некоторые трейдеры ожидают увидеть равное распределение ценовых значений по оси Y – линейная шкала.

Например, линейный ценовой график может иметь одинаковое расстояние в 5 единиц по оси Y (т. е. 0, 5, 10, 15).

На приведенной ниже диаграмме показан пример линейной шкалы для Apple (AAPL). Вы можете видеть, что ценовой график имеет ось Y с единицей измерения 0,20.

Пример диаграммы с линейной шкалой с расстоянием 0,20 доллара США

Логарифмическая шкала

И наоборот, логарифмическая диаграмма отображает значения с использованием масштабирования цены, а не уникальной единицы измерения.

На логарифмической диаграмме ось Y структурирована таким образом, что расстояния между единицами представляют процентное изменение ценной бумаги. Например, эта процентная разница может составлять 5%, 10% или 15%.

На следующем графике показан тот же график акций Apple, но с включенной логарифмической шкалой.

Пример диаграммы логарифмической шкалы с расстоянием примерно 0,30%

Хотя цены выглядят довольно перегруженными внизу, например, 140,40, 140,70 и т. д., распределение становится все более рассредоточенным по мере увеличения ценовых значений.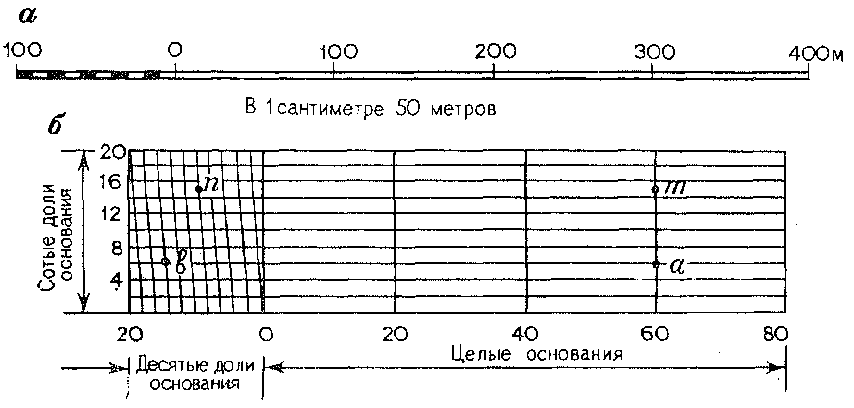

Это связано с тем, что по мере увеличения размера значений предшествующие единицы измерения становятся меньше и поэтому визуально выглядят меньше на диаграмме.

Теперь представьте себе акции, которые сначала торговались по 50 долларов, а со временем торгуются выше 300 долларов (например, Netflix). Первые годы торговли на более низких ценовых уровнях будут выглядеть как крыши, когда вы смотрите в окно самолета перед тем, как приземлиться.

Развивайте свое торговое 6-е чувство

Больше никакой паники, никаких сомнений.принимать правильные решения, потому что вы видели это на своем торговом симуляторе TradingSim.

2. Больше волатильности = логарифмическая шкала

Если ценная бумага имеет небольшие движения цены и изменчивые торговые действия, линейный график, вероятно, будет лучшим методом для построения графика акций.

Однако мы знаем, что движение цен на грошовые акции и биотехнологии совсем не скучно.

Для этих типов ценных бумаг логарифмический ценовой график имеет больше смысла, так как он может визуально отразить значимость больших ценовых движений.

На следующей диаграмме показано сравнение линейной и логарифмической диаграмм для Intel (INTC).

Сравнение линейной и логарифмической шкал для ценового графика INTC

Хотя линейная и логарифмическая шкалы могут выглядеть очень похожими, различия становятся очевидными, если внимательно рассмотреть распределение цены по оси Y.

Видно, что линейный график цены имеет более изогнутую линию. Вы также можете видеть, что линейный график в некоторой степени отражает идею о том, что цена двигалась довольно медленно в начальные периоды, прежде чем цена начала двигаться быстрее в более поздних частях.

Это искажение происходит из-за того, что цена указана в абсолютном долларовом выражении. С другой стороны, логарифмическая диаграмма показывает устойчивое приблизительное процентное изменение значений на 1% и показывает более равномерную шкалу изменения цены за период времени.

Таким образом, логарифмический график больше подходит для приведенного выше примера, поскольку он изображает рост цены акций на устойчивой ноте с довольно прямой траекторией. Когда темпы роста начинают меняться, логарифмическая диаграмма также соответствующим образом корректируется и соответствующим образом отображает изменение, чего нельзя сказать о линейной диаграмме, поскольку значения остаются неизменными, независимо от того, изменилась ли цена всего на 0 долларов.50 или 5%.

3. Логарифмические шкалы полезны для долгосрочной перспективы

Подводя итог, можно сказать, что ценовая шкала аналогична линейным графикам. Это означает, что движение от 100 до 150 долларов, что составляет 40%-ное движение, такое же, как движение от 200 до 250 долларов.

Вы можете видеть, что распределение здесь составляет 50 долларов за единицу, но в процентном выражении у вас есть первоначальное движение на 40% (от 100 до 150 долларов) и приблизительное движение на 22% от 200 до 250 долларов.

В таких случаях для больших ценовых движений лучше использовать логарифмические графики, которые фокусируются на процентах движения.

4. Линейная шкала для внутридневных трейдеров

С другой стороны, линейная ценовая шкала больше подходит для анализа ценной бумаги, которая движется в узком диапазоне или в пределах короткого промежутка времени, например, внутридневных торговых сессий.

Линейная шкала идеально подходит для внутридневных или краткосрочных графиков.

В приведенном выше примере показан 10-минутный ценовой график для AAPL с использованием линейной шкалы цен. Опять же, единицы находятся на равном расстоянии в 0,20 цента. Вы также можете увидеть пример простого метода прорыва, который относительно легко определить и торговать.

Из-за равного распределения в абсолютном долларовом выражении ценовой диапазон в 0,20 доллара, который был установлен на боковом рынке, дает цель вверх и вниз на расстоянии 0,20 доллара, что позволяет относительно легко торговать на краткосрочных ценовых графиках.

Даже если вы будете использовать логарифмическую шкалу на внутридневных графиках, поскольку ценовые движения обычно ограничены, вы получите те же результаты, что и на графике с линейной шкалой.

5. Какую шкалу цен использовать?

Когда дело доходит до анализа акций, цена ценной бумаги обычно анализируется в относительном выражении. Показатели, такие как соотношение цены и прибыли, балансовая стоимость, являются популярными финансовыми коэффициентами. Таким образом, при отображении цены рассматриваемой ценной бумаги имеет смысл представлять или анализировать движение ценной бумаги в процентном выражении, а не в абсолютных величинах.

Таким образом, есть вероятность, что трейдерам автоматически будет показана соответствующая ценовая шкала, даже не зная разницы между двумя типами ценовых шкал.

В конце концов, безопасность диктует, следует ли вам выбрать линейную шкалу цен, полулогарифмическую или логарифмическую шкалу.

Даже среди акций не все ценные бумаги ведут себя одинаково. В то время как, с одной стороны, есть акции, которые имеют взрывные колебания цен, есть также акции, которые обычно ограничиваются диапазоном в течение многих лет.

Бонус — 6. Тенденции улучшаются с логарифмической диаграммой

Я решил дополнить эту статью шестым разделом, посвященным линиям тренда на двух типах диаграмм.

Давайте начнем с простого примера рисования линий тренда для одной и той же ценной бумаги и сравним, как развиваются линии тренда между линейным и логарифмическим графиком.

Линии тренда, построенные на линейной и логарифмической диаграмме

На приведенной выше диаграмме показана корпорация Intel (INTC). Слева у нас линейный ценовой график, а справа логарифмический график.

Линии тренда на обоих графиках абсолютно одинаковы.

Это подводит нас к вопросу о том, какой из двух графиков точно отображает тренд? Это график логарифмической шкалы цен справа, который показывает линии тренда намного лучше, чем линии тренда слева.

Ответ на этот вопрос я оставлю на ваше усмотрение.

Резюме – логарифмическая шкала или линейная шкала: какая шкала лучше?

Ответ на этот вопрос зависит от ряда факторов, таких как рассматриваемая ценная бумага, поведение цены и, конечно же, временные рамки. Однако логарифмическая или полулогарифмическая шкала цен более популярна, чем линейная шкала.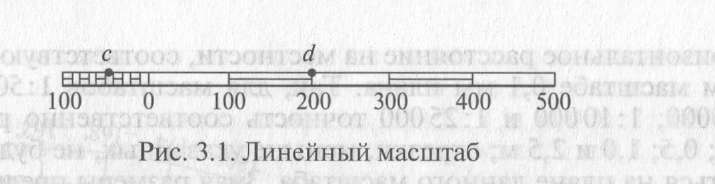

Почти все графические платформы по умолчанию используют логарифмическую шкалу, поскольку единицы измерения равномерно распределены в процентах выражений, что упрощает использование логарифмической шкалы в качестве базового графика для любой ценной бумаги, которую трейдер хочет проанализировать.

Как показано выше в некоторых примерах, существуют определенные сценарии, в которых использование одного типа ценовой шкалы определенно лучше. В конце дня тип и поведение цены определят правильную ценовую шкалу.

Проверьте свои новые знания

Хотите попрактиковаться в информации из этой статьи?
получите опыт торговли без риска с нашим торговым симулятором.

Посетите TradingSim.com ПОПУЛЯРНЫЕ УРОКИ В КУРСЕ: Введение в биржевые графики .