Основы классификации (объектов)
Изучив эту тему, вы узнаете:
— что такое классы и подклассы;
— что такое основание для классификации;
— что такое наследование свойств;
— для чего нужна классификация;
— как проводить классификацию разнообразных объектов;
— как классифицируются компьютерные документы.
Классы и классификация
Человеку присуща способность обобщать и упорядочивать все многообразие объектов. Каждое имя существительное отражает представление человека об обширной группе объектов: дом, стол, книга. Объекты одной группы обладают общими для всей группы характеристиками, а также некоторыми чертами, позволяющими отличить их от других объектов.
Человеку свойственно отождествлять несколько объектов, родственных по какому-то признаку, рассматривая их как самостоятельный объект.
Например, про скрипку, виолончель, альт, контрабас, флейту, гобой, фагот, трубу мы говорим, что это «музыкальные инструменты».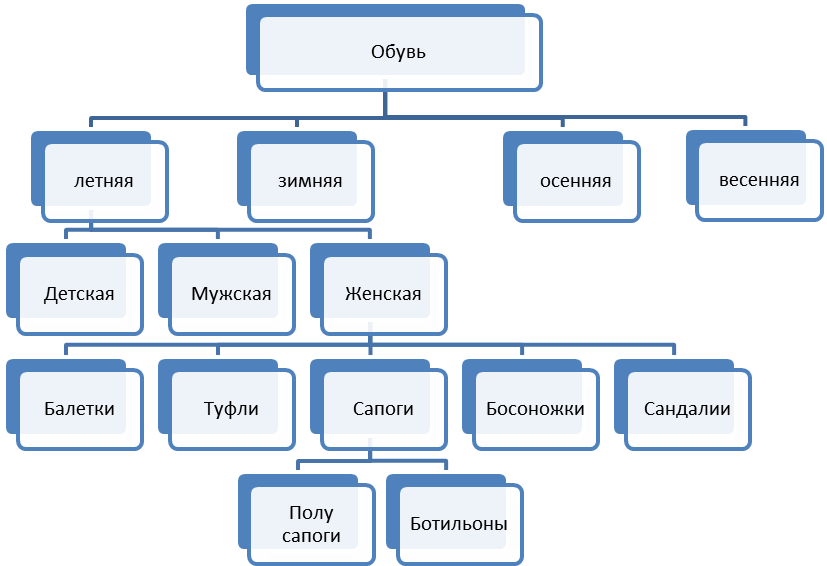
Класс — группа объектов с одинаковым набором характеристик.
Объекты, входящие в класс, называются экземплярами класса. Необходимо понять, что объекты, которые вы по каким-то параметрам объединили в класс с общим названием, отличаются друг от друга конкретными значениями параметров. Например, мячи, сохраняя основные свойства данного класса объектов (легкость, упругость), могут различаться материалом (каучуковые, резиновые, кожаные), цветом, размером. Птицами называют орла и курицу, страуса и колибри. Даже внутри узкого класса экземпляры могут сильно различаться: среди крылатых насекомых под названием «пчелы» существует матки, трутни, рабочие пчелы.
Классификация — распределение объектов на классы и подклассы на основании общих признаков.
Результаты классификации принято отображать в виде иерархической (древовидной) схемы. Общий вид такой схемы изображен на рисунке 9.1.
Внешне схема классификации напоминает перевернутое дерево, за что и получила название иерархической (древовидной). Пунктирными линиями на схеме выделены уровни иерархии. Самый верхний уровень (корень дерева) задает основные признаки, позволяющие отличить объекты данного класса от других. Каждый следующий нижестоящий уровень выделяет из вышестоящего группы объектов на основании совпадения одного или нескольких признаков. На нижнем уровне располагаются конкретные экземпляры выделенных подклассов.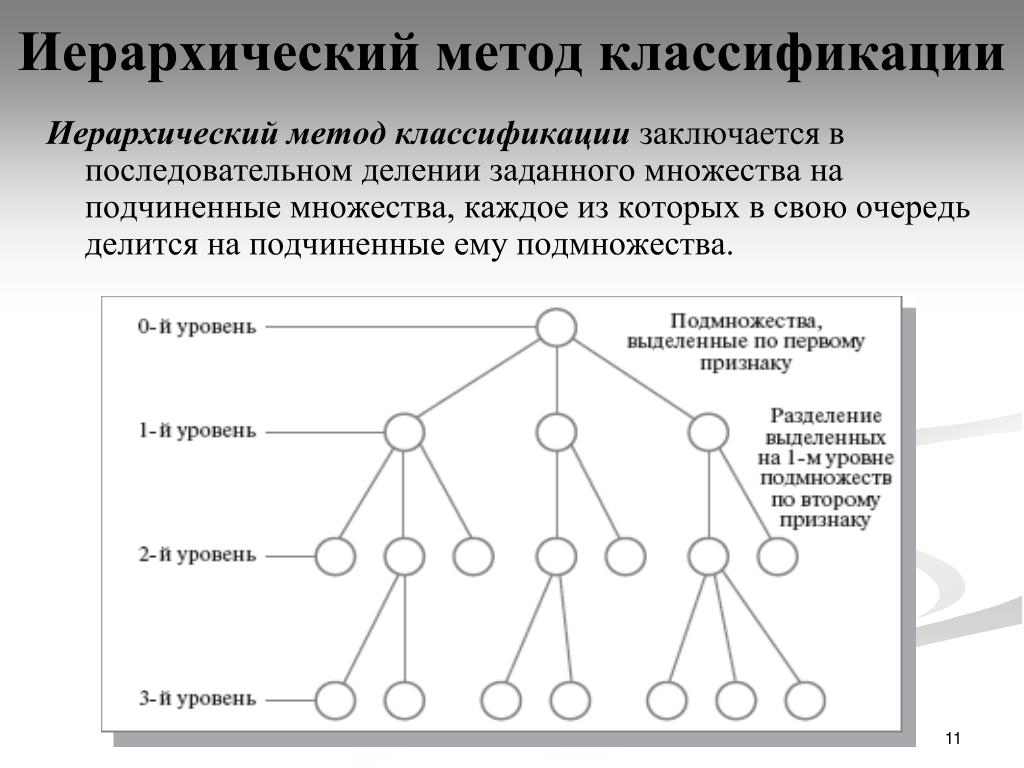
С подобными схемами вы, возможно, уже встречались при изучении биологии, истории и других предметов.
Рис. 9.1. Общий вид иерархической схемы
В виде такой схемы часто изображают родословную. Ее принято называть генеалогическим древом.
Родословная — перечень поколений одного рода, устанавливающий происхождение и степени родства.
Основание классификации
С известными примерами классификации вы уже знакомы. Например, в биологии это классификация растений и животных. С глубокой древности люди, знакомясь с многообразием форм жизни на Земле, стремились распределить это многообразие по группам. Так сложилась естественная классификация, основанная на наблюдении и группировке по некоторым признакам. Идеи, изложенные в книге К. Линнея «Виды растений», изданной в 1753 году, до сих пор служат исходной точкой йри классификации растений. С того времени используется и двойное название растений: первая часть имени указывает на подкласс (семейство), а вторая — на конкретные особенности экземпляра этого подкласса.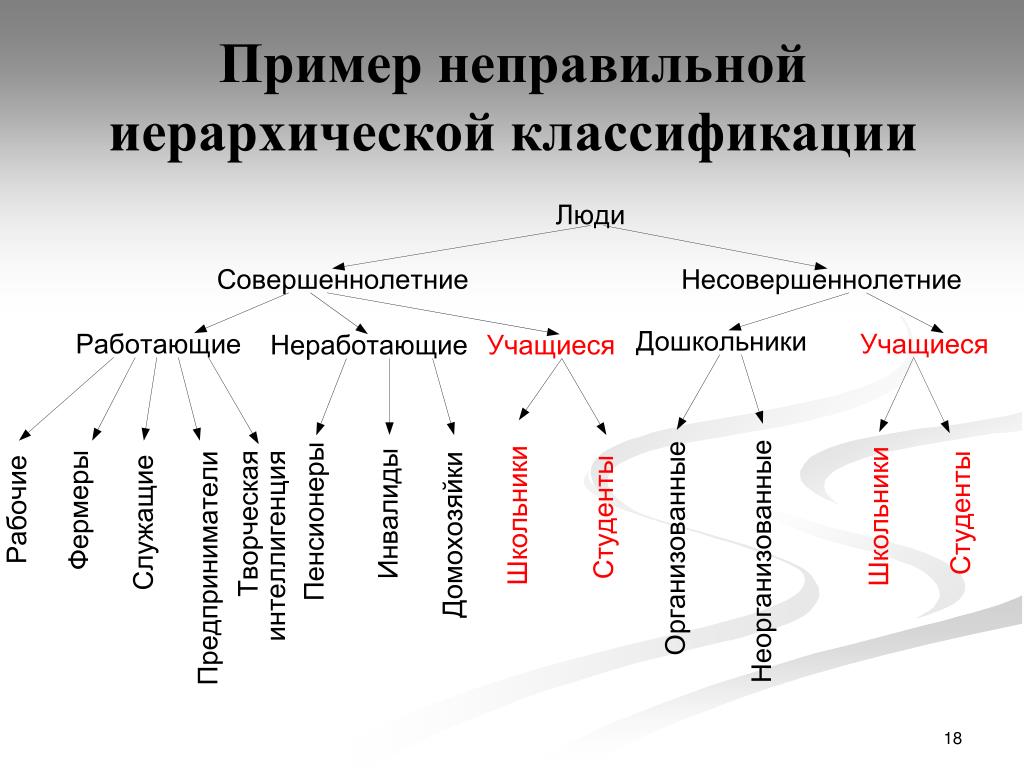
Классификации поддаются не только природные, но и искусственные объекты: в грамматике принято разделение слов по частям речи, в физике — классификация видов движения, в математике — классификация чисел. В их основе лежит группировка объектов по одному или нескольким намеренно выбранным признакам. В разных отраслях науки и техники классы и подклассы могут иметь свои специфические названия: виды, семейства, отделы, разряды, группы и т. п. При этом суть их не меняется.
Рассмотрим объект «книга». Под этим словом мы подразумеваем множество разнообразных книг: художественных и технических, разных авторов, разной стоимости, толстых и тонких, в подарочном издании и в мягкой обложке…
А теперь представьте, что вам необходимо разложить все это многообразие «по полочкам» в буквальном смысле слова, например упорядочить свою библиотеку.
Каждый подойдет к этому вопросу по-разному. Один человек расставит все книги в алфавитном порядке, по фамилии автора. Другой разделит их на жанры: детективы, фантастика, приключения, любовные или исторические романы. Третий поместит их на полки, руководствуясь цветом переплета и размером книг (наверняка вы сталкивались и с таким подходом). Несмотря на разницу в способах классификации, все эти примеры роднит нечто общее: подразделение объектов на «родственные» группы (классы), для которых существует один или несколько общих параметров.
Один человек расставит все книги в алфавитном порядке, по фамилии автора. Другой разделит их на жанры: детективы, фантастика, приключения, любовные или исторические романы. Третий поместит их на полки, руководствуясь цветом переплета и размером книг (наверняка вы сталкивались и с таким подходом). Несмотря на разницу в способах классификации, все эти примеры роднит нечто общее: подразделение объектов на «родственные» группы (классы), для которых существует один или несколько общих параметров.
Во всех приведенных примерах при группировке был выбран общий признак: в первом случае это автор, во втором — жанр, в третьем — цвет и размер. Именно по этим признакам затем производилось выделение из общей массы тех объектов, у которых его значение совпадает.
Таких общих признаков может
быть несколько. Они являются основанием классификации. Выбрав основание, из класса с общим названием «книга» можно выделить подклассы: «книга определенного автора», «книга определенного жанра», «книга определенного размера».
Классификация — творческий процесс, поэтому у каждого человека может получиться своя схема. Один из возможных вариантов выделения подклассов из класса книг показан на рисунке 9.2.
Рис. 9.2. Классификация книг
На первом уровне за основу разбиения книг на две группы выбран признак «вымысел» (да, нет). По этому признаку произошло разделение на художественную и техническую литературу.
На втором уровне признак выделения подклассов можно было бы назвать «форма подачи информации» (художественная проза, поэзия, словари и т. д.).
Третий уровень разбиения можно охарактеризовать признаком «стиль изложения».
Четвертый уровень классификации выделен только для романов, чтобы не загромождать схему. Признаком этого уровня выбран «жанр».
На самом нижнем уровне находятся конкретные экземпляры разнообразных книг.
Наследование свойств
Важнейшим свойством классов является наследование. Это слово вам хорошо знакомо. Дети наследуют от родителей черты характера и внешние признаки. Каждый подкласс, выделяющийся из класса, наследует свойства и действия, присущие этому классу. В приведенном на рисунке 9.2 примере и роман Д. С. Мережковского, и все другие изданные романы, и вся художественная литература вообще — наследуют от класса «книга» общие свойства и действия. Все они напечатаны на бумаге, переплетены и предназначены для чтения.
Из приведенной выше классификации видно, что образовалась иерархическая структура (дерево). Во главе ее класс-пра- родитель — «книга». В самом основании экземпляры подклассов — конкретные книги конкретных авторов.
Такая древовидная структура с общим корнем называется «иерархией наследования». Характеристики и поведение, связанные с экземплярами определенного класса, становятся доступны любому классу, расположенному ниже в иерархическом дереве.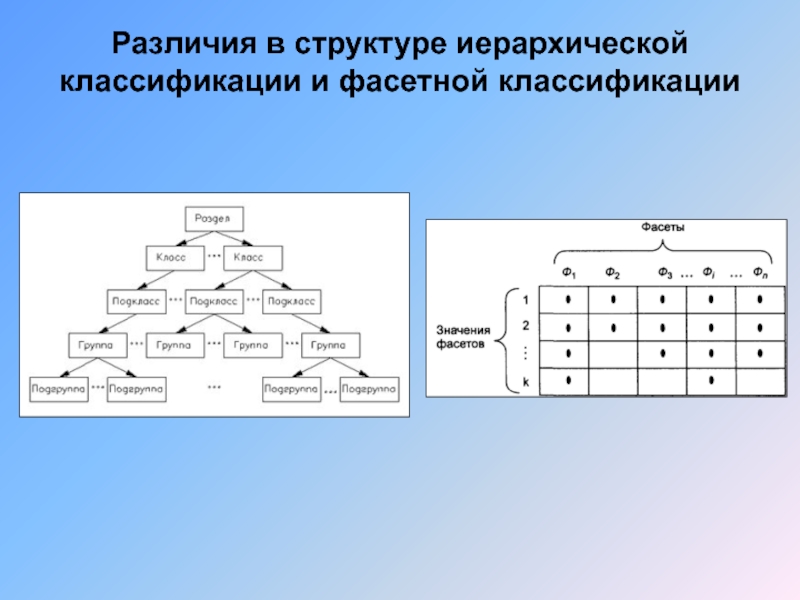
Утверждая, что «книга — источник знаний», вы подразумеваете как все книги вообще, так и конкретную книгу, например «О вкусной и здоровой пище». В этом проявляется наследование.
Для чего же нужна классификация?
□ Классификация позволяет выделить из всего многообразия объектов группы с интересующими исследователя свойствами и сосредоточиться на их изучении.
Предположим, что вы — неопытный огородник, но хотите, используя достижения науки, выращивать на своем участке хорошие урожаи помидоров. Вам незачем штудировать толстый том «Растениеводство», достаточно прочесть книги о семействе пасленовых, а еще лучше — об особенностях выращивания помидоров в вашей местности.
□ Классификация объектов проводится с целью установления наследственных связей между объектами. Свойство наследования позволяет изучать характеристики всех объектов класса, не привязываясь к конкретному экземпляру.
В геологии существует «теория единообразных изменений», которая гласит, что все природные факторы действуют повсюду одинаково. Не надо изучать, как действуют ветры на Уральские горы, так как механизм разрушения гор под воздействием ветров давно исследован, он един для всех случаев. То же относится к землетрясениям, вулканам, наводнениям, селям и т. п.
□ Классификация позволяет систематизировать знания об объектах любой природы и назначения.
Иллюстрацией этого утверждения служит то, что нет ни одной школьной дисциплины, в которой не использовалась бы классификация объектов изучения как средство обобщения информации, получаемой на уроках. Откройте любой учебник и убедитесь в этом.
Примеры классификации различных объектов
Исследуя один и тот же объект с разными целями, можно увидеть его различные грани. Например, врач, описывая конкретного человека, сделает акцент на симптомах возможной болезни.
Психолога заинтересуют черты характера и особенности психики. Социальные службы обратят внимание на возраст, наличие родственников, условия жизни. Поэтому одни и те же объекты можно классифицировать по-разному, выбрав те или иные основания. Вы уже столкнулись в учебнике с примерами различных классификаций. Например, изучая раздел 1, вы классифицируете информацию по разным признакам: по способу восприятия и по форме представления.
На рисунке 9.3 приведен еще один пример классификации информации — по содержанию.
Рис. 9.3. Классификация информации по содержанию
В этой классификации на основании признака «содержание» на первом уровне выделены следующие группы информации:
♦ статистическая — показатели развития производства и общества;
♦ коммерческая — наиболее важные сведения о производственных, торговых и финансовых операциях;
♦ экологическая — сведения о состоянии окружающей среды и влиянии деятельности человека на природу;
♦ политическая — информация о деятельности государственной власти, общественных движений и партий;
♦ другая (демографическая, медицинская и т. д.).
д.).
Все выделенные подклассы характеризуются теми же свойствами (ясность, полнота, актуальность и т. п.) и действиями (обмен, хранение, обработка), что и вышестоящий класс «информация».
Приведем еще один пример классификации, касающейся наиболее значимых систем (рисунок 9.4).
В качестве основания для классификации на первом уровне выбрано участие человека в создании системы (естественные и искусственные).
На втором уровне основанием для классификации был выбран признак «сфера жизнедеятельности человека». Здесь выделены такие подклассы систем:
♦ духовные у касающиеся духовной жизни человека;
♦ технологические у связанные с производственной деятельностью человека;
♦ организационные у обеспечивающие обслуживание всех видов деятельности.
Рис. 9.4. Классификация наиболее значимых систем
На схеме не показано дальнейшее разветвление дерева, так как это сделало бы рисунок громоздким. Но подразумевается, что дальнейшее выделение подклассов возможно. Например, рассматривая класс систем, называемых «Искусство», можно было выделить следующие подклассы по средствам воплощения замыслов авторов: Живопись, Скульптура, Архитектура, Литература, Театр, Музыка, Кино и т. д.
Но подразумевается, что дальнейшее выделение подклассов возможно. Например, рассматривая класс систем, называемых «Искусство», можно было выделить следующие подклассы по средствам воплощения замыслов авторов: Живопись, Скульптура, Архитектура, Литература, Театр, Музыка, Кино и т. д.
Наряду с устоявшимися и общепризнанными классификациями имеет право существовать любая классификация объектов, если за ее основу взят характерный признак и соблюдены правила выделения классов и подклассов. На рисунке 9.5 приведен пример классификации используемых в реальной жизни и встречающихся в сказках средств передвижения.
Здесь на нулевом уровне расположен класс объектов с общим названием «средства передвижения».
На первом уровне выделено два подкласса по признаку «реальность» (существуют в реальной жизни или в сказках, фантазиях).
Рис. 9.5. Классификация средств передвижения
Второй уровень выделяет из реальных и сказочных средств передвижения новые подгруппы по признаку «среда передвижения».
Третий уровень делит реальные средства передвижения на подгруппы по признаку «вид транспортйого средства». На схеме не указано выделение подгрупп из реальных наземных средств передвижения, чтобы не загромождать ее. Но эти группы могли быть следующими: рельсовые, дорожные. Возможно и дальнейшее подразделение. Важно понять, что нижние уровни наследуют все характерные признаки, свойственные более высоким уровням: например, объект Ка-26, принадлежащий к подклассу вертолетов, наследует от вышестоящего уровня среду перемещения (воздух), а также является реальным средством передвижения со всеми сопутствующими признаками (существует в реальной жизни, осуществляет перевозки людей и грузов).
Классификация компьютерных документов
В самом общем смысле компьютер можно назвать инструментом для обработки информации. Для этого существует множество разнообразных программных сред. Разработчики постоянно совершенствуют программы, упрощая работу с ними и предусматривая в них новые возможности.
Чтобы не «утонуть» в море программных продуктов, пользователь очень хорошо должен представлять, с какой информацией ему предстоит работать. Каждая программная среда предназначена для создания документов определенного вида.
На практических занятиях вы уже познакомились со многими видами компьютерных документов, которые будут упоминаться при классификации документов.
Приведенная на рисунке 9.6 схема показывает классификацию, в которой в качестве основания выбран признак «назначение документа». Основным назначением компьютерных документов является представление информации в удобном для пользователя виде. В таблице 9.1 дана более конкретная характеристика каждого класса документов.
Рис. 9.6. Классификация компьютерных документов
Обратите внимание, что название среды, как правило, совпадает с видом документа и формой представленной в нем информации.
Приведенная классификация поможет вам выбрать среду в соответствии с предполагаемой формой представления информации.
В настоящее время документы, используемые в различных областях человеческой деятельности, создаются на компьютере. Рассмотрим примеры документов различного назначения и сферы применения.
Литературное произведение, газетная статья, приказ — примеры текстовых документов.
Рисунки, чертежи, схемы — это графические документы.
Таблица 9.1. Виды компьютерных документов
Бухгалтер на предприятии представляет в табличном виде данные для расчета зарплаты сотрудников. Основная особенность электронных таблиц состоит в том, что они позволяют не только представлять информацию в табличной форме, но и производить автоматические вычисления по формулам, связывающим ячейки таблицы.
Один из видов компьютерных документов — база данных. Она представляет собой совокупность упорядоченных сведений об объектах. В обычной жизни вы не раз встречались с базами данных. Это и картотека с названиями книг в библиотеке, и телефонный справочник, и каталог товаров. В настоящее время вместо обычных «бумажных» баз данных повсеместно создаются компьютерные, представленные документами соответствующего вида. Диспетчер справочной службы имеет в своем распоряжении всеобъемлющую компьютерную базу данных, позволяющую ответить на любой ваш вопрос. Система управления базой данных обеспечивает быстрый поиск интересующей вас информации.
В настоящее время вместо обычных «бумажных» баз данных повсеместно создаются компьютерные, представленные документами соответствующего вида. Диспетчер справочной службы имеет в своем распоряжении всеобъемлющую компьютерную базу данных, позволяющую ответить на любой ваш вопрос. Система управления базой данных обеспечивает быстрый поиск интересующей вас информации.
Текст, графика, таблица, база данных — это примеры документов, в которых представлена информация какого-то одного вида.
Однако наиболее часто мы имеем дело с составными документами, в которых информация присутствует в разных формах. Такие документы могут содержать и текст, и формулы, и рисунки, и таблицы, и многое другое. Школьные учебники, журналы, газеты — это хорошо знакомые всем примеры составных документов.
Для создания составных документов используются программные среды, в которых предусмотрена возможность представлять информацию в разных формах.
Развитие программного обеспечения привело к тому, что в настоящее время появились новые виды компьютерных документов. В частности, это презентации и гипертекстовые документы.
В частности, это презентации и гипертекстовые документы.
Презентация представляет собой совокупность компьютерных слайдов. Специальная программа обеспечивает не только подготовку информации, но и показ ее по заранее созданному сценарию.
Гипертекст — это документ, который содержит так называемые гиперссылки на другие части документа или другие файлы, где содержится дополнительная информация.
Контрольные вопросы и задания
1. Для чего нужно классифицировать объекты?
2. Что лежит в основе любой классификации?
3. Приведите пример классификации объектов по общим свойствам.
4. Приведите пример классификации объектов по общим действиям.
5. Может ли среда существования стать основанием классификации?
6. Произведите классификацию объектов с общим названием «велосипед».
7. Классифицируйте домашнюю посуду по следующим признакам: материал, назначение, долговечность.
8. Предложите несколько вариантов упорядочения (классификации) разнообразных объектов на вашем письменном столе.
9. Назовите основание, по которому в одну группу могли бы попасть следующие объекты:
■ кенгуру, утконос, кролик, броненосец;
■ роза, колесо, футбольные бутсы, кактус;
■ молоко, бензин, кислота, магма.
10. Назовите разнородные объекты окружающего мира, которые вошли бы в одну группу по основанию «одно вещество».
11. Какие классификации используют в вашей школьной среде?
12. Перечислите наиболее распространенные группы компьютерных документов.
13. Приведите примеры классов программных продуктов. Какое можно выбрать для этого основание классификации?
14. Какое основание классификации можно использовать для выделения групп аппаратной части компьютера?
15. Какие вы знаете классы памяти компьютера?
примеры и заблуждения / Хабр
Это завершающая статья из цикла классификации моделей. В данной статье я классифицирую конструкции. Должен извиниться за отсутствие иллюстраций, но так получилось. Поэтому сегодня просто текст. Должен предупредить, что данная статья опирается на предыдущие мои статьи, в которых подробно описано, что объект, операция и функция — объекты, имеющие лишь разную трактовку.
Термины
Начнем с термина «есть часть». В быту мы встречаем следующие высказывания: слоны – есть часть млекопитающих. Речь идет о том, что множество слонов есть подмножество множества млекопитающих. В этой статье термин «есть часть» будет употребляться в другом смысле. Мы будем употреблять этот термин только в отношении конкретных объектов. Например, конкретная ветка дерева – есть часть конкретного дерева. При этом не надо думать, что речь идет о любой ветке дерева, как тогда, когда мы даем определение понятию: ветка дерева – есть часть дерева. В терминах матлогики это утверждение читается так: для любой ветки дерева найдется такое дерево, что данная ветка есть часть этого дерева. Такое утверждение относится уже не к конкретному объекту, а к понятию, определяющему объекты. Если в статье понадобиться сказать так, я скажу явно. В противном случае я буду говорить о конкретных объектах.
Следующий термин «включает в себя». Если я говорю, что дерево включает в себя ветку, то это значит, что конкретная ветка – это часть конкретного дерева. И речь по-прежнему идет о конкретных объектах, а не о множествах или понятиях.
Еще один термин, разобраться с которым будет немного сложнее. Это термин «состоит из» Кажется, что он близок к термину «включает в себя», но мы будем их различать. Мы говорим, что дерево состоит из веток, ствола и корней. При этом подразумеваем, что части дерева перечислены полностью, чтобы дать нам полное представление о строении дерева. То есть, термин «состоит из» употребляется в отношении строений (конструкций) объектов. Если взять часть из этих объектов, то сказать, что над-объект состоит из этих под-объектов уже не получится (что-то упущено). Поэтому правильна такая иерархия: над-объект, конструкция над-объекта, элементами которой являются под-объекты и из которых она состоит, под-объект, являющийся частью над-объекта и являющийся элементом конструкции над-объекта.
Парадигмы конструкций
Один над-объект может быть представлен в виде разных конструкций. Над-объект может быть поделен на части в соответствии с разными принципами деления (разными основаниями). Есть принцип деления, сохраняющий компактность пространственных частей — пространственное деление. Пример: здание состоит из помещений. Напомню, что тезис «здание состоит из помещений» равносилен утверждению: есть здание, есть конструкция здания, выполненная в рамках пространственной парадигмы, элементами которой (конструкции) являются помещения. Другое основание – функциональное. Пример: здание состоит из ограждающих конструкций, кровли и инженерных подсистем. Другими словами, можно сказать, что основание для деления над-объекта – это парадигма конструкции.
Конструкции человеческого тела часто рассматривается в двух парадигмах: одна называется внешнее строение человека, вторая — внутреннее строение. Внешнее строение описывает части человеческого тела: руки, ноги, голову, туловище. Внутреннее строение описывает подсистемы человека: кровеносную, пищеварительную, нервную и проч. Внешнее строение равносильно пространственному делению здания на помещения. Внутреннее строение равносильно функциональному делению здания по подсистемы.
Классификация конструкций
Обычно мы рассматриваем конструкцию просто: вот над-объект, вот под-объекты, вот связи между под-объектами, которые объясняют нам свойства над-объекта. Мы будем классифицировать конструкции через классификацию элементов конструкции.
Элементы конструкции принадлежат тому же классу, что и объект
Рассмотрим конструкцию, в которой элементы принадлежат тому же классу, что и над-объект. Например, вода состоит из частей, каждая из которых – тоже вода. Или куча песка, элементы которой – тоже кучи песка. Если объект делится подобным образом, то для него зачастую можно ввести меру. Это — особенность такого рода конструкций. Например, масса объекта равна сумме масс ее частей, площадь фигуры равна сумме площадей ее частей, объем материи равен сумме объемов ее частей и тд. Рассмотрим пример менее очевидный. Пусть есть операция и ее части – под-операции. Тогда мерой может стать ее четырехмерный объем. Пример: человек выполнял операцию 4 часа. Объем операции– 4 человеко-часа. Пусть мы разделили операцию на 4 под-операции. Каждая под-операция пусть имеет объем – 1 человеко-час. Таким образом, сумма объемов под-операций равна объему над-операции.
Заблуждение
Замечу, что многие здесь сделают ошибку и подумают, что я говорил о понятии операции. Нет, в данном контексте речь шла о конкретной операции, совершенной Васильевым с 12-00 по 16-00 12-го апреля 2016 года. Если же говорить о понятии операции, то нельзя сказать, что понятие длится 4 часа. Можно сказать, что операции подобного типа длятся в среднем 4 часа. Я же часто (даже от ведущих аналитиков) слышу ошибочные высказывания на эту тему. Они говорят, что операция, которую они обозначили в нотации BPMN в виде прямоугольника длится 4 часа. Но нотация BPMN не моделирует операции, она моделирует понятие операции. Поэтому в этой нотации нельзя сказать, сколько длится конкретная операция. В свойствах объекта, созданного в нотации BPMN может быть атрибут: средняя длительность операций данного типа, но не может быть атрибута длительность операции. В продукте
Businessstudioименно так и сделано. В свойствах объекта, созданного в нотации EPC или в нотации можно указать распределение длительностей операций определенного типа. И это верно.
Примеры конструкций первого типа
Примеры подобных конструкций: операция по постройке дома представлена в виде конструкции, состоящей из операций, которую мы наблюдаем на сетевом графике строительства дома. Диаграмма в нотации IDEF0 моделирует конструкцию функции, состоящую из функций.
Ошибочный пример: некоторые могут подумать, что на диаграмме BPMN подпроцесс – это конструкция операции, но это не так. На диаграмме BPMN нет моделей операций. Там есть концептуальные модели операций. Очень похоже на определение понятия, и так оно и есть. Квадратик в BPMN моделирует не операцию, а понятие об операции. Диаграмма в нотации BPMN – концептуальная модель, а не модель объекта.
Класс конструкций, в котором элементы принадлежат одному классу
Конструкция такого рода состоит из элементов, относящихся к одному классу в то время, как над-объект относится к другому классу.
Например, конкретная будка состоит из конкретных четырех досок. Понятно, что объем будки не равен сумме объемов досок, поэтому ввести меру не удастся. Пример из описания активности: операция состоит из участников. Мы воспринимаем участников как материальные, либо как функциональные объекты, но не воспринимаем их как операции. В данном случае я опять хочу подчеркнуть, что мы говорим не о концептах операций, модель которых можно найти в нотациях BPMN, а об операциях, модели которых можно найти на диаграммах Ганта. Например, участниками операции «забить гвоздь», которая состоялась в 9-00 13-го мая 2011 года были: Сидоров, молоток, гвоздь, две доски, табуретка, лампа, стол, помещение.
Если кто-то попытается сказать что-то подобное об объектах, созданных в нотации BPMN, то это должно звучать так: каждая операция данного типа, модель которого (типа) мы видим в нотации BPMN, имеет участников перечисленных далее типов:… Например, в каждой операции типа «забить гвоздь» будут участвовать объекты следующих типов: «исполнитель», «гвоздь» и «молоток». Правда, есть исключения. Например, иногда в определении типа операции можно встретить ссылку не на тип участника, а на модель конкретного ресурса. Тогда речь идет о том, что в любой операции данного типа участником будет конкретный объект, а не объект какого-то типа, например, в каждой операции класса «получить согласование на постройку здания» указан участник: администрация города Москвы (объект).
Все объекты конструкции принадлежат разным классам
Следующий кейс наиболее распространен: объекты над- и под- относятся к разным классам. Например, трансформатор состоит из сердечника и двух обмоток. В применении к описанию активности можно рассмотреть предыдущий пример в разрезе того, что исполнители относятся к разным классам. Сидоров – к людям, молоток – к инструментам, а гвоздь – к материалам. Все зависит от того, как мы классифицируем объекты.
Описание конструкции без перечисления ее элементов
Следующий кейс посложнее. Мы говорим о конструкции, в которой нет перечисления ее элементов, но есть упоминание о типах объектов, из которых состоит конструкция. Например, здание состоит из кирпичей. Конкретное здание состоит из объектов типа «кирпич». Нет перечисления конкретных кирпичей, но есть указание типа, к которому относятся эти объекты. Моделирование таких конструкций довольно затруднено в современных языках моделирования. Дело в том, что для моделирования таких утверждений нужны предикаты второго порядка. Но языков, которые были бы заточены для моделирования предикатов второго порядка, нет. Причина этого в том, что, если модель, созданная в предикатах первого порядка вычислима, то модель в предикатах второго порядка — нет. То есть, на основе фактов, записанных в предикатах первого порядка, можно строить однозначные выводы. Если же модель построена в предикатах второго порядка, то выводы могут быть только с некоторой долей вероятности. Например, если мы говорим, что лес состоит из осин на 60 процентов и из берез на 30 процентов (остальные деревья относятся к другим породам), то сказать наверняка о породе произвольно взятого дерева в этом лесу можно будет только с некоторой долей вероятности.
Создание ИС ставит перед собой задачу автоматизации некоторых операций. Чаще всего, это детерминированные операции, в которых нет места вероятностным исходам. Программисты в большинстве своем решают именно такие задачи. Поэтому все их инструменты заточены под моделирование предикатов первого порядка, ООП в частности. Поэтому там, где надо моделировать предикаты второго порядка, ООП не справляется.
Примеры
Можно подумать, что такой кейс и правда редкий, однако, моделирование активности предприятия напрямую связано с моделированием такого рода отношений между объектами. Например, мы моделируем конструкцию бизнес-функции. Есть три распространенных способа представить ее конструкцию (парадигмы конструкции). Первый способ был упомянут выше – над-функция представляется в виде конструкции, состоящей из под-функций (нотация IDEF0). Второй способ – конструкция функции состоит из набора ее участников (например, функция продаж состоит из продавца, потенциального покупателя и товара). Этот тип конструкции моделируется в нотации IDEF0 при помощи стрелок, входящих в квадрат «снизу». Третий тип конструкций соответствует текущему кейсу: функция состоит из операций определенного типа. Например, функция продаж состоит из операций по продаже товаров. Функция – объект, операция – объект. Операции по продаже – объекты одного типа. То есть тезис о том, что здание состоит из кирпичей похож на тезис: функция состоит из операций определенного типа. Языка для моделирования такого рода утверждений нет. Как я уже говорил, причина в том, что это утверждение в предикатах второго порядка. Еще один пример такого рода утверждений: кристалл состоит из атомов. Через аналогию с кристаллом мы перейдем к самому сложному для понимания кейсу, связанному с описанием конструкций.
Конструкция из ячеек с объектами разных типов
Пусть есть кристалл. До сего момента мы не рассматривали связи между элементами конструкции как часть конструкции. С этого момента связи нам понадобятся. Понятно, что разделение объекта на части требует описания связей между элементами. При делении на перечисляемые элементы мы можем перечислить и все связи между элементами. Однако, при делении на объекты одного типа без перечисления всех элементов возникает вопрос о том, как описать связи между элементами конструкции? Например, в здании большинство кирпичей имеют связи с другими кирпичами через кладочный раствор. Тогда мы говорим, что здание состоит из кирпичей, каждый кирпич имеет связи с соседними кирпичами. При этом 60 процентов кирпичей имеют 5 соседей, 30 процентов – 4 соседа, 5 процентов – 3 соседа и 5 процентов- 2 соседа. Таким образом, для любого выбранного кирпича из первой группы найдется пять, которые тоже являются частью здания и которые связаны с выбранным кирпичом через кладочный раствор. Теперь напишем то же утверждение относительно бизнес-функции. Функция по продаже состоит из операций по продаже. Предположим, что операции следуют одна за другой. Тогда мы можем сказать, что для любой операции существует предшествующая ей операция того же типа и существует последующая ей операция того же типа. Так мы смоделировали тип связи в конструкции, которая описана типами объектов, но не объектами. Теперь представим себе кристалл более сложного строения, в котором участвуют атомы разных элементов и расположены в сложной кристаллической решетке. Как описать строение такого кристалла? Те, кто занимается описанием и классификацией кристаллов, знают, что способов описания такого рода решетки – бесконечно много. Например, пусть есть одномерная цепочка атомов двух разных типов А и В, чередующихся друг с другом с шагом в один ангстрем. Можно сказать, что кристалл состоит из ячеек, каждая из которых состоит из атомов типа А и В, расположенных через 1 ангстрем, сдвиг между ячейками — 2 ангстрема. (Также верным будет утверждение о том, что кристалл состоит из ячеек, каждая из которых состоит из атомов типа А и В, расположенных через 3 ангстрема. Сдвиг между ячейками – 2 ангстрема и ячейки пересекаются в пространстве. Каждая такая регулярная структура видна на ренгенограмме кристалла. Чтобы ограничить количество вариантов обычно берут наиболее близко расположенные атомы). С другой стороны, можно сказать, что кристалл состоит из атомов двух типов: А и В. Это утверждение похоже на предыдущее, но отличается от него тем, что в первом случае конструкция кристалла состоит из ячеек, а конструкция ячеек, в свою очередь, — из атомов. Во втором случае конструкция кристалла напрямую состоит из атомов. Другой пример: пусть в функции продаж выполняются два типа операций: согласование условий и отгрузка товара. Можно сказать, что функция состоит из ячеек, в каждой из которых есть операция по согласованию условий и операция по отгрузке товара. А можно сказать: функция состоит из операций по согласованию условий и операций по отгрузке товаров. Это два разных утверждения.
Выбор последовательности элементов в типовой ячейке
Посмотрим на последовательность операций: АВАВАВАВ… Мы видим, что цепочка бесконечная и начинать выделение ячеек можно с любого места. Например, сначала птица Феникс родилась из пепла, затем она сгорела, затем родилась из пепла, затем сгорела. Или: сначала птица Феникс сгорела, затем родилась из пепла, затем снова сгорела. Ячейку можно начать в любом месте. Поэтому, чтобы иметь основания для начала, выбирают некоторое условие, которое выполняется для всех операций ячейки. Например, все операции относятся к одной сделке. Условия могут быть любыми, и в общем случае ячейка может начинаться с операции любого типа. Аналитики обычно этого не знают и, чтобы как-то оправдать выбор начальной операции в ячейке, гипнотизируют себя мыслями о том, что цепочка должна иметь мистическую цель. Вместо того, чтобы сказать, что операции в цепочке могут быть объединены в группу по какому-то (в общем случае произвольному) признаку, аналитики придумывают алхимические формулы. Более того, эта алхимия присутствует в определении процесса.
Моделирование предикатов второго порядка при помощи OWL
Стандарт OWL Full позволяет моделировать высказывания второго порядка благодаря тому, что в роли предметов высказывания в нем могут выступать как объекты, так и классы (множества объектов) и даже типы связей, которые могут существовать между объектами (предикаты). Все эти виды сущностей для OWL являются узлами графа, ребра в котором – конкретные утверждения.
Высказывания второго порядка, записанные в виде OWL, как правило, не обеспечивают вычислимости (возможности получения выводов средствами машин логического вывода). Однако не стоит считать это препятствием для реализации автоматизированных систем. В большинстве случаев работа с OWL-моделями происходит в прикладном программном коде и учитывает особенности и ограничения конкретной задачи, а не претендует на «вычисление всего». На практике полностью полагаться на стандартный логический вывод не получается даже при работе даже с высказываниями первого порядка – при большом объеме и разнообразии данных такие задачи требуют слишком больших вычислительных ресурсов.
Существует несколько способов моделирования высказываний о классах на языке OWL. Один из наиболее практически удобных способов состоит в введении специальных классов, объекты которых представляют собой высказывания о классах или предикатах. Приведем пример (для не знакомых со стандартом запишем его на естественном языке):
- Существует класс «Здание»
- Существует класс «Кирпич»
- Существует класс «Требование к составу объекта»
- Существует связь «Относится к объектам класса» между объектами класса «Требование к составу объекта» и классами
- Существует связь «Должны иметь в составе» между объектами класса «Требование к составу объекта» и классами
- Существует объект A, относящийся к классу «Требование к составу объекта», имеющий следующие связи:
- Требование А – относится к объектам – класс «Здание» (это высказывание можно записать как предикат: Относится к объектам (Требование А, класс «Здание») ).
- Требование А – должны иметь в составе – класс «Кирпич»
Можно обобщить функционал требований – изъять из названия класса слова «… к составу объекта», а в число связей класса «Требование» включить указание на предикат, к которому оно относится («Состоит из», «Расположен в»). Таким же способом можно исключить из названия класса и модальность («должен», «может» и др.). Тогда класс будет называться даже не «Требование», а «Утверждение» или «Аксиома». Это добавит полноценный второй уровень к структуре модели, представленной в виде графа. Выбор уровня формализма зависит исключительно от решаемой прикладной задачи.
Автоматизированная система считывает и интерпретирует приведенные выше высказывания, например, таким образом: в составе каждого объекта класса «Здание» должен присутствовать хотя бы один объект класса «Кирпич». Можно и не опускаться на уровень конкретных кирпичей, интерпретируя высказывание по-другому – как утверждение о том, что здание в принципе состоит из объектов класса «Кирпич» (каких именно – не известно). В таком случае могут использоваться другие высказывания о классе «Кирпич» – например о том, что кирпичи (то есть все объекты класса «Кирпич») имеют определенную плотность, массу, теплопроводность и др. Из этого программа сможет сделать вывод о свойствах здания.
В любом случае эта логика – способность интерпретировать объекты класса «Требование к составу объекта» как требования – должна быть заложена в коде, что допустимо в рамках решения конкретных прикладных задач.
Можно пойти немного другим путем – ставить классы не только на вторую позицию в предикате, но и на первую, то есть делать высказывания о классах как таковых:
- Существует класс «Здание»
- Существует класс «Кирпич»
- Существует связь (предикат) «Должен включать объекты, имеющие в составе только объекты класса» между классами и классами
- Класс «Здание» – должен включать объекты, имеющие в составе только объекты класса – класс «Кирпич»
Интерпретация утверждений такого рода, конечно, тоже остается на прикладном программном обеспечении.
Заметим, что некоторые утверждения о классах можно делать и в рамках более строгого формализма OWL, не теряя вычислимости модели при помощи стандартных машин логического вывода. Это достигается использованием ограничений значений свойств (кардинальностей) с квантификаторами: some, only, exactly и др. Еще один способ записи нашего примера таков:
- Существует класс «Здание»
- Существует класс «Кирпич»
- Существует связь «Состоит из»
- Класс «Здание» есть подкласс анонимного класса, для объектов которого значением связи «Состоит из» являются объекты класса «Кирпич»
При сохранении такого высказывания в граф образуются так называемые «пустые узлы». В данном случае пустым узлом будет анонимный класс, для которого задано ограничение. В соответствии с замыслом стандарта OWL, пустые узлы представляют собой утверждения с квантором существования – то есть, в нашем случае, утверждение о том, что существуют такие объекты, которые состоят из кирпичей. Подклассом таких объектов являются здания.
Такая конструкция довольно громоздка, а правила логического вывода – медленны и капризны в применении, поэтому на практике обычно проще обойтись первым или вторым способом.
Заметим, что все это время мы обсуждали высказывание «Здание состоит из кирпичей», смысл которого с логической точки зрения не слишком точен. Не понятно, что мы хотели сказать:
- Что все, что состоит из кирпичей, есть здание,
- Что здание должно состоять только из кирпичей,
- Что здание состоит в том числе и из кирпичей,
и так далее. При реализации автоматизированной системы такие смысловые «люфты» необходимо устранять. Именно поэтому в начале статьи я сразу дал определения терминам, которые буду употреблять в рамках текущей статьи.
Смешанные конструкции
Вернемся к конструкции дерева и посмотрим на тезис: дерево состоит из ветвей, ствола и корней. Этот тезис говорит о том, что конструкция дерева состоит из объекта – ствола и объектов двух разных типов — ветвей и корней.
Пример псевдоконструкции
Рассмотрим частый случай, когда строится диаграмма в нотации IDEF0. Затем одна из функций на этой диаграмме, как часто говорят, «декомпозируется» на диаграмму в нотации BPMN. Это можно встретить в упомянутой мной ранее программе Businessstudio. Поскольку функция – это объект в предметной области, а диаграмма в нотации BPMN – это модель понятия, то мы видим, что происходит ошибка: функция делится на понятие. Этого быть не может. Функция может делиться на ячейки с операциями. В каждой ячейке несколько операций, связанных между собой темпоральными связями. Для всех ячеек вводится понятие ячейки подобного типа. Это понятие моделируется в нотации BPMN. Так будет правильно.
Корреляция конструкций в двух разных парадигмах
Часто встречающийся способ описания объекта выглядит так: рассмотрим конструкцию объекта в двух разных парадигмах, например в парадигме «внешнего» и «внутреннего» строения. Тогда мы пойдем делить объект на части двумя совершенно разными способами. Например, здание будем делить с одной стороны на помещения, а с другой — на технические подсистемы. И вот тут срабатывает очень важный фактор, который мы, как правило, не замечаем, но он работает на уровне интуиции. Мы делим объект на части в двух разных парадигмах таким способом, что между элементами конструкций в двух разных парадигмах тоже можно установить соответствие. Например, после деления здания на помещения и подсистемы мы можем сказать, что и помещения можно поделить на части — части тех подсистем, которые находятся в этих помещениях. То есть, деление на части в двух разных парадигмах интуитивно делается зависимым друг от друга образом. И это отнюдь не очевидно. Современные стандарты инженерного проектирования основаны именно на таком делении объекта, хотя, я уверен, что в них нет прописанного требования о подобном ограничении на моделирование.
Задача классификации (Classification problem) · Loginom Wiki
Разделы: Бизнес-задачи, Алгоритмы
Loginom: Логистическая регрессия (обработчик), Нейросеть (классификация) (обработчик)
В искусственном интеллекте и машинном обучении — задача разделения множества наблюдений (объектов) на группы, называемые классами, на основе анализа их формального описания. При классификации каждая единица наблюдения относится определенной группе или номинальной категории на основе некоторого качественного свойства.
Пусть X — множество описаний объектов, Y — конечное множество номеров (имен, меток) классов. Существует неизвестная целевая зависимость — отображение y∗:X→Y, значения которой известны только на объектах конечной обучающей выборки Xm=(x1,y1),…,(xm,ym). Требуется построить алгоритм a:X→Y, способный классифицировать произвольный объект x∈X.
В математической статистике задачи классификации называются также задачами дискриминантного анализа.
В машинном обучении задача классификации решается с использованием обучения с учителем, поскольку классы определяются заранее и для примеров обучающего множества метки классов заданы. Аналитические модели, решающие задачу классификации, называются классификаторами.
Задача классификации представляет собой одну из базовых задач прикладной статистики и машинного обучения, а также искусственного интеллекта в целом. Это связано с тем, что классификация является одной из наиболее понятных и простых для интерпретации технологий анализа данных, а классифицирующие правила могут быть сформулированы на естественном языке.
К числу распространенных методов решения задачи классификации относятся:
Задача классификации применяется во многих областях:
- в торговле — классификация клиентов и товаров позволяет оптимизировать маркетинговые стратегии, стимулировать продажи, сокращать издержки;
- в сфере телекоммуникаций — классификация абонентов позволяет определять уровень лояльности, разрабатывать программы лояльности;
- в медицине и здравоохранении — диагностика заболеваний, классификация населения по группам риска;
- в банковской сфере — кредитный скоринг.
1.3. Методы классификации информации — СтудИзба
· 1.3. Методы классификации информации
Классификация –это система распределения объектов (предметов, явлений, процессов, понятий) по классам в соответствии с определенным признаком.
Под объектом понимается любой предмет, процесс, явление материального или нематериального свойства. Применительно к информации существуют информационные объекты.
Пример. В университете, например, существуют объекты: информация о студентах – объект «студент»; информация о преподавателях – объект «преподаватель»; информация о факультетах – объект «факультет» и т.д.
Свойства информационного объекта определяются реквизитами. Реквизиты представляются либо числовыми данными, например, все, стоимость, год, либо признаками, например, цвет, марка машины, фамилия.
Реквизит – логически неделимый информационный элемент, описывающий определенное свойство объекта, процесса, явления и т.п.
Пример. Информация в студенте представлена следующими реквизитами: фамилия, имя, отчество, пол, год рождения, место рождения, адрес домашний, факультет и т.д.
Классификация нужна для выявления общих свойств информационного объекта, а также для разработки правил (алгоритмов) и процедур обработки информации. При классификации необходимо соблюдать следующие требования:
Рекомендуемые файлы
-полнота охвата объектов рассматриваемой области;
-однозначность реквизитов;
-возможность включения новых объектов.
В любой стране разработаны и применяются государственные, отраслевые, региональе классификаторы. Например, классифицированы отрасли промышленности, оборудование, профессии, единицы измерения, статьи затрат и т.д.
Классификатор – систематизированный свод наименований и кодов классификационных группировок.
Код – это условное обозначение объекта или явления в виде знака или системы знаков, построенное по определенным правилам.
При классификации пользуются понятием классификационного признака, который позволяет установить сходство или различие объектов.
Разработаны три метода классификации объектов: иерархический, фасетный, дескрипторный.
Иерархический метод классификации устанавливает между классификационными группировками иерархические отношения подчинения, с последовательной детализацией их свойств: класс, подкласс, группа, подгруппа, вид и т.д.
0 уровень
1уровень
2 уровень
3 уровень
Достоинства:
-простота построения;
-использование независимых классификационных признаков в различных ветвях иерархической структуры.
Недостатки:
-жесткая структура, которая приводит к сложности внесения изменений, т.к. приходится перераспределять все классификационные группировки;
-невозможность группировать объекты по заранее не предусмотренным сочетаниям признаков.
Пример иерархической системы классификации для информационного объекта «факультет»:
0 уровень
1-название ф-та Коммерческий Информационные
(классификационный системы
признак)
2-возраст до 20 лет 20-30 лет свыше 30 лет до 20 лет 20-30 лет свыше 30 лет
3-пол м ж м ж м ж м ж м ж м ж
4-наличие детей есть нет есть нет есть нет есть нет есть нет есть нет
у женщин
Метод фасетной классификации основан на множестве независимых признаков. Набор таких признаков может быть произвольным, что позволяет группировать объекты по любому сочетанию признаков. Является одноуровневым, исходное множество объектов разбивается на подмножества классификационных группировок в соответствии со значениями признаков отдельных фасетов. Фасеты независимы между собой.
Схема построения фасетной системы классификации в виде таблицы:
|
| фасеты | ||||||
|
| |||||||
значения фасетов |
| Ф1 | Ф2 | Ф3 | … | Фi | … | Фn |
1 |
|
|
|
|
|
|
| |
2 |
|
|
|
|
|
|
| |
… |
|
|
|
|
|
|
| |
k |
|
|
|
|
|
|
| |
Достоинства:
-возможность создания большой емкости классификации, т.е. использование большого числа признаков классификации и их значений для создания группировок;
-возможность простой модификации всей структуры существующих группировок.
Недостатком фасетной системы классификации является сложность ее построения, т.к. необходимо учитывать все многообразие классификационных признаков.
Пример.
Наименование факультета | Возраст | Пол | Дети |
Радиотехнический | до 20 лет | м | есть |
Машиностроительный | 20-30 лет | ж | нет |
Коммерческий | свыше 30 лет |
|
|
Информационные системы |
|
|
|
Математический |
|
|
|
Суть дескрипторного метода классификации:
-отбирается совокупность ключевых слов или словосочетаний, описывающих определенную предметную область или совокупность однородных объектов, среди которых могут находиться синонимы;
Лекция «4. Способы подготовки шахтных полей» также может быть Вам полезна.
-выбранные ключевые слова нормализуются, т.е. из совокупности синонимов выбираются наиболее употребимые;
-создается словарь дескрипторов, т.е. словарь отобранных слов и словосочетаний.
Пример. Объект классификации – успеваемость студентов. Ключевые слова: оценка, экзамен, зачет, преподаватель, студент, семестр, название предмета. Синонимов нет, эти ключевые слова можно использовать как словарь дескрипторов.
Предметная область: учебная деятельность в вузе. Ключевые слова: студент, обучаемый, учащийся, преподаватель, учитель, педагог, лектор, ассистент, доцент, профессор, коллега, факультет, аудитория, лекция, практическое занятие и т.д. Встречаются синонимы. После нормализации словарь дескрипторов будет состоять из следующих слов: студент, преподаватель, лектор, ассистент, доцент, профессор, факультет, аудитория, лекция, практическое занятие и т.д.
Иерархическая классификация товаров, примеры
Понятие и сущность иерархической классификации товаров в маркетинге
Определение 1
Иерархическая классификация товаров – это группировка товарного ассортимента компании по подчиненным подмножествам.
Многие фирмы производят и/или продают множество различных видов товарной продукции. Для целей маркетинга и управления их принято подвергать определенной группировке по тем или иным основаниям, то есть классификации. Классификация представляет собой ни что иное как процедура группировки, проводимая на качественном уровне и основанная на выделении однородных свойств объектам. В маркетинге классификация товаров используется довольно часто.
Товары могут быть классифицированы по различным основаниям. В соответствии с этими основаниями выделяются различные классификационные методы. Метод иерархической классификации товарной продукции подразумевает необходимость последовательного разделения множества товарных групп на подчиненные классификационные группировки.
Отличительной особенностью данного метода классификации выступает наличие тесной связи между отдельными классификационными группировками, которая выявляется посредством анализа общности и различий основополагающих признаков. Фундаментальной основой деления множества товаров на подмножества выступает ступень классификации.
Под ступенью классификации принято понимать этап классификационного процесса, основанного на иерархическом методе, по окончании которого выделяется определенная совокупность классификационных группировок. Глубина классификации определяется количеством ступеней и признаков. Если глубина слишком большая, классификация товаров становится слишком запутанной и громоздкой. В этом случае многие низшие ступени начинают дублировать друг друга. Все это ограничивает возможности практического использования иерархической классификации товаров. Согласно общепринятому правилу количество ступеней, то есть глубина классификации не должна превышать десяти.
Замечание 1
Каждую группировку и ступень классификации следует выделять по основополагающему признаку, выбору которого в маркетинге отводится особая роль.
Готовые работы на аналогичную тему
В основе выбора классификационных признаков лежит целевое назначение классификации. Число признаков ограничено, если их требуется увеличить, следует отказаться от иерархического метода классификации товаров в пользу использования фасетного метода.
Использование иерархической классификации товарной продукции предполагает необходимость подразделения всего множество товарной продукции на подчинённые подмножества, которые все вместе составляют единую систему, состоящую из элементов, сходных как минимум по одному признаку. Структура иерархической классификации товаров включает в себя:
- группы;
- подгруппы;
- виды;
- подвиды и пр.
Иерархическая классификация позволяет структурировать множественные товары, формирующие собой ассортиментный ряд продукции фирмы и использовать полученные группы для дальнейшего анализа, оптимизации и управления. Используется подобного рода классификация и в сфере разработки стратегии продвижения продукции, совершенствовании ассортиментного ряда, формирования системы сбыта и пр.
Иерархическая методика классификации товаров, используемая в маркетинге, имеет свои преимущества и недостатки. К основным достоинством данной классификационной системы принято относить:
- высокую информативную насыщенность;
- способность к выделению общности и сходства признаков товарной продукции на одной и/или разных ступенях.
В то же время иерархическая классификация не лишена недостатков, которые наиболее ярко проявляются при ее чрезмерной глубине, ограничивая тем самым возможности ее использования для исследовательских и управленческих целей. К подобного рода ограничениям и недостаткам принято относить громоздкость структуры, высокие затраты на ее построение, а также трудность применения. К числу прочих недостатков, проявляющихся при незначительной глубине, относятся: неполный охват признаков и объектов, а также информационная недостаточность.
Замечание 2
Несмотря на наличие описанных выше недостатков, данная система классификации товарной продукции получила широкое общественное признание и была взята на вооружение многими специалистами в сфере товароведения, маркетинга и управления.
Примеры иерархической классификации товаров в маркетинге
Иерархическая система классификации товарной продукции весьма часто используется на практике. Рассмотрим лишь некоторые примеры ее применения, но прежде обратится к типовой классификационной схеме, представленной на рисунке 1.
Рисунок 1. Базовая схема иерархической классификации. Автор24 — интернет-биржа студенческих работ
Таким образом, заданное на нулевом уровне множество по первому классификационному признаку делится на подмножества первого уровня. Выделенные на первом уровне подмножества, в свою очередь, также делятся на подмножества по второму классификационному признаку и так далее, максимально – вплоть до 10 уровня. Приведем пример.
Предположим, что магазин специализируется на продаже клея. По природе своего происхождения клей может быть природным или синтетическим. В данном случае природа возникновения выступает классификационным признаком первого уровня. Каждая из групп подлежит дальнейшей классификации. Клей природного происхождения может быть минеральным, растительным или животным. Клей природного животного происхождения в свою очередь делится на альбуминовую, казеиновую и колагеновую группу, состоящую из мездрового и костного клея. Клей синтетического происхождения делится на созданные на основе термоактивных и термопластичных смол, а также синтетических каучуков. Таким образом, данная иерархическая классификационная цепочка состоит из пяти уровней.
Рассмотрим другие примеры.
Виноградные вина подлежат множественной классификации. По насыщенности диоксидом углерода их подразделяют на тихие и перенасыщенные. Тихие вина, в свою очередь, делятся на натуральные и специальные. Группа пересыщенных вид состоит из газированных или шипучих вин, игристых вин и шампанского. В данном случае классификационная структура имеет три уровня иерархии.
Широкой иерархической классификации может быть подвержена обувь. Так, например, в зависимости от сезона года, для которого она предназначена, ее делят на четыре укрупненных группы:
- весенняя;
- летняя;
- осенняя;
- зимняя.
Рассмотрим дальнейшую классификацию на примере летней обуви. Летняя обувь в зависимости от того, кто ее носит, делится на детскую, мужскую и женскую. Женская обувь по своему типу делится на туфли, балетки, сандалии, босоножки.
Весьма часто иерархическая классификация используется в рамках товарной номенклатуры. В этом случае используются следующие уровни классификации товаров. Первый уровень составляют разделы, на втором уровне используются группы, третий уровень представлен товарными позициями, четвертый уровень и ниже – более низкие уровни детализации.
VIII. Принципы классификации
Информация об изобретении Дополнительная информация Технические объекты изобретений Подразделения в классификации для классифицирования технических объектов изобретений Функционально-ориентированные и отраслевые подразделения Классификация технической сущности изобретений Общие замечания Категории тематики, для которой нет соответствующего точного заголовка рубрики МПК Периодическая Таблица химических элементов Химические соединения Химические смеси или композиции (составы) Получение и обработка химических соединений Устройства или способы Изделия Многоступенчатые способы, агрегаты (установки) Детали, конструктивные элементы Общие химические формулы Комбинаторные библиотеки 75. Основным назначением классификации, как отмечено в п. 6, является облегчение поиска технических решений. В связи с этим классификация разработана и должна использоваться таким образом, чтобы одинаковые технические решения классифицировались одинаково и, следовательно, могли быть найдены в одном и том же месте классификации. Это место должно быть самым подходящим для проведения поиска таких технических решений.
76. В патентном документе может быть два типа информации. Это «изобретательская информация» и «дополнительная информация». Значение этих выражений объясняется ниже в п.п. 77-80. Правила выбора классификационных индексов одинаковы для обоих типов информации (см. также главу XI ниже). Хотя в «Руководстве к МПК» упоминаются только изобретения или технические объекты изобретений, это в равной мере относится к техническим объектам, охватываемым дополнительной информацией.
ИНФОРМАЦИЯ ОБ ИЗОБРЕТЕНИИ
77. Изобретательская информация — это техническая информация, раскрываемая в патентном документе (например, описании, рисунках, патентной формуле), которая представляет дополнение к уровню техники. Изобретательская информация определяется в контексте с уровнем техники, используя в качестве руководства патентную формулу патентного документа, уделяя дополнительное внимание описанию и рисункам.
78. «Дополнение к уровню техники» означает все новое и неочевидное в технической сущности, особо раскрытое в патентном документе, что не является частью предшествующего уровня, т.е. разница между технической сущностью патентного документа и подборкой всех знаний о технической сущности, доступной публике.
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
79. Дополнительная информация — это техническая информация, которая сама по себе не является дополнением к уровню техники, но может представлять полезную информацию для поиска.
80. Дополнительная информация сопровождает изобретательскую информацию, указывая, например, составляющие композиции или смеси, или элементы или компоненты способа или конструкции, или использование классифицируемых технических объектов.
КАТЕГОРИИ ТЕХНИЧЕСКИХ ОБЪЕКТОВ ИЗОБРЕТЕНИЯ
81. Техническими объектами изобретений могут быть новые и неочевидные способы, продукты, устройства или материалы (или способы их использования или применения). Эти термины, обычно используемые для категории технического объекта, следует интерпретировать в широком смысле, как указано в следующих примерах:
(а) Примеры способов: полимеризация, ферментация, разделение, формование, транспортирование, обработка текстиля, передача и преобразование энергии, строительство, приготовление пищи, испытание, методы работы на машинах и способы их работы, обработка и передача информации.
(б) Примеры продуктов: химические соединения, составы, ткани, промышленные изделия.
(в) Примеры устройств: установки для проведения химических или физических процессов, инструменты, орудия, машины, устройства для выполнения технических операций.
(г) Примеры материалов: ингредиенты смеси.
82. Следует отметить, что устройство можно также рассматривать как продукт, в том смысле, что каждое устройство произведено в результате выполнения определенного процесса. Термин «продукт», однако, используется для обозначения конечного результата процесса независимо от его последующей функции, например, конечный продукт химического или производственного процесса, тогда как термин «устройство», как правило, предполагает его использование по определенному назначению или для определенной цели, например устройство для генерирования газов, устройство для резания. Материалы сами по себе могут составлять продукты.
ПОДРАЗДЕЛЕНИЯ В КЛАССИФИКАЦИИ ДЛЯ КЛАССИФИЦИРОВАНИЯ ТЕХНИЧЕСКИХ ОБЪЕКТОВ ИЗОБРЕТЕНИЙ
83. Классификация разработана для обеспечения классифицирования любой технической сущности изобретения в целом, а не по отдельным составным частям.
84. Составные части технического объекта изобретения могут также составлять изобретательскую информацию, если они сами по себе представляют дополнение к уровню техники, т.е. являются новыми и неочевидными объектами.
ФУНКЦИОНАЛЬНО-ОРИЕНТИРОВАННЫЕ И ОТРАСЛЕВЫЕ ПОДРАЗДЕЛЕНИЯ
85. Техническая сущность изобретений, описываемая в патентных документах, касается либо самой природы или функции какого-либо объекта, либо способа применения или использования объекта. В связи с этим термин «объект» используется для обозначения как осязаемых, так и неосязаемых технических объектов, например, способа, продукта, устройства. Вышеупомянутое находит отражение в строении схемы классификации. Она содержит рубрики для классифицирования:
а) объекта «вообще», т.е. характеризующегося своей природой или функцией; объекта, который либо не зависит от какой-либо конкретной области его применения, либо остается технически неизменным, если отвлечься от области применения, т.е. не приспособленным специально для использования в какой-то области;
Примеры:
(1) Подкласс F 16К предусмотрен для клапанов, характеризуемых конструктивными или функциональными свойствами, которые не зависят от особенностей текучей среды, проходящей через него, или от системы, частью которой он является.
(2) Класс С07 предусмотрен для органических химических соединений, характеризующихся их химической структурой, а не их применением.
(3) Подкласс В01D предусмотрен для фильтров вообще.
(б) объекта «специально приспособленного для» особого использования или цели, т.е. модифицированного или сконструированного специально для данного использования или цели;
Пример: A61F 2/24 – рубрика для механического клапана, специально приспособленного для человеческого сердца.
(в) особого использования или применения объекта;
Пример: Фильтры, специально приспособленные для особых целей, или комбинации их с другими устройствами, классифицируются в отраслевых рубриках, например A24D 3/00, A47J 31/06.
(г) встраивание объекта в большую систему.
Пример: B60G имеет подразделение для встраивания рессор в подвеску колес транспортного средства.
86. Подразделения категории (а), указанные выше, называются “функционально-ориентированными подразделениями”. Подразделения категории (б) — (г), указанные выше, называются «ориентированными по применению» подразделениями.
87. Подразделения, например, подклассы, не всегда следует рассматривать как полностью функционально — ориентированными или полностью ориентированными по применению по отношению к другим подразделениям МПК.
Пример: Несмотря на то, что подклассы F16K (клапаны и т.д.) и F16N (смазка) являются по своему содержанию функциональными, подкласс F16N содержит рубрики для некоторых клапанов, специально предназначенных для смазочных устройств или систем (например, F16N 23/00 – обратные клапаны для смазочных устройств), и, наоборот, подкласс F16К содержит отраслевые рубрики для смазочных устройств в шиберных затворах или золотниках (например, F16К 3/36 – конструктивные особенности, относящиеся к смазке).
Выражения «функционально-ориентированное подразделение» и «ориентированнoе по применению подразделение» не всегда могут рассматриваться в их абсолютном значении. Подразделение может быть более функциональным, чем другое рассматриваемое подразделение, но менее функциональным, чем другие подразделения по отношению к какой-либо тематике.
Пример: Группа F02F 3/00 относится к поршням двигателей внутреннего сгорания вообще и, следовательно, является более функционально-ориентированной, чем группа F02B 55/00, которая специально предназначена для вращающегося типа поршней двигателей внутреннего сгорания, но менее функционально-ориентированной, чем подкласс F16J, который предназначен для поршней вообще.
87 бис. В МПК существуют также подразделения, которые применяются для классифицирования только при условии, если не существует другого места в МПК для рассматриваемой тематики. Такие подразделения относятся к «остаточным».
Выражения, приведённые ниже и используемые в заголовках соответствующих подразделений, ясно указывают на «остаточный» характер этих подразделений:
— «не предусмотренные в других рубриках МПК»,
— «не предусмотренные в…»,
— «не охватываемые …».
«Остаточная» природа подразделения может быть относительной по отношению к другим подгруппам, другим основным группам того же подкласса, другим подклассам или даже ко всей МПК. Основные группы с номером 99/00 по всей МПК являются специально выделенными остаточными подразделениями.
Примеры: F21S 15/00 Неэлектрические осветительные устройства или системы с применением источников света, не отнесенных к основным группам F21S 11/00, F21S 13/00 или F21S 19/00
G06Q 99/00 Тематика, не предусмотренная в других группах данного подкласса
A99Z Тематика, не предусмотренная в этом разделе
F21K источники света, не предусмотренные в других рубриках МПК
КЛАССИФИКАЦИЯ ТЕХНИЧЕСКОЙ СУЩНОСТИ ИЗОБРЕТЕНИЙ
Общие замечания
88. Очень большое значение имеет правильное определение или выявление технической сущности изобретений. При этом следует иметь в виду, что для определения наиболее подходящего места в классификации объект следует рассмотреть в отношении каждой категории, представленной в п.п. 81-85.
Пример: Если в патентном документе раскрыт поршень, то необходимо рассмотреть вопрос о том, является ли технической сущностью изобретения поршень как таковой или, например, специальное приспособление поршня для использования в особых устройствах, или размещение поршней в целой системе, например, в двигателе внутреннего сгорания.
89. Часто информация об изобретении касается только определенной технической области использования. В этом случае изобретение будет полностью классифицировано в ориентированном по применению подразделении. Функционально-ориентированные подразделения разработаны на основании другого подхода. Его суть в том, что конструктивные и функциональные особенности объекта изобретения, которые классифицируются в этих подразделениях, относятся к нескольким областям применения и применение в какой-то определенной области не является информацией об изобретении.
Пример: Группа С09D 5/00 охватывает составы для нанесения покрытий для различных областей применения (например, С09D 5/16 охватывает противообрастающие краски). Группы С09D 101/00-201 /00 охватывают функционально-ориентированные аспекты составов для покрытия, а именно полимер, на котором состав основан.
90. Когда при классифицировании технической сущности возникают сомнения в выборе функционально-ориентированного или ориентированнoго по применению подразделения, необходимо руководствоваться следующим:
(а) Если определенная область применения упомянута, но детально не раскрыта или не определена полностью, классифицирование проводится в функционально-ориентированном подразделении, если таковое имеется. То же относится к случаю, когда широко заявлено несколько областей применения.
(б) Если технически существенные характеристики объекта относятся к самой природе или функции объекта, а также к области его применения или специальному приспособлению или встраиванию в целую систему, то классифицирование проводится и в функционально-ориентированном и в ориентированнoм по применению подразделениях, если таковые имеются.
(в) Если таких ориентиров, как (а) и (б), нет, классифицирование проводится и в функционально-ориентированном, и в ориентированнoм по применению подразделении.
91. При классифицировании большой системы (комбинации) в целом следует уделять внимание частям или деталям. Если они являются новыми и неочевидными, классифицирование и системы, и этих частей или деталей является необходимым.
Пример: В том случае, если документ относится к встраиванию какого-либо объекта, например, листовой рессоры, в целую систему, например, в подвеску колес транспортного средства, это означает, что он относится к целой системе и должен быть проклассифицирован в подразделении для этой системы (B60G). Если документ относится также к объекту как таковому, например, к листовой рессоре как таковой, и является новым и неочевидным, документ необходимо классифицировать также в подразделении для этого объекта (F16F).
Категории тематики, для которой нет соответствующего точного заголовка рубрики МПК
92. Из п.п. 81 и 82 следует, что техническая сущность изобретения может выражаться различными категориями объектов. Если для одной из этих категорий нельзя подобрать точно рубрику с соответствующим заголовком, для классифицирования выбирается наиболее подходящая рубрика, предусмотренная для других категорий объектов (см. п.п. 93-99 для конкретных ситуаций). В таких ситуациях, даже если заголовок рубрики не совсем явно предусматривает эту категорию объекта, возможны другие указания на нее, такие как отсылки, примечания, определения или упоминания о подобной тематике в других группах (подгруппах) данной части схемы. Определения, если таковые имеются, должны давать конкретную информацию о классификационных рубриках для подходящих категорий объектов, не указанных в заголовках рубрик.
Периодическая Таблица химических элементов
92 бис. Во всех разделах МПК при отсутствии особого указания Периодическая Система химических элементов, на которую содержится ссылка, является Системой с восьмью группами, как представлено ниже в Таблице. Например, в группе C07F 3/00 “Соединения, содержащие элементы 2-ой группы Периодической системы” имеются в виду элементы колонок IIA и IIB.
Химические соединения
93. Сущность изобретения, относящегося к химическому соединению (органическому, неорганическому или высокомолекулярному), классифицируется в разделе C в соответствии с его химической структурой. Если сущность изобретения относится также к определенной области его применения, то химическое соединение классифицируется также и в рубрике для этой области применения, если таковая является существенно важной технической характеристикой предмета изобретения. Однако, в случае, когда химическое соединение уже известно, а сущность изобретения относится исключительно к применению химического соединения, то изобретение классифицируется в рубрике, соответствующей области его применения, как информация об изобретении. При этом химическая структура соединения может быть также проклассифицирована в рубрике для химического соединения, как такового.
Химические смеси или композиции (составы)
94. Сущность изобретения, относящаяся к смесям или композициям (составам), классифицируется в тех подразделениях, которые соответствуют (если они существуют) их химическому составу, например в С03С (стекло), С04B (цемент, керамика), С08L (композиции органических высокомолекулярных соединений), С22С (сплавы). Если подходящее подразделение отсутствует, объект изобретения классифицируется в соответствии с областью его применения или использования. В тех случаях, когда применение или использование является существенным признаком изобретения, смесь или композиция классифицируются как по их химическому составу, так и по области применения или использования. Но, если данная химическая смесь или композиция известна, а сущность изобретения относится только к ее применению, то она классифицируется в рубрике, соответствующей области применения, как информация об изобретении. При этом смесь или композиция может также быть проклассифицирована в рубрике для данной химической смеси или композиции, как таковой.
Получение и обработка химических соединений
95. Сущность изобретения, касающаяся способа получения или обработки химического соединения, классифицируется в подразделении, соответствующем данному способу получения или обработки рассматриваемого химического соединения, а если такой рубрики не существует, то в рубрике, соответствующей данному химическому соединению. Если соединение, образующееся в результате данного процесса получения, является новым, то его следует также классифицировать в рубрике, соответствующей его химическому строению. Техническая сущность изобретения, касающаяся общих способов получения или обработки целых классов химических соединений, классифицируется в рубриках для способов, если такие рубрики существуют.
Устройства или способы
96. Сущность изобретения, касающаяся устройства, классифицируется в рубрике для данного устройства, если таковая существует. Если же для такого устройства специальной рубрики не существует, то устройство классифицируется в рубрике, соответствующей способу, в котором используется это устройство. Сущность изобретения, касающаяся способа изготовления или обработки продуктов, классифицируется в рубрике для применяемого способа. Если такой рубрики не существует, то изготовление или обработка продуктов классифицируется в рубрике для устройства, которое используется в данном способе. Если не существует рубрики для изготовления продукта, то устройство для изготовления или способ классифицируется в рубрике, соответствующей данному продукту.
Изделия
97. Сущность изобретения, касающаяся изделия, классифицируется в рубрике, соответствующей этому изделию. Если для изделия как такового не существует подходящей рубрики, оно классифицируется в подходящем функционально-ориентированном подразделении (т.е. в соответствии с функцией, выполняемой данным изделием) или, если таковое отсутствует, в соответствии с областью применения этого изделия.
Например: Если изделием, подлежащим классифицированию, является распылитель клея, специально предназначенный для книжных переплетов, то оно классифицируется в группе B42C 9/00 «Использование клея или склеивающих веществ в переплетном производстве». Поскольку не существует специальной рубрики для распылителей клея для переплетных работ, то они классифицируются в рубрике, соответствующей их функции, т.е. «использование клея».
Многоступенчатые способы, агрегаты (установки)
98. Сущность изобретения, заключающаяся в многоступенчатом способе или промышленном агрегате, которые состоят из комбинации стадий процесса или комбинации нескольких устройств в едином агрегате, классифицируется как нечто целое, т.е. в подразделении, соответствующем такой комбинации, например в подклассе B09B. Если такого подразделения не существует, изобретение классифицируется в подразделении, соответствующем продукту, получаемому в результате использования такого многоступенчатого способа или агрегата. Если сущность изобретения касается также отдельного элемента комбинации, например, отдельной стадии процесса или отдельной машины агрегата, то такой элемент классифицируется обособленно в соответствующей рубрике.
Детали, конструктивные элементы
99. В тех случаях, когда техническая сущность изобретения касается конструктивных элементов или деталей объекта, например, устройств, применяются следующие правила:
(а) если конструктивные элементы или детали предназначены или могут использоваться только для одного определенного объекта, то они классифицируются в рубриках, соответствующих этому объекту, если такие рубрики существуют;
(б) при отсутствии таких рубрик эти конструктивные элементы или детали классифицируются в рубрике, предназначенной для рассматриваемой тематики;
(в) конструктивные элементы или детали, которые могут использоваться в нескольких видах объектов, классифицируются в рубриках более общего характера, если таковые существуют;
(г) при отсутствии таких рубрик более общего характера, данные конструктивные элементы или детали классифицируются в рубриках, соответствующих всем видам объектов, к которым они точно относятся.
Например: В подклассе A45B группы 11/00-23/00 охватывают различные виды зонтов, а группа 25/00 – детали зонтов, которые могут использоваться более, чем для одного типа зонтов.
Общие химические формулы
100. Большое количество химических соединений часто выражается или заявляется в виде общих формул. Общие формулы представляют родовое химическое соединение, по крайней мере, с одним компонентом формулы, являющимся переменным, выбранным из специфической подборки альтернатив (например, формулы «Маркуша»). Использование общих формул вызывает проблемы при классифицировании, когда они охватывают большое количество соединений, которые могут быть отдельно проклассифицированы в большом количестве рубрик. В таких ситуациях классифицируются только индивидуальные химические соединения, наиболее полезные для поиска. Если химические соединения описываются с использованием общей химической формулы, должна применяться следующая процедура классифицирования.
| Стадия 1: | Классифицируются все «полностью идентифицированные» соединения, которые являются новыми и неочевидными, при условии, что они: |
Стадия 2: | Если «полностью определенные» соединения не раскрыты, например, когда соединения получают методом компьютерного моделирования, и они не подвергаются реальному эксперименту, классификация проводится по соединениям с точным химическим наименованием или по развёрнутой химической формуле. Классификацию следует ограничивать одной или очень малым количеством групп. |
Стадия 3 | Когда раскрыта только общая формула Маркуша, классификация проводится в наиболее специфических группе или группах, которые охватывают все или большинство возможных видов реализации. Классификацию следует ограничивать одной или очень малым количеством групп. |
Стадия 4 | В дополнение к вышеуказанной обязательной классификации, может быть представлена необязательная классификация, если другие соединения в объеме общей формулы представляют интерес. |
Если классификация всех «полностью определенных» соединений в их наиболее специфических рубриках приведет к большому числу классификационных рубрик (например, более 20), классифицирующий может уменьшить число индексов. Это может быть сделано, если классификация «полностью определенных» соединений приведет к присвоению большого числа подгрупп под одной иерархически старшей группой. Классификация таких соединений может быть выполнена только в группе более высокой иерархии. В других случаях классификация соединений проводится во всех более специфичных подгруппах.
Комбинаторные библиотеки
101. Совокупность большого количества химических соединений, биологических единиц или других веществ, может быть представлена в виде «библиотек». Библиотека обычно включает огромное число членов, которые, если их классифицировать по отдельности в большом количестве классификационных подразделений, перегрузят поисковую систему. Поэтому только индивидуальные члены, которые считаются «полностью определенными» каким-то образом как соединения общей формулы, классифицируются обязательно в группах, наиболее специфичных для них, например соединения в разделе С. Библиотека в целом классифицируется в соответствующей группе в подклассе С40В. В дополнение к вышеупомянутому обязательному классифицированию необязательное классифицирование проводится, если члены библиотеки представляют интерес.
Сведения о классификации данных — Microsoft 365 Compliance
- Чтение занимает 2 мин
В этой статье
В качестве администратора Microsoft 365 или администратора соответствия требованиям вы можете оценивать и затем помечать содержимое в своей организации, чтобы отслеживать, куда оно направляется, защищать его независимо от расположения, а также гарантировать его сохранность и удаление в соответствии с потребностями вашей организации. Это можно сделать посредством применения меток конфиденциальности, меток храненияи классификации типов конфиденциальной информации. Существуют различные способы обнаружения, оценки и пометки, но в результате вы можете иметь очень большое количество документов и электронных писем, которые помечены и классифицированы одним или обоими из этих ярлыков. После того, как вы примените свои метки хранения и метки чувствительности, вы захотите увидеть, как метки используются вашим арендатором и что делается с этими элементами. На странице классификации данных можно увидеть этот текст содержимого, а именно:
- количество элементов, которые были классифицированы как тип конфиденциальной информации, и характер этих классификаций
- наиболее часто используемые метки конфиденциальности, применяемые в Microsoft 365 и Azure Information Protection
- наиболее часто используемые метки хранения
- сводка действий, выполняемых пользователями с вашим конфиденциальным содержимым
- расположение ваших конфиденциальных и сохраненных данных
Вы также управляете этими функциями на странице классификации данных:
Классификация данных приведена в Центре соответствия требованиям Microsoft 365 или Центре безопасности Microsoft 365 > Классификация > Классификация данных.
Посмотрите видео о наших возможностях классификации данных.
Классификация данных будет сканировать ваш конфиденциальный контент и помеченный контент, прежде чем создавать какие-либо политики. Она называется управлением изменениями нулевого состояния. Такая возможность позволит вам определить влияние всех меток хранения и меток конфиденциальности в вашей среде и начать оценку требований политики защиты и управления.
Предварительные требования
Защиту от потери данных в конечной точке поддерживают несколько разных подписок. Параметры лицензирования для защиты от потери данных в конечной точке см. в руководстве по лицензированию Information Protection.
Разрешения
Чтобы получить доступ к странице классификации данных, учетной записи необходимо назначить членство в любой из этих ролей или групп ролей.
Группы ролей Microsoft 365
- Глобальный администратор
- Администратор соответствия требованиям
- Администратор безопасности
- Администратор данных о соответствии требованиям
Примечание
Для предоставления доступа к классификации данных Microsoft 365 рекомендуется всегда использовать роль с наименьшими привилегиями.
Типы конфиденциальных данных, которые наиболее часто используются в вашем содержимом
Microsoft 365 поставляется со многими определениями типов конфиденциальной информации, такими как элемент, содержащий номер социального страхования или номер кредитной карты. Для получения дополнительной информации о типах конфиденциальной информации см. Определения объектов типа конфиденциальной информации.
На карточке типа конфиденциальной информации отображаются наиболее часто используемые типы конфиденциальной информации, которые были найдены и помечены в вашей организации.
Чтобы узнать количество элементов в той или иной категории классификации, наведите указатель мыши на панель этой категории.
Примечание
Если на карточке отображается сообщение «Данные с конфиденциальной информацией не найдены», то это означает, что в вашей организации отсутствуют элементы, классифицированные как тип конфиденциальной информации, или отсутствуют обойденные элементы. Чтобы приступить к работе с метками, см. следующие статьи:
Наиболее часто используемые метки конфиденциальности, применяемые для содержимого
Когда вы применяете метку конфиденциальности к элементу с использованием Microsoft 365 или Azure Information Protection (AIP), то происходят две вещи:
- тег, который обозначает значение элемента для вашей организации, встраивается в документ и будет повсюду следовать за ним
- наличие тега включает различные защитные действия, такие как обязательные водяные знаки или шифрование. С включенной защитой конечной точки вы можете даже не позволить элементу выйти из под управления вашей организации.
Дополнительные сведения о метках конфиденциальности см. в статье Сведения о метках конфиденциальности.
Для файлов SharePoint и OneDrive должны быть включены метки конфиденциальности, чтобы соответствующие данные отображались на странице классификации данных. Дополнительные сведения см. в статье Включение меток конфиденциальности для файлов Office в SharePoint и OneDrive.
На карточке с меткой конфиденциальности отображается количество элементов (электронная почта или документ) по уровню конфиденциальности.
Примечание
Если вы не создали или не опубликовали какие-либо метки конфиденциальности или к содержимому не применена метка конфиденциальности, то на этой карточке будет отображаться сообщение «Метки конфиденциальности не обнаружены». Чтобы приступить к работе с метками конфиденциальности, см. следующие статьи:
Наиболее часто используемые метки хранения, применяемые для содержимого
Метки хранения используются для управления хранением и ликвидацией содержимого в вашей организации. В случае применения их можно использовать для управления способом хранения документа до удаления, необходимостью проверки перед удалением, завершением срока хранения и необходимостью помечать документ в качестве записи. Дополнительные сведения см. в статье Сведения о политиках и метках хранения.
Карточка наиболее часто используемых меток хранения показывает количество элементов, которым была присвоена метка хранения.
Примечание
Если в этой карточке отображается сообщение «Метки хранения не обнаружены», это означает, что вы не создали или не опубликовали метки хранения либо к содержимому не была применена метка хранения. Чтобы приступить к работе с метками хранения, см. следующие статьи.
Основные обнаруженные действия
В этой карточке представлен краткий обзор основных действий, которые пользователи выполняют с элементами, отмеченными в качестве конфиденциальных. Используйте Обозреватель действий, чтобы углубленно изучить различные действия, которые Microsoft 365 отслеживает по отмеченному содержимому и содержимому, размещенному в конечных точках Windows 10.
Примечание
Если в этой карточке отображается сообщение «Действие не обнаружено», то это означает отсутствие действий с файлом или то, что аудит пользователя и администратора не включен. Для включения журналов аудита см. сведения в следующих статьях:
Данные с метками конфиденциальности и хранения по расположению
Суть отчетов о классификации данных заключается в обеспечении наглядного представления о количестве элементов с меткой, а также об их расположении. Эти карточки дадут вам представление о количестве отмеченных элементов в Exchange, SharePoint, OneDrive и т. д.
Примечание
Если в этой карточке отображается сообщение: «Расположения не обнаружены», то это обозначает, что вы не создали или не опубликовали какие-либо метки конфиденциальности или к содержимому не была применена метка хранения. Чтобы приступить к работе с метками конфиденциальности, см. следующие статьи:
См. также
Сведения о том, как использовать классификацию данных в соответствии с требованиями к конфиденциальности данных, см. в разделе Развертывание защиты информации в соответствии с требованиями к конфиденциальности данных в Microsoft 365 (aka.ms/m365dataprivacy).
4 типа классификационных задач в машинном обучении
Последнее обновление 19 августа 2020 г.
Машинное обучение — это область исследований, которая занимается алгоритмами, которые учатся на примерах.
Классификация — это задача, которая требует использования алгоритмов машинного обучения, которые учатся назначать метку класса примерам из предметной области. Простой для понимания пример — это классификация писем как « спам » или « не спам ».
Существует множество различных типов задач классификации, с которыми вы можете столкнуться в машинном обучении, и специальные подходы к моделированию, которые можно использовать для каждой из них.
В этом руководстве вы познакомитесь с различными типами прогнозного моделирования классификации в машинном обучении.
После прохождения этого руководства вы будете знать:
- Классификационное прогнозирующее моделирование включает присвоение метки класса входным примерам.
- Двоичная классификация относится к предсказанию одного из двух классов, а мультиклассовая классификация предполагает предсказание одного из более чем двух классов.
- Классификация с несколькими метками включает в себя прогнозирование одного или нескольких классов для каждого примера, а несбалансированная классификация относится к задачам классификации, в которых распределение примеров по классам неодинаково.
Начните свой проект с моей новой книги «Мастерство машинного обучения с Python», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.
Приступим.
Типы классификации в машинном обучении
Фото Рэйчел, некоторые права защищены.
Обзор учебного пособия
Это руководство разделено на пять частей; их:
- Классификация Прогнозное моделирование
- Двоичная классификация
- Мультиклассовая классификация
- Классификация по нескольким этикеткам
- Несбалансированная классификация
Классификация Прогнозное моделирование
В машинном обучении классификация относится к задаче прогнозного моделирования, когда метка класса прогнозируется для данного примера входных данных.
Примеры проблем классификации:
- Рассмотрим пример, классифицируйте, является это спам или нет.
- Дан рукописный символ, классифицируйте его как один из известных символов.
- С учетом недавнего поведения пользователей, классифицировать как отток или нет.
С точки зрения моделирования для классификации требуется обучающий набор данных с множеством примеров входных и выходных данных, из которых можно учиться.
Модель будет использовать обучающий набор данных и вычислить, как лучше всего сопоставить примеры входных данных с конкретными метками классов.Таким образом, обучающий набор данных должен быть достаточно репрезентативным для проблемы и иметь много примеров каждой метки класса.
Метки классов часто представляют собой строковые значения, например « спам », « не спам » и должны быть сопоставлены с числовыми значениями перед предоставлением алгоритму моделирования. Это часто называют кодированием метки, когда каждой метке класса присваивается уникальное целое число, например « спам » = 0, « без спама » = 1.
Существует много различных типов алгоритмов классификации для моделирования задач прогнозного моделирования классификации.
Нет хорошей теории о том, как отображать алгоритмы на типы задач; вместо этого, как правило, рекомендуется, чтобы практикующий проводил контролируемые эксперименты и выяснял, какой алгоритм и конфигурация алгоритма дают наилучшие результаты для данной задачи классификации.
Алгоритмы прогнозного моделирования классификации оцениваются на основе их результатов. Точность классификации — это популярный показатель, используемый для оценки производительности модели на основе предсказанных меток классов.Точность классификации не идеальна, но это хорошая отправная точка для многих задач классификации.
Вместо меток классов для некоторых задач может потребоваться прогнозирование вероятности членства в классе для каждого примера. Это обеспечивает дополнительную неопределенность в прогнозе, который затем может интерпретировать приложение или пользователь. Популярной диагностикой для оценки предсказанных вероятностей является кривая ROC.
Есть, пожалуй, четыре основных типа задач классификации, с которыми вы можете столкнуться; их:
- Двоичная классификация
- Мультиклассовая классификация
- Классификация по нескольким этикеткам
- Несбалансированная классификация
Давайте рассмотрим каждый по очереди.
Двоичная классификация
Двоичная классификация относится к тем задачам классификации, которые имеют две метки класса.
Примеры включают:
- Обнаружение спама в электронной почте (спам или нет).
- Прогноз оттока (отток или нет).
- Прогноз конверсии (покупать или нет).
Обычно задачи двоичной классификации включают один класс, который является нормальным состоянием, и другой класс, который является ненормальным состоянием.
Например, « не спам, » — нормальное состояние, а « спам » — ненормальное состояние.Другой пример: « рак не обнаружен » — это нормальное состояние задачи, которая включает медицинский тест, а « рак обнаружен » — ненормальное состояние.
Классу для нормального состояния присваивается метка класса 0, а классу с ненормальным состоянием назначается метка класса 1.
Обычно для моделирования задачи двоичной классификации используется модель, которая предсказывает распределение вероятностей Бернулли для каждого примера.
Распределение Бернулли — это дискретное распределение вероятностей, которое охватывает случай, когда событие будет иметь двоичный исход как 0 или 1.Для классификации это означает, что модель предсказывает вероятность принадлежности примера к классу 1 или ненормальному состоянию.
Популярные алгоритмы, которые можно использовать для двоичной классификации, включают:
- Логистическая регрессия
- k-Ближайшие соседи
- Деревья решений
- Машина опорных векторов
- Наивный Байес
Некоторые алгоритмы специально разработаны для двоичной классификации и изначально не поддерживают более двух классов; примеры включают логистическую регрессию и машины опорных векторов.
Далее, давайте внимательнее рассмотрим набор данных, чтобы развить интуицию при решении задач двоичной классификации.
Мы можем использовать функцию make_blobs () для создания набора данных синтетической двоичной классификации.
В приведенном ниже примере создается набор данных из 1000 примеров, которые принадлежат одному из двух классов, каждый с двумя входными объектами.
# пример задачи бинарной классификации из импорта numpy, где из коллекций счетчик импорта из склеарна.наборы данных импортируют make_blobs из matplotlib import pyplot # определить набор данных X, y = make_blobs (n_samples = 1000, центры = 2, random_state = 1) # суммировать фигуру набора данных печать (X.shape, y.shape) # суммировать наблюдения по меткам класса counter = Counter (y) печать (счетчик) # подвести итоги первых нескольких примеров для i в диапазоне (10): print (X [i], y [i]) # рисуем набор данных и раскрашиваем метку по классам для метки _ в counter.items (): row_ix = where (y == label) [0] пиплот.разброс (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 18 19 20 21 | # пример задачи двоичной классификации из импорта numpy, где из импорта коллекций Counter из sklearn.datasets import make_blobs from matplotlib import pyplot # define dataset X, y = make_blobs (n_samples = 1000, center = 2, random_state = 1) # summarize dataset shape print (X.shape). shape) # суммировать наблюдения по метке класса counter = Counter (y) print (counter) # суммировать первые несколько примеров для i в диапазоне (10): print (X [i], y [i]) # построить набор данных и раскрасить метку по классам для метки, _ в счетчике.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show () |
При выполнении примера сначала суммируется созданный набор данных, показывающий 1000 примеров, разделенных на входные ( X ) и выходные ( y ) элементы.
Затем суммируется распределение меток классов, показывающее, что экземпляры принадлежат либо классу 0, либо классу 1, и что в каждом классе имеется 500 примеров.
Затем суммируются первые 10 примеров в наборе данных, показывая, что входные значения являются числовыми, а целевые значения — целыми числами, которые представляют членство в классе.
(1000, 2) (1000,) Счетчик ({0: 500, 1: 500}) [-3,05837272 4,48825769] 0 [-8.60973869 -3.72714879] 1 [1.37129721 5.23107449] 0 [-9,33
3 -2,9544469] 1 [-11,57178593 -3,85275513] 1 [-11,42257341 -4,85679127] 1 [-10,44518578 -3,76476563] 1 [-10.44603561 -3,26065964] 1 [-0,61947075 3,48804983] 0 [-10.591 -4.5772537] 1(1000, 2) (1000,) Счетчик ({0: 500, 1: 500}) [-3.05837272 4.48825769] 0 [-8.60973869 -3.72714879] 123 1 [1.3 5,23107449] 0 [-9,33 3 -2,9544469] 1[-11,57178593 -3,85275513] 1 [-11,42257341 -4,85679127] 1 [-10.44518578 -3.76476563] 1 [-10.44603561 -3.26065964] 1 [-0.61947075 3.48804983] 0 [-10. | 591 -4.5772537] 1
Наконец, для входных переменных в наборе данных создается диаграмма рассеяния, и точки окрашиваются в соответствии со значением их класса.
Мы видим два различных кластера, которые, как мы могли ожидать, легко различить.
Точечная диаграмма набора данных двоичной классификации
Мультиклассовая классификация
Мультиклассовая классификация относится к тем задачам классификации, которые имеют более двух меток классов.
Примеры включают:
- Классификация лиц.
- Классификация видов растений.
- Оптическое распознавание символов.
В отличие от бинарной классификации, мультиклассовая классификация не имеет понятия нормальных и аномальных результатов. Вместо этого примеры классифицируются как принадлежащие к одному из ряда известных классов.
Для некоторых задач количество меток классов может быть очень большим. Например, модель может предсказать фотографию как принадлежащую одному из тысяч или десятков тысяч лиц в системе распознавания лиц.
Задачи, связанные с предсказанием последовательности слов, например модели перевода текста, также могут считаться особым типом мультиклассовой классификации. Каждое слово в последовательности слов, которые должны быть предсказаны, включает в себя классификацию на несколько классов, где размер словаря определяет количество возможных классов, которые могут быть предсказаны, и может составлять десятки или сотни тысяч слов.
Обычно для моделирования задачи классификации нескольких классов используется модель, которая предсказывает распределение вероятностей Мультинулли для каждого примера.
Распределение Мультинулли — это дискретное распределение вероятностей, которое охватывает случай, когда событие будет иметь категориальный исход, например K в {1, 2, 3,…, K }. Для классификации это означает, что модель предсказывает вероятность принадлежности примера к каждой метке класса.
Многие алгоритмы, используемые для двоичной классификации, могут использоваться для классификации нескольких классов.
Популярные алгоритмы, которые можно использовать для мультиклассовой классификации, включают:
- к-ближайшие соседи.
- Деревья решений.
- Наивный Байес.
- Случайный лес.
- Повышение градиента.
Алгоритмы, разработанные для двоичной классификации, могут быть адаптированы для использования в мультиклассовых задачах.
Это включает в себя использование стратегии подбора нескольких моделей бинарной классификации для каждого класса по сравнению со всеми другими классами (называемых «один против остальных») или одной модели для каждой пары классов (называемой «один против одного»).
- Один против остальных : Подобрать одну бинарную модель классификации для каждого класса vs.все остальные классы.
- Один против одного : Подберите одну модель бинарной классификации для каждой пары классов.
Алгоритмы двоичной классификации, которые могут использовать эти стратегии для мультиклассовой классификации, включают:
- Логистическая регрессия.
- Машина опорных векторов.
Далее давайте более подробно рассмотрим набор данных, чтобы развить интуицию для решения задач классификации нескольких классов.
Мы можем использовать функцию make_blobs () для создания синтетического набора данных классификации нескольких классов.
В приведенном ниже примере создается набор данных из 1000 примеров, которые принадлежат одному из трех классов, каждый с двумя входными объектами.
# пример задачи мультиклассовой классификации из импорта numpy, где из коллекций счетчик импорта from sklearn.datasets импортировать make_blobs из matplotlib import pyplot # определить набор данных X, y = make_blobs (n_samples = 1000, центры = 3, random_state = 1) # суммировать фигуру набора данных print (X.shape, y.форма) # суммировать наблюдения по меткам класса counter = Counter (y) печать (счетчик) # подвести итоги первых нескольких примеров для i в диапазоне (10): print (X [i], y [i]) # рисуем набор данных и раскрашиваем метку по классам для метки _ в counter.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 18 19 20 21 | # пример задачи классификации нескольких классов из импорта numpy, где из импорта коллекций Counter из sklearn.datasets import make_blobs from matplotlib import pyplot # define dataset X, y = make_blobs (n_samples = 1000, center = 3, random_state = 1) # summarize dataset shape print (X.shape). shape) # суммировать наблюдения по метке класса counter = Counter (y) print (counter) # суммировать первые несколько примеров для i в диапазоне (10): print (X [i], y [i]) # построить набор данных и раскрасить метку по классам для метки, _ в счетчике.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show () |
При выполнении примера сначала суммируется созданный набор данных, показывающий 1000 примеров, разделенных на входные ( X ) и выходные ( y ) элементы.
Затем суммируется распределение меток классов, показывающее, что экземпляры принадлежат классу 0, классу 1 или классу 2 и что в каждом классе имеется примерно 333 примера.
Затем суммируются первые 10 примеров в наборе данных, показывающие, что входные значения являются числовыми, а целевые значения — целыми числами, которые представляют членство в классе.
(1000, 2) (1000,) Счетчик ({0: 334, 1: 333, 2: 333}) [-3,05837272 4,48825769] 0 [-8.60973869 -3.72714879] 1 [1.37129721 5.23107449] 0 [-9,33
3 -2,9544469] 1 [-8,63895561 -8,05263469] 2 [-8,48974309 -9,05667083] 2 [-7,51235546 -7,96464519] 2 [-7.51320529 -7,46053919] 2 [-0,61947075 3,48804983] 0 [-10.591 -4.5772537] 1(1000, 2) (1000,) Счетчик ({0: 334, 1: 333, 2: 333}) [-3.05837272 4.48825769] 0 [-8.60973869 -3.72714879] 1 [1,37129721 5,23107449] 0 [-9,33 3 -2,9544469] 1[-8,63895561 -8,05263469] 2 [-8,48974309 -9,05667083] 2 [-7.51235546 -7,96464519] 2 [-7,51320529 -7,46053919] 2 [-0,61947075 3,48804983] 0 [-10, | 591 -4,5772537] 1
Наконец, для входных переменных в наборе данных создается диаграмма рассеяния, и точки окрашиваются в соответствии со значением их класса.
Мы видим три отдельных кластера, которые, как мы могли ожидать, будет легко различить.
Точечная диаграмма набора данных мультиклассовой классификации
Классификация нескольких этикеток
Классификация с несколькими метками относится к тем задачам классификации, которые имеют две или более меток классов, где одна или несколько меток классов могут быть предсказаны для каждого примера.
Рассмотрим пример классификации фотографий, где данная фотография может иметь несколько объектов в сцене, а модель может предсказать присутствие нескольких известных объектов на фотографии, например « велосипед », « яблоко », «». человек и др.
В этом отличие от бинарной классификации и мультиклассовой классификации, где для каждого примера прогнозируется одна метка класса.
Распространено моделирование задач классификации с несколькими метками с помощью модели, которая прогнозирует несколько выходных данных, причем для каждого выхода прогнозируется как распределение вероятностей Бернулли.По сути, это модель, которая делает несколько прогнозов двоичной классификации для каждого примера.
Алгоритмы классификации, используемые для двоичной или мультиклассовой классификации, не могут использоваться напрямую для классификации по нескольким меткам. Могут использоваться специализированные версии стандартных алгоритмов классификации, так называемые версии алгоритмов с несколькими метками, в том числе:
- Дерево принятия решений с несколькими метками
- Случайные леса с несколькими метками
- Повышение градиента с несколькими этикетками
Другой подход — использовать отдельный алгоритм классификации для прогнозирования меток для каждого класса.
Далее, давайте более подробно рассмотрим набор данных, чтобы развить интуицию для задач классификации с несколькими метками.
Мы можем использовать функцию make_multilabel_classification () для создания синтетического набора данных классификации с несколькими метками.
В приведенном ниже примере создается набор данных из 1000 примеров, каждый с двумя входными объектами. Есть три класса, каждый из которых может иметь одну из двух меток (0 или 1).
# пример задачи классификации с несколькими метками из склеарна.наборы данных импортировать make_multilabel_classification # определить набор данных X, y = make_multilabel_classification (n_samples = 1000, n_features = 2, n_classes = 3, n_labels = 2, random_state = 1) # суммировать фигуру набора данных печать (X.shape, y.shape) # подвести итоги первых нескольких примеров для i в диапазоне (10): print (X [i], y [i])
# пример задачи классификации с несколькими метками из sklearn.datasets import make_multilabel_classification # define dataset X, y = make_multilabel_classification (n_samples = 1000, n_features = 2, n_ random_classes = 3 1) # форма суммирования набора данных печать (X.shape, y.shape) # суммируем первые несколько примеров для i в диапазоне (10): print (X [i], y [i]) |
При выполнении примера сначала суммируется созданный набор данных, показывающий 1000 примеров, разделенных на входные ( X ) и выходные ( y ) элементы.
Затем суммируются первые 10 примеров в наборе данных, показывающие, что входные значения являются числовыми, а целевые значения — целыми числами, которые представляют принадлежность к метке класса.
(1000, 2) (1000, 3) [18. 35.] [1 1 1] [22. 33.] [1 1 1] [26. 36.] [1 1 1] [24. 28.] [1 1 0] [23. 27.] [1 1 0] [15. 31.] [0 1 0] [20. 37.] [0 1 0] [18. 31.] [1 1 1] [29. 27.] [1 0 0] [29. 28.] [1 1 0]
(1000, 2) (1000, 3) [18. 35.] [1 1 1] [22. 33.] [1 1 1] [26. 36.] [1 1 1] [24.28.] [1 1 0] [23. 27.] [1 1 0] [15. 31.] [0 1 0] [20. 37.] [0 1 0] [18. 31.] [1 1 1] [29. 27.] [1 0 0] [29. 28.] [1 1 0] |
Несбалансированная классификация
Несбалансированная классификация относится к задачам классификации, в которых количество примеров в каждом классе распределяется неравномерно.
Обычно задачи несбалансированной классификации представляют собой задачи бинарной классификации, в которых большинство примеров в обучающем наборе данных относятся к нормальному классу, а меньшая часть примеров относится к ненормальному классу.
Примеры включают:
- Обнаружение мошенничества.
- Обнаружение выбросов.
- Медицинские диагностические тесты.
Эти проблемы моделируются как задачи двоичной классификации, хотя могут потребовать специальных методов.
Специализированные методы могут использоваться для изменения состава выборок в наборе обучающих данных путем недостаточной выборки класса большинства или передискретизации класса меньшинства.
Примеры включают:
Могут использоваться специализированные алгоритмы моделирования, которые уделяют больше внимания классу меньшинства при подгонке модели к набору обучающих данных, например, чувствительные к стоимости алгоритмы машинного обучения.
Примеры включают:
Наконец, могут потребоваться альтернативные показатели производительности, поскольку сообщение о точности классификации может вводить в заблуждение.
Примеры включают:
- Точность.
- Напомним.
- F-Мера.
Далее давайте более подробно рассмотрим набор данных, чтобы развить интуицию в отношении несбалансированных проблем классификации.
Мы можем использовать функцию make_classification () для создания набора данных синтетической несбалансированной двоичной классификации.
В приведенном ниже примере создается набор данных из 1000 примеров, которые принадлежат одному из двух классов, каждый с двумя входными объектами.
# пример задачи несбалансированной двоичной классификации из импорта numpy, где из коллекций счетчик импорта из sklearn.datasets импортировать make_classification из matplotlib import pyplot # определить набор данных X, y = make_classification (n_samples = 1000, n_features = 2, n_informative = 2, n_redundant = 0, n_classes = 2, n_clusters_per_class = 1, weights = [0.99,0.01], random_state = 1) # суммировать фигуру набора данных печать (X.shape, y.shape) # суммировать наблюдения по меткам класса counter = Counter (y) печать (счетчик) # подвести итоги первых нескольких примеров для i в диапазоне (10): print (X [i], y [i]) # рисуем набор данных и раскрашиваем метку по классам для метки _ в counter.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 18 19 20 21 | # пример задачи несбалансированной двоичной классификации из импорта numpy, где из импорта коллекций Counter из sklearn.наборы данных import make_classification из matplotlib import pyplot # define dataset X, y = make_classification (n_samples = 1000, n_features = 2, n_informative = 2, n_redundant = 0, n_classes = 2_, n_clights_clights, n_classes_ , 0,01], random_state = 1) # суммировать фигуру набора данных print (X.shape, y.shape) # суммировать наблюдения по метке класса counter = Counter (y) print (counter) # суммировать первые несколько примеров для i в диапазоне (10): print (X [i], y [i]) # построить набор данных и раскрасить метку по классам для метки, _ в счетчике.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show () |
При выполнении примера сначала суммируется созданный набор данных, показывающий 1000 примеров, разделенных на входные ( X ) и выходные ( y ) элементы.
Затем суммируется распределение меток классов, показывающее серьезный дисбаланс классов с примерно 980 примерами, принадлежащими классу 0, и примерно 20 примерами, принадлежащими классу 1.
Затем суммируются первые 10 примеров в наборе данных, показывающие, что входные значения являются числовыми, а целевые значения — целыми числами, которые представляют членство в классе. В этом случае мы видим, что большинство примеров относятся к классу 0, как и ожидалось.
(1000, 2) (1000,) Счетчик ({0: 983, 1: 17}) [0,86
5 1,18613612] 0 [1,55110839 1,81032905] 0 [1.236 1.01094607] 0 [1.11988947 1.63251786] 0 [1.04235568 1.12152929] 0 [1.18114858 0,
607] 0 [1.1365562 1.17652556] 0 [0,4620,72
8] 0 [0,18315826 1,07141766] 0 [0,32411648 0,53515376] 0
(1000, 2) (1000,) Счетчик ({0: 983, 1: 17}) [0,86 5 1,18613612] 0 [1,55110839 1,81032905] 0 [1,236] 1,0 [1.11988947 1.63251786] 0 [1.04235568 1.12152929] 0 [1.18114858 0, 607] 0[1,1365562 1,17652556] 0 [0,462 0,72 8] 0 [0,18315826 1,07141766] 0 [0,32411648 0,53515376] 0 |
Наконец, для входных переменных в наборе данных создается диаграмма рассеяния, и точки окрашиваются в соответствии со значением их класса.
Мы можем видеть один главный кластер для примеров, которые принадлежат классу 0, и несколько разрозненных примеров, которые принадлежат классу 1. Интуиция подсказывает, что наборы данных с этим свойством несбалансированных меток классов сложнее моделировать.
Точечная диаграмма набора данных несбалансированной двоичной классификации
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Сводка
В этом руководстве вы открыли для себя различные типы прогнозного моделирования классификации в машинном обучении.
В частности, вы выучили:
- Классификационное прогнозирующее моделирование включает присвоение метки класса входным примерам.
- Двоичная классификация относится к предсказанию одного из двух классов, а мультиклассовая классификация предполагает предсказание одного из более чем двух классов.
- Классификация с несколькими метками включает в себя прогнозирование одного или нескольких классов для каждого примера, а несбалансированная классификация относится к задачам классификации, в которых распределение примеров по классам неодинаково.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Откройте для себя быстрое машинное обучение на Python!
Разрабатывайте собственные модели за считанные минуты
… всего несколько строк кода scikit-learn
Узнайте, как это сделать, в моей новой электронной книге:
Мастерство машинного обучения с Python
Охватывает руководств для самостоятельного изучения и сквозных проектов , например:
Загрузка данных , визуализация , моделирование , настройка и многое другое…
Наконец-то доведите машинное обучение до
Ваши собственные проекты
Пропустить академики. Только результаты.
Посмотрите, что внутриКак использовать кривые ROC и кривые прецизионного вызова для классификации в Python
Последнее обновление 13 января 2021 г.
Может быть более гибким прогнозирование вероятностей принадлежности наблюдения к каждому классу в задаче классификации, а не непосредственное прогнозирование классов.
Эта гибкость проистекает из способа интерпретации вероятностей с использованием различных пороговых значений, которые позволяют оператору модели найти компромисс между ошибками, допущенными моделью, такими как количество ложных срабатываний по сравнению с количеством ложноотрицательных результатов.Это требуется при использовании моделей, в которых стоимость одной ошибки превышает стоимость ошибок других типов.
Два диагностических инструмента, которые помогают в интерпретации вероятностного прогноза для задач прогнозного моделирования бинарной (двухклассовой) классификации, — это ROC Curves и Precision-Recall Curves .
В этом руководстве вы познакомитесь с кривыми ROC и кривыми точного восстановления, а также узнаете, когда их использовать для интерпретации прогнозов вероятностей для задач двоичной классификации.
После прохождения этого руководства вы будете знать:
- Кривые ROC суммируют компромисс между частотой истинных положительных и ложных положительных результатов для прогнозной модели с использованием различных пороговых значений вероятности. Кривые
- Precision-Recall суммируют компромисс между истинным положительным значением и положительным прогнозным значением для прогнозной модели с использованием различных пороговых значений вероятности. Кривые
- ROC подходят, когда наблюдения сбалансированы между каждым классом, тогда как кривые точности-отзыва подходят для несбалансированных наборов данных.
Начните свой проект с моей новой книги «Вероятность для машинного обучения», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.
Приступим.
- Обновление августа / 2018 : исправлена ошибка в представлении строки без навыков для графика точного отзыва. Также исправлена опечатка, когда я называл ROC родственником, а не получателем (спасибо за проверку орфографии).
- Обновление ноябрь 2018 г. : исправлено описание интерпретации размера значений на каждой оси, спасибо Карлу Хамфрису.
- Обновление июнь / 2019 : исправлена опечатка при интерпретации несбалансированных результатов.
- Обновление, октябрь / 2019 г. : обновлены графики кривой ROC и кривой точности отзыва для добавления меток, использования модели логистической регрессии и фактического вычисления производительности классификатора без навыков.
- Обновление ноябрь / 2019 : Улучшено описание классификатора отсутствия навыков для кривой точного отзыва.
Как и когда использовать кривые ROC и кривые прецизионного вызова для классификации в Python
Фото Джузеппе Мило, некоторые права защищены.
Обзор учебного пособия
Это руководство разделено на 6 частей; их:
- Прогнозирование вероятностей
- Что такое кривые ROC?
- Кривые ROC и AUC в Python
- Что такое кривые прецизионного вызова?
- Кривые прецизионного вызова и AUC в Python
- Когда использовать кривые ROC в сравнении с кривыми прецизионного вызова?
Прогнозирование вероятностей
В задаче классификации мы можем решить спрогнозировать значения классов напрямую.
В качестве альтернативы он может быть более гибким для прогнозирования вероятностей для каждого класса. Причина в том, чтобы предоставить возможность выбирать и даже откалибровать порог для интерпретации предсказанных вероятностей.
Например, по умолчанию может использоваться порог 0,5, означающий, что вероятность в [0,0, 0,49] является отрицательным результатом (0), а вероятность в [0,5, 1,0] — положительным результатом (1).
Этот порог можно настроить, чтобы настроить поведение модели для конкретной проблемы.Примером может служить уменьшение количества ошибок того или иного типа.
При прогнозировании задачи двоичной или двухклассовой классификации мы можем сделать два типа ошибок.
- Ложно-положительный . Предскажите событие, когда события не было.
- Ложноотрицательный . Не предсказывайте никаких событий, хотя на самом деле событие имело место.
Путем прогнозирования вероятностей и калибровки порога баланс этих двух проблем может быть выбран оператором модели.
Например, в системе прогнозирования смога нас может гораздо больше заботить низкий уровень ложноотрицательных результатов, чем низкий уровень ложных срабатываний. Ложноотрицательный результат означал бы отсутствие предупреждения о дне смога, когда на самом деле это день сильного смога, что приводит к проблемам со здоровьем среди населения, которое не может принять меры предосторожности. Ложноположительный результат означает, что общественность будет принимать меры предосторожности, когда в этом нет необходимости.
Распространенный способ сравнения моделей, предсказывающих вероятности двухклассовых задач, — использовать кривую ROC.
Что такое кривые ROC?
Полезным инструментом при прогнозировании вероятности двоичного результата является кривая рабочих характеристик приемника или кривая ROC.
Это график частоты ложных срабатываний (ось x) по сравнению с частотой истинных положительных результатов (ось y) для ряда различных возможных пороговых значений от 0,0 до 1,0. Другими словами, он отображает частоту ложных срабатываний в зависимости от частоты совпадений.
Коэффициент истинных положительных результатов рассчитывается как количество истинных положительных результатов, деленное на сумму количества истинных положительных результатов и количества ложных отрицательных результатов.Он описывает, насколько хороша модель в прогнозировании положительного класса, когда фактический результат положительный.
Коэффициент истинно положительных результатов = истинно положительных результатов / (истинных положительных результатов + ложно отрицательных)
Частота истинно положительных результатов = истинно положительных результатов / (истинных положительных результатов + ложных отрицательных результатов) |
Уровень истинных положительных результатов также называется чувствительностью.
Чувствительность = истинно положительные / (истинные положительные + ложно отрицательные)
Чувствительность = истинно положительные / (истинные положительные + ложноотрицательные) |
Коэффициент ложных срабатываний рассчитывается как количество ложных срабатываний, деленное на сумму количества ложных срабатываний и количества истинно отрицательных результатов.
Его также называют частотой ложных тревог, поскольку он суммирует, как часто прогнозируется положительный класс, когда фактический результат отрицательный.
Частота ложных срабатываний = ложные срабатывания / (ложные срабатывания + истинные отрицательные результаты)
Частота ложных срабатываний = ложные срабатывания / (ложные срабатывания + истинные отрицательные результаты) |
Частота ложных срабатываний также называется инвертированной специфичностью, где специфичность — это общее количество истинно отрицательных результатов, деленное на сумму количества истинно отрицательных и ложных срабатываний.
Специфичность = Истинно-отрицательные / (Истинно-отрицательные + ложно-положительные)
Специфичность = истинно отрицательные / (истинно отрицательные + ложные положительные результаты) |
Где:
Частота ложноположительных результатов = 1 — Специфичность
Частота ложных срабатываний = 1 — Специфичность |
Кривая ROC — полезный инструмент по нескольким причинам:
- Кривые разных моделей можно сравнивать напрямую в целом или для разных порогов.
- Площадь под кривой (AUC) может использоваться как сводка навыков модели.
Форма кривой содержит много информации, включая то, что нас может больше всего заботить при возникновении проблемы, ожидаемую частоту ложных срабатываний и частоту ложных отрицательных результатов.
Чтобы прояснить это:
- Меньшие значения на оси x графика указывают на меньшее количество ложных срабатываний и более высокие истинно отрицательные.
- Большие значения по оси Y на графике указывают на большее количество истинных положительных результатов и меньшее количество ложных отрицательных результатов.
Если вы запутались, помните, что когда мы прогнозируем двоичный результат, это либо правильный прогноз (истинно положительный), либо нет (ложный положительный результат). Между этими вариантами существует противоречие, как и между истинно отрицательными и ложноотрицательными.
Искусная модель приписывает в среднем более высокую вероятность случайно выбранному действительному положительному событию, чем отрицательное. Это то, что мы имеем в виду, когда говорим, что модель обладает навыками. Как правило, искусные модели представлены кривыми, доходящими до верхнего левого угла графика.
Классификатор без навыков — это классификатор, который не может различать классы и предсказывает случайный класс или постоянный класс во всех случаях. Модель без навыков представлена в точке (0,5, 0,5). Модель без навыков на каждом пороге представлена диагональной линией от нижнего левого угла графика до верхнего правого и имеет AUC 0,5.
Модель с безупречным мастерством представлена в точке (0,1). Модель с безупречным мастерством представлена линией, которая проходит от левого нижнего угла графика к левому верхнему, а затем по верхнему краю к правому верху.
Оператор может построить кривую ROC для окончательной модели и выбрать порог, который дает желаемый баланс между ложными срабатываниями и ложными отрицаниями.
Хотите узнать о вероятности машинного обучения
Пройдите бесплатный 7-дневный ускоренный курс по электронной почте (с образцом кода).
Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.
Загрузите БЕСПЛАТНЫЙ мини-курс
Кривые ROC и AUC в Python
Мы можем построить кривую ROC для модели на Python, используя функцию scikit-learn roc_curve ().
Функция берет как истинные результаты (0,1) из набора тестов, так и предсказанные вероятности для класса 1. Функция возвращает частоту ложных срабатываний для каждого порога, истинно положительную частоту для каждого порога и пороговых значений.
… # вычислить кривую roc fpr, tpr, thresholds = roc_curve (y, probs)
… # вычислить кривую roc fpr, tpr, thresholds = roc_curve (y, probs) |
AUC для ROC можно рассчитать с помощью функции roc_auc_score ().
Как и функция roc_curve (), функция AUC принимает как истинные результаты (0,1) из тестового набора, так и предсказанные вероятности для класса 1. Он возвращает показатель AUC от 0,0 до 1,0 для отсутствия навыка и идеального навыка соответственно.
… # вычислить AUC auc = roc_auc_score (y, вероятность) print (‘AUC:% .3f’% auc)
… # вычислить AUC auc = roc_auc_score (y, probs) print (‘AUC:%.3f ‘% auc) |
Полный пример расчета кривой ROC и ROC AUC для модели логистической регрессии для небольшой тестовой задачи приведен ниже.
# roc curve и auc из sklearn.datasets импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics импортировать roc_curve из sklearn.metrics import roc_auc_score из matplotlib import pyplot # создать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, random_state = 1) # разделить на наборы поездов / тестов trainX, testX, тренировочный, testy = train_test_split (X, y, test_size = 0.5, random_state = 2) # генерировать прогноз отсутствия навыков (класс большинства) ns_probs = [0 для _ в диапазоне (len (testy))] # соответствовать модели model = LogisticRegression (решатель = ‘lbfgs’) model.fit (trainX, trainy) # прогнозировать вероятности lr_probs = model.predict_proba (testX) # сохраняем вероятности только положительного результата lr_probs = lr_probs [:, 1] # подсчитать баллы ns_auc = roc_auc_score (testy, ns_probs) lr_auc = roc_auc_score (testy, lr_probs) # подвести итоги print (‘Нет навыка: ROC AUC =%.3f ‘% (ns_auc)) print (‘Логистика: ROC AUC =%. 3f’% (lr_auc)) # вычислить кривые roc ns_fpr, ns_tpr, _ = roc_curve (testy, ns_probs) lr_fpr, lr_tpr, _ = roc_curve (testy, lr_probs) # построить кривую roc для модели pyplot.plot (ns_fpr, ns_tpr, linestyle = ‘-‘, label = ‘Нет навыков’) pyplot.plot (lr_fpr, lr_tpr, marker = ‘.’, label = ‘Logistic’) # метка оси pyplot.xlabel (‘Ложноположительная ставка’) pyplot.ylabel (‘Истинная положительная оценка’) # показать легенду пиплот.легенда () # показать сюжет pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 24 25 26 27 28 29 30 000 000 34 35 36 37 38 39 | # roc curve и auc от sklearn.наборы данных импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import roc_curve из sklearn.metrics import class 000 9_scenerate data import roc_auc 9_scenerate X, y = make_classification (n_samples = 1000, n_classes = 2, random_state = 1) # разделить на наборы поездов / тестов trainX, testX, trainy, testy = train_test_split (X, y, test_size = 0.5, random_state = 2) # генерировать прогноз отсутствия навыков (класс большинства) ns_probs = [0 for _ in range (len (testy))] # соответствовать модели model = LogisticRegression (solver = ‘ lbfgs ‘) model.fit (trainX, trainy) # предсказать вероятности lr_probs = model.predict_proba (testX) # сохранить вероятность только положительного результата lr_probs = lr_probs [: ] # подсчитать баллы ns_auc = roc_auc_score (testy, ns_probs) lr_auc = roc_auc_score (testy, lr_probs) # суммировать баллы print (‘No Skill: ROC AUC =%.3f ‘% (ns_auc)) print (‘ Logistic: ROC AUC =%. 3f ‘% (lr_auc)) # вычислить кривые ROC ns_fpr, ns_tpr, _ = roc_curve (testy, ns_probs) ls_probs) ls_probs lr_tpr, _ = roc_curve (testy, lr_probs)# построить кривую roc для модели pyplot.plot (ns_fpr, ns_tpr, linestyle = ‘-‘, label = ‘No Skill’) pyplot.plot ( lr_fpr, lr_tpr, marker = ‘.’, label = ‘Logistic’) # метки оси pyplot.xlabel (‘False Positive Rate’) pyplot.ylabel (‘True Positive Rate’) # показать легенду pyplot.legend () # показать график pyplot.show () |
При выполнении примера распечатывается ROC AUC для модели логистической регрессии и классификатор отсутствия навыков, который прогнозирует только 0 для всех примеров.
Без навыков: ROC AUC = 0,500 Логистика: ROC AUC = 0,903
Нет навыка: ROC AUC = 0.500 Логистика: ROC AUC = 0,903 |
Также создается график кривой ROC для модели, показывающий, что модель обладает навыками.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
График кривой ROC для классификатора без навыков и модели логистической регрессии
Что такое кривые прецизионного вызова?
Есть много способов оценить навыки модели прогнозирования.
Подход в смежной области поиска информации (поиск документов на основе запросов) измеряет точность и отзывчивость.
Эти меры также полезны в прикладном машинном обучении для оценки моделей двоичной классификации.
Точность — это отношение количества истинных положительных результатов к сумме истинных положительных и ложных срабатываний. Он описывает, насколько хороша модель в предсказании положительного класса. Точность называется положительной прогностической ценностью.
Прогнозирующая мощность положительных результатов = истинные положительные результаты / (истинные положительные результаты + ложные положительные результаты)
Положительная прогнозируемая мощность = Истинные положительные результаты / (Истинные положительные результаты + ложные положительные результаты) |
или
Точность = истинные положительные результаты / (истинные положительные результаты + ложные положительные результаты)
Точность = истинные положительные результаты / (истинные положительные результаты + ложные положительные результаты) |
Отзыв рассчитывается как отношение количества истинно положительных результатов к сумме истинных положительных и ложно отрицательных результатов.Напоминание — это то же самое, что и чувствительность.
Отзыв = Истинно-положительные / (Истинно-положительные + ложно-отрицательные)
Отзыв = Истинно-положительные / (Истинно-положительные + ложно-отрицательные) |
или
Чувствительность = истинно положительные / (истинные положительные + ложно отрицательные)
Чувствительность = истинно положительные / (истинные положительные + ложноотрицательные) |
Проверка точности и отзыва полезна в случаях, когда наблюдается несбалансированность наблюдений между двумя классами.В частности, существует множество примеров отсутствия события (класс 0) и только несколько примеров события (класс 1).
Причина этого в том, что обычно большое количество примеров класса 0 означает, что нас меньше интересует умение модели правильно предсказывать класс 0, например высокие истинные негативы.
Ключом к вычислению точности и напоминания является то, что в расчетах не используются истинные отрицания. Это касается только правильного предсказания класса меньшинства, класса 1.
Кривая точности-отзыва — это график точности (ось y) и отзыва (ось x) для различных пороговых значений, как и кривая ROC.
Классификатор без навыков — это классификатор, который не может различать классы и предсказывает случайный класс или постоянный класс во всех случаях. Линия отсутствия навыков меняется в зависимости от распределения положительных классов на отрицательные. Это горизонтальная линия со значением отношения положительных случаев в наборе данных. Для сбалансированного набора данных это 0.5.
В то время как базовая линия фиксируется с помощью ROC, базовая линия [кривая точности-отзыва] определяется соотношением положительных (P) и отрицательных (N) как y = P / (P + N). Например, для сбалансированного распределения классов y = 0,5…
— График точности-отзыва более информативен, чем график ROC при оценке двоичных классификаторов на несбалансированных наборах данных, 2015.
Модель с совершенными навыками изображена точкой в точке (1,1). Искусная модель представлена кривой, изгибающейся в сторону (1,1) над плоской линией отсутствия навыков.
Существуют также составные баллы, которые пытаются суммировать точность и отзывчивость; два примера включают:
- Оценка F-Measure или F1: вычисляет среднее гармоническое значение точности и отзыва (среднее гармоническое, потому что точность и отзыв являются коэффициентами).
- Площадь под кривой : как и AUC, суммирует интеграл или аппроксимацию площади под кривой точного отзыва.
С точки зрения выбора модели, F-Measure суммирует навыки модели для определенного порога вероятности (например,грамм. 0,5), тогда как область под кривой суммирует навыки модели по пороговым значениям, например ROC AUC.
Это делает точный вызов и график зависимости точности от отзыва и сводных показателей полезными инструментами для задач двоичной классификации, которые имеют дисбаланс в наблюдениях для каждого класса.
Кривые прецизионного вызова в Python
Точность и отзывчивость можно рассчитать в scikit-learn.
Точность и отзыв могут быть рассчитаны для пороговых значений с помощью функции precision_recall_curve (), которая принимает истинные выходные значения и вероятности для положительного класса в качестве входных данных и возвращает значения точности, отзыва и пороговых значений.
… # вычислить кривую точности-отзыва точность, отзыв, пороги = precision_recall_curve (testy, probs)
… # вычислить кривую точности-отзыва precision, recall, thresholds = precision_recall_curve (testy, probs) |
F-Measure можно вычислить, вызвав функцию f1_score (), которая принимает истинные значения класса и предсказанные значения класса в качестве аргументов.
… # вычислить оценку F1 f1 = f1_score (testy, yhat)
… # вычислить оценку F1 f1 = f1_score (testy, yhat) |
Площадь под кривой точности-отзыва может быть аппроксимирована путем вызова функции auc () и передачи ей значений отзыва (x) и точности (y), рассчитанных для каждого порога.
… # вычислить AUC с точностью до отзыва auc = auc (отзыв, точность)
… # вычислить точность-отзыв AUC auc = auc (отзыв, точность) |
При нанесении на график точности и отзыва для каждого порогового значения в виде кривой важно, чтобы отзыв был представлен по оси x, а точность — по оси y.
Полный пример расчета кривых точности-отзыва для модели логистической регрессии приведен ниже.
# кривая точности-отзыва и f1 из sklearn.datasets импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import precision_recall_curve из sklearn.metrics import f1_score из sklearn.metrics import auc из matplotlib import pyplot # создать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, random_state = 1) # разделить на наборы поездов / тестов trainX, testX, тренировочный, testy = train_test_split (X, y, test_size = 0.5, random_state = 2) # соответствовать модели model = LogisticRegression (решатель = ‘lbfgs’) model.fit (trainX, trainy) # прогнозировать вероятности lr_probs = model.predict_proba (testX) # сохраняем вероятности только положительного результата lr_probs = lr_probs [:, 1] # предсказать значения класса yhat = model.predict (testX) lr_precision, lr_recall, _ = precision_recall_curve (testy, lr_probs) lr_f1, lr_auc = f1_score (testy, yhat), auc (lr_recall, lr_precision) # подвести итоги print (‘Логистика: f1 =%.3f auc =%. 3f ‘% (lr_f1, lr_auc)) # построить кривые точности-отзыва no_skill = len (вздорный [testy == 1]) / len (проворный) pyplot.plot ([0, 1], [no_skill, no_skill], linestyle = ‘-‘, label = ‘Нет навыков’) pyplot.plot (lr_recall, lr_precision, marker = ‘.’, label = ‘Logistic’) # метка оси pyplot.xlabel (‘Отзыв’) pyplot.ylabel (‘Точность’) # показать легенду pyplot.legend () # показать сюжет pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 24 25 26 27 28 29 30 000 000 34 35 36 | # кривая прецизионного вызова и f1 из sklearn.наборы данных импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import precision_recall_curve из sklearn.metrics импортировать из sklearn.metrics 000# сгенерировать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, random_state = 1) # разделить на наборы для обучения / тестирования trainX, testX, trainy, testy = train_test_split (X, y , test_size = 0.5, random_state = 2) # соответствие модели model = LogisticRegression (solver = ‘lbfgs’) model.fit (trainX, trainy) # прогноз вероятностей lr_probs = model.predict_proba (testX) 9000 # сохранять вероятности только для положительного результата lr_probs = lr_probs [:, 1] # прогнозировать значения класса yhat = model.predict (testX) lr_precision, lr_recall, _ = precision_recall_curve_curve (testy), lr0003_probsy lr_f1, lr_auc = f1_score (testy, yhat), auc (lr_recall, lr_precision) # подвести итоги print (‘Логистика: f1 =%.3f auc =%. 3f ‘% (lr_f1, lr_auc)) # построить кривые точности-отзыва no_skill = len (testy [testy == 1]) / len (testy) pyplot.plot ([0 , 1], [no_skill, no_skill], linestyle = ‘-‘, label = ‘No Skill’) pyplot.plot (lr_recall, lr_precision, marker = ‘.’, Label = ‘Logistic’) # ось метки pyplot.xlabel (‘Recall’) pyplot.ylabel (‘Precision’) # показать легенду pyplot.legend () # показать график pyplot.показать () |
При выполнении примера сначала печатается F1, площадь под кривой (AUC) для модели логистической регрессии.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Логистика: f1 = 0,841 auc = 0,898
Логистика: f1 = 0.841 auc = 0,898 |
Затем создается график кривой точности-отзыва, показывающий точность / отзыв для каждого порога для модели логистической регрессии (оранжевый) по сравнению с моделью без навыков (синий).
График точного отзыва для классификатора без навыков и модели логистической регрессии
Когда использовать кривые ROC по сравнению с кривыми прецизионного восстановления?
Как правило, используются следующие кривые ROC и кривые прецизионного возврата:
- Кривые ROC следует использовать при примерно равном количестве наблюдений для каждого класса. Кривые
- Precision-Recall следует использовать при наличии среднего или большого дисбаланса класса.
Причина этой рекомендации заключается в том, что кривые ROC представляют оптимистичную картину модели на наборах данных с дисбалансом классов.
Однако кривые ROC могут представлять излишне оптимистичное представление о производительности алгоритма, если имеется большой перекос в распределении классов. […] Кривые Precision-Recall (PR), часто используемые при поиске информации, упоминались как альтернатива кривым ROC для задач с большим перекосом в распределении классов.
— Взаимосвязь между точным воспроизведением и кривыми ROC, 2006.
Некоторые идут еще дальше и предполагают, что использование кривой ROC с несбалансированным набором данных может быть обманчивым и привести к неправильной интерпретации навыка модели.
[…] визуальная интерпретируемость графиков ROC в контексте несбалансированных наборов данных может быть обманчивой в отношении выводов о надежности выполнения классификации из-за интуитивной, но неправильной интерпретации специфичности.Графики [Кривая точности-отзыва], с другой стороны, могут предоставить зрителю точный прогноз будущей эффективности классификации благодаря тому факту, что они оценивают долю истинно положительных результатов среди положительных прогнозов
— График точности-отзыва более информативен, чем график ROC при оценке двоичных классификаторов на несбалансированных наборах данных, 2015.
Основная причина такой оптимистической картины заключается в использовании истинно отрицательных результатов в показателе ложных положительных результатов на кривой ROC и тщательном избегании этого показателя на кривой точности-отзыва.
Если соотношение положительных и отрицательных экземпляров в тестовой выборке изменится, кривые ROC не изменятся. Такие показатели, как точность, точность, рост и оценка F, используют значения из обоих столбцов матрицы неточностей. По мере изменения распределения классов эти показатели также изменятся, даже если не изменится производительность основного классификатора. Графики ROC основаны на скорости TP и FP, в которых каждое измерение является строгим столбцовым соотношением, поэтому не зависит от распределений классов.
— Графы ROC: заметки и практические соображения для исследователей интеллектуального анализа данных, 2003.
Мы можем сделать этот бетон на небольшом примере.
Ниже приведен тот же пример кривой ROC с модифицированной задачей, где соотношение наблюдений класса = 0 и класса = 1 составляет примерно 100: 1 (в частности, Class0 = 985, Class1 = 15).
# кривая roc и auc на несбалансированном наборе данных из sklearn.datasets импортировать make_classification из склеарна.linear_model импорт LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics импортировать roc_curve из sklearn.metrics import roc_auc_score из matplotlib import pyplot # создать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, weights = [0.99,0.01], random_state = 1) # разделить на наборы поездов / тестов trainX, testX, trainy, testy = train_test_split (X, y, test_size = 0,5, random_state = 2) # генерировать прогноз отсутствия навыков (класс большинства) ns_probs = [0 для _ в диапазоне (len (testy))] # соответствовать модели model = LogisticRegression (решатель = ‘lbfgs’) модель.подходят (trainX, trainy) # прогнозировать вероятности lr_probs = model.predict_proba (testX) # сохраняем вероятности только положительного результата lr_probs = lr_probs [:, 1] # подсчитать баллы ns_auc = roc_auc_score (testy, ns_probs) lr_auc = roc_auc_score (testy, lr_probs) # подвести итоги print (‘Нет навыков: ROC AUC =%. 3f’% (ns_auc)) print (‘Логистика: ROC AUC =%. 3f’% (lr_auc)) # вычислить кривые roc ns_fpr, ns_tpr, _ = roc_curve (testy, ns_probs) lr_fpr, lr_tpr, _ = roc_curve (testy, lr_probs) # построить кривую roc для модели пиплот.сюжет (ns_fpr, ns_tpr, linestyle = ‘-‘, label = ‘Нет навыков’) pyplot.plot (lr_fpr, lr_tpr, marker = ‘.’, label = ‘Logistic’) # метка оси pyplot.xlabel (‘Ложноположительная ставка’) pyplot.ylabel (‘Истинная положительная оценка’) # показать легенду pyplot.legend () # показать сюжет pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 24 25 26 27 28 29 30 000 000 34 35 36 37 38 39 | # roc curve и auc для несбалансированного набора данных из sklearn.наборы данных импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import roc_curve из sklearn.metrics import class 000 9_scenerate data import roc_auc 9_scenerate X, y = make_classification (n_samples = 1000, n_classes = 2, weights = [0.99,0.01], random_state = 1) # разделить на наборы для обучения / тестирования trainX, testX, trainy, testy = train_test_split (X, y , test_size = 0.5, random_state = 2) # генерировать прогноз отсутствия навыков (класс большинства) ns_probs = [0 for _ in range (len (testy))] # соответствовать модели model = LogisticRegression (solver = ‘ lbfgs ‘) model.fit (trainX, trainy) # предсказать вероятности lr_probs = model.predict_proba (testX) # сохранить вероятность только положительного результата lr_probs = lr_probs [: ] # подсчитать баллы ns_auc = roc_auc_score (testy, ns_probs) lr_auc = roc_auc_score (testy, lr_probs) # суммировать баллы print (‘No Skill: ROC AUC =%.3f ‘% (ns_auc)) print (‘ Logistic: ROC AUC =%. 3f ‘% (lr_auc)) # вычислить кривые ROC ns_fpr, ns_tpr, _ = roc_curve (testy, ns_probs) ls_probs) ls_probs lr_tpr, _ = roc_curve (testy, lr_probs)# построить кривую roc для модели pyplot.plot (ns_fpr, ns_tpr, linestyle = ‘-‘, label = ‘No Skill’) pyplot.plot ( lr_fpr, lr_tpr, marker = ‘.’, label = ‘Logistic’) # метки оси pyplot.xlabel (‘False Positive Rate’) pyplot.ylabel (‘True Positive Rate’) # показать легенду pyplot.legend () # показать график pyplot.show () |
Выполнение примера предполагает, что модель обладает навыками.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Нет навыка: ROC AUC = 0.500 Логистика: ROC AUC = 0,716
Нет навыков: ROC AUC = 0,500 Логистика: ROC AUC = 0,716 |
Действительно, у него есть навыки, но все эти навыки измеряются как правильные истинные отрицательные прогнозы, и есть много отрицательных прогнозов.
Если вы просмотрите прогнозы, вы увидите, что модель предсказывает класс большинства (класс 0) во всех случаях в наборе тестов. Счет вводит в заблуждение.
График ROC-кривой подтверждает интерпретацию AUC умелой модели для большинства пороговых значений вероятности.
График кривой ROC для классификатора без навыков и модель логистической регрессии для несбалансированного набора данных
Мы также можем повторить тест той же модели на том же наборе данных и вместо этого вычислить кривую точности-отзыва и статистику.
Полный пример приведен ниже.
# кривая точности-отзыва и f1 для несбалансированного набора данных из склеарна.наборы данных импорт make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import precision_recall_curve из sklearn.metrics import f1_score из sklearn.metrics import auc из matplotlib import pyplot # создать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, weights = [0.99,0.01], random_state = 1) # разделить на наборы поездов / тестов trainX, testX, тренировочный, testy = train_test_split (X, y, test_size = 0.5, random_state = 2) # соответствовать модели model = LogisticRegression (решатель = ‘lbfgs’) model.fit (trainX, trainy) # прогнозировать вероятности lr_probs = model.predict_proba (testX) # сохраняем вероятности только положительного результата lr_probs = lr_probs [:, 1] # предсказать значения класса yhat = model.predict (testX) # вычисляем точность и отзыв для каждого порога lr_precision, lr_recall, _ = precision_recall_curve (testy, lr_probs) # подсчитать баллы lr_f1, lr_auc = f1_score (testy, yhat), auc (lr_recall, lr_precision) # подвести итоги print (‘Логистика: f1 =%.3f auc =%. 3f ‘% (lr_f1, lr_auc)) # построить кривые точности-отзыва no_skill = len (вздорный [testy == 1]) / len (проворный) pyplot.plot ([0, 1], [no_skill, no_skill], linestyle = ‘-‘, label = ‘Нет навыков’) pyplot.plot (lr_recall, lr_precision, marker = ‘.’, label = ‘Logistic’) # метка оси pyplot.xlabel (‘Отзыв’) pyplot.ylabel (‘Точность’) # показать легенду pyplot.legend () # показать сюжет pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 24 25 26 27 28 29 30 000 000 34 35 36 37 38 | # кривая прецизионного вызова и f1 для несбалансированного набора данных из sklearn.наборы данных импортировать make_classification из sklearn.linear_model import LogisticRegression из sklearn.model_selection import train_test_split из sklearn.metrics import precision_recall_curve из sklearn.metrics импортировать из sklearn.metrics 000# сгенерировать набор данных 2 классов X, y = make_classification (n_samples = 1000, n_classes = 2, weights = [0.99,0.01], random_state = 1) # разделить на наборы для обучения / тестирования trainX, testX, trainy , testy = train_test_split (X, y, test_size = 0.5, random_state = 2) # соответствие модели model = LogisticRegression (solver = ‘lbfgs’) model.fit (trainX, trainy) # прогноз вероятностей lr_probs = model.predict_proba (testX) 9000 # сохранять вероятности только для положительного результата lr_probs = lr_probs [:, 1] # прогнозировать значения класса yhat = model.predict (testX) # вычислять точность и отзыв для каждого порога lr_precision, lr_recall , _ = precision_recall_curve (testy, lr_probs) # вычислить баллы lr_f1, lr_auc = f1_score (testy, yhat), auc (lr_recall, lr_precision) # Log summarize scores 3f auc =%. 3f ‘% (lr_f1, lr_auc)) # построить кривые точности-отзыва no_skill = len (testy [testy == 1]) / len (testy) pyplot.plot ([0 , 1], [no_skill, no_skill], linestyle = ‘-‘, label = ‘No Skill’) pyplot.plot (lr_recall, lr_precision, marker = ‘.’, Label = ‘Logistic’) # ось метки pyplot.xlabel (‘Recall’) pyplot.ylabel (‘Precision’) # показать легенду pyplot.legend () # показать график pyplot.показать () |
При выполнении примера сначала печатаются оценки F1 и AUC.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Мы видим, что модель получает штраф за предсказание класса большинства во всех случаях. Оценки показывают, что модель, которая хорошо выглядела в соответствии с кривой ROC, на самом деле едва ли является умелой, если рассматривать использование точности и вспомнить, что фокусировка на положительном классе.
Логистика: f1 = 0,000 auc = 0,054
Логистика: f1 = 0,000 auc = 0,054 |
График кривой точности-отзыва показывает, что модель чуть выше линии отсутствия навыков для большинства пороговых значений.
Это возможно, потому что модель предсказывает вероятности и не дает точных сведений о некоторых случаях. Они выставляются через различные пороги, оцениваемые при построении кривой, переводя некоторый класс 0 в класс 1, предлагая некоторую точность, но очень низкую отзывчивость.
График точного отзыва для классификатора без навыков и модель логистической регрессии для несбалансированного набора данных
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Документы
API
Статьи
Сводка
В этом руководстве вы открыли для себя кривые ROC, кривые прецизионного восстановления и когда их использовать для интерпретации прогнозов вероятностей для задач двоичной классификации.
В частности, вы выучили:
- Кривые ROC суммируют компромисс между частотой истинных положительных и ложных положительных результатов для прогнозной модели с использованием различных пороговых значений вероятности. Кривые
- Precision-Recall суммируют компромисс между истинным положительным значением и положительным прогнозным значением для прогнозной модели с использованием различных пороговых значений вероятности. Кривые
- ROC подходят, когда наблюдения сбалансированы между каждым классом, тогда как кривые точности-отзыва подходят для несбалансированных наборов данных.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Получите представление о вероятности машинного обучения!
Развивайте свое понимание вероятности
… всего несколькими строками кода Python Узнайте, как это сделать, в моей новой электронной книге:
Probability for Machine Learning
Он предоставляет руководств для самообучения и сквозных проектов по:
Теорема Байеса , Байесовская оптимизация , Распределения , Максимальное правдоподобие , Кросс-энтропия , Модели калибровки
и многое другое…
Наконец-то используйте неопределенность в своих проектах
Пропустите академики. Только результаты. Посмотрите, что внутриЭкономически чувствительная логистическая регрессия для несбалансированной классификации
Последнее обновление 26 октября 2020 г.
Логистическая регрессия не поддерживает несбалансированную классификацию напрямую.
Вместо этого алгоритм обучения, используемый для соответствия модели логистической регрессии, должен быть изменен, чтобы учесть искаженное распределение. Этого можно достичь, указав конфигурацию взвешивания классов, которая используется для влияния на количество обновляемых коэффициентов логистической регрессии во время обучения.
Взвешивание может меньше наказывать модель за ошибки, допущенные на примерах из класса большинства, и больше наказывать модель за ошибки, сделанные на примерах из класса меньшинства. Результатом является версия логистической регрессии, которая лучше справляется с несбалансированными задачами классификации, обычно называемая зависимой от затрат или взвешенной логистической регрессией.
В этом руководстве вы обнаружите чувствительную к стоимости логистическую регрессию для несбалансированной классификации.
После прохождения этого руководства вы будете знать:
- Как стандартная логистическая регрессия не поддерживает несбалансированную классификацию.
- Как логистическая регрессия может быть изменена для взвешивания ошибки модели по весу класса при подборе коэффициентов.
- Как настроить вес класса для логистической регрессии и как выполнить поиск по сетке для различных конфигураций веса класса.
Начните свой проект с моей новой книги «Несбалансированная классификация с Python», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.
Приступим.
- Обновление февраль / 2020 : Исправлена опечатка при расчете веса.
- Обновление октябрь / 2020 : Исправлена опечатка в описании соотношения баланса.
Экономически чувствительная логистическая регрессия для несбалансированной классификации
Фотография Naval S, некоторые права защищены.
Обзор учебного пособия
Это руководство разделено на пять частей; их:
- Несбалансированный набор данных классификации
- Логистическая регрессия для несбалансированной классификации
- Взвешенная логистическая регрессия с помощью Scikit-Learn
- Взвешенная логистическая регрессия поиска по сетке
Несбалансированный набор данных классификации
Прежде чем мы углубимся в модификацию логистической регрессии для несбалансированной классификации, давайте сначала определим несбалансированный набор данных классификации.
Мы можем использовать функцию make_classification () для определения синтетического несбалансированного двухклассового набора данных классификации. Мы сгенерируем 10 000 примеров с приблизительным соотношением меньшинства к большинству 1: 100.
… # определить набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2)
… # определить набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, weights = [0.99], flip_y = 0, random_state = 2) |
После создания мы можем суммировать распределение классов, чтобы подтвердить, что набор данных был создан, как мы и ожидали.
… # суммировать распределение классов counter = Counter (y) печать (счетчик)
… # обобщить распределение классов counter = Counter (y) print (counter) |
Наконец, мы можем создать диаграмму разброса примеров и раскрасить их по метке класса, чтобы помочь понять проблему классификации примеров из этого набора данных.
… # точечная диаграмма примеров по метке класса для метки _ в counter.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) пиплот.легенда () pyplot.show ()
… # точечная диаграмма примеров по метке класса для метки, _ в counter.items (): row_ix = where (y == label) [0] pyplot.scatter (X [ row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show () |
Полный пример создания синтетического набора данных и построения графиков приведен ниже.
# Создание и построение набора данных синтетической несбалансированной классификации из коллекций счетчик импорта из sklearn.datasets импортировать make_classification из matplotlib import pyplot из импорта numpy, где # определить набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # суммировать распределение классов counter = Counter (y) печать (счетчик) # точечная диаграмма примеров по метке класса для ярлыка _ в счетчике.Предметы(): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show ()
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 | # Сгенерировать и построить набор данных синтетической несбалансированной классификации из коллекции импорта Counter из sklearn.наборы данных import make_classification from matplotlib import pyplot from numpy import, где # определить набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, _performance = 0,_кластер =, nights_class = _кластеры =], flip_y = 0, random_state = 2) # суммировать распределение классов counter = Counter (y) print (counter) # точечная диаграмма примеров по метке класса для label, _ in counter.items (): row_ix = where (y == label) [0] pyplot.scatter (X [row_ix, 0], X [row_ix, 1], label = str (label)) pyplot.legend () pyplot.show () |
При выполнении примера сначала создается набор данных и резюмируется распределение классов.
Мы видим, что набор данных имеет приблизительное распределение классов 1: 100 с немногим менее 10 000 примеров в классе большинства и 100 в классе меньшинства.
Счетчик ({0: 9900, 1: 100})
Счетчик ({0: 9900, 1: 100}) |
Затем создается диаграмма разброса набора данных, показывающая большое количество примеров для класса большинства (синий) и небольшое количество примеров для класса меньшинства (оранжевый) с некоторым небольшим перекрытием классов.
Точечная диаграмма набора данных двоичной классификации с дисбалансом классов от 1 до 100
Затем мы можем подогнать к набору данных стандартную модель логистической регрессии.
Мы будем использовать повторную перекрестную проверку для оценки модели с тремя повторениями 10-кратной перекрестной проверки. Характеристики режима будут представлены с использованием средней ROC-площади под кривой (ROC AUC), усредненной по повторам и всем складкам.
… # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (модель, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # подвести итоги print (‘Среднее значение ROC AUC:%.3f ‘% среднее (баллы))
… # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (model, X, y, scoring = ‘roc_auc =’ roc_auc ‘, cv = cv, n_jobs = -1) # подвести итоги производительности print (‘ Среднее ROC AUC:% .3f ‘% среднее (баллы)) |
Собирая все вместе, ниже приводится полный пример оцененной стандартной логистической регрессии по проблеме несбалансированной классификации.
# подобрать модель логистической регрессии на несбалансированном наборе данных классификации из среднего значения импорта из sklearn.datasets импортировать make_classification из sklearn.model_selection импорт cross_val_score из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # создать набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (решатель = ‘lbfgs’) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (модель, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # подвести итоги print (‘Среднее ROC AUC:% .3f’% среднее (баллы))
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 | # соответствует модели логистической регрессии на несбалансированном наборе данных классификации из numpy import mean from sklearn.наборы данных импортировать make_classification из sklearn.model_selection импорт cross_val_score из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # generate dataset_ , nduclass = 2 0003 0,n_clusters_per_class = 1, weights = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (solver = ‘lbfgs’) # определить процедуру оценки cv = Repeated (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (model, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # summarize performance отпечаток (‘Среднее значение ROC AUC:%.3f ‘% среднее (в баллах) |
При выполнении примера оценивается стандартная модель логистической регрессии для несбалансированного набора данных и отображается среднее значение ROC AUC.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Мы видим, что у модели есть навык, достигающий ROC AUC выше 0.5, в этом случае средний балл составляет 0,985.
Это обеспечивает основу для сравнения любых модификаций, выполненных в стандартном алгоритме логистической регрессии.
Хотите начать работу с классификацией дисбаланса?
Пройдите бесплатный 7-дневный ускоренный курс по электронной почте (с образцом кода).
Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.
Загрузите БЕСПЛАТНЫЙ мини-курс
Логистическая регрессия для несбалансированной классификации
Логистическая регрессия — эффективная модель для задач двоичной классификации, хотя по умолчанию она не эффективна при несбалансированной классификации.
Логистическая регрессия может быть изменена, чтобы лучше подходить для логистической регрессии.
Коэффициенты алгоритма логистической регрессии подбираются с использованием алгоритма оптимизации, который минимизирует отрицательную логарифмическую вероятность (потерю) для модели в наборе обучающих данных.
- минимизировать сумму i до n — (log (yhat_i) * y_i + log (1 — yhat_i) * (1 — y_i))
Это включает в себя повторное использование модели для прогнозирования с последующей адаптацией коэффициентов в направлении, которое снижает потери модели.
Расчет потерь для данного набора коэффициентов может быть изменен с учетом баланса классов.
По умолчанию, ошибки для каждого класса могут считаться имеющими одинаковый вес, например 1.0. Эти веса могут быть скорректированы в зависимости от важности каждого класса.
- минимизировать сумму i до n — (w0 * log (yhat_i) * y_i + w1 * log (1 — yhat_i) * (1 — y_i))
Взвешивание применяется к потерям, так что меньшие значения веса приводят к меньшему значению ошибки и, в свою очередь, к меньшему обновлению коэффициентов модели.Большее значение веса приводит к большему вычислению ошибки и, в свою очередь, к большему обновлению коэффициентов модели.
- Малый вес : Меньше значение, меньше обновлений для коэффициентов модели.
- Большой вес : Больше важности, больше обновлений для коэффициентов модели.
Таким образом, модифицированная версия логистической регрессии называется взвешенной логистической регрессией, взвешенной логистической регрессией или логистической регрессией с учетом затрат.
Веса иногда называют весами важности.
Несмотря на простоту реализации, проблема взвешенной логистической регрессии заключается в выборе веса для каждого класса.
Взвешенная логистическая регрессия с помощью Scikit-Learn
Библиотека машинного обучения Python scikit-learn предоставляет реализацию логистической регрессии, которая поддерживает взвешивание классов.
Класс LogisticRegression предоставляет аргумент class_weight, который можно указать как гиперпараметр модели.Class_weight — это словарь, который определяет каждую метку класса (например, 0 и 1) и вес, применяемый при вычислении отрицательной логарифмической вероятности при подборе модели.
Например, весовой коэффициент 1 к 1 для каждого класса 0 и 1 можно определить следующим образом:
… # определить модель веса = {0: 1.0, 1: 1.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights)
… # определить модель weights = {0: 1.0, 1: 1.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights) |
Классовое взвешивание может быть определено несколькими способами; например:
- Экспертиза в предметной области , определяется путем бесед с экспертами в предметной области.
- Настройка , определяется поиском гиперпараметров, например поиском по сетке.
- Эвристика , определенная в соответствии с общими рекомендациями.
Лучшим способом использования взвешивания классов является использование обратного распределения классов, присутствующего в наборе обучающих данных.
Например, распределение классов обучающего набора данных — это соотношение 1: 100 для класса меньшинства к классу большинства. Можно использовать инверсию этого отношения с 1 для класса большинства и 100 для класса меньшинства; например:
… # определить модель веса = {0: 1.0, 1: 100.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights)
… # определить модель weights = {0: 1.0, 1: 100.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights) |
Мы могли бы также определить такое же соотношение, используя дроби, и получить тот же результат; например:
… # определить модель веса = {0: 0,01, 1: 1,0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights)
… # определить модель weights = {0: 0.01, 1: 1.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights) |
Мы можем оценить алгоритм логистической регрессии с помощью взвешивания классов, используя ту же процедуру оценки, которая была определена в предыдущем разделе.
Мы ожидаем, что взвешенная по классам версия логистической регрессии будет работать лучше, чем стандартная версия логистической регрессии без какого-либо взвешивания классов.
Полный пример приведен ниже.
# взвешенная модель логистической регрессии для несбалансированного набора данных классификации из среднего значения импорта из sklearn.datasets импортировать make_classification из sklearn.model_selection импорт cross_val_score из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # создать набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # определить модель веса = {0: 0,01, 1: 1,0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (модель, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # подвести итоги print (‘Среднее ROC AUC:% .3f’% среднее (баллы))
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 | # взвешенная модель логистической регрессии для несбалансированного набора данных классификации из numpy import mean from sklearn.наборы данных импортировать make_classification из sklearn.model_selection импорт cross_val_score из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # generate dataset_ , n0002 0,n_clusters_per_class = 1, weights = [0.99], flip_y = 0, random_state = 2) # определить модель weights = {0: 0.01, 1: 1.0} model = LogisticRegression (solver = ‘lbfgs’, class_weight = weights) # определение процедуры оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценка модели = cross_val_score (model, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1)# подвести итоги print (‘Среднее ROC AUC:% .3f’% среднее (баллы)) |
При выполнении примера подготавливается набор данных синтетической несбалансированной классификации, затем оценивается взвешенная по классам версия логистической регрессии с использованием повторной перекрестной проверки.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Сообщается средний показатель ROC AUC, в этом случае он показывает лучший результат, чем невзвешенная версия логистической регрессии, 0,989 по сравнению с 0,985.
Библиотека scikit-learn предоставляет реализацию эвристики лучших практик для взвешивания классов.
Реализуется с помощью функции compute_class_weight () и рассчитывается как:
- n_samples / (n_classes * n_samples_with_class)
Мы можем проверить этот расчет вручную на нашем наборе данных. Например, у нас есть 10 000 примеров в наборе данных, 9900 в классе 0 и 100 в классе 1.
Весовой коэффициент для класса 0 рассчитывается как:
- взвешивание = n_samples / (n_classes * n_samples_with_class)
- взвешивание = 10000 / (2 * 9900)
- взвешивание = 10000/19800
- весовой коэффициент = 0.05
Весовой коэффициент для класса 1 рассчитывается как:
- взвешивание = n_samples / (n_classes * n_samples_with_class)
- взвешивание = 10000 / (2 * 100)
- взвешивание = 10000/200
- взвешивание = 50
Мы можем подтвердить эти вычисления, вызвав функцию compute_class_weight () и указав class_weight как « сбалансированный ». Например:
# вычислить эвристический вес класса из склеарна.utils.class_weight импорт compute_class_weight из sklearn.datasets импортировать make_classification # создать набор данных 2 классов X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # вычислить вес класса weighting = compute_class_weight (‘сбалансированный’, [0,1], y) печать (взвешивание)
# вычислить эвристический вес класса из sklearn.утилиты ], flip_y = 0, random_state = 2) # вычислить вес класса weighting = compute_class_weight (‘сбалансированный’, [0,1], y) print (weighting) |
Запустив пример, мы видим, что можем достичь веса около 0.5 для класса 0 и 50 для класса 1.
Эти значения соответствуют нашему ручному расчету.
Значения также соответствуют нашему эвристическому расчету выше для инвертирования отношения распределения классов в наборе обучающих данных; например:
Мы можем использовать баланс классов по умолчанию непосредственно с классом LogisticRegression, установив для аргумента class_weight значение «сбалансированный». Например:
… # определить модель model = LogisticRegression (solver = ‘lbfgs’, class_weight =’balanced ‘)
… # определить модель model = LogisticRegression (solver = ‘lbfgs’, class_weight =’balanced ‘) |
Полный пример приведен ниже.
# взвешенная логистическая регрессия для дисбаланса классов с эвристическими весами из среднего значения импорта из sklearn.datasets импортировать make_classification из sklearn.model_selection импорт cross_val_score из sklearn.model_selection import RepeatedStratifiedKFold из склеарна.linear_model импорт LogisticRegression # создать набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (решатель = ‘lbfgs’, class_weight = ‘сбалансированный’) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (модель, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # подвести итоги print (‘Среднее значение ROC AUC:%.3f ‘% среднее (баллы))
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 | # взвешенная логистическая регрессия для дисбаланса классов с эвристическими весами из numpy import mean from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.linear_model import LogisticRegression # сгенерировать набор данных X, y = make_classification (n_sample_ass = 10000, n_feclassification, n_samples = 10000, n_feclassification, n_samples = 10000, n_feclassification, n_samples weights = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (solver = ‘lbfgs’, class_weight = ‘balance’) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # оценить модель scores = cross_val_score (model, X, y, scoring = ‘roc_auc’, cv = cv, n_jobs = -1) # подвести итоги print (‘Среднее значение ROC AUC:%.3f ‘% среднее (в баллах) |
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
Выполнение примера дает то же среднее значение ROC AUC, которое мы получили, задав обратное соотношение классов вручную.
Взвешенная логистическая регрессия поиска по сетке
Использование взвешивания класса, которое является обратным соотношением обучающих данных, является всего лишь эвристикой.
Возможно, что лучшая производительность может быть достигнута с другим весовым коэффициентом класса, и это также будет зависеть от выбора метрики производительности, используемой для оценки модели.
В этом разделе мы проведем сеточный поиск по диапазону различных весов классов для взвешенной логистической регрессии и выясним, какие результаты дают лучший результат ROC AUC.
Мы попробуем следующие веса для классов 0 и 1:
- {0: 100,1: 1}
- {0: 10,1: 1}
- {0: 1,1: 1}
- {0: 1,1: 10}
- {0: 1,1: 100}
Их можно определить как параметры поиска по сетке для класса GridSearchCV следующим образом:
… # определить сетку баланс = [{0: 100,1: 1}, {0: 10,1: 1}, {0: 1,1: 1}, {0: 1,1: 10}, {0: 1,1: 100}] param_grid = dict (class_weight = баланс)
… # определить сетку balance = [{0: 100,1: 1}, {0: 10,1: 1}, {0: 1,1: 1}, {0: 1, 1:10}, {0: 1,1: 100}] param_grid = dict (class_weight = balance) |
Мы можем выполнить поиск по сетке по этим параметрам, используя повторную перекрестную проверку, и оценить производительность модели, используя ROC AUC:
… # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # определить поиск по сетке grid = GridSearchCV (оценка = модель, param_grid = param_grid, n_jobs = -1, cv = cv, scoring = ‘roc_auc’)
… # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # определить поиск по сетке grid = GridSearchCV (оценка = модель, param_grid, n_bsgrid, = -1, cv = cv, scoring = ‘roc_auc’) |
После выполнения мы можем суммировать лучшую конфигурацию, а также все результаты следующим образом:
… # сообщить о лучшей конфигурации print («Лучшее:% f с использованием% s»% (grid_result.best_score_, grid_result.best_params_)) # сообщить обо всех конфигурациях означает = grid_result.cv_results _ [‘mean_test_score’] stds = grid_result.cv_results _ [‘std_test_score’] params = grid_result.cv_results _ [‘параметры’] для mean, stdev, param в zip (means, stds, params): print («% f (% f) with:% r»% (mean, stdev, param))
… # сообщить о лучшей конфигурации print («Best:% f using% s»% (grid_result.best_score_, grid_result.best_params_)) # сообщить обо всех конфигурациях means = grid_result.cv_results _ [‘mean_test_score’ ] stds = grid_result.cv_results _ [‘std_test_score’] params = grid_result.cv_results _ [‘params’] для среднего, stdev, param в zip (means, stds, params): print («% f (% f) с:% r «% (среднее, стандартное отклонение, параметр)) |
В приведенном ниже примере сетки выполняется поиск пяти различных весов классов для логистической регрессии в несбалансированном наборе данных.
Можно ожидать, что эвристическое взвешивание классов является наиболее производительной конфигурацией.
# поиск по сетке весов классов с логистической регрессией для классификации дисбаланса из среднего значения импорта из sklearn.datasets импортировать make_classification из sklearn.model_selection import GridSearchCV из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # создать набор данных X, y = make_classification (n_samples = 10000, n_features = 2, n_redundant = 0, n_clusters_per_class = 1, веса = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (решатель = ‘lbfgs’) # определить сетку баланс = [{0: 100,1: 1}, {0: 10,1: 1}, {0: 1,1: 1}, {0: 1,1: 10}, {0: 1,1: 100}] param_grid = dict (class_weight = баланс) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # определить поиск по сетке grid = GridSearchCV (оценка = модель, param_grid = param_grid, n_jobs = -1, cv = cv, scoring = ‘roc_auc’) # выполнить поиск по сетке grid_result = сетка.подходят (X, y) # сообщить о лучшей конфигурации print («Лучшее:% f с использованием% s»% (grid_result.best_score_, grid_result.best_params_)) # сообщить обо всех конфигурациях означает = grid_result.cv_results _ [‘mean_test_score’] stds = grid_result.cv_results _ [‘std_test_score’] params = grid_result.cv_results _ [‘параметры’] для mean, stdev, param в zip (means, stds, params): print («% f (% f) with:% r»% (mean, stdev, param))
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 18 19 20 21 22 23 24 25 26 27 28 | # веса классов поиска сетки с логистической регрессией для классификации дисбаланса из numpy import mean from sklearn.наборы данных импортировать make_classification из sklearn.model_selection import GridSearchCV из sklearn.model_selection import RepeatedStratifiedKFold из sklearn.linear_model import LogisticRegression # generate dataset_ 0,n_clusters_per_class = 1, weights = [0.99], flip_y = 0, random_state = 2) # определить модель model = LogisticRegression (solver = ‘lbfgs’) # define grid balance = [{ 0: 100,1: 1}, {0: 10,1: 1}, {0: 1,1: 1}, {0: 1,1: 10}, {0: 1,1: 100}] param_grid = dict (class_weight = balance) # определить процедуру оценки cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # определить поиск по сетке grid = GridSearchridCV (param. = param_grid, n_jobs = -1, cv = cv, scoring = ‘roc_auc’) # выполнить поиск по сетке grid_result = сетка.fit (X, y) # сообщить о лучшей конфигурации print («Best:% f using% s»% (grid_result.best_score_, grid_result.best_params_)) # сообщить обо всех конфигурациях means = grid_result.cv_results_ [‘mean_test_score’] stds = grid_result.cv_results _ [‘std_test_score’] params = grid_result.cv_results _ [‘params’] для среднего, stdev, param в zip (means, stds, params):: print («% f (% f) с:% r»% (среднее, стандартное отклонение, параметр)) |
При выполнении примера оценивается вес каждого класса с использованием повторной k-кратной перекрестной проверки и отображается лучшая конфигурация и соответствующий средний показатель ROC AUC.
Примечание : Ваши результаты могут отличаться из-за стохастической природы алгоритма или процедуры оценки или различий в числовой точности. Попробуйте запустить пример несколько раз и сравните средний результат.
В этом случае мы видим, что соотношение 1: 100 от большинства к классу меньшинства дает лучший средний балл ROC. Это соответствует конфигурации для общей эвристики.
Было бы интересно изучить еще более строгие веса классов, чтобы увидеть их влияние на средний показатель ROC AUC.
Лучшее: 0,989077 при использовании {‘class_weight’: {0: 1, 1: 100}} 0,982498 (0,016722) с: {‘class_weight’: {0: 100, 1: 1}} 0,983623 (0,015760) с: {‘class_weight’: {0: 10, 1: 1}} 0,985387 (0,013890) с: {‘class_weight’: {0: 1, 1: 1}} 0,988044 (0,010384) с: {‘class_weight’: {0: 1, 1: 10}} 0,989077 (0,006865) с: {‘class_weight’: {0: 1, 1: 100}}
Best: 0,989077 с использованием {‘class_weight’: {0: 1, 1: 100}} 0.982498 (0,016722) с: {‘class_weight’: {0: 100, 1: 1}} 0,983623 (0,015760) с: {‘class_weight’: {0: 10, 1: 1}} 0,985387 (0,013890) с: {‘class_weight’: {0: 1, 1: 1}} 0,988044 (0,010384) с: {‘class_weight’: {0: 1, 1: 10}} 0,989077 (0,006865) с: {‘ class_weight ‘: {0: 1, 1: 100}} |
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Документы
Книги
API
Сводка
В этом руководстве вы обнаружили чувствительную к стоимости логистическую регрессию для несбалансированной классификации.
В частности, вы выучили:
- Как стандартная логистическая регрессия не поддерживает несбалансированную классификацию.
- Как логистическая регрессия может быть изменена для взвешивания ошибки модели по весу класса при подборе коэффициентов.
- Как настроить вес класса для логистической регрессии и как выполнить поиск по сетке для различных конфигураций веса класса.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Разберитесь с несбалансированной классификацией!
Разработка несбалансированных моделей обучения за считанные минуты
… всего несколькими строками кода Python
Узнайте, как в моей новой электронной книге:
Несбалансированная классификация с Python
Он предоставляет учебных пособий для самообучения и сквозных проектов по:
Показателям производительности , Методы пониженной дискретизации , SMOTE , Пороговое перемещение , Калибровка вероятности , Экономически чувствительные алгоритмы
и многое другое…
Привнесите несбалансированные методы классификации в свои проекты машинного обучения
Посмотрите, что внутри12 примеров обобщения
Обобщение — это формирование знания путем определения общих свойств и структур в вещах. Это важный мыслительный процесс, который позволяет формулировать, передавать и использовать сложные знания. Ниже приведены иллюстративные примеры обобщения.Концепция
Концепции — это абстракции, отличные от конкретной реальности.Часто они основаны на обобщениях. Например, слово «дерево» — это обобщение тысяч видов растений, имеющих общие черты, такие как ствол и продолжительность жизни, обычно превышающая два года. Многие слова можно рассматривать как обобщения, в которых они описывают общую концепцию в отличие от конкретных вещей. Следующая таблица дает несколько примеров слов, которые являются обобщениями.| Животное | Красивое | |||||||||
| Город | Океан | |||||||||
| Человек | Планета | |||||||||
| Завод | Запуск | |||||||||
| Общество | Технологии | AdageПословицы — это обобщения, которые дают представление о природе вещей.Это тип традиционной поговорки, которая передается из поколения в поколение из уст в уста.
Индуктивное рассуждениеИндуктивное рассуждение — это процесс построения обобщенной гипотезы или заключения с использованием примеров, служащих доказательствами.Например: Учитель был в плохом настроении 7 понедельников подряд. Доказательство на примереДоказательство на примере — это заблуждение, основанное на ленивых индуктивных рассуждениях, которое неверно предполагает, что у вещей, которые имеют одно общее, есть и другое общее. В Чжэнчжоу плохое качество воздуха. Эвристика— это эмпирические правила, которые позволяют быстро и эффективно решать проблемы, которые являются неоптимальными, но «достаточно хорошими».Любое хорошее французское вино имеет заниженную этикетку, не привлекающую внимания. Приведенная выше эвристика, вероятно, не очень точна, но может быть полезна для человека, который ничего не знает о вине и которому нужно быстро выбрать бутылку без долгих исследований.СтереотипыСтереотипы — это чрезмерные обобщения о людях. Термин подразумевает несправедливое обобщение.Иностранцы в Японии говорят по-английски. Приведенный выше стереотип основан на распространенном в Японии предположении, что люди, которые не кажутся азиатами, являются иностранцами, говорящими по-английски. Часто это может быть правдой, но также создает несправедливые ситуации. Например, черный или белый человек, родившийся и выросший в Японии и являющийся японцем, постоянно считается иностранцем и не может говорить по-японски.Агрессивное применение эвристики к людям может быть болезненным и несправедливым, поскольку люди заслуживают того, чтобы с ними обращались как с личностями.ПринципыПринципы — это обобщенные правила, которые принимаются отдельным лицом, организацией или обществом для управления своим будущим. Они могут быть закодированы как конституции, законы, основополагающие правила или руководящие принципы. Конгресс не принимает никаких законов, касающихся установления религии или запрещающих ее свободное исповедание; или ограничение свободы слова или печати; или право народа на мирные собрания и ходатайство перед правительством о возмещении жалоб. ЭтикаЭтика — это общие моральные принципы, которые могут быть приняты человеком, профессией, организацией или обществом. Я буду использовать лечение, чтобы помочь больным, в соответствии со своими способностями и суждениями, но никогда не с целью причинить вред или совершить проступок. КатегорииКатегория, такая как жанр фильма, является обобщением, которое можно использовать для систематизации вещей и передачи их основных свойств. Например, научная фантастика — это категория художественной литературы и кино, которая включает в себя элементы будущих технологий, социальных и экологических изменений.Темы и предметыШирокие области знаний сгруппированы в такие предметы, как математика и философия. Более конкретные группы знаний известны как темы. Например, тема «Американские джазовые музыканты 20-х годов».КлассификацииКлассификация — это система маркировки вещей в соответствии с общими свойствами. Например, классификация животных на основе их рациона с такими ярлыками, как травоядные, плотоядные и всеядные.Концептуальная модельКонцептуальная модель — это концепция, имеющая некоторую структуру. Например, идея о том, что капиталистические общества основаны на таких элементах, как рынки, потребители и производители.Классификация | Концепция | ОпределениеКлассификация определяется как систематическое распределение объектов по группам или категориям в соответствии с установленными критериями.Это часть фундаментальной концепции предварительного числового обучения. Сравнение предметов по сходству и различию подпадает под классификацию. Есть разные аспекты, которым мы можем научить детей с помощью классификации. Три основных фактора:
Что такое классификация по математике?Классификация означает организацию или сортировку объектов по группам на основе общего свойства, которым они обладают. Если у вас есть группа вещей, например фрукты или геометрические фигуры, вы можете классифицировать их по свойству, которым они обладают. Например, вы можете отнести яблоки к одной категории, бананы — к другой и так далее. Точно так же геометрические фигуры можно разделить на треугольники, четырехугольники и так далее.Давайте разберемся с этим на другом примере. Если вас попросят определить связь между данными парами по обе стороны от \ (:: \), и вам нужно найти недостающую цифру из четырех предложенных вариантов, вы сможете это сделать? Здесь точное совпадение — это «мяч», то есть вариант A.
Способы классификацииКлассификация может производиться по различным параметрам. Это могут быть предметы разного цвета, разного размера и т. Д. Давайте рассмотрим различные способы классификации вместе с примерами классификации.
Классификация по формеПо форме объектов их можно разделить на различные известные категории. Например, обратите внимание на следующие формы и попробуйте их классифицировать. Все формы можно классифицировать не только по форме, но и по сторонам. Как видите, мы классифицировали все формы по количеству сторон.
Давайте узнаем, как можно провести классификацию на основе размера Классификация по размеруОбратите внимание на круги на рисунке и их расположение.Все круги расположены в порядке возрастания их размера. Самая маленькая ставится первой, затем большая и так далее. Классификация по цветуТеперь разделим кружки по цвету. На приведенном выше рисунке у нас было 6 кругов разного размера. Если мы классифицируем их по цвету, мы получим три круга зеленого и три голубых. Далее мы можем расположить эти круги в порядке увеличения их размера. Классификация на основе чиселМы также можем расположить данный набор предметов по номерам. Обратите внимание на следующий пример. В столбце слева отображаются числа от 1 до 4. В столбце справа отображаются строки различных объектов. Числа соответствуют количеству, которое они представляют. Часто задаваемые вопросы по классификацииЧто такое математические классификации?Классификация — это математический навык с предварительным числом, позволяющий определять классы.Сортировка — это сортировка элементов по заранее определенным характеристикам или атрибутам различных категорий. Что такое классификация простыми словами?Классификация — это систематическое расположение объектов по группам и категориям. Какие две классификации фигур?Формы могут быть следующих типов:
Что означает «классификация фигур»?Классифицировать формы означает различать различные формы на основе их размера, сторон, свойств и т. Д. Сколько существует классификаций действительных чисел?Вещественные числа можно разделить на рациональные и иррациональные числа. Рациональные числа можно далее классифицировать как целые числа, целые числа, натуральные числа и дроби. Почему используется сортировка?Используется в основном для систематического расположения предметов. Как классифицируются треугольники?Треугольники классифицируются на основе их сторон и углов.Они могут быть острыми, тупыми или равноугольными треугольниками, если классифицировать их по углам. Они могут быть разносторонними, равнобедренными или равносторонними, если классифицировать их по бокам. Какое еще слово для сопоставления?Равный, дублирующий, классифицирующий и сопоставимый — это несколько слов, используемых как синонимы для сопоставления. Примеры классификацииРуководство по конкретной темеМетод обнаруженияВ январе 2014 года у команды Verizon RISK возник вопрос о том, какой метод обнаружения использовать для конкретного инцидента.В этом случае заказчик приобрел антивирусную защиту, но не обновил сигнатуры. Антивирусная компания обнаружила вредоносную активность из сети жертв другим способом и уведомила их. Каков метод обнаружения в этом случае?
Команда RISK быстро отказалась от антивируса в качестве опции.Хотя вредоносная программа была обнаружена их антивирусной компанией, обнаружение не было внутренним и не должно указываться в этом списке. Вопрос о том, использовать ли службу мониторинга или стороннюю сторону, возник из-за того, что жертва не платит за службу мониторинга. Однако, поскольку существуют деловые отношения с антивирусной компанией, кажется, что сторонняя сторона тоже не лучший выбор. В конце концов, команда RISK решила, что уведомление жертвы произошло потому, что жертва была клиентом антивирусной компании, а мониторинг был «дополнительной ценностью», которую они получили от того, что они были клиентом антивируса.Поэтому мы решили использовать службу внешнего мониторинга. Но, допустим, для примера, что мы знаем, что устройство было украдено. В частности, кто-то ворвался в машину сотрудника и забрал с заднего сиденья корпоративный ноутбук. Этот инцидент несложно проверить, потому что (обычно) будет только один субъект, действие и актив. Здесь мы предполагаем, что устройство защищено паролем с полным шифрованием диска. Пример классификации: утерянное устройствоОдним из наиболее распространенных инцидентов, о которых сообщают организации всех типов и размеров, является потеря мобильных устройств, таких как ноутбуки или мобильные телефоны.Это может произойти либо из-за ошибки сотрудника, либо из-за кражи актива сторонней стороной. Во многих случаях будет сложно определить, было ли потеряно или украдено пропавшее устройство, но мы предлагаем классифицировать его как «Потеря» (внутренняя ошибка), а не как «Кража» (external.physical), если нет веских оснований подозревать последний. Это не слепое / необоснованное предположение; Если кто-то не уверен, что случилось с устройством, подходит вариант «Потеря», а исторические данные показывают, что устройства теряются гораздо чаще, чем украдены. Мы сосредоточим этот пример на сценарии утери устройства, в частности, утерянного ноутбука. Этот инцидент является одним из наименее сложных для ПРОВЕРКИ, потому что (обычно) будет только один субъект, действие и актив. Здесь мы предполагаем, что устройство защищено паролем с полным шифрованием диска. Очень распространенная ошибка, когда украденные ноутбуки моделируются как потеря конфиденциальности, но не как соответствующая потеря доступности.Помните, что организация потеряла возможность использовать актив. Доступность должна быть указана в затронутых атрибутах. Описание инцидентаАктёр: InternalМотив: N / A Актерское разнообразие: Конечный пользователь Действие: ошибкаРазновидность действия: Потеря Вектор: небрежность АктивРазновидность: Ноутбук Собственность: Жертва Атрибут: конфиденциальность, доступность.Раскрытие данных: № Примечания: Ноутбук защищен паролем и зашифрован Наличие Разновидности: Убыток ОбоснованиеКлассификация этого повседневного происшествия довольно проста.Предполагается, что субъект в этом примере является типичным «конечным пользователем», но также может быть любым другим инсайдером или партнером. Действие просто «Потеря» в категории «Ошибка», а разновидность актива — «Ноутбук», который можно легко изменить для записи потерянных телефонов, документов и т. Д. Поскольку атрибут конфиденциальности VERIS также включает понятие потери владения или контроля. , он включен для всех потерянных активов. Также записывается более очевидный атрибут доступности, если устройство и все данные с момента последней резервной копии не могут быть полностью восстановлены. В этом случае устройство защищено паролем и зашифровано, и, если нет положительных доказательств раскрытия данных, мы можем записать «Нет» для этой переменной в разделе «Конфиденциальность». * Если * он не был защищен паролем и / или зашифрован, нам нужно было бы изменить его на «Возможно», чтобы учесть тот факт, что наши данные теперь находятся под угрозой раскрытия. Кроме того, необходимо будет включить разнообразие и количество задействованных данных. * Если * мы получили доказательства того, что данные были раскрыты неуполномоченным лицам (например,g., он размещен в Интернете или используется для мошенничества), нам нужно будет записать «Да» для переменной data_disclosure. Вывод JSON Пример классификации: украденное устройствоОбычным инцидентом, о котором сообщают все организации, является кража мобильных устройств, таких как ноутбуки или мобильные телефоны.Во многих случаях будет сложно определить, было ли пропавшее устройство потеряно или украдено, но мы предлагаем классифицировать его как «потерю» (внутренняя ошибка), а не как «кража» (external.physical), если нет веских оснований подозревать последний. Это не слепое / необоснованное предположение; Если кто-то не уверен в том, что случилось с устройством, уместно использовать различные варианты «потеря или неправильное размещение», а исторические данные показывают, что устройства теряются гораздо чаще, чем украдены. Но, допустим, для примера, что мы знаем, что устройство было украдено.В частности, кто-то ворвался в машину сотрудника и забрал с заднего сиденья корпоративный ноутбук. Этот инцидент несложно проверить, потому что (обычно) будет только один субъект, действие и актив. Здесь мы предполагаем, что устройство защищено паролем с полным шифрованием диска. Очень распространенная ошибка, когда украденные ноутбуки моделируются как потеря конфиденциальности, но не как соответствующая потеря доступности. Помните, что организация потеряла возможность использовать актив.Доступность должна быть указана в затронутых атрибутах. Основное различие между классификацией потерянного портативного компьютера и украденного портативного компьютера состоит в том, чтобы изменить субъект угрозы и предпринятые действия. Предполагается, что субъект является внешним, а не внутренним. И вместо Error действие Physical . Описание инцидентаАктер: ВнешнийМотив: Финансовый Разнообразие актеров: Неаффилированные Действие: физическоеРазнообразие действий: Кража Местонахождение: личный автомобиль Вектор: отключенные элементы управления АктивРазновидность: Ноутбук Собственность: Жертва Атрибут: конфиденциальность, доступность.Раскрытие данных: № Примечания: Ноутбук защищен паролем и зашифрован Наличие Разновидности: Убыток ОбоснованиеКлассификация этого повседневного происшествия довольно проста.В этом примере предполагается, что субъектом является типичный вор («неаффилированный»), но также может быть любой другой вид внешнего, инсайдерского или партнера. Разновидность действий — «Кража» в разделе «Физическое действие», и мы записали вектор «Отключенные элементы управления» и местоположение «Личного автомобиля», чтобы запечатлеть, что вор разбил окно карточки сотрудника. Вариантом этого может быть то, что вор взломал замок, и в этом случае физический вектор «Обойденные элементы управления» будет более подходящим.Местоположение также можно изменить, если ноутбук был украден из корпоративного офиса («Рабочая зона жертвы»), магазина или ресторана («Общественное учреждение») или дома сотрудника («Личное место жительства»). И так далее. Разновидностью активов здесь является «Ноутбук», но его можно легко изменить для записи украденных телефонов, документов и т. Д. Поскольку атрибут конфиденциальности VERIS также включает в себя понятие потери владения или контроля, он включается для всех потерянных активов.Также записывается более очевидный атрибут доступности, если устройство и все данные с момента последней резервной копии не могут быть полностью восстановлены. В этом случае устройство защищено паролем и зашифровано, и, если нет положительных доказательств раскрытия данных, мы можем записать «Нет» для этой переменной в разделе «Конфиденциальность». * Если * он не был защищен паролем и / или зашифрован, нам нужно было бы изменить его на «Возможно», чтобы учесть тот факт, что наши данные теперь находятся под угрозой раскрытия.Кроме того, необходимо будет включить разнообразие и количество задействованных данных. * Если * мы получили доказательства того, что данные были раскрыты неавторизованным сторонам (например, опубликованы в Интернете или использованы для мошенничества), нам нужно будет записать «Да» для переменной data_disclosure. Вывод JSON Пример классификации: неправильная доставкаНеправильная доставка — это тип ошибки, при которой субъект случайно отправляет конфиденциальные активы или данные не тому получателю.Это может происходить посредством электронной связи, такой как электронная почта и мгновенные сообщения, а также с помощью физических активов, таких как документы и ленты с резервными копиями. Классификация неправомерных действий зависит от мотива актера; это должно быть непреднамеренное действие. Если субъект намеревался отправить конфиденциальную информацию неуполномоченному лицу, то действие будет считаться злоупотреблением, а не ошибкой. Мы сосредоточим этот пример на сценарии утери устройства, в частности, утерянного ноутбука. Этот инцидент является одним из наименее сложных для ПРОВЕРКИ, потому что (обычно) будет только один субъект, действие и актив.Здесь мы предполагаем, что устройство защищено паролем с полным шифрованием диска. Очень распространенная ошибка, когда украденные ноутбуки моделируются как потеря конфиденциальности, но не как соответствующая потеря доступности. Помните, что организация потеряла возможность использовать актив. Доступность должна быть указана в затронутых атрибутах. Описание инцидентаАктёр: InternalМотив: N / A Актерское разнообразие: Конечный пользователь Действие: ошибкаРазнообразие действий: неправильная доставка Вектор: неадекватные процессы АктивРазновидность: M — Документы Собственность: Жертва Атрибут: конфиденциальность.Раскрытие данных: Да Примечания: Документы были отправлены не тому получателю из-за ошибки нечеткости ОбоснованиеПредполагается, что субъект в этом примере является типичным «конечным пользователем», но также может быть любым другим инсайдером или партнером.Вариант действия — просто «Неправильная доставка» в категории «Ошибка», а разновидность актива — «M — Документы», который можно легко изменить для резервного копирования лент или любого другого автономного ресурса, который может быть отправлен по почте. Если электронная почта или «электронные» копии документов доставлены по ошибке, актив, скорее всего, будет «U-Desktop» или «U-Laptop», поскольку пользователь, скорее всего, составил электронную почту и / или прикрепленные документы, хранящиеся на таких устройствах. Естественно, это также может повлиять на другие разновидности устройств и серверов конечных пользователей; все зависит от того, где были данные до того, как они были доставлены по ошибке. С точки зрения атрибутов, неправильная доставка всегда ставит под угрозу Конфиденциальность актива из-за потери владения или контроля. В этом случае мы предполагаем, что конверт, содержащий документы, был открыт, и получатель затем связался с организацией, чтобы сообщить им о путанице. Это должно быть помечено как «Да» для раскрытия данных, даже если никто, кроме этого человека, не видел это, и он / она никогда не делал с этим ничего злонамеренного (т.е., документы все же были просмотрены посторонним лицом). Вариантом этого может быть отправка зашифрованных резервных копий на неправильный адрес; если нет убедительных доказательств обратного, мы отметим «Нет» в отношении раскрытия данных в этом сценарии. Часто неправильно доставленные документы сохраняются в электронном виде, и поэтому организация-жертва не лишается возможности пользоваться активом. Если, однако, активы или данные не могут быть восстановлены, целесообразно включить доступность в качестве затронутого атрибута. Вывод JSON Пример классификации: ошибка публикацииОшибка публикации — это тип ошибки, при которой субъект размещает закрытые данные на общедоступном форуме, таком как веб-сайт или газета.Обычно это ошибка, связанная с тем, что закрытые данные на сервере случайно помещаются в папку, обслуживаемую программным обеспечением веб-сервера. Описание инцидентаАктёр: InternalМотив: N / A Актерское разнообразие: Конечный пользователь Действие: ошибкаВариант действия: ошибка публикации Вектор: неадекватные процессы АктивВариант: S — Веб-приложение Собственность: Жертва Атрибут: конфиденциальность.Раскрытие данных: Да Метод обнаружения: внешняя несвязанная сторонаОбоснованиеПредполагается, что субъект в этом примере является типичным «конечным пользователем», но также может быть любым другим инсайдером или партнером.Вариантом действия является просто «Ошибка публикации» в категории «Ошибка», а в данном примере набором ресурсов является веб-сервер. Мотив — NA для ошибок, потому что субъект не намеревался, чтобы что-то произошло. С точки зрения атрибутов, неправильная доставка всегда ставит под угрозу Конфиденциальность актива из-за потери владения или контроля. Однако не всегда факт раскрытия данных имел место. В этом примере об ошибке публикации сообщила внешняя несвязанная сторона, что означает, что для раскрытия данных должно быть установлено значение «Да», поскольку мы знаем, что по крайней мере одно неавторизованное лицо видел неправильно опубликованные данные.Однако, если ошибка была обнаружена внутри, и нет никаких конкретных доказательств того, что документ был просмотрен неавторизованными лицами, тогда для этого можно установить значение «Потенциально». Вектор ошибки публикации — это неадекватный процесс в этом примере, хотя вектор часто неизвестен. Неадекватный процесс был бы подходящим выбором, если бы не было механизма проверки, чтобы гарантировать, что публикуются только авторизованные данные. Вывод JSON Пример классификации: злоупотребление электронной почтойДовольно часто можно увидеть, как сотрудники злоупотребляют электронной почтой, нарушая конфиденциальность личных данных организации.Один из распространенных примеров — когда пользователь отправляет конфиденциальный документ в личную учетную запись электронной почты, чтобы поработать над ним из дома. Эта ситуация может сбивать с толку, потому что есть несколько вариантов действий, которые могут описать это, и есть хороший аргумент в пользу более чем одного затронутого актива. При кодировании инцидента, в котором есть только одно действие, лучше всего найти единственный наиболее подходящий вариант. Например, если сотрудник использует корпоративную электронную почту в личных целях или для отправки рабочих документов на личную учетную запись электронной почты вопреки политике, то это пример неправильного использования: неправильное использование электронной почты.Похожий сценарий заключается в том, что сотрудник загружает конфиденциальные документы в такую службу, как Dropbox, что не является злоупотреблением электронной почтой, а является неправильным использованием: использование неутвержденного программного обеспечения. Обычно инцидент не включает в себя как злоупотребление электронной почтой, так и использование неутвержденного программного обеспечения, если выполняется только одно действие. Если в организации действует политика, которая требует, например, того, что все файлы, хранящиеся в некорпоративных системах, должны быть зашифрованы, включите «неправильное использование электронной почты» ИЛИ «несанкционированное программное обеспечение» И неправильное использование: неправильное обращение с данными. Во всех этих случаях затронутым активом является рабочая станция, которую пользователь использует для загрузки или отправки документов по электронной почте. Если только сам почтовый сервер не скомпрометирован, его нельзя указывать среди затронутых ресурсов. Описание инцидентаАктёр: InternalМотив: удобство Актерское разнообразие: Конечный пользователь Действие: неправильное использованиеРазнообразие действий: неправильное использование электронной почты Вектор: доступ к локальной сети АктивВариант: U — Настольный Собственность: Жертва Атрибут: конфиденциальность, доступность.Раскрытие данных: потенциально Вывод JSON Классификация: определение с примерамиВ риторике и композиции классификация — это метод разработки абзацев или эссе, в котором писатель объединяет людей, предметы или идеи с общими характеристиками в классы или группы.Классификационное эссе часто включает примеры и другие вспомогательные детали, которые организованы по типам, видам, сегментам, категориям или частям целого. Замечания по классификации«Основная поддержка в классификации состоит из категорий, которые служат цели классификации … Категории в классификации — это« стопки », по которым писатель сортирует тему (элементы, подлежащие классификации). Эти категории станут темой предложения для основных абзацев эссе… Вспомогательные детали классификации — это примеры или объяснения того, что входит в каждую категорию. Примерами классификации являются различные предметы, попадающие в каждую категорию. Они важны, потому что читатели могут не быть знакомы с вашими категориями ». — Из« Настоящих эссе с чтением »Сьюзан Анкер Использование классификации во вводном абзаце«Американцев можно разделить на три группы: курильщики, некурящие и все увеличивающееся количество бросивших курить.Те, кто никогда не курил, не знают, чего им не хватает, но бывшие курильщики, бывшие курильщики, исправившиеся курильщики никогда не смогут этого забыть. Мы — ветераны личной войны, которую связывает переломный момент — бросить курить и соблазн выкурить еще одну сигарету. Почти для всех из нас, бывших курильщиков, курение продолжает играть важную роль в нашей жизни. И теперь, когда это ограничено в ресторанах по всей стране и будет запрещено почти во всех закрытых общественных местах в штате Нью-Йорк, начиная со следующего месяца, жизненно важно, чтобы все понимали различные эмоциональные состояния, которые может вызвать прекращение курения.Я наблюдал четыре из них; и в интересах науки я классифицировал их как фанатиков, евангелистов, избранных и безмятежных. Каждый день каждая категория набирает новых сотрудников ». — Из« Признаний бывшего курильщика »Франклина Зимринга Использование классификации для определения места«Каждый из четырех великих садов Ямайки, хотя и основан на схожих принципах, приобрел свою особую ауру. Сады Надежды, расположенные в самом сердце Кингстона, напоминают открыточные изображения общественных парков 1950-х годов, милые и смутно пригородные, наполненные знакомыми фаворитами — лантана и бархатцы, а также экзотика.Баня сохранила свой характер Старого Света; его легче всего вызвать, как он, должно быть, выглядел во времена Блая. Хина облаков потусторонняя. А Каслтон, сад, созданный вместо Бата, на мгновение напоминает о том золотом веке ямайского туризма, когда посетители прибывали на своих яхтах — эпоху Яна Флеминга и Ноэля Кауарда, до того, как коммерческие авиаперелеты выгружали простых смертных по всему острову ». —Из «Проклятых плодов хлеба капитана Блая» Кэролайн Александр Использование классификации для определения характера: пример 1«Местные телеинтервьюеры бывают двух видов.Один из них — блондин, страдающий булимией, с искривленной перегородкой и тяжелым когнитивным расстройством, который пошел на радиовещание, потому что был слишком эмоционально взволнован для работы по продажам по телефону. Другой вариант — учтивый, проницательный, чрезмерно квалифицированный для работы и слишком подавленный, чтобы с вами разговаривать. Хорошие местные телеведущие всегда в депрессии, потому что их поле очень многолюдно ». — Из« Книжного тура »П.Дж. О’Рурка Использование классификации для определения характера: Пример 2«Англоязычный мир можно разделить на (1) тех, кто не знает и не заботится о том, что такое раздвоенный инфинитив; (2) тех, кто не знает, но очень заботится; (3) тех, кто знает и осуждает; (4) ) те, кто знает и одобряет; (5) те, кто знает и различает.« — Из« Словаря современного использования »Х. В. Фаулера и Эрнеста Гауэрса Известные параграфы классификации и эссе для изученияИсточники
|
