Масса-К Производитель компании Мир Весов
«МАССА-К» — российский производитель электронной весовой техники
ЗАО «МАССА–К» основано в 1991 году на базе Государственного Института Метрологии им. Д.И.Менделеева. На протяжении 25-ти лет предприятие разрабатывает и производит электронные весы, которые применяются в различных областях торговли, медицины и промышленного хозяйства. Их надежность, высокое качество, простота эксплуатации и сервисное обслуживание пользуются неизменным спросов более чем в тридцати странах мира. Продукция компании «МАССА-К» имеет все необходимые сертификаты для использования в странах СНГ и европейского союза.
Компания «МАССА-К» производит торговые электронные весы, крановые, промышленные пандусные и паллетные, настольные, медицинские, лабораторные, счетные, товарные, а так же весы, печатающие этикетки. Торговые электронные весы «МАССА-К» широко применяются в технологических, торговых и учетных операциях для взвешивания в сферах общественного питания и торговли как штучного, так и весового товара, расчета его стоимости и фасовки. Все товарные настольные и напольные электронные весы имеют широкий температурный диапазон, повышенную точность и возможностью долгой и непрерывной работы от встроенного аккумулятора. Медицинские электронные весы «МАССА-К» используются в оздоровительных, медицинских и спортивных учреждениях для взвешивания людей. Лабораторные электронные весы применяются в научно-производственных лабораториях для измерений массы различных материалов и веществ. Вся продукция «МАССА-К» отличается высокой точностью, надёжностью, современным дизайном, многофункциональностью и конструкцией, основанной на цифровых датчиках взвешивания
Все товарные настольные и напольные электронные весы имеют широкий температурный диапазон, повышенную точность и возможностью долгой и непрерывной работы от встроенного аккумулятора. Медицинские электронные весы «МАССА-К» используются в оздоровительных, медицинских и спортивных учреждениях для взвешивания людей. Лабораторные электронные весы применяются в научно-производственных лабораториях для измерений массы различных материалов и веществ. Вся продукция «МАССА-К» отличается высокой точностью, надёжностью, современным дизайном, многофункциональностью и конструкцией, основанной на цифровых датчиках взвешивания
Продукция компании «МАССА-К» поставляется региональными представительствами как по всей России, так и в большинство стран дальнего и ближнего зарубежья. Авторизированный сервисный центр оказывает полную гарантийную и послегарантийную поддержку всей производимой продукции.
В интернет магазине компании «Мир Весов» продукция «МАССА-К» широко представлена лабораторными, техническими, счетными, пыле-водозащищенными весами, а так же торговыми весами-регистраторами с принтером этикеток и весами с термопечатью, стандартные платформенные весы, крановые и паллетные весы, а так же пандусные и балочные с различным НПВ. Кроме весов Вы можете приобрести калибровочные гири, опалубку (врезное исполнение), сканеры штрихкодов, кабели, индикаторы и различные терминалы к весам «МАССА-К».
Кроме весов Вы можете приобрести калибровочные гири, опалубку (врезное исполнение), сканеры штрихкодов, кабели, индикаторы и различные терминалы к весам «МАССА-К».
Запчасти для товарных весов Масса-К ТВ-М
Компания Zipstore.ru поставляет оптом и в розницу оригинальные запчасти к товарным весам Масса-К ТВ-М. Серия ТВ-М представлена электронными весами с широкими функциональными возможностями и современным программным обеспечением. Весовое оборудование Масса-К ТВ-М относится к III классу точности в соответствии с ГОСТ и имеет два варианта исполнения: без стойки и с вертикальной усиленной стойкой. В каталоге сайта Вы можете найти такие популярные комплектующие, как адаптер, амортизатор, кабель, индикатор, крышка, опора, тензодатчик и др.
Товарные электронные весы Масса-К ТВ-М помогут оптимизировать торговые, учетные и технологические операции. Весовое оборудование серии ТВ-М используется для взвешивания и фасовки товара в торговых точках, складских помещениях и на промышленных предприятиях. Наша компания предлагает широкий выбор запчастей для расширения функциональных возможностей, ремонта и замены комплектующих весов Масса-К ТВ- М.
Наша компания предлагает широкий выбор запчастей для расширения функциональных возможностей, ремонта и замены комплектующих весов Масса-К ТВ- М.
Каталог запчастей для весов Масса-К ТВ-М
В каталоге сайта представлен большой выбор оригинальных запчастей для товарных весов Масса-К серии ТВ- М. Комплектующие в каталоге могут иметь фотографию, краткое описание, каталожный номер, технические характеристики и список моделей весов, с которыми они совместимы.
Купить запчасти для весов Масса-К ТВ-М оптом и в розницу
Оформить заказ можно одним из следующих способов:
- отправить заявку по электронной почте [email protected]
- связаться с нашим менеджером при помощи формы обратной связи
- с помощью активной кнопки «Купить» в каталоге товаров или в конкретном товаре
- с помощью формы «Купить в 1 клик» в конкретном товаре
Мы осуществляем поставки во все города России, а также в Республику Беларусь, Казахстан и другие страны СНГ. Продажа запчастей осуществляется за наличный и безналичный расчет. На сайте указаны розничные цены в рублях и долларах, с учетом НДС. Узнать оптовые цены на запчасти можно, отправив нам запрос по электронной почте. Подробнее о способах доставки и оплаты Вы можете узнать в разделе сайта «Оплата и доставка». Наиболее выгодные предложения и скидки размещены в разделе «%Скидки и акции».
Продажа запчастей осуществляется за наличный и безналичный расчет. На сайте указаны розничные цены в рублях и долларах, с учетом НДС. Узнать оптовые цены на запчасти можно, отправив нам запрос по электронной почте. Подробнее о способах доставки и оплаты Вы можете узнать в разделе сайта «Оплата и доставка». Наиболее выгодные предложения и скидки размещены в разделе «%Скидки и акции».
Техподдержка
На сайте работает раздел «Инструкции и программы для весов» где вы можете найти информацию технического характера. На нашем форуме Вы можете получить консультацию по обслуживанию, эксплуатации, установке, ремонту или замене комплектующих для весов Масса-К ТВ-М, а также запросить сертификаты и подробные технические характеристики.
Ремонт весов Масса-К ТВ-М
Вы можете к нам обратиться, чтобы произвести ремонт, диагностику и профилактическое обслуживание товарных весов Масса-К ТВ-М. На нашем складе всегда в наличие ходовые запчасти, что обеспечивает замену комплектующих и ремонт в кратчайшие сроки.
Молярная масса — что это? Как рассчитать? Формулы и примеры
Что такое моль
Прежде чем говорить о том, как найти молярную массу вещества, определимся с понятием «моль». Его ввели как искусственную величину для упрощения расчетов. Это количество вещества, в котором содержится столько же мельчайших частиц, сколько в 12 г одного из изотопов углерода — C12.
Для всех химических веществ это количество одинаково и представляет собой число Авогадро 6,02 · 1023. Постоянная Авогадро обозначается NA, а измеряется в моль-1.
Число Авогадро — это количество молекул, ионов или других мельчайших частиц в 1 моле вещества.
NA = 6,02 · 1023 моль-1.
Историческая справка
В 1811 году химик Амедео Авогадро предположил, что если взять два равных объема газов в равных значимых условиях (при одинаковой температуре и давлении), то количество молекул в этих объемах тоже будет одинаковым.
Что такое молярная масса
Молярная масса — это масса одного моля вещества, она измеряется в граммах деленных на моль (г/моль). Данная величина представляет собой отношение массы вещества к его количеству, которое измеряется в молях.
Как обозначается молярная масса: М.
, где — это масса вещества, а — количество вещества.
Единица измерения молярной массы: г/моль.
Запоминаем!
Правильно говорить именно молярная, а не мольная масса.
Несмотря на то, что в 1 моле любого химического вещества содержится одинаковое количество молекул (и оно равно числу Авогадро), молярные массы разных веществ отличаются.
Как определить молярную массу
Данная величина тесно связана с такими понятиями, как относительные атомная и молекулярная массы. Именно относительные, потому что абсолютную массу молекулы или атома вещества в химии не используют для решения задач — это слишком малые величины.
Относительная атомная масса вещества (Ar) показывает, во сколько раз его атом больше 1/12 атома углерода. Это значение для каждого химического элемента можно увидеть в таблице Менделеева.

, где — это количество атомов.
Разберемся на примерах.
В молекуле хлорида натрия NaCl есть 1 атом натрия и 1 атом хлора, при этом Ar(Na) = 23, Ar (Cl) = 35,5.
Mr(NaCl) = 23 + 35,5 = 58,5.
В молекуле NaNO2 есть 1 атом натрия, 1 атом азота и 2 атома кислорода.
Ar(Na) = 23, Ar(N) = 14, Ar(O) = 16.
Mr(NaNO2) = 23 + 14 + 16 · 2 = 69.
Собственно, для вычисления молярной массы больше ничего и не требуется.
Важно
Молярная масса вещества численно равна относительной молекулярной массе. Но путать эти два понятия не стоит — у них разный физический смысл. Молярная масса характеризует 1 моль, а относительная молекулярная — 1 молекулу.
Количество вещества
Из предыдущих формул понятно, что молярная масса и количество вещества тесно связаны. Рассмотрим эту связь подробнее. Начнем с того, что количество вещества может обозначаться как латинской буквой , так и греческой буквой (ню). Международное обозначение — , но не стоит удивляться, встретив в формулах любую из этих букв.
Рассмотрим эту связь подробнее. Начнем с того, что количество вещества может обозначаться как латинской буквой , так и греческой буквой (ню). Международное обозначение — , но не стоит удивляться, встретив в формулах любую из этих букв.
В формуле нахождения молярной массы мы обозначили количество вещества через :
, следовательно .
Пользуясь этим, можно найти количество вещества (в молях), если нам известны его абсолютная и молярная масса.
Пример 1
Как определить, какое количество вещества включают 350 г сульфата бария BaSO4?
Воспользуемся формулой .
Мы помним, что M = Mr (значение молярной массы равно значению относительной молекулярной).
Mr(BaSO4) = Ar(Ba) + Ar(S) + Ar(O) · 4 = 137 + 32 + 16 · 4 = 233.
М(BaSO4) = Mr(BaSO4) = 233 г/моль.
Подставим значение молярной массы в формулу:
моль.
Есть и еще одна формула количества вещества, которая позволяет найти его, если известно число молекул или других структурных единиц.
, где — число структурных единиц, — число Авогадро.
Пример 2
Допустим, некий объем CaCO3 содержит 3,01 · 1023 молекул. Как найти количество вещества, соответствующее данному объему?
Воспользуемся формулой моль.
Молярный объем
Выше мы находили количество вещества через молярную массу, но для газов это можно сделать и через молярный объем. Согласно закону Авогадро количество любого газа, равное 1 моль, будет занимать один и тот же объем, если газы рассматриваются при одинаковой температуре и давлении.
При стандартных физических условиях — температуре 0°С и давлении 1 атм или 760 мм ртутного столба, 1 моль газа занимает объем 22,4 л.
Молярный объем — это объем газа, взятого в количестве 1 моль. Он обозначается Vm.
При нормальных условиях Vm = 22,4 л/моль.
Значения молярного и фактического объема газа помогают найти количество вещества.
, где — фактический объем газа, а — молярный объем.
Пример 1
Сколько молей содержится в 120 литрах газа при нормальных условиях?
Рассчитаем по формуле моль.
Ответ: 120 литров любого газа при стандартных условиях содержат 5,36 моль.
Относительная плотность одного газа по другому
Иногда для решения задачи нужно знать, как найти молярную массу газа, о котором сообщается лишь его плотность по воздуху или по другому газу. Это возможно, если знать формулу относительной плотности, которая обозначается буквой D.
, где и — некие газы.
Пример 1
Как определить, во сколько раз угарный газ плотнее водорода?
Для начала найдем молярную массу CO и H2:
М(CO) = Mr(CO) = Ar(C) + Ar(O) = 12 + 16 = 28.
М(H) = Mr(H2) = 2 · Ar(H) = 2 · 1 = 2.
.
Ответ: угарный газ в 14 раз плотнее водорода.
Пример 2
Как посчитать молярную массу газа х, о котором известно, что он в 10 раз плотнее углекислого газа CO2?
Подсчитаем для начала молярную массу углекислого газа:
M(CO2) = Mr(CO2) = 12 + 2 · 16 = 44.
Ориентируясь на формулу относительной плотности, произведем расчет молярной массы искомого газа х.
М(х) = D(х/CO2) · M(CO2) = 10 · 44 = 440 г/моль.
Ответ: у данного газа молярная масса 440 г/моль.
Примеры задач
Итак, мы разобрались, как находить молярную массу жидкости, газа или твердого тела и как это понятие связано с количеством вещества, а также с относительной плотностью одного газа по другому. Чтобы закрепить знания, посмотрите, как эти сведения применяются в решении задач.
Задача 1
Известно, что 300 г неустановленного вещества содержат 12,04 · 1023 молекул. Чему равна молярная масса данного вещества?
Дано:
N(х) = 12,04 · 1023.
m(х) = 300 г.
M(х) = ?
Решение:
Найдем количество вещества моль.
Подставим количество вещества в формулу :
г/моль.
Ответ: молярная масса данного вещества 150 г/моль.
Задача 2
Какой объем займет водород в количестве 0,7 моль?
Дано:
моль.
Решение:
По формуле мы можем найти объем .
Зная, что молярный объем при обычных условиях составляет 22,4 л/моль, вычислим фактический объем водорода:
л.
Ответ: объем водорода составляет 15,68 литров.
Задача 3
В порции оксида серы SO3 содержится 8,356 · 1023 атомов кислорода. Какова масса этой порции?
Дано:
N(O) = 8,356 · 1023.
m(SO3) = ?
Решение:
Для решения задачи нам подходит формула , т. е. . Но для начала нужно найти количество вещества.
Мы знаем, что в одной молекуле SO3 есть 3 атома кислорода, исходя из этого можно вычислить количество молекул в порции оксида:
, следовательно .
Зная количество молекул, рассчитаем количество вещества:
моль.
Теперь можно узнать молярную массу SO3:
M(SO3) = 32 + 16 · 3 = 80 г/моль.
Рассчитаем фактическую массу через молярную массу:
г.
Ответ: абсолютная масса порции оксида серы 36,8 грамм.
Задача 4
Как рассчитать молярную массу простого вещества, о котором известно, что в порции 100 г содержится 15,05 · 1023 молекул? Назовите это вещество.
Дано:
m(x) = 100 г.
N(x) = 15,05 · 1023.
М(х) = ?
Решение:
В данном случае поможет вычислить молярную массу NA, с помощью которого мы сначала узнаем количество вещества:
моль.
Исходя из этого, рассчитаем молярную массу:
г/моль.
Ответ: согласно таблице Менделеева можно предположить, что это кальций Ca.
Задача 5
Определите, насколько сероводород H2S плотнее водорода H2?
Решение:
Нам требуется вычислить относительную плотность сероводорода по водороду:
.
Для этого вычислим молярные массы H2S и H2:
М(H2S) = 1 · 2 + 32 = 34 г/моль.
М(H2) = 1 · 2 = 2 г/моль.
Подставим значения в формулу:
.
Ответ: сероводород в 17 раз плотнее водорода.
Вопросы для самопроверки
Что такое число Авогадро и чему оно равно?
В чем измеряется молярная масса?
Напишите формулу молярной массы вещества.
Какая формула связывает количество вещества и его объем?
Как узнать количество вещества, если известно число молекул в порции?
Массам непонятно — Маяковский.
 Полный текст стихотворения — Массам непонятно
Полный текст стихотворения — Массам непонятноМежду писателем
и читателем
стоят посредники,
и вкус
у посредника
самый средненький.
Этаких
средненьких
из посреднической рати
тыща
и в критиках
и в редакторате.
Куда бы
мысль твоя
ни скакала,
этот
все
озирает сонно:
— Я
человек
другого закала.
Помню, как сейчас,
в стихах
у Надсо̀на…
Рабочий
не любит
строчек коротеньких.
А еще
посредников
кроет Асеев.
А знаки препинания?
Точка —
как родинка.
Вы
стих украшаете,
точки рассеяв.
Товарищ Маяковский,
писали б ямбом,
двугривенный
на строчку
прибавил вам бы. —
Расскажет
несколько
средневековых легенд,
объяснение
часа на четыре затянет,
и ко всему
присказывает
унылый интеллигент:
— Вас
не понимают
рабочие и крестьяне. —
—
Сникает
автор
от сознания вины.
А этот самый
критик влиятельный
крестьянина
видел
только до войны,
при покупке
на даче
ножки телятины.
А рабочих
и того менее —
случайно
двух
во время наводнения.
Глядели
с моста
на места и картины,
на разлив,
на плывущие льдины.
Критик
обошел умиленно
двух представителей
из десяти миллионов.
Ничего особенного —
руки и груди…
Люди — как люди!
А вечером
за чаем
сидел и хвастал:
— Я вот
знаю
рабочий класс-то.
Я
душу
прочел
за их молчанием —
ни упадка,
ни отчаяния.
Кто может
читаться
в этаком классе?
Только Гоголь,
только классик.
А крестьянство?
Тоже.
Никак не иначе.
Как сейчас, помню —
весною, на даче… —
Этакие разговорчики
у литераторов
у нас
часто
заменяют
знание масс.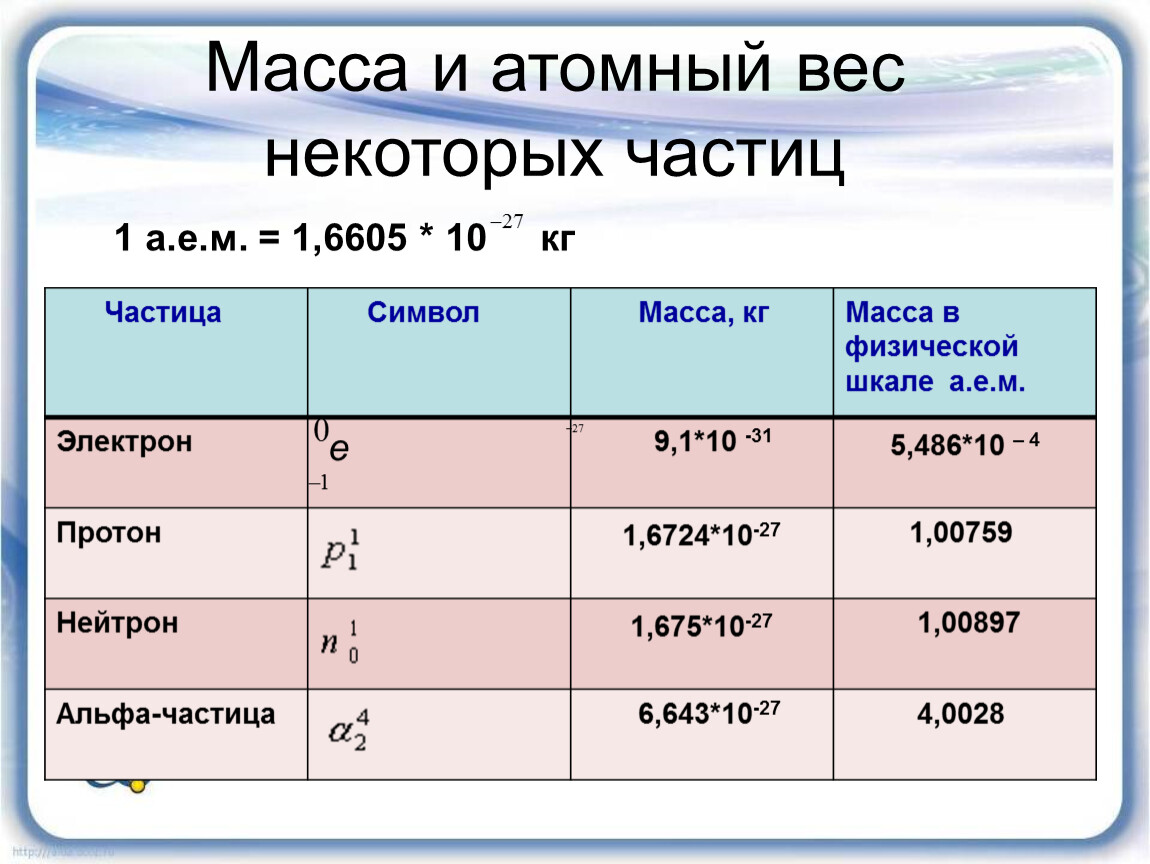
И идут
дореволюционного образца
творения слова,
кисти
и резца.
И в массу
плывет
интеллигентский дар —
грезы,
розы
и звон гитар.
Прошу
писателей,
с перепугу бледных,
бросить
высюсюкивать
стихи для бедных.
Понимает
ведущий класс
и искусство
не хуже вас.
Культуру
высокую
в массы двигай!
Такую,
как и прочим.
Нужна
и понятна
хорошая книга —
и вам,
и мне,
и крестьянам,
и рабочим.
1927 г.
Масса, относительные массы, молярная масса, массовые доли — урок. Химия, 8–9 класс.
Особенности применения физической величины «масса»
Масса обозначается буквой m и измеряется в граммах, килограммах или миллиграммах.
Пример:
m(h3SO4)= \(98\) г — масса серной кислоты равна \(98\) г.
Обрати внимание!
Связь между единицами измерения массы:
\(1\) кг \(=\) \(1000\) г, \(1\) г \(= 1000\) мг, \(1\) г \(= 0,001\) кг, \(1\) мг \(= 0,001\) г.
Массу атомов и молекул тоже можно выражать в граммах, килограммах или миллиграммах.
Пример:
масса одного атома серы:
ma(S)= 5,312⋅10−23 г.
Масса одной молекулы серной кислоты:
mm(h3SO4)= 1,627⋅10−22 г.
Это очень маленькие числа, которыми пользоваться неудобно. Поэтому для характеристики масс атомов и молекул введена атомная единица массы.
Атомная единица массы (а. е. м.) — 112 часть массы атома углерода. Её международное обозначение — u («unit»).
\(1\) u \(= 1\) а. е. м. \(=\) 1,66⋅10−24 г \(=\) 1,66⋅10−27 кг.
В атомных единицах массы атомов и молекул равны небольшим целым числам.
Пример:
ma(S)= \(32\) а. е. м. \(= 32\) u,
е. м. \(= 32\) u,
mm(h3SO4)= \(98\) а. е. м. \(= 98\) u.
Относительные массы
Применяются также относительные массы. Эти величины показывают, во сколько раз масса атома или молекулы больше одной атомной единицы массы.
Относительная атомная масса Ar — это отношение массы атома к \(1\) атомной единице массы. Величина безразмерная.
Пример:
Ar(S)= \(32\).
Относительная молекулярная масса Mr — это отношение массы молекулы к \(1\) атомной единице массы. Величина безразмерная.
Пример:
Mr(h3SO4)= \(98\).
Молярная масса
В расчётах используется также понятие «молярная масса».
Молярная масса численно равна массе \(1\) моль вещества. Она обозначается буквой M и измеряется в г/моль.
Пример:
M(h3SO4)= \(98\) г/моль.
Массовые доли
Массовая доля — это отношение массы компонента к массе образца вещества, в котором он содержится. Вычисляют массовую долю химического элемента в веществе, вещества в смеси, растворённого вещества в растворе, примесей и т. д.
Вычисляют массовую долю химического элемента в веществе, вещества в смеси, растворённого вещества в растворе, примесей и т. д.
Массовая доля обозначается буквой w. Это безразмерная величина. Может вычисляться также в %.
| 06 фев 2022 | Творог 5% ( короб 20кг) | 175 руб / кг | Москва | ООО «РЕСУРС МАРКЕТ» |
| 06 фев 2022 | Творог 9 | от 195 руб / кг | Москва | ООО «РЕСУРС МАРКЕТ» |
| 06 фев 2022 | Творожный продукт 20 | от 89.00 руб / кг | Москва | ООО «РЕСУРС МАРКЕТ» |
| 06 фев 2022 | Творог 5% ГОСТ | от 185 руб / кг | Москва | ООО «РЕСУРС МАРКЕТ» |
| 06 фев 2022 | Творог (ГОСТ) 5%, 9%, 18%, 29 | от 175 руб / кг | Москва | ООО «РЕСУРС МАРКЕТ» |
| 06 фев 2022 | Творог 200 г | 46. 00 руб / шт 00 руб / шт | Москва | ООО ТД «МОЛГРАДЪ» |
| 06 фев 2022 | Творожный продукт 9%, 18%, 23%,Творог ГОСТ | 98.50 руб / кг | Москва | ООО ТД «МОЛГРАДЪ» |
| 06 фев 2022 | Творог | от 185 руб / кг | Москва | ООО «МИЛКО» |
| 06 фев 2022 | Мягкий творожный продукт «Твороговск» 500 грамм | 50.00 руб / шт | Нижний Новгород | ООО «КМП» |
| 06 фев 2022 | Альбумин молочный без ЗМЖ замороженный | 30.00 руб / кг. | Нижний Новгород | ООО «КМП» |
| 06 фев 2022 | Творог 5%, 9%, 18%, творог из козьего молока | от 206 руб / кг | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД ПРИНЕВ. .. .. |
| 06 фев 2022 | Творог обезжиренный и жирный. Нижний Новгород | от 267 руб / кг | Нижний Новгород | ИП Бехтерев Дмитрий Васильевич |
| 06 фев 2022 | Творог «Световеж» 9 | 185 руб / кг | Липецк | ООО «СВЕТОВЕЖ» |
| 06 фев 2022 | Творог Световеж 5 | 175 руб / кг | Липецк | ООО «СВЕТОВЕЖ» |
| 06 фев 2022 | Творожный продукт «Световеж». Термостабильный | 87.00 руб / кг | Липецк | ООО «СВЕТОВЕЖ» |
| 06 фев 2022 | Творог ГОСТ 5%, 9%, 0 | от 230 руб / кг | Москва | Татьяна |
| 06 фев 2022 | Творог обезжиренный (не более 1,8%), 5%, 9 % ТОЛЬКО ГОСТ | 199 руб / кг | Суздаль | ООО «СМЗ» |
| 06 фев 2022 | Продаём творог ГОСТ, ж. 5 5 | 175 руб / кг | Санкт-Петербург | ООО «ПК ЭСТИНА» |
| 06 фев 2022 | Продаем молочную продукцию собственного производства | 115 руб / кг | Санкт-Петербург | ООО «ПК ЭСТИНА» |
| 06 фев 2022 | Творог ГОСТ 1,8%,5%,9%,18%, творог ТУ, творожный продукт 18%,23% от производителя | от 65.00 руб / кг | Нижний Новгород | ООО «ЗАСНЕЖЕННАЯ РУСЬ» |
| 06 фев 2022 | Творожный продукт 18%,23 | 64.00 руб / кг | Нижний Новгород | ООО «ЗАСНЕЖЕННАЯ РУСЬ» |
| 06 фев 2022 | Творог ГОСТ 1,8%,5%,9%,18%, творог ТУ от производителя | 125 руб / кг | Нижний Новгород | ООО «ЗАСНЕЖЕННАЯ РУСЬ» |
| 06 фев 2022 | Творожная масса, короб 5 кг. , С Курагой, изюм, чернослив, клубника, ванилин, вишня, с орехом и вар. сгущенкой , С Курагой, изюм, чернослив, клубника, ванилин, вишня, с орехом и вар. сгущенкой | 22.00 руб / кг | Александров | Дмитрий |
| 06 фев 2022 | Творог 100%, ПРЕМИУМ, ГОСТ, 9% и 18%, МЕРКУРИЙ, короб 5 кг, ведро 5 кг, пачка 200 г | 185 руб / кг | Александров | Дмитрий |
| 06 фев 2022 | Творожный продукт, короб 5 кг, ведро 3,5,10 кг, 9%, 18 | 89.00 руб / кг | Александров | Дмитрий |
| 06 фев 2022 | Творог, 9% и 18%, ГОСТ, МЕРКУРИЙ, короб 5 кг, пачка 200 г, Эконом | 33.00 руб / кг | Александров | Дмитрий |
| 06 фев 2022 | Сырки глазированные с длительным сроком хранения 120 суток, все регионы РФ и СНГ | от 6.00 руб / шт | Москва | ООО «МЕГАМОЛПРОД» |
| 06 фев 2022 | Творог обезжиренный | 150 руб / кг | Смоленск | ООО «ЛАКТИС» |
| 06 фев 2022 | Творог ГОСТ пластовой на марле 18 | 210 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Творог ГОСТ пластовой на марле 9 | 195 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Творог ГОСТ пластовой на марле 5 | 185 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Масса творожная с цукатами БЗМЖ | 195 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Масса творожная с курагой БЗМЖ | 195 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Масса творожная с изюмом БЗМЖ | 195 руб / кг | Санкт-Петербург | Сергей |
| 06 фев 2022 | Творог | Нижний Новгород | Андрей Юрьевич | |
| 06 фев 2022 | Творого домашний | 80. 00 руб / 500 гр 00 руб / 500 гр | Уфа | ГКФХ Багаутдинов Ильдус Рау… |
| 05 фев 2022 | Творог | 300 руб / кг | Алексеевка | ГКФХ Плешков Дмитрий Никола… |
| 05 фев 2022 | Товрог м.д.ж. 9% ГОСТ | 260 руб / кг | Москва | ИП Козлов Евгений Николаевич |
| 05 фев 2022 | Натуральный творог | Чебоксары | Светлана | |
| 05 фев 2022 | ТВОРОГ ГОСТ | от 185 руб / кг | Москва | ООО «КУРЬЯНОВСКИЙ МОЛОЧНЫЙ … |
| 05 фев 2022 | Творог замороженный для дальнейшей переработки | от 130 руб / кг | Москва | ООО «КУРЬЯНОВСКИЙ МОЛОЧНЫЙ … |
| 05 фев 2022 | Творог Классический 9 | Москва | ООО «КУРЬЯНОВСКИЙ МОЛОЧНЫЙ . .. .. | |
| 05 фев 2022 | Творог мягкий оптом производство под торговой маркой | Москва | ООО «НВС» | |
| 04 фев 2022 | Продукт творожный СЗМЖ | Новосибирск | ООО «ПРОМПРОДУКТ» | |
| 04 фев 2022 | Творог 9% в коробах по 10 кг (охлажденный и замороженный) | 237 руб / кг | Серебряные Пруды | АО АИСФЕР |
| 04 фев 2022 | Творог 12% в коробах по 10 кг (охлажденный и замороженный) | 280 руб / кг | Серебряные Пруды | АО АИСФЕР |
| 04 фев 2022 | Творог 12% 400г (без сычужного фермента) | Серебряные Пруды | АО АИСФЕР | |
| 04 фев 2022 | Творог 9% 400г (без сычужного фермента) | Серебряные Пруды | АО АИСФЕР | |
| 04 фев 2022 | Творог ГОСТ | от 160 руб / кг | Москва | ООО «НОРМОЛТОРГ» |
| 04 фев 2022 | Масса творожная | 82. 00 руб / кг 00 руб / кг | Москва | ООО «НОРМОЛТОРГ» |
| 04 фев 2022 | Сырки глазированные | 5.40 руб / шт | Москва | ООО «НОРМОЛТОРГ» |
| 04 фев 2022 | Творжная масса | 22.00 руб / шт | Москва | ООО «НОРМОЛТОРГ» |
| 04 фев 2022 | Творог, творожный продукт | от 70.00 руб / кг | Москва | ООО «НОРМОЛТОРГ» |
| 04 фев 2022 | ТВОРОГ 9/18 | 260 руб / кг | Москва | Лилия |
| 04 фев 2022 | Творожный продукт «Деревенский», 18% м.д.ж | от 104 руб / кг | Новосибирск | ООО «МОЛКОМБИНАТ КОЧЕНЕВСКИЙ» |
| 04 фев 2022 | Творожная паста и масса в ассортименте | от 96. 00 руб / кг 00 руб / кг | Новосибирск | ООО «МОЛКОМБИНАТ КОЧЕНЕВСКИЙ» |
| 04 фев 2022 | Творожный продукт 18% м. д. ж. «Термостабильный» | 112.80 руб / кг | Казань | ООО «СИНЕРГИЯ УСПЕХА» |
| 04 фев 2022 | Творожный продукт 18%, «Термостабильный» | 117.60 руб / кг | Казань | ООО «СИНЕРГИЯ УСПЕХА» |
| 04 фев 2022 | Масса творожная | от 99.00 руб / кг | Новосибирск | ООО «ДОБРЫЕ ТРАДИЦИИ» |
| 04 фев 2022 | Творог ГОСТ | от 169 руб / кг | Новосибирск | ООО «ДОБРЫЕ ТРАДИЦИИ» |
| 04 фев 2022 | Творожный продукт | от 88.00 руб / кг | Новосибирск | ООО «ДОБРЫЕ ТРАДИЦИИ» |
| 04 фев 2022 | Паста творожная | 89. 00 руб / кг 00 руб / кг | Новосибирск | ООО «ДОБРЫЕ ТРАДИЦИИ» |
| 04 фев 2022 | Творог ГОСТ 5%,9% зерновой/пастообразный | 179 руб / кг | Санкт-Петербург | ООО «ТОРГОВЫЙ ДОМ «МИЛБЛАГОДА» |
| 04 фев 2022 | Масса, паста творожная | Новосибирск | Ирина | |
| 04 фев 2022 | Творог, творожный продукт | Новосибирск | Ирина | |
| 04 фев 2022 | Творог «Домашний» 9% ведро 5 кг | 142 руб / кг | Волгоград | ИП Парфенов Андрей Игорьевич |
| 04 фев 2022 | Творожная масса | 103 руб / кг | Красный Сулин | ООО «ЮГ ХОЛДИНГ» |
| 04 фев 2022 | Творожный продукт | 95. 00 руб / кг 00 руб / кг | Красный Сулин | ООО «ЮГ ХОЛДИНГ» |
| 04 фев 2022 | Творог ГОСТ | 240 руб / кг | Красный Сулин | ООО «ЮГ ХОЛДИНГ» |
| 03 фев 2022 | Творог зерненый сухой и в сливках | Калуга | ООО ТД «БЕЛТРЕЙД» | |
| 03 фев 2022 | Творог замороженный | от 180 руб / кг | Калуга | ООО ТД «БЕЛТРЕЙД» |
| 03 фев 2022 | Творог 0% 5% 9 | от 180 руб / кг | Калуга | ООО ТД «БЕЛТРЕЙД» |
| 03 фев 2022 | Творожный продукт оптом | от 110 руб / кг | Калуга | ООО ТД «БЕЛТРЕЙД» |
| 03 фев 2022 | Творог ГОСТ 5 | 150 руб / кг | Великие Луки | ООО «АГРОПРОМЫШЛЕННЫЙ КОМПЛ. .. .. |
| 02 фев 2022 | Творожный продукт, рассыпчатый, термостабильный 18-32% жирности от Производителя | 85.00 руб / кг | Москва | ООО «МИЛКТРИ» |
| 02 фев 2022 | Молочные продукты | Можайск | ЗАО ЗСМ «МОЖАЙСКИЙ» | |
| 02 фев 2022 | Творог замороженный ГОСТ | Можайск | ЗАО ЗСМ «МОЖАЙСКИЙ» | |
| 02 фев 2022 | Творог, масло сливочное | Можайск | ЗАО ЗСМ «МОЖАЙСКИЙ» | |
| 02 фев 2022 | Творог натуральный 5% ГОСТ | Можайск | ЗАО ЗСМ «МОЖАЙСКИЙ» | |
| 02 фев 2022 | Увеличение выхода творога (100%) по технологии Семаргл | Химки | ООО «СЕМАРГЛ» | |
| 02 фев 2022 | Творожный продукт «Крестьянский» | от 120 руб / кг | Новосибирск | ООО ТПК «ЯСНА» |
| 02 фев 2022 | Творожная масса | от 116 руб / кг | Новосибирск | ООО ТПК «ЯСНА» |
| 02 фев 2022 | Творожная паста | от 110 руб / кг | Новосибирск | ООО ТПК «ЯСНА» |
| 02 фев 2022 | Творожный продукт «Крестьянский» 18% фасованный | от 120 руб / кг | Новосибирск | ООО ТПК «ЯСНА» |
| 02 фев 2022 | Творог 0%5% 9% ГОСТ Беларусь короб 20 кг | 149 руб / кг. | Москва | Дмитрий Анатольевич |
| 02 фев 2022 | Творог ГОСТ 5 | 155 руб / кг | Санкт-Петербург | ООО «ЛАКШМИЛК» |
| 02 фев 2022 | Творог ГОСТ 9 | 165 руб / кг | Санкт-Петербург | ООО «ЛАКШМИЛК» |
| 02 фев 2022 | Творог 9% для социального питания | 135 руб / кг | Санкт-Петербург | ООО «ЛАКШМИЛК» |
| 02 фев 2022 | Творог 5, 9 % МДЖ | 175 руб / кг | Санкт-Петербург | Алексей |
| 02 фев 2022 | Творог ГОСТ 9 | Самара | ИП Марисов Денис Михайлович | |
| 02 фев 2022 | Творог обезжиренный натуральный замороженный, короб 20 кг, ОПТ | 110 руб / кг | Ижевск | ООО «Площадка Ш» |
| 01 фев 2022 | Сливочно-творожный продукт Бэллочиз, от производителя | от 165 руб / кг | Москва | ООО «БЭЛЛОЧИЗ» |
| 01 фев 2022 | Творог ГОСТ м. д.ж 18% и 9% термостабильный от производителя д.ж 18% и 9% термостабильный от производителя | от 155 руб / кг | Москва | ООО «БЭЛЛОЧИЗ» |
| 01 фев 2022 | Творожный продукт (Молокосодержащий продукт) | 103 руб / кг | Самара | ООО «ОРИОН» |
| 31 янв 2022 | Творог ГОСТ м.д.ж. 9 | Москва | ООО КМЗ «РОСТМОЛПРОМ» | |
| 31 янв 2022 | Творог, Творожный продукт весовой м.д.ж. 9%, 18 Термостабильный | Москва | ООО КМЗ «РОСТМОЛПРОМ» | |
| 31 янв 2022 | Творог «Гармония» м.д.ж. обезжиренный, 5%, 9% ГОСТ | 169.70 руб / кг | Москва | ООО «МОЛОЧНЫЙ ЗАВОД «ЯНИНО» |
| 31 янв 2022 | Творогосодержащий продукт м.д.ж.9%,18 | 77. 95 руб / кг 95 руб / кг | Москва | ООО «МОЛОЧНЫЙ ЗАВОД «ЯНИНО» |
| 31 янв 2022 | Творожный продукт silver | 85.00 руб / кг | Воронеж | ООО «НАШ ПАРТНЕР» |
| 31 янв 2022 | ТВОРОГ 1.8 | 120 руб / кг | Москва | ООО «ЧИСТЫЕ МОЛОЧНЫЕ ПРОДУКТЫ» |
| 31 янв 2022 | Творожный продукт «Сельский» | от 70.00 руб / кг | Красноярск | ООО «МОЛКОМБИНАТ «НОВОНИКОЛ… |
| 31 янв 2022 | Продукт молокосодержащий (выработанный по технологии творого) творожный сладкий с змж «СЛАСТЕНА» с массовой долей жира 16,5 % с курагой 0,2 к | Красноярск | ООО «МОЛКОМБИНАТ «НОВОНИКОЛ… | |
| 31 янв 2022 | Продукт творожный Сельский 18% (вакуум) 1 кг | Красноярск | ООО «МОЛКОМБИНАТ «НОВОНИКОЛ. .. .. | |
| 31 янв 2022 | Продукт творожный «Новониколаевский» Сельский 18% 5кг | Красноярск | ООО «МОЛКОМБИНАТ «НОВОНИКОЛ… | |
| 31 янв 2022 | Творог 9% «Новониколаевский» ГОСТ упак 0,5 кг | Красноярск | ООО «МОЛКОМБИНАТ «НОВОНИКОЛ… | |
| 28 янв 2022 | Продукт творожный термостабильный | 115 руб / кг | Липецк | ООО «МСЗ ЛИПЕЦКИЙ» |
| 28 янв 2022 | Продукт творожный | 120 руб / кг | Липецк | ООО «МСЗ ЛИПЕЦКИЙ» |
| 27 янв 2022 | Творожный продукт «Золотое качество» | от 90.00 руб / кг | Москва | ООО «РИККОТА» |
| 27 янв 2022 | Творожный продукт и масса | 86. 00 руб / кг 00 руб / кг | Москва | ООО «АДЕЛАНТЕ-М» |
| 27 янв 2022 | Творог 9% и обезжиренный | Славянск-на-Кубани | ООО АГРОФИРМА «ПРИВОЛЬЕ» | |
| 26 янв 2022 | Творог | Санкт-Петербург | ООО «ГАРАНТ Т» | |
| 26 янв 2022 | Творожный порошок | 16.00 euro / кг | Москва | ООО «АЛЬЦИОНА ИНГРЕДИЕНТС» |
| 26 янв 2022 | Организация продаёт творог ( гост)в пром переработку | Ярославль | Ольга | |
| 25 янв 2022 | Творог, творожные продукты в ассортименте | 80.00 руб / кг | Липецк | ООО «ЛИПЕЦКМОЛОКО» |
| 25 янв 2022 | Продаём творог замороженный ГОСТ, ж. 0 до 5 0 до 5 | 135 руб / кг | Екатеринбург | Алексей |
| 25 янв 2022 | Творог 9%, ГОСТ, 250 гр | 75.00 руб / шт | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 25 янв 2022 | Творог 9%, ГОСТ, 500 гр | 145 руб / шт | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 25 янв 2022 | Творог 18%, ГОСТ, 250 гр | 90.00 руб / шт | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 25 янв 2022 | Творог 18%, ГОСТ, 500 гр | 150 руб / шт | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 25 янв 2022 | Творог 9%, ГОСТ | 250 руб / кг | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 25 янв 2022 | Творог 18%, ГОСТ | 280 руб / кг | Санкт-Петербург | ЗАО «ПЛЕМЕННОЙ ЗАВОД «РУЧЬИ» |
| 24 янв 2022 | Творог ГОСТ 0% 5% и 9 | Пушкино | ООО «ЧАПЛЫГИНМОЛОКО» | |
| 24 янв 2022 | Творог обезжиренный, 5 | 150 руб / кг | Заречный | ООО «БЕЛОЯРСКАЯ МОЛОЧНАЯ КО. .. .. |
| 20 янв 2022 | Творожный продукт | 77.00 руб / кг | Рязань | ООО ПО «РАЗДОЛЬЕ» |
| 20 янв 2022 | Творог ГОСТ 0%, 5%, 9 | Рязань | ООО ПО «РАЗДОЛЬЕ» | |
| 19 янв 2022 | Творожная масса (ассортимент) | 169 руб / кг | Владивосток | ООО «КВАЗАР» |
| 19 янв 2022 | Творог замороженный срок годности 6 месяце | 159 руб / кг | Владивосток | ООО «КВАЗАР» |
| 19 янв 2022 | Творог 9 | 220 руб / кг | Красноярск | Юлия |
| 19 янв 2022 | Творожный продукт, 9 и 18 | от 91.00 руб / кг | Санкт-Петербург | Айза |
| 19 янв 2022 | Творожный продукт весовой от производителя | 70. 00 руб / кг 00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творожная масса от производителя | от 82.00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творожный продукт «Нежный» от производителя | от 64.00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творожный продукт «Для пекаря» от производителя | от 66.00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творожный продукт супертермостабильный от производителя | от 75.00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творожный продукт рассыпчатый термостабильный от производителя | от 68. 00 руб / кг 00 руб / кг | Москва | ООО «НОВОМОСКОВСК-МОЛОКО» |
| 19 янв 2022 | Творог весовой рассыпчатый 0%,5%, 9 | от 200 руб / кг | Камышин | ООО «ЛЮБИМЫЙ ГОРОД» |
| 18 янв 2022 | Творог натуральный 5%, 9 | Санкт-Петербург | ООО «МОЛОЧНОЕ НЕБО» | |
| 18 янв 2022 | Творог замороженный | Казань | Мария | |
| 17 янв 2022 | Творог | от 190 руб / кг | Москва | ООО «ОПТТОРГ» |
| 17 янв 2022 | Творожный продукт | от 95.00 руб / кг | Москва | ООО «ОПТТОРГ» |
| 17 янв 2022 | Творог МЗ «Янино». Красноярск | 90. 00 руб / кг 00 руб / кг | Красноярск | ООО «ЭВЕРЕСТ» |
| 15 янв 2022 | Творог домашний пластовой на марле (2%, 5%, 9) | 195 руб / кг | Санкт-Петербург | Максим |
| 14 янв 2022 | Творог | Нижний Новгород | ООО «ВОСХОД» | |
| 12 янв 2022 | Творог ГОСТ 0%2%5 | Москва | ООО ТК «БАЛТЭНЕРГЕТИКА» | |
| 12 янв 2022 | Творожный продукт | от 88.00 руб / кг | Камень-на-Оби | ООО «ХОРОШИЙ ВЫБОР» |
| 11 янв 2022 | Творог. Молочная весовая продукция в ведрах по 3 кг, 5 кг, в коробках по 5 кг. Сметана, Творожный продукт, Сметанный продукт, Творожная масса, Йогу… | Екатеринбург | ООО «ЮНИТ» | |
| 11 янв 2022 | Творожный продукт 18 | от 105 руб / кг | Омск | ООО «СЫТНОЕ ДЕЛО» |
| 11 янв 2022 | Творог обезжиренный / 5% / 9 | Омск | ООО «СЫТНОЕ ДЕЛО» | |
| 11 янв 2022 | Творог и творожный продукт | 84. 00 руб / кг 00 руб / кг | Екатеринбург | ООО «САННИ ВУД» |
| 10 янв 2022 | Творог жирность от 3 до 9 | 85.00 руб / кг | Нижний Новгород | ИП Федулов Роман Борисович |
| 08 янв 2022 | Творог 9% ГОСТ | 140 руб / кг | Москва | Тимур |
| 07 янв 2022 | Творог 5 % ГОСТ | 135 руб / кг | Москва | ООО «МБ» |
| 07 янв 2022 | Творог в больших тарах (ведро 3,5,10 кг) разной жирности | 67.00 руб / кг | Москва | ООО «МБ» |
2.2. Моль, молярная масса
2.2. Моль, молярная масса2.2. Моль, молярная масса
В химических процессах участвуют мельчайшие частицы – молекулы, атомы, ионы, электроны. Число таких частиц даже в малой порции вещества очень велико.
Поэтому, чтобы избежать математических операций с большими числами, для характеристики количества вещества, участвующего в химической реакции, используется
специальная единица – моль.
Число таких частиц даже в малой порции вещества очень велико.
Поэтому, чтобы избежать математических операций с большими числами, для характеристики количества вещества, участвующего в химической реакции, используется
специальная единица – моль.
Моль — это такое количество вещества, в котором содержится определенное число частиц (молекул, атомов, ионов), равное постоянной Авогадро
Постоянная Авогадро NA определяется как число атомов, содержащееся в 12 г изотопа 12С:
Таким образом, 1 моль вещества содержит 6,02 • 1023 частиц этого вещества.
Исходя из этого, любое количество вещества можно выразить определенным числом молей ν (ню). Например, в образце вещества содержится 12,04 • 1023 молекул. Следовательно, количество вещества в этом образце составляет:
В общем виде:
где N – число частиц данного вещества;NA – число частиц, которое содержит 1 моль вещества (постоянная Авогадро).

Молярная масса вещества (M) – масса, которую имеет 1 моль данного вещества.
Эта величина, равная отношению массы m вещества к количеству вещества ν, имеет размерность кг/моль или г/моль. Молярная масса, выраженная в г/моль, численно равна относительной относительной молекулярной массе Mr (для веществ атомного строения – относительной атомной массе Ar).
Например, молярная масса метана CH4 определяется следующим образом:
M(CH4)=16 г/моль, т.е. 16 г CH4 содержат 6,02 • 1023 молекул.
Молярную массу вещества можно вычислить, если известны его масса m и количество (число молей) ν, по формуле:
Соответственно, зная массу и молярную массу вещества, можно рассчитать число его молей: или найти массу вещества по числу молей и молярной массе: m = ν • MНеобходимо отметить, что значение молярной массы вещества определяется
его качественным и количественным составом, т. е. зависит от Mr и Ar.
Поэтому разные вещества при одинаковом количестве молей имеют
различные массы m.
е. зависит от Mr и Ar.
Поэтому разные вещества при одинаковом количестве молей имеют
различные массы m.
Пример
Вычислить массы метана CH4 и этана С2H6,
взятых в количестве ν = 2 моль каждого.
Молярная масса метана M(CH4) равна 16 г/моль;
молярная масса этана M(С2Н6) = 2 • 12+6=30 г/моль.
Отсюда: m(CH4) = 2 моль • 16 г/моль = 32 г;
m(С2Н6) = 2 моль • 30 г/моль = 60 г.
Таким образом, моль – это порция вещества, содержащая одно и то же число частиц, но имеющая разную массу для разных веществ, т.к. частицы вещества (атомы и молекулы) не одинаковы по массе.
n(CH4) = n(С2Н6), но m(CH4) (С2Н6)
Вычисление ν используется практически в
каждой расчетной задаче.
Что такое масса (м)? — Определение из WhatIs.com
ОтМасса (обозначается как m ) — безразмерная величина, представляющая количество материи в частице или объекте. Стандартной единицей массы в Международной системе (СИ) является килограмм (кг).
Масса измеряется путем определения степени, в которой частица или объект сопротивляется изменению своего направления или скорости при приложении силы. Исаак Ньютон утверждал: «Неподвижная масса остается неподвижной, а масса, движущаяся с постоянной скоростью и в постоянном направлении, сохраняет это состояние движения, если на нее не действует внешняя сила.При данной приложенной силе большие массы ускоряются в малой степени, а малые массы ускоряются в большой степени. Применяется следующая формула:
F = мА
, где F — приложенная сила в ньютонах, м — масса объекта или частицы в килограммах, а a — результирующее ускорение в метрах в секунду в квадрате. Массу тела можно вычислить, если известны сила и ускорение.
Массу тела можно вычислить, если известны сила и ускорение.
Масса — это не то же самое, что вес. Вес имеет значение только тогда, когда объект, имеющий определенную массу, помещается в поле ускорения, такое как гравитационное поле Земли. Например, на поверхности земли килограмм массы весит около 2,2 фунта. Но на Марсе такая же масса килограмма будет весить всего около 0,8 фунта, а на Юпитере — примерно 5,5 фунта.
При выражении больших или малых масс используются префиксные множители. В таблице ниже показаны наиболее распространенные альтернативные единицы массы и их отношение к килограмму.
| Блок (и символ) | Чтобы преобразовать в килограммов, умножьте на: | И наоборот, умножить на: |
| метрическая тонна (т) | 1000 | 0,001 |
| грамм (г) | 0,001 | 1000 |
| миллиграмм (мг) | 10 -6 | 10 6 |
| микрограмм (мкг) | 10 -9 | 10 9 |
| нанограмм (нг) | 10 -12 | 10 12 |
| пикограмм (пг) | 10 -15 | 10 15 |
Последний раз это было обновлено в январе 2016 года.
Масса (М) — обзор
2.1.3 Метод Галеркина на простом примере
Как уже упоминалось, целесообразно анализировать системы с распределенными параметрами (или непрерывными ) путем преобразования их в дискретные методом Галеркина, или, если на то пошло, коллокацией или конечным элементом методами или методом прямой лагранжевой дискретизации (раздел 2.1.7), а затем с использованием методов, описанных в разделе 2.1.2. Метод Галеркина будет рассмотрен здесь на примере.
Рассмотрим однородную консольную трубу длиной L, массой на единицу длины m и жесткостью на изгиб EI.Простейшее уравнение, описывающее его изгибное движение, имеет вид
(2.22)EI∂4w∂x4+m∂2w∂t2=0,
, где w(x,t) — боковой прогиб — согласно балочной теории Эйлера-Бернулли, в отличие от теории Тимошенко или других теорий более высокого порядка. Граничные условия:
(2.23)wx=0=0,∂w∂xx=0=0,EI∂2w∂x2x=L=0,EI∂3w∂x3x=L=0.
Решение этой проблемы хорошо известно [напр. Бишоп и Джонсон (1960), Мейрович (1997)]. После разделения переменных с константой разделения λr4 пространственное уравнение допускает решение, состоящее из экспонент от ±λr и ±λri, где i =-1.Подстановка в (2.23) дает систему четырех однородных уравнений, условие нетривиальности решения которой приводит к характеристическому уравнению
(2.24)cosλrLcoshλrL+1=0.
Это трансцендентное уравнение дает бесконечный набор собственных значений, первые три из которых таковы:
(2,25)λ1L=1,87510,λ2L=4,69409,λ3L=7,85476;
соответствующие собственные частоты, собственные частоты, равны
(2,26)Ωr=(λrL)2EImL412.
Модальные формы или собственные функции равны
(2.27)ϕr(x)=chλrx-cosλrx-σrsinhλrx-sinλrx,
, где
(2.28)σr=sinhλrL-sinλrL/chλrL+cosλrL.
Прежде чем продолжить, необходимо сделать важное примечание . В теории колебаний и в классической математике принято определять собственное значение как квадрат или, как в уравнении (2. 26), квадратный корень из частоты, за исключением, возможно, размерного фактора, как в (2.26); главное состоит в том, что положительное собственное значение здесь связано с положительной собственной частотой .Однако в теории динамики и устойчивости решения выражаются как пропорциональные exp(iΩt) или exp(λt), так что Ω и λ не совпадают по фазе на 90°; положительное собственное значение в этом случае представляло бы расходящееся движение , т. е. неустойчивую систему! Это может привести к путанице, без сомнения. Однако эти различные значения и обозначения так глубоко укоренились в этой области [ср. уравнения (2.26) и (2.36)], что, по мнению автора, попытка унификации обозначений и значений привела бы к еще большей путанице.Вместо этого предпочтительны контекст и случайные напоминания, чтобы читатель знал, какое из двух обозначений для собственного значения используется.
26), квадратный корень из частоты, за исключением, возможно, размерного фактора, как в (2.26); главное состоит в том, что положительное собственное значение здесь связано с положительной собственной частотой .Однако в теории динамики и устойчивости решения выражаются как пропорциональные exp(iΩt) или exp(λt), так что Ω и λ не совпадают по фазе на 90°; положительное собственное значение в этом случае представляло бы расходящееся движение , т. е. неустойчивую систему! Это может привести к путанице, без сомнения. Однако эти различные значения и обозначения так глубоко укоренились в этой области [ср. уравнения (2.26) и (2.36)], что, по мнению автора, попытка унификации обозначений и значений привела бы к еще большей путанице.Вместо этого предпочтительны контекст и случайные напоминания, чтобы читатель знал, какое из двух обозначений для собственного значения используется.
Когда на свободный конец трубы добавляется сосредоточенная масса Me, † уравнение движения то же, но граничные условия
(2. 29)wx=0=0,∂w∂xx=0 =0,EI∂2w∂x2x=L=0,EI∂3w∂x3x=L=Me∂2w∂t2x=L;
29)wx=0=0,∂w∂xx=0 =0,EI∂2w∂x2x=L=0,EI∂3w∂x3x=L=Me∂2w∂t2x=L;
, следовательно, на свободном конце действует сила сдвига, связанная с инерцией дополнительной массы. Конечно, для такой простой задачи можно действовать обычным образом и определить собственные значения и собственные функции модифицированной задачи.Тем не менее окажется удобным преобразовать такие системы в дискретные методом Галеркина. С этой целью для рассматриваемой задачи торцевой сдвиг переносится из граничных условий в уравнение движения, которое можно переписать в виде
(2.30)EI∂4w∂x4+m+Meδ(xL) ∂2w∂t2=0,
, где δ(xL) — дельта-функция Дирака; граничные условия (2.29) при этом сводятся к (2.23). По методу Галеркина решение (2.30) можно представить как
(2.31)w(x,t)≃wN(x,t)=∑j=1Nψj(x)qj(t),
, где ψj(x) – соответствующие функции сравнения , т. е. функции в одной области, D=[0,L], удовлетворяющая всем граничным условиям (как геометрическим, так и естественным * ), а qj(t) — обобщенные координаты дискретизированной системы, которая в итоге получится при применении этого метода (Мейрович, 1967, 1997). , 1967Мейрович, 1997). Теперь понятно, почему выгодно переформулировать эту задачу в виде уравнений (2.30) и (2.23), так как тогда можно использовать ψj(x)≡ϕj(x), т. е. использовать собственные функции (2.27) в качестве подходящих функций сравнения: подходящих, так как они удовлетворяют граничным условиям, связанным с ( 2.30), а также удобно, так как они уже известны.
, 1967Мейрович, 1997). Теперь понятно, почему выгодно переформулировать эту задачу в виде уравнений (2.30) и (2.23), так как тогда можно использовать ψj(x)≡ϕj(x), т. е. использовать собственные функции (2.27) в качестве подходящих функций сравнения: подходящих, так как они удовлетворяют граничным условиям, связанным с ( 2.30), а также удобно, так как они уже известны.
Если в левую часть (2.30) подставить аппроксимацию (2.31), то результат вообще будет не нулевым, а будет равен функции ошибок, которую можно обозначить E[wN]. Метод Галеркина требует, чтобы
(2.32)∫DE[wN]ψr(x)dD=0,r=1,2,…N;
, т. е. по области интегральная ошибка, взвешенная по ψr(x), † должна быть равна нулю (Finlayson & Scriven 1966).
Таким образом, в этом примере подстановка приближения (2.31) с ψj(x)=ϕj(x) в уравнение (2.30), умножение на ϕr(x) и интегрирование по D=[0,L] приводит к
(2.33)∑j=1NEIλj4qjLδrj+mLδrj+Meϕr(L)ϕj(L)q¨j=0,r=1,2,…,N,
в силу ортогональности собственных функций (2. 27), т.е. из
27), т.е. из
(2.34)∫0Lϕr(x)ϕj(x)dx=Lδrj,
, где δrj — дельта Кронекера (0forr≠jan и 1forr=j). Очевидно, что система теперь дискретизирована. Таким образом, если используется двухмодовое приближение (N=2), уравнение (2.33) может быть записано в следующей матричной форме:
(2.35)mL+Meϕ12(L)Meϕ1(L)ϕ2(L)Meϕ1( L)ϕ2(L)mL+Meϕ22(L)q¨1q¨2+EIλ14L00λ24Lq1q2={0}.
Собственные значения и собственные частоты этой матричной системы являются приближениями младших двух из непрерывной системы; таким образом, если Me=12 мл, то Ω1=2.018(EI/мл4)12, Ω2=17,165(EI/мл4)12. Соответствующие собственные векторы дают в некотором смысле «смесь» собственных функций первого и второго режима исходной системы, необходимую для аппроксимации собственных функций модифицированной; таким образом, для этого примера
{A}1=1-0,02,{A}2=11,48.
В общем, N должно быть достаточно большим, чтобы обеспечить сходимость. Таблица 2.1 показывает, что сходимость может быть очень быстрой. Точные значения при решении (2. 22) с граничными условиями (2.29) равны Ωr(EI/mL4)-12=2.0163,16.901,51.701дляр=1,2,3.
22) с граничными условиями (2.29) равны Ωr(EI/mL4)-12=2.0163,16.901,51.701дляр=1,2,3.
Таблица 2.1. Аппроксимации трех низших собственных частот модифицированной консольной трубы для различных N в случае Me=12 мл.
+ N| 2 | 4 | 6 | 8 | 10 | |
|---|---|---|---|---|---|
| Ω1 (ЭИ / МЬ4) -12 | 2,0184 2,0166 2,0164 | 2,0163 2,0163 | |||
| Ом2(ЭИ/мл4)-12 | 17.166 | +16,936 | 16,912 | 16,906 | 16,904 |
| Ω3 (EI / МЬ4) -12 | — | 52,125 | 51,826 | 51,754 | 51,728 |
Метод Галеркина теперь будет выражены формально в обобщенной форме, полезной для дальнейшего развития. Задача на собственные значения, связанная с уравнениями (2.22) и (2.30), может быть выражена как
(2.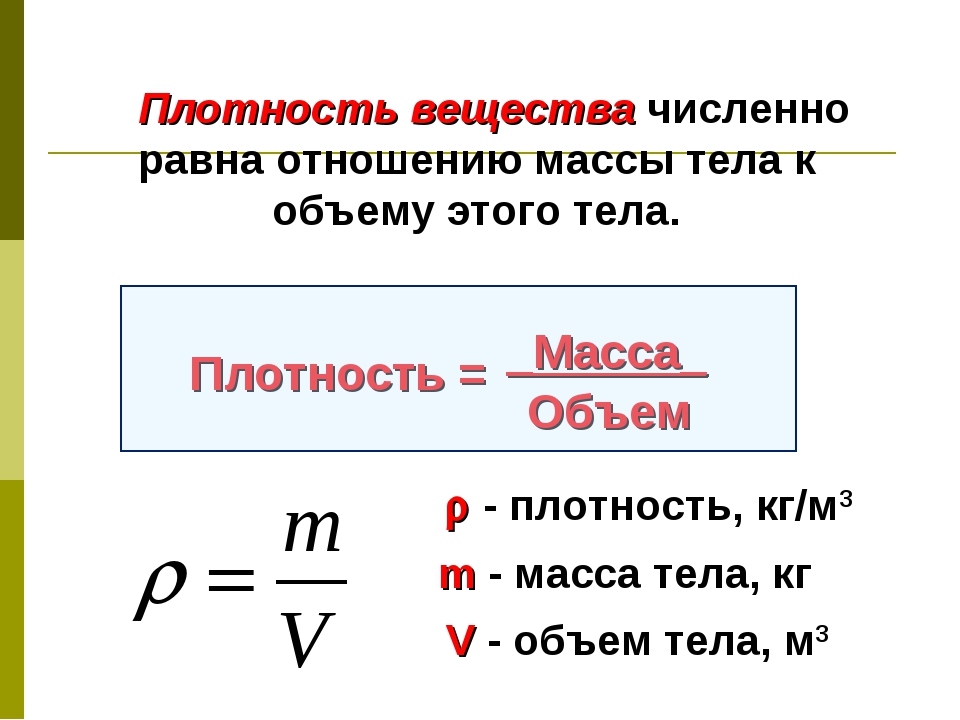 36)L[w]=λM[w],
36)L[w]=λM[w],
при соответствующих граничных условиях.Обычно L и M — линейные дифференциальные операторы, хотя M во многих случаях — скаляр, а λ(=Ω2) — собственное значение. В случае уравнения (2.30) L=EI(∂4/∂x4) и M=m+Meδ(x-L), так что M[w]=Mw. Эквивалент утверждения (2.31) теперь равен
(2.37)wN(x)=∑j=1Najψj(x).
Элементы матриц масс и жесткости [ср. уравнения (2.1)], две матрицы в (2.35) могут быть получены как х)]dx.
В случае, когда Me включен в M и граничные условия (2.23), это стандартная проблема. Если же Me исключить из уравнений движения, то граничные условия (2.29) можно переписать в виде
(2.39)w(0)=0,w′(0)=0,w″(L) =0,EIw‴(L)=-λMew(L),
, в котором ()′≡∂/∂x, а задача необычна тем, что собственное значение появляется в граничных условиях. Следовательно, строго (Фридман, 1956) область D зависит от λ. В этом примере для расчетов с уравнением (2.22) и граничными условиями (2.29), приводящими к «точным результатам», к которым приводят результаты из таблицы 2. 1, мы беспечно проигнорировали эту тонкость (сохранив D=[0,1]), но тем не менее получили правильные результаты. Однако это не всегда так, как будет показано в разделе 2.1.4.
1, мы беспечно проигнорировали эту тонкость (сохранив D=[0,1]), но тем не менее получили правильные результаты. Однако это не всегда так, как будет показано в разделе 2.1.4.
Масса | КОСМОС
Портрет сэра Исаака Ньютона, который помог определить понятие массы.Авторы и права: Архив Калифорнийского технологического института
На Земле термины масса и вес часто используются взаимозаменяемо, но в астрономии и ньютоновской физике масса объекта связана с тем, сколько материи он содержит.Массу объекта можно охарактеризовать его способностью сопротивляться данной силе (мы иногда называем это инерционной массой тела , и, таким образом, масса тесно связана с понятием инерции). Это простое следствие второго закона Ньютона, где сила F , действующая на тело, равна массе m , умноженной на ускорение a , которое оно испытывает, то есть:
F=ma или m=F/a .
В глубоком космосе, вдали от гравитационного поля Земли (или другого крупного тела), объект будет «невесомым» — однако он все еще будет иметь массу и, следовательно, сопротивление заданной силе.
Массы часто выражаются в килограммах (кг), граммах (г) или солнечных массах (M ⊙ ). Тело массивнее другого, когда оно имеет большую массу. Одним из наименее массивных объектов во Вселенной является электрон, масса которого составляет всего 9,11 × 10 -31 кг, в то время как масса Солнца равна 1.989 × 10 30 кг, а массы галактик, подобных Млечному Пути, превышают 10 42 кг.
Универсальный закон всемирного тяготения Ньютона гласит, что все массы во Вселенной притягиваются друг к другу.
В специальной теории относительности существует эквивалентность между массой м , и энергия , и энергия E , учитывая известное уравнение E = MC 2 где C — скорость света . Таким образом, все частицы и даже свет имеют связанную с ними массу.
Таким образом, все частицы и даже свет имеют связанную с ними массу.
В специальной теории относительности Эйнштейна масса тела изменяется, когда оно имеет скорость v по отношению к наблюдателю. Если масса покоя равна м 0 , то масса м тела становится:
, где снова c — скорость света.
В общей теории относительности Эйнштейна наличие массы искажает пространственно-временной континуум и делает его «искривленным».В общей теории относительности массы — и даже свет — движутся по прямым линиям в кривизне пространства. Другим следствием массы в общей теории относительности является то, что она приводит к замедлению времени или гравитационному красному смещению. Это заставляет часы в присутствии массы идти медленнее, чем в вакууме. Гравитационная сила, которую тело ощущает в присутствии другой массы, равна гравитационной массы , а в общей теории относительности Эйнштейна гравитационная и инерционная массы идентичны.
Движение массы на пружине
В предыдущей части этого урока движение массы, прикрепленной к пружине, было описано как пример колебательной системы. Масса при пружинном движении обсуждалась более подробно, поскольку мы стремились понять математические свойства объектов, находящихся в периодическом движении. Теперь мы исследуем движение массы на пружине еще более подробно, сосредоточившись на том, как различные величины изменяются с течением времени.Такие величины будут включать в себя силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Закон Гука
Мы начнем наше обсуждение с исследования сил, действующих пружиной на подвешенный груз. Рассмотрим систему, показанную справа, с пружиной, прикрепленной к опоре. Пружина висит в расслабленном, нерастянутом положении. Если бы вы взялись за нижнюю часть пружины и потянули вниз, пружина растянулась бы.Если бы вы потянули с небольшим усилием, пружина немного растянулась бы. И если бы вы тянули с гораздо большей силой, пружина растянулась бы в гораздо большей степени. Какова именно количественная связь между силой тяги и степенью растяжения?
И если бы вы тянули с гораздо большей силой, пружина растянулась бы в гораздо большей степени. Какова именно количественная связь между силой тяги и степенью растяжения?
Чтобы определить это количественное соотношение между величиной силы и величиной растяжения, к пружине можно прикрепить предметы известной массы. Для каждого добавленного объекта можно измерить величину растяжения.Сила, приложенная в каждом случае, будет весом объекта. Можно провести регрессионный анализ данных силы-растяжения, чтобы определить количественную взаимосвязь между силой и степенью растяжения. В приведенной ниже таблице данных показаны некоторые репрезентативные данные для такого эксперимента.
Масса (кг) | Усилие на пружине (Н) | Величина растяжения (м) |
0.000 | 0,000 | 0,0000 |
0,050 | 0,490 | 0,0021 |
0,100 | 0,980 | 0. |
0,150 | 1.470 | 0,0063 |
0,200 | 1,960 | 0,0081 |
0,250 | 2.450 | 0,0099 |
0,300 | 2,940 | 0,0123 |
0,400 | 3,920 | 0,0160 |
0.500 | 4.900 | 0,0199 |
Построив график данных силы-растяжения и выполнив линейный регрессионный анализ, можно определить количественное соотношение или уравнение. Сюжет показан ниже.
Анализ линейной регрессии дает следующую статистику:
наклон = 0.00406 м/с
y-перехват = 3,43 x 10 -5 ( per почти близко к 0,000)
константа регрессии = 0,999
Уравнение для этой линии
Растяжение = 0,00406•Сила + 3,43×10 -5
Тот факт, что константа регрессии очень близка к 1,000, указывает на то, что существует сильное соответствие между уравнением и точками данных. Эта сильная посадка придает достоверность результатам эксперимента.
Эта сильная посадка придает достоверность результатам эксперимента.
Эта взаимосвязь между силой, приложенной к пружине, и степенью растяжения была впервые обнаружена в 1678 году английским ученым Робертом Гуком. Как выразился Гук: Ut tensio, sic vis . В переводе с латыни это означает «Как протяженность, так и сила». Другими словами, величина растяжения пружины пропорциональна величине силы, с которой она тянет. Если бы мы завершили это исследование около 350 лет назад (и если бы мы знали немного латыни), мы были бы знамениты! Сегодня эта количественная зависимость между силой и растяжением называется законом Гука и часто приводится в учебниках как
.F пружина = -k•x
, где Fspring — сила, действующая на пружину, x — степень растяжения пружины относительно ее расслабленного положения, а k — константа пропорциональности, часто называемая константой пружины.Постоянная пружины — это положительная константа, значение которой зависит от исследуемой пружины. Жесткая пружина будет иметь высокую жесткость пружины. Это означает, что потребуется относительно большое количество силы, чтобы вызвать небольшое смещение. Единицами жесткости пружины являются ньютон/метр (Н/м). Знак минус в приведенном выше уравнении указывает на то, что направление растяжения пружины противоположно направлению силы, действующей на пружину. Например, когда пружина была растянута ниже своего расслабленного положения, x равно вниз .Пружина реагирует на это растяжение, оказывая направленное вверх усилие. X и F находятся в противоположных направлениях. Последнее замечание относительно этого уравнения заключается в том, что оно работает для пружины, растянутой по вертикали, и для пружины, растянутой по горизонтали (такой, которая будет обсуждаться ниже).
Жесткая пружина будет иметь высокую жесткость пружины. Это означает, что потребуется относительно большое количество силы, чтобы вызвать небольшое смещение. Единицами жесткости пружины являются ньютон/метр (Н/м). Знак минус в приведенном выше уравнении указывает на то, что направление растяжения пружины противоположно направлению силы, действующей на пружину. Например, когда пружина была растянута ниже своего расслабленного положения, x равно вниз .Пружина реагирует на это растяжение, оказывая направленное вверх усилие. X и F находятся в противоположных направлениях. Последнее замечание относительно этого уравнения заключается в том, что оно работает для пружины, растянутой по вертикали, и для пружины, растянутой по горизонтали (такой, которая будет обсуждаться ниже).
Анализ силы массы на пружине
Ранее в этом уроке мы узнали, что на объект, который вибрирует, действует восстанавливающая сила.Возвращающая сила заставляет вибрирующий объект замедляться по мере удаления от положения равновесия и ускоряться по мере приближения к положению равновесия. Именно эта возвращающая сила отвечает за вибрацию. Так какова возвращающая сила массы на пружине?
Именно эта возвращающая сила отвечает за вибрацию. Так какова возвращающая сила массы на пружине?
Мы начнем обсуждение этого вопроса с рассмотрения системы на диаграмме ниже.
На схеме показаны воздушная трасса и планер.Планер крепится пружиной к вертикальной опоре. Трение между планером и воздушной гусеницей незначительно. Таким образом, на планер действуют три доминирующие силы. Эти три силы показаны на диаграмме свободного тела справа. Сила гравитации (Fgrav) довольно предсказуема — как по величине, так и по направлению. Сила тяжести всегда действует вниз; его величина может быть найдена как произведение массы на ускорение свободного падения (m•9.8 Н/кг). Опорная сила (Fsupport) уравновешивает силу тяжести. Он питается воздухом от воздушной дорожки, в результате чего планер левитирует над поверхностью гусеницы. Конечная сила – это сила пружины (Fspring). Как обсуждалось выше, сила пружины изменяется по величине и направлению.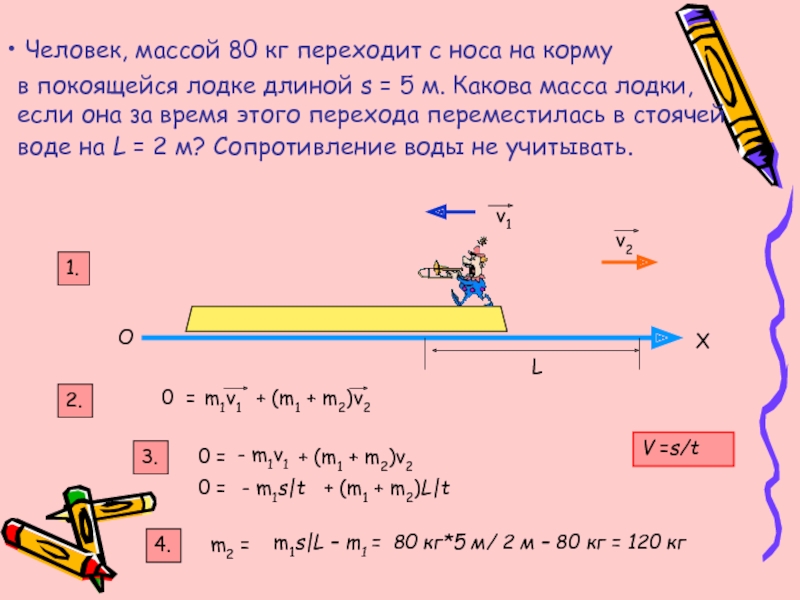 Его величину можно найти с помощью закона Гука. Его направление всегда противоположно направлению растяжения и к положению равновесия. Поскольку планер с воздушной гусеницей совершает возвратно-поступательные движения , сила пружины (Fspring) действует как восстанавливающая сила.Он действует на планер влево, когда он расположен справа от положения равновесия; и он действует на планер вправо, когда он расположен слева от положения равновесия.
Его величину можно найти с помощью закона Гука. Его направление всегда противоположно направлению растяжения и к положению равновесия. Поскольку планер с воздушной гусеницей совершает возвратно-поступательные движения , сила пружины (Fspring) действует как восстанавливающая сила.Он действует на планер влево, когда он расположен справа от положения равновесия; и он действует на планер вправо, когда он расположен слева от положения равновесия.
Предположим, что планер оттягивается вправо от положения равновесия и выходит из состояния покоя. На приведенной ниже диаграмме показано направление силы пружины в пяти различных положениях на протяжении пути параплана. Когда планер перемещается из положения А (точка освобождения) в положение В, а затем в положение С, сила пружины действует влево на движущийся влево планер.Когда планер приближается к положению C, степень растяжения пружины уменьшается, а сила пружины уменьшается в соответствии с законом Гука. Несмотря на это уменьшение силы пружины, все еще существует ускорение, вызванное восстанавливающей силой, для всего размаха от положения А до положения С. В положении С планер достиг максимальной скорости. Как только планер проходит влево от положения C, сила пружины действует вправо. Во время этой фазы цикла планера пружина сжимается.Чем дальше от положения С перемещается планер, тем больше степень сжатия и больше сила пружины. Эта сила пружины действует как восстанавливающая сила, замедляя планер при его перемещении из положения C в положение D и в положение E. К тому времени, когда планер достигает положения E, он замедляется до положения мгновенного покоя, прежде чем изменить свое направление и возвращаясь к положению равновесия. Во время движения планера из положения E в положение C степень сжатия пружины уменьшается, и сила пружины уменьшается.На протяжении всего расстояния от положения Е до положения С сохраняется ускорение. В положении С планер достиг максимальной скорости. Теперь планер начинает двигаться вправо от точки C. При этом сила пружины действует влево на планер, движущийся вправо. Эта восстанавливающая сила заставляет планер замедляться на всем пути от положения C до положения D и положения E.
В положении С планер достиг максимальной скорости. Как только планер проходит влево от положения C, сила пружины действует вправо. Во время этой фазы цикла планера пружина сжимается.Чем дальше от положения С перемещается планер, тем больше степень сжатия и больше сила пружины. Эта сила пружины действует как восстанавливающая сила, замедляя планер при его перемещении из положения C в положение D и в положение E. К тому времени, когда планер достигает положения E, он замедляется до положения мгновенного покоя, прежде чем изменить свое направление и возвращаясь к положению равновесия. Во время движения планера из положения E в положение C степень сжатия пружины уменьшается, и сила пружины уменьшается.На протяжении всего расстояния от положения Е до положения С сохраняется ускорение. В положении С планер достиг максимальной скорости. Теперь планер начинает двигаться вправо от точки C. При этом сила пружины действует влево на планер, движущийся вправо. Эта восстанавливающая сила заставляет планер замедляться на всем пути от положения C до положения D и положения E.
Ранее на этом уроке обсуждались изменения положения груза на пружине во времени.В то время было показано, что положение груза на пружине зависит от синуса времени. Обсуждение относилось к массе, которая колебалась вверх и вниз, будучи подвешенной к пружине. Обсуждение было бы в равной степени применимо и к нашему планеру, движущемуся по воздушной трассе. Если бы детектор движения был размещен в правом конце воздушной дорожки для сбора данных для графика зависимости положения от времени, график выглядел бы так, как показано ниже. Положение А — это крайнее правое положение на воздушной дорожке, когда планер находится ближе всего к детектору.
Позиции, отмеченные на приведенной выше диаграмме, — это те же позиции, которые использовались при обсуждении восстанавливающей силы выше. Вы могли вспомнить из этого обсуждения, что положения А и Е были положениями, в которых масса имела нулевую скорость. Положение С было положением равновесия и было положением максимальной скорости. Если бы тот же детектор движения, который собирал данные о положении и времени, использовался для сбора данных о скорости и времени, то данные на графике выглядели бы так, как показано на графике ниже.
Положение С было положением равновесия и было положением максимальной скорости. Если бы тот же детектор движения, который собирал данные о положении и времени, использовался для сбора данных о скорости и времени, то данные на графике выглядели бы так, как показано на графике ниже.
Обратите внимание, что график зависимости массы пружины от скорости от времени также имеет синусоидальную форму. Единственная разница между графиками положение-время и скорость-время состоит в том, что один смещен на одну четверть колебательного цикла от другого. Также обратите внимание на графики, что абсолютное значение скорости наибольшее в положении C (соответствующем положению равновесия). Скорость любого движущегося объекта, независимо от того, вибрирует он или нет, — это скорость с направлением.Величина скорости есть скорость. Направление часто выражается как положительный или отрицательный знак. В некоторых случаях скорость имеет отрицательное направление (планер движется влево) и ее скорость откладывается под осью времени. В остальных случаях скорость имеет положительное направление (планер движется вправо) и ее скорость отложена над осью времени. Вы также заметите, что скорость равна нулю всякий раз, когда положение находится в экстремальном положении. Это происходит в положениях А и Е, когда планер начинает менять направление.Так же, как и в случае маятникового движения, скорость наибольшая, когда смещение массы относительно ее положения равновесия наименьшее. И скорость наименьшая, когда смещение массы относительно ее положения равновесия наибольшее.
В остальных случаях скорость имеет положительное направление (планер движется вправо) и ее скорость отложена над осью времени. Вы также заметите, что скорость равна нулю всякий раз, когда положение находится в экстремальном положении. Это происходит в положениях А и Е, когда планер начинает менять направление.Так же, как и в случае маятникового движения, скорость наибольшая, когда смещение массы относительно ее положения равновесия наименьшее. И скорость наименьшая, когда смещение массы относительно ее положения равновесия наибольшее.
Энергетический анализ массы на пружине
На предыдущей странице обсуждался энергетический анализ колебаний маятника. Здесь мы проведем аналогичный анализ для движения массы на пружине.В нашем обсуждении мы будем ссылаться на движение планера без трения по воздушной дорожке, которое было введено выше. Планер потянет вправо от положения равновесия и выйдет из состояния покоя (положение А). Как уже упоминалось, планер затем ускоряется к положению C (положение равновесия). Как только планер проходит положение равновесия, он начинает замедляться, поскольку сила пружины тянет его назад против движения. К тому времени, когда он достигает положения E, планер замедляется до мгновенной паузы, прежде чем изменить направление и разогнаться обратно к положению C.Еще раз, после того, как планер проходит точку C, он начинает замедляться по мере приближения к точке A. Оказавшись в позиции A, цикл начинается сначала… и снова… и снова.
Как только планер проходит положение равновесия, он начинает замедляться, поскольку сила пружины тянет его назад против движения. К тому времени, когда он достигает положения E, планер замедляется до мгновенной паузы, прежде чем изменить направление и разогнаться обратно к положению C.Еще раз, после того, как планер проходит точку C, он начинает замедляться по мере приближения к точке A. Оказавшись в позиции A, цикл начинается сначала… и снова… и снова.
Кинетическая энергия, которой обладает объект, — это энергия, которой он обладает благодаря своему движению. Это величина, которая зависит как от массы, так и от скорости. Уравнение, связывающее кинетическую энергию (KE) с массой (m) и скоростью (v), равно
.КЭ = ½•m•v 2
Чем быстрее движется объект, тем большей кинетической энергией он обладает.Мы можем объединить эту концепцию с приведенным выше обсуждением того, как скорость изменяется в ходе движения. Это смешение концепций привело бы нас к выводу, что кинетическая энергия массы на пружине увеличивается по мере ее приближения к положению равновесия; и уменьшается по мере удаления от положения равновесия.
Эта информация представлена в таблице ниже:
Этап цикла | Изменение скорости | Изменение кинетической энергии |
от А до В до С | Увеличение | Увеличение |
C-D-E | По убыванию | По убыванию |
от В до Г до С | Увеличение | Увеличение |
С до В до А | По убыванию | По убыванию |
Кинетическая энергия — это только одна из форм механической энергии. Другая форма – потенциальная энергия. Потенциальная энергия — это накопленная энергия положения, которым обладает объект. Потенциальная энергия может быть гравитационной потенциальной энергией, и в этом случае положение относится к высоте над землей. Или потенциальная энергия может быть упругой потенциальной энергией, и в этом случае положение относится к положению массы на пружине относительно положения равновесия. Для нашего планера с вибрирующей воздушной гусеницей нет изменения высоты. Поэтому гравитационная потенциальная энергия не меняется.Эта форма потенциальной энергии не представляет большого интереса для нашего анализа изменений энергии. Однако происходит изменение положения массы относительно ее положения равновесия. Каждый раз, когда пружина сжимается или растягивается относительно ее расслабленного положения, происходит увеличение упругой потенциальной энергии. Количество упругой потенциальной энергии зависит от степени растяжения или сжатия пружины. Уравнение, связывающее величину потенциальной энергии упругости (PEspring) с величиной сжатия или растяжения (x), имеет вид
Другая форма – потенциальная энергия. Потенциальная энергия — это накопленная энергия положения, которым обладает объект. Потенциальная энергия может быть гравитационной потенциальной энергией, и в этом случае положение относится к высоте над землей. Или потенциальная энергия может быть упругой потенциальной энергией, и в этом случае положение относится к положению массы на пружине относительно положения равновесия. Для нашего планера с вибрирующей воздушной гусеницей нет изменения высоты. Поэтому гравитационная потенциальная энергия не меняется.Эта форма потенциальной энергии не представляет большого интереса для нашего анализа изменений энергии. Однако происходит изменение положения массы относительно ее положения равновесия. Каждый раз, когда пружина сжимается или растягивается относительно ее расслабленного положения, происходит увеличение упругой потенциальной энергии. Количество упругой потенциальной энергии зависит от степени растяжения или сжатия пружины. Уравнение, связывающее величину потенциальной энергии упругости (PEspring) с величиной сжатия или растяжения (x), имеет вид

PE пружина = ½ • k•x 2
, где k — жесткость пружины (в Н/м), а x — расстояние, на которое пружина растянута или сжата относительно расслабленного, нерастянутого положения.
Когда планер с воздушной гусеницей находится в положении равновесия (положение C), он движется с наибольшей скоростью (как обсуждалось выше). В этой позиции значение x равно 0 метру. Таким образом, количество упругой потенциальной энергии (PEspring) равно 0 Дж. Это положение, при котором потенциальная энергия минимальна. Когда планер находится в положении А, пружина растягивается на максимальное расстояние и потенциальная энергия упругости максимальна. Аналогичное утверждение можно сделать и для положения E. В положении E пружина сжата больше всего, и упругая потенциальная энергия в этом месте также максимальна.Поскольку пружина растягивается в той же мере, в какой сжимается, потенциальная энергия упругости в положении А (растянутое положение ) такое же, как и в положении Е (положение сжатое ). В этих двух положениях — А и Е — скорость равна 0 м/с, а кинетическая энергия равна 0 Дж. Таким образом, как и в случае вибрирующего маятника, колеблющаяся масса на пружине имеет наибольшую потенциальную энергию, когда она имеет наименьшую кинетическая энергия. И он также имеет наименьшую потенциальную энергию (положение C), когда он имеет наибольшую кинетическую энергию.Эти принципы показаны на анимации ниже.
В этих двух положениях — А и Е — скорость равна 0 м/с, а кинетическая энергия равна 0 Дж. Таким образом, как и в случае вибрирующего маятника, колеблющаяся масса на пружине имеет наибольшую потенциальную энергию, когда она имеет наименьшую кинетическая энергия. И он также имеет наименьшую потенциальную энергию (положение C), когда он имеет наибольшую кинетическую энергию.Эти принципы показаны на анимации ниже.
При проведении анализа энергопотребления обычно используется гистограмма энергопотребления. Гистограмма энергии использует гистограмму для представления относительного количества и формы энергии, которой обладает движущийся объект. Это полезный концептуальный инструмент для демонстрации того, какая форма энергии присутствует и как она меняется с течением времени. На приведенной ниже диаграмме представлена гистограмма энергии для планера с воздушной гусеницей и пружинной системы.
Гистограмма показывает, что по мере того, как масса на пружине перемещается от A к B и C, кинетическая энергия увеличивается, а потенциальная энергия упругости уменьшается. Однако общее количество этих двух форм механической энергии остается постоянным. Механическая энергия переходит из потенциальной формы в кинетическую; но общее количество сохраняется . Аналогичное явление сохранения энергии происходит, когда масса перемещается от C к D и E. Когда пружина сжимается, а масса замедляется, ее кинетическая энергия преобразуется в упругую потенциальную энергию.При этом преобразовании общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в предыдущей главе — главе «Энергия» — учебника по физике.
Однако общее количество этих двух форм механической энергии остается постоянным. Механическая энергия переходит из потенциальной формы в кинетическую; но общее количество сохраняется . Аналогичное явление сохранения энергии происходит, когда масса перемещается от C к D и E. Когда пружина сжимается, а масса замедляется, ее кинетическая энергия преобразуется в упругую потенциальную энергию.При этом преобразовании общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в предыдущей главе — главе «Энергия» — учебника по физике.
Очевидно, не все пружины одинаковы. И не все пружинно-массовые системы одинаковы. Одной измеряемой величиной, которую можно использовать для отличия одной системы массы пружины от другой, является период.Как обсуждалось ранее в этом уроке, период — это время, за которое вибрирующий объект совершает один полный цикл вибрации. Переменными, влияющими на период системы пружина-масса, являются масса и постоянная пружины. Уравнение, связывающее эти переменные, напоминает уравнение для периода маятника. Уравнение
Переменными, влияющими на период системы пружина-масса, являются масса и постоянная пружины. Уравнение, связывающее эти переменные, напоминает уравнение для периода маятника. Уравнение
T = 2•Π•(m/k) .5
, где T — период, m — масса объекта, прикрепленного к пружине, а k — жесткость пружины.Уравнение можно интерпретировать так, что более массивные объекты будут вибрировать с более длительным периодом. Их большая инерция означает, что для завершения цикла требуется больше времени. А пружины с большей жесткостью (более жесткие пружины) имеют меньший период; массам, прикрепленным к этим пружинам, требуется меньше времени для завершения цикла. Их более высокая жесткость пружины означает, что они оказывают более сильное восстанавливающее усилие на прикрепленную массу. Эта большая сила сокращает время, необходимое для завершения одного цикла вибрации.
С нетерпением жду урока 2
Как мы видели в этом уроке, вибрирующие объекты качаются на месте . Они колеблются взад и вперед вокруг фиксированного положения. Простой маятник и груз на пружине — классические примеры такого колебательного движения. Хотя это и не очевидно при простом наблюдении, использование детекторов движения показывает, что колебания этих объектов имеют синусоидальный характер. Существует тонкое волнообразное поведение, связанное с тем, как положение и скорость изменяются во времени.На следующем уроке мы будем исследовать волны. Как мы скоро узнаем, если масса на пружине — это покачиваний во времени , то волна — это совокупность покачиваний, разбросанных по пространству . Когда мы начнем изучение волн в Уроке 2, понятия частоты, длины волны и амплитуды останутся важными.
Они колеблются взад и вперед вокруг фиксированного положения. Простой маятник и груз на пружине — классические примеры такого колебательного движения. Хотя это и не очевидно при простом наблюдении, использование детекторов движения показывает, что колебания этих объектов имеют синусоидальный характер. Существует тонкое волнообразное поведение, связанное с тем, как положение и скорость изменяются во времени.На следующем уроке мы будем исследовать волны. Как мы скоро узнаем, если масса на пружине — это покачиваний во времени , то волна — это совокупность покачиваний, разбросанных по пространству . Когда мы начнем изучение волн в Уроке 2, понятия частоты, длины волны и амплитуды останутся важными.
 Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивная масса на пружине предоставляет учащимся простую среду для изучения влияния массы, жесткости пружины и продолжительности движения на период и амплитуду вертикально вибрирующей массы.
Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивная масса на пружине предоставляет учащимся простую среду для изучения влияния массы, жесткости пружины и продолжительности движения на период и амплитуду вертикально вибрирующей массы.
Проверьте свое понимание
1.Чтобы растянуть пружину на 40 см от исходного положения, требуется усилие 16 Н. Какая сила (в ньютонах) нужна, чтобы растянуть ту же пружину …
а. … в два раза больше?
б. … в три раза больше?
в. …половина дистанции?
2. Постоянно обеспокоенный привычкой белок на заднем дворе нападать на его кормушки для птиц, мистер Х. решает использовать немного физики для лучшей жизни. Его текущий план включает в себя оснащение кормушки для птиц пружинной системой, которая растягивается и колеблется, когда масса белки приземляется на кормушку.Он желает иметь максимально возможную амплитуду вибрации. Должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
Должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
3. По предыдущему вопросу. Если г-н Х хочет, чтобы его кормушка для птиц (и прикрепленная к ней белка) вибрировала с максимально возможной частотой, должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
4. Используйте энергосбережение, чтобы заполнить пробелы на следующей диаграмме.
5. Какая из следующих систем масса-пружина будет иметь самую высокую частоту вибрации?
Случай A: Пружина с k = 300 Н/м и массой 200 г подвешена к ней.
Случай B: Пружина с k = 400 Н/м и массой 200 г подвешена к ней.
6. Какая из следующих систем масса-пружина будет иметь самую высокую частоту вибрации?
Случай A: Пружина с k = 300 Н/м и массой 200 г подвешена к ней.
Случай B: Пружина с k = 300 Н/м и массой 100 г подвешена к ней.
Калькулятор плотности p = м/В
Использование калькулятора
Выберите расчет плотности p, массы m или объема V. Введите два других значения, и калькулятор вычислит третье значение в выбранных единицах измерения. Вы также можете ввести экспоненциальное представление, например 3.45е22.
Уравнение плотности для этих расчетов:
\( p = \dfrac{m}{V} \)
Где:
р = плотность
м = масса
В = объем
Калькулятор плотности использует формулу p=m/V, или плотность (p) равна массе (m), деленной на объем (V). Калькулятор может использовать любые два значения для расчета третьего.Плотность определяется как масса на единицу объема. Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет конвертировать между единицами.
Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет конвертировать между единицами.
Значимые цифры
Для значения 165778 при выборе 4 значащих цифр будет возвращено 165800. Для значения 0,00165778 при выборе 4 значащих цифр будет возвращено 0,001658. См. также наши справочные заметки по значимые фигуры.
Расчет плотности:
Решая плотность, массу или объем, мы можем использовать следующие формулы:
Рассчитать p Учитывая m и V
Рассчитать плотность по массе и объему.
\( p = \dfrac{m}{V} \)
Вычислить m Учитывая p и V
Рассчитать массу по плотности и объему.
\(м = пВ\)
Рассчитать V по данным p и m
Рассчитать объем по плотности и массе.
\(V = \dfrac{m}{p} \)
Кубический корень объема помогает в мысленной визуализации фактического объема.Еще раз спасибо пользователю, который предложил этот калькулятор!
\(\sqrt[3]{V} \)
96q22.html
Обзорный вопрос по физике Часть: Энергия
Год: 1996 Вопрос №: 22
Вопрос: Тележка массой (m), движущаяся со скоростью (v), имеет кинетическую энергию KE. Если масса
тележку удвоить, а ее скорость уменьшить вдвое, кинетическая энергия тележки будет:
(1 ) вдвое меньше
(2 ) в два раза больше
(3 ) вчетверо больше
(4 ) в четыре раза больше
Что на самом деле задает этот вопрос?
Объяснение: Дастин С.
[ Вернуться к меню вопросов ]
Ответ 1
вдвое меньше
ПРАВИЛЬНО
Вспоминая KE = 0,5 mv 2
Сначала мы удваиваем массу, которая равна удвоенной кинетической энергии. Тогда скорость
уменьшается вдвое, что дает четверть кинетической энергии. При объединении удвоение
умноженная на четверть, равна половине, поэтому она в два раза меньше. вернуться к началу
Ответ 2
вдвое больше
НЕПРАВИЛЬНО
Это неверно, потому что при удвоении массы кинетическая энергия удваивается.Но тогда вы должны учитывать уменьшение скорости вдвое.
Помните KE = 0,5 мВ 2 вернуться к началу
Ответ 3
вчетверо больше
НЕПРАВИЛЬНО
Вы, кажется, правильно учли уменьшение скорости, но забыли
об удвоении массы. Помните KE = 0,5 мВ 2 вернуться к началу
Помните KE = 0,5 мВ 2 вернуться к началу
Ответ 4
в четыре раза больше
НЕПРАВИЛЬНО
Это неверно, потому что, когда масса 2x, кинетическая = 2x.Когда скорость
вдвое это равно 1/4 кинетической. Объединение 2x четверть равно половине, а не четырем
раз как здорово.
Помните KE = 0,5 мВ 2 вернуться к началу
Что на самом деле означает этот вопрос?
Этот вопрос действительно спрашивает, как найти кинетическую энергию описанной тележки
когда во время движения изменяются и масса, и скорость. вернуться наверх
вернуться наверх
q21-тело-массы-m-движется- | ЛИДО
Решение:
(a) Когда тело массой m в точке A, стоящее на земле, поднимается над землей на высоту h в точке B, к нему прилагается сила.
Приложенная сила = вес тела
Сила, действующая на массу m = F = мг
‘g’ – ускорение свободного падения при массе 1 кг
(b) Проделанная работа = Сила х перемещение (расстояние)
Вт = мгч
(c) Совершенная работа сохраняется в организме в виде потенциальной энергии
С.Е = мгч
привет студенты добро пожаловать в Лидо
обучающие видео с вопросами и ответами
Меня зовут Паллави, и я преподаю математику и
наука на Лидо
давайте посмотрим на это самое
интересный вопрос здесь
это тело массой m
перемещается с земли на высоту
хорошо, прежде чем продолжить
вопрос давайте предположим, что эти
фотографии, как вы видите здесь это
рисунок
все бутылки имеют массу m
ну допустим у всех одинаково
масса m
и допустим синие бутылки
поднял на высоту
ч б или ч
красные бутылки будут высотой h r
желтый будет высотой h y, а розовый
один лс так ясно синие бутылки
находятся в
максимальная высота правильно ладно давайте двигаться
вперед с вопросом сейчас
так что нам нужно, если сила тяжести
на массу 1 кг г
Ньютон, то найти силу
требовалось или требовалось поднять тело так
сила тяжести на
масса 1 кг означает, что мы знаем, что сила
массу в g справа и дано, что для
масса 1 кг, т. м равен 1 сила тяжести
г ньютонов, что также дано в
вопрос
нам нужно найти силу, необходимую для подъема
тело
так как вы можете видеть, что это магазин
менеджер, он хранит бутылки
на этих стойках прямо так
здесь, когда он поднимает синий
бутылка все бутылки имеют одинаковую массу
поэтому, когда он продолжает брать синюю бутылку
держит его на высоте HB
затем он берет красную бутылку скажем
и держит его на высоте
h он делает для желтого и розового
бутылки
а, следовательно, сила, необходимая
поскольку
масса одинакова, а g равно
ускорение свободного падения такое же
приложенная сила равна
вес тела мы знаем, что m g
вот как теперь измеряется сила
должен найти
сила, необходимая для подъема тела на
когда он поднимает бутылки
это то, что сила требуется и
он равен весу тела
так что если масса равна 1, то сила равна м в g
g — ускорение под действием силы тяжести
масса 1 кг
поэтому приложенная сила будет просить
j ньютона в данном случае
давайте перейдем к следующей части, которая
найти работу
сделано в подъеме тела, так что теперь он
поднимая тело и удерживая его над
вот это мы все знаем
совершенная работа отдается в виде силы в
смещение
мы уже рассчитали силу
разве это не мг
а в этом случае, так как масса равна 1 кг, значит
поэтому мы приняли это как
следовательно, сила равна g, если масса равна единице.
м равен 1 сила тяжести
г ньютонов, что также дано в
вопрос
нам нужно найти силу, необходимую для подъема
тело
так как вы можете видеть, что это магазин
менеджер, он хранит бутылки
на этих стойках прямо так
здесь, когда он поднимает синий
бутылка все бутылки имеют одинаковую массу
поэтому, когда он продолжает брать синюю бутылку
держит его на высоте HB
затем он берет красную бутылку скажем
и держит его на высоте
h он делает для желтого и розового
бутылки
а, следовательно, сила, необходимая
поскольку
масса одинакова, а g равно
ускорение свободного падения такое же
приложенная сила равна
вес тела мы знаем, что m g
вот как теперь измеряется сила
должен найти
сила, необходимая для подъема тела на
когда он поднимает бутылки
это то, что сила требуется и
он равен весу тела
так что если масса равна 1, то сила равна м в g
g — ускорение под действием силы тяжести
масса 1 кг
поэтому приложенная сила будет просить
j ньютона в данном случае
давайте перейдем к следующей части, которая
найти работу
сделано в подъеме тела, так что теперь он
поднимая тело и удерживая его над
вот это мы все знаем
совершенная работа отдается в виде силы в
смещение
мы уже рассчитали силу
разве это не мг
а в этом случае, так как масса равна 1 кг, значит
поэтому мы приняли это как
следовательно, сила равна g, если масса равна единице. тогда сила g
Ньютон прав, так что мы уже знаем
сила здесь
так что будет расстояние или
смещение
в этом случае сейчас идут эти высоты
на картинке, как вы можете видеть
он берет бутылку, сохраняя
синяя бутылка на большем расстоянии
поэтому он больше, чем hr больше, чем
поэтому hb больше, чем больше, чем
h желтого больше, чем h розового
так что явно больше работы сделано
чтобы сохранить тело тело, которое имеет массу одинаковую массу все тела такие же, как но
синяя бутылка
большая часть работы выполняется там, потому что
смещение
больше почему, потому что проделанная работа
равна силе смещения
возьмем водоизмещение л.с. или ч
скажем
поэтому совершенная работа равна
сила, которую мы уже рассчитали
что мг
и смещение h поэтому работают
сделано
m g h теперь, как только мы сохраним
бутылка вон там, когда у нас есть
хранил это здесь
найти потенциальную энергию, запасенную в
тело
поэтому эта проделанная работа сохраняется в теле
в виде потенциальной энергии, и это
потенциальная энергия также равна
мг, так что в случае с синими бутылками это будет
быть может
в случае с красными бутылками это может быть
в случае с желтой бутылкой это будет моя
и то же самое для розовой бутылки, которая
мог бы
поэтому отсюда мы также можем узнать, какой
один имеет наибольшую потенциальную энергию
правильно, так что я надеюсь, что вы поняли это
вопрос, если есть какие-либо дополнительные вопросы, пожалуйста, оставьте свои комментарии ниже
спасибо
тогда сила g
Ньютон прав, так что мы уже знаем
сила здесь
так что будет расстояние или
смещение
в этом случае сейчас идут эти высоты
на картинке, как вы можете видеть
он берет бутылку, сохраняя
синяя бутылка на большем расстоянии
поэтому он больше, чем hr больше, чем
поэтому hb больше, чем больше, чем
h желтого больше, чем h розового
так что явно больше работы сделано
чтобы сохранить тело тело, которое имеет массу одинаковую массу все тела такие же, как но
синяя бутылка
большая часть работы выполняется там, потому что
смещение
больше почему, потому что проделанная работа
равна силе смещения
возьмем водоизмещение л.с. или ч
скажем
поэтому совершенная работа равна
сила, которую мы уже рассчитали
что мг
и смещение h поэтому работают
сделано
m g h теперь, как только мы сохраним
бутылка вон там, когда у нас есть
хранил это здесь
найти потенциальную энергию, запасенную в
тело
поэтому эта проделанная работа сохраняется в теле
в виде потенциальной энергии, и это
потенциальная энергия также равна
мг, так что в случае с синими бутылками это будет
быть может
в случае с красными бутылками это может быть
в случае с желтой бутылкой это будет моя
и то же самое для розовой бутылки, которая
мог бы
поэтому отсюда мы также можем узнать, какой
один имеет наибольшую потенциальную энергию
правильно, так что я надеюсь, что вы поняли это
вопрос, если есть какие-либо дополнительные вопросы, пожалуйста, оставьте свои комментарии ниже
спасибо


 0040
0040