Модель это в информатике: 1. Понятие модели — Информатика

11 Понятие модели. Материальные и информационные модели

11 Понятие модели. Материальные и информационные модели

Понятиемодели. Материальные и информационные модели. Формализация как замена реальногообъекта его информационной моделью.

Моделирование.

Человечество в своей деятельности (научной, образовательной,технологической, художественной) постоянно создает и использует моделиокружающего мира. Строгие правила построения моделей сформулировать невозможно,однако человечество накопило богатый опыт моделирования различных объектов ипроцессов.

Модели позволяют представить в наглядной форме объекты и процессы, недоступныедля непосредственного восприятия (очень большие или очень маленькие объекты,очень быстрые или очень медленные процессы и др.). Наглядные модели частоиспользуются в процессе обучения. В курсе географии первые представления онашей планете Земля мы получаем, изучая ее модель — глобус, в курсе физикиизучаем работу двигателя внутреннего сгорания по его модели, в химии приизучении строения вещества используем модели молекул и кристаллических решеток,в биологии изучаем строение человека по анатомическим муляжам и др.

Модели играют чрезвычайно важную роль в проектировании и создании различныхтехнических
устройств, машин и механизмов, зданий, электрических цепей и т. д. Безпредварительного создания чертежа — невозможно изготовить даже простуюдеталь, не говоря уже о сложном механизме.

В процессе проектирования зданий и сооружений кроме чертежей частоизготавливают макеты. В процессе разработки летательных аппаратов поведение ихмоделей в воздушных потоках исследуют в аэродинамической трубе. Разработка электрическойсхемы обязательно предшествует созданию электрических цепей и так далее.

Развитие науки невозможно без создания теоретических моделей (теорий,законов, гипотез и пр.), отражающих строение, свойства и поведение реальныхобъектов. Создание новых теоретических моделей иногда коренным образом меняетпредставление человечества об окружающем мире (гелиоцентрическая система мираКоперника, модель атома Резерфорда-Бора, модель расширяющейся Вселенной, модельгенома человека и пр.).

Адекватность теоретических моделей законам реальногомира проверяется с помощью опытов и экспериментов.

Все художественное творчество фактически является процессом созданиямоделей. Например, такой литературный жанр, как басня, переносит реальныеотношения между людьми на отношения между животными и фактически создает моделичеловеческих отношений. Более того, практически любое литературное произведениеможет рассматриваться как модель реальной человеческой жизни. Моделями, вхудожественной форме отражающими реальную действительность, являются такжеживописные полотна, скульптуры, театральные постановки и пр.

Моделирование — это метод познания, состоящий в создании иисследовании моделей.

Модель.

Каждый объект имеет большое количество различных свойств. В процессепостроения модели выделяются главные, наиболее существенные для проводимогоисследования свойства. В процессе исследования аэродинамических качеств моделисамолета в аэродинамической трубе важно, чтобы модель имела геометрическоеподобие оригинала, но не важен, например, ее цвет.

При построении электрическихсхем — моделей электрических цепей — необходимо учитывать порядок подключенияэлементов цепи друг к другу, но не важно их геометрическое расположение друготносительно друга и так далее.

Разные науки исследуют объекты и процессы под разными углами зрения и строятразличные типы моделей.

В физике изучаются процессы взаимодействия и изменения объектов, в химии —их химический состав, в биологии — строение и поведение живых организмов и такдалее.

Возьмем в качестве примера человека: в разных науках он исследуется в рамкахразличных моделей. В рамках механики его можно рассматривать как материальнуюточку, в химии — как объект, состоящий из различных химических веществ, вбиологии — как систему, стремящуюся к самосохранению, и так далее.

Модель — это некий новый объект, который отражает существенныеособенности изучаемого объекта, явления или процесса.

С другой стороны, разные объекты могут описываться одной моделью. Так, вмеханике различные материальные тела (от планеты до песчинки) могутрассматриваться как материальные точки.
Один и тот же объект может иметь множество моделей, а разные объекты могутописываться одной моделью.

Никакая модель не может заменить сам объект. Но при решении конкретнойзадачи, когда нас интересуют определенные с
войства изучаемого объекта, модельоказывается полезным, а подчас и единственным инструментом исследования.

Модели материальные и модели информационные.

Все модели можно разбить на два больших класса: модели предметные(материальные) и модели информационные. Предметные модели воспроизводятгеометрические, физические и другие свойства объектов в материальной форме(глобус, анатомические муляжи, модели кристаллических решеток, макеты зданий исооружений и др.).

Информационные модели представляют объекты и процессы в образной илизнаковой форме.
Образные модели (рисунки, фотографии и др.) представляют собой зрительныеобразы объектов, зафиксированные на каком-либо носителе информации (бумаге,фото- и кинопленке и др.). Широко используются образные информационные модели вобразовании (учебные плакаты по различным предметам) и науках, где требуетсяклассификация объектов по их внешним признакам (в ботанике, биологии,палеонтологии и др. ).

Знаковые информационные модели строятся с использованием различных языков(знаковых систем). Знаковая информационная модель может быть представлена вформе текста (например, программы на языке программирования), формулы (например,второго закона Ньютона F=ma), таблицы (например, периодической таблицыэлементов Д. И. Менделеева) и так далее.

Иногда при построении знаковых информационных моделей используютсяодновременно несколько различных языков. Примерами таких моделей могут служитьгеографические карты, графики, диаграммы и пр. Во всех этих моделяхиспользуются одновременно как язык графических элементов, так и символьныйязык.

Моделирование и формализация

На протяжении своей истории человечество использовало различные способы и инструментыдля создания информационных моделей. Эти способы постоянно совершенствовались.Так, первые информационные модели создавались в форме наскальных рисунков, внастоящее же время информационные модели обычно строятся и исследуются сиспользованием современных компьютерных технологий.

Формализация. —

Естественные языки используются для создания описательных информационныхмоделей. В истории науки известны многочисленные описательные информационныемодели- например, гелиоцентрическая модель мира, которую предложил Коперник,формулировалась следующим образом:

• Земля вращается вокругсвоей оси и вокруг Солнца-
• орбиты всех планет проходятвокруг Солнца.

С помощью формальных языков строятся формальные информационные модели(математические, логические и др.). Одним из наиболее широко используемыхформальных языков является математика. Модели, построенные с использованиемматематических понятий и формул, называются математическими моделями. Языкматематики является совокупностью формальных языков. —

Язык алгебры позволяет формализовать функциональные зависимости междувеличинами. Так, Ньютон формализовал гелиоцентрическую систему мира, открывзаконы механики и закон всемирного тяготения и записав их в виде алгебраическихфункциональных зависимостей.

В школьном курсе физики рассматривается многоразнообразных функциональных зависимостей, выраженных на языке алгебры, которыепредставляют собой математические модели изучаемых явлений или процессов.

Язык алгебры логики (алгебры высказываний) позволяет строить формальныелогические модели. С помощью алгебры высказываний можно формализовать (записатьв виде логических выражений) простые и сложные высказывания, выраженные наестественном языке. Построение логических моделей позволяет решать логическиезадачи, строить логические модели устройств компьютера (сумматора, триггера) итак далее.

В процессе познания окружающего мира человечество постоянно используетмоделирование и формализацию. При изучении нового объекта сначала обычностроится его описательная информационная модель на естественном языке, затемона формализуется, то есть выражается с использованием формальных языков(математики, логики и др.).

Визуализация формальных моделей. —

В процессе исследования формальных моделей часто производится ихвизуализация. Для визуализации алгоритмов используются блок-схемы:пространственных соотношений между объектами — чертежи, моделей электрическихцепей — электрические схемы, логических моделей устройств — логические схемы итак далее.

Так при
визуализации формальных физических моделей с помощью анимации можетотображаться динамика процесса, производиться построение графиков измененияфизических величин и так далее. Визуальные модели обычно являютсяинтерактивными, то есть исследователь может менять начальные условия и параметрыпротекания процессов и наблюдать изменения в поведении модели.

—

Что такое модель (определение)

Понятие модели (Н.В.Макарова) В отличие от концепции обучения моделированию предлагаемой А.И.Бочкиным, Н.В.Макарова вынесла понятия модели и моделирования в самое начало раздела «Компьютерное моделирование» (Информатика 9 класс). «..,все многообразие моделей отличает нечто общее, а именно моделью может стать искусственно созданный человеком абстрактный или материальный объект. Анализ модели и наблюдение за ней позволяют познать суть реально существующего объекта, процесса или явления, называемого прототипом или >оригиналом. Значит можно дать более простое определение и модели и процесса моделирования. Модель — упрощенное представление о реальном объекте, процессе или явлении. Моделирование — построение моделей для исследования и изучения объектов, процессов, явлений. Может возникнуть вопрос, почему бы ни исследовать сам оригинал, зачем создавать его модель? Во-первых, в реальном времени оригинал может уже не существовать или его нет в действительности. Для моделирования время не помеха. На основании известных фактов методом гипотез и аналогий можно построить модель событий или природных катаклизмов далекого прошлого (гибель Атлантиды, вымирание динозавров). С помощью такого же метода можно заглянуть в будущее (модель «ядерной зимы», мальтусовская модель перенаселения Земли, модель глобального потепления планеты и пр. ) Во-вторых, оригинал может иметь много свойств и взаимосвязей. Чтобы изучить какое — либо конкретное, интересующее нас свойство, иногда полезно отказаться от менее существенных, не рассматривая их. Что же поддается моделированию? Это может быть объект, явление или процесс. Моделями объектов могут быть уменьшенные копии архитектурных сооружений, наглядные пособия и пр. Модель может отражать нечто реально существующее, скажем атом водорода или Солнечную систему, структуру парламентской власти, грозовой разряд и пр. Для изучения явлений живой природы, для предотвращения катастрофы, для применения природных сил на благо человечества создаются модели явлений. Академик Георг Рихман , сподвижник и друг Ломоносова, еще в начале 18 века моделировал магнитные и электрические силы, чтобы изучить их и найти им дальнейшее применение. Когда речь на уроках географии идет о природных явлениях (землетрясения, цунами и пр.), мы имеем в виду не какой-то конкретный случай, а его обобщение. В моделях объектов или явлений отражаются свойства оригинала — его характеристики, параметры. Можно также создавать модели процессов, т.е. моделировать действия над материальными объектами: ход, последовательную смену состояний, стадий развития одного объекта или их системы. Примеры тому общеизвестны: это модели экологических или процессов, развития Вселенной или общества и т.п.. И, наконец, любым действиям человека, будь то разрешение конкретной житейской проблемы или выполнение какой-либо работы, предшествует возникновение модели будущего поведения. Это главное отличие человека мыслящего от всех других существ на земле.» На начало

Ответы на вопросы по информатике

1. Моделирование

Моделирование – это метод воспроизведения и исследования определённого фрагмента действительности (предмета, явления, процесса, ситуации) или управления им, основанный на представлении объекта с помощью его копии или подобия — модели. Модель обычно представляет собой либо материальную копию оригинала, либо некоторый условный образ, представленный в абстрактной (мысленной или знаковой) форме и содержащий существенные свойства моделируемого объекта. Процедуры создания моделей широко используются как в научно-теоретических, так и в прикладных сферах человеческой деятельности.

В научном познании модель рассматривается как «объект-подобие» или «объект-заместитель» объекта-оригинала, воспроизводящий определённые его характеристики. В этом смысле модель всегда соответствует объекту-оригиналу — в тех свойствах, которые подлежат изучению, но в то же время отличается от него по ряду других признаков, что делает модель удобной для исследования изучаемого объекта. Результаты разработки и исследования моделей при определённых условиях, принимаемых в методологии науки и специфических для различных областей и типов моделей, распространяются на оригинал. Использование метода моделирования в научном познании диктуется необходимостью раскрыть такие стороны объектов, которые либо невозможно постигнуть путём непосредственного изучения, либо непродуктивно изучать их таким образом в силу каких-либо ограничений.

В научном познании возможны два способа моделирования:

1. Эмпирический способ моделирования— подразумевает воссоздание эмпирически выявленных свойств и связей объекта в его модели.
2. Теоретический способ моделирования— подразумевает теоретическое воссоздание объекта в его модели.

Модели, применяемые в научном познании, разделяются на два больших класса:

1. Материальные модели представляют собой природные объекты, подчиняющиеся в своём функционировании естественным законам. Подразделяются на два основных вида: предметно-физические и предметно-математические модели.
2. Идеальные модели представляют собой идеальные образования, зафиксированные в соответствующей знаковой форме и функционирующие по законам логики мышления, отражающей мир. Подразделяются на два основных вида: идеализированные модельные представления и знаковые модели.

Соответственно указанным различениям выделяют основные разновидности моделирования. Каждое из них применяется в зависимости от особенностей изучаемого объекта и характера познавательных задач.

2. Графические информационные модели

В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.

Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта.

Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.

Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.

График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.

Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.

3. Табличные модели

Представление информации в табличной форме широко распространено. Уже в школьной жизни приходится встречаться с массой таблиц: расписание занятий, журнал успеваемости, график дежурств, таблица Менделеева, таблицы физических свойств веществ, таблицы исторических дат и многое другое. Информация в таблицах обязательно упорядочена по какому-то принципу. Например, в классном журнале — в алфавитном порядке фамилий учеников; в расписании занятий — по дням недели и номерам уроков и т.д. Такая упорядоченность позволяет быстро находить в таблице нужные сведения.

Чаще всего используются прямоугольные таблицы, состоящие из строк и столбцов (граф). В верхней строке таблицы обычно располагаются заголовки граф. Вот пример прямоугольной таблицы, содержащей сведения о погоде в течение нескольких дней.

Погода

Дата	Осадки	Температура (градусы С)	Давление (мм рт. ст.)	Влажность (проценты)
15.03.97	Снег	-3,5	746	67
16.03.97	Без осадков	0	750	62
17.03.97	Туман	1,0	740	100
18.03.97	Дождь	3,4	745	96
19. 03.97	Без осадков	5,2	760	87

Данная таблица является примером таблицы типа «объект-свойство». Каждая строка такой таблицы относится к конкретному объекту. В нашем примере это определенный день, заданный датой. Первая графа обычно идентифицирует этот объект, последующие графы отражают свойства (характеристики) объекта.

Другой тип таблиц называется «объект-объект». Такие таблицы отражают взаимосвязь между различными объектами. Примером является таблица успеваемости учеников по разным предметам.

4. Информационное моделирование

Многие процессы, происходящие в природе, в технике, в экономических и социальных системах, описываются сложными математическими соотношениями. Это могут быть уравнения, системы уравнений, системы неравенств и пр., которые являются математическими моделями описываемых процессов.

Математическая модель — это описание моделируемого процесса на языке математики.

Компьютерная математическая модель — это программа, реализующая расчеты состояния моделируемой системы по ее математической модели.

Что такое вычислительный эксперимент

Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом.

Вычислительный эксперимент в некоторых случаях может заменить реальный физический эксперимент.

Впечатляющий пример использования такой возможности — прекращение испытаний ядерного оружия, которые сопровождались значительным экологическим ущербом. Благодаря очень точным математическим моделям и мощным компьютерам стало возможно просчитать все последствия, к которым приводит изменение в конструкции ядерной бомбы. Образно говоря, удалось «взорвать бомбу» внутри компьютера, ничего не разрушив.

Важным свойством компьютерных математических моделей является возможность визуализации результатов расчетов. Этим целям служит использование компьютерной графики.

Представление результатов в наглядном виде — важнейшее условие для их лучшего понимания. Например, результаты расчетов распределения температуры в некотором объекте представляются в виде его разноцветного изображения: участки с самой высокой температурой окрашиваются в красный цвет, а с самой холодной — в синий. Участки с промежуточными значениями температуры окрашиваются в цвета спектра, равномерно переходящие от красного к синему.

Для изображения изменяющихся со временем (динамических) результатов используют графическую анимацию.

Компьютерная графика позволяет человеку в процессе проведения численного эксперимента «заглянуть» в недоступные места исследуемого объекта. Можно получить изображение любого сечения объекта сложной формы с отображением рассчитываемых характеристик: температурных полей, давления и пр. В реальном физическом эксперименте такое можно сделать далеко не всегда. Например, невозможно выполнить измерения внутри работающей доменной печи или внутри звезды. А на модели это сделать можно.

Управление на основе моделей

Еще одно важное направление компьютерного математического моделирования связано с использованием компьютеров в управлении. Компьютеры используют для управления работой химических реакторов на заводах, атомных реакторов на электростанциях, ускорителей элементарных частиц в физических лабораториях, полета автоматических космических станций и т. д.

Управляя производственной или лабораторной установкой, компьютер должен просчитывать ее I характеристики для того, чтобы вовремя снять показания с датчиков или оказать управляющее воздействие: включить реле, открыть клапан и т. п.

Все расчеты производятся по заложенным в программу управления математическим моделям. Важно, чтобы результаты этих расчетов получались в режиме реального времени управляемого процесса.

Имитационное моделирование

Имитационное моделирование — особая разновидность моделирования на компьютере.

Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.

Такое поведение в математике называется стохастическим. Из курса физики вам знакомо явление броуновского движения: хаотического перемещения легких частиц на поверхности жидкости из-за неравномерных ударов молекул с разных сторон. Нельзя точно рассчитать траекторию броуновской частицы, но ее можно сымитировать на экране компьютера. Отсюда и происходит название — имитационная модель.

К имитационным моделям относятся модели систем массового обслуживания: например, системы торговли, автосервиса, скорой помощи, в которых появление заявок на обслуживание и длительность обслуживания одной заявки — события случайные.

Задачи, решаемые с помощью имитационных моделей систем массового обслуживания, заключаются в поиске режимов работы служб сервиса (магазинов, автозаправок и пр.), уменьшающих время ожидания клиентов.

Еще одним популярным объектом для имитационного моделирования являются транспортные системы: сеть городских дорог, перекрестки, светофоры, автомобили. Модель имитирует движение транспортных потоков по городским улицам. Эксперименты на такой модели позволяют найти режимы управления движением (работа светофоров), уменьшающие возможность возникновения пробок. Работа имитационной модели всегда визуализируется на экране компьютера.

5. Системы, модели, графы

Графы

Составными частями графа являются вершины и ребра. На рисунке вершины отображены кружками – это элементы системы, а ребра изображены линиями – это связи (отношения) между элементами. Глядя на этот граф, легко понять структуру дорожной системы в данной местности.

Построенный граф позволяет, например, ответить на вопрос: через какие поселки надо проехать, чтобы добраться из Репкино в Мышкино? Видно, что есть два возможных пути: 1) Р — К — Б — М  и 2) Р- К — Д — Б — М. Можно ли отсюда сделать вывод, что 1-й путь короче 2) –го?  Нет, нельзя.  Данный граф не содержит количественных характеристик. Это не карта, где соблюдается масштаб и есть возможность измерить расстояние.

Граф, приведенный на следующем рисунке, содержит количественные характеристики. Числа около ребер обозначают длины дорог в километрах. Это пример взвешенного графа. Взвешенный граф может содержать количественные характеристики не только связей, но и вершин. Например, в вершинах может быть указано население каждого поселка. Согласно данным взвешенного графа, оказывается, что второй путь длиннее первого.

Подобные графы еще называют сетью. Для сети характерна возможность множества различных путей перемещения по ребрам между некоторыми парами вершин. Для сетей также характерно наличие замкнутых путей, которые называются циклами. В данном случае имеется цикл: К-Д-Б-К

На рассмотренных схемах каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать и от М к Б (предполагаем, что действует двустороннее движение). Такие графы являются неориентированными, а их связи называются симметричными.

Весьма распространенным типом систем являются системы с иерархической структурой. Иерархическая структура естественным образом возникает, когда объекты или некоторые их свойства находятся в отношении соподчинения (вложения, наследования). Как правило иерархическую структуру имеют системы административного управления, между элементами которых установлены отношения подчиненности (директор завода – начальники цехов – начальники участков – бригадиры — рабочие).  Иерархическую структуру имеют также системы, между элементами которых существуют отношения вхождения одних в другие.

Граф иерархической структуры называется деревом. Основным свойством  дерева является то, что между любыми двумя его вершинами  существует единственный путь. Деревья не содержат циклов и петель.

Дерево административной структуры РФ

Граф, отражающий иерархическую административную структуру нашего государства: РФ делится на семь административных округов; округа делятся на регионы (области и национальные республики), в состав которых входят города и другие населенные пункты. Такой граф называется деревом.

У дерева существует одна главная вершина, которая называется корнем дерева. Эта вершина изображается вверху; от нее идут ветви дерева. От корня начинается отсчет уровней дерева. Вершины, непосредственно связанные с корнем, образуют первый уровень.  От них идут связи к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин на следующем уровне. Такой принцип связи называется “один ко многим”. Вершины, которые не имеют порожденных, называются листьями (на нашем графе это вершины, обозначающие города).

Графическое моделирование результатов научных исследований.

Общую цель научной графики можно сформулировать так: сделать невидимое и абстрактное “видимым”.  Последнее слово заключено в кавычки, т.к. эта видимость часто весьма условна. Можно увидеть распределение температуры внутри неоднородно нагретого тела сложной формы без введения в него сотен микродатчиков, т.е. по существу его разрушения? – Да, можно, если есть соответствующая математическая модель и, что очень важно, договоренность о восприятии определенных условностей на рисунке. Можно увидеть распределение металлических руд под землей без раскопок? Строение поверхности чужой планеты по результатам радиолокации? Да, можно, с помощью компьютерной графики и предшествующей ей математической обработки.

Более того, можно “увидеть” и то, что, строго говоря, вообще плохо соответствует слову “видеть”. Так, возникшая на стыке химии и физики наука – квантовая химия – дает нам возможность “увидеть” строение молекулы. Эти изображения – верх абстракции и системы условностей, так как в атомном мире обычные наши понятия о частицах (ядрах, электронах и т.п.) принципиально неприменимы. Однако многоцветное “изображение” молекулы на экране компьютера для тех, кто понимает всю меру его условности, приносит большую пользу, чем тысячи чисел, являющихся результатами вычислений.

Изолинии.

Стандартный прием обработки результатов вычислительного эксперимента – построение линий (поверхностей), называемых изолиниями (изоповерхностями), вдоль которых некоторая функция имеет постоянное значение. Это очень распространенный прием визуализации характеристик некоторого скалярного поля в приближении сплошной среды: изотермы – линии равной температуры; изобары – линии равного давления; изолинии численности экологической популяции на местности и т.д.

Условные цвета, условное контрастирование

Это прием современной научной графики – условная раскраска. Она находит широчайшее применение в самых разных приложениях науки и представляет собой набор приемов по максимально удобной визуализации результатов компьютерного моделирования.

В различных исследованиях температурных полей встает проблема наглядного представления результатов, например, температур на метеорологических картах. Для этого можно рисовать изотермы на фоне карты местности. Но можно добиться еще большей наглядности, учитывая, что большинству людей свойственно воспринимать красный цвет как “горячий”, синий – как “холодный”. Переход по спектру от красного к синему отражает промежуточные значения температур.  При поиске полезных ископаемых методами аэросъемки с самолетов или космических спутников компьютеры строят условные цветовые изображения распределений плотности под поверхностью Земли и т.д.

Изображения в условных цветах и контрастах – мощнейший прием научной графики.

6. Объектно-информационные модели

Объектный подход к информационному моделированию берет свое начало в парадигме объектно-ориентированного программирования (ООП), возникшей в 1970-х годах. Главным понятием здесь является «объект».

Объект — часть окружающей нас действительности.

Понятие объекта является очень широким и объединяет в себе как реальные, осязаемые предметы (например: кресло, автомобиль, мост), так и образы, созданные мышлением человека (например: стихотворение, музыкальное произведение, математическая теорема).

Информационная модель объекта должна отражать некоторый набор его свойств.

Свойства объекта — это совокупности  признаков, которые отличают его от других объектов. В следующей таблице даны примеры объектов и их свойств.

Имя объекта	Свойства
Мой преподаватель	Имя Стаж работы Читаемый курс
Мой жесткий диск	Объем Количество занятой памяти
Важный документ	Имя Дата создания Объем занимаемой памяти Местоположение

У каждого конкретного объекта свойства имеют определенные значения. В нашем примере добавим значения свойств объектов.

Эти значения могут быть количественными величинами (10 лет, 5 Гб), но могут быть и именами других объектов. Например, «Иван Иванович Иванов» и «Математика» сами могут рассматриваться как объекты.

Состояние объекта характеризуется перечнем всех возможных его свойств и текущими значениями каждого из этих свойств.

Имя объекта	Свойства	Значения свойств
Мой преподаватель	Имя Стаж работы Читаемый курс	Иванов Иван Иванович 10 дет Математика
Мой  жесткий диск	Объем Количество занятой памяти	10 Гб 5 Гб
Важный документ	Имя Дата создания Объем занимаемой памяти Местоположение	main.doc 20 июня 2002 года 50Кб С: \ Documents

Изменение состояния объекта отражается в его информационной модели изменением значений его свойств. Как правило, объекты не остаются неизменными. Например, растет стаж работы учителя И.И. Иванова; на жестком диске изменяется объем занятой памяти; документ может быть перенесен на другой диск, в другую папку и пр. Все эти процессы в информационной модели отражаются изменениями значений свойств.

В объектно-информационной модели отражаются не только свойства, но также и поведение объекта. Поведение объекта — действия, которые могут выполняться над объектом или которые может выполнять сам объект. Теперь опишем поведение объектов из нашего примера.

Имя объекта	Поведение (действия)
Мой преподаватель	Чтение лекции Прием экзамена Проведение консультации
Мой жесткий диск	Форматирование Копирование
Важный документ	Открытие Чтение Запись Копирование Переименование

Графические информационные модели.

Многообразие графических информационных моделей

Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. Графические информационные модели являются простейшим видом моделей. С их помощью передаются внешние признаки объекта – размер, форма, цвет. Графические модели несут в себе больше информации, чем словесные.

Для более наглядного и понятного представления информации в графических информационных моделях используются графические изображения (образные элементы), которые могут быть дополнены текстами, числами и символами. Примерами графических информационных моделей являются схемы, карты, чертежи, графики, диаграммы и много другое.

Разберёмся более подробно с каждой из них.

Cхема – это графическое отображение состава и структуры сложной системы. Можно обратиться к ранее рассматриваемому примеру: две электрические схемы соединения переключателей.

Схема последовательного соединения переключателей

Схема параллельного соединения переключателей

На первой представлено последовательное соединение, а на второй – параллельное. Можно заметить, что с помощью схемы легче разбираться с такими задачами, нежели использовать словесное описание. Схемы используются на уроках биологии, истории и так далее.

Следующая графическая информационная модель – чертеж. Чертеж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования. При построении чертежа используются изображения, числа, текст. С помощью изображений мы получаем представление о форме объекта, с помощью чисел – о размере, с помощью текста – о названии объектов, размерах, в которых выполнены изображения. Примером чертежа является изображение детали перед её изготовлением.

На чертеже изображена деталь в разрезе, чтобы лучше было видно все части, составляющие нашу деталь, присутствуют размеры (числа).

Рассмотрим такую графическую информационную модель как карта. Карта используется для отображения местности в уменьшенном масштабе, которая является для нее объектом моделирования. Например, с помощью карты мы можем узнать сколько километров от Москвы до Санкт-Петербурга, как добраться на метро или автобусе с одного остановочного пункта до другого, где находится Будапешт и много другое. Для различных целей используются разнообразные карты: политическая, географическая, тематическая и другие.

Перейдем к графикам. График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

Например, Максим учится в девятом классе. В течение 8 лет учёбы в школе он получал следующие годовые оценки по математике: первый класс – 5, второй класс – 4, третий класс – 4, четвёртый – 5, пятый – 4, шестой – 3, седьмой – 4, восьмой — 3. Посмотрим, как это можно отобразить на графике. Ось X будет отображать классы с 1 по 8. Ось Y оценки с 1 до 5. Обратите внимание, что в данном графике за единицу будем брать две клеточки.

Расставим точки в соответствии с данными на координатной плоскости и соединим их линиями.

Мы получили необходимый график, с помощью которого можно сделать вывод, что знания Максима по математике ухудшились. Ещё одним примером графика является кардиограмма сердца. Кардиограмма точно определяет в каком ритме бьётся сердце.

Перейдём к диаграммам. Диаграмма – это графическое изображение, которое даёт наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Диаграммы бывают нескольких видов, но более подробно мы с ними познакомимся при изучении электронных таблиц.

А сейчас рассмотрим несколько примеров.

Первый: Наша планета состоит из воды и суши. Вода составляет семьдесят процентов от планеты, а суша – тридцать. Изобразим всё это с помощью круговой диаграммы. Нарисуем круг. Он будет изображать планету и соответственно будет равен ста процентам. Затем изобразим семьдесят процентов суши и тридцать процентов воды.

На данной диаграмме мы можем увидеть соотношение воды и суши.

Теперь рассмотрим ещё один пример. Саша тратит на дорогу от дома до школы 10 минут, Таня – 15 минут, Ира – 7 минут и Игорь – 20 минут. Давайте все это изобразим с помощью диаграммы. На оси X напишем имена учащихся, а на оси Y – время, затраченное на дорогу. Затем каждому учащемуся нарисуем столбик по высоте соответствующий времени его пути.

 

 Таким образом мы получили столбчатую диаграмму.

Важно запомнить:

·     Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений.

·     Схема – это графическое отображение состава и структуры сложной системы.

·     Чертёж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования.

·     График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

·     Диаграмма – это графическое изображение, которое дает наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений.

Идеальные и материальные модели

Неоднозначность термина «модель», огромное число типов моделирования и их быстрое развитие затрудняют в настоящее время построение логически законченной, удовлетворяющей всех классификации моделей. Любая подобная классификация условна в силу того, что она отражает, с одной стороны, субъективную точку зрения авторов, а с другой — ограниченность их знаний в конечном числе областей научного познания.

Данную классификацию следует рассматривать как попытку построения некоторого инструмента или модели для исследования свойств и характеристик самого процесса моделирования. Моделирование относится к общенаучным методам познания. Использование моделирования на эмпирическом и теоретическом уровнях исследования приводит к условному делению моделей на материальные и идеальные.

Материальное моделирование — это моделирование, при котором исследование объекта выполняется с использованием его материального аналога, воспроизводящего основные физические, геометрические, динамические и функциональные характеристики данного объекта. Основными разновидностями материального моделирования являются натурное и аналоговое. При этом оба вида моделирования основаны на свойствах геометрического или физического подобия.

Идеальное моделирование отличается от материального тем, что оно основано не на материализованной аналогии объекта и модели, а на аналогии идеальной, мыслимой и всегда носит теоретический характер. Идеальное моделирование является первичным по отношению к материальному. Вначале в сознании человека формируется идеальная модель, а затем на ее основе строится материальная.

Материальное моделирование

Основными разновидностями материального моделирования являются натурное и аналоговое. При этом оба вида моделирования основаны на свойствах геометрического или физического подобия. Две геометрические фигуры подобны, если отношение всех соответственных длин и углов одинаковы. Если известен коэффициент подобия — масштаб, то простым умножением размеров одной фигуры на величину масштаба определяются размеры другой, ей подобной геометрической фигуры. Два явления физически подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой. Изучением условий подобия явлений занимается теория подобия.

Натурное моделирование — это такое моделирование, при котором реальному объекту ставится в соответствие его увеличенный или уменьшенный материальный аналог, допускающий исследование (как правило, в лабораторных условиях) с помощью последующего перенесения свойств изучаемых процессов и явлений с модели на объект на основе теории подобия.

Аналоговое моделирование — это моделирование, основанное на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими соотношениями, логическими и структурными схемами). В основу аналогового моделирования положено совпадение математических описаний различных объектов.

Модели физического и аналогового типов являются материальным отражением реального объекта и тесно связаны с ним своими геометрическими, физическими и прочими характеристиками. Фактически процесс исследования моделей данного типа сводится к проведению ряда натурных экспериментов, где вместо реального объекта используется его физическая или аналоговая модель.

Идеальное моделирование

Идеальное моделирование разделяют на два основных типа: интуитивное и научное.

Интуитивное моделирование — это моделирование, основанное на интуитивном (не обоснованном с позиций формальной логики) представлении об объекте исследования, не поддающимся формализации или не нуждающимся в ней. В качестве наиболее яркого примера интуитивной модели окружающего мира можно считать жизненный опыт любого человека. Любое эмпирическое знание без объяснения причин и механизмов наблюдаемого явления также следует считать интуитивным.

Научное моделирование — это всегда логически обоснованное моделирование, использующее минимальное число предположений, принятых в качестве гипотез на основании наблюдений за объектом моделирования.

Главное отличие научного моделирования от интуитивного заключается не только в умении выполнять необходимые операции и действия по собственно моделированию, но и в знании «внутренних» механизмов, которые используются при этом. Можно сказать, что научное моделирование знает не только, как необходимо моделировать, но и почему так нужно делать. Необходимо подчеркнуть чрезвычайно важную роль интуиции, интуитивных моделей в науке, без них не обходится не одно сколь-нибудь новое знание. Последнее недостижимо только методами формальной логики.

Интуитивное и научное (теоретическое) моделирование ни в коей мере нельзя противопоставлять одно другому. Они хорошо дополняют друг друга, разделяя области своего применения.

Знаковым называют моделирование, использующее в качестве моделей знаковые изображения какого-либо вида: схемы, графики, чертежи, наборы символов, включающее также совокупность законов и правил, по которым можно оперировать с выбранными знаковыми образованиями и элементами. В качестве примеров таких моделей можно назвать любой язык, например: устного и письменного человеческого общения, алгоритмический и т.д. Знаковая форма используется для передачи как научного, так и интуитивного знания. Моделирование с помощью математических соотношений также является примером знакового моделирования.

Интуитивное знание является генератором нового знания. Однако далеко не все догадки и идеи выдерживают последующую проверку экспериментом и методами формальной логики, свойственными научному подходу, выступающему в виде своеобразного фильтра для выделения наиболее ценных знаний.

 

Модель

Моделирование

Процесс моделирования

Процесс математического моделирования

 

На главную страницу

 

 

 

 

Абстрактная модель — это… Что такое Абстрактная модель?

Абстрактная модель — это модель, отражающая лишь самые общие характеристики моделируемого явления. Чаще всего абстрактная модель дает лишь качественные характеристики моделируемого объекта или явления.

Сферы применения абстрактных моделей

Такие модели могут применяться в физике, химии, экономике и других науках. Они нужны везде, где нужно составить самое общее, первичное представление об объекте. Особенно часто абстрактные модели применяются в социальных науках, где невозможно произвести непосредственный эксперимент, а также часто требуется вычленить определенное явление. Хорошим примером могут быть гуманитарные науки, такие как социология. Предметом её изучения является общество, над которым не представляется возможным ставить эксперименты. Поэтому социология вынуждена ограничиваться лишь мысленным экспериментом. Также из-за невообразимого количества взаимосвязей, присутствующих в обществе, социологу требуется выделить наиболее важные для его исследования объекты и взаимоотношения, то есть сформулировать абстрактную модель. Обычно абстрактная модель является первым шагом в изучении явления и необходимым условием для появления математической модели изучаемого явления. Обычно абстрактная модель также позволяет исследовать явление «в первозданной чистоте», т.к. большинство является максимально идеализированным представлением определенного объекта/явления. Особенно важна абстрактная модель в информатике, т.к. там очень часто разработчику высокоуровневого приложения требуется доступ к функциям и возможностям более низкого уровня, при необходимости абстрагирования от деталей его реализации. Примером такой модели может быть например Сетевая модель OSI, которая дает видение общих принципов реализации сетевого взаимодействия, абстрагируясь от конкретных деталей реализации в различных системах.

Источники

Лопатников Л. И. Экономико-математический словарь:Словарь современной экономической науки. — 5-е изд., перераб. и доп. — М.: Дело, 2003. — 520 с.

Модели и моделирование – Сайт учителя математики и информатики

Как вы понимаете слово «модель»?

Окружающий нас мир очень многообразен. Объекты вокруг нас имеют сложное строение и обладают присущими им отличительными свойствами. В процессе познания мира невозможно учесть все свойства объектов. И поэтому нередко в процессе изучения объектов используют их модели. Другими словами, намного удобнее изучать не сам реальный объект, а его модель, которая отражает определенные его свойства.

Для примера рассмотрим в качестве объекта человека. Для маленьких детей первой моделью человека является кукла. С возрастом эта модель становится им неинтересной. Поэтому кукла должна быть заменена другой моделью. Как и сам человек, его модели разнообразные. То есть конкретная модель будет изменяться в зависимости от цели. Например, портному в работе пригодится манекен, так как его в первую очередь интересуют размеры человека — рост, объем груди, ширина спины и т.д.

А для учителя, преподающего анатомию, или медицинского работника, изучающего структуру костей человека, ничто не заменит скелета человека. В моделях, созданных скульптором или художником, большое значение имеет внешний вид человека. Таким образом, для одного и того же объекта можно создать разные модели. Кукла, манекен, скульптура, картина — это модели, отражающие разные свойства человека.

В зависимости от формы реализации модели делят на два вида: материальные и информационные.

Материальную модель можно потрогать руками. Приведенные выше кукла, скульптура материальные модели человека.

Информационная модель — это представленная в определенном виде информация, описывающая существенные свойства объекта или события. Информационные модели широко распространены. Например, описание любого события или объекта в литературном произведении, изображение материального объекта на бумаге (рисунок, схема) тоже являются информационными моделями.

Таким образом, когда говорят о модели объекта, имеют в виду образ, отражающий его определенные свойства. Сам объект, по которому создают модель, называют объектом-оригиналом. Процесс создания и изучения моделей называют моделированием. На протяжении жизни человек постоянно сталкивается с разными задачами: как создавать новые машины и механизмы, как строить новое, комфортабельное жилье, как уберечься от болезней и т. д. Моделирование дает возможность решать такие задачи намного быстрее и с меньшими затратами.
Для информатики, естественно, интересны именно информационные модели. Для представления информационных моделей пользуются как естественными, так и формальными языками. Естественные языки предпочтительнее при создании словесных, изобразительных моделей. Например, между литературным произведением и понятием модели есть непосредственная связь, так как произведение обращает внимание читателя на разные стороны жизни. Наиболее ярко это видно в баснях.

При создании математических, логических и специальных моделей используют формальные языки. Примером математической модели может быть любая формула, знакомая вам с урока математики.

Одной из простейших форм информационной модели является графическая модель. Графические модели отражают внешние свойства объектов — размеры, форму, цвет. В отличие от словесных моделей графические модели более информационны. На уроках биологии, географии, военного дела, истории широко используют карты. Прежде чем приступить к созданию технических устройств, строительству зданий, готовят их чертежи.

Для того чтобы наглядно показать цифровые и статистические данные, используют графики и диаграммы.

После того, как появились компьютеры, их стали широко применять для создания моделей. Современные компьютеры позволяют создавать очень сложные компьютерные модели.

Компьютерные модели могут заменить как материальные, так и нематериальные (информационные) модели. Когда-то, чтобы заранее изучить, как будут работать машины и механизмы, создавали их материальные модели. Сегодня, в некоторых случаях, нет необходимости в таких моделях. С этой задачей гораздо успешнее справляются современные компьютерные программы.

Обобщение урока №1 про 

модели и моделирование:

• Когда говорят о модели объекта, имеют в виду образ, который отражает его определенные свойства. Объект, по которому создают модель, называют объектом-оригиналом.
• Модели разделяют на два вида: материальные и информационные.
• Процесс создания и изучения модели называют моделированием.
• Кукла, манекен, скульптура, портрет — это разнообразные модели человека.
• Моделирование дает возможность решать задачи, с которыми сталкивается человек, намного быстрее и с меньшими затратами.
• Для представления информационной модели в той или иной форме используют как естественные, так и формальные языки.
• Компьютерные модели могут заменить материальные и информационные модели.

В следующем уроке мы рассмотрим — Графический редактор Google SketchUP.

Компьютерное моделирование

Моделирование распространения инфекционных заболеваний для определения эффективных вмешательств . Точное моделирование инфекционных заболеваний опирается на множество больших наборов данных. Например, оценка эффективности социального дистанцирования в отношении распространения гриппоподобного заболевания должна включать информацию о дружбе и общении между людьми, а также стандартные биометрические и демографические данные. Исследователи, финансируемые NIBIB, разрабатывают новые вычислительные инструменты, которые могут включать новые доступные наборы данных в модели, предназначенные для определения наилучшего курса действий и наиболее эффективных вмешательств во время пандемического распространения инфекционных заболеваний и других чрезвычайных ситуаций в области общественного здравоохранения.

Многомасштабное моделирование (МСМ) — это сложный тип вычислительного моделирования, который включает несколько уровней биологической системы. Изображение предоставлено ISB.

Отслеживание вирусной эволюции во время распространения инфекционного заболевания. РНК-вирусов, таких как ВИЧ, гепатит В и коронавирус, постоянно мутируют, чтобы развить лекарственную устойчивость, избежать иммунного ответа и вызвать новые инфекции. Образцы секвенированных патогенов от тысяч инфицированных людей можно использовать для идентификации миллионов эволюционирующих вирусных вариантов.Исследователи, финансируемые NIBIB, создают вычислительные инструменты для включения этих важных данных в анализ инфекционных заболеваний, проводимый специалистами здравоохранения. Новые инструменты будут созданы в партнерстве с CDC и будут доступны в Интернете для исследователей и медицинских работников. Проект усилит эпидемиологический надзор и лечение заболеваний во всем мире и позволит разработать более эффективные стратегии искоренения болезней.

Преобразование беспроводных данных о здоровье в улучшение здоровья и здравоохранения. Устройства для мониторинга состояния здоровья в больницах и носимые датчики, такие как умные часы, генерируют огромные объемы данных о состоянии здоровья в режиме реального времени. Медицинское обслуживание, основанное на данных, обещает быть быстрым, точным и менее дорогостоящим, но постоянные потоки данных в настоящее время ограничивают возможность использования информации. Исследователи, финансируемые NIBIB, разрабатывают вычислительные модели, которые преобразуют потоковые данные о состоянии здоровья в полезную форму. Новые модели будут обеспечивать физиологический мониторинг в реальном времени для принятия клинических решений в Национальной детской больнице.Команда математиков, биомедицинских информатиков и персонала больниц будет генерировать общедоступные данные и программное обеспечение. Проект будет использовать рынок беспроводной связи в здравоохранении с оборотом в 11 миллиардов долларов для значительного улучшения здравоохранения.

Человеческое и машинное обучение для индивидуального управления вспомогательными роботами. Чем тяжелее у человека нарушение моторики, тем сложнее управлять вспомогательными механизмами, такими как инвалидные коляски с электроприводом и роботизированные руки. Доступные средства управления, такие как устройства для затягивания и затягивания, не подходят для людей с тяжелым параличом.Исследователи, финансируемые NIBIB, разрабатывают систему, которая позволит людям с тетраплегией управлять роботизированной рукой, одновременно поощряя упражнения и поддерживая остаточные двигательные навыки. Технология использует интерфейсы тела и машины, которые реагируют на минимальное движение конечностей, головы, языка, плеч и глаз. Первоначально, когда пользователь двигается, машинное обучение дополняет сигнал для выполнения задачи с помощью роботизированной руки. Помощь сокращается по мере того, как машина передает управление все более опытному пользователю. Этот подход направлен на расширение возможностей людей с тяжелым параличом и предоставление интерфейса для безопасного обучения управлению роботами-помощниками.

Обновлено в мае 2020 г.

Роль моделей в информатике в JSTOR

Абстрактный

Взяв за отправную точку исследование Брайана Кантуэлла Смита «Пределы корректности компьютеров», эта статья исследует роль моделей в информатике. Смит выделяет два типа моделей, которые играют важную роль: спецификации — это модели проблем, а программы — модели возможных решений. Оба предполагают существование концептуализаций как способов восприятия мира «определенными ограниченными способами». «Но языки программирования высокого уровня также функционируют как модели виртуальных (или абстрактных) машин, в то время как языки программирования низкого уровня функционируют как модели причинных (или физических) машин. Итоговый отчет предполагает, что наборы моделей, встроенные в модели, незаменимы для компьютерное программирование.

Информация о журнале

The Monist, основанный в 1888 году Эдвардом К. Хегелером, является одним из старейших и важнейших философских журналов в мире.Он помог сделать философию профессиональной дисциплиной в Соединенных Штатах, опубликовав таких философов, как Льюис Уайт Бек, Джон Дьюи, Готтлоб Фреге, Ханс-Георг Гадамер, Сидни Хук, К. Льюис, Эрнст Мах, Чарльз Сандерс Пирс, Хилари Патнэм, Уиллард Ван Орман Куайн, Бертран Рассел и Грегори Властос. The Monist ежеквартально издает тематические выпуски по определенным философским темам, которые редактируют ведущие философы в соответствующих областях. В результате каждый выпуск представляет собой сборную антологию, вызывающую постоянный интерес.

Информация об издателе

Oxford University Press — это отделение Оксфордского университета. Издание во всем мире способствует достижению цели университета в области исследований, стипендий и образования. OUP — крупнейшая в мире университетская пресса с самым широким присутствием в мире. В настоящее время он издает более 6000 новых публикаций в год, имеет офисы примерно в пятидесяти странах и насчитывает более 5500 сотрудников по всему миру. Он стал известен миллионам людей благодаря разнообразной издательской программе, которая включает научные работы по всем академическим дисциплинам, библии, музыку, школьные и университетские учебники, книги по бизнесу, словари и справочники, а также академические журналы.

Абстрактная модель — обзор

2 Нейронные сети с прямой связью: частотный и байесовский подход

Нейронные сети изначально задумывались как абстрактные модели мозга. Однако с годами их область применения значительно расширилась, и теперь они используются во множестве приложений, включая регрессию и классификацию. Интерес к моделям нейронных сетей возродился благодаря работе Rumelhart et al. (1996), Цибенко (1989) и др.Нейронная сеть — это набор простых вычислительных единиц, которые сильно взаимосвязаны (рис. 1). Эти единицы также называются узлами и в общих чертах представляют собой биологический нейрон. Для простоты здесь мы рассматриваем только сети с «обратным распространением» или «с прямой связью». Эти сети принимают набор входов xi = (xi1,…, xip) T и вычисляют из них некоторые выходы Oi, используя определенное количество слоев. В типичной нейронной сети с одним скрытым слоем выходы могут быть вычислены как

(1) Oi = β0 + ∑j = 1Mβjψ (γj0 + ∑s = 1pxisγjs), i = 1,…, n.

В (1) γjs — вес от входа xis до скрытой единицы j. Точно так же βj — это вес, прикрепленный к скрытой единице j. Γj0 и β0 — смещения для скрытых узлов и выходных блоков. Однако при необходимости они могут абсорбироваться в γjs и βj (Риос Инсуа и Мюллер, 1998). Количество скрытых узлов обозначено M. Функция ψ упоминается как функция активации .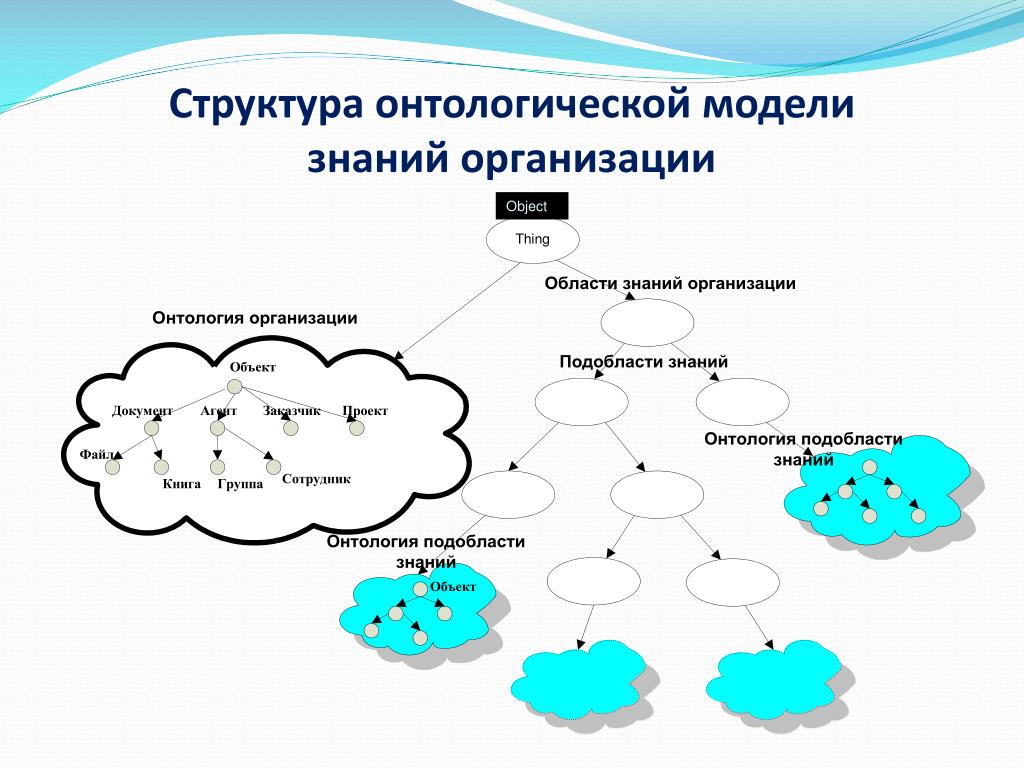 Обычно ψ нелинейна. Некоторые из наиболее распространенных вариантов ψ — это функции логистики exp (x) 1 + exp (x) и гиперболического тангенса exp (x) -exp (-x) exp (x) + exp (-x).

Cybenko (1989) показал, что если количество скрытых узлов стремится к бесконечности, то их можно использовать как универсальный аппроксиматор любой непрерывной функции в компактном диапазоне. Обозначим через In n-мерный единичный куб [0,1] n. Пространство непрерывных функций на In обозначается C (In) и использует || f || для обозначения нормы супремума f∈C (In). Цибенко (1989) показал, что если ψ — произвольная непрерывная сигмоидальная функция, то суммы вида (1) плотны в C (In). В классическом подходе веса и смещения в нейронных сетях изучаются на основе набора обучающих примеров (xi, yi) с входными данными xi и целями yi.Стандартные процедуры обучения нейронной сети регулируют веса и смещения в сети, чтобы минимизировать некоторую меру ошибок, чаще всего сумму квадратов отклонений между выходами сети и целями, то есть R (Θ) = ∑i (Oi-yi ) 2, где Θ — множество всех параметров сети (весов и смещений). Это составляет оценку максимального правдоподобия, когда добавляется член ошибки, скажем ei, в определение Oi в (1) и предполагается нормальность ошибок. Чтобы избежать переобучения, мы добавляем штрафную функцию C (Θ) к мере ошибки, и штрафная мера ошибки определяется следующим образом:

(2) Rp (Θ) = R (Θ) + λC (Θ).

Функция ошибок R (Θ) или Rp (Θ) невыпуклая и имеет множество локальных минимумов. В результате полученное окончательное решение во многом зависит от выбора начальных весов.

В байесовской перспективе аппроксимация сетевой модели путем минимизации (2) может рассматриваться как максимизация апостериорной

(3) π (θ | Training Set) ∝exp {-R (Θ) -λC (Θ)},

где exp (-R (Θ)) — это вероятность, а exp {-λC (Θ)} — априорная оценка весов и смещения сети. В начале девяностых годов Бантин и Вейганд (1991) и Маккей (1992) показали, что принципиальный байесовский подход к обучению нейронных сетей может привести ко многим улучшениям.В частности, Маккей показал, что путем аппроксимации распределений весов гауссианами и принятия априорных значений сглаживания можно получить оценки весов и дисперсии выходных данных и автоматически установить коэффициенты регуляризации. Нил (1996) ввел передовые методы байесовского моделирования, особенно гибридный метод Монте-Карло, в анализ нейронных сетей.

В байесовском подходе к обучению нейронной сети цель состоит в том, чтобы найти прогнозирующее распределение для целевых значений в новом «тестовом» случае (xn + 1, yn + 1), учитывая входные данные в этом случае и входные данные. и цели в учебных случаях.

(4) P (yn + 1 | xn + 1, обучающий набор) = ∫P (yn + 1 | xn + 1, Θ) P (Θ | обучающий набор) dΘ.

Апостериорное распределение для Θ обычно очень сложное, с множеством мод. Таким образом, поиск прогнозного распределения для тестового примера путем вычисления интеграла (4) является сложной задачей. Для вычисления интеграла используется метод Монте-Карло цепи Маркова, основанный на гибридном алгоритме Монте-Карло. Гибридный алгоритм Монте-Карло — это разновидность алгоритма Метрополиса, в котором состояния-кандидаты находятся посредством динамического моделирования.

Моделирование и симуляция: информатика иллюзий

От редакции Предисловие.

Предисловие.

Глава 1. Основные концепции и инструменты.

1.1. Моделирование и симуляция: что это?

1.2. Валидность, достоверность, сговорчивость и проверка.

1.3. Состояние системы и причинные системы.

1.4. Классификация динамических систем.

1.5. Дискретное и непрерывное моделирование.

1.6. Эволюция программного обеспечения для моделирования.

Глава 2. Непрерывное моделирование.

2.1. Вступление.

2.2 Обыкновенные дифференциальные уравнения и модели систем с сосредоточенными параметрами.

2.3. Непрерывное моделирование с помощью аналоговых компьютеров.

2.4. Численные методы решения обыкновенных дифференциальных уравнений (ОДУ).

2.5. Графики прохождения сигналов.

2.6. Графики облигаций.

2.7. Альтернативные инструменты моделирования и динамической неопределенности.

2.8. Системы с распределенными параметрами.

2.9. Системная динамика.

2.10. Галактическое моделирование и проблема N тел.

Глава 3. Дискретное и комбинированное моделирование — пример реализации PASION.

3.1. Действительны ли дискретные модели ?.

3.2. Система моделирования PASION.

3.3. Генератор модели массового обслуживания QMG.

3.4. Комплексный системный симулятор PASION.

Глава 4. Дифференциальные включения в моделировании и симуляции.

4.1. Дифференциальные включения.

4.2. Возможные приложения.

4.3. Решатель дифференциального включения.

4.4. Применение в обработке неопределенности.

4.5. Неопределенное будущее и дифференциальные включения.

4.6. Выводы и дальнейшие исследования.

Глава 5. Гидродинамика — моделирование колеблющегося потока газа.

5.1. Вычислительная гидродинамика.

5.2. Численные задачи.

5.3. Инструмент моделирования.

5.4. Примеры.

5.5. Колеблющийся поток газа.

5.6. Двумерные гидродинамические модели недействительны.

5.7. Выводы.

Глава 6. Моделирование явлений общей теории относительности.

6.1. Некоторые основные понятия.

6.3. Инструмент моделирования и модельное время.

6.4. Имитационные эксперименты.

Глава 7. Взаимодействие враждебных иерархических структур: моделирование борьбы террористических и антитеррористических организаций .

7.1. Вступление.

7.2. Модель.

7.3. Структуры.

7.4. Инструмент и реализация модели.

7.5. Имитационные эксперименты.

7.6. Выводы.

Глава 8. О метрической структуре в пространстве моделей динамических систем.

8.1. DEVS.

8.2. Определения.

8.3. Расстояние между моделями.

8.4. Примеры.

8.5. Выводы.

Глава 9. Оптимизация моделирования: пример параллельного алгоритма оптимизации.

9.1. Вступление.

9. 2. Постановка задачи.

9.3. Имитационный эксперимент.

9.4. Выводы.

Список литературы.

Индекс.

Компьютерное моделирование | Encyclopedia.com

█ JUDSON KNIGHT

Моделирование в техническом использовании этого термина относится к преобразованию объектов или явлений из реального мира в математические уравнения.Компьютерное моделирование — это представление трехмерных объектов на компьютере с использованием программного обеспечения, разработанного для этой цели. Среди применений компьютерного моделирования — военные игры и моделирование бедствий, ситуации, в которых компьютеры предлагают безопасные, относительно недорогие средства создания или воссоздания событий без сопутствующих потерь жизни или имущества.

Математика, компьютеры и программное обеспечение для моделирования

Математическое моделирование восходит к достижениям в геометрии и других дисциплинах в конце восемнадцатого века.Среди них была начертательная геометрия французского математика Гаспара Монжа, техника которого была настолько ценной для артиллерии Наполеона, что долгие годы оставалась засекреченной оборонной тайной. Спустя почти полтора столетия, в конце Второй мировой войны, математики и ученые, работавшие на военные нужды Соединенных Штатов, разработали машину для быстрого перевода математических моделей в формы, легко понятные нематематикам.

Этой машиной был компьютер, и в течение последних двух десятилетий двадцатого века множество разновидностей программного обеспечения для трехмерного моделирования получили распространение.Сюда входило любое количество компьютерных анимационных и игровых пакетов, а также различные системы автоматизированного проектирования / автоматизированного производства (CAD / CAM). CAD позволял инженерам и архитекторам, например, создавать сложные модели, которые позволяли им «заглядывать» в незастроенные конструкции и тестировать уязвимости этих структур, не рискуя жизнями или деньгами.

Одним из примечательных вариантов трехмерного программного обеспечения является язык моделирования виртуальной реальности, сокращенно VRML и произносится как «вер-мал». «Необходимый для представления трехмерных объектов во всемирной паутине (той части Интернета, к которой обычные пользователи наиболее привыкли), VRML создает виртуальный мир или гиперпространство, которое можно просматривать через двумерный экран компьютера. Автор нажимая назначенные клавиши, пользователь может перемещаться не только вверх, вниз, вправо и влево, но и вперед и назад в этом виртуальном мире.

Катастрофы, войны и другие симуляции

После того, как космический шаттл Columbia разбился 1 февраля 2003 г. аналитики Национального управления по аэронавтике и исследованию космического пространства (НАСА) использовали программное обеспечение для моделирования, применяемое Национальным советом по безопасности на транспорте (NTSB) для изучения аварий.В приложениях, таких как приложения для исследований NASA и NTSB, цель состоит в том, чтобы понять не только то, что произошло, но и как и почему это произошло, и чем это вызвано.

Чем больше данных о бедствии доступно, тем лучше модель, а это, в свою очередь, дает следователям более точные инструменты для анализа. Однако в конце концов человеческому рассуждению ничто не заменит. Например, симуляция NTSB авиакатастрофы Swissair Flight 111 в сентябре 1998 года отслеживала курс огня из кабины, который в конечном итоге сбил самолет, но не объясняла, что вызвало пожар.

Тем не менее, симуляция бесценна, поскольку она предоставляет человеческому разуму чрезвычайно точный и яркий источник информации о точной последовательности событий, произошедших во время бедствия. Аналитики НАСА использовали компьютерное моделирование для изучения первой крупной катастрофы шаттла Challenger в 1986 году, но технологии 2003 года были намного лучше. Мало того, что компьютер за 2000 долларов был способен запускать симуляции, для которых 17 лет назад требовалась машина за 75000 долларов, но и достижения в области графики, вызванные, по иронии судьбы, кажущимися легкомысленными требованиями игр и фильмов, привели к гораздо более точной картине того, что произошло. .

Военные игры и симуляторы террора. Связь между развлечением и симуляцией в целом, а также технологией компьютерного моделирования в частности, не была потеряна для руководства США в области безопасности и обороны. Сразу после теракта 11 сентября 2001 г. федеральные чиновники собрали команду, в которую вошли Дэвид Финчер, директор бойцовских клубов Seven, и ; Стивен Э.

Де Соуза, сценарист Крепкий орешек; и Спайк Джонз, директор Быть Джоном Малковичем. Задача, поставленная перед этими творческими умами, идеально подходила для Голливуда: представить сценарии нападения террористов на Соединенные Штаты.

Эти сценарии, наряду с другими формами ввода, помогли сформировать основу для моделирования такими группами, как Институт творческих технологий (ИКТ), исследовательский центр Университета Южной Калифорнии в Лос-Анджелесе. ИКТ — одна из многих организаций, в которые федеральное правительство инвестирует почти 100 миллионов долларов в год с целью разработки военных симуляторов — исследований, которые, в отличие от моделей бедствий для NTSB или NASA, касаются не столько того, что произошло, сколько того, что может случиться . Министерство обороны также имеет свои собственные аналитические центры по моделированию, в том числе Командование по моделированию, обучению и приборостроению армии США, известное как STRICOM.

Моделирование, разработанное компанией ICT, ошеломляет своей степенью правдоподобия. «Виртуальные люди» на экране — не автоматы; скорее, они были запрограммированы личностями и эмоциями, как персонажи в кино. Новейшие компьютерные технологии позволяют даже имитировать запахи. В результате необычного слияния государственного и частного секторов ICT продала коммерческие версии игр, которые она производила совместно с U.С. Армия.

Цель моделирования, производимого ICT и другими организациями, участвующими в компьютерном моделировании, выходит далеко за рамки простого развлечения: за небольшую часть затрат и рисков, связанных с военными играми с участием реальных войск и оборудования, командиры и их подчиненные могут учиться и извлекать уроки из боя. Компьютерное моделирование также позволяет изучать десятки различных видов террора, но без каких-либо человеческих или финансовых затрат. Предоставляя лаборатории для обучения, моделирование может предотвратить потери в реальных ситуациях.

█ ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ:

КНИГИ:

Дэнби, Дж. М. А. Компьютерное моделирование: от спорта к космическим полетам — от порядка к хаосу. Ричмонд, Вирджиния: Willmann-Bell, 1997.

Emmer, Michele. Визуальный разум: искусство и математика. Кембридж, Массачусетс: MIT Press, 1993.

Моделирование и имитация: увязка развлечений и обороны. Вашингтон, округ Колумбия: National Academy Press, 1997.

ЭЛЕКТРОННЫЙ:

Ли, Дэвид Б., лейтенант.Полковник, ВВС США. «War Gaming: думая о будущем». Airpower Journal (14 марта 2003 г.).

Военный институт ВВС США. (14 марта 2003 г.).

Исполнительный офис программы армии США по моделированию, обучению и оснащению. mil/> (14 марта 2003 г.).

СМОТРИ ТАКЖЕ

Интернет
НАСА (Национальное управление по воздуху и исследованию космического пространства)
NTSB (Национальный совет по безопасности на транспорте)
Суперкомпьютеры

Образцы для подражания пробуждают интерес студентов к компьютерным наукам

Основные моменты истории

• Учащиеся, являющиеся образцами для подражания, более чем в 10 раз чаще проявляют интерес
• 53% U.Студенты S. говорят, что у них есть образец для подражания в области информатики
• Девочки, сельские жители и темнокожие школьницы с наименьшей вероятностью будут такими образцами для подражания

Примечание редактора. Приведенное ниже исследование было проведено в партнерстве между Amazon и Gallup.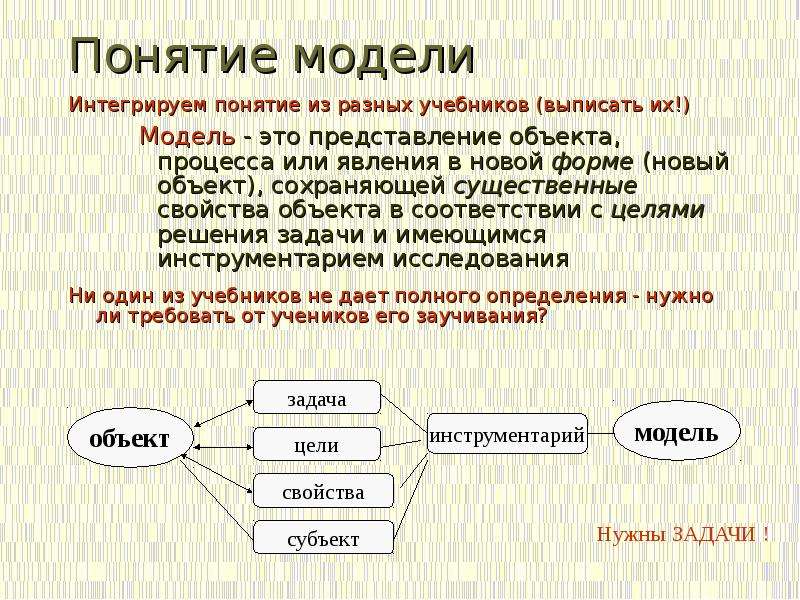

ВАШИНГТОН, округ Колумбия — Недавно опубликованное исследование, проведенное Gallup в партнерстве с Amazon Future Engineer, подтверждает давние анекдотические и качественные доказательства того, что образцы для подражания важны для пробуждения серьезного интереса студентов к карьере в области информатики.Исследование показало, что американские ученики с 5 по 12 классы, которые полностью согласны с тем, что у них есть образец для подражания в области информатики, более чем в 10 раз чаще, чем те, кто категорически не согласен с тем, чтобы сказать, что они планируют продолжить такую ​​карьеру — 73% vs. 7% соответственно.

Интерес студентов к информатике, уверенность в том, что они могут преуспеть в этом, и планы заниматься этим в колледже и за его пределами — все это во многом связано с наличием в их жизни образцов для подражания. Восемьдесят процентов тех, кто полностью или частично согласен с тем, что у них есть образец для подражания в области информатики, заинтересованы в изучении этой темы, по сравнению с 43% тех, кто категорически или несколько не согласен.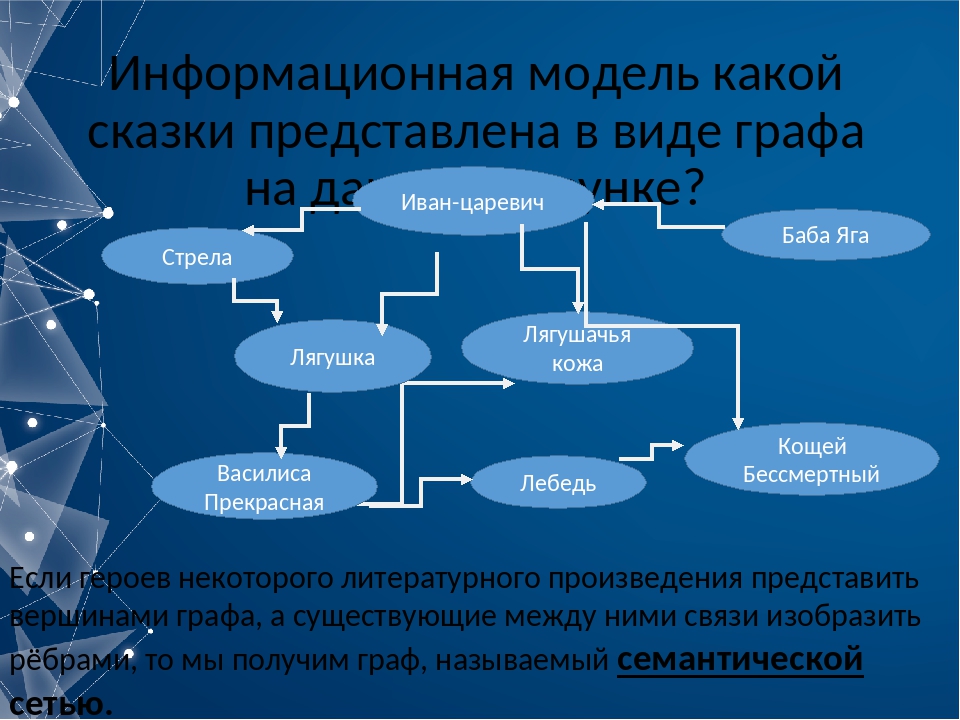

Вы заинтересованы в изучении информатики?

	Да, заинтересовались	Нет, не интересует
	%	%
Студенты, которые согласны с тем, что у них есть образец для подражания в информатике	80	20
Студенты, которые не согласны с тем, что у них есть образец для подражания в информатике	43	57
Исследование Amazon Future Engineer / Gallup, 2021 год

Эти отношения между образцами для подражания и стремлениями к информатике являются постоянными среди учащихся каждого пола, расы / этнической принадлежности и группы доходов домохозяйства.

Небольшое большинство студентов согласны с тем, что у них есть ролевые модели по информатике

Исследование, проведенное 2–20 июня 2021 года более чем 4000 учащихся с пятого по двенадцатый классы, показало, что 53% американских студентов согласны с тем, что у них есть образцы для подражания в области информатики.

Оцените, насколько вы согласны со следующим утверждением: У меня есть образцы для подражания в информатике.

Полностью согласен	26%
Скорее согласен	27%
Скорее не согласен	21%
Совершенно не согласен	26%
Исследование Amazon Future Engineer / Gallup, 2021

Шестьдесят один процент тех, кто посещал уроки информатики в школе, говорят, что у них есть образцы для подражания в этой области, по сравнению с 45%, которые не посещали уроки.

Эти выводы относятся к числу более подробных сведений, доступных в полном отчете.

У меньшего числа девочек, сельских или чернокожих студентов есть ролевые модели по информатике

Однако традиционно недостаточно обслуживаемые группы населения, включая сельских студентов, чернокожих студентов и девочек, реже, чем их сверстники, сообщают, что у них есть образцы для подражания в информатике.

Наибольшие различия наблюдаются среди сельских студентов по сравнению с городскими студентами. Только 15% студентов, живущих в сельской местности, полностью согласны с тем, что у них есть образцы для подражания в области компьютерных наук, по сравнению с 46% студентов, живущих в больших городах.Этот пробел в доступе к ролевым моделям, вероятно, связан с соответствующей разницей в доступе к урокам информатики, которые менее распространены в сельских школах, потому что учителя часто выступают в качестве этих ролевых моделей.

Наличие ролевых моделей в компьютерных науках, по городскому хозяйству

Оцените, насколько вы согласны со следующим утверждением: У меня есть образцы для подражания в информатике.

	Полностью согласен	Скорее согласен	Скорее не согласен	Совершенно не согласен
	%	%	%	%
Крупные города	46	26	13	14
Пригород	19	31	22	28
Малые города	14	25	28	33
Сельская местность	15	21	26	38
Исследование Amazon Future Engineer / Gallup, 2021

азиатских и белых учащихся с большей вероятностью, чем латиноамериканских студентов, полностью согласны с тем, что у них есть образцы для подражания в области информатики, а темнокожие студенты — наименее вероятны.Мальчики на 10 процентных пунктов чаще, чем девочки, сообщают, что у них есть такие образцы для подражания.

Наличие ролевых моделей в компьютерных науках по расе / этнической принадлежности и полу

Оцените, насколько вы согласны со следующим утверждением: У меня есть образцы для подражания в информатике.

	Полностью согласен	Скорее согласен	Скорее не согласен	Совершенно не согласен
	%	%	%	%
Белые студенты	29	28	19	23
Черные студенты	17	28	21	33
Латиноамериканские студенты	23	26	23	28
Азиатские студенты	35	24	25	16
Учащиеся	31	27	20	22
Студентки	21	28	22	29
Исследование Amazon Future Engineer / Gallup, 2021

Итог

Исследование Amazon Future Engineer / Gallup Student Study поддерживает прошлые исследования, показывающие, что ролевые модели важны для пробуждения интереса студентов к информатике.Ролевые модели представляют собой зеркало, в котором учащиеся могут увидеть свое настоящее и будущее, а также окно в область, которая имеет решающее значение для того, чтобы помочь им увидеть возможности, которые она может им предложить.

Хотя важность ролевой модели информатики очевидна, существует неравенство в доступе к ней. Эти дисбалансы тесно связаны с другими различиями в доступе к информатике и участии в ней в сельских районах, для исторически недопредставленных и маргинализированных студентов и девочек.Еще предстоит проделать большую работу, чтобы предоставить студентам видение карьеры и помочь им понять практическое применение этой востребованной области, в которой отсутствует разнообразие кадров.

Прочтите полный отчет, чтобы получить более подробные сведения о доступе к информатике и интересе к ней. Узнайте больше о программе Amazon Future Engineer Program здесь.

% PDF-1.3 % 1 0 объект > транслировать / GS4 GS BT / F0 1 Тс 8.96638 0 0 8.96638 285,36 ​​727,6801 тм 0 г [(T) 80 (o) 27 (w) 27 (ards) -347 (a) -347 (Mo) -27 (del) -362 (of) -347 (Computer) -347 (Science) -349 (Graduate) ) -347 (Прием) -360 (Решения)] TJ / F1 1 Тс 9,96264 0 0 9,96264 72,48 685,8 тм [(P) 25 (ap) -25 (er:) — 482 (jc * — ** — ** — ****)] TJ / F2 1 Тс 17,21544 0 0 17,21544 86,76 663,72 тм [(T) 77 (o) 27 (w) 28 (ards) -294 (a) -299 (Mo) -29 (del) -299 (of) -300 (Computer) -301 (Science) -314 (Graduate) ) -308 (Прием)] TJ 10,33723 -1,1571 ТД (Решения) Tj / F3 1 Тс 11,95517 0 0 11,95517 267,6 620,88 тм [(Найджел) -330 (W) 80 (ard)] TJ / F4 1 Тс 7.97011 0 0 7,97011 204,12 601,44 тм [(Компьютер) -361 (Наука,) — 376 (Univ) 30 (ersit) 32 (y) -362 (of) -346 (T) 90 (exas) -361 (at) -376 (El) -346 ( P) 31 (aso)] TJ -1,64113 -1,43034 ТД [(500) -376 (W) 90 (est) -360 (Univ) 30 (ersit) 31 (y) -361 (Av) 30 (en) 30 (ue,) — 362 (El) -361 (P) 31 (aso,) — 346 (T) 90 (exas) -360 (79968,) — 377 (США)] TJ 8,77779 -1,4454 ТД [(nigelw) 30 ([email protected])] TJ -4,80294 -1,49057 ТД [([Получение) 31 (ред.) -377 (00/00/00;) — 376 (принято) -390 (00/00/00])] TJ / F5 1 Тс 10,90909 0 0 10,90909 275,88 528,2401 тм (Аннотация) Tj -18,645 -1,65 TD [(Абстрактный.) -418 (P) 33 (oten) 33 (tial) -264 (Applican) 33 (ts) -242 (to) -231 (выпускник) -242 (sc) 33 (ho) -33 (ol) -242 ( \ fnd) -209 (it) -231 (di \ 016cult) -231 (to) -242 (прогнозировать,) — 242 (ev) 33 (en) -242 (приблизительно) 33 (ximately) 88 (,)] TJ 0 -1,1 TD [(whic) 33 (h) -396 (sc) 33 (ho) -33 (ols) -407 (будет) -407 (принять) -418 (им.) — 649 (W) 88 (e) -418 ( га) 33 (v) 33 (e) -407 (создано) -418 (a) -407 (прогнозирующее) 33 (e) -407 (mo) -33 (del) -396 (из) -407 (поступление) — 396 (решение -)] TJ Т * [(изготовление,) — 429 (pac) 33 (k) 55 (возраст) -418 (in) -407 (the) -407 (form) -396 (of) -407 (a) -407 (w) 33 ( eb) -407 (page) -407 (that) -418 (allo) 33 (ws) -418 (studen) 33 (ts) -396 (to) -418 (en) 33 (ter) -407 (их) — 407 (информация)] TJ 0 -1.089 ТД [(а) -297 (см.) -308 (а) -297 (список) -308 (из) -308 (сбн) 33 (хо) -33 (ols) -308 (где) -286 (они) -308 (are) -297 (lik) 33 (ely) -319 (to) -308 (b) -33 (e) -297 (принято) — 451 (This) -286 (pap) -33 (er) -297 (объясняет) -297 (the) -297 (обоснование)] TJ 0 -1,1 TD [(для) -341 (the) -352 (mo) -33 (del’s) -352 (design) -341 (and) -341 (параметр) -352 (v) 55 (alues.) — 484 (In) 33 (интерес) -363 (вопросы) -341 (включить) -341 (в) -352 (ш) 33 (а) 33 (у) -352 (тот) -352 (доказательства)] TJ 0 -1,089 TD [(is) -341 (com) 33 (bined,) — 330 (the) -341 (оценка) -352 (of) -330 (parameters,) — 341 (и) -330 (the) -341 (mo) » -33 (делинг) -330 (из) -341 (неточно) 33 (т) 33 (у) 88 (.)] TJ / F0 1 Тс 8,96638 0 0 8,96638 271,44 426,84 тм [(Индекс) -322 (T) 81 (erms)] TJ -19,7538 -1,

ТД [(studen) 26 (t) -320 (оценка) 29 (t,) — 361 (принятие) -348 (критерии,) — 360 (заявка) -347 (ev) 53 (оценка,) — 347 (принятие решений) ,) — 360 (com) 27 (bination) -348 (of) -347 (evi -)] TJ 0 -1,23127 ТД [(dence,) — 349 (заказано) -334 (w) 26 (восемь) 27 (ted) -348 (a) 27 (v) 27 (erage,) — 360 (неопределенно) 27 (t) 27 (y) 81 (,) — 335 (GRE) -334 (баллы,) — 373 (GP) 80 (A,) — 335 (буквы) -359 (из) -348 (рекомендации)] TJ / F5 1 Тс 10,90909 0 0 10,90909 71,88 72,96 тм [(V) 88 (ол.0) -363 (№ 0,) — 352 (200x) -5654 (журнал) -330 (из) -330 (Adv) 55 (anced) -330 (вычислительный) -352 (In) 33 (интеллигентный) -11473 (1)] TJ 17,655 -1,089 TD [(и) -319 (In) 33 (Telligen) 33 (t) -363 (Информатика)] TJ ET конечный поток эндобдж 2 0 obj > эндобдж 3 0 obj > транслировать / GS4 GS BT / F0 1 Тс 8,96638 0 0 8,96638 71,52 731,76 тм 0 г [(Найджел) -348 (W) 80 (ard)] TJ / F3 1 Тс 11,95517 0 0 11,95517 71,52 696,72 тм [(1) -60 (.) — 412 (В) 30 (тро) -31 (воздуховод)] ТДж / F5 1 Тс 10,90909 0 0 10,90909 81,96 673,8 тм [(The) -440 (pro) -33 (cess) -429 (b) 33 (y) -440 (whic) 33 (h) -440 (p) -33 (oten) 33 (tial) -462 (выпускник) ) -440 (студент) 33 (ц) -440 (и) -440 (выпускник) -440 (сбн) 33 (хо) -33 (олс) -451 (пришел) -451 (вместе) -462 (есть)] TJ -0.957 -1,089 ТД [(требует много времени) -407 (для) -407 (для) -407 (для) 33 (ts,) — 429 (для) -407 (для) -396 (p) -33 (для людей) -407 (для ) -396 (написать) -407 (буквы) -418 (из) -407 (рекомендация,) — 429 (и)] TJ 0 -1,1 TD [(для) -385 (поступлений) -385 (комитетов) -407 ([1) -11 (,) — 385 (2) -11 (].) — 616 (В) -374 (ан) -396 (попытка ) -396 (to) -396 (mak) 33 (e) -396 (the) -396 (pro) -33 (cess) -385 (подробнее) -385 (e \ 016cien) 33 (t,) — 429 ( w) 33 (e) -396 (га) 33 (v) 33 (e)] TJ 0 -1,09999 ТД [(created) -308 (a) -308 (w) 33 (eb) -297 (to) -33 (ol) -308 (that) -308 (can) -308 (help) -286 (inform) -297 ») (p) -33 (oten) 33 (tial) -319 (выпускник) -308 (studen) 33 (ts) -297 (in) -297 (Computer) -286 (Science) -308 ((CS))] TJ 0 -1.089 ТД [(ab) -33 (out) -418 (ho) 33 (w) -418 (application) -429 (are) -418 (ev) 55 (aluated.) — 715 (This) -407 (w) »33 ( as) -418 (dev) 33 (elop) -33 (ed) -418 (at) -429 (the) -418 (Departmen) 33 (t) -429 (of) -429 (Computer)] TJ 0 -1,09999 ТД [(Наука) -385 (at) -374 (UT) -374 (El) -374 (P) 33 (aso) -385 (as) -385 (a) -374 (service) -385 (to) -385 (the) -374 (computer) -374 (science) -385 (comm) 33 (unit) 33 (y) 88 (.) — 583 (Using) -374 (this) -374 (to) -33 (ol) -385 (ma) 33 (y)] TJ 0 -1,089 TD [(включить) -341 (заявка) 33 (ts) -341 (к) -341 (b) -33 (etter) -341 (цель) -341 (их) -341 (e \ 013orts,) — 341 (к ) -341 (the) -341 (b) -33 (ene \ ft) -319 (of) -341 (all.)] TJ 0,957 -1,09999 TD [(А) 33 (т) -363 (в) -363 (сердце) -352 (из) -352 (в) -363 (в) -33 (ол) -363 (в) -352 (а) -363 (mo) -33 (del) -352 (of) -352 (the) -363 (b) -33 (eha) 33 (vior) -352 (of) -363 (компьютер) -352 (наука) -363 ( выпускник) -363 (поступление)] TJ -0,957 -1,1 TD [(комитеты.) — 451 (предыдущий) -286 (w) 33 (ork) -297 (имеет) -286 (sho) 33 (wn) -286 (тот) -297 (a) -286 (подчиненные) 33 ( t’s) -297 (отказ) -308 (решения) -286 (can) -297 (b) -33 (e) -286 (предсказано)] TJ 0 -1.08899 TD [(b) 33 (y) -264 (a) -264 (линейный) -275 (mo) -33 (del) -264 (производный) 33 (ed) -264 (b) 33 (y) -264 (m) ) 33 (конечный) -275 (регресс) -264 ([1) -11 (].) -429 (Наш) -253 (mo) -33 (del) -264 (go) -33 (es) -264 (b) -33 (ey) 33 (ond) -264 (this) -264 (to) -275 (pro) -33 (duce) -253 (ac -)] TJ 0 -1,1 TD [(cept / reject) -319 (предсказания) -286 (для) -297 (a) -297 (большой) -308 (n) 33 (um) 33 (b) -33 (er) -286 (of) — 286 (отдел) 33 (ц,) — 308 (для) -297 (скорее) -297 (разнородный) -308 (аппликан) 33 (ц,)] TJ 0 -1,09999 ТД [(и) -308 (для) -308 (заявка) 33 (ts) -330 (для) -308 (кого) -308 (только) -319 (частичная) -319 (информация) -319 (есть) -308 (a) 33 (v) 55 (больной.) — 473 (С) -308 (the) -319 (data) -319 (a) 33 (v) 55 (нездоровый) -341 (w) 33 (as)] TJ 0 -1.089 ТД [(неадекватно) -264 (для) -253 (автоматический) -286 (мес.) -33 (дел-билдинг,) — 264 (наш) -253 (пн.) -33 (дел) -253 (использует) -253 ( вычисления) -275 (WHIC) 33 (H) -253 (точно) -275 (затем) 33 (W) -275 (the)] TJ 0 -1,09999 ТД [(соображения) -352 (и) -341 (обоснование) -363 (использовалось) -330 (б) 33 (у) -352 (допуски) -341 (комитеты,) — 385 (тамб) 33 (у) -341 (включение) -352 (параметр) -352 (параметр)] TJ 0 -1,089 TD [(v) 55 (alues) -341 (to) -341 (b) -33 (e) -319 (выведено) -330 (логически) -363 (и) -330 (justi \ fed) -319 (in) 33 (tuitiv) 33 (ely) 88 (.)] TJ 0,957 -1,1 TD [(Это) -220 (pap) -33 (er) -220 (fo) -33 (cuses) -220 (on) -231 (те) -231 (asp) -33 (ects) -231 (of) — 231 (the) -231 (mo) -33 (del) -231 (whic) 33 (h) -220 (are) -231 (in) 33 (teresting) -242 (in) -231 (terms) -231 ( оф) -220 (com) 33 (bination)] TJ -0.957 -1,1 TD [(из) -407 (доказательства,) — 429 (параметр) -418 (оценка,) — 440 (и) -396 (обоснование) -418 (меньше) -385 (неуверенно) 33 (t) 33 (y) 88 (.) — 682 (Меньше) -407 (дюйм) 33 (интерес) -418 (подробности)] TJ 0 -1,089 TD [(are) -308 (do) -33 (cumen) 33 (ted) -297 (в другом месте) -308 ([3].) — 440 (хотя) -308 (the) -297 (pap) -33 (er ) -297 (только) -297 (адреса) -297 (один) -308 (домен,) -308 (в) -297 (вопросы) -297 (столкнулись)] TJ 0 -1,1 TD [(ma) 33 (y) -264 (также) -275 (возникают) -264 (in) -264 (другие) -264 (проблемы) -253 (in) 33 (v) 33 (olving) -275 (сложные) ) -275 (принятие решений) -275 (и) -253 (в) -264 (вывод) -264 (из) -264 (скрыто)] TJ Т * [(принятие решения) -341 (b) -33 (eha) 33 (vior) -341 (из) -330 (неполное) -341 (информация.)] TJ 0,957 -1,089 TD [(Это) -297 (pap) -33 (er) -308 (состояния) -319 (the) -308 (k) 33 (ey) -319 (предположения) -308 (in) -308 (Section) -319 (2,) — 319 (присутствует) 33 (ts) -308 (the) -308 (mo) -33 (del) -308 (for) -308 (computing) -319 (appli -)] TJ -0,957 -1,1 TD [(can) 33 (t) -352 (сила) -352 (in) -341 (Section) -352 (3,) — 352 (объясняет) -352 (ho) 33 (w) -341 (v) 55 ( arious) -352 (допуски) -341 (p) -33 (olicies) -352 (are) -352 (mo) -33 (deled) -341 (in) -341 (Section) -352 (4,)] TJ 0 -1,089 TD [(и) -330 (обсуждает) -319 (некоторые) -341 (направления) -341 (для) -330 (будущее) -330 (w) 33 (ork) -330 (in) -330 (Section) -341 (5.)] TJ / F3 1 Тс 11,95517 0 0 11,95517 71,52 373,92 тм [(2) -60 (.) — 412 (Ключ) -340 (Упрощение) -332 (Предположения)] TJ / F5 1 Тс 10,90909 0 0 10,90909 81,96 351 тм [(The) -374 (\ frst) -374 (предположение) -385 (b) -33 (ehind) -363 (the) -385 (mo) -33 (del) -374 (is) -385 (that) -396 (в) -385 (сила) -385 (из) -385 (ан) 33 (у) -385 (аппликан) 33 (т) -396 (может) -385 (б) -33 (д) -374 (представляют -)] TJ -0,957 -1,089 TD [(сен) 33 (ted) -429 (b) 33 (y) -429 (a) -429 (single) -429 (n) 33 (um) 33 (b) -33 (er,)) — 440 (указано ) -418 (к) -440 (b) -33 (elo) 33 (w) -429 (as) -429 (the) -429 (GQ) -418 (оценка) -440 (\ (GQ) -429 ( стоит) -418 (для) -429 (\ Generalized)] TJ 0 -1.1 TD [(Quan) 33 (titativ) 33 (e »,) — 363 (или) -341 (ma) 33 (yb) -33 (e) -330 (\\ Предположительно) -352 (Qualit) 33 (y» \ ).)] TJ 0,957 -1,089 TD [(The) -484 (второй) -495 (предположение) -495 (is) -495 (that) -495 (there) -495 (is) -495 (a) -506 (single,) — 539 (univ) 33 (внешне) -495 (общий) -495 (w) 33 (a) 33 (y) -495 (to) -506 (ev) 55 (aluate) -517 (CS)] TJ -0,957 -1,1 TD [(выпускник) -341 (sc) 33 (ho) -33 (ol) -341 (Applican) 33 (ts.) — 451 (хотя) -341 (ясно) -341 (a) -330 (упрощенный \ fcation, ) -352 (это) -330 (есть) -330 (не) -330 (ан) -330 (необоснованно) -330 (один,)] TJ Т * [(в) -385 (минимум) -396 (судейство) -374 (из) -374 (в) -374 (прием) -385 (комитет) -396 (дискуссии) -374 (при свидетелях) -374 (б) 33 (у) -374 (в) -385 (автор) -374 (в) -396 (три)] TJ 0 -1.089 ТД [(v) 33 (ery) -396 (di \ 013eren) 33 (t) -407 (институты:) — 583 (the) -396 (Univ) 33 (ersit) 33 (y) -418 (of) -396 » (Калифорния) -407 (в) -407 (Берк) 33 (эли) 88 (,) — 440 (в) -396 (Унив) 33 (эрсит) 33 (у) -418 (из) -396 (Т) 88 (оки) 33 (о,)] TJ 0 -1,1 TD [(и) -440 (the) -451 (Univ) 33 (ersit) 33 (y) -473 (of) -451 (T) 88 (exas) -462 (at) -451 (El) -451 (P ) 33 (aso.) — 814 (Di \ 013erences) -462 (in) -451 (the) -451 (ev) 55 (aluation) -473 (критерии) -462 (that) -462 (v) 55 (arious )] TJ Т * [(отправление) 33 (тс) -385 (присутствует) 33 (т) -374 (о) -385 (их) -385 (ш) 33 (эб) -374 (с.) -385 (ар) -396 (так ) 33 (ru) -385 (к) -396 (b) -33 (e) -374 (только) -374 (the) -385 (результат) -385 (из) -385 (случайный) -374 (пропуски) ] TJ 0 -1.089 ТД [(и) -220 (другое) -220 (шум.) — 418 (Это) -220 (подразумевает) -220 (это) -231 (то) -231 (признание) -220 (p) -33 (olicy) » -231 (из) -231 (ан) 33 (у) -220 (отдел) 33 (т) -231 (может) -231 (также) -231 (б) -33 (д) -220 (описать) -33 (ред)] TJ 0 -1,1 TD [(с) -330 (a) -341 (одиночный) -341 (n) 33 (um) 33 (b) -33 (er,) — 319 (the) -341 (порог) -319 (GQ.)] TJ 0,957 -1,1 TD [(The) -330 (третий) -319 (предположение) -330 (is) -341 (that) -341 (a) -330 (mo) -33 (del) -341 (need) -330 (not) — 330 (b) -33 (e) -330 (p) -33 (ошибочно) -330 (to) -341 (b) -33 (e) -330 (полезно.)] TJ / F3 1 Тс 11.95517 0 0 11.95517 71,52 182,64 тм [(3) -60 (.) — 412 (Mo) -30 (делинг) -341 (Applican) 31 (t) -332 (прочность)] TJ / F5 1 Тс 10,90909 0 0 10,90909 81,96 159,72 тм [(In) -418 (сущность,) — 462 (the) -418 (mo) -33 (del) -429 (нормализует) -429 (все) -440 (the) -429 (факторы) -429 (in)) 33 (v) 33 (olv) 33 (ed) -440 (to) -440 (one) -429 (scale) -440 (and) -418 (com) 33 (bines) -429 (them)] TJ -0,957 -1,089 TD [(используя) -330 (a) -352 (w) 33 (восемь) 33 (ting) -352 (whic) 33 (h) -341 (is) -341 (c) 33 (hosen) -341 (di \ 013eren) 33 (tly) -352 (дюйм) -341 (eac) 33 (h) -352 (case) -352 (to) -341 (захват) -341 (the) -341 (фактический) -363 (imp) -33 (ortance) -341 (или)] TJ 0 -1.1 TD [(informativ) 33 (eness) -341 (of) -341 (eac) 33 (h) -341 (factor.) — 462 (This) -319 (section) -352 (считает) -330 (eac) 33 ( з) -352 (коэффициент) -341 (дюйм) -330 (об.)] ТДж -0,055 -5,764 TD [(2) -12199 (Journal) -330 (of) -341 (Adv) 55 (anced) -330 (Computational) -341 (In) 33 (telligence) -4928 (V) 88 (ol.0) -352 (№0,) — 352 (200x)] TJ 17,644 -1,089 TD [(и) -330 (In) 33 (теллиген) 33 (t) -363 (информатика)] TJ ET конечный поток эндобдж 4 0 obj >] >> транслировать

.