Относительные показатели динамики: Задача №18. Расчёт относительных показателей динамики

Содержание

Задача №18. Расчёт относительных показателей динамики

Имеются следующие данные о производстве одной из моделей iPhone компанией Apple за 2013 год:

 I кварталII кварталIII кварталIV квартал
Произведено смартфонов, млн. штук 82,0 75,3 60,1 50,8

Определите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь.

 

Решение:

Относительная величина динамики характеризует развитие изучаемого явления во времени.

Относительный показатель динамики (ОПД) представляет собой отношение уровня изучаемого процесса или явления за данный период времени и уровня этого же процесса или явления в прошлом:

Относительный показатель динамики с переменной базой сравнения рассчитывается тогда, когда происходит сравнение с предыдущим уровнем. Его ещё также называют цепным темпом роста, так как основание относительной величины последовательно меняется.

Темп роста может быть выражен в процентах или коэффициентах.

где

уi – уровень текущего периода,

уi-1 – уровень предшествующего периода.

Относительный показатель динамики с постоянной базой (базисный) рассчитывается тогда, когда происходит сравнение с одним и тем же базисным уровнем. Его ещё также называют базисным темпом роста. Темп роста может быть выражен в процентах или коэффициентах.

где

у0 – уровень базисного периода.

  I кварталII кварталIII кварталIV квартал
Произведено смартфонов, млн. штук 82,0 75,3 60,1 50,8
Темп роста базисный, % 100,0 91,8 73,3 62,0
Темп роста цепной, % — 91,8 79,8 84,5

Из полученных базисных относительных величин динамики (темпов роста) видно, что за 2013 год объём производства смартфонов Apple неуклонно снижалось от квартала к кварталу:

91,8 ˃ 73,3 ˃ 62,0

Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходил спад производства.

Такое решение компании, возможно, вызвано тем, что спрос на устройства данной модели упал в связи с появлением новой более современной модели.

Между относительными показателями динамики с переменной и постоянной базой сравнения существует взаимосвязь: произведение цепных темпов роста (в коэффициентах) равно конечному базисному.

Так, для рассчитанных показателей получим:

0,918 * 0,798 * 0,845 = 0,619 ≈ 0,62.

Относительные показатели динамики численности населения

Будучи вполне приемлемым как первая характеристика динамики численности населения, его абсолютный прирост тем не менее обладает тем весьма существенным недостатком, что он сильно зависит от величины самой абсолютной численности населения, а также от длины рассматриваемого периода. Чем больше абсолютная численность населения и длина периода, тем больше при прочих равных условиях и абсолютная величина абсолютного прироста (убыли). Поэтому необходим переход к относительным показателям, которые очищены от влияния этих параметров. При этом в зависимости от того, рассчитываются ли эти относительные показатели по отношению к начальной или средней численности населения, принято различать соответственно темпы роста и прироста и коэффициенты роста и прироста. Ниже пойдет речь о темпах роста и прироста.

Темпы роста и прироста за период

Самыми простыми из них являются темпы роста и прироста за период. Первый из них равен отношению численности населения в конце периода к численности населения в его начале

Таблица 3.3

Темпы прироста населения России. 1961-2000 гг.. %

Годы Темпы прироста за год Годы Темпы прироста за год Годы Темпы прироста за год Годы Темпы прироста за год
1,36 0,57 0,57 0,11
1,18 0,58 0,68 -0,02
1,07 0,55 0,76 -0,21
0,90 0,63 0,69 -0,04
0,70 0,68 0,71 -0,22
0,66 0,71 0,89 -0,32
0,52 0,70 0,85 -0,27
0,53 0,68 0,71 -0,28
0,52 0,55 0,45 -0,53
0,50 0,53 0,34 -0,51

В табл.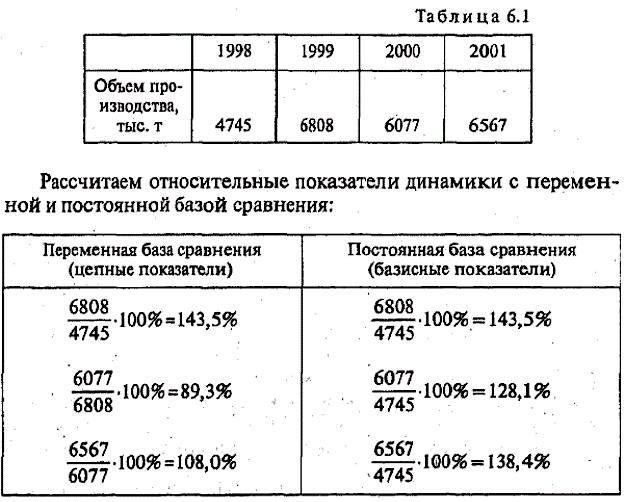 3.3 и на графике 3.2 приведены значения темпов прироста численности населения России за 40 лет, с 1960 по 2000 г. Как видно из этих данных, на протяжении всего этого периода от десятилетия к десятилетию происходило неуклонное сокращение величины этого показателя. При этом начиная с 1992 г. величины темпов прироста стали отрицательными, так как численность населения стала уменьшаться.

Темпы роста и прироста за период свободны от одного из недостатков, свойственных абсолютному приросту, а именно от зависимости от абсолютной численности населения. Они дают возможность сравнивать между собой динамику численности населения различных стран и регионов, различные периоды в истории одного и того же населения и т.д. Однако их крупным недостатком остается то, что они сильно зависят от длины периода, для которого рассчитываются: чем длиннее этот период, тем, при прочих равных условиях, они больше. К тому же эти показатели ничего не говорят об изменениях скорости роста или убыли численности населении внутри периода. И чем больше длительность периода, тем сильнее эта «маскировка».

Абсолютные и относительные величины в статистике. Примеры решения задач

Статистическое исследование, независимо от его масштабов и целей, всегда завершается расчетом и анализом различных по виду и форме выражения статистических показателей, величин.

Система статистических показателей — это совокупность взаимосвязанных показателей, имеющая одноуровневую или многоуровневую структуру, и нацеленная на решение конкретной статистической задачи. В отличие от признака, статистические показатели получаются расчетным путем. Это может быть простой подсчет единиц совокупности, суммирование их значений признака, сравнение двух или нескольких величин или более сложные расчеты.

Исходной, первичной формой выражения статистических показателей являются абсолютные величины. Статистические показатели в форме абсолютных величин характеризуют абсолютные размеры изучаемых статистикой процессов и явлений, а именно, их массу, площадь, объем, протяженность, отражают их временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц.

При решении особых аналитических задач абсолютные величины представляют в форме баланса по источникам формирования и по направлениям использования.

Абсолютные статистические показатели всегда являются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.

  • Натуральные единицы измерения отражают естественные свойства явлений и измеряются в физических единицах меры веса, объема, протяженности и т. д. В международной практике используются такие натуральные единицы измерения как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д.
  • Стоимостные единицы измерения отражают несоизмеримые в натуральном выражении процессы и представляют собой их денежное выражение. Денежная оценка социально-экономических явлений и процессов приобретает наибольшее значение в условиях рыночной экономики.
  • К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.

Относительный статистический показатель представляет собой результат деления (отношение) одного абсолютного показателя на другой и показывает соотношение между количественными характеристиками социально-экономических процессов и явлений.

При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения.

Относительные показатели могут выражаться в коэффициентах, процентах (%), промилле (‰).

Все используемые на практике относительные статистические показатели можно подразделить на следующие виды

:

  • Относительные показатели динамики – показывают изменение явления во времени, например: Д = факт 2013г. / факт 2012г. Пример определения динамики представлен в задаче 2.
  • Относительные показатели плана (плановое задание) – отношение планируемой величины показателя на предстоящий период к достигнутой величине этого показателя в данном периоде, например: ПЗ = план 2013г. / факт 2012г.
  • Относительные показатели реализации плана (выполнение плана) – отношение величины фактического к величине планируемого показателя за один период, например: ВП = факт 2012г. / план 2012г.
  • Относительные показатели структуры – определяют удельные веса отдельных частей в целом, находят как отношение структурной части изучаемого объекта к его целому. Пример определения структуры представлен в задачах 1 и 2.
  • Относительные показатели координации — представляют собой отношение одной части совокупности к другой части этой же совокупности.
  • Относительные показатели интенсивности и уровня экономического развития — характеризуют степень распространения изучаемого процесса или явления, находят как отношение исследуемого показателя к размеру присущей ему среды.
  • Относительные показатели сравнения – находят как отношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т. п.).

Примеры решения задач по теме «Абсолютные и относительные величины в статистике»

Задача 1. В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.

Марка автомобиля Число проданных автомобилей
Skoda 245
Hyundai 100
Daewoo 125
Nissan 274
Renault 231
Kia 170
Итого 1145

Решение

Расширим предложенную таблицу и определим структуру продаж автомобилей:

Марка автомобиля Число проданных автомобилей Структура, %
Skoda 245 (245:1145)×100=21,40
Hyundai 100 8,73
Daewoo 125 10,92
Nissan 274 23,93
Renault 231 20,17
Kia 170 14,85
Итого 1145 100

Задача 2. По региону имеются следующие данные о вводе в эксплуатацию жилой площади:

Определить динамику ввода жилья в эксплуатацию и структуру введенного жилья.

Решение

Расширим предложенную таблицу и определим структуру продаж автомобилей:

Задача 3. Закупочная цена пшеницы в августе текущего года в России составила 70 долларов за тонну. При этом планировалось, что цена закупки в сентябре сократится до 60 долларов. Фактически она составила 72 доллара за тонну. В то же время в США цена пшеницы достигла соответственно: 90 долларов в августе и 84 доллара в сентябре. Определить все возможные относительные величины.

Решение

Для решения составим таблицу закупочных цен в Росси и США за два месяца в долларах за тонну:

Вычислим относительные показатели для России:
Плановое задание за сентябрь ПЗ = (60:70)*100 = 85,71%
Выполнение плана за сентябрь ВП = (72:60)*100 = 120%
Динамика Д = (72:70)*100 = 102,86%

Вычислим возможные относительные показатели для США:
Динамика Д = (84:90)*100 = 93,33 %

Другие статьи по данной теме:

Список использованных источников

  1. Белобородова С. С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
  2. Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003;
  3. Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
  4. Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;

Примеры решения задач по общей теории статистики

Ниже приведены условия  и решения задач. Закачка решения в формате doc  начнется автоматически через 10 секунд.

     Задача 2.

На предприятии в начале года имелось 720 рабочих и 55 инженерно-технических работников (ИТР). В течении года уволилось 180 рабочих и 20 ИТР и было принято на работу 60 рабочих и 40 ИТР.

Определить относительные  величины, характеризующие соотношения между рабочими и ИТР на начало и конец года. К какому виду относительных величин принадлежат результаты этих вычислений? Проанализировать полученный результаты.

Решение.

Относительная величина характеризующая соотношение между рабочими и ИТР является относительным показателем координации, который характеризует соотношение отдельных частей целого между собой.

Определим на начало года относительную величину координации между рабочими и ИТР:

WР/ИТР0 = 720/55 = 13,091.

Это свидетельствует о том, что в начале года рабочих на предприятии было в 13,091 раз больше, нежели инженерно-технических работников.

Определим наконец года относительную величину координации между рабочими и ИТР:

WР/ИТР1 =P1 / ИТР1 = (720 – 180 + 60) / (55 – 20 + 40) = 600/75 = 8.

В конце года рабочих на предприятии было в 8 раз больше, нежели инженерно-технических работников.

Относительная величина координации уменьшилась к концу года на (13,091/8 – 1 )∙100 = 63,6. Это говорит об относительном уменьшении числа рабочих к числу ИТР.

 

 

 

Задача 3.

Определите среднюю себестоимость одного километра пробега ведомственного автотранспорта и показатели колеблемости для трех предприятий по следующим данным:

Предприятие

Себестоимость 1 км пробега, тыс. р.

Сумма расходов на авто­транспорт, млрд р.

№1

60

6,6

№2

80

9

№3

100

6

того

…

21,6

Решение.

Среднюю себестоимость одного километра пробега ведомственного автотранспорта определим по формуле средней гармонической взвешенной:

тыс. р.

где хi – i-й вариант усредняемого признака

mi – вес i-го варианта.

Как было посчитано нами выше величина пробега по каждому предприятию составляет 110 тыс. км.; 112,5 тыс. км.; 60 тыс. км. Соответственно.

Определим дисперсию и среднее квадратическое отклонение для себестоимости 1 км. пробега.

   Найдем дисперсию по следующей формуле:

                                    

(тыс. р.)2

 

 

6074,336 – 76,462 = 228,205 (тыс. р.)2

 

        Дисперсия показывает среднее арифметическое квадратов отклонений каждого значения признака от средней арифметической.

    Среднее квадратическое отклонение находим по специальной формуле: = 15,106 тыс. р.

    Коэф. вариации   =(15,106/76,46)·100%= 19,8%

Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние характеристики достаточно надежно характеризуют совокупность по варьирующему признаку. В нашем же случае коэффициент вариации  меньше 35%, т.е. полученная величина  средней себестоимости пробега надежно характеризует данную совокупность по этому признаку.

 

 

 

 

Задача 4.

По сгруппированным данным задачи 1:1) определите среднее значение изучаемого показателя, моду и медиану; 2) постройте гистограмму; 3) оцените характер асимметрии.

Решение.

Группы организаций по величине остатков на счетах, млн. р.

Середина интервала, млн. р.

Число организаций

417 – 612,8

514,9

6

612,8 – 808,6

710,7

8

808,6 – 1004,4

906,5

14

1004,4 – 1200,2

1102,3

8

1200,2 – 1396

1298,1

4

И т о г о:

—

40

1. Для того чтобы вычислить среднее значение признака перейдем от интервального ряда к дискретному, т.е. найдем середину каждого интервала как полусумму нижней и верхней границ. Для удобства вычислений составляем таблицу.

Найдем средний стаж: = (514,9∙6 + 710,7∙8 + 906,5∙14 + 1102,3∙8 + 1298,1∙4)/40 = 35476,8/40 = 886,92 млн. р.

Найдем моду Мо и медиану Ме:

Мо=ХМо + iМо млн. р.

fM0,fM0-1,fM+1 –частоты модального, до и после модального интервалов соответственно, ХМ0 – начало модального интервала, iМО- величина модального интервала.

      Мода показывает варианту наиболее часто встречающегося в данной совокупности, т.е. наибольшее число организаций имеют остаток 906,5 млн. р.

Ме=ХМе + iМе млн. р.

ХМе- начало медианного интервала; iМе — величина медианного интервала;SМе- сумма накопленных частот до медианного интервала: fМе – частота медианного интервала.

Медиана – это варианта, располагающаяся в середине ранжированного ряда распределения.

    Вывод: половина предприятий имеют остаток на счете до 892,5 млн. р., а вторая половина рабочих – более 892,5 млн.р.

2. Построим гистограмму распределения организаций по величине остатков на текущих счетах.

Рис. 4.1. Гистограмма распределения организаций по величине остатков на текущих счетах.

3. Оценим характер ассиметрии. При сравнительном изучении ассиметрии вычисляется относительный показатель ассиметрии:

(886,92 – 906,5)/ = — 19,58 <0, так же

<0.

Следовательно мы имеем левостороннюю ассиметрию.

 

  

 Задача 5.

Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице базисные показатели динами­ки по следующим данным о производстве продукции «А».

Год

Производство продукции «А», тыс. шт.

Базисные показатели динамики

Абсолютный прирост, тыс. шт.

Темпы роста, %.

Темпы прироста, %

1-й

55,1

—

100,0

—

2-й

…

2,8

…

…

3-й

…

 

110,3

…

4-й

…

…

…

14,9

5-й

…

…

. ..

17,1

6-й

…

…

121,1

…

Проанализируйте полученные показатели. Сделайте вывод о характере общей тенденции изучаемого явления.

Решение.

Определим недостающие показатели в таблице.

Год

Производство продукции «А», тыс. шт.

Базисные показатели динамики

Абсолютный прирост, тыс. шт.

Темпы роста, %.

Темпы прироста, %

1-й

55,1

—

100,0

—

2-й

57,9

2,8

105,1

5,1

3-й

60,8

5,7

110,3

10,3

4-й

63,3

8,2

114,9

14,9

5-й

64,5

9,4

117,1

17,1

6-й

66,7

11,6

121,1

. ..

 

У0 = 55,1 тыс. шт..

У1 = У0 + ∆1 = 55,1 + 2,8 = 57,9 тыс. шт.

Тр1 = У1/У0 = 57,9/55.1 = 1,051 или 105,1%.

Тпр1 = Тр1 – 100% = 5,1%.

У2 = У0∙Тр2 = 55,1∙1,103 = 60,8 тыс. шт.

∆2 = У2 – У0 = 60,8 – 55,1 = 5,7 тыс. шт.

Тпр2 = 110,3 – 100 = 10,3%.

Тр3 = Тпр3 + 100% = 14,9 + 100 = 114,9%.

У3 = У0∙Тр3 = 55,1∙1,149 = 63,3 тыс. шт.

∆3 = 63,3 – 55,1 = 8,2 тыс. шт.

Тр4 = Тпр4 + 100% = 17,1 + 100 = 117,1%.

У4 = У0∙Тр4 = 55,1∙1,17,1 = 64,5 тыс. шт.

∆4 = У4 – У0 = 64,5 —  55,1 = 9,4 тыс. шт.

Тпр5 = Тр5 — 100% = 121,1 – 100 = 21,1%.

У5 = У0∙Тр5 = 55,1∙1,211 = 66,7 тыс. шт.

∆5 = У5 – У0 = 66,7 —  55,1 = 11,6 тыс. шт.

   Все базисные показатели с каждым годом имеют тенденцию роста. Это свидетельствует о положительной динамики рассматриваемого нами ряда. Ни за один период не наблюдается снижение исследуемого показателя.

 

 

 

 

Задача 6.

По следующим данным вычислить: 1) базисные индексы объема продукции в целом по предприятию; 2) цепные индексы объема продукции в целом по предприятию. Покажите взаимосвязь между базисными и цепными индексами.

 

Цех

Объем продукции по годам, млрд р.

1-й год

2-й год

3-й год

4-й год

№1

975

1200

1240

1300

№2

620

630

540

660

№3

25

30

35

50

Решение.

Так как объем продукции представлен в денежном выражении, то по всему предприятию в целом можем найти объем продукции, суммировав объемы каждого из цехов.

Цех

Объем продукции по годам, млрд р.

1-й год

2-й год

3-й год

4-й год

№1

975

1200

1240

1300

№2

620

630

540

660

№3

25

30

35

50

Итого

1620

1860

1815

2010
  1. Определим базисные индексы по формуле:

Тiб = yi/y0,

Где yi – значение показателя за i-ый период, y0 – значение показателя, принятого за базу сравнения.

Находим:

Т1б = 1860/1620 = 1,148 или 114,8%;

Т2б = 1815/1620 = 1,12 или 112%;

Т3б = 2010/1620 = 1,241 или 124,1%.

2. Определим цепные индексы по формуле:

Тiц = yi/yi-1,

Где yi – значение показателя за i-ый период, yi-1 – значение предшествующего показателя.

Находим:

Т1ц = 1860/1620 = 1,148 или 114,8%;

Т2ц = 1815/1860 = 0,976 или 97,6%;

Т3ц = 2010/1815 = 1,107 или 110,7%.

Между исчисленными индексами существует взаимосвязь:

Т1б = Т1ц;

Т2б = Т1ц ∙ Т2ц = 1,148 ∙ 0,976 = 1,12;

Т3б = Т1ц ∙ Т2ц ∙ Т3ц = 1,148 ∙ 0,976 ∙ 1,107 = 1,241.

 

 

 

 

 

 

Задача 7.

Среднее снижение цен на группу товаров в июле по сравнению с июнем составило 8%, а в августе по сравнению с июлем — 12%. Определите, как изменился физический объем продукции, если объем реализации товаров за этот период вырос в 2,1 раза (среднее изменение цен определялось с помощью цепных индексов с весами августа). Проанализируйте взаимосвязь между пока­зателями.

Решение.

Определим индекс изменения цен в августе по сравнению с июнем, умножая соответствующие цепные индексы:

Ip = ip1 ∙ ip2 = 0,92 ∙ 0,88 = 0,8096.

Определим индекс физического объема по группе товаров с июня по август:

Iq = Ipq/Ip = 2,1/0,8096 = 2,594 или 259,4 %.

В августе месяце по сравнению с июнем физический объем реализации группы товаров возрос на 159,4%, в то время как цены на продукцию снизились на 19,04%.

 

 

Задача 8.

Изменение численности городского и сельского населения об­ласти характеризуется следующими данными (млн чел.):

Год

Все население, тыс. чел.

В том числе

городское

сельское

1990

10,1

6,73

3,46

2000

10,0

6,99

3,03

По этим данным постройте столбиковые и круговые диаграммы. Какие выводы можно сделать на основе сравнения площадей соответствующих пря­моугольников и секторов, относящихся к двум сравниваемым годам?

Решение.

Для наглядного изображения структуры населения области за 1990 и за 2000 годы построим столбиковые круговые и столбиковые диаграммы.

 

Сравнивая построенные диаграммы, можем отметить, что в 2000 году доля сельского населения области стала меньше доли городского населения по сравнению с 1990 годом.

 

 

 Задача 9.

Определите: а) как изменится ошибка повторной выборки, если среднее квадратическое отклонение признака будет больше в 2 раза, на 10%; б) как изменится при тех же условиях объем выборки; в) как изменится объем выборки, если вероятность, гарантирующую репрезентативность, увеличить с 0,954 до 0,997.

Решение.

  1.             Предельная ошибка повторной выборки:

,

Где n – объем выборки, t – коэффициент доверия,  — среднее квадратическое отклонение.

  При увеличении среднего квадратическаго отклонения в два раза получим:

, увеличение среднего квадратического отклонения в два раза.

При увеличении среднего квадратическаго отклонения на 10%, предельная ошибка выборки увеличится на 10%.

  1. Объем выборки при повторном отборе:

.

  При увеличении среднего квадратическаго отклонения в два раза получим:

= 4, увеличение объема выборки в четыре раза.

 

При увеличении среднего квадратическаго отклонения на 10% получим:

= 1,21, увеличение объема выборки на 21%.

3. При увеличении доверительной вероятности с 0,954 до 0,997, коэффициент доверия возрастет с 2-х до 3-х и объем выборки изменится следующим образом:

, т. е. увеличится в 2,25 раза.

Список из 26 сотрудников Relative Dynamics Inc. — адреса электронной почты и телефоны

Джорджи Брофи Старший директор по развитию бизнеса — Aerospace + Defense Соединенные Штаты Америки xx@relativedynamics. space
Эдвард Левин Аэрокосмический инженер Мэриленд, США xx @ relativedynamics.пространство
Стивен Йен Инженер по системам радиосвязи Флорида, США [email protected]
Натали Младший инженер по навигации, навигации и контролю Мэриленд, США xx @ relativedynamics.космос
Майкл Крайнак Главный технический директор Мэриленд, США xx@relativedynamics. space
Джон Бостер Инженер 3 Техас, США xx @ relativedynamics.космос
Куш Патель Генеральный директор Мэриленд, США [email protected]
Джефф Джиллетт Старший инженер GNC Мичиган, США xx @ relativedynamics.космос
Ричард Беркат Спутник Aqua / Aura GNC Engineer Мэриленд, США xx@relativedynamics. space
Ушма Директор по персоналу и привлечению талантов Иллинойс, США xx @ relativedynamics.космос
Кассандра Кастильо Спутниковый инженер Мэриленд, США [email protected]
Хорхе Кадена Группа передовых разработок — инженер FPGA Соединенные Штаты Америки xx @ relativedynamics.космос
Аакаш Патель Инженер по эксплуатации FOT Мэриленд, США xx@relativedynamics. space
Генри Хайм Младший инженер GNC Мэриленд, США xx @ relativedynamics.пространство
Рене Уильямс Менеджер проекта Вирджиния, США [email protected]
Thomas Just Инженер по бортовым системам Мэриленд, США xx @ relativedynamics.космос
Адекунле Старший инженер РФ Соединенные Штаты Америки xx@relativedynamics. space
Калеб Марти Инженер по системам радиосвязи Техас, США xx @ relativedynamics.космос
Джон Драганов Инженер по мехатронике Мэриленд, США [email protected]
Лаура Худ Старший инженер системы связи Техас, США xx @ relativedynamics.космос
Эрин Рассел Инженер миссии Вирджиния, США xx@relativedynamics. space
Jordan Logue Инженер по инструментам Мэриленд, США xx @ relativedynamics.космос
Кевин Хиш Инженер-электронщик Мэриленд, США [email protected]
Сюзанна Дершайд Аналитик по качеству Мэриленд, США xx @ relativedynamics.space
Энди Йе Инженер по системной интеграции и тестированию Калифорния, США xx@relativedynamics. space
Антрикш Пател Главный операционный директор Соединенные Штаты Америки xx @ relativedynamics.космос

Относительная динамика аналитического космического аппарата с гравитационным воздействием, сопротивлением и возмущениями от третьего тела

https://doi.org/10.1016/j.actaastro.2021.04.043Получить права и контент

Основные моменты

•

Аналитический космический аппарат относительная динамика

•

Гравитация, сопротивление и возмущения третьего тела Луны Солнечные возмущения

•

Влияние возмущений на относительное движение космического корабля на НОО и ВОО

•

Периодические эффекты длинных и коротких вариации из-за J 2 относительного движения космического корабля

Abstract

Растет интерес к построению космических кораблей для космических исследований. Такие миссии потребуют наличия точной и эффективной модели динамики на борту бортового компьютера для расчета и управления желаемым относительным движением. Следовательно, аналитическая модель динамики, которая может быть применена к эксцентрическим орбитам и включает возмущения, может обеспечить повышение точности и эффективности. В этой статье разрабатывается точное аналитическое решение относительного движения двух космических аппаратов с использованием классических орбитальных элементов. Аналитическое решение получено путем распространения элементов орбиты вперед во времени с учетом гравитационного поля до пятой гармоники, вековых и периодических возмущений третьего тела и сопротивления, а также расчета относительного движения в локально-вертикальном – локально-горизонтальном опорный кадр на каждом временном шаге.Было обнаружено, что аналитическое решение точно описывает относительное движение по сравнению с численным симулятором, давая ошибки порядка метров для расстояний разноса порядка сотен метров.

Ключевые слова

Полет космического корабля

Относительное движение космического корабля

Динамика космического корабля

Аналитический

Орбитальные элементы

Рекомендуемые статьиЦитирующие статьи (0)

Полный текст

© 2021 IAA.Опубликовано Elsevier Ltd. Все права защищены.

Рекомендуемые статьи

Цитирование статей

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

  • В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
  • Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
  • Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
  • Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
  • Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Свидетельства из зоны евро Йоханнеса Гарейса, Эрика Майера :: SSRN

33 стр. Добавлено: 4 авг. 2020 г.

Дата написания: 2020

Абстрактные

Мы разрабатываем модель расширенного реального делового цикла (RBC) с финансово ограниченными фирмами и нематериальным капиталом, не являющимся залогом.На основе последовательной модели условий заимствования фирм мы обнаружили, что в рамках структурной векторной авторегрессии (SVAR), в ответ на неблагоприятный финансовый шок, материальные инвестиции падают больше, чем нематериальные инвестиции. Это позитивное совместное движение между материальными и нематериальными инвестициями, а также относительная устойчивость нематериальных инвестиций создают проблему для теоретической модели. Мы показываем, что корректировочные затраты, связанные с инвестициями, помогают согласовать модель с наблюдаемыми эмпирическими данными.Оценка теоретической модели с использованием байесовского подхода с ограниченной информацией подтверждает наличие гораздо больших затрат на корректировку для нематериальных инвестиций, чем для материальных инвестиций.

Ключевые слова: материальные инвестиции, нематериальные инвестиции, финансовые шоки, зона евро

Классификация JEL: C32, E32, E44

Рекомендуемое цитирование: Предлагаемая ссылка

Гарейс, Йоханнес и Майер, Эрик, Финансовые шоки и относительная динамика материальных и нематериальных инвестиций: данные из зоны евро (2020).Документ для обсуждения Deutsche Bundesbank No. 39/2020, доступен на SSRN: https://ssrn.com/abstract=3669517