Моделирование — это… Что такое Моделирование?
Модели́рование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.
Виды моделирования
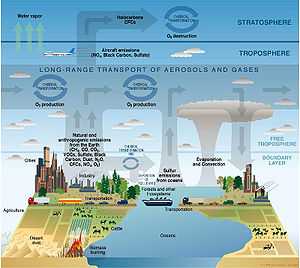Пример научного моделирования. Схема химических процессов и процессов переноса в атмосфере.В силу многозначности понятия «модель» в науке и технике не существует единой классификации видов моделирования: классификацию можно проводить по характеру моделей, по характеру моделируемых объектов, по сферам приложения моделирования (в технике, физических науках, кибернетике и т. д.). Например, можно выделить следующие виды моделирования:
и т. д.
Процесс моделирования
Процесс моделирования включает три элемента:
- субъект (исследователь),
- объект исследования,
- модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.
На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.
Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.
Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.
Математическое моделирование исторической динамики
В последнее время интенсивно развивается математическое моделирование исторической динамики (клиодинамика). К настоящему времени основными достижениями клиодинамики можно считать разработку математических моделей «вековых» социально-демографических циклов [1][2][3][4] и достаточно успешное математическое моделирование долгосрочного развития Мир-Системы[5][6][7].
См. также
Примечания
- ↑ Нефёдов С. А. Концепция демографических циклов. — Екатеринбург: Изд-во УГГУ, 2007
- ↑ Коротаев А. В., Комарова Н. Л., Халтурина Д. А. Законы истории. Вековые циклы и тысячелетние тренды. Демография, экономика, войны. 2-е изд. — М.: УРСС, 2007
- ↑ Турчин П. В. Историческая динамика: На пути к теоретической истории. — М.: УРСС, 2007
- ↑ Малков С. Ю. Математическое моделирование исторической динамики: подходы и модели // Моделирование социально-политической и экономической динамики. Ред. М. Г. Дмитриев. — М.: Изд-во РГСУ, 2004. — С. 76—188.
- ↑ Коротаев А. В., Малков А. С., Халтурина Д. А.
- ↑ Цирель С. В. Историческое время и пути исторической эволюции. Статья I. История и Математика. Модели и теории / Ред. Л. Е. Гринин, А. В. Коротаев, С. Ю. Малков. М.: ЛКИ, 2008. С. 246—278
- ↑ Капица С. П. Общая теория роста человечества: Сколько людей жило, живёт и будет жить на Земле М.: Наука, 1999. ISBN 5-02-008299-6
Литература
Ссылки
dic.academic.ru
33.Математические модели в физике, химии, биологии и экономике
Мы будем рассматривать в данном разделе аналитические модели. В аналитических моделях вход. и выход. Параметры связаны явными выражениями: уравнениями, неравенствами и т.д. Если мы решаем системы уравнений Колмогорова-Эрланга, это аналитическое моделирование, если же мы останавливаемся на графовой модели и проводим статистический эксперимент, определяем как обслуживает система поток заявок, то это имитационное моделирование. Для решения аналитической модели обычно приходится применять численные методы решения задач, но некоторые модели дают и аналитическое решение, т.к. для решения разных математических задач используются разные методы, иногда аналитические модели делят по методам (интегральные, дифференциальные, линейные и т.д.), но обычно по сферам применения (физические, химические, биологические, педагогические, технические). Рассмотрим некоторые примеры аналитической мат. моделей, которые являются наиболее простыми и в то же время классическими.
Математические модели в физике и технике
В физике моделирование
в основном используется для описания
процессов в производстве, связанных с
решением дифференциальных уравнений
и частных производных. Все другие модели,
это обычно упрощенный вариант этих
процессов. Основой для построения
моделей являются следующими з
Часть уравнений записывается в одномерном виде или с помощью радиус-вектора
; 
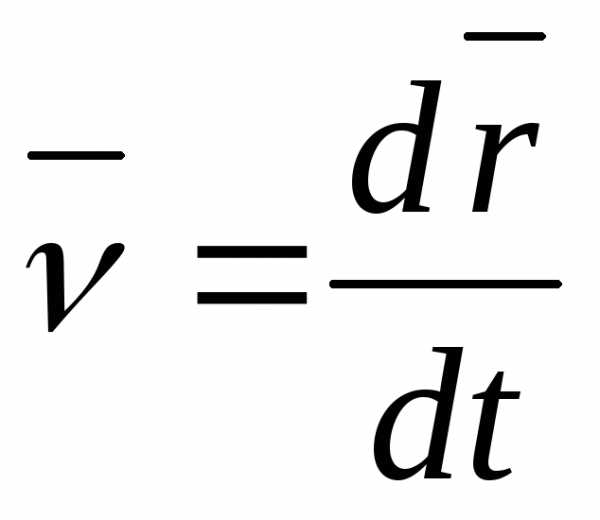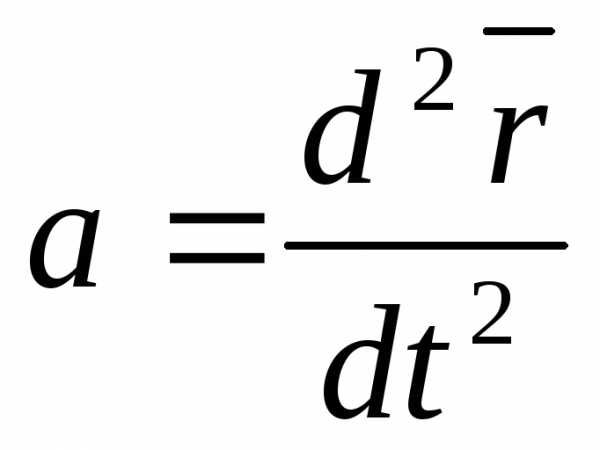
2. Модель колебательной системы
Рассмотрим ее от простого к сложному. В качестве примера могут служить очень многие окружающие на предметы, где важна вибрация (двигатели). Колебания свойственны и электрическим системам. Будем считать, что у нас одномерные колебания (вдоль одной оси).
Положение
предмета определяется одной координатой
х, уравнение будет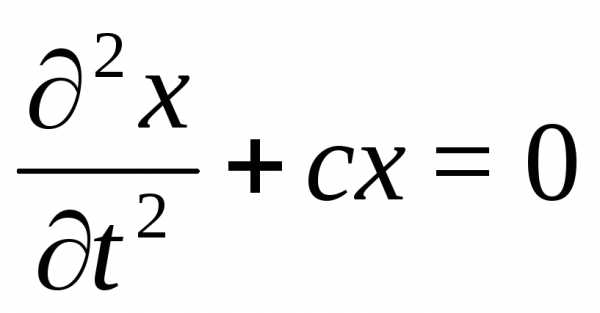 
.
Решение этого диф. уравнения хорошо известно, оно представляет из себя
Колебания Гармонические со сдвигом фазы, незатухающие.
Усложняем модель — вводим затухание
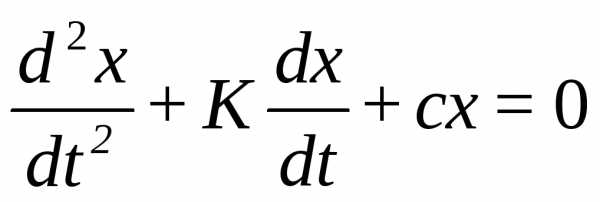(К-
коэффициент затухания)
Если К мало (К<<1), то решение не будет сильно отличаться. Решение системы приводит к возникновению .
К=0,1- затухание
хорошо видно (переодич.). При увеличении
К (
)-
апериодическое затухание, когда нет ни
одного периода.
Дальше Усложняем задачу- введение периодичность внешней силы
Собственная частота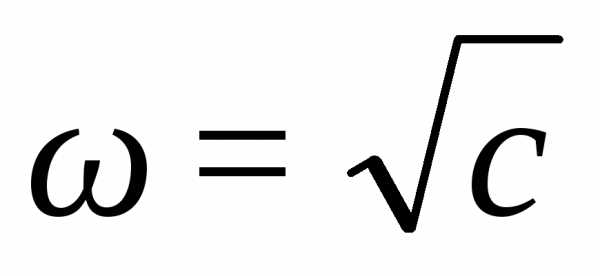 
К<<1, W>>p.
Модуляция. Внутри собственные колебания, их амплитуда моделируется с частотой собственных колебаний (биения)
Если К<0, м.б. (т.к. она только мешает) – параметрический резонанс.
Фактически параметрический резонанс при отрицательном затухании — это получение энергии извне. Процессы собственных колебаний важны, когда колебания паразитные (вредны), когда делают демпферы (делают затухания апериодичными).
Пример: рессоры автомобиля (обычно полезны для раскачки колебаний).
Резонанс может быть отрицательным и положительным по значению. Излучение электромагнитных волн основано на резонансах, как обычных, так и параметрических. Излучение и прием электромагнитных волн резонансные. Параметрический резонанс выгоден тем, что гораздо мощнее обычного. Это удобное средство для генерации, например, СВЧ-колебаний (магнитофон). Для параметрического резонанса собственная частота не нужна, поэтому можно вкачивать энергию до самого разрушения этого резонатора. Но может быть и вред, разрушение, что неприятно.
Модуляция – основа радиосвязи. Есть несущая частота, которую модулируют, а потом де модулируют. Звук низкочастотен (36 КГц), а радиоволна распространяется на высокой частоте, значит, нужны мегагерцы. Есть амплитудная, фазовая и частотная модуляция. Эффект биений обычно вредный, мешающий – это источник шума. Иногда с помощью биений делают специальные шумовые генераторы.
Модель теплопроводности тонкого слоя
стекло (тонкое,
длинное),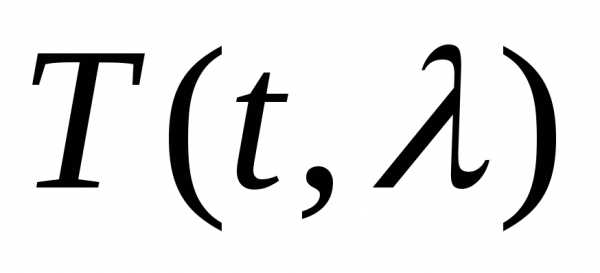 
—
температура будет равномерна,
следовательно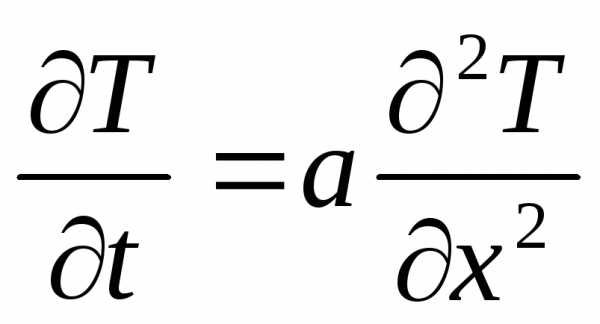
. 
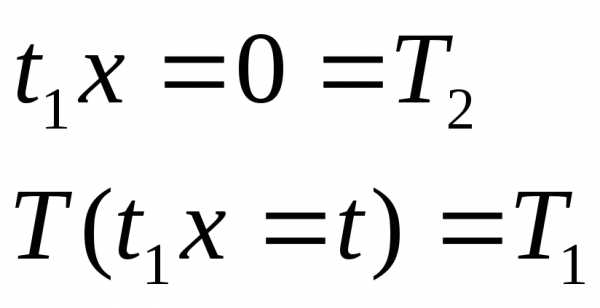гранич.
Обычно это уравнение не решается в явном
виде, а с помощью клеточной аппроксимации.
Решая эту систему уравнений, мы находим
значения в узлах сетки. Подобным же
способом моделируются другие задачи
теплопроводности, электростатики и
электродинамики. Основная проблема –
сложность вычисления, поэтому требуются
мощные ЭВМ.
Еще одна модель – движение тела, брошенного под углом к горизонту. Для ее решения используют так называемый метод стрельбы, он уже близок к имитационному моделированию.
Еще – модель движения ракеты:
— уравнение Циолковского.
Кинетические и структурные модели в химии
В химии в основном распространены модели химических реакций и строение модели хим. соединений. Для хим. реакций самое важное –кинетика, т.е. изменение течение реакций со временем, т.е. чем быстрее идет реакция, тем меньше остается реагирующего вещества, и наоборот. В начале ХХ века Адольф Лотка сформулировал модель кинетических реакций, которая была названа модель Вольтерра-Лотки. Цепочка превращений веществ:
Получена система диф. уравнений. Эти уравнения по смыслу похожи на уравнения Колмогорова- Эрланга. Это показывает, что то были тоже кинетические уравнения и все кинетические процессы похожи друг на друга.
В химии кинетические уравнения усложняются тем, что величины не являются постоянными, а зависят от таких величин как ,
химический состав
веществ (температура подчиняется закону
теплоемкости, р зависит от диффузии, которая определяется
уравнением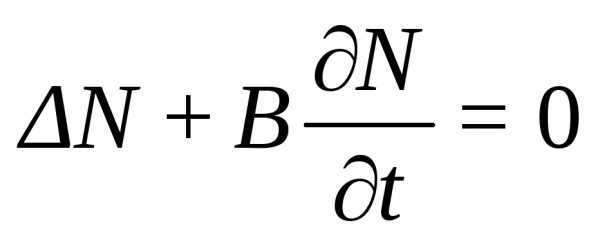 
—
закон диффузии Фика. Похожее соотношение
имеет и закон фильтрационного переноса
Дарси). В результате приходится решать
одновременно с кинетической еще и эти
сложные уравнения.
В химии большое значение имеют структурные модели молекул: Н-О-Н, особенно удобна для органических веществ (у них очень сложная структура).
При изучении нового хим. вещества делают новый хим. анализ — определяют пропорции содержащие тех или иных веществ. Тогда можно определить из каких атомов состоит молекула, но и от того, как они соединены. Вводится валентная связь. Одни атомы имеют 1-ю валентную связь, другие 2-ю и т.д. Были обнаружены изомеры вещества с одинаковым количеством молекул, но с разными свойствами.
2
задачи:
Определить внутреннюю структуру молекулы и связать ее структуру и хим. свойства, т.е. изучение изомеров.
Проектирование изомеров — научиться создавать устойчивые структуры для молекул различных видов и давать их предположит. свойства.
Обе эти задачи стали настолько популярны в органической химии, что даже были созданы специальные системы моделирования молекул.
Математические модели в биологии
Биология чрезвычайно связана с химией и биохимией => структурное моделирование из химии перешло и в биологию. Биологические структуры – очень сложные химические структуры => появилась наука биохимия, которая изучает химию биологических структур. Здесь методы структурного моделирования оказались очень полезны. Наиболее известные задачи, связанные с моделированием генов.
Гены – молекулы, из которых формируется так называемые информационные компоненты живых существ-ДНК, РНК. В основном гены уже изучены и известны, но остались вопросы какие гены входят в ту или иную ДНК и как они связаны между собой. Т.к. даже в простейшем ДНК генов десятки тысяч, возник мировой проект «модель ДНК» , сначала у простейших существ, теперь человека (завершение) . Структурное моделирование- ведущее в биохимии.
Модели внутривидовой борьбы
Особи одного вида конкурируют между собой. В начале, когда особей мало, а условия благоприятные идет быстрый рост популяции, ограничения наступают из-за борьбы между особями одного вида. Самой первой простой моделью стала модель роста – модель безудержного роста. В этой модели отсутствует внутривидовая конкуренция, она будет модернизироваться.
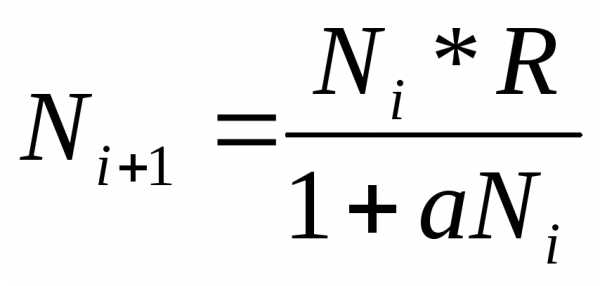
Чем больше a, тем меньше рост, однако, и эта модель не могла описать некоторые явления, которые возникали в реальных экосистемах. В некоторых системах возникали колебания численности из года в год. Ввели еще один параметр, усложнили модель
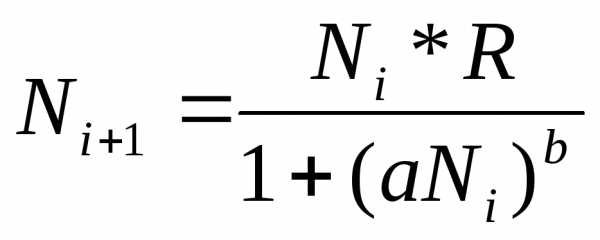
Коэффициент b определяет нелинейную зависимость скорости роста R от численности. Численное изучение этой модели позволило обнаружить 4 характерные ситуации:
— монотонный рост
— ситуация затухающих колебаний
— ситуация незатухающих колебаний
— ситуация флуктуаций (случайных изменений)
Данные модели дискретные, но можно построить и непрерывную, кинетическую, ее уравнение:
.
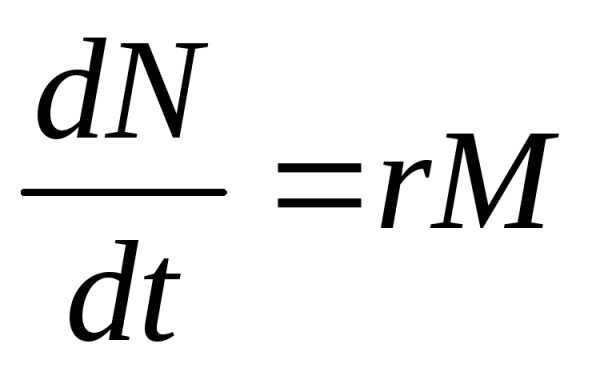при этом r – некий аналог скорости. Эта
двухпараметричная модель называется
логистической кинетической моделью
(модель Вольтера — Лоттки).
Модели межвидовой конкуренции
Если сосуществуют 2 вида, которые активно воздействуют друг на друга, то возникают процессы межвидовой конкуренции и борьбы. Наиболее известна модель (кинетическая) Вольтера — Лотки конкуренция двух видов:
Коэффициенты определяют связь между 2 видами. Если, то увеличение особей второго вида идет к уменьшению особей первого вида. Второй вид подавляет первый. Если, то особи второго вида не влияют. Очевидно, чем больше волков, тем меньше зайцев. В модели 6 параметров – ее изучение очень сложно, поэтому обычно фиксируют часть параметров. В общем случае изучение этой параметрической модели показало, что популяции хищников и жертв испытывают циклические изменения. В биологии очень часто используют так же имитационное моделирование.
Имитационное моделирование в биологии
Модель «жизнь»
В ней имитируется размножение простейших существ, задаются некоторые ограничения на размножение, гибель и т.д., а затем запускается эксперимент и прослеживается динамика со временем. Простейший вариант (школьный). Берем таблицу клеток пустых и заполненных (живых). Задаются правила, например если живая клетка окружена 4 и более живыми, то она погибает от перенаселения, если возле нее один или нет, погибает от одиночества. Если к мертвой примыкает 3 живые, она оживает. Эксперимент:
— задается начальная случайная конфигурация живых клеток
— задается количество моментов времени, которое будет прослежено
— в цикле по моментам времени производят обновление таблицы по заданным правилам, и наблюдают за изменением картинки. Подобные системы изучались, и оказалось, что в такой таблице могут существовать устойчивые конфигурации, которые не разрушаются.
Модели в экономике
Экономические науки – одна из наиболее важных сфер применения моделирования, именно здесь модели дают наибольшую эффективность, например если оптимизировать в одной модели траты всего государства, эффект будет выражаться в миллиардах долларов. Можно выделить следующие типы моделей:
— модель ЛП (линейные) – модель ресурсов, запасов и т.д.
— модели, построенные на транспортной задаче (распространение и перевозка грузов)
— модели целочисленного программирования (результат принадлежит области целых чисел, количество человек, число заводов и т.д.) – модели первого типа с целочисленными параметрами.
— модели динамического программирования – в основном связанные с развитием какого-либо производства, фирмы и т.д.
— игровые модели, связанные с противоборством, конкуренцией.
— прогностические модели, связанные с прогнозом ситуации при недостатке информации или случайных событиях.
— модели автоматического управления (сделать систему управления оптимальной)
нелинейные модели решаются только в отдельных случаях.
34. Стохастическое моделирование. Метод Монте-Карло в моделировании. Генерирование случайных и псевдослучайных чисел. Методы и алгоритмы генерации. Генерирование случайных чисел распределенных по экспоненциальному, нормальному и произвольно заданному закону распределения.
Стохастическое программирование – раздел математического программирования, совокупность методов решения оптимизационных задач вероятностного характера. Это означает, что либо параметры ограничений (условий) задачи, либо параметры целевой функции, либо и те и другие являются случайными величинами (содержат случайные компоненты).
Оптимизационная задача — экономико-математическая задача, цель которой состоит в нахождении наилучшего распределения наличных ресурсов. Решается с помощью оптимальной модели методами математического программирования, т. е. путем поиска максимума или минимума некоторых функций при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). Решение оптимизационной задачи называется оптимальным решением, оптимальным планом, оптимальной точкой.
Случайные величины характеризуются средними значениями, дисперсией, корреляцией, регрессией, функция распределения и т.д.
Статистическое моделирование – моделирование с использованием случайных процессов и явлений.
Существует 2 варианта использования статистического моделирования:
– в стохастических моделях может существовать случайные параметры или взаимодействия. Связь между параметрами носит случайный или очень сложный характер.
– даже для детерминированных моделей могут использоваться статистические методы. Практически всегда используются статическое моделирование в имитационных моделях
Модели, где между параметрами существует однозначная связь и нет случайных параметров называются детерминированными.
Детерминированные процессы – определенные процессы, в которых всякие процессы определены законами.
Человек считает все процессы детерминированными, однако со временем обнаружены случайные процессы. Случайный процесс – это такой процесс, течение которого может быть различным в зависимости от случая, причем вероятность того или иного течения определена.
Исследование процессов показало, что они бывают 2-х типов:
а) Случайные по своей природе процессы;
б) Очень сложные детерминированные процессы;
Доказана центральная теорема, в соответствии с которой сложение различных процессов увеличивает случайный характер. Так, если сложить совершенно разные последовательности, не связанные между собой, то результат в пределе стремится к нормальному распределению. Но известно, что нормальное распределение – независимые события, следовательно, объединение детерминированных событий в пределе ведет к их случайности.
Т.о. в природе не существует совершенно чисто детерминированных процессов, всегда есть смесь детерминированных и случайных процессов. Действие случайного фактора называется “шумом”. Источники шума – сложные детерминированные процессы (броуновское движение молекул).
В имитационном моделировании часто сложные процессы заменяют случайными, следовательно, для того чтобы сделать имитационную модель, нужно научиться моделировать случайные процессы методами статического моделирования. Представляют случайные процессы в КМ последовательностью случайных чисел, величина которых случайно меняется.
В статистическом моделировании очень часто используется метод статистических испытаний Монте-Карло. Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.
Суть метода:
для того, чтобы определить постоянную
или детерминированную характеристику
процесса можно использовать статический
эксперимент, параметры которого в
пределе связаны с определяемой величиной. Сущность
метода Монте-Карло состоит в следующем: требуется
найти значение а некоторой изучаемой
величины. Для этого выбирают такую
случайную величину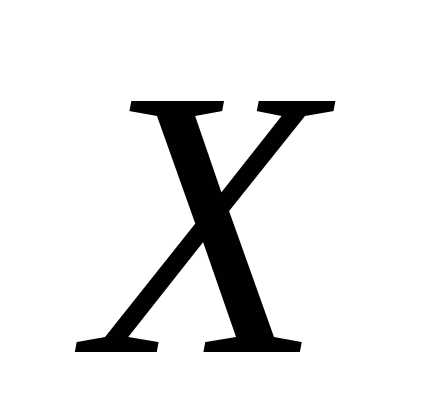 
,
математическое ожидание которой равно 
:
.
Практически же поступают так: производят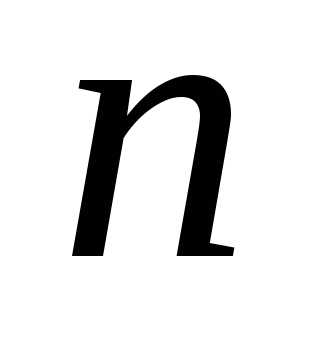 
испытаний, в результате которых получают 
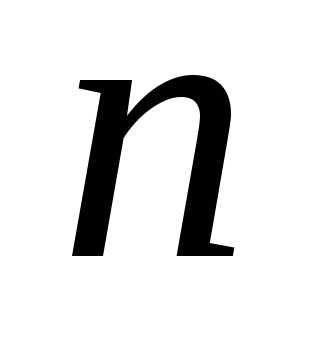возможных значений 
;
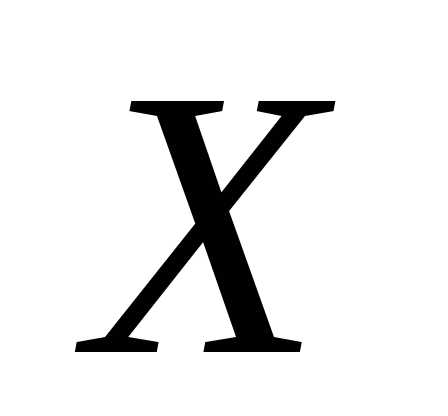вычисляют их среднее арифметическое и принимают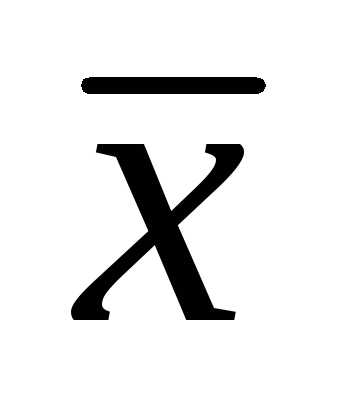 
в качестве оценки (приближенного
значения) 
искомого числа
:
.
Рассмотрим суть метода на примерах его использования:
studfiles.net
Моделирование определение — Справочник химика 21
Цель этого этапа моделирования — определение границ кинетической области, а также оптимальных пористой структуры, формы и размеров зерен катализатора. Работами многих ученых » -созданы методы анализа скорости протекания химических процессов в пористых зернах и даны важнейшие рекомендации -зо, 52,5з JJo выбору указанных оптимальных параметров. Развитие математического моделирования при помощи ЭВМ открыло новые возможности дальнейшего совершенствования методов расчета и детального изучения механизмов химических реакций на пористых катализаторах. [c.472]Несмотря на реальную возможность моделирования определенных процессов экстракции, имеются определенные трудности в ее реализации. [c.8]
Такое ограничение содержания книги позволило авторам развить единый подход к математическому моделированию определенной группы гетерогенных [c.3]
Реакция (1) является медленной, поэтому авторы [3] смогли определить только верхнюю границу значений константы скорости /с ионная сила 1 моль/л, 23°С) . Одна из целей настоящего моделирования — определение значения константы скорости реакции (1). [c.83]
Анализ является важнейшим этапом проектирования процессов перегонки и ректификации и характеризуется определением оптимальных режимных параметров процесса и конструктивных размеров аппаратов при заданных технологических требованиях и ограничениях на процесс. Анализ сложных систем ректификации проводится методом декомпозиции их на ряд подсистем с де-тальным исследованием полученных подсистем методом математического моделирования. Проведение анализа сложных систем возможно также при одновременном решении всех уравнений си-стемы с учетом особенностей взаимного влияния режимов разделения в каждом элементе системы. Последний метод анализа является более перспективным для однородных систем сравнительно небольшой размерности, так как в этом методе не требуется рассмотрения сложной проблемы оптимальной декомпозиции системы. [c.99]
Переменные, характеризующие состояние процесса, которые измеряются и поддерживаются на заданном уровне или изменяются по определенно>7 закону, принято называть управляемыми величинами. Как правило, управляемые переменные легко измеряются, но иногда их вычисляют по другим измеряемым переменным, используя математическое моделирование процесса. [c.6]
Основные понятия и определения, принятые в моделировании на ЭВМ объектов и систем управления………….. 4 [c.96]
Вместе с тем, для понимания сложных пластовых процессов обычно требуется разумное сочетание физического и математического модели- рования. Но при этом всегда следует помнить, что модель-это приближенное описание объекта, отражающее не все, а только определенные его свойства, характеристики, что результаты математического (как и любого другого) моделирования нельзя использовать за пределами условий адекватности модели объекту. [c.381]
Под чувствительностью оптимума будем понимать величину относительного изменения критерия оптимальности при отклонении управляющих воздействий от оптимальных значений. Вообще говоря, в приведенное определение чувствительности оптимума следует включить не только зависимость указанного критерия от управляющих воздействий, но также и от всех остальных параметров математической модели, для которых в процессе моделирования необходимо задавать численные значения. В этом случае постановка задачи исследования чувствительности оптимума, найденного на математической модели процесса, окажется наиболее широкой. Однако принципиально анализ чувствительности оптимума несмотря на то, по какому параметру ее исследуют, проводят аналогичными методами. Поэтому в дальнейшем ограничимся рассмотрением чувствительности только по отношению к управляющим воздействиям. [c.36]
В отличие от статистических математические модели, которые построены с учетом основных закономерностей процессов, протекающих в моделируемом объекте, качественно более правильно характеризуют его даже при наличии недостаточно точных в количественном отнои]ении параметров модели. Поэтому с пх помощью можно изучать общие свойства объектов моделирования, относя-и ихся к определенному классу. [c.47]
Описанный выше способ развития процесса на основе теории подобия имеет существенные недостатки. В лучшем случае мы можем рассчитывать на получение в промышленной установке таких же показателей, как и в опытной. Если даже эти показатели являются оптимальными для установки меньшего масштаба, они не обязательно должны быть оптимальными для большего масштаба. Теория подобия не может сформулировать правила определения оптимальных условий работы образца по результатам исследований на модели. Другой недостаток моделирования — необходимость применения небольших промежуточных изменений масштаба при разработке сложных операций и процессов, что не позволяет значительно сократить время доведения технологического процесса до промышленного внедрения. Продолжительные исследования и проектирование могут привести к тому, что продукт устареет к моменту его выпуска. [c.472]
Уравнения (2.3) и (2.4) являются незамкнутыми. Помимо неизвестных функций р,- и щ они содержат члены Зц, 1,1 и которые не выражены через указанные функции. Поток массы характеризующий кинетику фазового пере сода, может быть определен только при совместном решении уравнений гидродинамики и уравнений тепло- и массообмена, рассмотрение которых не входит в задачу данной главы. Напротив, тензор поверхностных сил в фазах 2,- и сила межфазного взаимодействия являются чисто гидродинамическими параметрами. Их определение означает, по существу, формулировку реологических уравнений состояния для исследуемой смеси и представляет собой основную и наиболее сложную проблему при моделировании двухфазных течений. [c.60]
Таким образом, при помощи системотехники, вероятно, удастся установить единство между исследоват
www.chem21.info
МОДЕЛИРОВАНИЕ — это… Что такое МОДЕЛИРОВАНИЕ?
- МОДЕЛИРОВАНИЕ
- МОДЕЛИРОВАНИЕ, исследование каких-либо явлений, процессов или систем объектов путем построения и изучения их моделей; использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов. На идее моделирования по существу базируется любой метод научного исследования — как теоретический (при котором используются различного рода знаковые, абстрактные модели; например, математическое моделирование), так и экспериментальный (использующий предметные модели).
Современная энциклопедия. 2000.
Смотреть что такое «МОДЕЛИРОВАНИЕ» в других словарях:
МОДЕЛИРОВАНИЕ — метод исследования объектов познания на их моделях; построение и изучение моделей реально существующих предметов и явлений (органич. и неорганич. систем, инженерных устройств, разнообразных процессов физических, химических, биологических … Философская энциклопедия
моделирование — Процесс распознавания последовательности идей и поведении, которая позволяет справиться с задачей. Основа ускоренного обучения. Процесс наблюдения и копирования успешных действий и поведения других людей; процесс распознавания последовательностей … Большая психологическая энциклопедия
МОДЕЛИРОВАНИЕ — физическое, замена изучения нек рого объекта или явления эксперим. исследованием его модели, имеющей ту же физ. природу. В науке любой эксперимент, производимый для исследования тех или иных закономерностей изучаемого явления или для проверки… … Физическая энциклопедия
моделирование — ия, ср. modeler ,> нем. modellieren. Употреблять резного дела мастера для моделирования из воску фигур и арнаментов. ДАЭ 33. Напоследок и в модулировании, как в нужнейшем всякому медалеру художестве, обучать. МАН 4 580. Что до серебряной и… … Исторический словарь галлицизмов русского языка
МОДЕЛИРОВАНИЕ — экономическое (франц. modelle, от лат. modulus мера, образец) воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в искусственно созданных условиях (натурное моделирование). В экономике чаще… … Экономический словарь
моделирование — Метод исследования сложных процессов и явлений на их моделях или на натурных установках с применением теории подобия при постановке и обработке эксперимента [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)]… … Справочник технического переводчика
Моделирование — (simulation) Имитация маркетинговой ситуации в целях ее исследования. При машинном моделировании (computer simulation) вся имеющаяся информация загружается в компьютер, что позволяет сопоставить возможные варианты стратегий маркетинга. При… … Словарь бизнес-терминов
МОДЕЛИРОВАНИЕ — исследование каких либо явлений, процессов или систем объектов путем построения и изучения их моделей; использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.… … Большой Энциклопедический словарь
МОДЕЛИРОВАНИЕ ЗВЁЗД — методы нахождения распределений физ. характеристик звёздного вещества (давления, плотности, темп ры, массы, хим. состава) от центра до поверхности звезды и изменений этих характеристик со временем. Построение моделей даёт возможность установить… … Физическая энциклопедия
моделирование — имитация, имитирование, макетирование, моделировка Словарь русских синонимов. моделирование сущ., кол во синонимов: 9 • автомоделирование (1) • … Словарь синонимов
dic.academic.ru
Моделирование — Википедия. Что такое Моделирование
Модели́рование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.
Виды моделирования
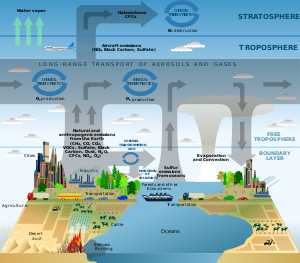Пример результата научного моделирования. Схема химических процессов и процессов переноса в атмосфере.В силу многозначности понятия «модель» в науке и технике не существует единой классификации видов моделирования: классификацию можно проводить по характеру моделей, по характеру моделируемых объектов, по сферам приложения моделирования (в технике, физических науках, кибернетике и т. д.).
В настоящее время по технологии моделирования и области применения выделяют такие основные виды моделирования:
и др.
Процесс моделирования
Процесс моделирования включает три элемента:
- субъект (исследователь),
- объект исследования,
- модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.
На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.
Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.
Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.
См. также
Примечания
Литература
- Глинский Б. А. Моделирование как метод научного исследования. М., 1965;
- Кодрянц И. Г. Философские вопросы математического моделирования. Кишинев, 1978;
- Мамедов Н. М. Моделирование и синтез знаний. Баку, 1978;
- Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. — М.: Наука, 1997. — 320 с. — ISBN 5-9221-0120-X.
- Уемов А. И. Логические основы метода моделирования. М., 1971
- Аристов А. О. Теория квазиклеточных сетей : научная монография — М: МИСиС, 2014. — 188с. ISBN 978-5-600-00321-7
- Кононюк А. Е. Обобщенная теория моделирования. Начала. К.1. Ч.1. «Освіта України», 2012. — 602 с. ISBN 978-966-7599-50-8
Ссылки
wiki.sc
Моделирование химических процессов — МегаЛекции
Моделирование (лат. modus — мера, образ, способ) издавна применялось в научном познании. Например, возникновение представлений Демокрита и Эпикура об атомах, их форме, и способах соединения, об атомных вихрях и ливнях, объяснения физических свойств различных веществ с помощью представления о круглых и гладких или крючковатых частицах, сцеп ленных между собой. Эти представления являются прообразами современных моделей, отражающих ядерно-электронное строение атома. В науке Нового времени первоначально применялись различные механические модели. Постепенно метод моделирования стал приобретать все большее распространение, проникая во все отрасли научного знания. XX век принес методу моделирования новые успехи, связанные с расцветом кибернетики.
Моделирование на современном этапе приобрело значение общенаучного метода. Его особенностью является то, что для изучения объекта используется опосредующее звено — объект-заместитель. Исходный объект исследования при моделировании называется оригиналом, объект-заместитель — моделью.
По мнению большинства выдающихся химиков, в том числе лауреата нобелевской премии Г. Сиборга, теоретическое моделирование является основным методом познания в химии. Сущность химических явлений скрыта от непосредственного наблюдения исследователя, поэтому познание осуществляют путем построения модели невидимого объекта по косвенным данным.
Контрольные вопросы:
1. В чем заключаются научные методы познания вещества?
2. Раскройте роль эксперимента и теории в химии
3. Для чего проводится моделирование химических процессов?
Раздел 1. Общая и неорганическая химия
Тема 1.1 Основные понятия и законы химии
Перечень изучаемых вопросов:
1.Вещество. Атом. Молекула. Химический элемент. Аллотропия. Простые и сложные вещества. 2.Качественный и количественный состав веществ. Химические знаки и формулы.
3.Относительные атомная и молекулярная массы. Количество вещества.
4.Стехиометрия. Закон сохранения массы веществ. Закон постоянства состава веществ молекулярной структуры. Закон Авогадро и следствия из него.
Вещество. Атом. Молекула. Химический элемент. Аллотропия. Простые и сложные вещества.
Химия —наука о веществах, закономерностях их превращений (физических и химических свойствах) и применении. В настоящее время известно более 100 тыс. неорганических и более 4 млн. органических соединений.
Химические явления: одни вещества превращаются в другие, отличающиеся от исходных составом и свойствами, при этом состав ядер атомов не изменяется. Физические явления: меняется физическое состояние веществ (парообразование, плавление, электропроводность, выделение тепла и света, ковкость и др.) или образуются новые вещества с изменением состава ядер атомов.
Вещество –один из видов материи, который характеризуется массой покоя. Это совокупность атомов, ионов или молекул, состоящих из одного или нескольких химических элементов.
Вещества:
· Чистые(химические соединения) — НСl, NaCl, H2SO4.
· Смеси веществ –молоко, природная вода, руда, песок, воздух
Химические соединения:
· Простые (состоят из атомов одного вида) — H2, O2, F2, J2, и др.
· Сложные(молекулы состоят из различных элементов) – H2O, NaCl, CuO, NaNO3.
Молекулы— это мельчайшие частицы вещества, состав которых и химические свойства такие же, как у данного вещества.
Атомы —это мельчайшие химически неделимые частицы, из которых состоят молекулы. Атом – мельчайшая частица химического элемента.
Химический элемент –это атомы одного и того же вида.
Например: все атомы водорода – это элемент водород; Н – химический знак (символ)
Основоположником современного атомно-молекулярного учения о строении веществ является выдающийся русский учёный М.В. Ломоносов. Учение создано в 1741 году.
Сущность учения состоит в том, что:
· Все вещества состоят из молекул.
· Молекулы состоят из атомов.
· Молекулы и атомы находятся в постоянном непрерывном движении, чем объясняются физические и химические явления.
Атомное ядро — центральная часть атома, состоящая из Z протонов и N нейтронов, в которой сосредоточена основная масса атомов.
Заряд ядра — положительный, по величине равен количеству протонов в ядре или электронов в нейтральном атоме и совпадает с порядковым номером элемента в периодической системе. Сумма протонов и нейтронов атомного ядра называется массовым числом A = Z + N.
Изотопы — химические элементы с одинаковыми зарядами ядер, но различными массовыми числами за счет разного числа нейтронов в ядре.
Химическая формула— это условная запись состава вещества с помощью химических знаков (предложены в 1814 г. Й. Берцелиусом) и индексов (индекс — цифра, стоящая справа внизу от символа. Обозначает число атомов в молекуле). Химическая формула показывает, атомы каких элементов и в каком отношении соединены между собой в молекуле.
Аллотропия— явление образования химическим элементом нескольких простых веществ, различающихся по строению и свойствам. Простые вещества- молекулы, состоят из атомов одного и того же элемента.
Cложные вещества— молекулы, состоят из атомов различных химических элементов.
Все вещества постоянно подвергаются всевозможным изменениям называемым явлениями.
Явления:
· Физические(изменение агрегатного состояния) – помол пшеницы, плавка металла, испарение воды.
· Химические(изменение состава и свойств вещества) – выпечка хлеба из муки, скисание молока.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Молекулярное моделирование — это… Что такое Молекулярное моделирование?
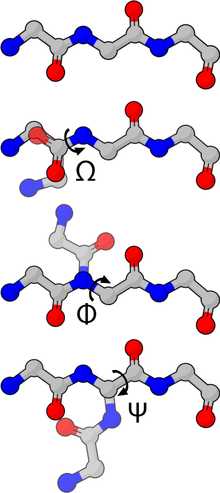
Молекулярное моделирование (ММ) — собирательное название методов исследования структуры и свойств молекул вычислительными методами с последующей визуализацией результатов, обеспечивающие их трехмерное представления при заданных в расчете условиях[1].
Методы молекулярного моделирования используются в компьютерной химии, вычислительной биологии и науке о материалах для изучения как индивидуальных молекул, так и взаимодействия в молекулярных системах.
Расчеты простейших систем при молекулярном моделировании могут быть выполнены вручную, но из-за большого объема вычислений при молекулярном моделировании сколь либо сложных систем, особенно при исследовании молекулярной динамики, используются компьютерные методы расчета и визуализации, эта техника получила название компьютерного молекулярного моделирования (англ. computer-assisted molecular modeling, CAMM)[2].
Общей чертой методов ММ является атомистический уровень описания молекулярных систем — наименьшими частицами являются атомы или небольшие группы атомов. В этом состоит отличие ММ от квантовой химии, где в явном виде учитываются и электроны. Таким образом, преимуществом ММ является меньшая сложность в описании систем, позволяющая рассмотрение большего числа частиц при расчётах.
Молекулярная механика
Молекулярная механика — один из подходов в ММ, использующий классическую механику для описания физических основ модели. Атомы (ядра с электронами) представляются точечными массами с соответствующими зарядами. Взаимодействия между соседними атомами включают упругие взаимодействия (соответствующие химическим связям) и силы Ван-дер-Ваальса, описываемые традиционно потенциалом Леннарда-Джонса. Электростатические взаимодействия вычисляются по закону Кулона. Атомам в пространстве присваиваются Декартовы или внутренние координаты; в динамических расчётах атомам также могут быть присвоены скорости, соответствующие температуре. Обобщающее математическое выражение известно как потенциальная функция (см. уравнения) и соответствует внутренней энергии системы (U) — термодинамической величине, равной сумме потенциальной энергии и кинетической. Потенциальная функция представляет потенциальную энергию как сумму энергетических членов, соответствующих отклонению от равновесных значений в длинах связей, валентных и торсионных углах, и членов для не связанных пар атомов, соответствующих ван-дер-Ваальсовым и электростатическим взаимодействиям.
Набор параметров, состоящий из равновесных значений длин связей, валентных углов, величин парциальных зарядов, силовых констант и ван-дер-Ваальсовских параметров, называется силовым полем. Различные реализации молекулярной механики используют слегка отличающиеся математические выражения и, следовательно, различные константы в потенциальной функции. Распространенные силовые поля, используемые в настоящее время, были разработаны с использованием точных квантовых расчетов и/или подгонкой под экспериментальные данные.
Для поиска локального минимума потенциальной энергии используются соответствующие методы минимизации (например, метод наискорейшего спуска и метод сопряженных градиентов), а для изучения поведения систем с течением времени используются методы молекулярной динамики. Низшие энергетические состояния более стабильны и имеют более важное значение из-за своей роли в химических и биологических процессах. Молекулярно-динамические расчеты, с другой стороны, показывают поведение системы как функцию от времени. И для минимизации, и для молекулярной динамики главным образом используется второй закона Ньютона — (или, что равносильно, ). Интегрирование этого закона движения с помощью различных алгоритмов приводит к получению траекторий атомов в пространстве и времени. Сила, действующая на атом, определяется как отрицательная производная функции потенциальной энергии.
Молекулы могут быть смоделированы как в вакууме, так и в присутствии растворителя, например воды. Расчёты систем в вакууме называются расчётами «в газовой фазе», в то время как расчёты, включающие молекулы растворителя, называются расчётами «с явно заданным растворителем». Другая группа расчётов учитывает наличие растворителя оценочно, с помощью дополнительных членов в потенциальной функции — так называемые расчёты «с неявным растворителем».
В настоящее время методы молекулярного моделирования стали обыденными при изучении структуры, динамики и термодинамики неорганических, биологических и полимерных систем. Среди биологических явлений, которые исследуются методами ММ, сворачивание белков, ферментативный катализ, стабильность белков, конформационные превращения и процессы молекулярного узнавания в белках, ДНК и мембранах.
Популярные программы для молекулярного моделирования
См. также
Литература
- A. R. Leach, Molecular Modelling: Principles and Applications, 2001, ISBN 0-582-38210-6
- D. Frenkel, B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, 1996, ISBN 0-12-267370-0
- D. C. Rapaport, The Art of Molecular Dynamics Simulation, 2004, ISBN 0-521-82586-7
- R. J. Sadus, Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation, 2002, ISBN 0-444-51082-6
- K.I.Ramachandran, G Deepa and Krishnan Namboori. P.K. Computational Chemistry and Molecular Modeling Principles and Applications 2008[1] ISBN 978-3-540-77302-3 Springer-Verlag GmbH
- А. В. Погребняк Молекулярное моделирование и дизайн биологически активных веществ. — Ростов-на-Дону: Издательство СКНЦ ВШ, 2003. — ISBN 5-87872-258-5
- Х.-Д. Хельтье, В. Зиппль, Д. Роньян, Г. Фолькерс, Молекулярное моделирование Теория и практика, 2010, ISBN 978-5-9963-0156-0
Ссылки
Примечания
- ↑ molecular modeling // IUPAG Gold Book
- ↑ computer-assisted molecular modeling (CAMM) // IUPAC Gold Book
dic.academic.ru