Графические информационные модели. Многообразие графических информационных моделей
Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. Графические информационные модели являются простейшим видом моделей. С их помощью передаются внешние признаки объекта – размер, форма, цвет. Графические модели несут в себе больше информации, чем словесные.
Для более наглядного и понятного представления информации в графических информационных моделях используются графические изображения (образные элементы), которые могут быть дополнены текстами, числами и символами. Примерами графических информационных моделей являются схемы, карты, чертежи, графики, диаграммы и много другое.
Разберёмся более подробно с каждой из них.
Cхема – это графическое отображение состава и структуры сложной системы. Можно обратиться к ранее рассматриваемому примеру: две электрические схемы соединения переключателей.
Схема последовательного соединения переключателей
Схема параллельного соединения переключателей
На первой представлено последовательное соединение, а на второй – параллельное. Можно заметить, что с помощью схемы легче разбираться с такими задачами, нежели использовать словесное описание. Схемы используются на уроках биологии, истории и так далее.
Следующая графическая информационная модель – чертеж. Чертеж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования. При построении чертежа используются изображения, числа, текст. С помощью изображений мы получаем представление о форме объекта, с помощью чисел – о размере, с помощью текста – о названии объектов, размерах, в которых выполнены изображения. Примером чертежа является изображение детали перед её изготовлением.
На чертеже изображена деталь в разрезе, чтобы лучше было видно все части, составляющие нашу деталь, присутствуют размеры (числа).
Рассмотрим такую графическую информационную модель как карта. Карта используется для отображения местности в уменьшенном масштабе, которая является для нее объектом моделирования. Например, с помощью карты мы можем узнать сколько километров от Москвы до Санкт-Петербурга, как добраться на метро или автобусе с одного остановочного пункта до другого, где находится Будапешт и много другое. Для различных целей используются разнообразные карты: политическая, географическая, тематическая и другие.
Перейдем к графикам. График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.
Например, Максим учится в девятом классе. В течение 8 лет учёбы в школе он получал следующие годовые оценки по математике: первый класс – 5, второй класс – 4, третий класс – 4, четвёртый – 5, пятый – 4, шестой – 3, седьмой – 4, восьмой — 3. Посмотрим, как это можно отобразить на графике. Ось X будет отображать классы с 1 по 8. Ось Y оценки с 1 до 5. Обратите внимание, что в данном графике за единицу будем брать две клеточки.
Расставим точки в соответствии с данными на координатной плоскости и соединим их линиями.
Мы получили необходимый график, с помощью которого можно сделать вывод, что знания Максима по математике ухудшились. Ещё одним примером графика является кардиограмма сердца. Кардиограмма точно определяет в каком ритме бьётся сердце.
Перейдём к диаграммам. Диаграмма – это графическое изображение, которое даёт наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Диаграммы бывают нескольких видов, но более подробно мы с ними познакомимся при изучении электронных таблиц.
А сейчас рассмотрим несколько примеров.
Первый: Наша планета состоит из воды и суши. Вода составляет семьдесят процентов от планеты, а суша – тридцать. Изобразим всё это с помощью круговой диаграммы. Нарисуем круг. Он будет изображать планету и соответственно будет равен ста процентам. Затем изобразим семьдесят процентов суши и тридцать процентов воды.
На данной диаграмме мы можем увидеть соотношение воды и суши.
Теперь рассмотрим ещё один пример. Саша тратит на дорогу от дома до школы 10 минут, Таня – 15 минут, Ира – 7 минут и Игорь – 20 минут. Давайте все это изобразим с помощью диаграммы. На оси X напишем имена учащихся, а на оси Y – время, затраченное на дорогу. Затем каждому учащемуся нарисуем столбик по высоте соответствующий времени его пути.
Таким образом мы получили столбчатую диаграмму.
Важно запомнить:
· Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений.
· Схема – это графическое отображение состава и структуры сложной системы.
· Чертёж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования.
· График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.
· Диаграмма – это графическое изображение, которое дает наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений.
videouroki.net
Графические информационные модели
Свойства графических информационных моделей
Определение 1
Графическая информационная модель – способ представления описываемых объектов и процессов в виде изображений. С помощью таких моделей передаются внешние признаки – форма, размер, цвет.
Поскольку человек с помощью зрения получает большую часть информации (порядка 70%), то по эффективности восприятия рисунок зачастую оказывается более эффективным, чем текст, формулы или устный рассказ.
Замечание 1
Текст, как и реалистичное изображение, воспринимается посредством зрения, но для его восприятия нервной системой должна быть проделана дополнительная работа — преобразование во взаимосвязанные, удерживаемые в сознании мыслительным усилием образы.
Графические информационные модели, видимо, появились в человеческой практике раньше других. Рисунки, отображающие план местности и места охоты, археологи находят на стенах пещер, где обитали доисторические люди.
Типы графических моделей
Примеры графических моделей:
- карта – отображение местности в уменьшенном масштабе;
- схема – графическое отображение структуры системы;
- чертёж – условное изображение предмета с точным соотношением размеров;
- график – изображение, которое отражает зависимость одной величины от другой;
- диаграмма – изображение, дающее наглядное представление о соотношении величин или значений одной величины; диаграмма отличается от графика большей наглядностью, меньшим количеством задействованных данных.

Рисунок 1. Чертеж. Автор24 — интернет-биржа студенческих работ
Способы исполнения карт, схем, чертежей регламентированы отраслевыми стандартами. Так, географические карты выполняются в заданном масштабе, с использованием определенных правил преобразования трехмерной поверхности в двухмерную (проекции), с нанесением сетки координат, с использованием определенных цветов для обозначения высот и глубин. Кроме того, географические карты изображаются по-разному в зависимости от назначения: физические, экономические, климатические, демографические, военные и т.д.
Схемы также различаются в зависимости от отрасли. Существуют стандарты для черчения электронных схем, схем монтажа оборудования (например, электросилового, водопроводного) и т.п.
Чертежи также изготавливаются по ГОСТам: осевые линии наносятся штрихпунктирными линиями, невидимые — штриховыми, внешние — жирными, размерные — тонкими. Для обозначения различных материалов используются штриховки. Надписи на чертежах выполняются особым шрифтом по определенным правилам. Чертеж должен быть обрамлен особой рамкой со штампом.
Существуют менее регламентированные формы графических моделей, такие, как эскизы. Они применяются там, где требуется быстро зафиксировать конструкторскую мысль, передать ее исполнителю. Нет строгих правил при формировании графиков и диаграмм. Однако и при рисовании произвольных графических моделей принято придерживаться определенных правил и рекомендаций.
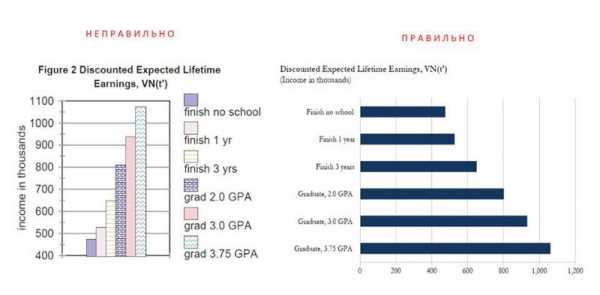
Рисунок 2. Рекомендации по отображению диаграммы. Автор24 — интернет-биржа студенческих работ
В приведенном примере нужно расположить информацию на осях таким образом, чтобы данные легко считывались. Если нанести информацию об уровне образования на горизонтальную ось, большое количество текста помешает восприятию. Кроме того, придется задействовать большое количество цветов и штриховок. Но при упрощении второй оси (умеренные цифры) график легко разворачивается на 90 градусов, дополнительная фактура становится ненужной.
Графические модели и вычислительная техника
Современное программное обеспечение предоставляет широкие возможности для подготовки графических моделей. Приведем несколько примеров таких приложений:
- Microsoft Ecxel — для отображения в графическом виде информации на основе данных электронных таблиц;
- Microsoft PowerPoint — для подготовки насыщенных графикой офисных презентаций;
- Adobe Photoshop — для работы с растровой графикой;
- Adobe Illustrator — для работы с векторной графикой;
- AutoCAD — для подготовки машиностроительных чертежей и т.д.
Особо следует отметить то обстоятельство, что графические модели используются и при разработке самого программного обеспечения: с помощью диаграмм семейства UML проектируются компьютерные программы. Такие диаграммы не зависят от предметной области и могут применяться в любом программном проекте. Кроме того, для подготовки таких диаграмм не нужна компьютерная техника (хотя ее применение и возможно). Диаграммы и схемы рисуются фломастерами на пластиковых досках или ватмане в ходе «мозговых штурмов», к которым могут быть привлечены как непосредственные разработчики, так и представители заказчика.
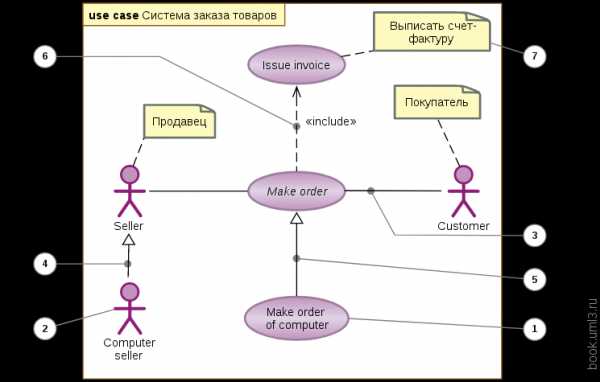
Рисунок 3. Диаграмма случаев использования из семейства UML. Автор24 — интернет-биржа студенческих работ
Проектирование с помощью UML начинается от определения случаев использования (Use Case). Дальнейшие уточнения могут идти многими способами, но конечной целью процесса проектирования является формирование диаграмм классов. На их основе с помощью специального программного обеспечения может быть даже частично сформирован компьютерный код, который программистам останется только конкретизировать и отладить.
spravochnick.ru
4. 8 Графические информационные модели
скачать 4.8 Графические информационные модели.Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. К ним относятся: чертежи, графики, диаграммы, образные модели, схемы (карты, графы, блок-схемы).
Графические (геометрические) информационные модели передают внешние признаки объекта — размеры, форму, цвет, расположение. В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы). Часто графические модели дополняются числами, символами и текстами (знаковыми элементами). В этом случае их называют смешанными моделями.
Образные модели представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кинопленке и др.). К ним относятся рисунки, фотографии.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. Схема – это графическое отображение состава и структуры сложной системы. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта.
В информатике особое место занимает построение блок-схем. Блок-схемы наглядно отражают алгоритм, т.е. последовательность действий при решении задачи. Они строятся при программировании – создании новых программ.
Карта описывает конкретную местность, которая является для нее объектом моделирования. Это уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений.
Карта создается с определенными целями для определения:
-
местоположения населенных пунктов; -
рельефа местности; -
расположения автомагистралей; -
измерения расстояний между реальными объектами на местности -
и т.д.
Сейчас получили большое распространение геоинформационные модели (Например, http://maps.google.ru/ — спутниковая съемка карты местности).
Чертеж – точная геометрическая копия реального объекта. Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения. Чертежи создаются конструкторами, проектировщиками, они должны быть очень точным, т.к. на них указываются все необходимые размеры реального объекта. Существует масса различных компьютерных сред для создания конструкторских чертежей: Автокад, Адем, Компас, 3D MАХ — для трехмерного моделирования и т.д.
Графики и диаграммы — это информационные модели, которые в наглядной форме представляют числовые и статистические данные.
График — линия, дающая наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График – отображение и визуализация различных процессов (природных, экономических, общественных и технических). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
Отдельное место среди графических моделей занимают графы.
4.9 Графы
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. В информатике по графам строятся программы. В этом параграфе рассмотрены только самые основные понятия, свойства графов и некоторые способы решения задач.
Если объекты некоторой системы изобразить точками (кругами, овалами, прямоугольниками…), а связи между ними — линиями (дугами, стрелками…), то мы получим информационную модель рассматриваемой системы в форме графа. Граф представляет собой набор вершин и соединяющих их ребер. Вершины графа могут быть обозначены буквами, числами, словами…
Если рёбра графа характеризуются некоторой дополнительной информацией (выраженной числами), его называют взвешенным, а числа — весами рёбер. Вес рёбер может соответствовать, например, расстоянию между объектами (городами).
Если ребра графа указывают направление (представлены стрелками), то граф называют ориентированным (орграфом). Движение в ориентированном графе возможно тольеко в одном направлении (по стрелкам). Связи между объектами – вершинами в таком случае считаются несимметричными. У неориентированного графа связи между объектами – вершинами симметричны.
Одинаковые, но по-разному нарисованные графы, называют изоморфными. У изоморфных графов соединены одни и те же вершины.
Степенью вершины графа называется количество выходящих из нее ребер. Вершина, имеющая четную степень, называется четной вершиной, Вершина, имеющая нечетную степень, называется нечетной вершиной. На рисунке вершины A, B, D – чётные. Их степень равна 2. Вершины С, Е – нечётные. Их степень равна 3.
С понятием степени вершины связана одна из основных теорем теории графов – теорема о чётности числа нечетных вершин.
Теорема: Любой граф содержит четное число нечетных вершин.
Для иллюстрации рассмотрим задачу.
В городе Маленьком 5 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с 3-мя другими?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 3 провода, т.е. степень каждой вершины нашего графа – 3. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца и при суммировании степеней каждый провод взят 2 раза). (3*5)/2=15/2=7,5
Но это число не целое, то есть количество проводов получится разным. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Есть еще одно важное понятие, относящееся к графам – понятие связности. Граф называется связным, если любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа. Граф на рисунке ниже имеет три компоненты связности (состоит из трёх отдельных частей).
Вершина, не имеющая рёбер, называется изолированной вершиной и составляет отдельную компоненту связности. Вершина, имеющая только одно ребро, называется концевой или висячей.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью (1). Цепь, начальная и конечная вершины которой совпадают, называется циклом (2). Дерево (иерархия) – это граф, в котором нет циклов (3), т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
(1) (2) (3)
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный им объект входит в один класс1 высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Например, родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
4.10 Использование графов при решении задач
Пример 1. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом)
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить.
Пример 2. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусем без присмотра нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное размещение персонажей на берегу реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё. Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существует два решения этой задачи. Приведём соответствующий одному из них план переправы:
-
крестьянин перевозит лису; -
крестьянин возвращается; -
крестьянин перевозит собаку; -
крестьянин возвращается с лисой; -
крестьянин перевозит гуся; -
крестьянин возвращается; -
крестьянин перевозит лису.
Пример 3. Рассмотрим следующую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если игрок I оставил 4 спички, игрок II может своим ходом оставить 3 или 2 спички. Если же после хода первого игрока осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну.
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 2.8 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Контрольные вопросы.
-
Какие информационные модели относят к графическим? -
Приведите примеры графических информационных моделей, с которыми вы имеете дело:
а) при изучении других предметов; б) в повседневной жизни.
-
Что такое граф? Что является вершинами и рёбрами графа? Укажите на собственном графе-примере. -
Какой граф называют ориентированным? Взвешенным? -
Какие графы называют изоморфными? -
Что такое степень вершины? Укажите степени вершин в вашем графе. -
Сформулируйте теорему о чётности числа нечетных вершин. -
Какой граф называют связным? Изобразите граф с двумя компонентами связности. -
Какую вершину называют изолированной? Висячей? Укажите на собственном примере – графе. -
Что такое путь? Цепь? Цикл? Приведите примеры цепей и циклов, имеющихся в вашем графе. -
Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы. -
Составьте семантическую сеть по русской народной сказке «Колобок».
nenuda.ru
§1.3 Графические информационные модели
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (учебник ФГОС Л.Л. Босова, А.Ю. Босова) | §1.3 Графические информационные модели
Ключевые слова:
• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево
1.3.1. Многообразие графических информационных моделей
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта. Примеры схем приведены на рис. 1.5.
Рис. 1.5. Примеры схем, используемых на уроках физики, биологии, истории
Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.
Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.
График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
1.3.2. Графы
Если некоторые объекты изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой; при этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной.
Граф называется неориентированным, если его вершины соединены рёбрами (рис. 1.6, а). Вершины ориентированного графа соединены дугами (рис. 1.6, б). Путь — это последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую.
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. На рис. 1.6, в с помощью взвешенного неориентированного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Рис. 1.6. Графы
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс1* высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Ресурс «Живая Родословная» (145555) — инструмент для формирования и анализа генеалогических деревьев, содержащий примеры родословных. С его помощью вы можете изучить генеалогические деревья многих известных семей и построить генеалогическое дерево своей семьи (http://sc.edu.ru/).
Класс — множество объектов, обладающих общими признаками.
1.3.3. Использование графов при решении задач
Графы удобно использовать при решении некоторых классов задач.
Пример 1. На рисунке 1.7 изображена схема дорог, связывающих торговые точки А, В, С, D, Е. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки Е?
Рис. 1.7. Схема дорог, представленная ориентированным графом
В вершину Е можно попасть только из вершин С и D. Если мы будем знать число путей из вершины А в вершину С и из вершины А в вершину D, то, сложив их, получим искомое число путей из А в Е. Действительно, для того чтобы попасть из вершины А в вершину Е, мы просто все пути из вершины А в вершину С дополним дугой СЕ, а пути из вершины А в вершину D дополним дугой DE. Число путей при этом не изменится. Итак, число путей из вершины А в вершину Е равно сумме путей из А в С и из А в П.
Можно сказать, что наша задача распалась на две более простые задачи. Решим каждую из них в отдельности.
В вершину С можно попасть непосредственно из вершины А и из вершины В. В свою очередь, существует единственный путь из вершины А в вершину В. Таким образом, из вершины А в вершину С можно попасть двумя путями: 1 (напрямую из А) + 1 (через В) = 2.
Попробуйте доказать, что путь из вершины А в вершину В — единственный.
Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин А, В и С:
1 (напрямую из А) + 1 (через В) + 2 (через С) = 4.
Итак, существуют четыре пути из вершины А в вершину D.
Теперь выполним подсчёт путей из А в Е:
2 (через С) + 4 (через D) = 6.
Решение задачи будет гораздо проще, если двигаться от вершины А (начало маршрута) к вершине Е и проставлять веса вершин — число путей из А в текущую вершину (рис. 1.8). При этом вес вершины А можно принять за 1. Действительно, существует единственный способ попасть из А в А — оставаться на месте.
Рис. 1.8. Схема дорог, представленная взвешенным ориентированным графом
Пример 2. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.9.
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
Рис. 1.9. Дерево для решения задачи о записи трёхзначных чисел
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. (Вспомните правило умножения из комбинаторики!)
Пример 3. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.10).
Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:
1) крестьянин перевозит лису;
2) крестьянин возвращается;
3) крестьянин перевозит собаку;
4) крестьянин возвращается с лисой;
5) крестьянин перевозит гуся;
6) крестьянин возвращается;
7) крестьянин перевозит лису.
Пример 4. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если игрок I оставил 4 спички, игрок II может своим ходом оставить 3 или 2 спички. Если же после хода первого игро- . ка останутся 3 спички, второй игрок может выиграть, взяв две спички и оставив одну.
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 1.11 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Рис. 1.11. Дерево игры
САМОЕ ГЛАВНОЕ
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы.
Граф состоит из вершин, связанных линиями — рёбрами или дугами. Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весами вершин (рёбер, дуг).
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Какие информационные модели относят к графическим?
3. Приведите примеры графических информационных моделей, с которыми вы имеете дело:
а) при изучении других предметов;
б) в повседневной жизни.
4. Что такое граф? Что является вершинами и рёбрами графа на рис. 1.6, в? Приведите примеры цепей и циклов, имеющихся в этом графе. Определите, какие два пункта наиболее удалены друг от друга (два пункта считаются самыми удалёнными, если длина кратчайшего пути между ними больше, чем длина кратчайшего пути между любыми другими двумя пунктами). Укажите длину кратчайшего пути между этими пунктами.
5. Приведите пример системы, модель которой можно представить в форме графа. Изобразите соответствующий граф.
6. Грунтовая дорога проходит последовательно через населённые пункты А, В, С и D. При этом длина грунтовой дороги между А и В равна 40 км, между В и С — 25 км, и между С и D — 10 км. Между А и D дороги нет. Между А и С построили новое асфальтовое шоссе длиной 30 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.
7. На рисунке изображена схема дорог, связывающих торговые точки А, Б, В, Г, Д, Б, К. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки К?
8. Работая в группе, составьте семантическую сеть по одной из русских народных сказок: «Колобок», «Курочка Ряба», «Репка».
9. Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы.
10. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8 при условии, что в записи числа не должно быть одинаковых цифр?
11. Сколько существует трёхзначных чисел, все цифры которых различны?
12. Для составления цепочек используются бусины, помеченные буквами А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
13. Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Электронное приложение к уроку
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
xn—-7sbbfb7a7aej.xn--p1ai
Понятие модели. Назначение и свойства моделей. Графические информационные модели
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год | Понятие модели
Содержание урока
Что такое моделирование. Натурные и информационные модели
Что такое моделирование. Формализация
Графические информационные модели. Карта, чертежи и схемы
Графические информационные модели. График — модель процесса
Графические информационные модели
Карта, чертежи и схемы
Основные темы параграфа:
• карта как информационная модель;
• чертежи и схемы;
• график — модель процесса.
Карта как информационная модель
Можно ли назвать информационной моделью карту местности (рис. 2.2)?
Безусловно, можно! Ведь карта описывает (графически) конкретную местность, которая является для нее объектом моделирования. Кроме того, карта создается с определенной целью: с ее помощью можно добраться до нужного населенного пункта. Используя линейку и учитывая масштаб карты, можно определить расстояние между различными пунктами. Однако никаких более подробных сведений о населенных пунктах, кроме их расположения, эта карта не дает.
Чертежи и схемы
Другими знакомыми вам примерами графических информационных моделей являются чертежи, схемы, графики.
Чертеж должен быть очень точным, на нем указываются все необходимые размеры. Например, чертеж болта нужен для того, чтобы, глядя на него, токарь мог выточить болт на станке (рис. 2.3).
У схемы электрической цепи нет никакого внешнего сходства с реальной электрической цепью (рис. 2.4). Электроприборы (лампочка, источник тока, конденсатор, сопротивление) изображены символическими значками, а линии обозначают соединяющие их проводники электрического тока. Электрическая схема нужна для того, чтобы понять принцип работы цепи, чтобы можно было рассчитать в ней значения силы тока и напряжения, чтобы при сборке цепи правильно соединить ее элементы.
Схема — это графическое отображение состава и структуры сложной системы.
Структура — это порядок объединения элементов системы в единое целое.
На рисунке 2.5 приведена схема Московского метрополитена. Структуру Московского метрополитена называют радиально- кольцевой.
xn—-7sbbfb7a7aej.xn--p1ai
Графические информационные модели. Графы
Граф – это совокупность объектов со связями между ними. Графически это будет выглядеть следующим образом:
Вершины (точки) – это объекты, а ребра (линии между ними) – это связи. Помимо точек вершины графа могут изображаться овалами, кругами, прямоугольниками и так далее. Связи между вершинами могут быть различными: дуги, рёбра, петли.
На данном уроке мы с вами познакомимся с ориентированными и неориентированными графами. В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.
Решим задачу: В соревнованиях по шахматам участвовало 6 учащихся с 9 по 11 класс. При встрече они все обменялись рукопожатиями. Вопрос: сколько всего было сделано рукопожатий?
Для решения данной задачи будем использовать граф. Вершинами графов будут являться шесть учащихся, которые участвовали в турнире. Пронумеруем их от одного до шести. Проведем от каждой вершины линии (ребра) к оставшимся пяти вершинам.
Для ответа на вопрос остается сосчитать, сколько линий изображено на графе. Ответ: на турнире было сделано 15 рукопожатий.
Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
Давайте сами нарисуем взвешенный граф на основе задачи со следующим условием: Между городами A, B, C, D, Е построены дороги. Необходимо найти кратчайший путь из города А в город Е, если известно, что из города А в город В расстояние 100 километров, из А в С – 260 километров, из В в С – 140 километров, из В в Е – 400 километров, из С в D – 50 километров, из С в Е – 100 километров и из D в Е – 40 километров.
Итак, для решения данной задачи необходимо нарисовать взвешенный граф, так как нам дано расстояние, то есть вес рёбер. Для начала нарисуем вершину А. Из неё будут выходить два ребра в вершины В и С. Ребро из А в В будет короче, чем из А в С, так как расстояние из пункта А в пункт В 100 километров, а из пункта А в пункт С – 260 километров.
Далее нарисуем ребро из В в С и его вес будет равен 140.
Теперь нарисуем ребро из вершины С в вершину D и укажем вес 50
и так далее.
У нас получился взвешенный граф.
Нам осталось найти кратчайший путь. Для этого из вершины А будем идти в вершину В – это 100 километров, затем сразу в вершину Е. Слаживаем 100 и 400, получим 500 километров.
Аналогичным образом проходим по остальным рёбрам и получим, что путь через вершины A, B, C, E равен 340 километров. Через вершины A, C, E 360 километров. A, B, C, D, E - 330, A, C, B, E 800 километров и через вершины A, C, D, E равен 350 километров. Нам необходимо выбрать кратчайший – это путь через города A, B, C, D, E и равен он 330 километров.
Следующее понятие, с которым мы должны познакомится — Цепь. Итак, цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза. То есть при построении пути по одному и тому же ребру можно пройти только один раз. Например, всем известная детская задача, где необходимо нарисовать домик не отрывая ручки от бумаги и в то же время нельзя дважды проходить по одной и той же линии.
В свою очередь, цикл – это цепь, в которой начальная и конечная вершины совпадают. В детстве, наверное, каждый из вас рисовал звезду, не отрывая ручки от бумаги и не проходя дважды по одной и той же линии или ребру. При изображении такой звезды начальная и конечная вершины совпадают. Сеть – это граф с циклом.
Разберём ещё один пример. У Антона в семье есть мама Татьяна, папа Юрий и сестра Маша. Изобразим каждого члена семьи как вершину нашего графа и обозначим первыми буквами имён. От каждого из них проведём рёбра к оставшимся троим. Над каждым из рёбер укажем, кто кем и кому приходится. Например, если идти от вершины Антона к Юрию, то Антон является сыном. А если идти наоборот, от Юрия к Антону, то Юрий является отцом. Аналогичным образом можно провести отношения между всеми членами семьи. Данный граф является примером семантической, или же смысловой сети.
Таким образом, Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними. Все связи данного графа различны, поэтому их необходимо подписывать.
Графы широко распространены как информационные модели. Их можно применять, например, при планировании жилого района, где вершинами будут являться дома, а рёбрами – дороги или дорожки, которые их связывают. Ещё одним примером будет являться карта проезда по городу на любом из видов транспорта, где остановки – это вершины, а путь движения транспорта – это рёбра и так далее.
Следующее определение в данной теме: дерево. Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь. Корень дерева – это одна и единственная главная его вершина.
Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков. Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Листья – это вершины, которые не имеют потомков.
Разберёмся более подробно на примере:
Ученик Антон решил составить генеалогическое дерево своей семьи. Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он является сыном своего отца Юрия и мамы Татьяны. В свою очередь Татьяна является дочерью Леонида (дедушки Антона) и Елены (бабушки Антона). Юрий является сыном Григория (дедушки Антона) и Марии (бабушки Антона). У Антона есть сестра Маша. Так как словесное описание трудно для восприятия, давайте поможем Антону представить это все в виде дерева и построим генеалогическое дерево.
Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху. У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок. У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.
Таким образом, мы построили родословное дерево.
Важно запомнить:
· Граф – это совокупность объектов со связями между ними.
· Вершины – это объекты, а ребра – это связи.
· Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
· Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза.
· Цикл – это цепь, в которой начальная и конечная вершины совпадают.
· Сеть – это граф с циклом.
· Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними.
· Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину.
videouroki.net
Понятие модели. Назначение и свойства моделей. Графические информационные модели
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год | Понятие модели
Содержание урока
Что такое моделирование. Натурные и информационные модели
Что такое моделирование. Формализация
Графические информационные модели. Карта, чертежи и схемы
Графические информационные модели. График — модель процесса
Что такое моделирование
Натурные и информационные модели
Изучаемые вопросы:
— Модель – упрощённое подобие реального объекта.
— Натурные и информационные модели.
— Понятие моделирования и формализации.
— Карта как информационная модель.
— Чертежи, схемы и графики – примеры графических информационных моделей.
Что такое моделирование
Основные темы параграфа:
• натурные модели;
• информационные модели;
• формализация.
Натурные модели
Сейчас речь пойдет об очень важном в науке понятии — понятии модели. Это слово многим знакомо. Возможно, кто-то из вас занимается техническим моделированием — строит модели кораблей, автомобилей или самолетов. Такие модели воспроизводят некоторые свойства реальных устройств, например, форму, способность плавать, ездить или летать. Можно привести и другие примеры моделей: глобус — это модель земного шара, манекен в магазине — модель человека, макет в мастерской архитектора — модель застройки города.
Выше перечислены примеры материальных моделей. Их еще называют натурными моделями.
Как правило, моделируемый объект представляет собой сложную систему. Например, автомобиль состоит из корпуса, двигателя, колес, рулевого управления, салона и пр.
Модель автомобиля, построенная школьником, много проще. В ней, например, может отсутствовать двигатель, электропитание, рулевое управление и другие части, размер ее меньше размера настоящего автомобиля.
Любая модель воспроизводит только те свойства оригинала, которые понадобятся человеку при ее использовании. Например, манекен и производственного робота можно назвать моделями человека. Манекен нужен для того, чтобы на него можно было надеть одежду для рекламы или для удобства работы портного, но способности ходить, мыслить или разговаривать от него не требуется. Поэтому манекен должен воспроизводить лишь форму и размер человеческого тела.
Цель создания производственного робота совсем другая. Робот должен воспроизводить некоторые физические действия человека: уметь брать и перемещать детали, закручивать и раскручивать болты и пр. Но для достижения этих целей внешнего сходства с человеком совсем не требуется.
Свойства объекта, отраженные в модели, зависят от цели моделирования. Модели одного и того же объекта будут разными, если они создаются для разных целей.
Информационные модели
Кроме натурных существуют еще информационные модели. Нетрудно понять, что для информатики именно они и представляют наибольший интерес .
Если натурная модель объекта моделирования — это его физическое подобие, то информационная модель — это его описание. Способ описания может быть самым разным: вербальным, т. е. словесным описанием на естественном языке, математическим, графическим и др. Например, чертеж корабля является его графическим описанием, а стало быть, информационной моделью корабля (рис. 2.1).
Понятие объект моделирования надо понимать в самом широком смысле. Это может быть материальный объект: корабль, комета, живая клетка; явление природы: гроза, солнечное затмение; процесс: полет ракеты, изменение стоимости акций на фондовой бирже.
Моделирование — это деятельность человека по созданию модели (натурной или информационной).
В науке существует еще одна разновидность моделей: воображаемые (идеальные) модели. Например, в физике: материальная точка, абсолютно твердое тело, идеальный газ; в математике: геометрическая точка, бесконечность и пр.
Так же как и натурные, информационные модели одного и того же объекта, предназначенные для разных целей, могут существенно различаться.
Вот пример. Нередко людям приходится заполнять всевозможные анкеты, личные карточки. Такие документы можно рассматривать как различные информационные модели человека. По форме они одинаковые (анкеты), а по содержанию разные. Например, в личной карточке работника предприятия, которая хранится в отделе кадров, о нем имеются следующие сведения: фамилия, имя, отчество, пол, год рождения, место рождения, национальность, адрес проживания, образование, семейное положение. А в медицинскую карточку того же самого человека заносятся следующие данные: фамилия, имя, отчество, пол, год рождения, группа крови, вес, рост, хронические заболевания. В обществе охотников, членом которого является этот же человек, о нем хранится третий набор сведений. Как видите, разные цели моделирования — разные информационные модели.
Современным инструментом для информационного моделирования является компьютер. С его помощью воспроизводятся самые сложные объекты, процессы, явления. Такая модель обычно отображается на экране в виде статического (неподвижного) или анимированного (подвижного) изображения, может сопровождаться звуком, т. е. использовать технологию мультимедиа.
Модель — это упрощенное подобие реального объекта. Модель отражает лишь некоторые свойства объекта, существенные с точки зрения цели моделирования.
Для обозначения сложных объектов, состоящих из множества взаимосвязанных частей, в науке используется термин система. В большинстве случаев объектами моделирования являются сложные системы: природные, технические, общественные и др.
Модель используется как заменитель реальной системы для воспроизведения отдельных ее функций, для прогноза ее поведения в определенных условиях.
xn—-7sbbfb7a7aej.xn--p1ai
