Какие существуют типы моделей систем – Системы и модели систем Понятие модели

2. Виды моделей

По способу отображения действительности различают три ос­новных вида моделей — эвристические, физические и матема­тиче­ские.

Эвристические модели,как правило, представляют собой об­разы, рисуемые в воображении человека. Их описание ве­дется словами естественного языка и, обычно, неоднозначно и субъек­тивно. Эти модели неформализуемы, т. е. не описыва­ются фор­мально-логическими и математическими выраже­ниями, хотя и рождаются на основе представления реальных процессов и явле­ний. Эвристическое моделирование — основное средство вырвать­ся за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии че­ловека, его опыта и эрудиции. Эвристиче­ские модели используют­ся на начальных этапах проектирова­ния (или других видов дея­тельности), когда сведения о разраба­тываемом объекте еще скуд­ны. На последующих этапах проек­тирования эти модели заменя­ются на более конкретные и точ­ные.

Физические модели —материальны, но могут отличаться от реального объекта или его части размерами, числом и материа­лом элементов. Выбор размеров ведется с соблюдениемтеории подобия.К физическим моделям относятся реальные изделия, образцы, экспериментальные и натурные модели.

Физические модели подразделяются на объемные (модели и ма­кеты) и плоские (тремплеты).

Под модельюпонимают изделие, являющееся упрощенным по­добием исследуемого объекта.

Под тремплетомпонимают изделие, являющееся плоским мас­штабным отображением объекта в виде упрощенной ортого­нальной проекции или его контурным очертанием. Тремплеты вырезают из пленки, картона и т. п. и применяют при исследова­нии и проектировании зданий, установок, сооружений.

Под макетомпонимают изделие, собранное из моделей или тремплетов.

Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчетов. Такая модель позволяет охватить явление или процесс во всем их многообра­зии, наиболее адекватна и точна, но достаточно дорога, трудо­емка и менее универсальна. В том или ином виде с физическими моделя­ми работают на всех этапах проектирования.

Математические модели —формализуемые, т. е. представля­ют собой совокупность взаимосвязанных математических и фор­мально-логических выражений, как правило, отображающих ре­альные процессы и явления (физические, психические, социаль­ные и т. д.). Модели по форме представления могут быть:

• аналитические, их решения ищутся в замкнутом виде, в виде функциональных зависимостей. Удобны, при анализе сущности описываемого явления или процесса, но отыскание их решений бывает весьма затруднено;

• численные, их решения — дискретный ряд чисел (таблицы). Модели универсальны, удобны для решения сложных задач, но не наглядны и трудоемки при анализе и установлении взаимо­связей между параметрами. В настоящее время такие модели реализуют в виде программных комплексов —пакетов программ для расчета на компьютере. Программные ком­плексы бывают прикладные, привязанные к предметной об­ласти и конкретной системе, явлению, процессу, и общие, реализующие универ­сальные математические соотношения (например, расчет сис­темы алгебраических уравнений).

Построение математических моделей возможно следующими способами:

• аналитическим путем, т. е. выводом из физических законов, математических аксиом или теорем;

• экспериментальным путем, т. е. посредством обработки ре­зультатов эксперимента и подбора аппроксимирующих (при­ближенно совпадающих) зависимостей.

Математические модели более универсальны, дешевы, позво­ляют поставить «чистый» эксперимент (т. е. в пределах точности модели исследовать влияние какого-то отдельного фактора при постоянстве других), прогнозировать развитие явления или про­цесса. Математические модели — основа построения компьютер­ных моделей и применения вычислительной техники. Резуль­таты математического моделирования нуждаются в обязатель­ном со­поставлении с данными физического моделирования — с целью проверки полученных данных и для уточнения самой мо­дели.

К промежуточным между эвристическими и математическими моделями можно отнести графические модели,представляю­щие различные изображения — схемы, графики, чертежи. Так, эскизу (упрощенному изображению) некоторого объекта в зна­чительной степени присущи эвристические черты, а в чертеже уже конкрети­зируются внутренние и внешние связи моделируе­мого объекта.

Промежуточными также являются и

аналоговые модели.Они позволяют исследовать одни физические явления или математи­че­ские выражения посредством изучения других физических явле­ний, имеющих аналогичные математические модели.

Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом объекте и возможностей проек­тировщика, исследователя. По возрастанию степени соответст­вия реальности модели можно расположить в следующий ряд: эври­стические (образные) — математические — физические (экс­пери­ментальные).

Технические системы различаются по назначению, устрой­ст­ву и условиям функционирования. Следовательно, можно и нужно вносить соответствующие различия и в их модели.

В зависимости от целей исследования выделяют следующие модели:

• функциональные, предназначенные для изучения функцио­нального назначения элементов системы, внутренних связей и связей с другими системами;

• функционально-физические, предназначенные для изучения сущности и назначения физических явлений, используемых в системе, их взаимосвязей;

• модели процессов и явлений, таких как кинематические, проч­ностные, динамические и другие, предназначенные для иссле­дования тех или иных характеристик системы, обеспечиваю­щих ее эффективное функционирование.

Модели также подразделяют на простые и сложные, однород­ные и неоднородные, открытые и закрытые, статические и дина­мические, вероятностные и детерминированные.

Часто говорят о технической системе как простой или слож­ной, закрытой или открытой и т. п. В действительности же под­ра­зумевается не сама система, а возможный вид ее модели, ак­центи­руется особенность ее устройства или условий работы.

Четкого правила разделения систем на сложныеипростыене существует. Обычно признаком сложных систем служит много­об­разие выполняемых функций, большое число составных час­тей, разветвленный характер связей, тесная взаимосвязь с внеш­ней средой, наличие элементов случайности, изменчивость во времени и другие. Понятие сложности системы — субъективно и определя­ется необходимыми для ее исследования затратами времени и средств, потребным уровнем квалификации, т. е. за­висит от кон­кретного случая и конкретного специалиста.

Подразделение систем на однородные и неоднородные произ­водится в соответствии с заранее выбранным призна­ком: исполь­зуемые физические явления, материалы, формы и т. д. При этом одна и та же система при разных подходах может быть и однород­ной, и неоднородной. Так, велосипед — однородная механическая система, поскольку использует механические способы передачи движения, но неоднородная по типам материалов, из которых из­готовлены отдельные части (резиновая шина, стальная рама, ко­жаное седло).

Все системы взаимодействуют с внешней средой, обменива­ются с нею сигналами, энергией, веществом. Системы относят к

открытым,если их влиянием на окружающую среду или воз­дей­ствием внешних условий на их состояние и качество функ­циони­рования пренебречь нельзя. В противном случае системы рассмат­ривают какзакрытые,изолированные.

Динамические системы, в отличие отстатических,нахо­дятся в постоянном развитии, их состояние и характеристики изменяют­ся в процессе работы и с течением времени.

Характеристики вероятностных(иными словами,стохас­ти­ческих)систем случайным образом распределяются в про­странст­ве или меняются во времени. Это является следствием как случай­но, о распределения свойств материалов, геометриче­ских размеров и форм объекта, так и случайного характера воз­действия на него внешних нагрузок и условий. Характеристикидетерминирован­ных

систем заранее известны и точно предска­зуемы.

Знание этих особенностей облегчает процесс моделирова­ния, так как позволяет выбрать вид модели, наилучшим образом соот­ветствующей заданным условиям.

Выбор модели того или иного вида основывается на выделе­нии в системе существенных и отбрасывании второстепенных факторов и должен подтверждаться исследованиями или пред­ше­ствующим опытом. Наиболее часто в процессе моделирова­ния ориентируются на создание простой модели, поскольку это позво­ляет сэкономить время и средства на ее разработку. Од­нако повы­шение точности модели, как правило, связано с рос­том ее сложно­сти, так как необходимо учитывать большое число факторов и связей. Разумное сочетание простоты и по­требной точности и ука­зывает на предпочтительный вид мо­дели.

studfiles.net

Модели систем

Характерной особенностью систем является множественность их моделей [2]. Остановимся на четырех типах моделей, которых, как правило, достаточно для описания системы:

модель «Черный ящик»,

модель состава системы,

модель структуры системы,

математическая модель функционирования системы.

Модель «Черный ящик» отображает связи системы с внешней средой в виде указания входов и выходов системы и использует две группы параметров: действием на входе и реакцией на выходе. Эта модель не отображает внутреннее устройство системы и используется, когда внутреннее содержание системы либо неизвестно, либо слишком сложно.

Модель состава системы представляет собой только перечень элементов системы и имеет вид таблицы или списка.

Модель структуры системы содержит функциональные элементы вместе со связями между ними и представляется в виде различного рода схем: блок-схема, функциональная схема, принципиальная схема и т.п. Модель структуры показывает связность элементов, их взаимодействие.

Математическая модель функционирования системы представляет собой зависимость одних параметров системы от других, включая, иногда, параметры внешней среды и время.

8. Математическая модель функционирования системы

Эта модель является одной из главных моделей системы, так как она позволяет проводить не только исследование ее функционирования, но и решать задачи, возникающие при проектировании, производстве и эксплуатации систем, например, оценить параметры системы, проводить их оптимизацию и т.д.

При составлении математической модели исходят из весьма общих предположений о характере функционирования системы:

1. Система функционирует во времени: в каждый момент времени система находится в одном из возможных состояний;

2. На вход системы могут поступать входные сигналы;

3. Система способна выдавать выходные сигналы;

4. Состояния системы в данный момент времени определяются предыдущими состояниями и входными сигналами, поступившими в данный момент времени и ранее;

5. Выходной сигнал в данный момент времени определяется состояниями системы и входными сигналами, относящимися к данному и предшествующему моментам времени.

Эти предположения означают следующее. В первом из них отражается динамический характер функционирования системы в пространстве и времени. То есть процесс функционирования системы представляет собой последовательную смену состояний под действием внешних и внутренних причин.

Второе и третье предположения имеют целью описать взаимодействие системы с внешней средой.

В четвертом и пятом предположениях отражается реакция системы на внутренние факторы и воздействия внешней среды.

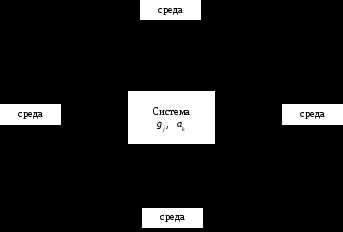
Модель системы представим в следующем виде с учетом переменных, характеризующих систему [8].

На рис. 1.8 введены следующие обозначения переменных:

–внешние (выходные) параметры системы, m – их количество;

–параметры состояний системы, w – их количество;

–внутренние параметры системы, l – их количество;

–параметры необходимых воздействий для системы, d – их

количество;

–параметры возмущающих воздействий на систему, s – их

количество;

–параметры управления системой, v – их количество.

z₁ z_S

входы

d₁y₁

входы выходы

d_n входы y_m

u₁u_v

Рисунок 1.8.

Все перечисленные параметры являются компонентами многомерных векторов. На все параметры накладываются ограничения типа равенств или неравенств. Приведем характеристики указанных параметров.

Внешние (выходные, характеристики качества) параметры – y_i(t) – описывают систему с точки зрения заказчика или потребителя (системы более высокого ранга). Их называют также функционалами. Типичные внешние параметры: пропускная способность, помехоустойчивость, чувствительность, производительность, надежность, габариты, масса, стоимость, годовые приведенные затраты и т.п.

Эти параметры служат для количественной характеристики основных свойств системы, т.е. возможностей ее использования для выполнения поставленной цели (использования по назначению).

Совокупность внешних параметров y_i(t) образует вектор внешних параметров . На внешние параметры обычно накладываются ограничения (сверху, снизу, с обеих сторон). Они определяют требуемые по техническому заданию (ТЗ) значения внешних параметров или области их допустимых изменений. Например:y₁ = a, y₂ ≤ b, y₃ ≥ c, d ≤ y₄ ≤ e, и т.д.

Совокупность всех ограничений определяет допустимое множество (пространство) внешних параметров Y. При этом любой допустимый (с точки зрения ТЗ) вектор внешних параметров принадлежит этому множеству.

Состояния системы – g(t) – это переменные или параметры, которые обычно характеризуют управляемые системы (например, технологический процесс производства и т.п.). Они представляют собой набор значений параметров системы в некоторый момент времени t. Эти значения можно рассматривать как координаты определенной точки в w-мерном пространстве, которое называется пространством состояний G.

Вектор состояний системы 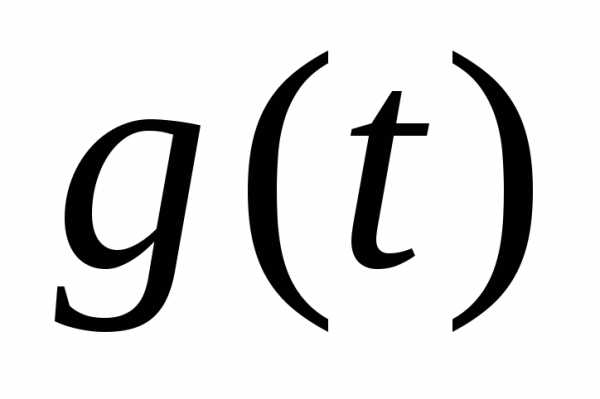это набор состояний системы . Совокупность ограничений, накладываемых на состояния системы, определяют допустимое пространство состояний и принадлежность к нему вектора состояний. В этом пространстве состояний и функционирует система, т.е. переходит из одного состояния в другое или сохраняет какое-то состояние в течение некоторого промежутка времени. А функция системы проявляется в движении изображающей точки по некоторой траектории в пространстве состояний.

Внешние параметры системы полностью определяются состояниями системы

где Ф_i – некоторый оператор, ставящий в соответствие траектории z(t) конкретное число или функцию.

Внутренние параметры – а_k(t) – описывают систему с точки зрения разработчика. Типичные внутренние параметры: вид модуляции, длительность сигнала, полоса частот и т.п. К внутренним параметрам относятся и параметры электрорадиоэлементов.

Вектор внутренних параметров системы 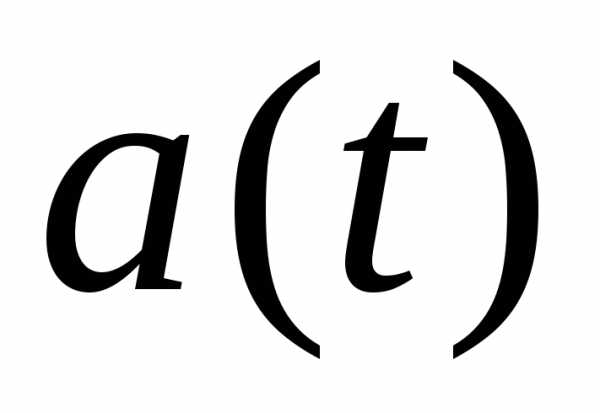есть совокупность всех внутренних параметров. На них также накладываются ограничения, которые в совокупности определяют допустимое множество (пространство) внутренних параметровА так, что .

Строгой границы между внешними и внутренними параметрами не существует. Одни и те же параметры могут быть и внутренними и внешними. Обычно к внешним параметрам относятся те параметры, которые задаются в ТЗ, а к внутренним те, которые подлежат определению в процессе проектирования. Например, если в ТЗ задаются мощность передатчика и чувствительность приемника (для системы связи или радиолокатора), то это будут внешние параметры. Но в ТЗ могут быть указаны дальность связи или обнаружения, тогда это будут внешние параметры, а мощность передатчика и чувствительность приемника, выбранные проектировщиком, будут внутренними параметрами.

Параметры необходимых воздействий – d_r(t) – это те воздействия внешней среды, которые обеспечивают выполнение системой поставленной цели и ее эффективное функционирование. Представление то же, что и ранее, т.е. .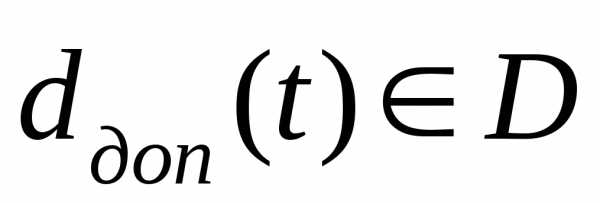

Параметры возмущающих воздействий – z_p(t) – это те воздействия внешней среды, которые определяют условия функционирования системы. К ним относятся воздействия климата, различного рода помехи, радиация различного рода и т.п. Представление то же, что и ранее т.е. .

Параметры управления – u_q(t) – это воздействия на управляемый объект внешней среды, в качестве которой выступает управляющая система.

Представление то же, что и ранее т.е. .

Внешние параметры и состояния системы зависят от внутренних параметров системы, необходимых и возмущающих воздействий и параметров управления.

Математическая модель функционирования системы – это совокупность математических соотношений между всеми перечисленными параметрами, описывающие поведение системы с требуемой точностью. Примеры моделей:

Вид оператора Ф или φ учитывает структуру системы, характер связей между элементами, закономерности функционирования системы.

Используется большое разнообразие моделей функционирования системы. Например, модель технической системы, техническая функция которой состоит в преобразовании входной величины d_r в выходную величину y_i, может иметь вид (рис. 1.9).

d_r y_i

Рисунок 1.9.

Очень часто техническую систему описывают моделью (системой уравнений), в которой установлены связи между внутренними и внешними параметрами:

— — — — — — — — — — — — — — —

Такие равенства называют также уравнениями связи.

studfiles.net

Основные типы моделей

Единая классификация видов моделирования затруднена в силу многозначности понятия «модель» в науке. Ее можно проводить по различным основаниям: по характеру моделей (по средствам моделей), по характеру моделируемых объектов, по сферам их приложения и его уровням. В связи с этим любая классификация обречена на неполноту.

В зависимости от средств моделирования различают материальные и идеальные модели. Материальное (субстанциональное) моделирование основывается на материальной аналогии объекта и его модели. Для построения данного типа моделей необходимо выделить функциональные характеристики (геометрические, физические) исследуемого объекта. Процесс исследования связан с материальным воздействием на объект.

К материальным (субстанциальным) моделям социально-психологических явлений можно отнести те, которые моделируют один вид групповой деятельности посредством другого. Примером этого типа моделирования являются исследования на кибернометре, проводившиеся Н.Н. Обозовым, проигрывание ситуаций в социально-психологическом тренинге. Например, в моделировании ситуаций в группах активного социально-психологического обучения субъектом является ведущий и группа используется как «материал» для построения и определения моделей. Субъектом может являться группа вместе с ведущим. Такое моделирование подразумевает включение в модель проявлений личности в целом, затрагивая аффективную, ценностную и неосознаваемую часть опыта человека. В итоге внутриличностный опыт участников переформулируется.

Также к субстанциональным моделям можно отнести социально-психологические эксперименты. Так, колония А. Макаренко являлась субстанциональной моделью организации и осуществления воспитательной работы с подростками.

Большой класс моделей представляют идеальные модели. Идеальное моделирование основано на мыслимой аналогии. Идеальное моделирование подразделяется на знаковое (формализованное) и интуитивное моделирование. Последнее применяется там, где процесс познания только начинается или системные взаимосвязи очень сложные. Жизненный опыт человека можно рассматривать как интуитивную модель межличностных отношений. Возможен вариант построения модели, при котором формальная структура выбирается на интуитивных основаниях.

Моделями знакового моделирования являются схемы, графики, чертежи, формулы. Важнейшим видом знакового моделирования является математическое моделирование. Не всякая знаковая система выступает в качестве модели, так как знаковая система лишь в том случае становится моделью, если она становится предметом исследования, если в ее пределах и ее средствами решаются задачи, решение и смысл которых лежат за пределами данной знаковой системы. Так, естественный язык может выступать в роли модели при изучении быта, культуры, экономических и социальных отношений; естественные языки выступают в роли моделей при исследовании закономерностей мышления, представляющего собой отражения объективного мира.

Существенным моментом создания любой знаковой модели является формализация. Всякая формализация сопровождается следующими процедурами:

1. Задается алфавит (конечный или бесконечный).

2. Задаются правила, порождающие из исходных знаков алфавита «слова», «формулы».

3. Формулируются правила, по которым от одних слов, формул данной системы можно переходить к другим словами и формулам (так называемые правила вывода).

4. В зависимости от характера и целей создаваемой модели могут формулироваться (но могут и не формулироваться) предложения, считающиеся исходными (аксиомы или постулаты). Как правило, формулируются не сами аксиомы данной знаковой системы, а схемы аксиом с соответствующими правилами подстановки.

Знаковые модели обладают некоторой самостоятельностью. В их пределах и их средствами зачастую ставятся и решаются задачи, реальный смысл которых может быть первоначально не ясен. В знаковых моделях теория подобия абсолютно не применима.

Сегодня большая часть исследований по знаковым моделям ведется в русле логико-математических. В этих моделях природа прототипа и модели уже не играет никакой роли. В этих моделях важны чисто логические и математические свойства. Описание модели в этом случае не отделимо от самой модели. Возможность экспериментирования отсутствует и заменяется выводом. Новые знания получаются путем логического и математического выводов из первоначального описания модели. Математическое моделирование в социальной психологии не ограничивается операциями количественными, оно может иметь дело также и с качественными характеристиками. Некоторые социально-психологические процессы — такие, как принятие решений на выборах или распределение голосов избирателей, могут быть определены полностью в математических терминах. В подобных случаях математические модели являются средством изучения логических следствий из наблюдаемых правил.

В случае сложных систем, когда неясно количественное выражение множества целевых функций, используются имитационные модели. Имитационное моделирование применяется для анализа поведения системы, здесь не исследуются фундаментальные законы динамики системы. При этом функционирование сложной системы представляется в виде определенного алгоритма, который реализуется на ЭВМ.

Возможен вариант построения модели, при котором формальная структура выбирается на интуитивных основаниях. Принятая формальная модель может подсказать нам общее структурное представление об изучаемой системе. В этом случае осознание и вербализация концепции следуют за уже готовой ее математической формой. Множество возможных абстрактных структур заведомо меньше множества их конкретных интерпретаций.

Математические и компьютерные модели. Примером математической модели социального поведения может служить модель Льюиса Ф.Ричардсона, или модель гонки вооружений. Рассмотрим ее для иллюстрации компактности, трансформируемости и эффективности математических моделей. Эта модель учитывает действие всего лишь трех факторов:

а) государство Х ощущает наличие военной угрозы со стороны государства Y, точно такая же логика действует со стороны государства Y;

б) бремя расходов;

в) прошлые обиды.

Хt +1 = kYt – aXt + g

Yt+1 = mXt – bYt + h

Xt и Yt – величины уровней вооружения в момент времени t

Коэффициенты k, m, a, b – являются положительными величинами, а g и h – положительными или отрицательными в зависимости от того, насколько в целом враждебно или дружественно настроены государства.

Величина угрозы отражена в членах kYt и mXt, поскольку, чем больше эти числа, тем больше количество вооружений у противной стороны.

Величина расходов отражена в членах aXt и mYt, поскольку за счет этих членов снижается уровень вооружений в следующем году.

Константы g и h отражают величину прошлой обиды, которая в рамках данной модели считается неизменной.

К концу семидесятых годов модель была испробована уже сотни раз на самых разных вариантах гонки вооружений. Модель Ричардсона в целом эффективна в случаях краткосрочных прогнозов; характера гонки вооружений и, следовательно, прогнозирования войн, так как почти всем современным войнам предшествует нестабильная гонка вооружений.

Модель Ричардсона – это только один из представителей большого класса динамических моделей, т.е. таких, которые моделируют развитие некоторого процесса во времени. Многие из таких моделей реализуются в виде дифференциальных уравнений, а многие заимствуют математический аппарат из моделей демографического роста и других биологических процессов.

Одна из наиболее развитых областей математического моделирования социального поведения называется теорией игр. «Игры» в рамках данной теории – это ситуации, в которых два или более участника делают выбор в отношении своих действий, и выигрыш каждого участника зависит от совместного выбора обоих (всех). Игры, изучаемые теорией игр, обычно более формализованы, чем традиционные, и вознаграждения в них представляют собой не просто выигрыш или проигрыш, а нечто боле сложное, но принцип соревнования здесь и там один и тот же.

Теория игр вначале рассматривалась на материале одного из типов соревнования, которое носит название игры с нулевой суммой. Условие этого типа игры: сколько один игрок выигрывает, столько же другой проигрывает. К этой категории принадлежит большая часть обычных игр. Однако большая часть социально-психологических ситуаций являются играми с ненулевой суммой, или кооперативными, когда оба игрока при определенных условиях могут оказаться в выигрыше (то есть тот факт, что один из игроков выиграл вовсе не означает тот факт, что другой столько же проиграл). Из кооперативных игр лучше всего изучена игра «дилемма заключенного». Эта модель может применяться для обоюдного контроля выполнения деловых контрактов, принятие решений о начале активных действий (забастовки, коллективные сговоры). В реальной действительности игроки чаще выбирают сотрудничество, несмотря на все факторы, подталкивающие их к обману.

Третьим примером математических моделей, которые очень хорошо известны, является модель Даунса. Модель позволяет объяснить, почему кандидаты на всеобщих выборах не занимают совпадающие позиции и почему кандидаты часто меняют свои идеологические позиции в промежутке между первичными и повторными выборами. Простейший вариант модели Даунса представляет собой колоколообразную кривую, проходящую вдоль единой фиксированной идеологической оси.

Кроме рассмотренных моделей, к математическим моделям относятся модели ожидаемой полезности. Они эффективны при решении вопросов, какие меры следует предпринять (прескриптивные модели), но предсказать действительное поведение людей (дескриптивные модели) они не могут. К этим моделям близки модели оптимизации, которые по большей части были заимствованы из экономической науки и инженерного дела. Эти модели полезны для определения оптимального поведения, например когда в качестве соперника выступает непредсказуемое будущее, в ситуациях конкуренции с малым числом участников, а кроме того в условиях конкуренции, когда обстановка определяется большим числом участников. Математическое описание колебательных процессов вызывает интерес в связи с изучением мотивации, модели формирования общественного мнения описывают с помощью кинетических уравнений. Статические задачи как правило записываются в виде алгебраических выражений, динамические – в виде дифференциальных и конечноразностных уравнений.

Многомерность социально-психологических явлений может быть достаточно полно описана в настоящее время методами современного многомерного анализа, включающего в частности, методы многомерной статистики, кластерный анализ и анализ латентных структур, многомерное шкалирование и др.

Компьютерные модели основываются на программировании с использованием не уравнений, а алгоритмов (строго сформулированных последовательных инструкций). Компьютерные модели бывают особенно эффективны при изучении ситуаций, сопряженных с обработкой большого количества информации, например, процессов обучения, нечисловых процессов. Очень часто применяется такая форма компьютерной модели как экспертная система. В ней используется большое количество установок типа «если … то». Экспертные системы проявили свои возможности в точном воспроизведении поступков людей в самых разнообразных областях.

Примерами компьютерных моделей социально-психологических процессов могут служить программы Talk и Search Man, разработанные учеными из Омска. Первая служит для комплексного моделирования транзактного общения индивидов. Вторая создана с целью проведения компьютерных экспериментов, касающихся проблемы выбора женщиной супруга с целью образования семьи.

Еще более сложными являются динамические компьютерные имитационные модели, которые моделируют сложные процессы с помощью больших систем уравнений, не поддающихся решению алгебраическими средствами. Объектами компьютерных имитационных моделей могут быть обширные социально-психологические процессы (смена настроений масс, массовое поведение) и эти модели все чаще используются для проигрывания сценариев типа «что будет, если…».

Модели нелинейных процессов.

Быстрое развитие синергетики, теории самоорганизации сложных систем, было обусловлено поиском моделей для описания нелинейных процессов. Синергетика имеет дело с открытыми нелинейными диссипативными системами, далекими от равновесия. Практически все объекты, с которыми сталкивается социальная психология можно отнести к этому классу. Под открытыми системами понимают такие, которые могут обмениваться энергией, веществом, информацией с окружающей средой. И отдельный человек и социальные группы относятся к открытым системам. Нелинейность систем предполагает, что в реальных социальных и социально-психологических системах последствия представляют собой результат воздействия множества причин. Более того, следствия оказывают обратное влияние на породившие их причины. Под свойством диссипативности в широком смысле понимается способность изучаемой системы «забывать» детали внешних воздействий. Основное свойство таких систем – необычайная чувствительность к всевозможным воздействиям и в связи с этим чрезвычайная неравновесность. Неравновесность социально-психологических явлений проявляется в их иррегулярном поведении. Сложные социально-психологические процессы напоминают бесконечный компьютер, в котором заложено бесконечное число коммуникантов, это делает невозможным выделение «начального сигнала» (руководства) и определение четкого адресата.

Неравновесное состояние изучаемых объектов иллюстрируют процессы спонтанной активности, активного характера восприятия, выбора цели индивидом или группой.

На принципиальное значение процессов самоорганизации для психики человека не раз обращали внимание крупные психологи. Ключевая категория К. Левина «динамическое поле» рассматривалась как целостная самоорганизующаяся система. Г. Олпорт обсуждал понятие самоконфронтации, которое, можно рассматривать в рамках идеи самоорганизации. Модели, иллюстрирующие связь явлений с теорией самоорганизации: модель тюремных бунтов, теория катастроф, модель миграции, Модель выработки единого мнения Г.А. Саймона и Г. Гутцкова.

В типологию моделей входят также структурные, функциональные и смешанные модели. Субстанциональные модели вызываются к жизни трудностями технического и организационного характера. Структурные модели имитируют внутреннюю организацию оригинала. Они могут быть как знаковыми, так и незнаковыми. Функциональные модели имитируют способ поведения оригинала. Они также как и структурные модели меньше привязаны к оригиналу. Эти модели могут быть как материальными, так и идеальными. Функциональное моделирование – это основной метод кибернетики на современном этапе. Объективной основой кибернетического подхода является относительная независимость функции от структуры, т.е. факт существования потенциального множества конкретных структур, способных выполнять данную функцию.

Отдельные типы моделей в чистом виде встречаются редко. Модели обычно из одномерных превращаются в многомерные. Субстанциональная модель должна быть либо структурной, либо функциональной, либо той и другой. Функционально-структурные модели по степени вероятности выводов значительно уступают структурно- функциональным моделям.

Модели также можно разделить по степени полноты. По этому основанию они делятся на полные и неполные. Чем полнее модель, тем она сложнее, поэтому совсем необязательно в каждом случае стремиться к созданию полной модели. В качестве начального этапа исследования выгоднее и удобнее бывает создавать неполные модели, так как они позволяют быстрее получить результат. Хотя этот результат менее точен, чем при использовании полной модели, но в большинстве случаев на первом этапе исследования его использование вполне оправдано. Чем больше модель, тем осторожнее следует к ней относиться. Построить эффективную модель, значит найти такое описание ее, которое дает ответ на конкретно поставленный вопрос. Общая модель сложного объекта называется агрегированной и составляется из детализированных моделей.

studfiles.net

40. Цель построения модели систем, определение моделей систем.

Модель системы – это математический или физический аналог реальной системы, в котором характер протекания основных процессов подобен протеканию таких же процессов в реальной системе.

Цель – это конкретное назначение модели, вытекающее из ее формального определения, и дающее полное, точное и адекватное описание моделируемой системы, для получения ответов на некоторую совокупность вопросов, возникших при проведении анализа моделируемого объекта. Цель отражает причину создания модели и определяет ее назначение. Целью модели является получение ответов на совокупность вопросов, которые неявно присутствуют (подразумеваются) в процессе анализа и, следовательно, они руководят созданием модели и направляют его. Это означает, что сама модель должна будет дать ответы на эти вопросы с заданной степенью точности. Четко определенная цель становится критерием окончания моделирования. Таким образом, цель модели – это: набор вопросов, на которые должна ответить модель и критерий окончания моделирования.

41. Формы информации циркулирующих систем, структура модели системы.

42. Системный анализ.

Системный анализ — научный метод познания, представляющий собой последовательность действий по установлениюструктурных связеймежду переменными или элементами исследуемойсистемы. Опирается на комплекс общенаучных, экспериментальных, естественнонаучных, статистических, математическихметодов.

Ценность системного подхода состоит в том, что рассмотрение категорий системного анализа создает основу для логического и последовательного подхода к проблеме принятия решений. Эффективность решения проблем с помощью системного анализа определяется структурой решаемых проблем.

Системный анализ возник в США и прежде всего в недрах ВПК.  Кроме того, в США системный анализ изучался во многих государственных организациях. Он считался наиболее ценным побочным  достижением в области обороны и изучения космического пространства. 

Объект системного анализав теоретическом аспекте — это процесс подготовки и принятия решений; в прикладном аспекте — различные конкретные проблемы, возникающие при создании и функционировании систем.

В теоретическом аспекте — это, во-первых, общие закономерности проведения исследований, направленные на поиск наилучших решений различных проблем на основе системного подхода (содержание отдельных этапов системного анализа, взаимосвязи, существующие между ними, и др.).

Во-вторых, конкретные научные методы исследования — определение целей и их ранжирование, дезагрегирование проблем (систем) на их составные элементы, определение взаимосвязей, существующих как между элементами системы, так и между системой и внешней средой и др.

В-третьих, принципы интегрирования различных методов и приемов исследования (математических и эвристических), разработанных как в рамках системного анализа, так и в рамках других научных направлений и дисциплин в стройную, взаимообусловленную совокупность методов системного анализа.

studfiles.net

Модели систем

Цели, которые ставит перед собой человек, редко достижимы только за счет его собственных возможностей или внешних средств, имеющихся у него в данный момент. Такое стечение обстоятельств называется проблемной ситуацией. Примером такой ситуации, требующей создания информационных систем, является случай, когда на крупных предприятиях обычные способы сбора и обработки первичных данных не обеспечивают необходимой полноты и оперативности контроля производственных показателей. В конечном итоге, это значительно снижает экономическую эффективность и качество принимаемых инженерных и управленческих решений.

Осознание объективных противоречий, неразрешимых в рамках существующего положения, является исходным толчком к выявлению новых, более эффективных средств решения этой проблемы и формулировке соответствующих целей. Цель — это субъективный образ (абстрактная модель) несуществующего, но желаемого состояния среды, которое решило бы возникшую проблему.

Все последующие действия, направленные на отбор из окружающей среды объектов, свойства которых можно использовать для достижения цели, и на объединение этих объектов надлежащим образом, представляют собой работу по созданию того, что называют системой. Другими словами, система есть средство достижения цели. Это и есть первое определение системы.

В инженерно-технической и экономической практике момент постановки целей (формулировки технического задания) — один из важнейших этапов создания систем. Специалисты отдают себе отчет в сложности этого этапа и на деле сугубо формально трактуют его результат только тогда, когда наступает юридическая ответственность за неудачу. Обычно же цели последовательно уточняются с многократными изменениями и дополнениями.

Первое определение (искусственной) системы как «средство достижения цели» выдвигает на первый план целевую подчиненность всех сторон организации системы. Однако даже на простых примерах обнаруживаются сложности: соответствие между целями и системами не всегда однозначно (одна система может быть связана с несколькими целями, одной цели могут отвечать разные системы) и не всегда очевидно (выявить действительные цели существующей системы непросто). Тем не менее, целевая предназначенность системы ‑ ее исходное, главное свойство.

1. Модель «черного ящика»

Важную роль при анализе сложных проблем играют наглядные, образные, визуальные модели. Перейдем от первого определения системы к его визуальному эквиваленту.

Во-первых, приведенное определение ничего не говорит о внутреннем устройстве системы. Поэтому ее можно изобразить в виде непрозрачного «ящика», выделенного из окружающей среды. Уже эта максимально простая модель по-своему отражает два следующих важных свойства системы: целостность и обособленность от среды.

Во-вторых, в определении системы косвенно говорится о том, что хотя «ящик» и обособлен, выделен из среды, но не является полностью от нее изолированным.

В самом деле, ведь достижение цели — это запланированные заранее изменения в окружающей среде, какие-то продукты работы, предназначенные для потребления вне системы. Иначе говоря, система связана со средой и с помощью этих связей воздействует на среду.

Графически связи изображают в виде стрелок, направленных от системы в среду. Эти связи называются выходами системы. Выходы системы в данной графической модели соответствуют слову «цель» в словесном определении модели системы.

Кроме того, в определении имеется указание и на наличие связей другого типа: система является средством, поэтому должны существовать и возможности ее использования, воздействия на нее, т.е. и такие связи со средой, которые направлены извне в систему. Эти связи изображают в виде соответствующих стрелок, направленных от среды в систему, и называют входами системы.

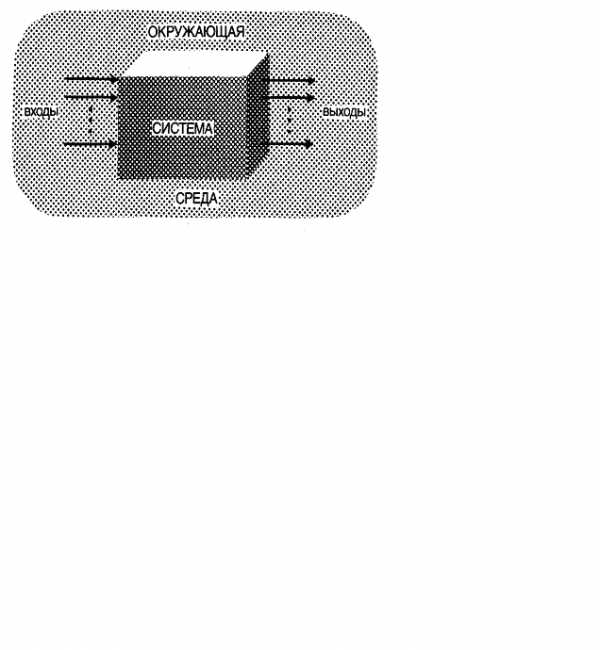
Рис.4.1. Модель «черного ящика»

Результатом является модель системы, которая получила название черного ящика. Это название образно подчеркивает полное отсутствие сведений о внутреннем содержании «ящика». В этой модели задаются, фиксируются, перечисляются только входные и выходные связи системы со средой. Даже «стенки ящика», т.е. границы между системой и средой, в этой модели обычно не описываются, а лишь подразумеваются, признаются существующими. Такая модель, несмотря на внешнюю простоту и на отсутствие сведений о внутренности системы, часто оказывается полезной на практике.

Во многих случаях достаточно содержательного словесного описания входов и выходов, тогда модель «черного ящика» просто является их списком. Например, бытовая модель телевизора такова: входы — шнур питания, антенна, ручки управления и настройки; выходы — экран кинескопа и звуковые динамики. В других случаях требуется только количественное описание некоторых или всех входов и выходов.

Для максимальной формализации модели «черного ящика», необходимо задать два множества X и Y входных и выходных переменных, но никаких других отношений между этими множествами фиксировать нельзя (иначе это уже будет не «черный», а прозрачный ящик).

Множественность входов и выходов. Построение модели «черного ящика» не является тривиальной задачей, так как на вопрос о том, сколько и какие именно входы и выходы следует включать в модель, ответ не прост и не всегда однозначен. Главной причиной множественности входов и выходов в модели «черного ящика» является то, что всякая реальная система, как и любой объект, взаимодействует с другими объектами окружающей среды практически неограниченным числом способов.

Строя модель системы, из этого бесчисленного множества взаимосвязей отбирают для включения в список входов и выходов конечное их число. Критерием отбора при этом является целевое назначение модели, существенность той или иной связи по отношению к заданной цели. Те, что представляются существенными, важными, включают в состав модели. И наоборот ‑ те, что несущественны, неважны, — в модель не включаются.

Именно здесь возможны ошибки. То, что в модели не учитываются, исключаются из рассмотрения некоторые связи, не лишает их реальности, они все равно действуют независимо от нашей воли. Нередко оказывается, что казавшиеся несущественными или даже неизвестные связи на самом деле являются важными и должны учитываться.

Особое значение это обстоятельство имеет при задании цели системы, т.е. при определении ее выходов. Оно относится и к описанию существующей системы по результатам ее обследования, и к проекту пока еще не существующей системы. Реальная система неизбежно вступает во взаимодействия со всеми объектами окружающей среды, поэтому необходимо как можно раньше, лучше всего еще на стадии построения (проектирования) модели, учесть все наиболее важное. В результате главную цель приходится сопровождать, уточнять заданием дополнительных целей, ограничений.

Следует подчеркнуть, что невыполнение дополнительных целей может сделать ненужным и даже вредным или опасным достижение основной цели. Этот факт заслуживает особого внимания, так как на практике часто обнаруживается незнание или недооценка важности указанного положения. Между тем оно является одним из центральных во всей науке, называемой системология.

Модель «черного ящика» часто оказывается не только очень полезной, но в ряде случаев единственно применимой при изучении систем. Например, при исследовании психики человека мы лишены возможности вмешательства в систему. Также при проведении исследований, в результате проведения которых нужно получить данные о системе в обычной для нее обстановке, следует специально заботиться о том, чтобы измерения как можно меньше влияли на саму систему.

Другая причина того, что приходится ограничиваться только моделью «черного ящика», — действительное отсутствие данных о внутреннем устройстве системы. Тогда простота модели «черного ящика» обманчива. Всегда существует опасность неполноты составления перечня входов и выходов как вследствие того, что важные из них могут быть сочтены несущественными, так и в силу неизвестности некоторых из них в момент построения модели.

studfiles.net

Информатика и ИКТ. Профильный курс.

Модели систем

Основные понятия

• системный анализ
  
• модель «черный ящик»
• модель состава
• структурная модель
• граф, дерево

Системный анализ

Исследование некоторой реальной системы состоит из двух этапов: анализ и синтеза.

Анализ системы — это выделение ее частей с целью прояснения состава системы. Систему можно раскладывать на части бесконечно. Момент остановки «дробления» системы зависит от цели исследования. Цель исследования, как правило, получение модели системы — приближенного представления об устройстве и функционировании системы. Модель можно далее использовать для прогнозирования поведения системы в некоторых условиях, для управления системой, для диагностики сбоев в функционировании системы и т.д.

Невозможно понять как работает система, выяснив только ее состав. Нужно знать структуру связей между частями системы. Только в совокупности состава и структуры можно понять состояни и поведение системы. Поэтому анализ системы — это первый этап ее исследования. Второй этап — синтез.

Слово «синтез» обозначает соединение. Синтез — это мысленное или реальное соединение частей в единое целое. В результате синтеза создается целостное представление о системе, объясняется механизм системного эффекта.

Системный анализ — это исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.

Всякое описание системы носит модельный характер (отражает ограниченное число ее свойств). Главный вопрос при построении модели системы: какие ее характеристики являются существенными с точки зрения целей использования будущей модели.

Модель «черный ящик»

В простейшем случае бывает достаточно иметь представление о взаимодействии системы с внешней средой, не вдаваясь в подробности ее внутреннего устройства. Такое описание системы называется моделью «черного ящика». Вход системы — это воздействие на систему со стороны внешней среды, выход — это воздействие, оказываемое системой на окржающую среду. В такой модели внутреннее устройство скрыто, поэтому ее называют «черный ящик». 

Модель состава

Если описание системы ограничить перечислением ее частей, то мы получи модель состава. Эта модель дает более подробное представлени о системе, чем модель «черного ящика».

Структурная модель системы

Структурную модель системы еще называют структурной схемой. На структурной схеме отражается состав системы и ее внутренние связи. Для отображения структурной схемы системы используются графы. Граф состоит из вершин, обозначающих элементы системы, и ребер — линий, обозначающих связи (отношения) между элементами системы. 

Графы могут быть неориентированными и ориентированными. Направленные линии связи на графе называют дугами. Граф системы с иерархической структурой называют дерево.

Дерево — ориентированный граф. Обычно вершины дерева располагаются по уровням всерху вниз. Дуги направлены от верхних к нижним вершинам. Каждая вершина может быть связана с одной вершиной верхнего уровня (исходной) и множеством вершин нижнего уровня (порожденными). Такая связь называется «один ко многим«. Единственная вершина самого верхнего уровня называется корнем дерева. Вершины самого нижнего уровня, у которых нет порожденных вершин, называются листьями дерева. В дереве отсутствуют петли — замкнутые траектории связей, поэтому маршрут перемещения по дереву между любыми двумя вершинами всегда является единственным.

---

Вопросы:

1. Какие существуют типы моделей систем? Чем они различаются? Приведите примеры.

2. Что такое граф? Из чего он состоит?

3. Приведите примеры ориентированных и неориентированных графов.

Компьютерный практикум

Нарисуйте два варианта графа системы «Компьютер», содержащего следующие вершины: процессор, оперативная память, внешняя память, клавиатура, монитор, принтер. 

а) линия связи обозначает отношение «передает информацию»

б) линия связи обозначает отношение «управляет».

doma10.ucoz.ru

Система моделей — это… Что такое Система моделей?

Система моделей [system of models, large-scale economic mo­del, multimodel system] — совокупность взаимно связанных экономико-математических моделей для описания сложных экономических систем, которые невозможно воспроизвести в одной модели, достаточно детализированной для практических целей: она была бы слишком громоздкой. Поэтому для планирования и прогнозирования экономики крупнейших хозяйственных объектов разрабатываются С.м., построенные обычно по иерархическому принципу, в несколько уровней — они называются многоуровневыми системами.

В СССР был разработан и в той или иной мере опробован на практике, в частности, в автоматизированной системе плановых расчетев ( АСПР), ряд крупных С.м. Среди них — предложенные Институтом экономики и организации промышленного производства СО АН СССР С.м. оптимального территориально-производственного планирования, ЦЭМИ АН СССР — С.м. многоступенчатой оптимизации экономики (включая межотраслевую модель, модели оптимизации многоотраслевых комплексов и ряд отраслевых моделей), Советом по изучению производительных сил при бывш. Госплане СССР — С.м. размещения производства ведущих отраслей народного хозяйства, б. НИЭИ латвийского Госплана — С.м. прогнозирования и планирования народного хозяйства республики, ЦЭМИ АН СССР — С.м. оценки, анализа и прогноза народного благосостояния и другие.

Среди разработанных к настоящему времени многоуровневых систем большинство имеют два уровня: верхний (народного хозяйства в целом) и нижний — отраслевой или региональный (в зависимости от типа системы).

Производственная программа отдельного предприятия тоже может рассчитываться с помощью С.м.: она включит в себя модели расчета общезаводских показателей на верхнем уровне, показателей отдельных цехов — на следующем и т.д.

С.м. создает возможность для самостоятельного решения отдельных планово-экономических задач и их последующего согласования. Расчеты (обычно итерационные, см. Итерация) проводятся так, что результаты (выходы) расчетов по одной модели оказываются входами для других и т.д. Есть два основных способа связи моделей в системе — алгоритмический и неформальный, когда процесс согласования результатов производится людьми.

Следует различать понятия “С.м.” и “комплекс моделей”. В последнем случае разные модели отражают в разных “языках” разные стороны исследуемого объекта (например, трудовые, финансовые, материальные потоки), но не связаны так, чтобы можно было получить из их решения общий результат — например, оптимальный план хозяйственного объекта.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

economic_mathematics.academic.ru