Метод экстраполяции пример – 8. Методы экстраполяции

8. Методы экстраполяции

Экстраполяцияпредставляет метод прогнозирования, заключающийся в изучении сложившихся в прошлом и настоящем устойчивых тенденций развития процессов и явлений и переносе их на будущее. Метод экстраполяции применим, если используются следующиедопущения: а) период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития; б) анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время; в) не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития. Прогнозирование с помощью метода экстраполяции – один из простейших методов статистического прогнозирования. Его использование оправдано при недостаточном знании о природе изучаемого явления или отсутствии данных, необходимых для применения более совершенных методов прогнозирования.

Различают а) простую экстраполяцию, которая предполагает, что все действовавшие в прошлом и настоящем тенденции сохранятся в полном объеме, так как все действовавшие факторы останутся неизменными; б)прогнозную экстраполяцию, которая базируется на предположении об изменении факторов, определяющих динамику изучаемого процесса или явления.

Основу экстраполяции составляет изучение динамических рядов, представляющих собой упорядоченные во времени наборы измерений тех или иных показателей исследуемого объекта. В основе динамического анализа лежит понятие траектории, которая описывает состояние изучаемого процесса как функцию от времени:Q=Q(t),t[0,T], [0,T] – отрезок времени.

При этом время может учитываться как по интервалам, так и непрерывно. В первом случае функция называется динамическим рядом.

Использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс представляет собой сочетание двух составляющих: регулярной составляющей (Х_t) и случайной переменной (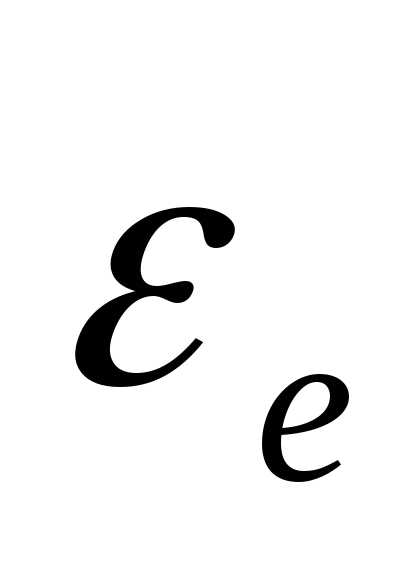). Временной ряд может условно представлен в виде:Y_t=X_t+ _t.

Регулярная составляющаяназывается трендом, тенденцией и характеризует существующую динамику развития процесса в целом.Случайная составляющаяотражает случайные колебания (шумы процесса).

Показателями развития процессаявляются абсолютный прирост, темп роста, темп прироста. Показатели изменения динамического ряда могут вычисляться на постоянной и переменой базе. Для обобщающей оценки скорости и интенсивности изменения динамического ряда используются различные средние характеристики, среди которых являются средний темп роста и средний темп прироста. Средний темп роста рассчитывают как среднее геометрическое и как среднее параболическое.

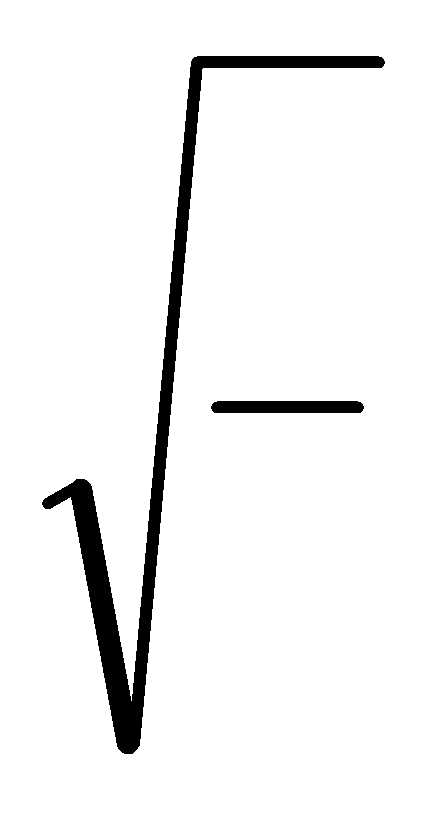Среднее геометрическоерассчитывается из последовательных цепных темпов роста:;среднее параболическоеориентировано на сумму динамического ряда и определяется из уравнения:

Задача ППЭсостоит в определении вида экстраполирующих функций Х_tи _tна основе исходных эмпирических данных и параметров выбранной функции.

Методика построениятрендовых моделей представляет сочетание качественного экономического анализа и формальных математико-статистических методов и включает несколько этапов: 1)Выбор класса функции тренда.Существует более 40 временных функций, отличающихся своими свойствами. Надо выбрать ту, которая отражает главные особенности динамики исследуемого показателя, прежде всего тип развития. Можно выделить 4 типа экономического роста: постоянный, увеличивающийся, уменьшающийся и рост с качественными изменениями характеристик на протяжении рассматриваемого периода. 2)

Оценка параметров функции. Он проводится методами регрессионного анализа. 3)Расчет значений формальных критериев аппроксимации. Для характеристики близости тренда к аппроксимируемому динамическому ряду применяют несколько формальных критериев: сумма квадратов отклонений значений тренда от фактических значений, значение коэффициента детерминации и т.д. 4)Анализ остаточной компоненты динамического ряда.5)Выбор функции тренда. Результатом предшествующих этапов является построение нескольких функций тренда для одного показателя. Выбор лучшей осуществляется путем сопоставления значений, возможностей экономической интерпретации и использования в прогнозировании.

МЕТОД ЛИНЕЙНОЙ экстраполяции. Сущность метода заключается в том, что прогнозные величины определяются на основе среднего прироста (снижения) исследуемого показателя за определенный период времени.

Пример. Предположим, у нас имеются данные об объеме ВНП страны за ряд лет:

Таблица — Объем ВНП страны

Год	Объем ВНП	Прирост ВНП
1995	16,0	—
1996	21,8	5,8
1997	27,0	5,2
1998	32,0	5,0
1999	36,8	4,8

Рассчитаем средний темп прироста за четыре года: (5,8 + 5,2 + 5,0 + 4,8)/4 = 5,2

Определив средний темп прироста, рассчитаем прогнозное значение ВНП страны на 2000 год: Y₂₀₀₀=Y₁₉₉₉+Y= 36,8 + 5,2 = 42,0

В тех случаях, когда показатели базисного и конечного прогнозного периода известны и следует определить годовые промежуточные показатели, используют метод линейной интерполяции, рассчитывая средний прирост за данный период времени:

Пример:Y₂₀₀₀= 205,Y₂₀₀₅ = 240. Y= (240 — 205)/5 = 7.

Y₂₀₀₂ =Y₂₀₀₀+ 2*Y= 205 + 2*7 = 219.

МЕТОД ПРОСТОЙ СРЕДНЕЙ. Применяется в тех случаях, когда в уравнении линейной зависимости Y=a+bx, коэффициентb= 0. При таком условии график будет представлен прямой параллельной горизонтальной оси графика, а прогноз будет состоять в расчете простой средней из всех имеющихся данных:Y=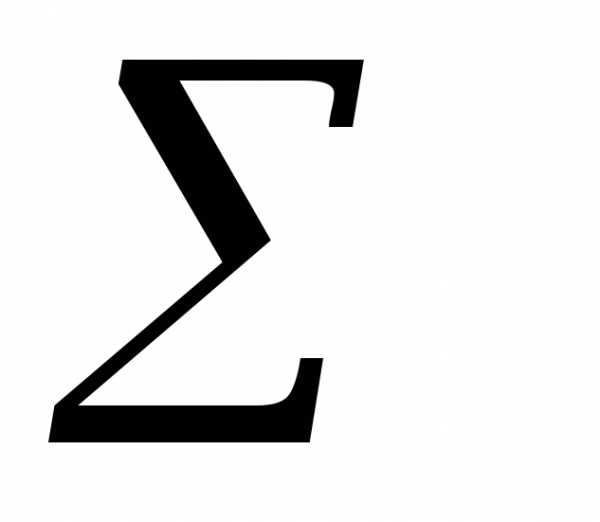Y/N.

Расчеты простой средней часто связывают с сезонными колебаниями, происходящими внутри общего тренда.

Пример.Имеются данные об объеме ВНП за ряд лет по кварталам:

Год	1 квартал	2 квартал	3 квартал		В целом за год
1995	190	370	300	220	1080
1996	280	420	310	180	1190
1997	270	360	280	190	1100
1998	300	430	290	200	1220
1999	320	440	320	220	1300
Итого	1360	2020	1500	1010	5890
Средний объем	272	404	300	203	294,5

Рассчитываем квартальный индекс: 1 квартал = 272:294,5 = 0,92; 2 квартал = 404:294,5 = 1,37;

3 квартал = 300:294,5 = 1,02; 4 квартал = 203:294,5 = 0,69.

Для того, чтобы составить прогноз объема ВНП по кварталам на 2000 год,надо прогнозное значение ВНП за данный год разделить на 4(количество кварталов) и умножить на соответствующий квартальный индекс. Предположим, что в 2000 году ВНП будет равен 1450. Тогда в 1 квартале будет произведено: (1450:4)*0,92= 333,5; 2 квартал = (1450:4)*1,37 = 496,625 и т.д.

МЕТОД наименьших квадратов. Позволяет подогнать функцию под некоторый набор численных значений и построить график функции по некоторой совокупности точек. Выбор этой функции считается наилучшим, если стандартное отклонение определяемое формулой:

E= 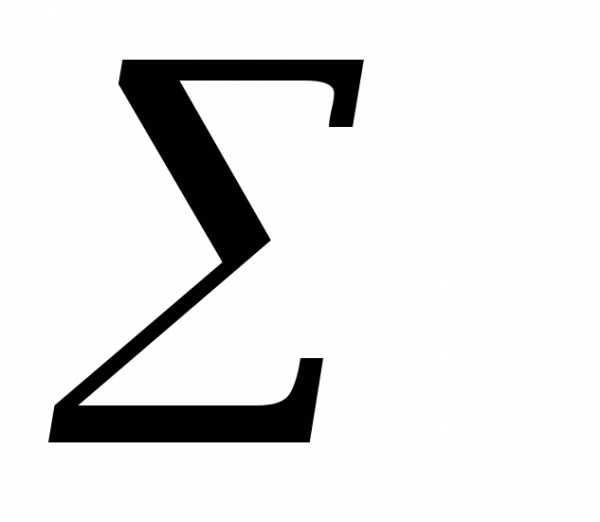(d_t–d’_t)²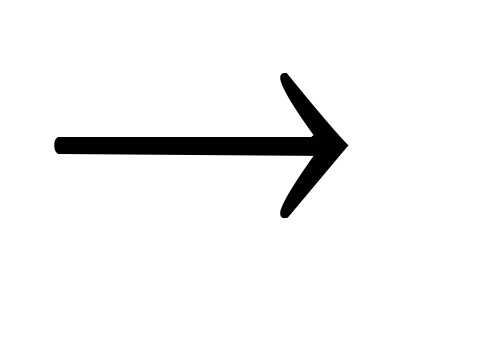minоказывается сведено к минимальному значению.

d_t– фактические данные,

d`_t– данные рассчитанной функции.

Как правило, используется линейная функция Y = a + bx.

Задача состоит в том, чтобы определить значения а и b, где

а – значение Yв базисном периоде,

b– угол наклона прямой.

Чтобы определить значения aиbиспользуется система уравнений:

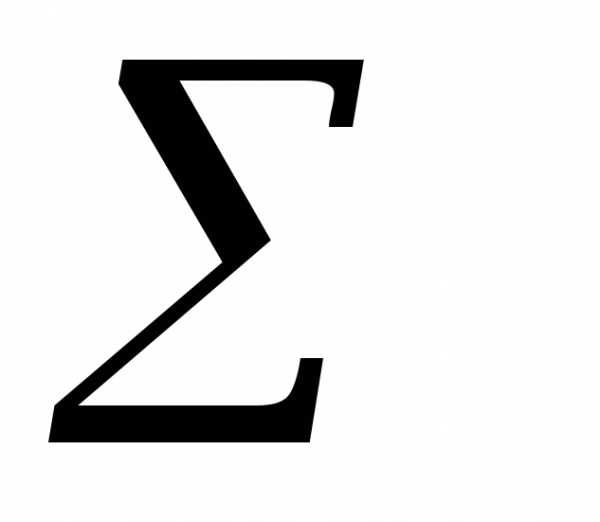Y=Na+b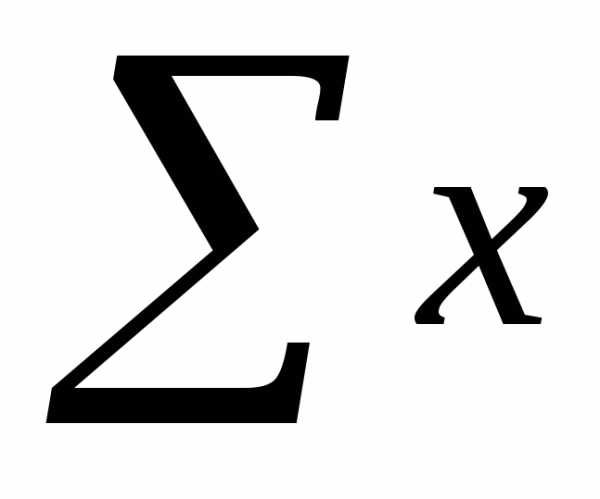

Y=ax+bx², гдеN- число периодов

х – номер периода.

Пример. Имеются данные об объеме ВНП.

Год	Y(ВНП)	x	x2	xY	Yсглаженный
1995	108	0	0	0	108,4
1996	119	1	1	119	108,4 + 4,7 = 113,1
1997	110	2	4	220	108,4 + 2* 4,7 = 117,8
1998	122	3	9	366	108,4 + 3* 4,7 = 122,5
1999	130	4	16	520	108,4 + 4* 4,7 = 127,2
	589	10	30	1225

Система уравнений выглядит следующим образом: 589 = 5а + 10b

1225 = 10ф + 30b.

Решая их, находим а = 108,4, b= 4,7.

Можно рассчитать ВНП 2000 года : Y₂₀₀₀=Y₁₉₉₅+ 5b= 108,4 + 5*4,7 = 131,9.

В отдельных случаях лучшего соответствия теоретических данных эмпирическим можно достигнуть вычерчивая по точкам кривой сглаживания вида Y=ab^x, т.е. используяпоказательную функцию.

Если показательное уравнение логарифмировать, то значения коэффициентов а и можно определить методом наименьших квадратов:

log Y = log a + x* log b.

logaиlogbнаходят, решая нормальные уравнения: 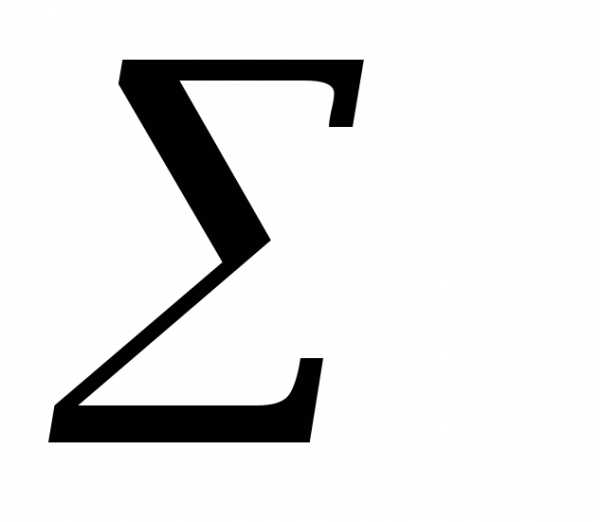logY=Nloga+ 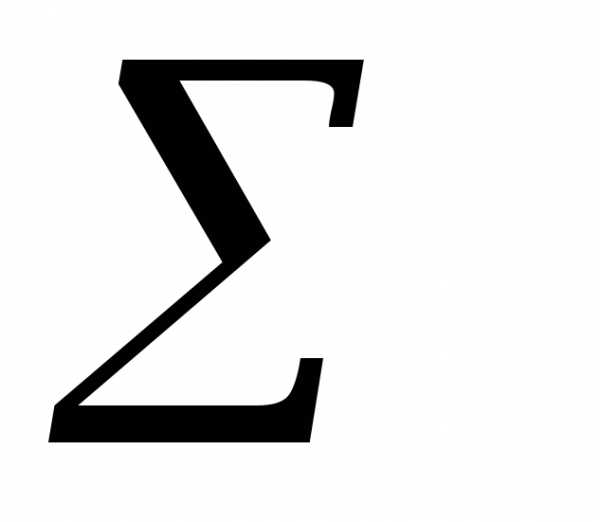xlogb.

x log Y = 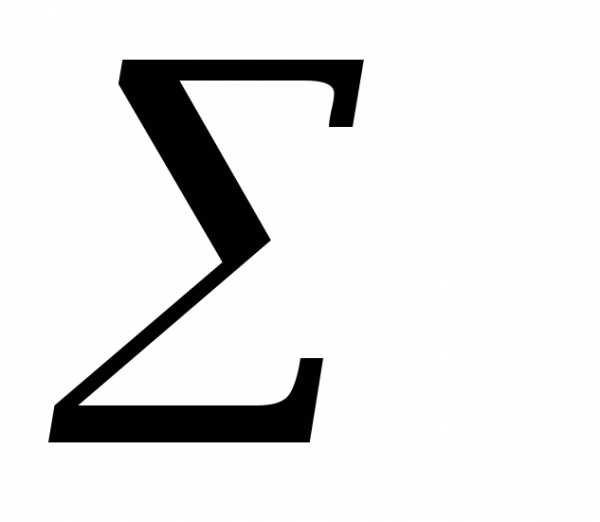x log a +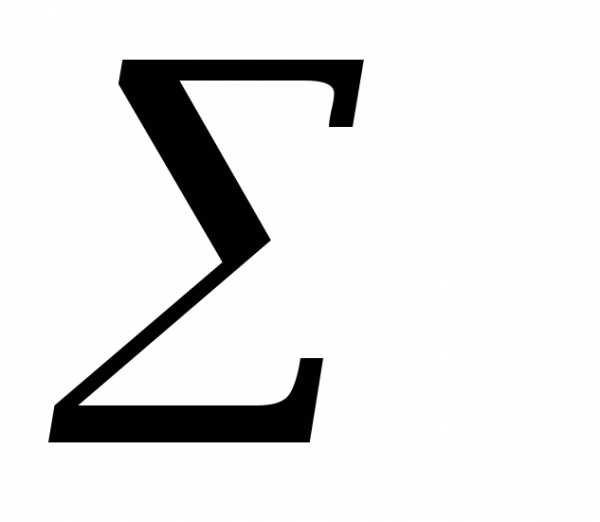x² log b.

Если определить х таким образом, что x= 0, то

log a = log Y/ N, log b =x log Y/x².

МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ. При подготовке прогноза методом скользящей привязки число периодов, по которым производится суммирование фактических данных, несколько больше того числа, которое было установлено и которое желательно иметь для проведения необходимых расчетов. Необходимость выравнивания сезонных колебаний требует, чтобы суммарная продолжительность всех периодов была равна 1 году. Выравнивание сезонных колебаний происходит в силу того, что крайние значения тренда имеют тенденцию к взаимному погашению. Вовлечение в расчет скользящей средней большего числа временных периодов увеличивает эффект сглаживания и одновременно уменьшает чувствительность прогноза к данным последних периодов.

Движение скользящей средней во времени дает возможность учесть самую последнюю информацию и отказаться от использования более старых данных. Использование скользящей средней позволит подготовить качественный прогноз только тогда, когда данные будут относительно стабильны.

Индекс сезонных колебаний, вычисленный на основе скользящей средней, дает возможность улучшить качество прогноза. Индекс получают путем деления объема фактического производства в соответствующем периоде на величину центрированной скользящей средней за тот же период. Повысить надежность можно за счет усреднения значения нескольких индексов общих временных периодов.

Пример. Для разработки прогноза на 2000 год используем данные о квартальных объемах производства. Скользящие средние определяются исходя из разбивки года на кварталы. Можно рассчитать скользящую среднюю только за 2 квартал 1995 года путем деления суммы данных за четыре квартала данного года на 4: (190+370+300+220)/4= 270.

Для расчета следующей скользящей средней берут данные за 2-4 кварталы 1995 года и 1 квартал 1996 года. Аналогично поступают в дальнейшем.

Центрированная скользящая средняя находится только для третьего квартала путем деления суммы данных скользящей средней за 2 и 3 кварталы 1995 года: (270+292)/2 = 281.

Дальнейшие расчеты делаются аналогично, заменяя одно значение другим.

Индекс сезонных колебаний получают путем деления фактического объема производства на величину центрированной скользящей средней за тот же период. Для 3 квартала 1995 года: 300:281 = 1,07.

Таблица. Расчет значений скользящей средней и индексов сезонных колебаний

Год	Квартал	Объем производства	Скользящая средняя	Центрированная скользящая средняя	Индекс сезонных колебаний
1995	1	190
	2	370	(190+370+300+220):4=270
	3	300	(370+300+220+280):4=292	(270+292):2 = 281	1.07
	4	220	(300+220+280+420):4=305	(292+305):2= 298,5	0,74
1996	1	280	(220+280+420+310):4=307	(305+307):2= 306	0,91
	2	420	(280+420+310+180):4=297	(307+297):2= 302	1,39
	3	310	295	296	1,04
	4	180	280	287,5	0,63
1997	1	270	273	276,5	0,98
	2	360	275	274	1,32
	3	280	283	279	1,00
	4	190	300	286,5	0,66
1998	1	300	303	301,5	1,00
	2	430	305	304	1,42
	3	290	310	307,5	0,94
	4	200	312	311	0,64
1999	1	320	320	316	1,01
	2	440	325	322,5	1,37
	3	320
	4	220

На основе рассчитанных данных индекса сезонных колебаний заполняем таблицу 2 и делаем расчет скорректированного индекса.

Таблица 2 Расчет скорректированного индекса сезонных колебаний

Год	1 квартал	2 квартал	3 квартал	4 квартал
1995			1.07	0,74
1996	0,91	1,39	1,04	0,63
1997	0,98	1,32	1,00	0,66
1998	1,00	1,42	0,94	0,64
1999	1,01	1,37
Итого	3,90	5,50	4,05	2,67
Средний индекс сезонных колебаний	0.975	1,375	1,0125	0,6675
Скорректированный индекс сезонных колебаний	0,97	1,37	1,00	0,66

Средний индекс сезонных колебаний рассчитываем путем деления суммы индексов за данный квартал на количество данных: для 1 квартала: 3,90:4 = 0,975 и т.д.

Полученные средние индексы сезонных колебаний проверяют на точность расчета. Среднее значение всех квартальных индексов не должна превышать 1. В нашем случае:

(0.975 + 1,375 + 1,0125 + 0,6675): 4 = 1,0075

Так как индекс больше 1, его следует скорректировать, уменьшив на 0.0075.

Завершающая стадия – составление прогноза. Для этого берут центрированную скользящую среднюю за определенный период и умножают на скорректированный индекс сезонных колебаний. Для 2000 года мы должны взять центрированную скользящую среднюю за 1 квартал 1999 года (316) и умножить на скорректированный индекс сезонных колебаний за 1 квартал (0,97):

1 квартал 2000 года = 316*0,97 = 307.

И т.д.

ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ. При экспоненциальном сглаживании в равенство вводится постоянный коэффициент сглаживания , придающий больший вес последним данным. Уравнение прогноза, учитывающее экспоненциальное сглаживание, записывается в виде:

F_n=Y_n-1+ (1 —)F_n-1,

где F_n– прогноз предстоящего периода

F_n-1— прогноз на текущий год

— коэффициент сглаживания

Y_n-1— фактический объем прогнозируемого показателя в текущем году.

Коэффициент находится в интервале от 0 до 1.Чувствительность к происходящим изменениям повышается с увеличением коэффициента сглаживания и уменьшением числа рассматриваемых периодов (N). Связь междуиNописывается отношением=.

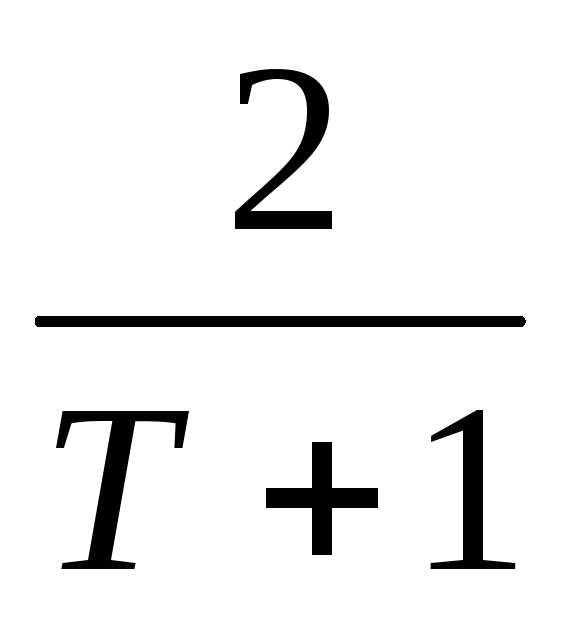Поэтому, если нас не устраивает найденное количество периодов N, то мы легко можем найти значение, которое нас устроит.

studfiles.net

Методы экстраполяции — Модели и методы принятия решений в анализе и аудите Библиотека русских учебников

Одним из наиболее распространенных методов краткосрочного прогнозирования экономических явлений является экстраполяция

Термин»экстраполяция»имеет несколько толкований. В широком смысле экстраполяция — это метод научного исследования, заключающийся в распространении выводов, полученных из наблюдений за одной частью явления, на а другую его часть. В узком смысле — это определение по ряду данных функции других ее значений вне этого рядоза цим рядом.

Экстраполяция заключается в изучении сложившихся в прошлом и настоящем устойчивых тенденций экономического развития и перенос их на будущее

Цель такого прогноза — показать, к каким результатам можно сделать в будущем, если двигаться к нему с той же скоростью или ускорением, что и в прошлом

Прогноз определяет ожидаемые варианты экономического развития исходя из гипотезы, что основные факторы и тенденции прошлого периода сохранятся на период прогноза или что можно обосновать и учесть напр рямок их изменений в рассматриваемой перспективе. Подобная гипотеза выдвигается исходя из инертности экономических явлений и процессев.

В прогнозировании экстраполяция применяется при изучении временных рядов

экстраполяции в общем виде можно представить в виде определенного значения функции

где у, — прогнозируемое значение уровня ряда динамики; I — период предубеждения;

Уи — уровень ряда, принятый за базу экстраполяции, а — параметры уравнения тренда

зависимости от особенностей изменения уровней в рядах динамики методы экстраполяции могут быть простыми и сложными (рис 147)

Рис 147. Группировка методов прогнозной экстраполяции

Простые методы экстраполяции основываются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего уровня ряда, среднего абсолютного прироста, среднего темпа роста

Рассмотрим подробнее названные методы экстраполяции

При экстраполяции на основе среднего уровня ряда используется принцип, при котором прогнозируемый уровень равен среднему значению уровней ряда в прошлом, т.е.

В таком случае экстраполяция дает прогностическую точечную оценку. Точное совпадение этих оценок с фактическими данными — явление маловероятное. Итак, прогноз должен быть в виде интервала значений. Доверительный интервал прог прогноза для средней при небольшом числе наблюдений находится по формулелою

где * о — табличное значение

В свою очередь среднее квадратическое отклонение для выборки равна:

где. Уи — текущий уровень ряда динамики; п — число уровней ряда динамики

Полученный доверительный интервал учитывает неопределенность, связанную с оценкой средней величины, и его применение для прогнозирования увеличивает степень надежности прогноза. Но недостатком рассматриваемого подходов периода является то, что доверительный интервал не связан с периодом предупреждениюя.

Экстраполяция по среднему абсолютному приросту может быть осуществлена ??тогда, если считать общую тенденцию развития явления линейной

Для вычисления прогнозного значения уровня необходимо определить средний абсолютный прирост. Л. Затем, зная уровень ряда динамики, принятый за базу экстраполяции уп, записать экстраполяционных формулу

Экстраполяция по среднему темпу роста может быть осуществлена, если есть основания считать, что общая тенденция ряда динамики характеризуется показательной кривой. Прогнозируемый уровень ряда в этом случае у определяется по формулею

где. ТР — средний темп роста, рассчитанный по формуле средней геометрической

Доверительный интервал прогноза по средним темпом роста может быть определен только в том случае, когда средний темп роста рассчитывается с помощью статистического оценивания параметров експоненц циальной криво.

Все три рассмотренные методы экстраполяции тренда являются простейшими, но одновременно и наиболее приближены

Сложные методы экстраполяции предусматривают выявление основной тенденции, т.е. применение статистических формул, описывающих тренд. Методы этой группы можно разделить на два основных типа: аналитические (кри иви роста) и адаптивныеі.

В основу аналитических методов прогнозирования (кривых роста) положен принцип получения с помощью метода наименьших квадратов оценки детерминированной компоненты, характеризующей основную тенденцию

Адаптивные методы прогнозирования основаны на том, что процесс реализации их заключается в вычислении последовательных во времени значений прогнозируемого показателя с учетом степени влияния предыдущих уровней. К ним х относятся методы текучей и экспоненциальной средних, метод гармонических весов, метод авто-регрессииї.

Метод аналитического выравнивания тренда (метод наименьших квадратов) может быть применен только в том случае, когда развитие явления достаточно хорошо описывается построенной модели и условия, определяющие тенденцию развития в прошлом, существенно не изменятся в будущем. При соблюдении этих требований прогнозирование осуществляется путем подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждениюя.

Процедура разработки прогноза по использованию аналитического выравнивания тренда состоит из следующих этапов:

1) выбор формы кривой, отражает тенденцию;

2) определение показателей, количественно характеризующие тенденции изменений;

3) оценка вероятности прогнозных расчетов

Выбор формы кривой можно осуществлять на основе построения графика, общий вид которого, как правило, позволяет установить:

а) имеет динамический ряд показателя четко выраженную тенденцию;

б) если так, то эта тенденция плавная;

в) каков характер тенденции

Отвечая на эти вопросы, необходимо помнить, что внешняя простота графика ложная. Любое динамическое задача гораздо сложнее от статического и каждая точка кривой является результатом изменения явления как в пр ростори, так и во времяі.

В связи с этим для повышения обоснованности и достоверности выравнивания с целью более точного выявления имеющейся тенденции необходимо провести вариантный расчет по нескольким аналитическими функциями и и на основе экспертных и статистических оценок определить лучшую форму связей.

На втором этапе необходимо определить параметры уравнения связи. Для их нахождения используют метод наименьших квадратов. В этом случае выравнивающая функция будет занимать такое положение среди факт политических значений показателей, при котором суммарное отклонение точек от функции будет минимальнойим.

Достоверную и обоснованную оценку полученным результатам можно дать, используя такие статистические показатели, как средний коэффициент роста, общая и остаточная дисперсия, коэффициент корреляции, др. ндекс корреляции, коэффициент корреляции исходного ряда и ряда отклонений определенного по разнице фактических и выровненных по любой аналитической функцией даны.

Для проверки гипотезы о наличии или отсутствии автокорреляции используют таблицы с критическими значениями коэффициента автокорреляции при различных уровнях значимости. Если табличное значение коефицие ента автокорреляции выше фактического, то можно утверждать, что автокорреляция отсутствует или устраняется, а значит, можно использовать формулы для вероятностной оценки значений, которые прогнозируются по этому и точками.

Пример 141

Рассмотрим использование метода аналитического выравнивания по данным деятельности TOB»Браво»г. Харькова, приведенными в табл 144

. Таблица 144. Динамика товарооборота TOB»Браво»

Луна	Товарооборот, тыс грн
	2005 г	2006 г
января	1156,3	1054,3
февраля	1254,3	1149,6
марта	1156,2	1098,2
апреля	1150,4	1135,2
мая	987,6	976,4
июня	1021,3	999,5
июля	1051,6	1045,6
августа	1115,4	1054,9
сентября	1254,2	1235,8
октября	1061,3	1035,4
ноября	1124,2	1108,5
декабря	1256,9	1249,4

Для прогноза были выбраны такие функции, как линейная, логарифмическая, полиномиальная, ступенчатая и экспоненциальная

Наглядное изображение колебаний объема товарооборота по указанным аналитическими функциями приведены на рис 148

Статистические оценки рассматриваемых аналитических функций приведены в табл 145 (с 539)

Как показывают данные таблицы, не все избранные аналитические функции хорошо выравнивают выходной динамический ряд. Об этом свидетельствует значение коэффициента (индекса) корреляции. Для прогнозирования, то есть продолжение сформ правленных тенденции на ближайшую перспективу, могут быть использованы только те функции, для которых коэффициент (индекс) корреляции превышает 0,7. К таковым относятся линейная, экспоненциальная и полиномиальная ф ункции. Последняя имеет наибольший коэффициент корреляции, равный 0,847, и наименьшую величину остаточной дисперсиирсії.

Рис 148. Исходящие выровнены по аналитическими функциями значения объема товарооборота TOB»Браво»

Итак, наиболее приемлемой формой аналитической функции для прогнозирования является полиномиальная функция, представленная уравнением:

Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на следующие три месяца: у25 = 654,83; у = 655,93; у»- 657,07 тыс грн 26 27

. Таблица 145. Характеристики выравнивающих функций для динамического ряда товарооборота

з / п	Показатель	Аналитическая функция
		линейная	логарифмическая	ступенчатая	экспоненциальная	полиномиальная
1	Коэффициент корреляции (индекс корреляции)	0,819	0,673	0,674	0,820	0,847
2	Остаточная дисперсия	6,40	10,66	10,64	6,39	5,52
3	Свободный член уравнения	639,27	637,46	637,51	639,29	641,65
4	Коэффициент при первом аргументе	0,522	3,651	0,0056	0,0008	-0,0278
5	Коэффициент при втором аргументе					0,022

Вероятность того, что прогнозируемый экономический показатель в заданный момент времени будет равна значению, которое соответствует точечной прогноза, практически равна нулю. Поэтому к точечному прогнозу визначают ться границы возможного изменения прогнозируемого значения показателя — доверительный интервал по формулею

где * (а,. Т — 20 — табличное значение распределения. Стьюдента. ВТ-д степенями свободы и уровнем значимости а;

а — среднеквадратичная ошибка прогноза

Среднеквадратическая ошибка прогноза вычисляется по формуле

где n — число уровней динамического ряда;

р — число параметров в уравнении прогноза;

Отметим, что в полученных при прогнозировании оценок доверительных интервалов следует относиться с осторожностью. Это связано со спецификой динамических рядов. Специфичность их заключается в том, что увеличение числа сп постережень в статической совокупности позволяет получить более точные характеристики этой совокупности, тогда как аналогичное удлинение ряда динамики не всегда приводит к подобным результатам, особенно в ты х случаях, когда ряды динамики используются для прогнозирования. Это обстоятельство связано с тем, что информационная ценность уровней теряется по мере их удаления от периода предубеждение, то есть знает ния уровней ряда динамики при прогнозировании неравноценно. Поэтому параметры уравнений аппроксимирующих кривых роста могут иметь погрешности и менять свои оценки при исключении части членов ряда или добавил. Анне новых членов ряда динамики, что отражается на точности расчетных значений уровней ряда динамики. Кроме того, параметры моделей тренда, полученные методом наименьших квадратов, остаются неизменным и в течение всего рассматриваемого периода. На практике часто встречаются случаи, когда параметры моделей меняются, а процедуры, сглаживающих с помощью метода наименьших квадратов не могут заметить такие изменения. Поэтому более эффективными оказываются адаптивные методы, в которых значимость уровней ряда динамики уменьшается по мере их удаления от прогнозируемого периода. К ним относятся: метод текучих с ередних, метод экспоненциального сглаживания, метод гармонических весов и другие, входят в класс адаптивных методе методів.

Часто ряды динамики характеризуются резкими колебаниями показателей по годам. Такие ряды, как правило, имеют слабую связь со временем и не проявляют четкой тенденции изменения. В этом случае методы аналитической ного выравнивания малоэффективен, так как вероятность расчетов резко падает. Доверительные границы прогноза иногда оказываются шире колебания показателя в ряде динамикіки.

При прогнозировании на основе временных рядов, очень колеблются, можно использовать метод текучих средних, с помощью которого можно исключить случайные колебания временного ряда, что достигается дорожно ом замены значений в середине выбранного интервала средней арифметической величины.

Интервал, величина которого остается постоянной, постепенно смещается на одно наблюдение. Если наблюдается определенная цикличность изменений показателей, интервал текучести должна равняться продолжительности цик клу. В случае отсутствия цикличности в изменении показателей рекомендуется выполнять разнообразный расчет при параметре сглаживания, изменяющийся. Лучший вариант определяется на основе дальнейшей оценки и выровненных рядедів.

По данным выровненных значений ряда динамики осуществляется подбор формы кривой, отражающей тенденции развития явления. Полученное уравнение регрессии используется для определения прогнозного значения испы лиджуваного показательа.

Пример 142

Рассмотрим использование метода текучих средних на основании данных, приведенных в табл 146,

Таблица 146. Выровненные за текучими средними значениями товарных запасов предприятия, тыс. грн

На основе выровненных значений товарных запасов предприятия получены следующие значения коэффициента корреляции (г):

Z	2	3	5	7		11
r	0,553	0,485	0,106	0,620	0,954	0,992

Приведенные данные свидетельствуют, что наилучшие результаты должны по данным, выровненными на основе 11 уровней исследуемого ряда динамики

В этом случае уравнение прямой будет иметь вид:

Используя это уравнение, в перспективе получаем:

Прогнозное значение товарных запасов на 16-й год можно определить по формуле

Отсюда уи = 38,63 тыс. грн

Для расчета у17 используется текучая средняя. У7, в формуле которой у1в будет уже известной величиной

Метод экспоненциального сглаживания

Экспоненциальное сглаживание — это выравнивание динамических рядов, очень колеблются, с целью последующего прогнозирования. По этому методу можно дать обоснованные прогнозы на основании рядов динамики, ма ають умеренный связь во времени, и обеспечить более учета показателей, достигнутых за последние годы. Сущность метода заключается в сглаживании временного ряда с помощью взвешенной текучей средней, в которые и веса подчинены экспоненциальному закону. Каждое сглажено значение рассчитывается путем объединения предыдущего сглаженного значения и текущего значения временного ряда. В этом случае текущее зна ния временного ряда решается с учетом константы, сглаживает. Расчет осуществляется по формулемулою

где ^ — значение экспоненциальной средней в момент *; у, — текущее значение ряда динамики;

— значение экспоненциальной средней в момент (

Значение а всегда находится в пределах от 0 до 1, и в каждом конкретном случае необходимо выбрать наиболее приемлемое значение

Величину в формуле (149) можно представить в виде суммы фактического значения уровня и сглаженного значение наблюдения, что ему предшествует разделения можно продлить для членов ряда $ ^ 2 $ и т д. В результате получим такое выражениераз:

в котором среднее сглажено значение является комбинацией всех предыдущих уровней ряда. Величина у0 характеризует начальные условия процесса. Сложив в формуле (1410) все члены, содержащие параметр а, получим:

где / — число периодов отставание от момента

Согласно формуле (1411) относительный вес каждого предыдущего уровня снижается по экспоненте по мере его удаления от момента, для которого вычисляется сглаженное значение. Отсюда и возникло название. Этому ого метода сглаживанияня.

Последовательное применение формулы (1410) дает возможность вычислить экспоненциальной средней через значения всех уровней данного ряда динамики. Кроме того, она определяет экспоненциальные средние первого порядка в, т.е. средние, полученные непосредственно при сглаживании исходных данных ряда динамики. В тех случаях, когда тенденция после сглаживания исходного ряда определена недостаточно четко, процедуру згладжува ния повторяют, т.е. вычисляют экспоненциальные средние 2-го, 3-го и последующих порядков, пользуясь такими выражениямими:

При практическом использовании метода экспоненциального сглаживания возникают некоторые трудности. Основными есть выбор константу а и определение начального условия у0. От численного значения параметра а зависит, насколько быстро будет уменьшаться вес предыдущих наблюдений и соответственно этому степень их влияния на уровень, сглаживается. Чем больше значение параметра а, тем меньше влияют предыдущие уровни и соответственно меньшим оказывается влияние экспоненциальной средней. Поиск компромиссного значения параметра сглаживания составляет задачу оптимизации модели, до сих пор до конца еще не водовороте шэншена.

Автор метода экспоненциального сглаживания, английский ученый. РГ. Браун, предложил такую ??формулу расчета а:

где г — число уровней, входящих в интервал сглаживания

Величина г определяется в этом случае эмпирически

Поиск оптимального значения параметра сглаживания адаптивных полиноминальной моделей может осуществляться также путем переборки различных его значений. В этом случае оптимальным будет то значение а, пр ри котором получена наименьшая дисперсия ошибки прогнозирования, исчисленная или при реализации процедуры сглаживания всего ряда динамики, или не использованном в расчетах отрезка ряда, специаль но оставлен для проверки качества прогнозных моделей.

Задача выбора параметра у0, определяющий начальные условия, предлагается решать следующим образом:

o если имеются данные о развитии явления в прошлом, то вместо у0 можно использовать среднюю арифметическую всех имеющихся уровней ряда динамики или какой-то их части;

o если сведений о развитии явления в прошлом нет, то вместо у0 используют исходное (первое) значение уровня ряда. Динамики в или специальные формулы. Брауна

Для линейной модели начальные условия определяются так:

Для определения значений коэффициентов а0 и ах необходимо рассчитать коэффициенты уравнения тренда, полученные методом наименьших квадратов

Затем осуществляется расчет экспоненциальных средних первого и второго порядков по формулам (1412), (1413)

Прогноз в случае линейного тренда вычисляется по формуле

Ошибка прогноза можно вычислить по формуле

где а — среднеквадратичная ошибка отклонения от линейного тренда, которая вычисляется по формуле

где к — число степеней свободы, которое определяется по числам членов ряда п и параметров выровненной кривой

Метод экспоненциального сглаживания по сравнению с другими методами прогноза имеет преимущества и недостатки. Среди преимуществ необходимо назвать его точность, увеличивается с увеличением числа уровней динамического в ряду. Недостатком метода является то, что нет точного метода для выбора оптимальной величины параметра сглаживания а. Точность прогноза по этому методу уменьшается с увеличением прогнозного интервала. Он эффе руктивных для краткосрочных прогнозов, в других условиях его можно использовать для получения приближенных. Оценитеінок.

Пример 143

Составим ретроспективный прогноз товарных запасов методом экспоненциального сглаживания для а = 0,1, а = 0,2 и а = 0,3 (табл 147)

Расчет экспоненциального взвешенного значения по по формуле (1410), которая в зависимости от величины сглаживающий-ной константы приобретает вид:

Независимо от величины а экспоненциальное сглаженное значение в первом году равняется фактическому значению уровня ряда динамики за этот год сглаженные значения в последующие годы определяется так:

Аналогично рассчитываются и последующие сглаженные значения, приведенные в табл 147

. Таблица 147 экспоненциально средние, рассчитанные за товарными запасами предприятия, тыс. грн

Луне	Значение исходного ряда	Экспоненциальное сглажено значение
		а = 0,1	а = 0,2	а = 0,3
1	25,6	25,60	25,60	25,60
2	26,1	25,65	28,26	25,75
3	27,2	25,81	25,33	26,19
4	27,5	25,97	25,55	26,58
5	28,4	26,22	25,83	27,13
6	28,6	26,46	26,11	27,57
7	27,1	26,52	26,21	27,43
8	27,8	26,65	26,37	27,54
9	26,2	26,60	26,35	27,14
10	27,1	26,65	26,42	27,13
11	28,7	26,86	26,65	27,60
12	27,5	26,92	26,74	27,57
13	30,7	27,30	27,13	28,51
14	29,7	27,54	27,39	28,87
15	31,4	27,93	27,79	29,63

Как видно из рис 149, значения, полученные при а = 0,3, лучше отражают общий тренд

Для расчета прогнозного значения остатка товарных запасов необходимо определить экспоненциальной средней второго порядка по формуле (1412), а также параметры линейного тренда по формулам (1419) и ( (142020).

экспоненциальная средняя первого порядка для 16 месяца определяется по формуле (149), где текущее значение товарных запасов рассчитано на основании уравнения тренда:

Результаты расчетов приведены в таблице 148

Таблица 148 Построение модели прогноза методом экспоненциального сглаживания

Таким образом, прогнозное значение остатка товарных запасов на 16-й месяц равен 30,67 тыс. грн

Более рациональным способом дисконтирования информации является метод гармонических весов, разработанный польским статистике 3. Хелвигом. Он подобен метода простого экспоненциального сглаживания и использует есть тот самый принцип. В его основе лежит взвешивания текущего показателя, но вместо текучей средней используется идея текущего тренда. Экстраполяция производится непостоянным трендом, отдельные точки л. Аман линии решаются с помощью гармонических весов, что позволяет позже наблюдением предоставлять большую весоввагу.

Метод гармонических весов базируется на следующих предпосылках:

1) период времени, за который изучается экономический процесс, должен быть достаточно длительным, чтобы можно было определить его закономерности;

2) исходный ряд динамики не должен иметь скачкообразных изменений;

3) прогнозируемый социально-экономическое явление должно быть инерционным, т.е. для наступления большого изменения в характеристиках процесса необходимо, чтобы прошло значительное время;

4) отклонения от текущего тренда носят случайный характер;

5) автокорреляционная функция, рассчитанная на основе последовательных приростов, должна уменьшаться с ростом времени (0″т.е. влияние более поздней информации имеет сильнее отражаться на прогнозируемой ве еличини, чем на ранней информациимації.

Для осуществления прогноза по этому методу исходный ряд динамики разбивается на фазы г. Число фаз должно быть меньше число членов ряда л, т.е. г п. Конечно фаза г равен 3 — 5 уровням

Для каждой фазы рассчитывается линейный тренд:

Для оценки параметров связи используется способ наименьших квадратов

С помощью полученных (п — г 1) уравнений определяются значения текущего тренда (и /, (/)), из которых находится среднее значение (УИ (п) по формуле арифметической простой

Для проверки гипотезы о том, что отклонение от текущего тренда является стационарным процессом, рассчитывается автокорреляционная функция. Если значение автокорреляционной функции уменьшаются от периода к перио периода, то пять предпосылка этого метода выполняетсяя.

Далее рассчитывают приросты по формуле

Средний прирост вычисляется по формуле

где. С»1 — гармоничные коэффициенты при следующих условиях:

По этим выражением поздней информации предоставляется больше веса, потому что приросты обратно пропорциональны времени, который отделяет раннюю информацию от поздней для момента и — п

В общем виде ряд гармонических весов определяют по формуле

Чтобы получить гармоничные коэффициенты. С (я 1, которые удовлетворяют условиям (1428), нужно гармоничные веса. ГНИ й разделить на (п -1), т.е.

Далее прогнозирование осуществляется так же, как и при простых методах прогноза, путем добавления до последнего значения ряда динамики среднего прироста, т.е.

Пример 144

Проиллюстрируем этот метод на примере динамики реализации продукции за 9 месяцев 2007 г (табл. 149)

Таблица 149. Исходные данные и результаты расчета прогноза объема реализации продукции методом гармонических весов

Предварительно ряд динамики был проверен на выполнение предпосылок, на которых базируется метод

Параметры уравнений отдельных фаз движения текущего тренда определены методом наименьших квадратов при условии, что интервал сглаживания (г) равна 3

С помощью полученных уравнений определяем значение текущего тренда

Если г = 1, имеем одно значение у1и) и которое получаем из уравнения

Если. И — 2, имеем два значения дт, получаемые из уравнений:

Если и = 3, имеем три значения ую), получаемые из уравнений:

Аналогично находим все значения в

Расчет прироста производится по формуле (1426). Например:

Гармонические веса определяются по формуле (1429). Например:

Гармонические коэффициенты получаем по формуле (1430):

и т.д.

Используя формулу (1427), находим средний абсолютный прирост (б) = 1,974) и рассчитаем прогнозные значения на производство реализованной продукции на следующие три месяца по формуле (1431):

Этот метод прогнозирования используется тогда, когда есть уверенность, что тенденция в будущем описывается плавной кривой, есть ряд динамики нет сезонных и циклических колебаний

uchebnikirus.com

Сущность и методы экстраполяции :: BusinessMan.ru

Сложное слово «экстраполяция» составлено из двух простых. Первое на латыни звучит extra и означает «вне», «за», «снаружи». Второе на той же латыни звучит polire и означает «изменять», «выправлять», «приглаживать». В целом экстраполяция может быть определена как значение вне двух заданных точек. Она считается оценкой того, что извлечено из известных фактов, которые расширяют данные в неизвестной области, чтобы прийти к предполагаемому результату. Эта концепция также может быть отнесена к предсказанию образа будущего, предполагающего истинность настоящих и прошлых тенденций.

Метод экстраполяции предполагает, что данные или наблюдения в будущем будут по-прежнему похожи. Таким образом, будущие результаты могут быть предсказаны. Ее можно рассматривать как математическую гипотезу. При экстраполяции используются данные и факты определенной ситуации и приводятся прогнозы о том, что может произойти в конечном итоге.

История процесса экстраполяции

Этот метод часто называют экстраполяцией Ричардсона или методом Ромберга. Но это не совсем правильно, поскольку на протяжении веков уже существовали похожие численные методы решения подобных задач. Поэтому знаменитая h3 Ричардсона (экстраполяция для численного решения) не является первой. Подобный метод был применим в вычислениях Гюйгенса еще в 1654 году. Сам термин «экстраполяция» был впервые введен Томасом Д. Кларесоном в 1959 году в книге о науке и художественной литературе.

Методы экстраполяции могут пониматься как расширение данных или процессов, предполагающих, что аналогичный процесс будет применяться и за их пределами. Экстраполяция — важная концепция, используемая не только в математике, но и в других областях, таких как социология, психология, прогнозирование. Например, водитель обычно экстраполирует дорожные условия за пределами своего видения. Экстраполяция может быть отнесена к способу, в котором значения данных рассматриваются как точки x1, x2 …, xn, а затем значение приближается к пределу заданного диапазона точек.

Преимущества использования:

1. Простой метод прогнозирования.
2. Не так много данных требуется.
3. Быстрая и дешевая аналитика.

Метод существует в статистических данных. Если какие-то значения периодически убираются, ответ приближается к следующей точке данных. Примером методом экстраполяции является прогноз погоды, в котором рассматривается предыстория данных и экстраполируется прогнозируемая модель будущего. Еще более простой пример, если есть информация о воскресеньях, понедельниках и вторниках, можно экстраполировать среду или четверг.

Недостатки использования экстраполяции:

1. Ненадежность, если имеются значительные колебания в исторических данных.
2. Предположение, что прошлая тенденция будет продолжаться и в будущем, вряд ли возможно во многих конкурентных бизнес-средах.
3. Игнорирует качественные факторы, например изменения вкусов и моды.

Ускорение последовательности

Методы экстраполяции заключается в создании касательной линии в конце известных данных и расширении ее за пределы этой области. Подобно интерполяции, экстраполяция использует множество методов, требующих предварительного знания процесса, который создает существующие точки данных. Метод включает в себя экстраполяцию линейную и полиномиальную, экстраполяцию коники и французской кривой.

Как правило, качество конкретного метода ограничено предположениями о функции. В численном анализе экстраполяция Ричардсона представляет собой метод ускорения последовательности, используемый для улучшения скорости ее сходимости. Он назван в честь Льюиса Фрая Ричардсона. Он представил технику расчета в начале XX века, полезность которой для практических вычислений вряд ли можно переоценить.

Практические применения экстраполяции Ричардсона включают интеграцию Ромберга, которая применяет ее к правилу трапеции и алгоритму Булирша — Стоера для решения обыкновенных дифференциальных уравнений.

Линейный метод

Метод линейной экстраполяции полезен, когда задана линейная функция. Это делается путем рисования касательной линии в конечной точке заданного графика и расширения ее за пределы. Этот метод экстраполяции в прогнозировании дает хорошие результаты, когда точка, которая должна быть предсказана, не слишком далека от данных. Линейная интерполяция полезна при поиске значения между заданными точками. Его можно рассматривать как «заполнение пробелов» таблицы данных.

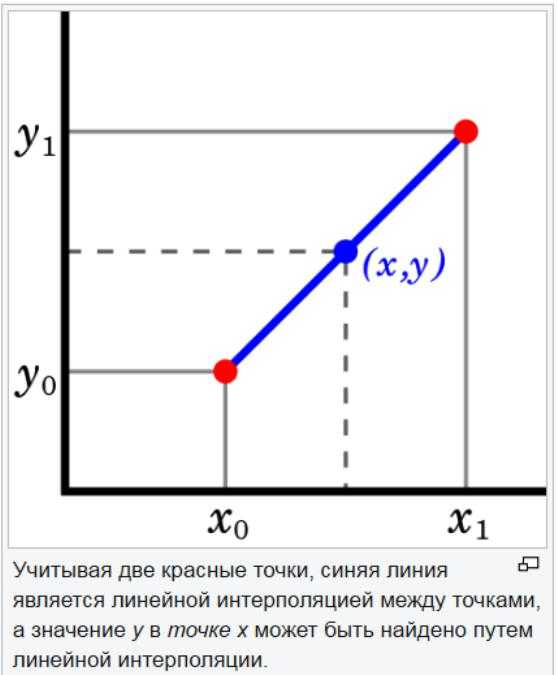
Стратегия линейной интерполяции заключается в использовании прямой линии для соединения известных точек значений по обе стороны от неизвестной. Линейная интерполяция неточна для нелинейных параметров. Если точки в наборе данных меняются на большую величину, линейная интерполяция может дать неправильную оценку.

Линейная экстраполяция может помочь оценить значения, которые выше или ниже значений в наборе данных. Стратегия ее заключается в использовании подмножества данных вместо всего набора. Для этого типа значений полезно применять в прогнозировании метод экстраполяции, используя последние две или три точки, чтобы оценить значение, превышающее диапазон данных.

Полиномиальная и коническая экстраполяции

Известно, что три точки дают уникальный многочлен. Полиномиальная кривая может быть продолжена после окончания таких данных. Она обычно выполняется методом Ньютона с конечной разностью или с использованием интерполяционной формулы Лагранжа. Полином высшего порядка должен быть экстраполирован с должным вниманием, потому что при полиномиальной экстраполяции есть справедливые шансы на ошибку. Если это произойдет, оценка ошибки будет экспоненциально возрастать вместе со степенью полинома.

В математике минимальная полиномиальная экстраполяция представляет собой преобразование последовательности, используемое для ускорения сходимости. Хотя метод Айткена является самым известным, он часто терпит неудачу, особенно для векторных последовательностей. При этом выполняется итерация, которая строит матрицу. Ее столбцы являются отличиями.

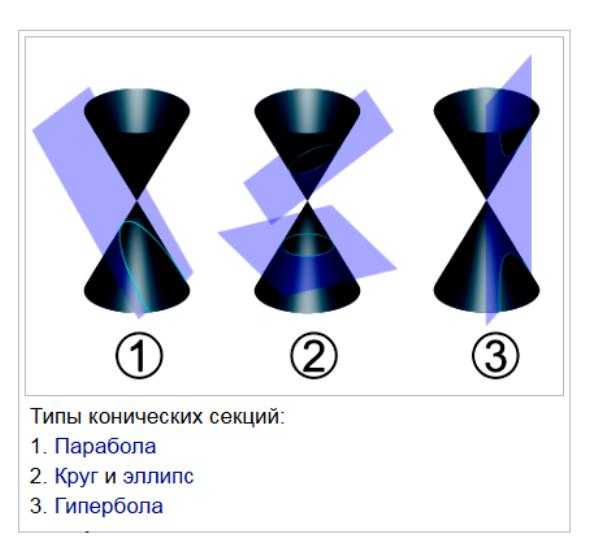
К примеру, методом экстраполяции для конического разреза может быть произведен с помощью 5 точек, указанных ближе к концу данных. В случае, если коническая секция представляет собой круг или эллипс, то она будет образовывать петли назад и воссоединиться с собой. Парабола или гипербола никогда не пересекутся. Но они могут быть изогнуты назад относительно оси X. Экстраполяция конуса может быть выполнена на бумаге с конической секцией или с помощью компьютера.

Математический метод оценки

В этом методе экстраполяции прогнозируется значение за базовый период. Действия, описанные ниже, автоматически выполняются системой и не видны пользователю. Описание предназначено для уточнения алгоритма, который выводит ожидаемые значения из количества, хранящегося в системе, и прогнозирует результат измерения счетчика.

Экстраполяция при использовании определения количества процедуры выполняется с помощью функции: Yt = f (yi, t, aj).

В качестве основы для экстраполяции добавляются округленные данные типичного базового периода, хранящегося в результатах считывания. Система определяет вес Yt данных временного ряда в t (время прогнозируемого периода) для получения правильного решения методом экстраполяции. Где в точке отсчета взяты yi – уровень ряда и aj – параметр уравнения тренда.

Прогнозирование функциональных возможностей

Метод фиксации статистической кривой применим к прогнозированию функциональных возможностей. Статистические процедуры соответствуют прошлым данным одной или нескольких математических функций, таких как линейные, логарифмические, Фурье или экспоненциальные. Наилучшие выбираются статистическим тестом. Тогда этот прогноз экстраполируется из этой математической связи методом математической экстраполяции. Одним из самых простых способов получения приблизительных оценок будущих (или прошлых) условий является экстраполяция данных, которые изменяются со временем.

Например, если нужно провести грубую оценку будущих уровней загрязняющих веществ в питьевых водах на 20 лет вперед, можно экстраполировать эту тенденцию с последних 20 лет. То же наблюдается, если нужно оценить распространенность курения или рак легких в фоновом режиме в будущем. Прогноз можно составить путем расчета тенденции за последние годы. Экстраполяции этого типа можно сделать с использованием менее сложных методов. Во многих случаях (особенно в областях маркетинга и управления бизнесом) традиционно используется метод экстраполяции, например путем просмотра последних данных и интуитивной оценки того, что подразумевается в будущем.

Методы, основанные на правилах, также могут быть использованы путем применения набора предопределенных принципов или ожиданий на основе предварительного понимания системы и учета последних данных для интерпретации будущих событий.

При любом методе в экстраполяции важна осторожность из-за наличия многочисленных неопределенностей. Любая процедура экстраполяции основана на предположении, что в прошлых данных и знаниях имеется достоверная информация. Следовательно, будущее обусловлено теми же факторами, которые действовали ранее.

Ошибки прогнозирования

Ошибочность экстраполяции (точнее, ошибочность неоправданной экстраполяции) возникает, когда явление, ответственное за ряд тривиальных локальных эффектов, считывается в качестве великих глобальных явлений. Еще одна причина ошибки заключается в том, что иногда обобщенные правила выводятся на основе слишком немногочисленных фактов. Так, теория Дарвина об эволюции является фантастическим примером применения метода экстраполяции, в которой механизмы случайных изменений и естественного отбора объявляются для учета развития таких сложных структур, как зрение млекопитающих или иммунная система живых организмов.

При попытке интерпретации результатов исследований ученый должен избегать экстраполяции вне диапазона данных и осознавать лежащие в основе предположения, чтобы избежать принятия недействительных выводов. В общем, экстраполяция является законным научным инструментом. Есть два аспекта, которые помогают различать действительную и ошибочную экстраполяцию. Вероятность ошибочной экстраполяции выше, когда для ее построения были получены точки на недостаточных данных.

Статистические инструменты Excel

Чтобы найти корреляцию между годами и результатами (например, в бизнесе), можно воспользоваться Excel.

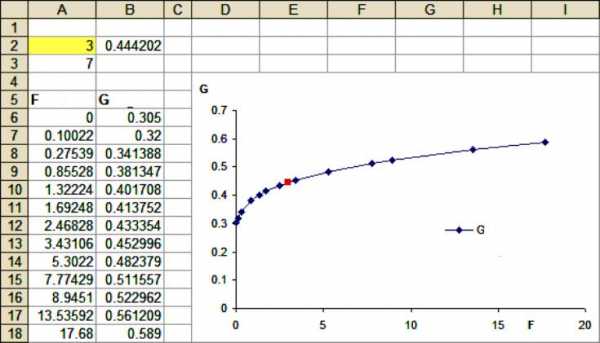
Для этих задач используют статистические инструменты для моделирования методом экстраполяции, встроенные во все версии Excel, начиная с 97. Порядок действия:

1. Ввести известные значения, например общие продажи за 2016-2017 годы, если нужно определить их за 2018 и 2020 годы.
2. Установить утилиту Analysis, функцию, требующую использования надстройки.
3. Чтобы установить ее, извлечь из меню «Инструменты», «Дополнения».
4. Проверить окно утилиты анализа и подтвердить с помощью «ОК».
5. Измерить корреляции между двумя сериями.
6. Экстраполяция, которую нужно сделать, имеет смысл только в том случае, если между двумя наборами чисел (годы и продажи) складывается четкая тенденция (корреляция) по методу экстраполяции тенденций.
7. Чтобы измерить эту корреляцию, используют меню «Инструменты», «Утилиты анализа».
8. В списке «Инструменты анализа» выбирают «Анализ корреляции» и нажимают «ОК».
9. В поле Input Range вводят анализируемый диапазон, например A6: B18, Excel добавит символ «$».
10. В области «Параметры вывода» проверяют выходной диапазон и вводят в соседнее поле.
11. Подтверждают с помощью OK.
12. Excel создает массив из двух строк по двум столбцам. Находят расчетное значение (например, 0.981). Поскольку это значение близко к 1, это означает, что существует сильная корреляция между годами и цифрами продаж. Если пользователь получит значение, близкое к нулю, это будет означать, что тенденция не возникает. В этом случае экстраполяция не имеет смысла.
13. Запускается оценка будущих значений.
14. Выбирают необходимый диапазон и нажимают кнопку «Мастер диаграмм».
15. Выбирают диаграмму (например, облака точек) и нажимают «Готово».

Применение скользящих средних

Эти два метода экстраполяции предполагают широкое использование данных по продажам для прогнозирования будущего. Скользящее среднее значение принимает серию данных и «сглаживает» флуктуации в них. Цель состоит в том, чтобы извлекать экстремумы данных из периода в период. Скользящие средние часто вычисляются ежеквартально или еженедельно. Для прогнозирования будущих значений экстраполяция предполагает использование трендов, установленных историческими данными. Основное предположение экстраполяции заключается в том, что образец будет продолжаться и в будущем, если фактические данные не указывают на иное. Чтобы подробнее разобраться в этих методах, можно рассмотреть диаграмму, показывающую продажи гаджетов для крупного бизнеса с 2012 по 2015 годы.

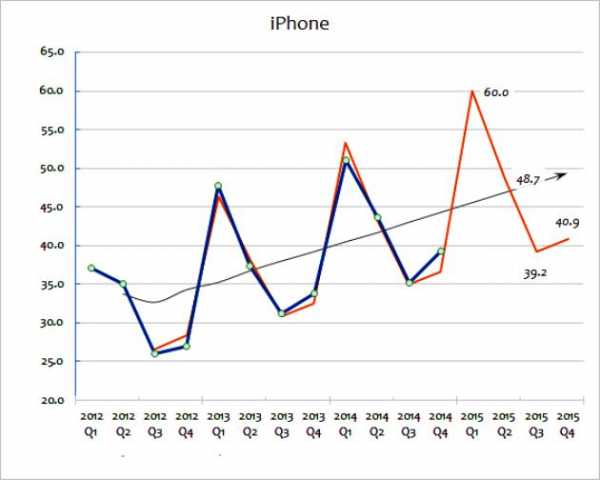
Этот метод экстраполяции расчета показывает фактическую цифру продаж. Как можно увидеть, общая сумма продаж колеблется от года к году, хотя можно догадаться (глядя на данные), что общая тенденция для роста продаж имеется. Черная линия показывает скользящую среднюю. Это рассчитывается путем добавления последних лет продаж (например, Q1 + Q2 + Q3 + Q4), а затем деления на четыре.

Этот метод сглаживает годовые изменения и дает хорошее представление об общей тенденции в годовых продажах. Скользящее среднее помогает указать тенденцию роста, выраженную в процентных значениях. Именно это экстраполяция будет использовать сначала, чтобы предсказать путь будущих продаж. Это можно сделать математически, используя электронную таблицу. В качестве альтернативы экстраполированный тренд можно просто нарисовать на диаграмме в качестве приблизительной оценки.

Корреляция трендов

Всегда одна технология является предшественником другой. Это случается, когда достижения, достигнутые в технологии прекурсоров, могут быть приняты технологией последователей. Когда такие отношения существуют, знание изменений в технологии предшественников может быть использовано для прогнозирования хода технологии последователей в будущем. Кроме того, экстраполяция предшественника позволяет прогнозировать продолжение следования за пределами времени запаздывания.

В этом случае используют метод экстраполяции трендов, в котором сравниваются, например, тенденции скорости боевых и транспортных самолетов. Другим примером прогноза корреляции трендов является прогнозирование размера и мощности будущих компьютеров, основанное на достижениях в области микроэлектронной технологии. Иногда технология последователей зависит от нескольких технологий прекурсоров, а не от одного предшественника.

Фиксированные комбинации предшественников могут влиять на изменение в последовательности, но чаще комбинации не фиксируются, а входы предшественников различаются как по комбинации, так и по силе. Например, увеличение скорости воздушных судов может происходить за счет улучшения двигателей, материалов, элементов управления, топлива, аэродинамики и различных комбинаций этих факторов.

Пример прогноза корреляции, полученной методом экстраполяции трендов: общие пассажирские мили, общие географические мили и средняя посадочная мощность. Экстраполяция статистически определенных тенденций позволяет объективно подходить к прогнозированию. Однако этот подход имеет серьезные ограничения и ловушки. Любые ошибки или неправильный выбор, сделанный при определении исторических данных, будут отражены в прогнозе, что снижает его ценность.

Приложения, атрибуты и лимиты

Метод экстраполяции относится к сфере прогнозирования. Он предполагает, что шаблоны, которые существовали в прошлом, будут продолжаться и в будущем, а также то, что эти шаблоны являются регулярными и могут быть измерены. Другими словами, прошлое является хорошим индикатором будущего. Приложения полезны для разработки базовых данных.

Атрибуты и лимиты — это простые и дешевые инструменты вычислений, как и сложные теоретические модели.

1. Данные процесса — графика и наблюдения.
2. Ключ — наличие хорошей базы данных и понимание структуры внутри нее.
3. Техника — наилучшая подгонка, соотношение и так далее.

Временные стандартные статистические процедуры не приводят к аккуратным подборам тенденций, которые прогнозист может экстраполировать с комфортом, выполняя прогноз методом экстраполяции. В таких случаях прогнозист может «скорректировать» статистические результаты, применяя суждение. Также он может полностью игнорировать статистику и экстраполировать тренд целиком на основе суждения.

Прогнозы, генерируемые таким образом, менее точны, чем статистические, но не обязательно неудовлетворительные. Одним из примеров такой экстраполяции качественного тренда является прогнозирование сложности воздушного судна. Попытки количественной оценки этой тенденции не были успешными. Но процент подвижных или регулируемых частей самолета был экстраполирован с частотой, с которой такие элементы были введены в прошлом. Эти прогнозы были достаточно точными.

Специфические технические изменения не могут быть предсказаны таким образом, но степень изменения может. Это дает полезные материалы для планирования, указывая тенденцию прошлого поведения.

businessman.ru

Метод экстраполяции, его основные черты :: SYL.ru

Существует довольно большое количество методов научных исследований, данная статья посвящена экстраполяции. Этот метод основывается на рассмотрении тенденций, закономерностей или связей, которые имеют место быть в настоящем или происходивших в прошлом, и перенесение их на будущее состояние объекта прогнозирования. Метод экстраполяции относится к группе формализованных. Его целью является отражение будущего состояния какого-либо объекта, если он будет развиваться так же, как раньше, не меняя скорости. На рисунке ниже представлен пример того, как выглядит линия тренда, составленная с помощью данного метода.

Метод экстраполяции имеет широкое применение в практической деятельности, поскольку он довольно прост в исполнении, не требует серьезных капитальных вложений. Кроме того, он нуждается в объемной базе статистических данных. Принято различать перспективную и ретроспективную экстраполяцию. Чаще встречается первый вариант. Это перенесение знаний на объект в будущем. Вторя предполагает экстраполяцию в прошлое.

Метод экстраполяции в прогнозировании

Предполагается два условия при его использовании. Во-первых, сохранение в будущем основных факторов, оказывающих влияние на исследуемый объект в прошлом. Во-вторых, развитие событий происходит плавно, траекторию можно описать с помощью математических символов и формул.

Что предпринять, если одно из указанных выше допущений не соблюдается? В данном случае проводится процедура «исправление линии тренда». Она заключается в отсечении показателей, возникших в результате воздействия измененных факторов. При этом необходимо соблюдать осторожность, лучше применить метод экспертных оценок. Исключить ошибки или хотя бы минимизировать их можно путем увеличения базы данных или уменьшения срока прогнозирования. Следует отметить одну особенность, которую имеет метод экстраполяции. Период прогнозирования должен быть больше, чем 1/3 его базы. Данный метод является механическим приемом. Его результаты нельзя использовать в качестве заключительного этапа при составлении прогноза. Полученные данные необходимо передать на оценку экспертам, которые способны внести коррективы в случае изменения каких-либо внешних факторов. Еще один пример графического изображения представлен на рисунке слева.

Метод экстраполяции. Пример использования в управлении

Существует несколько разновидностей данного метода, которые могут быть использованы для принятия решений. Первой из них является экстраполяция понятий. Она может быть применена при появлении новых явлений, факторов, которые требуют объяснения. Однако она может стать неудачной. Вторая разновидность – экстраполяция количественная. Возникает там, где необходимо произвести перенос тех или иных параметров объекта или системы из прошлого в будущее. Важно помнить, что экстраполируемые факторы, параметры или отношения могут быть как историческими, так и вневременными. Первые способны претерпевать изменения в количественном отношении. В данном случае прогнозы будут неточными. А вторые постоянны всегда. Яркий пример – соотношение радиуса и длины окружности, которые имеет идеальный круг. Прогнозы, построенные с использованием вневременного метода экстраполяции, будут отличаться высокой степенью точности.

www.syl.ru

3. Методы экстраполяции, их особенности.

Основой методов формализации является экстраполяция, основанная на изучении динамики изменения экономического явления в предшествующем периоде и перенесении найденной закономерности на будущее. Обязательным условием использования экстраполяционного подхода является познание и понимание природы исследуемого процесса, наличие устойчивости в экономическом процессе. В исследовании закономерностей процесса важное место принадлежитдинамическим (временным) рядам,представляющим совокупность числовых данных, характеризующих изменение показателя во времени.Зная закономерность изменения признака в предшествующем периоде, и перенося найденную зависимость на будущее, определяют вероятность количественного значения исследуемого показателя в будущем.

Условно выделяют следующие группы метода экстраполяции тенденций:

• упрощенныецелесообразны при недостаточной информации о предыстории развития объекта (нет длинного динамического ряда или информация задана только двумя точками: на начало и конец периода).

• аналитические основаны на применении МНК к динамическому ряду и представлении закономерности развития явления во времени в виде уравнения тренда.

• адаптивныеиспользуются в случаях сильной колебаемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. Относят: методы скользящих средних, экспоненциального сглаживания, метод гармонических весов, методы авто регрессионных преобразований.

Метод наименьших квадратов. Позволяет подобрать параметры прогнозирующей функции так, чтобы суммарные отклонения фактических значений динамического ряда от вычисленных были минимальны.

Метод скользящей средней. Если тренд имеет сложную форму, то проводится процесс сглаживания эмпирических кривых. Суть: замена фактических значений показателя их усредненными величинами, имеющими меньшую вариацию.

Метод по огибающим кривымучитывает в прогнозе качественных изменений, происходящих в самом объекте. Отличительная особенность: совместное изучение частных тенденций развития. Позволяет установить соподчиненность индивидуальных закономерностей, последовательность их чередования, наиболее вероятные значения показателей в будущем. Широко используется при прогнозировании НТП, агрегируемых показателей и т.д. Обязательным условием является рассмотрение всех форм проявления объекта в прошлом и настоящем.

Метод экспоненциального сглаживания. Выравнивание особенно сильно колеблющихся динамических рядов в целях последующего прогнозирования. Позволяет давать обоснованные прогнозы на основании рядов динамики, имеющих умеренную связь во времени, обеспечивает больший учет показателей, достигнутых в последние годы. Сущность заключается в сглаживании временного ряда с помощью взвешенной скользящей средней, в которой веса подчиненыэкспоненциальному закону: воздействие замыкающих наблюдений отражается на прогнозных оценках более заметно, чем влияние начальных уровней.

При экстраполяционном прогнозировании важным является заключительный этап – верификация, которая представляет совокупность критериев, способов и процедур, позволяющих на основе многостороннего анализа оценивать качество получаемого прогноза. Чаще осуществляется оценка метода прогнозирования, с помощью которого получен результат, чем оценка качества самого результата. Это связано с тем, что не найдено эффективного подхода к оценке качества прогноза до его реализации.

studfiles.net

Методы простой экстраполяции

Археология Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика

Метод среднего уровня ряда – прогнозируемый уровень изучаемой величины принимается равным среднему значению уровней ряда этой величины в прошлом. Этот метод используется, если средний уровень не имеет тенденции к изменению, или это изменение незначительно (нет явно выраженного тренда, рисунок 32А)   (59)   Где yi – значение iого уровня n – база прогноза В некотором смысле отрезок динамического ряда, охваченный наблюдением, можно уподобить выборке, а значит полученный прогноз будет выборочным, для которого можно указать доверительный интервал   (60)   где (61) – среднеквадратичное отклонение временного ряда   tα–критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n1).   Пример. В таблице 63 приведены данные временного ряда y(t). Рассчитать прогнозное значение y на момент времени t =13 методом среднего уровня ряда   Таблица 63. Результаты расчетов   t yi   прогноз         (80+98)/2 (80+98+94)/3 90,7 (80+98+94+103)/4 93,8 (80+98+94+103+84)/5 91,8 (80+98+94+103+84+115)/6 95,7 (80+98+94+103+84+115+98)/7 96,0 (80+98+94+103+84+115+98+113)/8 98,1 (80+98+94+103+84+115+98+113+114)/9 99,9 (80+98+94+103+84+115+98+113+114+87)/10 98,6 (80+98+94+103+84+115+98+113+114+87+107)/11 99,4   (80+98+94+103+84+115+98+113+114+87+107+85)/12 98,2     Рисунок 34. Методы простой экстраполяции   Доверительный интервал для прогноза в момент t =13 приведен в таблице 64   Таблица 64. Результаты статобработки   yпрог n t0.05 s Нижний предел 95ДИ% Верхний предел 95ДИ% 98,2 2,2 12,4 69,7 126,7                 Метод скользящих средних– метод прогнозирования на краткосрочный период, основан на процедуре сглаживания уровней изучаемой величины (фильтрации). Преимущественно используются линейные фильтры сглаживания с интервалом m т.е.   (62)   Доверительный интервал (63)   Где – среднеквадратичное отклонение временного ряда (64) tα–критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n1).   Пример. В таблице 65 приведены данные временного ряда y(t). Рассчитать прогнозное значение y на момент времени t =13 методом скользящих средних с интервалом сглаживания m=3. Таблица 65. Результаты расчетов   t yi   прогноз             (80+98+94)/3 90,7 (98+94+103)/3 98,3 (94+103+84)/3 93,7 (103+84+115)/3 100,7 (84+115+98)/3 (115+98+113)/3 108,7 (98+113+114)/3 108,3 (113+114+87)/3 104,7 (114+87+107)/3 102,7 прогноз (87+107+85)/3   Исходный и сглаженный ряд представлены на рисунке 35     Рисунок 35. Метод скользящих средних   Таблица 66. Результаты статобработки   yпрог n m t0.05 s Нижний предел 95ДИ% Верхний предел 95ДИ% 2,2 12,4 61,4 124,6                   Метод экспоненциального сглаживания –в процессе выравнивания каждого уровня используются значения предыдущих уровней, взятых с определенным весом. По мере удаления от какогото уровня вес этого наблюдения уменьшается. Сглаженное значение уровня на момент времени t определяется по формуле   (65)   где St – текущее сглаженное значение; yt – текущее значение исходного ряда; St – 1 – предыдущее сглаженное значение; α сглаживающая параметр S0 берется равным среднему арифметическому нескольких первых значений ряда Для расчета α предложена следующая формула   (66)   По поводу выбора α нет единого мнения, эта задача оптимизации модели пока еще не решена. В некоторых литературных источниках рекомендуется выбирать 0,1 ≤ α ≤ 0,3. Прогноз рассчитывается следующим образом   (67)   Доверительный интервал   (68)   Пример. Рассчитать прогнозное значение y на момент времени t =11 методом экспоненциального сглаживания. Зададим α=0,3, S0 – среднее значение по трем первым членам ряда. Таблица 67. Результаты расчетов   t yi   St   (80+98+94)/3 90,7 0,3*80+(10,3)*90,7 87,5 0,3*98+(10,3)*87,5 90,6 0,3*94+(10,3)*90,6 91,6 0,3*103+(10,3)*91,6 95,0 0,3*84+(10,3)*95 91,7 0,3*115+(10,3)*91,7 98,7 0,3*98+(10,3)*98,7 98,5 0,3*113+(10,3)*98,5 102,8 0,3*114+(10,3)*102,8 106,2 0,3*87+(10,3)*106,2 100,4 0,3*107+(10,3)*100,4 102,4 0,3*85+(10,3)*102,4 97,2 прогноз 97,2+0,3*(8597,2) 93,5   Рисунок 36. Метод экспоненциального сглаживания   Таблица 68. Результаты статобработки yпрог n α t0.05 s Нижний предел 95ДИ% Верхний предел 95ДИ% 93,5 0,3 2,2 12,4 63,8 123,2     Рассмотренные методы прогнозирования являются простейшими, и в тоже время самыми приближенными – это видно из широких доверительных интервалов в приведенных примерах. Большая погрешность прогноза наблюдается в случае сильных колебаний уровней. Также неправомерно использовать эти методы при наличии явной тенденции к росту (или падению) исходного временного ряда. Но все же для краткосрочных прогнозов их применение бывает оправданным.

studopedya.ru

22. Методы экстраполяции, достоинства и недостатки

Экстраполяция

сущность в анализе развития объекта прогнозирования во времени и распространения, продления особенностей развития этого объекта из прошлого/настоящего в будущее. То есть какие факторы и условия (природные, экономические, социальные, экологические, политические, рыночные, правовые, инвестиционные и т.д.) оказывали влияние на развитие объекта в прошлом и настоящем такие же оказывают влияние и в будущем. Исходной информацией для методов экстраполяции являются временные ряды. Временной рядимеет вид таблицы, когда каждому временному отрезку соответствует значение какого-то показателя. Для применения методов экстраполяции необходимо иметь временной ряд не менее, чем за 4 временных отрезка. Для применения методов экстраполяции необходима точная и достоверная статистическая информация, а развитие объекта можно охарактеризовать плавной линией (линией тренда). К условием применения методов экстраполяции можно отнести отсутствие форс-мажорных обстоятельств. Достоинство методов экстраполяции это простота, точность, а недостаток – это большое количество условий для применения. Мы не можем применять метод экстраполяции на объекте, по которому нет статистической информации.

Метод скользящих средних — Этот метод применятся когда нет четкой зависимости значения показателя от времени

Метод наименьших квадратов – выполняется с помощью расчетов среднего арифметического значения.

Метод экспоненциального сглаживания – позволяет давать обоснованные прогнозы на основании временных рядов, имеющих хорошую связь между показателями и временным отрезком.

Метод исторических и географических аналогий –это метод прогнозирования по образцу, по аналогии. Основной принцип географич аналогий состоит в том что прогнозирование использования зем ресурсов проводится и выполняется на основе уже выполненного прогноза в регионе или в городе с аналогичными географическими условиями плюс поправки. А метод исторических аналогий заключается в сопоставлении прогноза который был сделан в прошлом на этот же объект плюс поправки.

Классификация методов экстраполяции:

Метод простой экстраполяции – предполагает расчет простого среднего значения, который закладывается в основу прогноза.

Метод аналитического выравнивания – нахождение математической функции, которая наиболее точно описывает особенности развития объекта. Основными этапами аналитического выравнивания является выбор формы кривой, отражающей особенности развития объекта, а так же важными этапами является определение показателей , дающих показательную характеристику этим изменениям. Выбор формы кривой можно осуществить на основе построения графика.

23. Методы моделирования, классификация, особенности

Моделирование

Это научные методы отражающие как одни так и другие многосторонние связи, учет влияния различных факторов. Метолы моделирования позволяют давать обоснованные прогнозы для объектов не имеющих статистическую информацию для объектов развитие которых можно охарактеризовать не плавной траекторией а скачкообразной (с резкими колебаниями показателей).

Модель (с лат. Образец) эконом модель приставляет собой условный образ объекта и детальную информатизацию его элементов. Сложились требования к экономич моделям:

ограниченность времени решения

Устойчивость к ошибкам в исходных данных

Удобство для последующего математич описания. Варианты прогнозов можно рассматривать по одному уравнению, а можно и по множеству. Причем количество уравнений не влияет на качество прогнозов.

Структурное моделирование – строится на основе специальных метрик и мер близости, с помощью которых можно выделять качественно однородные группы на основе большего числа признаков. Структурное моделирование очень тесно связано с методом пастеризации.

Сетевое моделирование – в основу этого метода положено построение сетевого графика, который имеет множество разновидностей.

Самыми точными методами моделирования являются экономико-математические. Наиболее разработанными являются детерминированные экономико-математические методы, решаемые с помощью симплекс метода. В настоящее время особую популярность набирает нейросетевое моделирование. Эта группа методов позволяет математически описывать сложные объекты, процессы, показатели которых имеют разную размерность, а так же показатели имеют и количественные, и качественные. Нейросетевое моделирование позволяет решать множество экономических задач и получать множество прогнозов, так как в основе нейросетей лежать не статистические и линейные модели, а гибкие нелинейные нейросетевые модели.

Эконом модель после ее матем обработки называется ЭММ. Существуют различные методы моделирования, например статистическое.

studfiles.net