Задача №18. Расчёт относительных показателей динамики
Имеются следующие данные о производстве одной из моделей iPhone компанией Apple за 2013 год:
| I квартал | II квартал | III квартал | IV квартал | |
|---|---|---|---|---|
| Произведено смартфонов, млн. штук | 82,0 | 75,3 | 60,1 | 50,8 |
Определите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь.
Решение:
Относительная величина динамики характеризует развитие изучаемого явления во времени.
Относительный показатель динамики (ОПД) представляет собой отношение уровня изучаемого процесса или явления за данный период времени и уровня этого же процесса или явления в прошлом:
Относительный показатель динамики с переменной базой сравнения рассчитывается тогда, когда происходит сравнение с предыдущим уровнем. Его ещё также называют цепным темпом роста, так как основание относительной величины последовательно меняется. Темп роста может быть выражен в процентах или коэффициентах.
где
уi – уровень текущего периода,
уi-1 – уровень предшествующего периода.
Относительный показатель динамики с постоянной базой (базисный) рассчитывается тогда, когда происходит сравнение с одним и тем же базисным уровнем. Его ещё также называют базисным темпом роста. Темп роста может быть выражен в процентах или коэффициентах.
где
у0 – уровень базисного периода.
| I квартал | II квартал | III квартал | IV квартал | |
|---|---|---|---|---|
| Произведено смартфонов, млн. штук | 82,0 | 75,3 | 60,1 | 50,8 |
| Темп роста базисный, % | 100,0 | 91,8 | 73,3 | 62,0 |
| Темп роста цепной, % | — | 91,8 | 79,8 | 84,5 |
Из полученных базисных относительных величин динамики (темпов роста) видно, что за 2013 год объём производства смартфонов Apple неуклонно снижалось от квартала к кварталу:
91,8 ˃ 73,3 ˃ 62,0
Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходил спад производства.
Такое решение компании, возможно, вызвано тем, что спрос на устройства данной модели упал в связи с появлением новой более современной модели.
Между относительными показателями динамики с переменной и постоянной базой сравнения существует взаимосвязь: произведение цепных темпов роста (в коэффициентах) равно конечному базисному.
Так, для рассчитанных показателей получим:
0,918 * 0,798 * 0,845 = 0,619 ≈ 0,62.
ecson.ru
23. Относительные показатели динамики, показатели плана и реализации плана, связь между ними.
Относительный показатель динамики (ОПД) – характеризует динамику процесса, т.е. изменения во времени. Это отношение уровня (значения) показателя в более поздний период к уровню этого показателя в более ранний период.
ОПД= Текущий уровень/Предшествующий или Базовый уровень
Относительный показатель плана (прогноза) (ОПП) – характеризует планируемое (прогнозируемое) изменение показателя:
ОПП=Уровень,планируемй на (i+1) период/Уровень,достигнутый в i-ом периоде
Относительный показатель реализации плана (ОПРП) – отражает изменение фактического (достигнутого) уровня по сравнению с планом:
ОПРП= Уровень,достигнутый в( i+1) периоде/ Уровень,планируемй на (i+1) период
Между относительными показателями динамики, плана и реализации плана существует взаимосвязь:
ОПД= ОПП*ОПРП
24.Относительные показатели сравнения и интенсивности.
Относительный показатель интенсивности и уровня экономического развития (ОПИ) – представляет собой степень распространения или развития какого-либо явления в определенной среде.
ОПИ=Показатель, хар-щий явление А/Показатель,хар-щий среду распространения явления А
Эти показатели определяются сопоставлением разноименных, но связанных между собой абсолютных величин: фондоотдача, фондоемкость, плотность населения на один кв.км., число автомашин на сто семей и т.д.
Разновидностью этих показателей является относительные показатели уровня экономического развития. Они характеризуют размеры производства различных видов продукции на душу населения (среднедушевой уровень производства). При их вычислении необходимо годовой объем производства данного вида продукции разделить на среднегодовую численность населения за тот же год.
Относительные показатель сравнения (ОПСр) – отношение одноименных величин, относящихся к разным объектам или разным территориям и взятых за одно и тоже время.
ОПСр=Показатель, хар-щий объект А/Показатель, хар-щий объект В
25.Относительные показатели структуры и координации уровня экономического сравнения.
Относительный показатель структуры (ОПС) – это отношение части к целому. Он характеризует структуру совокупности и показывает какую долю (или удельный вес) во всей совокупности составляет отдельная ее часть: удельный вес женщин, мужчин, малых предприятий, частных предприятий.
ОПС=Показатель, хар-щий часть совокупности/Показатель по всей совокупности в целом
Изменения во времени ОПС, а также изменения части и целого, на основании которых рассчитан ОПС, связаны между собой следующим соотношением:
ОПД(ОПС)=ОПД(части)/ОПД(целого)
То есть относительная величина динамики, вычисленная для доли равна отношению относительной величина динамики, вычисленной для части и целого.
Относительный показатель координации (ОПК) – это отношение одной части совокупности к другой части этой же совокупности, обычно той части, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной точки зрения.
ОПК=Показатель,хар-щий одну часть совокупности/Показатель,хар-щий другую часть совокупности
studfiles.net
39. Статистические показатели динамики
Показатели динамики – это показатели, характеризующие изменение во времени уровней ряда. К ним относятся: абсолютный прирост, темп роста, темп прироста и абсолютное значение одного процента прироста, пункт роста.
1) Абсолютный прирост – определяется, как разность между текущим и базисным уровнями динамического ряда и показывает на сколько текущий уровень превышает базисный. Базисный абсолютный прирост вычисляется по формуле: DYiб =Yi-Y0; цепной абсолютный прирост: DYiц= Yi-Yi-1.
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному приросту последнего периода (момента) времени.
2) Темп роста — определяется как отношение текущего уровня к базисному и показывает, во сколько раз текущий уровень превышает базисный.
а)
базисный:  б)
цепной:
б)
цепной:
Между цепными и базисным коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь промежуток времени; а частное от деления текущего базисного коэффициента роста на предыдущий базисный коэффициент роста равно текущему цепному коэффициенту роста.
3) Темп прироста — показывает, на сколько процентов уровень текущего периода (момента) времени больше (или меньше) базисного уровня.
Базисный: Цепной:
4) Абсолютное значение 1% прироста — рассчитывается как отношение абсолютного цепного прироста к цепному темпу прироста за тот же период времени. Используется для правильной оценки значения полученного темпа прироста. Аi показывает какое абсолютное значение скрывается за относительным показателем 1% прироста.
40. Средние показатели ряда динамики
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели динамики: средний уровень ряда и средние показатели изменения уровней ряда.
Средние уровни ряда определяются для интервальных рядов с равноотстоящими интервалами по формуле средней арифметической простой
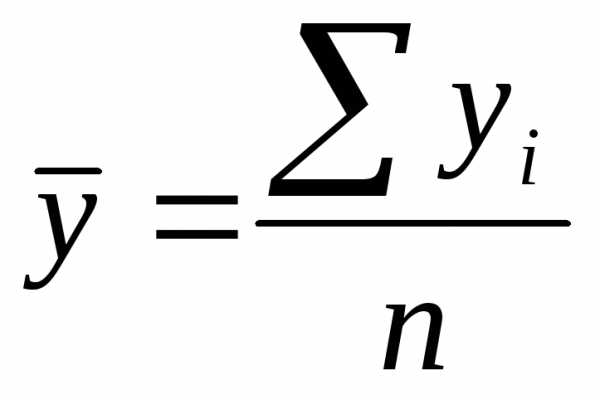 ;
n
– число уровней ряда
;
n
– число уровней ряда
Для интервального ряда с неравноотстоящими интервалами средние уровни ряда определяется по формуле средней арифметической взвешенной
 ;
; 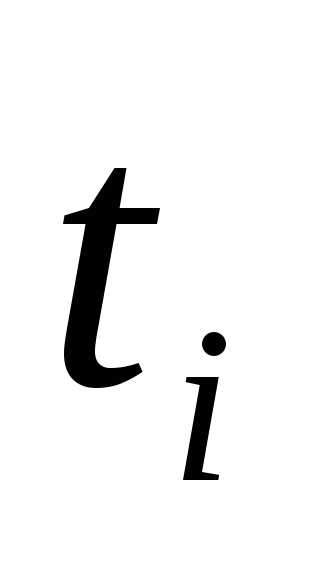 — длительность интервала времени между
уровнями
— длительность интервала времени между
уровнями
Для моментных рядов с равноотстоящими интервалами средние уровни ряда определяются по формуле средней хронологической простой
; n – количество дат
Для моментных рядов с неравноотстоящими датами средние уровни ряда определяются по формуле средней хронологической взвешенной
 —
период времени между двумя смежными
датами
—
период времени между двумя смежными
датами
Средние показатели изменения уровней ряда рассчитываются усреднением цепных показателей динамики.
1)
Средний абсолютный прирост определяется как простая средняя
арифметическая величина из цепных
абсолютных приростов и показывает, на
сколько в среднем изменялся показатель
в течение изучаемого периода времени: 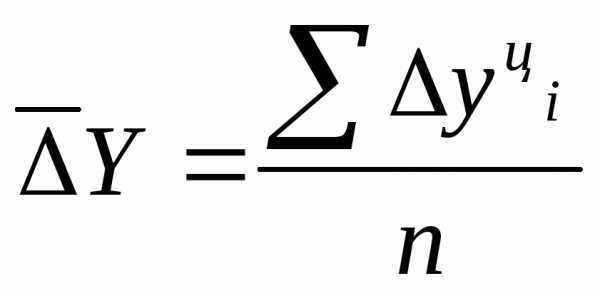
2) Средний темп роста определяется как средняя геометрическая из цепных темпов роста и показывает, сколько процентов в среднем составлял рост показателя.
,
где n – количество периодов времени.
4. Средний темп прироста показывает на сколько процентов в среднем рос показатель в течение изучаемого периода времени.
24.Относительные величины динамики.
Относительные статистические величины— это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.
Относительные показатели — представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений.
Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) и уровня этого же процесса или явления в прошлом:
ОПД = Текущий уровень / Предшествующий или базисный уровень
ОПД = ОПП * ОПРП
ОПД может быть с постоянной базой – базисный, и переменной –цепной.
Относительная величина динамики характеризует интенсивность, структуру, динамику экономических явлений, показывает во сколько раз текущий уровень превышает предшествующий (базисный).
Величина динамики называется коэффициентом роста, если выражена кратным отношением, или темпом роста, если выражена в процентах. Относительная величина динамики характеризует скорость развития явления или темпы изменения явления во времени.
Темп роста (Тр) – интенсивность изменения уровней ряда динамики. Представляет собой всегда положительное число и выражается в процентах.
Цепной: Тр = yi/yi-1*100%
Базисный: Тр = yi/y1*100%
Темп прироста (Тпр) определяется для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах.
Цепной: Тпр=Трцепной-100%
Базисный: Тпр=Трбазисный-100%
Относительные величины планового задания и выполнения плана.
Относительные статистические величины— это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.
Относительные показатели — представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений.
Относительные показатели плана (ОПП)характеризует напряженность, т.е. во сколько раз намечаемый объем производства (или какой-либо финансовый результат деятельности предприятия) превысит достигнутый уровень или сколько процентов от этого уровня составит.
ОПП = уровень, планируемый на (i+1)-й период / уровень, достигнутый в i-м периоде
Относительная величина планового задания (показатель планового задания) представляет собой отношение планируемого уровня показателя к его уровню, достигнутому в предыдущем периоде (или в периоде, рассматриваемом как базисный).
Относительная величина планового задания характеризует перспективу развития явления ОВПЗ = плановый уровень на будущий (следующий) период / фактический уровень текущего (предыдущего) периода
Относительная величина выполнения плана (показатель выполнения плана) характеризует степень реализации плана.
ОВВП = фактический уровень текущего периода / план текущего периода
Между и Относительной величиной планового задания и относительной величиной выполнения плана существует взаимосвязь выраженная в формуле: ОВВП = ОВД / ОВПЗ.
Относительные величины структуры.
Относительные статистические величины— это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.
Относительные показатели — представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений.
Относительный показатель структуры (ОПС)представляет собой соотношение структурных частей изучаемого объекта и их целого:
ОПС = показатель, характеризующий часть совокупности / показатель по всей совокупности в целом (*100%)
Относительные величины структуры характеризуют состав изучаемых совокупностей. Исчисляются они как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. как отношение части к целому, и представляют собой удельный вес части в целом. Как правило, относительные величины структуры выражаются в процентах (база сравнения принимается за 100). Показатели структуры могут быть выражены также в долях (база сравнения принимается за 1).
Сравнивая структуру одной и той же совокупности за разные периоды времени, можно проследить структурные изменения, происшедшие во времени.
Относительные величины координации и интенсивности.
Относительные статистические величины— это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.
Относительные показатели — представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений.
Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:
ОПК = показатель, характеризующий i-ю часть совокупности / показатель, характеризующий часть совокупности выбранную в качестве базы сравнения
Относительный показатель интенсивности (ОПИ)характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
ОПИ = показатель, характеризующий явление А / показатель, характеризующий среду распространения явления A
Относительная величина интенсивности выражается в процентах, промилле или может быть именованной величиной. Схема расчета диктуется сутью экономического показателя. Примерами данной величину являются: выход сельскохозяйственной продукции в расчете на 1000 га пашки, величина розничного товарооборота в расчете на 1 кв.метр торговой площади, и др. Такие показатели отражают объем количественного показателя деятельности организации по отношению к величине имеющихся в распоряжении организации пассивных основных фондов.
Разновидность ОПИ — Относительный показатель уровня экономического развития, характеризующий производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства.
Виды средних величин. 29. Понятие и назначение средних величин в статистике. 30. Средняя арифметическая и средняя гармоническая величины. 31. Средняя геометрическая, хронологическая величины. 32. Мода и медиана.
Средней величинойназывается статистический показатель, который дает обобщенную характеристикуварьирующего признакаоднородныхединиц совокупности.
Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.
Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Средняя агрегатная:
,где wi = xifi, xi– i-й вариант осредняемого признака, fi – вес i-ого варианта
Заработная плата одного рабочего = Совокупность фондов з.п. / общая численность рабочих предприятия
Виды средних величин
Средние величины делятся на два больших класса: степенные средние и структурные средние
Степенные средние:
Средняя арифметическая — используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Эта средняя используется, когда веса (f) отсутствуют (каждый вариант признака повторяется только один раз) или равны между собой.
где n – численность совокупностей
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническаяиспользуется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая — со скоростью 100 км/ч, вторая — 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000).
Дляпростой средней геометрической
, где nxi – x1*x2*…*xn
Длявзвешенной средней геометрической
, где nxi –
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).
Формулапростой средней квадратической
Формулавзвешенной средней квадратической
Средняя хронологическая (даны показатели за год, и присутствует месяц следующего года)
Средняя хронологическая простая:
Средняя хронологическая взвешенная:
Структурные средние:
Мода (Mо) – значение признака наиболее часто встречающегося в исследуемой совокупности, т.е. это одна из вариантов признака, которая в ряду распределения имеет наибольшую частоту (частость).
В дискретном ряду мода определяется визуально по максимальной частоте или частости.
В интервальном ряду по наибольшей частоте определяется модальный интервал, а конкретное значение моды в интервале рассчитывается по формуле: где,x0 и h – соответственно нижняя граница и величина модального интервала. FМо fМо-1 fМо+1 — частоты модального, предмодального и послемодального интервалов.
Медиана (Ме) – значение признака (варианта), приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части.
Медиана, как и мода, не зависит от крайних значений вариантов, поэтому меняется для характеристики центра в ряду распределения с неопределенными границами.
Для определения медианы в ранжированном ряду необходимо вначале найти номер медианы затем используются кумулятивные частотыSi(частость Sd).
В дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
(Нечетное число = среднее значение, четное число = полу сумма двух средних членов).
В интервальном вариационном ряду распределения медиана находится по формуле
В симметричных рядах распределения значения моды и медианы совпадают со средней величиной, а в умеренно ассиметричных они соотносятся как: 3(x-Ме)~x-Mо
Выбор формы средней величины зависит от исходной базы расчета средней и от имеющейся экономической информации для ее расчета.
Исходной базой расчета и ориентиром правильности выбора формы средней величины являются экономические соотношения, выражающие смысл средних величин и взаимосвязь между показателями.
studfiles.net
Абсолютные и относительные показатели рядов динамики.
Динамический ряд представляет собой ряд последовательных уровней, сопоставляя которые между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Если сравнению подлежат несколько последовательных уровней, то возможны следующие два варианта сопоставления:
1) каждый уровень ряда динамики сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. В качестве базисного уровня (базы сравнения) выбирается либо начальный уровень ряда динамики или же уровень, с которого начинается какой-то новый этап развития явления. Такое сравнение называется сравнением с постоянной базой;
2) каждый уровень ряда динамики сравнивается с непосредственно ему предшествующим. Такое сравнение называется сравнением с переменной базой.
Показатели динамики с постоянной базой – базисные показатели – характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i-гo) периода.
Показатели динамики с переменной базой – цепные показатели – характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
Абсолютный прирост определяется как разность между двумя уровнями ряда динамики и показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:
базисный абсолютный прирост: (11.1)
цепной абсолютный прирост: (11.2)
где – уровень сравниваемого периода;
– уровень базисного периода;
– уровень непосредственно предшествующего периода.
Темп роста определяется как отношение двух сравниваемых уровней, может быть выражен с помощью коэффициентов (коэффициент роста ) или в процентах, и показывает, во сколько раз данный уровень превышает уровень базисного периода:
базисный коэффициент роста: ; (11.3)
цепной коэффициент роста: ; (11.4)
базисный темп роста: ; (11.5)
цепной темп роста: . (11.6)
Темп прироста показывает на сколько процентов уровень данного периода больше (или меньше) базисного уровня:
базисный темп прироста: (11.7)
цепной темп прироста: (11.8)
При анализе относительных показателей ряда динамики (темпов роста и темпов прироста) не следует рассматривать их изолированно от абсолютных показателей (уровней ряда и абсолютных приростов) Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением одного процента прироста. Этот показатель рассчитывают как отношение абсолютного прироста к темпу прироста (в процентах) за тот же период времени:
(11.9)
Рассмотрим расчет вышеуказанных показателей по ряду динамики производства электроэнергии, представленному в табл. 11.4.
Таблица 11.4
Производство электроэнергии
Годы | Производство эл. энергии, млрд. кВт | Абсолютный прирост | Темп роста | Темп прироста | |||
базисный | цепной | базисный | цепной | базисный | цепной | ||
1990 | 1300 | — | — | 100,0 | 100,0 | — | — |
1991 | 1325 | 25 | 25 | 101,9 | 101,9 | 1,9 | 1,9 |
1992 | 1400 | 100 | 75 | 107,9 | 105,7 | 7,9 | 5,7 |
1993 | 1450 | 150 | 50 | 111,6 | 103,6 | 11,6 | 3,6 |
1994 | 1570 | 270 | 120 | 116,9 | 104,8 | 16,9 | 4,8 |
1995 | 1600 | 300 | 30 | 123,1 | 105,3 | 23,1 | 5,3 |
1996 | 1850 | 550 | 250 | 142,3 | 115,6 | 42,1 | 15,6 |
1. Определим абсолютный прирост.
Базисный:
Абсолютный прирост производства электроэнергии в 1992 г по сравнению с 1990 г составил 100 млрд. кВт.
Цепной:
Абсолютный прирост производства электроэнергии в 1992 г по сравнению с 1991 г составил 75 млрд. кВт.
Результаты расчета приведены в табл. 11.4.
2. Определим темп роста производства электроэнергии:
Производство электроэнергии в 1992 году по сравнению с 1990г. возросло до 107,9 %.
Результаты расчета приведены в табл. 22.
3. Определим темп прироста производства электроэнергии:
100 млрд. кВт электроэнергии произведенной в 1992 году дали 7,9% прироста.
4. Определим абсолютное значение одного процента прироста производства электроэнергии:
Абсолютное значение одного процента прироста в 1992 г. составило 13,25 млрд. кВт электроэнергии.
www.ekonomstat.ru
ОПД, ОПП и ОПРП, ОПС, ОПК, ОПИ, ОПСР.
Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.
По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня экономического развития, сравнения.
1. Относительный показатель динамики характеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде.
Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения).
2. Относительный показатель плана (прогноза) и выполнения плана. Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом:
Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.
3. Относительные показатели структуры (ОПС) характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:
ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию.
Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части, например: при изучении состава населения по различным признакам (возрасту, образованию, национальности и др.).
4. Относительные показатели координации (ОПК) характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или являющаяся приоритетной в совокупности.
5. Относительные показатели интенсивности и уровня экономического развития (ОПИ) характеризуют степень распространения или уровень развития изучаемых явлений или процессов в определённой среде и образуются как результат сравнения разноименных, но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:
ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек.
6. Относительные показатели сравнения (ОПСр) характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но за одинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.
С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д.
www.ekonomstat.ru
33. Абсолютные и относительные показатели анализа рядов динамики.
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчёта показателей динамики.Анализ интенсивности изменения во времени осуществляется с помощью показателей,получаемых в результате сравнения уровней между собой.
К таким показателям относят:
1.Абсолютный прирост- абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени(+,-,0)
2.Темп роста- относит. показатель, характеризующий интенсивность процесса роста или снижения. Он хар-ет относит. скорость изменения уровня ряда в единицу времени. Всегда представляет собой(+ число).
3.Темп прироста- относит. показатель, харак-ий величину прироста(+,-, или 1).
4.Абсолютное значение одного процента прироста- показывает какое значение скрывается за относит. показателем одного процента прироста.
Показатель анализа динамики может вычисляться на постоянной и переменной базе сравнения.
Для расчёта показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного уровня выбирается начальный уровень в ряду динамики.
Вычисленные при этом показатели называются — базисными.
Для расчёта показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим.
Вычисленные при этом показатели анализа динамики называют- ценными.
Таблица.
34. Система средних показателей рядов динамики.
Для обобщающей характеристики динамики исследуемого явления определяют средние уровни ряда и средние показатели изменения уровня ряда.
Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется:
1.а)Винтервальномряду динамикис равноотстоящими уровнямиво времени расчетсреднего уровня ряда ()производится по формуле средней арифметической простой:
где уi- абсолютные уровни ряда,n- число уровней ряда
Для интервальногоряда динамики снеравноотстоящими уровнями средний уровень рядавычисляется по формуле:
гдеti- длительность интервала по времени между смежными датами.
где t — число периодов времени, в течение которых уровень не изменяется.
б)Для моментного ряда сравноотстоящими уровнями средний уровень рядарассчитывается по формуле средней хронологической:
где n– число уровней ряда.
Средний уровеньмоментного рядасразноотстоящимиуровнями вычисляется по следующей формуле:
ti- интервал времени между смежными уровнями.
2.Средний абсолютный прирост –показатель, характеризующий среднюю абсолютную скорость роста (снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.д.). Определение среднего абсолютного прироста производится по формуле:
или,гдеn- число ценных абсолютных приростов в изучаемом периоде,
m- число уровней ряда в изучаемом периоде.
3.Средний темп роста –относительный показатель, выраженный в форме коэффициента и показывающий, во сколько раз увеличился уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежеквартально и т.п.). Среднегодовой темп роста вычисляется по формуле средней геометрической:
, или,
где m– число коэффициентов роста.
4.Средний темп прироста –относительный показатель, выраженный в процентах и показывающий, на сколько увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени ( в среднем ежегодно, ежемесячно и т.п.). Среднегодовой темп прироста получаем, вычтя из среднего темпа роста 100 %:
.
studfiles.net
