Как научить ребёнка быстро считать в уме с помощью счёт Абакус
Статья подготовлена при поддержке детского развивающего центра – London Express Junior.
По телевидению, обычно в выходной день, несколько каналов транслируют программы, в которых дети от двух лет и старше демонстрируют свои уникальные таланты, поражая и зрителей и жюри, если оно предусмотрено правилами проекта, и всё население страны. Кто-то выписывает замысловатые фигуры на роликах, кто-то навскидку может назвать столицу любого государства, кто-то декламирует по памяти стихи Пастернака, Цветаевой и Вознесенского, кто-то легко орудует кузнечными клещами и молотком. Это замечательно.
А вот некоторые детишки, чуть прикрыв глаза и совершая с виду хаотичные движения большим и указательным пальцами обеих рук, демонстрируют умение быстро считать в уме. Причём складывают, вычитают и перемножают не простые числа, а трёх и даже четырёхзначные. Со стороны это кажется волшебством, и многие родители, с восхищением уставившись в экран телевизора, задаются вопросом: как научить ребёнка быстро считать?
Многие после таких передач лезут в интернет и с удивлением узнают, что мудрые японцы и ещё более мудрые китайцы уже давно, пару тысячелетий, знают, как научить считать ребёнка в уме. Для этого они даже создали замечательные счёты Абакус, или Соробан по-японски, чем-то похожие на наши русские деревянные счёты, которые уже давно канули в лету, после изобретения калькуляторов, компьютеров и других умных гаджетов.
Чем хороша ментальная арифметика?
Счёты Абакус для развития логики
При помощи этого древнего метода можно за год-два научить ребёнка быстро и уверенно оперировать большими числами. Однако возникает справедливый вопрос: а не будет ли мозг малыша слишком занят математическими действиями, чтобы осталось место и время для других вещей?
Если включить логику и немного поразмыслить, то, глядя на азиатов, практикующих эту практику обучения не один век, становится понятно, что никаких побочных действий она не имеет. Мало этого, у детей, умеющих пользоваться счётами Абакус, отмечается:
- активизация зрительной и слуховой памяти.
- умение концентрироваться в нужный момент.
- усиление смекалки и интуиции.
- самостоятельность и уверенность.
- умение нестандартно мыслить.
- реализация способностей и успешная карьера.
- развитие творческого потенциала.
- развитие способности к изучению иностранных языков.
Список на первый взгляд абсолютно ничего общего с цифрами и математическими действиями не имеет. Но в этом и скрыта уникальность метода. Постоянные занятия на счётах Абакус позволяют наладить ускоренные связи между правым и левым полушариями мозга, одно из которых отвечает за логику, а второе за воображение. Именно на развитие воображения и сделан упор. А когда ребёнок способен логически объяснить то, что придумал – это уже не пустые фантазии – это изобретение, новация. Плюс отличная память, интуиция и концентрация. Мягко выражаясь, это не повредит. А если честно, то будет помогать всю дальнейшую жизнь.
Что такое счёты Абакус?
Классические счёты Абакус
Устройство, если этот термин здесь применим, довольно простое. Деревянная рамка, разделённая перекладиной на две неравные части. В верхней части ряд одиночных косточек, обозначающие пятёрки. В нижней части в каждом столбце по четыре косточки – единицы. Столбцы, справа налево обозначают последовательно единицы, десятки, сотни, тысячи и так далее. Манипулирование с косточками, помимо всего прочего, ещё и развивает у детей мелкую моторику, оказывая положительное влияние на центры речи.
Запоминается эта несложная конфигурация без труда и уже через несколько занятий ребёнок с успехом начинает постигать азы математики и может приступать к вычислениям.
Как проходит обучение
Обучение детей на счётах Абакус
Вопреки мнению некоторых специалистов, утверждающих, что счёты или линейка Абакус доступна только в возрасте от 5 до 11 лет, обучиться ментально считать можно даже в престарелом возрасте. Указанные возрастные ограничения являются оптимальными и именно в этот период приносят больше пользы не только в изучении математики. Начинать обучение раньше тоже не запрещается, а уж взрослому человеку освоить Абакус вообще не представляет никакой сложности. Другое дело, что менталитет и характер уже сформировался и кроме как быстро складывать и вычитать 40-летний человек больше ничему не научится.
С детьми другая история. На первых уроках они осваивают счёт непосредственно на самих счётах, перебирая костяшки пальчиками, что само по себе уже очень полезно. Как уже отмечалось, развивается мелкая моторика, полезная не только для суставов, но и речевых центров мозга. Мозг стимулируется, плюс его заставляют решать простенькие примеры, что тоже развивает внимание и память. Занятия обычно проводятся в игровой форме, чтобы не просто заинтересовать малыша, но и показать ему, что математика может быть абсолютно не скучной.
На втором этапе, когда ребёнок уже достаточно хорошо справляется с заданиями посчитать, сколько будет 234 прибавить 543 или из 421 вычесть 237 при помощи счётов, начинают делать упор на воображение. Малыш должен в уме представить счёты Абакус и мысленно передвигать костяшки. Дети уже привыкли делать это при помощи пальчиков и в большинстве случаев продолжают ими двигать в воздухе. Ни в коем случае нельзя заставлять их перестать это делать, а тем более убирать руки в карманы или за спину. Никакого вреда в этих непонятных постороннему человеку движениях нет, ребёнку так просто привычнее.
Обычно осваивается три математических действия: сложение, вычитание и умножение.
Может возникнуть вопрос: а как потом в школе учить таблицу умножения и не становится ли это требование учителей бесполезным? Абсолютно нет. Счёты Абакус учат оперировать многозначными числами, а сколько будет пятью пять или семью девять надо просто помнить. Как говориться одно другому не только не мешает, но дополняет.
Если вы отдали своего ребёнка в детский центр на изучение счёта при помощи линейки Абакус, будьте готовы немного удивиться. В отличие от спортивных секций и кружков всевозможной направленности ежедневных занятий здесь не понадобиться. Два часа один раз в неделю вполне достаточно, чтобы успешно постичь эту науку. Но главное, это выполнять домашние задания, которые будет давать преподаватель. Много времени на них тоже не понадобиться – 15-20 минут, но делать их надо обязательно. Постоянная практика, даже такая непродолжительная, позволит не просто сохранить полученные на занятиях навыки, но и усилить их. А дозированная и хорошо сбалансированная нагрузка на мозг ещё никому не вредила.
В хороших центрах, где работают опытные и квалифицированные педагоги, программа обучения ментальной арифметике корректируется, в зависимости от индивидуальных качеств ребёнка.
Немного из практики
Один небольшой пример для наглядности.
Итак, счёты Абакус состоят из:
- деревянной или пластмассовой рамки.
- разделительной перекладины.
- нижних косточек, означающих единицы.
- верхних косточек, означающих пятёрки.
Всё, больше ничего в них нет.
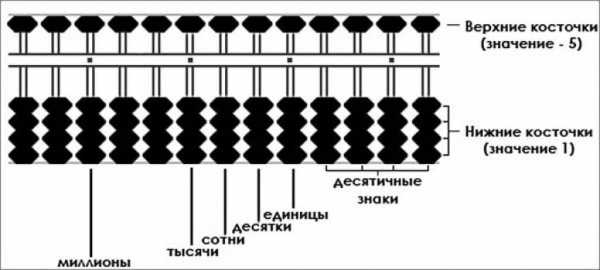
Расположение косточек на счетах Абакус
Теперь представим, как будет выглядеть на них число, например 375.
- на столбце с единицами опускаем верхнюю косточку к разделительной перекладине.
- на столбце с десятками проделываем тоже самое, но снизу поднимаем две косточки.
- в столбце сотни поднимаем три косточки.
Всё просто и понятно, не правда ли? Даже и добавить нечего.
Со сложением и вычитанием немного сложнее и лучше сначала посмотреть, как это делает опытный счетовод, который ещё и сможет всё доступно объяснить. Визуализация на первом этапе обучения просто необходима.
Внимательные и заинтересованные читатели, наверняка, уже давно решили, что обучение ребёнка математике на счётах Абакус полезно, с какой стороны не погляди. И пусть он не станет у вас выдающимся учёным, который будет играючи оперировать многозначными числами и сыпать многоуровневыми формулами. Обучение пригодится и в других сферах деятельности, ведь внимательность, хорошая память, уверенность в себе, способность нестандартно решать любые проблемы – это залог успешной карьеры и счастливой жизни.
detstvodetstvo.ru
| Сведение счЁтов или счетОв? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Top of Page | Разработано LiveJournal.com |
pishu-pravilno.livejournal.com
Как считать на счетах | Рождённые в СССР
Здравствуйте, дорогие читатели! Я заметил, что современные дети почти разучились совершать в уме простейшие арифметические действия. До того дошло, что вполне обычной стала картина: стоит стайка сорванцов в магазине с пакетами чипсов и мороженым в общей на всех корзинке – и нетерпеливо наблюдает за несложными манипуляциями самого смышленого их собрата. А тот с помощью смартфона высчитывает, хватит ли им ещё и на бутылку «Кока-колы». Да-а, представляю удивление ребят, если бы их любимая Марь Иванна заявила на очередном уроке математики: «А сегодня мы узнаем, как считать на счетах!»
Но ведь, скорее всего, многие из сегодняшних школьников и не слыхивали, что это за диво такое – деревянные счеты. А я помню, как весело было стучать приятными на ощупь костяшками и представлять себя самым важным по детскому разумению человеком в магазине – кассиром, счастливым обладателем больших, «настоящих» счетов! Можно было целый час простоять рядом с кассой, завороженно наблюдая, как кошка за мышкиной беготней, за веселыми деревяшками под ловкими пальцами молодой кассирши, резво облетающими счеты. Как считать, она, конечно, ни на секунду не задумывалась, это же было основным навыком в её профессии.
Если вам удастся раздобыть счеты, или с детства оставили на память – давайте вместе попробуем вспомнить эти навыки. Хотя бы сложение и вычитание припомним, ведь умножение и деление – более сложные операции на этом инструменте. Хотя я слышал, что сейчас есть люди, желающие и находящие такую возможность, чтобы их детей обучали так называемой ментальной математике. Для этих целей они приобретают малышам счеты абакус. Как считать на них, и что это за счеты? Я думаю, информации на эту тему в сети хватает.
Мы же с вами попытаемся вспомнить уроки счета. Итак, как считать на счетах – инструкция ). Сначала «обнуляем» наши счеты, сбрасывая все кругляшки на правый край. Числа представлены костяшками над тем рядом, где их четыре. Располагаются по разрядам – от единиц над вышеупомянутым рядом разряды увеличиваются к десяткам, сотням и далее. Ниже единиц размещаются четверти, десятые и сотые. Почему центральные костяшки обычно окрашены в черный цвет? Для более удобной ориентации при счете.
Для сложения набираем число, скажем, 937. Для этого влево отбрасываем нужное количество костяшек соответствующего разряда. Теперь, чтобы прибавить к этому, допустим, число 134 – добавляем его поразрядно, начиная с младшего разряда. Это делается для того, чтобы если в одном из разрядов не хватает костяшек – оставить их в данном ряду в том количестве, которого не хватило, и прибавить одну костяшку в старшем над этим ряду.
Разность чисел можно вычислить похожим на нахождение суммы способом, сверху вниз. В ряду, где имеется недостаток костяшек, следует оставить их в количестве, равном 10 минус Х. За Х принимаем число недостающих костяшек и сдвигаем одну костяшку верхнего ряда вправо. Думаю, если вы проделывали эти манипуляции на вытащенных из закромов счетах – разобрались быстро. Но не торопитесь давать объявление: «Учим считать на счетах!» Вот научитесь самостоятельно умножать и делить на них – тогда пора обзаводиться учениками ).
А я во время нашего урока вспомнил еще одно применение этого инструмента для счета, не самое математическое, возможно. После уроков берешь возле пустынной асфальтовой дорожки с уклоном у троих друзей волшебные колесики – и вот уже только ветер свистит в ушах, да как! Считать на счетах любой может научиться, а вы попробуйте удержаться на четвереньках на этом предвестнике скейтборда!
up-partner.ru
Счеты Википедия
Простые счёты.Счёты (русские счёты) — простое механическое устройство (счётная доска с костями) для выполнения арифметических расчётов, согласно одной версии происходят от китайского счётного приспособления суаньпань, согласно другой имеют собственно русское происхождение.
Представляют собой раму, имеющую некоторое количество спиц; на них нанизаны костяшки, которых обычно по 10 штук. Счёты являются одним из ранних вычислительных устройств и вплоть до конца XX века массово использовались в торговле и бухгалтерском деле, пока их не заменили калькуляторы.
История[ | ]
Николаас Витсен в своё время на основе внешнего сходства с суаньпанем предположил, что счёты пришли из Китая через золотоордынских татар в XIV веке[1] и даже называет того, кто их впервые ввёл в России — первого из Строгановых[2]. Однако И. Г. Спасский указывает на отличия от суаньпаня, в частности, что в счётах использовалась десятичная система счисления[3]. Он считал, что счёты произошли от прибора «дощаный счёт», который по его предположению возник в Московском государстве в XVI веке[4].
Первое известное упоминание счётов встречается в «Переписной книге домовой казны патриарха Никона», составленной в 1658 году, где они называются «счоты»
Система счисления и система ирования[ | ]
В русских счётах применяется позиционная десятичная система счисления с непозиционным унарным ированием внутри каждого разряда.
Каждый ряд костяшек представляет собой числовой разряд, который вверх от спицы с четырьмя костяшками возрастает от единиц до сотен тысяч, а вниз — уменьшается от десятых до тысячных. Максимальное значение для каждого ряда — десять, умноженное на вес разряда (для разряда единиц максимальное значение — 10, если все костяшки отложены влево, для десятков — 100 и так далее). «Набор» числа осуществляется сдвиганием костяшек из правого края прута в левый.
Прут, на котором находятся всего 4 костяшки, использовался для расчётов в полушках. Одна полушка равнялась половине одной деньги, то есть четверти копейки. Соответственно, четыре костяшки составляли одну копейку [7]. Также этот прут использовался для перевода фунтов в пуды (1 пуд = 40 фунтов). Такж
ru-wiki.ru
Счёты Википедия
Простые счёты.Счёты (русские счёты) — простое механическое устройство (счётная доска с костями) для выполнения арифметических расчётов, согласно одной версии происходят от китайского счётного приспособления суаньпань, согласно другой имеют собственно русское происхождение.
Представляют собой раму, имеющую некоторое количество спиц; на них нанизаны костяшки, которых обычно по 10 штук. Счёты являются одним из ранних вычислительных устройств и вплоть до конца XX века массово использовались в торговле и бухгалтерском деле, пока их не заменили калькуляторы.
История[ | ]
Николаас Витсен в своё время на основе внешнего сходства с суаньпанем предположил, что счёты пришли из Китая через золотоордынских татар в XIV веке
Первое известное упоминание счётов встречается в «Переписной книге домовой казны патриарха Никона», составленной в 1658 году, где они называются «счоты»[5][6].
Система счисления и система ирования[ | ]
В русских счётах применяется позиционная десятичная система счисления с непозиционным унарным ированием внутри каждого разряда.
Каждый ряд костяшек представляет собой числовой разряд, который вверх от спицы с четырьмя костяшками возрастает от единиц до сотен тысяч, а вниз — уменьшается от десятых до тысячных. Максимальное значение для каждого ряда — десять, умноженное на вес разряда (для разряда единиц максимальное значение — 10, если все костяшки отложены влево, для десятков — 100 и так далее). «Набор» числа осуществляется сдвиганием костяшек из правого края прута в левый.
Прут, на котором находятся всего 4 костяшки, использовался для расчётов в полушках. Одна полушка равнялась половине одной деньги, то есть четверти копейки. Соответственно, четыре костяшки составляли одну копейку[7]. Также этот прут использовался для перевода фунтов в пуды (1 пуд = 40 фунтов). Также этот прут может служить разделителем целой и дробной частей набранного на с
ru-wiki.ru
Счёты — Википедия
Простые счёты.Счёты (русские счёты) — простое механическое устройство для произведения арифметических расчётов, усовершенствованный аналог римского абака, являются одним из первых вычислительных устройств.
Счёты представляют собой раму с нанизанными на спицы костяшками, обычно по 10 штук.[1]
Русские счёты появились на рубеже XV — XVI веков и вплоть до конца XX века массово использовались в торговле и бухгалтерском деле для арифметических расчётов. В конце XX века их заменили электронные калькуляторы.
Система счисления и система кодирования[править]
В русских счётах применяется десятичная система счисления с унарным кодированием (Unary Coded Decimal, UCD).
Каждый ряд костяшек представляет собой числовой разряд, причём вверх от прута с четырьмя костяшками разряд возрастает от единиц до сотен тысяч, а вниз — уменьшается от десятых до тысячных. Максимальное значение для каждого ряда — десять, умноженное на вес разряда (для разряда единиц максимальное значение — 10, если все костяшки отложены влево, для десятков — 100 и так далее). «Набор» числа осуществляется сдвиганием костяшек из правого края прута в левый.
Прут, на котором находятся всего 4 костяшки, использовался для расчётов в полушках. 1 полушка была равна половине деньги, то есть четверти копейки, соответственно, четыре костяшки составляли одну копейку[2]. Также этот прут использовался для перевода фунтов в пуды (1 пуд = 40 фунтов). Также этот прут может служить разделителем целой и дробной частей набранного на счётах числа, и в вычислениях не использоваться.
Таким образом, максимальное число, которое можно набрать на счётах с семью рядами целых чисел, составляет 11`111`111,110.
После добавления к девяти костяшкам одного разряда десятой костяшки производится операция записи единицы переноса в следующий разряд, состоящая из трёх действий:
- сдвигом влево одной костяшки к девяти костяшкам добавляется десятая костяшка;
- сдвигом вправо всех десяти костяшек предыдущий разряд обнуляется;
- сдвигом влево одной костяшки в следующий разряд записывается единица переноса.
Выполнением этого правила исключается любое неоднозначное представление чисел. С точки зрения теории систем счисления для действий в показательной единично кодированной десятичной позиционной системе счисления достаточно девяти костяшек, о чём пишет и Я. И. Перельман[3], при этом операция записи единицы переноса производилась бы за два действия вместо трёх действий:
- сдвигом влево одной костяшки в следующий разряд записывается единица переноса;
- сдвигом вправо девяти костяшек предыдущий разряд обнуляется;
но для удобства счета (в частности, чтобы удобно получать дополнение до 10, необходимое для переноса разряда при вычитании) в русских счётах было выбрано число костяшек равное десяти, что формально соответствует единичнокодированной одиннадцатиричной системе счисления.
Русские счёты и значения костей на каждой проволокеОбщие замечания[править]
С помощью счётов можно выполнять все четыре базовые арифметических операции в пределах разрядности счёт. Однако на практике удобно и быстро на счётах можно только складывать и вычитать; операция умножения на произвольное число достаточно сложна, а деление в общем виде, скорее всего, займёт больше времени, чем выполнение той же операции на бумаге (с помощью известного алгоритма «деления столбиком»). Впрочем, есть достаточно большое количество специальных случаев, когда счёты вполне применимы для умножения и деления.
Кроме того, нужно учитывать следующие моменты:
- Счёты в принципе не предназначены для манипуляций с отрицательными числами. Поэтому любые операции должны приводиться к положительным числам, а знак, если это необходимо, должен просто учитываться отдельно.
- В операциях умножения и деления учитывать положение десятичного разделителя для обоих операндов достаточно неудобно. Вследствие этого при выполнении умножения и деления десятичных дробей либо только второй, либо оба операнда приводятся к целому числу, то есть десятичный разделитель в них просто игнорируется. После выполнения операции положение десятичного разделителя восстанавливается вручную.
«Набор» числа[править]
Представление чисел на счётах и порядок набора описан выше. Здесь необходимо лишь отметить, что правило расположения разрядов числа на проволоках (то есть помещение единичного разряда непременно перед проволокой с четырьмя косточками) в практических расчётах часто бывает необязательно соблюдать. Более того, в процессе расчётов бывает удобно иногда вместо перенабора числа просто мысленно перенести разделитель целой и дробной части на другое место.
В некоторых руководствах по вычислениям на счётах рекомендуется следующее «усовершенствование»: просверлить в раме счётов слева ряд небольших отверстий, расположенных напротив промежутков между проволоками. При расчётах какой-либо предмет (гвоздик, разогнутая скрепка и т. п.) помещается в отверстие, находящееся напротив промежутка, в данный момент разделяющего единицы и десятые доли. Таким образом в любой момент положение десятичного разделителя явно отмечено и может быть легко изменено.
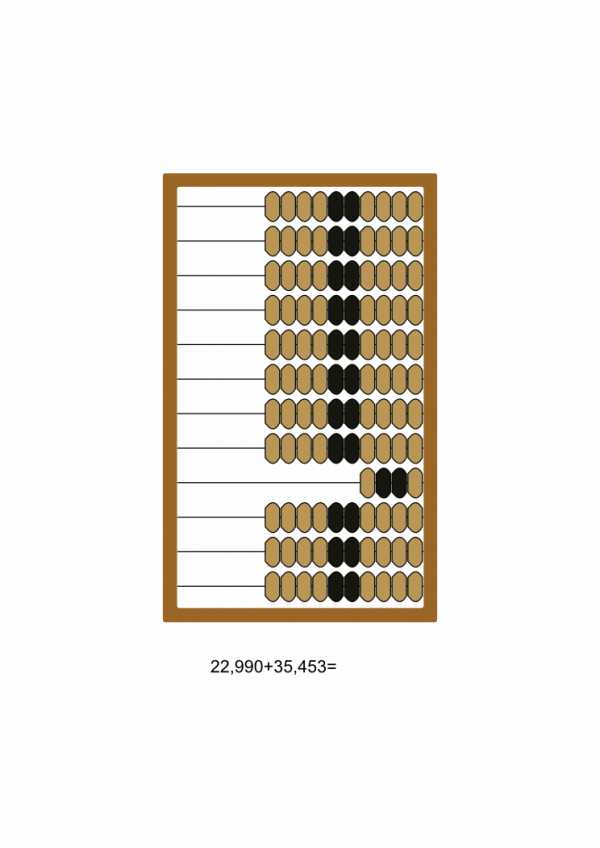Сложение на счётах от старших разрядов к младшимСложение[править]
Согласно одному из возможных способов, сложение на счётах выполняется «снизу вверх» (от младших разрядов к старшим). На счётах «набирается» первое слагаемое, после чего поразрядно, от младшего разряда к старшему, производятся следующие действия:
- На проволоке, соответствующей разряду, перебрасывается влево столько косточек, сколько единиц в соответствующем разряде второго слагаемого.
- Если на проволоке не хватает косточек для выполнения первого действия, то на проволоке слева оставляется столько косточек, сколько не хватило, а на следующей (находящейся выше) проволоке перебрасывается влево одна косточка.
- Если в результате действия (как первого, так и второго, и данного) слева на проволоке оказалось 10 косточек, то все косточки на этой проволоке перебрасываются вправо, а на следующей (находящейся выше) проволоке дополнительно перебрасывается влево одна косточка.
После того, как будут выполнены действия со всеми разрядами, «набранное» на счётах число и будет результатом сложения.
Есть и другой способ — сложение от старших разрядов к младшим[4], см. анимацию.
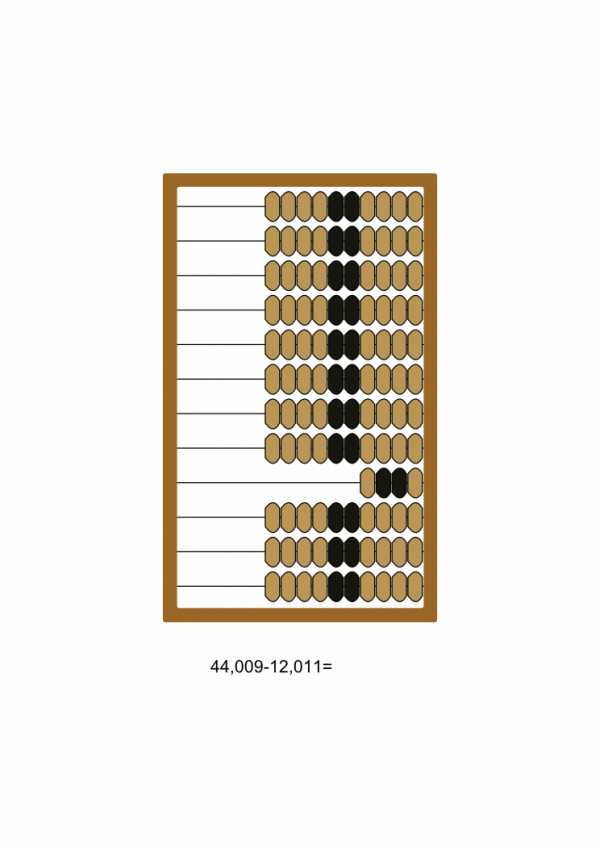Вычитание на счётахВычитание[править]
Вычитание на счётах выполняется «сверху вниз», то есть от старших разрядов к младшим. В силу неприспособленности счётов для работы с отрицательными числами всегда нужно из большего положительного числа вычитать меньшее положительное число. Если требуется вычесть из меньшего большее, числа следует поменять местами и оставить знак «в уме».
На счётах «набирается» уменьшаемое, после чего поразрядно, от старшего разряда к младшему, производятся следующие действия:
- На проволоке, соответствующей разряду, перебрасывается вправо столько косточек, сколько единиц в соответствующем разряде вычитаемого.
- Если на проволоке не хватает косточек для выполнения первого действия, производится перенос разряда: слева оставляется (10 — n) косточек, где n — «недостающее» число косточек (чтобы не делать второе вычитание в уме, можно весь десяток косточек на данной проволоке перенести влево, после чего отбросить недостающее число косточек), а на находящейся выше проволоке отбрасывается вправо одна косточка
- Если при переносе на проволоке, соответствующей старшему разряду, не хватает косточек, то выполняется перенос в следующий (ещё более старший) разряд и так до тех пор, пока на одной из проволок не окажется достаточного количества косточек. Так, например, при вычитании (1001 — 3) сначала на проволоке младшего разряда будет оставлено 8 косточек и потребуется перенос во второй разряд, затем — в третий, и только после этого на проволоке четвёртого разряда окажется достаточно косточек, чтобы завершить операцию.
Умножение[править]
Умножение на однозначное число в общем случае может быть заменено на сложение множимого с самим собой соответствующее количество раз. Целые многозначные числа перемножаются поразрядно, аналогично «умножению в столбик»:
- В качестве множимого выбирается то из двух чисел, которое содержит больше ненулевых цифр.
- Множимое прибавляется к самому себе столько раз, сколько единиц в младшем (первом) разряде множителя.
- Для каждого следующего разряда множителя множимое прибавляется к уже имеющемуся на счётах числу соответствующее количество раз, но со сдвигом на один разряд вверх. То есть для разряда десятков сложение производится со сдвигом на один разряд, сотен — н
www.wiki-wiki.ru
Счёты Википедия
Простые счёты.Счёты (русские счёты) — простое механическое устройство (счётная доска с костями) для выполнения арифметических расчётов, согласно одной версии происходят от китайского счётного приспособления суаньпань, согласно другой имеют собственно русское происхождение.
Представляют собой раму, имеющую некоторое количество спиц; на них нанизаны костяшки, которых обычно по 10 штук. Счёты являются одним из ранних вычислительных устройств и вплоть до конца XX века массово использовались в торговле и бухгалтерском деле, пока их не заменили калькуляторы.
В русских счётах применяется позиционная десятичная система счисления с непозиционным унарным кодированием внутри каждого разряда.
Каждый ряд костяшек представляет собой числовой разряд, который вверх от спицы с четырьмя костяшками возрастает от единиц до сотен тысяч, а вниз — уменьшается от десятых до тысячных. Максимальное значение для каждого ряда — десять, умноженное на вес разряда (для разряда единиц максимальное значение — 10, если все костяшки отложены влево, для десятков — 100 и так далее). «Набор» числа осуществляется сдвиганием костяшек из правого края прута в левый.
Прут, на котором находятся всего 4 костяшки, использовался для расчётов в полушках. Одна полушка равнялась половине одной деньги, то есть четверти копейки. Соответственно, четыре костяшки составляли одну копейку[7]. Также этот прут использовался для перевода фунтов в пуды (1 пуд = 40 фунтов). Также этот прут может служить разделителем целой и дробной частей набранного на счётах числа и в вычислениях не использоваться.
Таким образом, максимальное число, которое можно набрать на счётах с семью рядами целых чисел, составляет 11 111 111,110.
После добавления к девяти костяшкам одного разряда десятой костяшки производится операция записи единицы переноса в следующий разряд, состоящая из трёх действий:
- сдвигом влево одной костяшки к девяти костяшкам добавляется десятая костяшка;
- сдвигом вправо всех десяти костяшек предыдущий разряд обнуляется;
- сдвигом влево одной костяшки в следующий разряд записывается единица переноса.
Выполнением этого правила исключается любое неоднозначное представление чисел. С точки зрения теории систем счисления, для действий в показательной единично кодированной десятичной позиционной системе счисления достаточно девяти костяшек, о чём пишет и Я. И. Перельман[8], при этом операция записи единицы переноса производилась б
ruwikiorg.ru