Задачи с решениями по кривой производственных возможностей – Задача №139. Построение КПВ

Задача №139. Построение КПВ

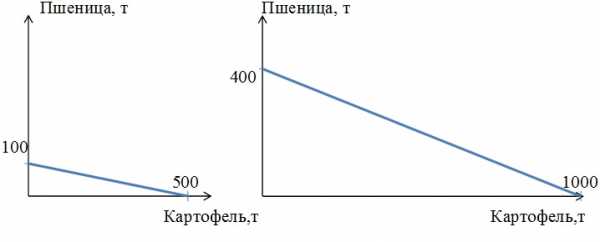
На одном поле фермер может произвести 500 т картофеля или 100 т пшеницы, а на другом альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля при максимальном производстве картофеля, равном 1000 т. Построить кривую производственных возможностей фермера.

 

Решение:

Кривая производственных возможностей (КПВ) – это кривая, каждая точка которой показывает максимальные количества двух экономических благ, которые способна произвести экономика страны при полном и эффективном использовании имеющихся ресурсов и текущем уровне технологий.

Из условия задачи известно, что на первом поле фермер может произвести либо 500 т картофеля, либо 100 т пшеницы.

Для построения кривой производственных возможностей первого поля откладываем по оси ординат (пшеница) максимальное количество выращенной пшеницы, которое производилось бы в экономике, если бы все имеющиеся ресурсы были направлены на производство пшеницы, то есть 100 т. Производство картофеля в этом случае равно нулю.

И наоборот, если все имеющиеся ресурсы направлены на производство картофеля, то максимальное количество – 500 т, которое может быть произведено при полном и эффективном использовании имеющихся ресурсов, мы откладываем по оси абсцисс (картофель). Производство пшеницы в этом случае равно нулю.

Соединив две эти точки, получим КПВ первого поля.

При этом альтернативные издержки (АИ) производства 1 т картофеля – это то количество пшеницы, от выращивания которого фермер вынужден отказаться:
100 / 500 = 0,2 т пшеницы.

На втором поле фермер может произвести максимально 1000 т картофеля или 400 т пшеницы, так как альтернативная стоимость выращивания 2 т пшеницы равна 5 т картофеля. Или альтернативные издержки 1 т картофеля равны 2 / 5 = 0,4 т пшеницы.

 

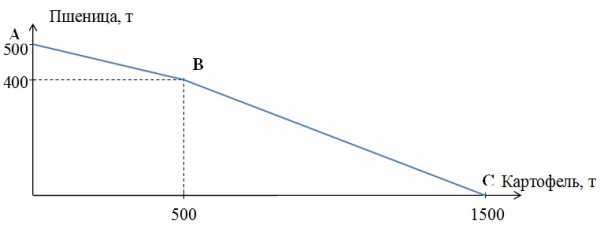
Построим суммарную КПВ для этого фермера.

Максимально возможный объём выращиваемой пшеницы – 500 тонн (на первом поле он может вырастить 100 тонн, на втором – 400 тонн). При этом объём картофеля будет нулевым. Отметим соответствующую точку на графике (точка А).

Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество.

Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие.

На первом поле альтернативные издержки 1 т картофеля равны 0,2 т пшеницы.

А на втором поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.

0,2 меньше чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать первое поле.

Максимально на первом поле можно вырастить 500 т картофеля, пожертвовав при этом 100 тонн пшеницы.

Координаты точки перелома (точки В) – 500 тонн картофеля, 400 тонн пшеницы.

Максимальное количество картофеля, которое можно вырастить на двух полях равно 1500 тонн (500 тонн на первом поле и 1000 тонн на втором). При этом объём пшеницы будет нулевым. Обозначим точку С на оси абсцисс.

Соединив последовательно три точки А, В и С получим суммарную кривую производственных возможностей нашего фермера.

ecson.ru

Задача № 144. Построение КПВ

Иван может получить на своем поле либо 400 т пшеницы, либо 1000 т картофеля. Для Петра альтернативной стоимостью выращивания одной тонны картофеля будет производство 0,25 т пшеницы при максимальном урожае картофеля, равном 1200 т. Два фермера – Иван и Петр – решили объединить свои усилия. Это не увеличит их производительности.

а) Построить кривую производственных возможностей «коллективного» хозяйства.

б) Верно ли, что альтернативной стоимостью производства первых 1200 т картофеля является производство 400 т пшеницы?

в) Верно ли, нельзя произвести 600 т картофеля и 550 т пшеницы?

г) Верно ли, что при производстве 1700 т картофеля альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы?

д) Верно ли, что для увеличения производства пшеницы с 200 т на 550 т нужно пожертвовать снижением урожая картофеля на 1100 т.

 

Решение:

а) Кривая производственных возможностей — это кривая, каждая точка которой показывает все возможные сочетания максимального производства двух экономических благ,  в условиях  полной занятости ресурсов и неизменной технологии.

Найдём координаты точек перелома:

А: Максимальное производство пшеницы обоих фермеров – 700 тонн. На поле Ивана можно вырастить 400 тонн, на поле Петра – 300 тонн:

1200 × 0,25 = 300.

При этом объём картофеля будет нулевым.

В: Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество.

Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие.

На поле Ивана альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.

А на поле Петра альтернативные издержки 1 т картофеля равны 0,25 т пшеницы.

0,25 меньше чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать поле Петра.

Максимально на его поле можно вырастить 1200 т картофеля, пожертвовав при этом 300 тонн пшеницы.

Точка В будет иметь координаты: 1200 тонн картофеля, 400 тонн пшеницы.

С: Максимальное количество картофеля, которое можно вырастить на двух полях равно 2200 тонн (1000 тонн на поле Ивана и 1200 тонн на поле Петра). При этом объём пшеницы будет нулевым.

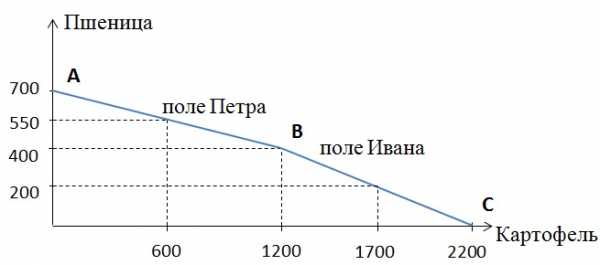
б) Неверно, так как альтернативной стоимостью производства первых 1200 т картофеля является производство 300 т пшеницы.

в) Точка, в которой производится 600 тонн картофеля, соответствует верхнему участку КПВ, отражающему производственные возможности поля Петра.

КПВ поля Петра является линейной функцией вида:

Y = a — b × X,

где а — максимально возможный объём пшеницы, когда все ресурсы используются только в производстве пшеницы,

b — коэффициент, характеризующий наклон КПВ и отражающий величину альтернативных издержек выращивания 1 т картофеля.

Итак, КПВ поля Петра описывается уравнением:

Y = 700 — 0,25 × X,

При производстве 600 тонн картофеля можно максимально вырастить:

Y = 700 — 0,25 × 600 = 550 тонн пшеницы.

Таким образом, можно произвести 600 т картофеля и 550 т пшеницы.

г) Точка, в которой производится 1700 т картофеля соответствует нижнему участку КПВ, отражающему производственные возможности поля Ивана.

На поле его поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.

Альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы:

8 / 20  = 0,4 т пшеницы — верно.

д) Да, это так.

1700 — 600 = 1100

ecson.ru

Решение типовых задач

1. Построить кривую производственных возможностей на основании исходных данных (табл. 1).

1. Объяснить методологическое значение кривой производственных возможностей.

2. Рассчитать альтернативные затраты производства единицы товара А.

3. Рассчитать альтернативные затраты производства единицы товара Б.

4. Объяснить закономерность изменения величин альтернативной стоимости.

Таблица 1.

Таблица данных для построения КПВ

Товар	Вариант производственной программы
	1	2	3	4	5	6	7
А	0	7	12	16	19	21	22
Б	6	5	4	3	2	1	0
А в Б
Б в А

Решение

Рис. 1.3. График кривой производственных возможностей

Методологическое значение кпв

Кривая (граница) производственных возможностей помогает определить любую комбинацию производства двух товаров предприятием:

1. При полной загруженности ресурсов (все точки на кривой).

2. При неполном использовании ресурсов (левее кривой).

3. Невозможное производство (правее кривой) из-за недостаточности ресурсов (рис. 1.3).

А также помогает определить объёмы производства товаров при увеличении ресурсов (смещение кривой вправо) и уменьшении ресурсов (смещение кривой влево).

Закономерность изменения величин альтернативной стоимости

Альтернативная стоимость товара или издержки на увеличение производство одного товара за счёт уменьшения другого возрастают. Эти издержки связаны с необходимостью дополнительных затрат, например, на переобучение рабочих, закупку сырья, переналаживание оборудования для производства большего количества одного из товаров. Альтернативная стоимость выражается в количестве товара, которым мы должны пожертвовать для увеличения производства другого.

; ; и т.д.

Расчёт альтернативных затрат

Товар	Вариант
	1	2	3	4	5	6	7
А	0	7	12	16	19	21	22
Б	6	5	4	3	2	1	0
А в Б		1/7	1/5	1/4	1/3	½	1/1
Б в А	7/1	5/1	4/1	3/1	2/1	1/1

Задачи по микроэкономике

Задача 1. На рынке товара Х известны функции 3 покупателей и 3 продавцов.

Qd1 = 2 – 0,2P Qd2 = 1,5 – 0,2P Qd3 = 1,5 – 0,6P

Qs1 = – 0,6 + 0,5P Qs2 =– 0,2 + 0,5Р Qs3 = – 0,2 + P

Определите равновесную рыночную цену и равновесный объём продукции

Решение:

Определяем функцию рыночного спроса аналитическим способом:

Qd = 5 – P (Qd₁ +Qd₂ + Qd₃ )

Определяем функцию рыночного предложения аналитическим способом:

Qs = — 1 + 2P(Qs₁ +Qs₂ + Qs₃ )

Определяем равновесную цену и равновесный объем продукции

Qd = Qs; 5 – P = -1 + 2P; Pe = 2 Qe = 3

Задача 2. Даны рыночные функции спроса и предложения:Qd = 5 – P и Qs = — 1 + 2P. Определите математически общественную выгоду торговли.

Решение:

Qd = 5 – P; Qs = -1 + 2P; Qd = Qs; 5 – P = -1 + 2P; Pe = 2 Qe = 3

Pd max: 5 – P = 0 Pd max = 5; Ps min: — 1 + 2P = 0 Ps min = 0,5

Излишек покупателя = ½ × (Pd max – Pe) × Qe = ½ (5 – 2) × 3 = 4,5

Излишек продавца = ½ × (Pe – Ps min) × Qe = ½ (2 – 0,5) × 3 = 2,25

Общественная выгода торговли = 4,5 + 2,25 = 6,75

Задача 3. Дана функция спроса Q_D = 8 – 0,5P. Определить коэффициент прямой эластичности спроса по цене, если цена равна 6 ден. ед.

studfiles.net

Учебно-методический материал (экономика, 10 класс) по теме: Алгоритм решения задач на построение графика общей кривой производственных возможностей

Подготовка к конкурсу «Стратег»

Экономика, 10-й класс

Алгоритм решения задач на построение графика общей кривой производственных возможностей

При решении задач такого тапа надо исходить из того условия, что современное производство основывается на разделении труда, а значит, на специализации и кооперации товаропроизводителей. Товаропроизводители объединяют свои усилия для совместного производства экономического продукта. При этом они могут все свои усилия направить на производство одного и того же продукта, или же распределить свои функции так, чтобы производить только тот продукт (или часть его), который у них получается быстрее и лучше.

1. Исходные данные задачи оформить в виде таблицы, заполнив колонки 1, 2, 3. По мере накопления опыта решения  задач такого типа, таблицу можно изменять. Для избежания путаницы первое место в таблице отводим тому товару (изделию), который первым упоминается в условии задачи.

Товаропроизводители	Товары (продукция), ед. изм.	Альтернативная стоимость
	Товар Х	Товар У
1	2	3	4
Товаропроизводитель 1
Товаропроизводитель 2
Товаропроизводитель 3
ИТОГО:			ХХХХХХХХХХХХХ

2. Рассчитать альтернативную стоимость, составив соотношение: сколько единиц товара Х приходится на 1 единицу товара У. Для этого заполняете в таблице колонку 4.

3. На основе альтернативной стоимости сделать вывод о специализации товаропроизводителей. Вывод записать под таблицей.

4. Заполнить в таблице строку «ИТОГО» для каждого товара. Для этого вы подсчитываете сумму  товара, которую можно получить в том случае, если все производители сосредоточат свои усилия только на его производстве.

5. Определить минимальное количество точек для построения общей КПВ и дать им обозначение.

Для простоты построения графиков используем частный вид КПВ – наклонную прямую. Если бы надо было построить КПВ для одного производителя, то достаточно найти две крайние точки. А вот для построения общей КПВ нужны промежуточные точки, так называемые точки перегиба или перелома, показывающие изменение альтернативной стоимости на разных участках графика.

---

Минимальное количество точек для построения общей КПВ находим по формуле:

 

n = N – 1,           где

n – количество точек перегиба;

N – количество товаропроизводителей.

Например, если у нас по условию задачи имеются два товаропроизводителя, то минимальное количество точек для построения графика равно трем. Это точки А, В, С.

6. Рассчитать координаты точек.

Если у нас три точки, то две из них – это крайние.

Расчет координат крайних точек прост:

— если все товаропроизводители сосредоточат свои усилия на производстве товара Х, то его будет получено в количестве Р ед, а товара У – 0 ед;

— если все товаропроизводители сосредоточат свои усилия на производстве товара У, то его будет получено в количестве S ед, а товара Б – 0 ед.

Координаты крайних точек:

А(P ед, 0 ед.)

С(0 ед, S ед.).

Расчет координат промежуточных точек производится только на основе альтернативной стоимости и того вывода, что уже записан вами под данными таблицы. Сравниваются потери товаропроизводителей. Тот из них, кто больше всего теряет в количестве товара У, специализируется на его производстве. Тот, чьи потери меньше всего, производит товар Х. Обратите на это внимание, так как у вас может появиться путаница, если производителей трое и даже больше.

7. Оформить таблицу координат для точек, по которым и  будет построен график.

	А	В	С
Товар Х
Товар У

8. Построить график.

Примеры графиков приводятся на рис.1 и рис.2

                            Рисунок 1                                                                    Рисунок 2

Запомните:

1. Оси координат показывают данные о количестве производимых благ, а не о количестве используемых ресурсов, необходимых для получения этих благ.
2. Если форма кривой вогнута, задача решена неправильно. Нарушен закон возрастания альтернативных издержек (вмененных затрат).

---

Решите задачи:

Задача 1.

Два фермера могут выращивать свеклу и картофель, засеивая им свои угодья в любой пропорции. Если Петр все свои поля отведет под свеклу, то он соберет урожай 3000т, а если под картофель, то получит 2000т. У Павла другая ситуация. Он может получить 4800т свеклы или 2400 картофеля. Построить общую кривую производственных возможностей.

Задача 2.

Фермер имеет три участка, которые использует под сливы и яблони. На первом участке фермер может вырастить либо 160ц слив либо 50ц яблок; а втором – 300 и 100 соответственно; а на третьем – 140 и 60. Определите точки перегиба КПВ фермера, за исключением крайних точек.

nsportal.ru

Задачи по экономике

Решение задач по экономике вызывает немало трудностей у школьников и студентов, так как требует знаний не только экономических терминов, законов и формул, но также и навыков пользования математическим аппаратом.  

В этом разделе собраны задачи по экономике с решением, задачи как типовые, так и повышенной сложности.

Данный раздел полезен:

---

1. школьникам, изучающим основы экономической теории, а также изучающим экономику в курсе обществознания.

Рекомендуем обратиться к разделам:

Микроэкономика

Макроэкономика

Национальное счетоводство

Экономическая статистика

Финансовая математика

---

2. студентам экономических и не экономических специальностей, изучающим экономику в ВУЗе и средних профессиональных образовательных учреждениях.

Этот раздел поможет подготовить домашнее задание по экономическим дисциплинам, приготовиться к контрольным мероприятиям, экзамену.

Для вас будут полезны разделы:

Анализ хозяйственной деятельности

Макроэкономика

Микроэкономика

Общая теория статистики

Система национальных счетов

Финансовая математика

Ценообразование

Эконометрика

Экономическая статистика

---

3. учителям обществознания и экономики в школе при подготовке к уроку или для составления домашних заданий и контрольных работ.

---

4. преподавателям высших учебных заведений, а также всем интересующимся и желающим разобраться в этом сложном мире, называемом экономикой.

---

Сайт регулярно пополняется новыми разделами, статьями, публикациями, а также задачами по экономике с решениями. Следите за обновлением списка задач в нашей группе В Контакте. Надеемся, что Вы найдёте для себя много полезного на нашем сайте.

Желаем успехов!

ecson.ru

Учимся решать экономические задачи

⇐ ПредыдущаяСтр 4 из 34Следующая ⇒

Типы задач:

— построение кривых производственных возможностей задач: (КПВ) на основании различных данных об альтернативных возможностях производителей;

— анализ возможностей построения КПВ по исходным данным;

— анализ кривых производственных возможностей.

2A. На одном однородном поле фермер может произвести 300 т картофеля или 100 т пшеницы, а на другом однородном поле везде альтернативная стоимость выращивания 1 т пшеницы равна 2 т картофеля при максимальном производстве картофеля, равном 400 т.

а) Какова альтернативная стоимость производства 1 т пшеницы на первом поле?

б) Построить кривую производственных возможностей для каждого поля.

в) Построить кривую общих производственных возможностей фермера.

Обсуждение и решение:

а) На первом поле, пожертвовав одной тонной пшеницы, фермер высвободил площадь для выращивания трех тонн картофеля. Следовательно, альтернативная стоимость производства 1 т пшеницы на первом поле равна 3 т картофеля. И, наоборот, 1 т картофеля стоит 1/3 т пшеницы.

Примечание. В дальнейшем предлагаем обозначать такое соотношение альтернативных стоимостей как 1П = 3К.

б) Построение кривой производственных возможностей для каждого поля очевидно. Кривой производственных возможностей будет прямая (это частный случай выпуклой кривой), соединяющая точки максимального производства пшеницы и наибольшего производства картофеля. Обозначим на первом поле эти точки следующим образом: (0П, 300К) и (100П, 0К).

Рис. 2-1. Кривая производственных возможностей первого поля

Обоснование: Поле можно разделить в любой пропорции. На одной части посеять пшеницу, а на другой посадить картофель.

Альтернативная стоимость единицы пшеницы на втором поле выражается следующим соотношением: 1П = 2К. В результате максимальное производство на этом поле пшеницы равно 200 т (400 / 2 = 200). Кривая производственных возможностей строится аналогично.

в)Построение общей кривой производственных возможностей может вызвать затруднения. Ключом к решению является понятие альтернативной стоимости. Максимум производства пшеницы на двух полях очевиден — это 100 + 200 = 300, если засеять оба поля пшеницей. Аналогично можно найти максимум производства картофеля. Таким образом, две точки КПВ мы получили: (300П, 0К)и (0П, 700К).

Что делать далее? Можно предложить два варианта использования производственных ресурсов:

Рис. 2-2. Два варианта использования ресурсов

 

Ясно, что первый вариант дает верное решение, а второй — нет, так как в первом получается выпуклая кривая, а во втором — нет.

Но это еще не все. Нужен более совершенный алгоритм решения задач подобного рода. Представьте, что у фермера не два, а пять полей. Ведь в этом случае пришлось бы перебирать 5! = 120 вариантов.

Алгоритм построения общей кривой производственных возможностей.Допустим, что мы всегда засевали все поля пшеницей, а на следующий год нам потребовалось немного картофеля. На каком поле его посадить? Ясно, что на том, где потери в виде недополученной пшеницы будут минимальными, т.е. там, где альтернативная стоимость картофеля наименьшая. При построении решения приведенной выше задачи следует посадить на первом поле. Если не хватит этого поля, то остаток картофеля надо посадить на поле со следующим по возрастанию значением альтернативной стоимости картофеля и т.д.

Например, если у фермера три поля, то графически процесс можно иллюстрировать так:

Рис. 2-3. Пример построения общей кривой производственных возможностей

 

Верхний треугольник соответствует полю 3, где стоимость картофеля минимальна (1К=0,4П). Второй треугольник соответствует полю 2, где стоимость картофеля следующая по возрастанию.

 

2Б. Королевство Рубляндия производит два знаменитых продукта: «масло» (образ мирной продукции) и «пушки» (образ военной продукции) и имеет следующую границу годовых производственных возможностей (рис. 2-4).

Рис. 2-4. Кривая производственных возможностей Рубляндии

 

Эту кривую можно представить в табличном виде по точкам перелома:

 

1) Каково максимально возможное производство пушек?

Ответ: Максимальное количество пушек, которое может быть произведено в Рубляндии, составляет 8 тыс. штук при отсутствии производства масла.

2) Сколько может быть произведено пушек при производстве 7 тыс. т масла?

Ответ: При производстве 7 тыс. т масла не может быть выпущено более 6 тыс. пушек.

3) Найти альтернативную стоимость увеличения производства пушек с 6 тыс. до 7 тыс. в год.

Ответ: Альтернативной стоимостью увеличения производства пушек с 6 тыс. до 7 тыс. в год будет уменьшение производства масла на 3 тыс. т в год (7 — 4 = 3). 4) На сколько может быть увеличен выпуск масла при производстве 4 тыс. т масла и 4 тыс. штук пушек?

Ответ: Выпуск масла может быть увеличен до 10 тыс. т, что даст прирост выпуска на 6 тыс. т.

5) Можно ли произвести с помощью имеющихся ресурсов 6,7 тыс. пушек и 5,5 тыс. т масла?

Ответ: Нет, нельзя, поскольку на кривой производственных возможностей выпуску 5,5 тыс. т масла соответствует производство 6,5 тыс. пушек. Постройте соответствующий график.

6) Какова максимальная альтернативная стоимость производства одной тысячи пушек? Какова — минимальная?

Ответ. В соответствии с законом возрастающих альтернативных затрат максимальная альтернативная стоимость производства одной тысячи пушек равна 4 тыс. т масла, так как увеличение выпуска пушек с 7 до 8 тыс., т. е. последней тысячи, ведет к уменьшению производства масла с 4 тыс. т до нуля.

Минимальная альтернативная стоимость производства одной тысячи пушек составляет 0,5 тыс. т масла.

7) Ведущие специалисты Рубляндии оценивают ценность 1 тыс. пушек в 1 млрд дукатов, а 1 тыс. т масла — в 1,5 млрд дукатов. Сколько нужно произвести пушек и масла, чтобы их общая ценность была наибольшей?

Ответ: Самый простой путь — это перебор точек перегиба. В результате нужно произвести пушек в количестве 4 тыс. штук, а масла — 10 тыс. т. Таким образом, общая ценность принятого королем решения оценивается в 19 млрд дукатов.

2В.Могут ли следующие точки лежать на одной кривой производственных возможностей: А(15,3), В(8, 13), С(13, 6), D(5,12)?

Ответ: Нет, не могут. Возможны два способа решения.

Способ 1 (графический). Если точки принадлежат некоторой кривой производственных возможностей, то, соединив эти точки, мы получим выпуклую кривую. В данном случае, соединив указанные точки, мы имеем кривую, которая не является выпуклой.

Способ 2 (аналитический). Заметим, что точки D и В связаны таким образом, что из точки D в точку В можно попасть, только увеличив сразу две координаты. Чего не может быть для точек кривой производственных возможностей.

Все эти методы не идеальны. Представьте себе, что в задаче указаны 23 точки. Что делать?

Общий алгоритм (аналитический). Расположить все точки по возрастанию одной из координат. Тогда, если они могут принадлежать некоторой кривой производственных возможностей, числа по другой координате будут убывать в соответствии с законом возрастающих альтернативных затрат. Если же этого нет, то данные точки не могут принадлежать никакой кривой производственных возможностей.

 

2Г*.Допустим, точки А, Б, В и Г лежат на одной кривой производственных возможностей: А(4000, 11000), Б(8000, 3000), В(7000, X)и Г(3000, Y). Определить полный набор соотношений с участием неизвестных X и Y.

Решение: Выпуклая форма кривой производственных возможностей и закон возрастающих альтернативных затрат позволяют определить искомые соотношения. Ясно, что X < Y, 11 000 < Y, 3000 < X, но это еще не все. Прирост производства первого продукта с 7000 до 8000 был обеспечен большими потерями второго продукта, чем с 3000 до 4000, т. е.

Х-3000 > Y — 11000.

Но и это еще не все.

Для удобства анализа расположим точки в таблице по возрастанию первой координаты:

 

Обратите внимание на расстояние по первой координате между точками В и А. Оно составляет 3000 единиц и в три раза больше, чем расстояние между точками А и Г, а также между точками В и Б. Поэтому

X — 3000 ≥ 1/3(11 000 — X) ≥Y — 11 000.

Ответ: Y > 11 000 > X > 3000 и

X — 3000 ≥(11 000 — X) ≥ Y — 11 000.

ОБМЕН

Основные понятия. Выгоды добровольного обмена. Абсолютное преимущество. Сравнительное преимущество.

Основные умения. Различать и измерять абсолютное и сравнительное преимущество.

Дополнительные умения.Анализировать и вычислять выгоду от обмена на условных примерах. Строить кривые производственных возможностей с учетом обмена.

mykonspekts.ru

2.4 Оптимизация на КПВ | Экономика для школьников

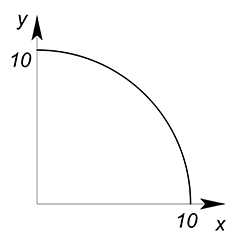
Нахождение максимальной выручки

Имеем: КПВ некоторый страны задана функцией $x^2+y^2=100$, цены товаров $x$ и $y$ соответственно равны $10$ и $5$, найти при каком объёме производства данных товаров выручка от их продажи будет максимальной.

Построим КПВ:

$x^2+y^2=100$

$y^2=100-x^2$

$y=\sqrt{100-x^2}$

Теперь разберемся с функцией выручки (выручка обозначается буквами $»TR»$ (от англ «total revenue»)):

$TR=PQ$, где $P$ — цена товара, $Q$ — его количество.

В данном случае у нас $2$ товара, поэтому функция $TR$ будет зависеть от двух переменных $Q_x$ и $Q_y$:

$TR=P_xQ_x+P_yQ_y=10Q_x+5Q_y$

Далее для простоты будем писать не $Q_x$, $Q_y$, а просто $x$, $y$

Данная функция выручки может быть построена в трехмерной плоскости. Что мы можем сделать с этой функцией, чтобы перевести её в двухмерное пространство? В первую очередь можно выразить $y$ через $2$ другие переменные ($TR$;$x$):

$y=\dfrac{TR}{5}-2x$.

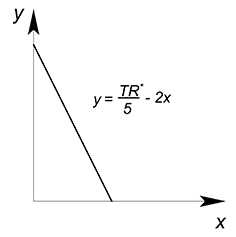
Так как значение $TR$ нам не задано, мы можем сами выбрать оптимальную для нас величину выручки. Будем фиксировать значение $TR$ на разных уровнях (будем преходить на более высокие графики — увеличивать значение выручки), пока не достигнем оптимального ($TR_1 \to TR_2 \to TR_3$). $TR_3$ будет оптимальной величиной, ибо точка, в которой функция выручки касается графика КПВ, будет на границе нашей области производственных возможностей, следовательно, точка касания будет приносить максимальную выручку, а график выручки будет занимать самое высокое положение из всех доступных (выручка будет наибольшей из всех возможных). Если бы мы выбрали меньшее значение выручки, то мы недополучили бы часть денег — мы смогли бы произвести ещё больше товаров $x$ и $y$ и продать их (в этом случае у нас была бы возможность улучшения ситуации). Если бы выбрали большее значение переменной $TR$ ($TR_4$), то не смогли бы произвести соответствующий ей объём товаров, ибо нет такой точки (с точки зрения производства), в которой мы бы получили такую выручку.

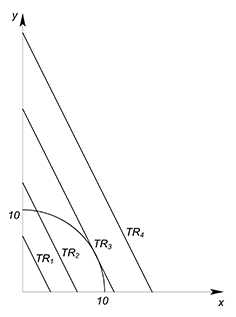
Как мы уже выяснили, оптимальная точка будет лежать на графике КПВ. Её положение на данной линии будет зависеть от соотношения цен товаров $x$ $y$, которые и задают наклон функции выручки.

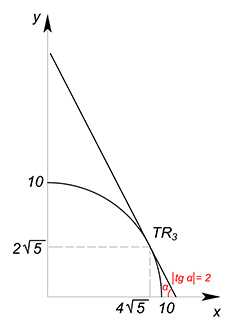
Линейная функция $y=\dfrac{TR}{5}-2x$ будет иметь постоянный $tg$ угла наклона, равный по модулю $2$. Чтобы найти положение оптимальной точки на графике КПВ необходимо взять производную функции КВП (обычно это делается по переменной $x$) и приравнять её к производной функции выручки (взятой также по $x$ — $y'(x)$) . То есть угол наклона касательной в оптимальной точке должен совпадать с углом наклона функции выручки.

КПВ:
$y=\sqrt{100-x^2}$
$y'(x)=\dfrac{-x}{\sqrt{100-x^2}}$

$TR$:
$y=\dfrac{TR_3}{5}-2x$
$y'(x)=-2$

$\dfrac{-x}{\sqrt{100-x^2}}=-2$

Отсюда находим $x$ и соответствующее ему значение $y$:

$x=4\sqrt5$
$y=2\sqrt5$

Считаем выручку:

$TR=10\cdot{4\sqrt5}+5\cdot{2\sqrt5}=50\sqrt5$

У этой задачи есть более легкое и быстрое решение: подставляем функцию КПВ вместо переменной $x$ в функции выручки:
$TR=10x+5\sqrt{100-x^2}$
Получаем функцию, зависимую от одной переменной. Максимизируем данную функцию обычным способом, беря производную и приравнивая её к 0.

В общем виде:

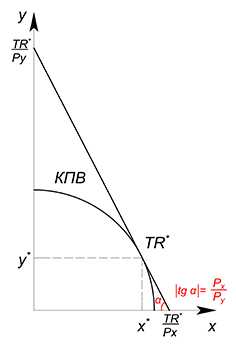
КПВ:
$y=f(x)$

$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$

Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:

$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$

Берем производные функций КПВ и выручки, приравниваем их:

$f'(x)=-\dfrac{P_x}{P_y}$

Находим оптимальные $x$, $y$, $TR$

Особого внимания заслуживает случай с линейной функцией КПВ (аналогично поступаем и с выпуклой).
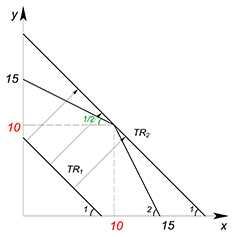
Имеем: КПВ задана функцией $y=10-2x$; $P_x=5$, $P_y=10$. Найти максимальную выручку.
В данном случае у нас нет возможности провести касательную к графику функции КПВ, но мы также можем воспользоваться методом фиксации значения $TR$ и поиска оптимальной точки.

$TR=5x+10y$
$y=\dfrac{TR^*}{10}-\dfrac{x}{2}$

Точно также будем двигать в право функцию выручки, пока она не займет наивысшее положение из всех возможных — пока значение выручки, приносимой комбинациями $x$ и $y$, не станет максимальным из всех доступных. Максимальную выручку в данном случае мы можем получить в точке $y=10$, $x=0$. Считаем $TR=10\cdot{10}=100$. При линейной функции КПВ метод тот же, но функция выручки уже не будет касательной.

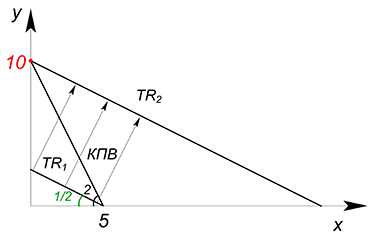
Также интересен случай с функцией КПВ, имеющей излом. Воспользуемся тем же методом, что и в двух предыдущих случаях, только опять же здесь функция выручки не будет касательной, проведенной к графику КПВ.

Имеем: график КПВ состоит из двух участков, заданных функциями $y=15-\dfrac{x}{2}$ при $x$ принадлежащем $[0;10]$, $y=30-2x$ при $x$ принадлежащем $[10;15]$. $P_x=P_y=5$.

$TR=5x+5y$
$y=\dfrac{TR}{5}-x$

Двигаем график выручки вправо, пока он не займет максимально доступное значение. В данном случае это значение оказалось в точке излома графика КПВ (такое бывает не всегда). Так случилось, потому что угол наклона графика выручки был меньше угла наклона одной из функций КПВ, но больше угла наклона второй.

$x=y=10$
$TR=5\cdot{10}+5\cdot{10}=100$

В общем виде:

КПВ:
$y=f(x)$

$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$

Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:

$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$

Двигаем функцию выручки вправо, пока не достигнем наибольшего уровня $TR$ из всех возможных. Находим соответствующие точке пересечения значения $x$, $y$, $TR$.

Вообще весь данный метод поиска максимальной выручки основан на фиксации переменной $TR$ и её движении вправо до того момента, пока мы не достигнем максимально высокого уровня графика, которому соответствует максимально возможное значение выручки и оптимальные $x$ и $y$. Просто методы подсчета этих оптимальных значений товаров различны для различных функций КПВ.

Еще одним распространённым типом задач является поиск оптимальных объёмов производства товаров при заданной пропорции их потребления.

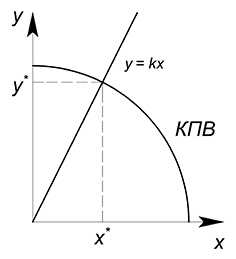
КПВ некоторой страны задана функцией $x^2+y^2=100$. Жители потребляют товары $x$ и $y$ только в пропорции $\dfrac{1}{2}$. Найти оптимальные объёмы производства данных благ.

Как обычно начнем с построения КПВ

Далее у нас имеется ограничение — потребление $x$ и $y$ в определенной пропорции. Если $\dfrac{x}{y}=\dfrac{1}{2}$, то $y=2x$. Все точки, для которых верна пропорция $\dfrac{x}{y}=\dfrac{1}{2}$, будут лежать на одной прямой, являющейся лучом решений.

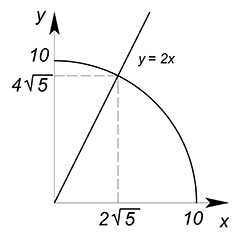
Как известно, эффективная точка будет лежать на границе производственных возможностей. Одновременно он будет принадлежать лучу решений. Найдем её:

$y=\sqrt{100-x^2}=2x$

Из уравнения находим $x$ и соответствующий ему $y$:

$x=2\sqrt{5}$

$y=4\sqrt{5}$

В общем виде:

КПВ:

$y=f(x)$

Пропорция производства товаров:

$y=kx$

Отсюда находим $x$ и $y$

iloveeconomics.ru