Русские счеты как считать: Как считать на счетах правильно (ВИДЕО)

Содержание

Как считать на древних приспособлениях для счета

Борисов А.Е. 1

1МБОУ «СОШ № 40 им. Героя Советского Союза В.А. Скугаря»

Пинчук Н.Н. 1

1ГБОУ ДО РК «ДДЮТ»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Человечество научилось пользоваться простейшими счётными приспособлениями тысячи лет назад. Наиболее востребованной оказалась необходимость определять количество предметов, используемых в меновой торговле. Одним из самых простых решений было использование весового эквивалента меняемого предмета. Для этих целей использовались простейшие балансирные весы.

С потребностью более сложного счета были изобретены счетные доски, применявшиеся для арифметических вычислений приблизительно с V века до н.

э. в Древней Греции, Древнем Риме, Древнем Китае и в других странах.

Общие принципы счетных досок — разделение линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов. Камешек для греческой счетной доски (абак) назывался псифос; от этого слова было произведено название для счёта — псифофория, «раскладывание камешков». У римлян камешек называли калькулюс, а счет на абаке получил название калькуляция. И сейчас подсчет расходов называют калькуляцией, а человека, выполняющего этот подсчет – калькулятором, также называется современный электронный прибор для счета. Среди применяющихся в современности вариантов абака — русские счёты и японский соробан.

Древние приспособления для счета заинтересовали меня при изучении темы «История развития вычислительной техники». Как древние приспособления для счета способствовали развитию вычислительной техники?

Актуальностьмоей работы состоит в том, что в наше время сложных информационных технологий важно понимать, что стояло у истоков зарождения вычислительной техники, как потребность в счете и обработке сложных вычислений способствовала развитию вычислительной техники и привела к появлению сложных современных вычислительных систем.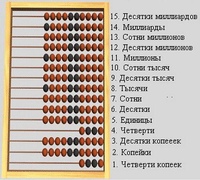

Выдвигаемая гипотеза:

Древние приспособления для счета позволяли выполнять сложные вычисления.

Цель:изучить способы счета на древних приспособлениях посредством проведения эксперимента.

Задачи:

изучить теоретический материал;

изучить способы математических действий на приспособлениях;

изготовить соробан;

провести эксперимент по выполнению вычислений на приспособлениях для счета;

зафиксировать результаты вычисления при помощи фотографий;

сделать выводы по полученным результатам.

В ходе проведения работы мною был изучен теоретический материал из источников, указанных в списке. Прочитана книга Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с., которая вызвала интерес к более углубленному изучению древних приспособлений для счета, практическому их использованию. Вместе с папой изготовлен соробан. Из других источников литературы, таких как Берназани Д. Соробан/Абакус: Справочное пособие 2013 г.-150 с. и Депман И.Я. История арифметики: Пособие для учителей, Издание второе, исправленное, М.: Просвещение, 1965 г.- 416 с.

Изучены способы счета на соробане и русских счетах. Произведен анализ и сделаны выводы по проделанной работе. Для представления защиты работы публике сделана презентация в Power Point.

Описание древних приспособлений счета

Абак

Предшественником абака была пыльная доска или доска, которая покрывалась песком. Путем разделения пыльного полотна на ряды острой палочкой, представлялись различные значения чисел. Это достигалось с использованием различных знаков, которые рисовались вдоль линий. Позднее, в Древнем Риме использовали доски, сделанные из камня, бронзы, слоновой кости. На сделанных углублениях считали камешками, косточками.

В неаполитанском музее древностей хранится римский абак, представляющий собой доску с прорезанными полосками, вдоль которых передвигались камешки. На доске располагалось восемь длинных полосок и восемь коротких, расположенных над длинными. Над каждой длинной полоской имеется обозначение, описывающее назначение полоски (слева на право):

— означает, что полоска используется для отложения разряда миллионов;

— для отложения разряда сотен тысяч;

— разряда десятков тысяч;

— разряда тысяч;

— разряда сотен;

— разряда десяток;

— разряда единиц.

— означает, что эта полоска используется для отложения унций.

На семи левых длинных полосках располагали четыре камешка, каждый из которых приравнивался к единице соответствующего разряда числа. На семи левых коротких полосках располагали по одному камешку, обозначавшего пять единиц разряда. Восьмая длинная полоса (служившая для отсчета унций) содержала пять камешков, каждый из которых обозначал единицу разряда унции. Восьмая короткая содержала один камешек, обозначающий шесть единиц. На доске справа имелись две короткие полоски с одним камешком означавшие: — пол унции; — четверть унции.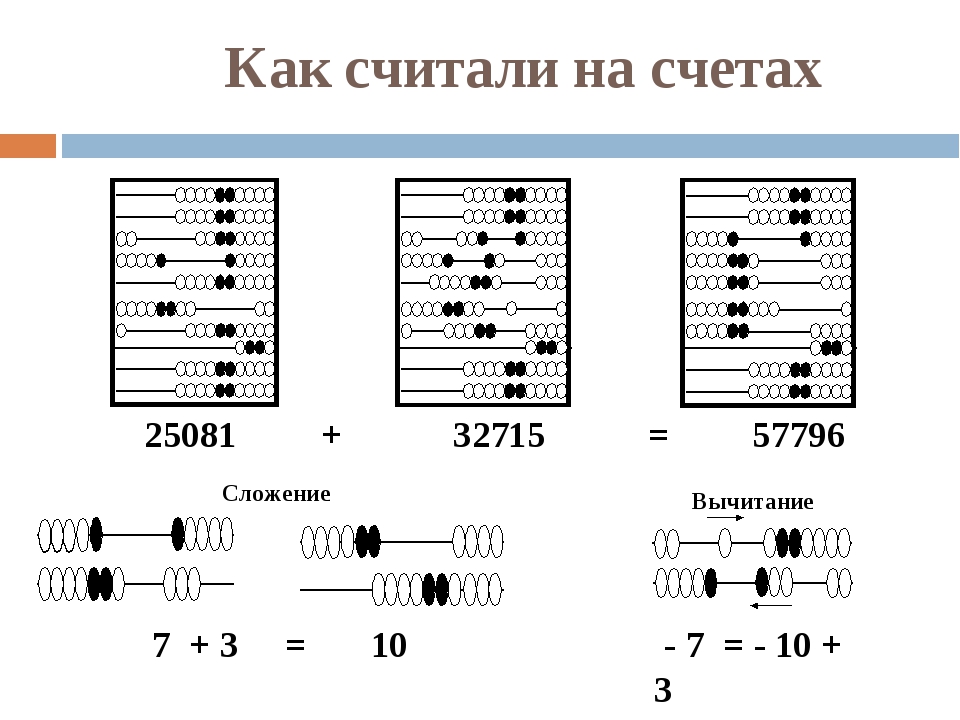 Одна длинная полоска с двумя камешками означала: — шестая часть унции.

Чаще всего абаком пользовались для денежных расчетов налогов и торговли.

Счет на абаке сменил более древний счет на пальцах.

Соробан

Соробан — это японские счёты, которые появились в Японии в XVI веке. Соробан является потомком абака.

Соробан состоит из нечётного количества вертикально расположенных спиц. Каждая спица представляет собой цифру. Обычно их 13, но встречаются соробаны и с 21, 23, 27 или даже с 31 спицей. Бо́льшее количество спиц позволяет набирать большие числа, или представлять сразу несколько чисел на одном соробане.

На каждой спице нанизано по 5 костяшек, причём верхняя костяшка на каждой спице отделена от нижних перегородкой.

Четыре нижние костяшки называются «земными», и каждая представляет собой единицу.

Верхняя костяшка называется «небесной» и считается за пять «земных».

В начальных классах японских школ, до сих пор обучают детей счету на соробане.

Русские счеты

Появились в России на рубеже XV — XVI веков и активно применялись в торговле вплоть до последнего десятилетия XX века. В русских счётах, используется десятичная система счисления и возможность оперировать четвертями, десятыми и сотыми дробными долями. С момента своего возникновения счёты практически не изменились.

С появлением дешёвых электронных калькуляторов счёты практически полностью вышли из употребления. Ещё раньше, в начале 1980-х годов, обучение пользованию счётами было исключено в СССР из школьной программы.

На Русских счетах одиннадцать полос спиц с костями.

Дробная часть начинается со спицы с 4-мя костями. И от нее вниз располагается еще три спицы для дробной части.

Вверх от дробной части идут спицы по 10 костей, начиная с разряда единиц до миллиона.

Способы вычислений на древних приспособлениях для счета

Способ и метод счета на абаке

В исходном положении в «обнуленном» устройстве все камни выровнены по нижнему краю, а верхний ряд по верхнему краю.

В первую полоску ставили столько камешков, сколько в числе единиц, во вторую полоску – сколько в нем десятков, в третью – сколько сотен, и так далее. В верхнем разделе каждый камешек равен 5 в первой полоске, 50 во второй и так далее. Три правые полоски предназначались для счета дробями.

Вычисления производились слева на право.

Сравнивая древний абак и русские счеты, можно заметить, что процесс вычислений совершался пятеричной системой счета, выкладывание камешек происходило снизу в верх, а в русских счетах процесс вычислений совершался десятеричной системой счета и передвижение косточек происходило справа налево.

Способ и метод счета на соробане

Счеты представляют собой рамку, разделенную перекладиной. В верхней части расположена одна линия косточек. Каждая косточка в ней означает «пять». Внизу расположены ряды косточек, в каждом из которых по 4 косточки. Каждая из них обозначает «один». Для удобства вычисления начинают с самого среднего ряда.

Для обнуления соробана счеты слегка ударяют о стол. После этого двумя пальцами отодвигают верхние бусинки от перегородки.На соробане работают всегда сверху вниз большим и указательным пальцами обеих рук.

Набор числа на соробане. Сложение

Сначала нужно отложить первое слагаемое в центре. Ряд за рядом формируя общее число, поразрядно. Все действия на соробане осуществляют слева направо. Сначала откладывается старший разряд и так до младшего, по порядку. Затем также слева направо поразрядно необходимо произвести прибавление следующего числа. Если разряд переполняется косточками, нужно добавить одну бусинку к старшему разряду (слева).

Например, 254+333=587:

1)Откладываем 254

2)Прибавляем 333

3)Получаем 587

Вычитание

Вычитание происходит по той же системе, что и сложение. Разница в том, что при

недостаче бусинок их берут у старшего разряда.

333-254=79

Откладываем 333, затем вычитаем из него 254

Получаем 79

Способ и метод счета на русских счетах

В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть копейки. Черным цветом выделены центральные костяшки (для удобства).

Набор числа:

Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.

Сложение

Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов. Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку.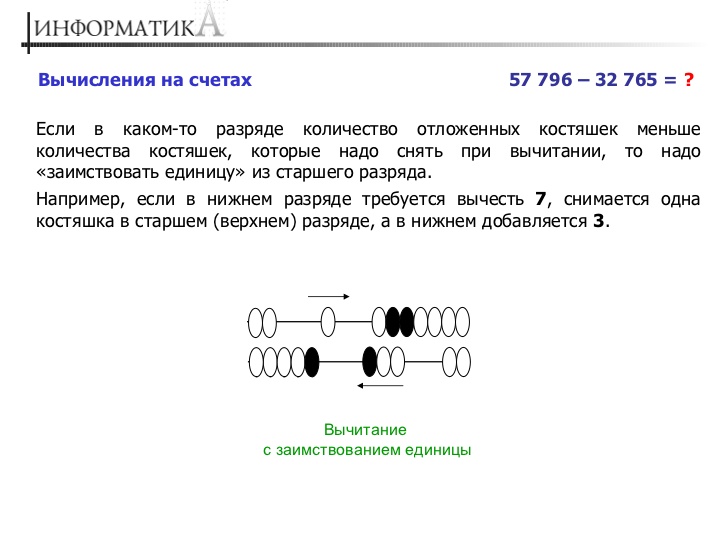 Чтобы лучше разобраться, как правильно складывать числа на счетах, посмотрим пример ниже (987 + 134 = 1 121):

Вычитание

Вычитание на счетах производится точно таким же образом как сложение, сверху вниз. Если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число не хвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже пример (121 – 98 = 23):

Умножение

Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой два раза или три раза соответственно. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Умножение на 5, это деление на 2 , а потом умножение на 10. В этом случае, после деления на 2 переносятся разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.

Умножение на счетах является не самым быстрым и простым.

Деление

Деление на русских счетах является достаточно сложной процедурой. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов.

Эксперимент с древними приспособлениями счета

Задача:

Расстояние от Москвы до Екатеринбурга по железной дороге 1667км., от Екатеринбурга до Новосибирска 1524 км. и от Москвы до Иркутска 5042 км. Чему равно расстояние от Новосибирска до Иркутска по железной дороге?

3.1 Решение задачи по математике при помощи соробана

Сначала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191 (км.)

Получаем 3191

Затем из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851 (км. )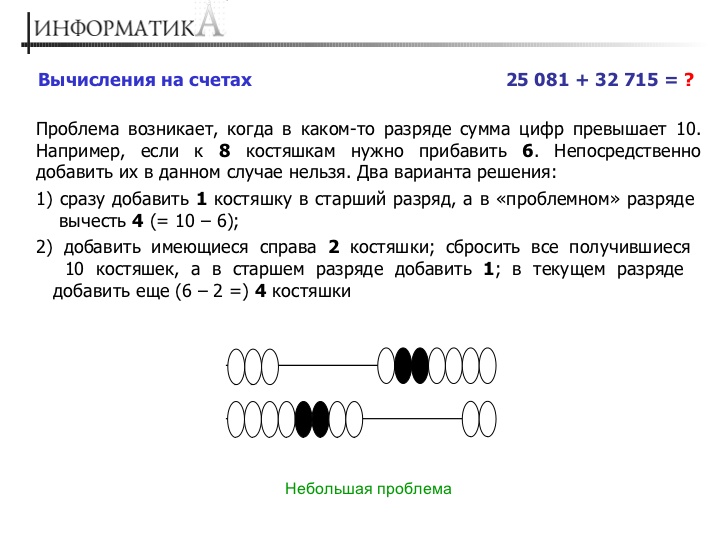

Получаем ответ 1851 (км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851 (км).

3.2. Решение задачи по математике при помощи русских счет

Так же для начала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191(км.)

Получаем 3191 (км.)

Из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851(км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851(км.).

Вывод

Благодаря исследованию, я узнал о различных видах древних приспособлений счета. Изучив методы и способы счета могу сделать вывод, что разные приспособления счета имели различные свойства, так, например, абак позволял вычислять способом сложения, вычитания, умножения и деления, а так же позволял выполнять действия с дробями. Но абак имел свои недостатки: невозможность сохранить результат, из него мог выпасть камешек, в результате весь расчет сбивался.

На протяжении нескольких столетий соробан активно применяется для обучения детей в странах Азии. В Европе и Америке заинтересовались соробаном в XXI веке. А в нашей стране первые школы обучения ментальной арифметике появились в 2013 году. Современные японцы считают, что и сегодня обучение счету с использованием соробана имеет ряд преимуществ по сравнению с традиционным подсчетом на бумаге. Этот метод тренирует мозг, увеличивая количество нейронных связей, и способствует развитию интеллекта и творческих способностей. Хорошо заменяет калькулятор при выполнении домашнего задания по математике начальной школы. Позволяет совершать такие математические действия как сложение, вычитание, умножение и деление.

Недостаток соробана заключается, что невозможно сохранить результат вычислений.

Вычисления на русских счетах, позволяет так же выполнять многие математические действия: сложение, вычитание, умножение, деление, и выполнять действия с дробями, которые будут изучаться мною в дальнейшем.

Недостатки использования русских счет заключаются в том, что нельзя сохранить результат, большие по размеру.

Гипотеза мною доказана на примерах: сложные математические вычисления можно выполнять на древних приспособлениях для счета. Возможно сложение, вычитание больших чисел до миллиарда и более. Конкретно на моем соробане до миллиона.

Таким образом, я считаю, что древние приспособления для счета, а именно, русские счеты и соробан являются достойными предшественниками современной вычислительной техники.

Список использованных источников и литературы

Апокин И.А., Майстров Л.Е. История вычислительной техники. М.: Наука, 1990г.- 400 с.

2. Берназани Д. Соробан/Абакус: Справочное пособие ,2013 г.-150 с.

3. Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с.

4. Депман И.Я. История арифметики: Пособие для учителей,

Издание второе, исправленное, М.: Просвещение, 1965 г.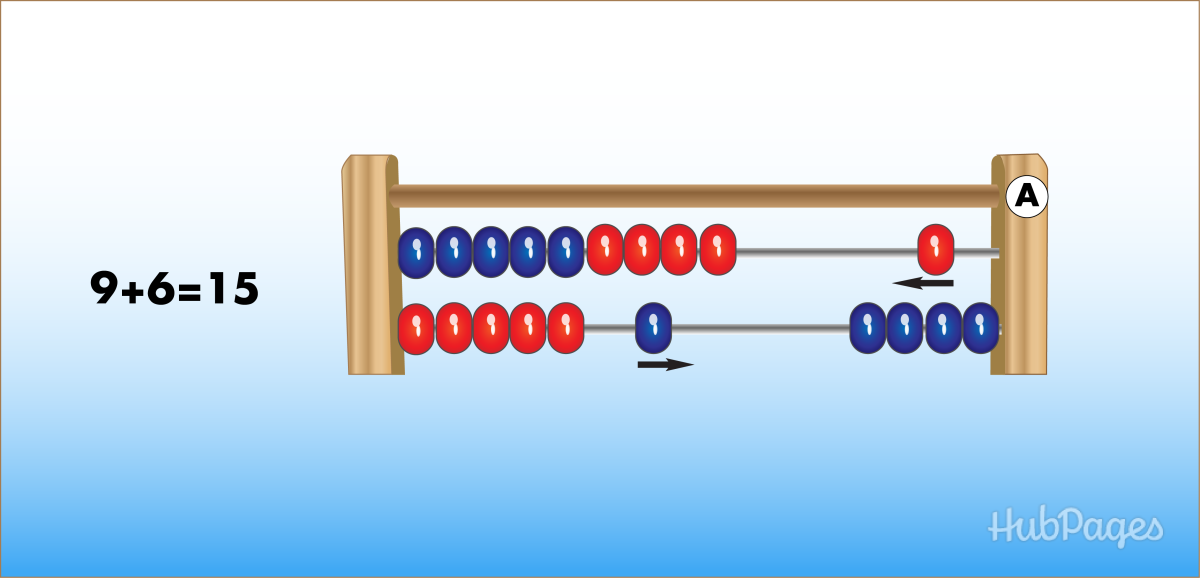 — 416 с.

Интернет ресурсы:

https://ru.wikipedia.org/wiki

http://all-ht.ru/inf/history/p_0_4.html

Просмотров работы: 1086

Счет на счетах обучение. Русские счеты: история, правила счета

Здравствуйте, дорогие друзья! Меня зовут Евгения Климкович. Я рада видеть вас на страничках блога «ШколаЛа»!

Чем сегодня займемся? Может быть, посчитаем? Не хотите? Да ладно вам! Это же очень интересно! Особенно если не просто ворон считать, а считать на абакусе. А вы, кстати, знаете, как считать на абакусе? Вот и я не знаю. Счеты в руках не держала, на курсы не ходила. Но понять, как же все-таки это делается, очень хочется. Вот и решила попробовать хотя бы немножко приоткрыть завесу тайны.

Вы со мной?

Тогда присаживайтесь поудобнее, включайте мозг. Наш ментально-арифметический поезд отправляется!

Предлагаю начать с главного! С абакуса или, как его еще называют, соробана. Что это за штуковина такая?

План урока:

Что такое абакус?

Вот она – эта загадочная счетная машинка.

Чем-то напоминает известные многим советские счеты с костяшками. И, насколько я поняла, принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Расположение чисел

Теперь о том, как же располагаются числовые линейки.

Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?

Давайте посмотрим на примере. Я нарисовала абакус!

Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на моем рисунке – это единицы.

Так будет выглядеть на абакусе число 3.

Поднимаем к разделительной планке три костяшки на линейке единиц.

Попробуем взять двойное число, например, 15.

На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

А вот это какое число получилось? Догадаетесь?

А давайте чего-нибудь посущественнее наберем. Например, 6482!

На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча.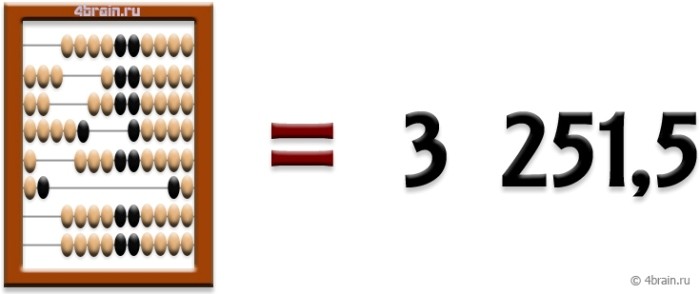 Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?

Как складывать?

А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.

Откладываем на абакусе 33.

К трем десяткам прибавим еще один. Получим 4 десятка или 40.

Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.

В результате получилось 47! Может на калькуляторе проверим?) Шучу, и так ясно, что результат мы получили верный!

Дополнительная литература

В общем, примерно вот по такой схеме на абакусе и считают. Я показала все самое простое. А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста! Обнаружила в интернете инструкцию по работе с соробаном. Вот здесь ее можно скачать.

Если не поможет инструкция, то может быть стоит обратить внимание на книгу «Ментальная арифметика. Знакомство»? Насколько я поняла, она ориентирована на обучение детишек. Такой своеобразный учебник. Нашла я ее в магазине «My-shop». Ссылка на эту книжку чуть ниже.

Ментальная арифметика. Знакомство — Багаутдинов Р. | Купить книгу с доставкой | My-shop.ru
[|urlspan]

Думаю, что и взрослым людям не повредят занятия с абакусом. Особенно бухгалтерам. Представляете, все коллеги на калькуляторах считают или на компьютерах. А вы такой деловой с абакусом) И батарейки-то не садятся, и кнопки не западают, и костяшки так приятно пощелкивают) Красота!

Уф, наверное, хватит на сегодня счета. Теперь давайте посмотрим, как другие считают. Настоящие маленькие абакус-мастера, только они уже на том уровне подготовки, когда хватает и воображаемых счет. Смотрим видео.

На сегодня, пожалуй, все. А завтра на блоге «ШколаЛа» вас ждет новая интересная информация!

Кстати, если есть желание каждое воскресение по почте получать анонсы статей на следующую неделю, то обязательно подпишитесь на новости блога. Тогда вы точно ничего не пропустите!

И не забудьте вступить в нашу группу «ВКонтакте» , там вас тоже ждет много всего интересного!

Удачи вам и вашим маленьким школьникам!

Евгения Климкович.

Инструкция

Счеты – простейший вычислительный аппарат, который представляет собой счетные кольца, нанизанные на тонкие спицы. Обрамленные единой канвой, счеты заключают в себе всю систему – единицы, сотни и т.д. На верхних рядах счет расположены целые числа, причем их уменьшается с каждой следующей спицей: от сотен тысяч к единицам. Под коротким «костяшек» расположены дробные числа: от десятых до тысячных.

Самыми простыми вычислениями на счетах являются сложение и вычитание. Числа набираются начиная с первого ряда целых: от 1 до 10. Следующий рад (на одну спицу вверх) – от 11 до 20 и т.д. Набирайте необходимое число, передвигая «костяшки» из соответствующего ряда справа налево. Когда один ряд на спице заполнится, воспользуйтесь числами большего значения – то есть одна «костяшка» верхнего ряда заменяет 10 «костяшек» нижнего. Складывая числа, добавляйте «костяшки» в соответствующие ряды. Чтобы окончательный , «спускайтесь» внизу вверх – миллионы, тысячи, сотни и т.д.

Вычитание на счетах производится таким же способом, что и сложение, только в обратном порядке. То есть вычитая из одного числа другое, убирайте «костяшки» из соответствующих рядов. Таким образом, во время подсчета двигайтесь сверху вниз. Окончательную сумму вы узнаете, подсчитав кольца, оставшиеся в левой стороне счет.

Для каждого числа умножение на счетах производится разными способами. Если вам нужно умножить на 2 или 3, замените это действие сложением, «плюсуя» число 2 или 3 раза соответственно. Умножение на 4 – это сложение (2*2).

Чтобы умножить число на 6, его нужно умножить на 5 описанным выше способом, затем к полученному результату прибавить число, которое было в начале вычислений.

Чтобы умножить на 7, сначала умножьте число на 10, а затем от полученного значения отнимите умножаемое число три раза.

Умножение на 8 или 9 заменяют умножением на 10, но без переноса 2х или 1й (при умножении на 8 и 9 соответственно) косточки наверх.

Множители, следующие после 10, «раскладывают» на . Например, вам нужно умножить на 12 – вы раскладываете этот множитель на 10 и 2. Сложите число с самим собой (умножьте на 2), затем прибавьте к нему удесятеренное значение.

Источники:

счеты как считать
Как правильно посчитать от 1 до 1000 на японском языке?

Умножение — одна из четырех арифметических операций, изучаемых с первого класса школы. Наряду со сложением она, пожалуй, чаще всего применяется в повседневной жизни. При этом под рукой не всегда есть калькулятор или листок бумаги. Именно поэтому знание того, как умножать в уме числа, просто необходимо любому современному человеку. Тем более что эффективность устного умножения достигается путем использования всего одного правила и нескольких простых приемов.

Вам понадобится

Знание таблицы умножения чисел от 0 до 9. Умение складывать и вычитать числа.

Инструкция

Проверьте, не описывается ли задача одним из случаев, позволяющих произвести быстрое умножение. Для этого проанализируйте, не является ли один из сомножителей числом 4, 5, 8, 9, 10, 11, 25 или числом, образованным путем умножения перечисленных на числа 10 (например, 40, 500, 1000, 250). В случае если это так, произведите быстрое умножение. При умножении на число 10 и его степени, допишите после умножаемого числа столько нулей, содержится в множителе, кратном . Это будет результатом. Так, 52 * 100 = 5200. При умножении на 4 дважды удвойте умножаемое число. При умножении на 8 удвойте умножаемое число. При умножении на 5, умножьте число на 10, а затем разделите на 2. При умножении на 25, умножьте число на 100, а затем дважды разделите на 2. Для умножения числа на 9, умножьте его на 10 (допишите один ноль) и вычтите его же из результата. Например, 56 * 9 = 56 * 10 — 56 = 560 — 56 = 504. Для умножения числа на 11, умножьте его на 10 и прибавьте его же к результату. Так, 56 * 11 = 56 * 10 + 56 = 560 + 56 = 616. Если задача не допускает быстрого умножения, перейдите к следующему шагу.

В советское время таким приспособлением, как русские арифметические счеты, пользовались продавцы практически во всех магазинах, а также финансисты в банках, кассиры, бухгалтеры и представители других профессий. Однако о том, как считать на счетах, в наше время имеют представление далеко не все, так как место этого счетного приспособления вытеснили более современные приборы.

Как считать на счетах: основные принципы

Когда все костяшки счет выровнены по краю с правой стороны, это означает, что счеты выставлены на нулевое положение. Всего на счетах 8 (или 10) рядов, каждый из которых обозначает определенный класс цифр — от единиц до десятков тысяч (или сотен и миллионов, если на счетах 10 рядов). Так, самый верхний ряд обозначает десятки тысяч, второй сверху — тысячи, третий — сотни, четвертый — десятки, пятый — единицы, шестой (в нем всего четыре костяшки) — четверти, седьмой — десятые (0,1), и восьмой — сотые (0,01).

Как работать на счетах: чтобы набрать любое число, требуется костяшки соответствующего класса цифр подвинуть влево. Например, чтобы набрать число 5 844,75, нужно передвинуть 5 тысяч, 8 сотен, 4 десятка, 4 единицы и три четвертака (или 7 десятых и 5 сотых). Если осталось непонятно, как считать, то советуем ознакомиться с нашей статьей .

Арифметические действия на счетах

Можно научиться считать на счетах как самостоятельно, так и под руководством кого-то, кто уже умеет это делать. Совершать сложение на счетах очень просто: необходимо сначала набрать костяшками первое число, а после этого перенести справа налево второе число из оставшихся костяшек. Если их не хватает, то нужно отодвинуть одну костяшку на один класс выше, при этом сложение всегда начинают с нижних рядов.

Вычитание — обратный процесс, только начинать вычитать необходимо с верхних рядов. При этом от большего числа, разумеется, отнимают меньшее, и, если костяшек в каком-то ряду не хватает, отнимают одну классом ниже.

Чтобы посчитать на счетах, как на калькуляторе, нужно иметь большой опыт. Так, умножение и деление на русских счетах — действие далеко не самое простое и быстрое. К примеру, чтобы умножить любое число на два, нужно сложить это число со вторым таким же числом, то же самое относится и к умножению на три. Умножение на 4 — это умножение числа на 2 и последующее его умножение снова на 2.

Чтобы умножить число на 5, нужно разделить число на 2 и умножить на 10 (чтобы умножить на 10, нужно перенести костяшки на уровень выше). Умножение на числа больше 5 производится благодаря комбинации описанных методов.

Что до деления, то проводить его при помощи счет довольно сложно и, чаще всего не рационально.

Для тех, кто интересуется историей и кому хочется узнать о первых навыках человека в счете, полезно будет ознакомиться с нашей статьей .

Введение

С потребностью более сложного счета были изобретены счетные доски, применявшиеся для арифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме, Древнем Китае и в других странах.

Общие принципы счетных досок — разделение линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов. Камешек для греческой счетной доски (абак) назывался псифос; от этого слова было произведено название для счёта — псифофория , «раскладывание камешков». У римлян камешек называли калькулюс, а счет на абаке получил название калькуляция . И сейчас подсчет расходов называют калькуляцией, а человека, выполняющего этот подсчет — калькулятором, также называется современный электронный прибор для счета. Среди применяющихся в современности вариантов абака — русские счёты и японский соробан.

Актуальность моей работы состоит в том, что в наше время сложных информационных технологий важно понимать, что стояло у истоков зарождения вычислительной техники, как потребность в счете и обработке сложных вычислений способствовала развитию вычислительной техники и привела к появлению сложных современных вычислительных систем.

Выдвигаемая гипотеза:

Древние приспособления для счета позволяли выполнять сложные вычисления.

Цель: изучить способы счета на древних приспособлениях посредством проведения эксперимента.

Задачи:

изучить теоретический материал;

изучить способы математических действий на приспособлениях;

изготовить соробан;

провести эксперимент по выполнению вычислений на приспособлениях для счета;

зафиксировать результаты вычисления при помощи фотографий;

сделать выводы по полученным результатам.

Описание древних приспособлений счета

Означает, что полоска используется для отложения разряда миллионов;

Для отложения разряда сотен тысяч;

Разряда десятков тысяч;

Разряда тысяч;

Разряда сотен;

Разряда десяток;

Разряда единиц.

Означает, что эта полоска используется для отложения унций.

Чаще всего абаком пользовались для денежных расчетов налогов и торговли.

Счет на абаке сменил более древний счет на пальцах.

Соробан — это японские счёты, которые появились в Японии в XVI веке. Соробан является потомком абака.

Четыре нижние костяшки называются «земными», и каждая представляет собой единицу.

Верхняя костяшка называется «небесной» и считается за пять «земных».

В начальных классах японских школ, до сих пор обучают детей счету на соробане.

Русские счеты

На Русских счетах одиннадцать полос спиц с костями.

Дробная часть начинается со спицы с 4-мя костями. И от нее вниз располагается еще три спицы для дробной части.

Вверх от дробной части идут спицы по 10 костей, начиная с разряда единиц до миллиона.

Способы вычислений на древних приспособлениях для счета

Способ и метод счета на абаке

В первую полоску ставили столько камешков, сколько в числе единиц, во вторую полоску — сколько в нем десятков, в третью — сколько сотен, и так далее. В верхнем разделе каждый камешек равен 5 в первой полоске, 50 во второй и так далее. Три правые полоски предназначались для счета дробями.

Вычисления производились слева на право.

Способ и метод счета на соробане

Набор числа на соробане. Сложение

Например, 254+333=587:

1)Откладываем 254

2)Прибавляем 333

3)Получаем 587

Вычитание

Вычитание происходит по той же системе, что и сложение. Разница в том, что при

недостаче бусинок их берут у старшего разряда.

Откладываем 333, затем вычитаем из него 254

Получаем 79

Способ и метод счета на русских счетах

В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц — десятки, сотни и т.д., ниже — четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть копейки. Черным цветом выделены центральные костяшки (для удобства).

Набор числа:

Сложение

Вычитание

Умножение

Умножение на счетах является не самым быстрым и простым.

Деление

Эксперимент с древними приспособлениями счета

Задача:

3.1 Решение задачи по математике при помощи соробана

Сначала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191 (км.)

Получаем 3191

Затем из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851 (км.)

Получаем ответ 1851 (км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851 (км).

3.2. Решение задачи по математике при помощи русских счет

Так же для начала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191(км.)

Получаем 3191 (км.)

Из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851(км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851(км.).

Вывод

Недостаток соробана заключается, что невозможно сохранить результат вычислений.

Недостатки использования русских счет заключаются в том, что нельзя сохранить результат, большие по размеру.

Список использованных источников и литературы

Апокин И.А., Майстров Л.Е. История вычислительной техники. М.: Наука, 1990г.- 400 с.

2. Берназани Д. Соробан/Абакус: Справочное пособие,2013 г.-150 с.

3. Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с.

4. Депман И.Я. История арифметики: Пособие для учителей,

Издание второе, исправленное, М.: Просвещение, 1965 г.- 416 с.

Интернет ресурсы:

https://ru.wikipedia.org/wiki

http://all-ht.ru/inf/history/p_0_4.html

Еще осталось в памяти то время, когда простейшие калькуляторы были роскошью, а о компьютерах и речи не было. Продавцы, почтовые работники и даже банковские служащие пользовались счетами.

Инструкция

1. Счеты – примитивный вычислительный агрегат, тот, что представляет собой счетные кольца, нанизанные на тонкие спицы. Обрамленные цельной канвой, счеты заключают в себе всю систему чисел – единицы, десятки, сотни и т.д. На верхних рядах счет расположены целые числа, причем их значение уменьшается с всей дальнейшей спицей: от сотен тысяч к единицам. Под коротким рядом «костяшек» расположены дробные числа: от десятых до тысячных.

2. Самыми примитивными вычислениями на счетах являются сложение и вычитание. Числа набираются начиная с первого ряда целых: от 1 до 10. Дальнейший рад (на одну спицу вверх) – от 11 до 20 и т.д. Набирайте нужное число, передвигая «костяшки» из соответствующего ряда справа налево. Когда один ряд на спице заполнится, воспользуйтесь числами большего значения – то есть одна «костяшка» верхнего ряда заменяет 10 «костяшек» нижнего. Складывая числа, добавляйте «костяшки» в соответствующие ряды. Дабы посчитать окончательный итог, «спускайтесь» внизу вверх – миллионы, тысячи, сотни и т.д.

3. Вычитание на счетах производится таким же методом, что и сложение, только в обратном порядке. То есть вычитая из одного числа другое, убирайте «костяшки» из соответствующих рядов. Таким образом, во время подсчета двигайтесь сверху вниз. Окончательную сумму вы узнаете, подсчитав кольца, оставшиеся в левой стороне счет.

4. Для всякого числа умножение на счетах производится различными методами. Если вам необходимо умножить на 2 либо 3, замените это действие сложением, «плюсуя» число 2 либо 3 раза соответственно. Умножение на 4 – это сложение (2*2).

5. Дабы умножить на 5, перенесите все косточки счет на одну линию вверх (то есть умножьте его на 10), после этого разделяете число напополам в уме.

6. Дабы умножить число на 6, его необходимо умножить на 5 описанным выше методом, после этого к полученному итогу прибавить число, которое было в начале вычислений.

7. Дабы умножить на 7, вначале умножьте число на 10, а после этого от полученного значения отнимите умножаемое число три раза.

8. Умножение на 8 либо 9 заменяют умножением на 10, но без переноса 2х либо 1й (при умножении на 8 и 9 соответственно) косточки наверх.

9. Множители, следующие позже 10, «раскладывают» на составляющие. Скажем, вам необходимо умножить на 12 – вы раскладываете данный множитель на 10 и 2. Сложите число с самим собой (умножьте на 2), после этого прибавьте к нему удесятеренное значение.

10. Деление на счетах – процесс непростой и доступный только специалистам. В бывшие времена необходимо было проходить особое обучение, дабы освоить деление.

Умножение – одна из четырех арифметических операций, постигаемых с первого класса школы. Наравне со сложением она, вероятно, почаще каждого используется в повседневной жизни. При этом под рукой не неизменно есть калькулятор либо лист бумаги. Именно следственно умение того, как умножать в уме числа, примитивно нужно любому современному человеку. Тем больше что производительность устного умножения достигается путем применения каждого одного правила и нескольких примитивных приемов.

Вам понадобится

Знание таблицы умножения чисел от 0 до 9. Знание складывать и вычитать числа.

Инструкция

1. Проверьте, не описывается ли задача одним из случаев, дозволяющих произвести стремительное умножение. Для этого проанализируйте, не является ли один из сомножителей числом 4, 5, 8, 9, 10, 11, 25 либо числом, образованным путем умножения перечисленных чисел на степени числа 10 (скажем, 40, 500, 1000, 250). В случае если это так, произведите стремительное умножение. При умножении на число 10 и его степени, допишите позже умножаемого числа столько нулей, сколько содержится в множителе, кратном десяти. Это будет итогом. Так, 52 * 100 = 5200. При умножении на 4 двукратно удвойте умножаемое число. При умножении на 8 трижды удвойте умножаемое число. При умножении на 5, умножьте число на 10, а после этого поделите на 2. При умножении на 25, умножьте число на 100, а после этого двукратно поделите на 2. Для умножения числа на 9, умножьте его на 10 (допишите один нуль) и вычтите его же из итога. Скажем, 56 * 9 = 56 * 10 – 56 = 560 – 56 = 504. Для умножения числа на 11, умножьте его на 10 и прибавьте его же к итогу. Так, 56 * 11 = 56 * 10 + 56 = 560 + 56 = 616. Если задача не допускает стремительного умножения, перейдите к дальнейшему шагу.

2. Расположите множители в последовательности убывания порядка их чисел. Для этого примитивно сравните длину сомножителей в символьном представлении и поставьте на первое место больше длинный множитель. Скажем, требуется помножить 47 на 526. Умножение легче будет изготавливать, если представить задачу как 526 * 47.

3. Мысленно разбейте всякий множитель на сумму чисел с точностью до порядка. Представьте задачу умножения в виде произведения этих сумм. Так, 526 * 47 = (500 + 20 + 6) * (40 + 7).

4. Умножьте в уме числа. Произведите последовательное умножение чисел суммы, на которую был разбит 1-й сомножитель на числа суммы второго сомножителя. Позже всякого умножения складывайте полученное число с предыдущим итогом. Используйте примитивные правила умножения, приведенные в первом шаге. Скажем, 526 * 47 = (500 + 20 + 6) * (40 + 7) = 500 * 40 + 20 * 40 + 6 * 40 + 500 * 7 + 20 * 7 + 6 * 7 = 20000 + 800 + 240 + 3500 + 140 + 42 = 24722.

Обратите внимание!
Изготавливаете главные расчеты только на калькуляторе либо в электронных таблицах на компьютере.

Полезный совет
Выучите таблицу умножения от 1*1 до 9*9. Это дозволит вам стремительно находить произведения маленьких чисел.

Как считать на счетах | Рождённые в СССР

Здравствуйте, дорогие читатели! Я заметил, что современные дети почти разучились совершать в уме простейшие арифметические действия. До того дошло, что вполне обычной стала картина: стоит стайка сорванцов в магазине с пакетами чипсов и мороженым в общей на всех корзинке – и нетерпеливо наблюдает за несложными манипуляциями самого смышленого их собрата. А тот с помощью смартфона высчитывает, хватит ли им ещё и на бутылку «Кока-колы». Да-а, представляю удивление ребят, если бы их любимая Марь Иванна заявила на очередном уроке математики: «А сегодня мы узнаем, как считать на счетах!»

Но ведь, скорее всего, многие из сегодняшних школьников и не слыхивали, что это за диво такое – деревянные счеты. А я помню, как весело было стучать приятными на ощупь костяшками и представлять себя самым важным по детскому разумению человеком в магазине – кассиром, счастливым обладателем больших, «настоящих» счетов! Можно было целый час простоять рядом с кассой, завороженно наблюдая, как кошка за мышкиной беготней, за веселыми деревяшками под ловкими пальцами молодой кассирши, резво облетающими счеты. Как считать, она, конечно, ни на секунду не задумывалась, это же было основным навыком в её профессии.

Если вам удастся раздобыть счеты, или с детства оставили на память – давайте вместе попробуем вспомнить эти навыки. Хотя бы сложение и вычитание припомним, ведь умножение и деление – более сложные операции на этом инструменте. Хотя я слышал, что сейчас есть люди, желающие и находящие такую возможность, чтобы их детей обучали так называемой ментальной математике. Для этих целей они приобретают малышам счеты абакус. Как считать на них, и что это за счеты? Я думаю, информации на эту тему в сети хватает.

Мы же с вами попытаемся вспомнить уроки счета. Итак, как считать на счетах – инструкция ). Сначала «обнуляем» наши счеты, сбрасывая все кругляшки на правый край. Числа представлены костяшками над тем рядом, где их четыре. Располагаются по разрядам – от единиц над вышеупомянутым рядом разряды увеличиваются к десяткам, сотням и далее. Ниже единиц размещаются четверти, десятые и сотые. Почему центральные костяшки обычно окрашены в черный цвет? Для более удобной ориентации при счете.

Для сложения набираем число, скажем, 937. Для этого влево отбрасываем нужное количество костяшек соответствующего разряда. Теперь, чтобы прибавить к этому, допустим, число 134 – добавляем его поразрядно, начиная с младшего разряда. Это делается для того, чтобы если в одном из разрядов не хватает костяшек – оставить их в данном ряду в том количестве, которого не хватило, и прибавить одну костяшку в старшем над этим ряду.

Разность чисел можно вычислить похожим на нахождение суммы способом, сверху вниз. В ряду, где имеется недостаток костяшек, следует оставить их в количестве, равном 10 минус Х. За Х принимаем число недостающих костяшек и сдвигаем одну костяшку верхнего ряда вправо. Думаю, если вы проделывали эти манипуляции на вытащенных из закромов счетах – разобрались быстро. Но не торопитесь давать объявление: «Учим считать на счетах!» Вот научитесь самостоятельно умножать и делить на них – тогда пора обзаводиться учениками ).

А я во время нашего урока вспомнил еще одно применение этого инструмента для счета, не самое математическое, возможно. После уроков берешь возле пустынной асфальтовой дорожки с уклоном у троих друзей волшебные колесики – и вот уже только ветер свистит в ушах, да как! Считать на счетах любой может научиться, а вы попробуйте удержаться на четвереньках на этом предвестнике скейтборда!

Русские счёты в учебном процессе и на столах бухгалтеров / Хабр

Вы будете несказанно удивлены, но компьютеры существовали не всегда – до их изобретения, в течение минимум двух с половиной веков, наши предки-бухгалтеры пользовались так называемыми русскими счётами.
Под катом находятся старые рисунки и фотографии, наглядно демонстрирующие, как это происходило.

Начнем с конца позапрошлого века: более ранние фотографии отсутствуют, поскольку с фотографическими аппаратами тогда было туго.
Образцово-показательное рабочее место бухгалтера – рисунок из журнала «Счетоводство» (первого русского бухгалтерского журнала, между прочим).

А это урок бухгалтерии в Московском коммерческом училище, фотография из юбилейного издания от 1904 г. Вон они счёты, на столе преподавателя.

Еще одно известное учебное заведение – Московская Практическая академия коммерческих наук. Тоже из юбилейного издания, но уже от 1910 г. Преподаватель – очень известный в бухгалтерских кругах человек: Александр Васильевич Прокофьев, автор курса двойной бухгалтерии, переиздававшегося не менее двадцать раз (ну и скукотища, наверное!).

А это – аудитория С.-Петербургских высших коммерческих счетоводных и железнодорожных курсов Михаила Владимировича Побединского, тоже очень известного человека. Где-то 1914 год или чуть раньше. На столах, естественно, счёты – куда без них?

Революция покончила с царскими учебными заведениями, но не смогла покончить с русскими счётами. Глядите, счёты на столах работниц Чрезучета – была в Петрограде такая контора, намеревавшаяся учитывать все имущество революционного города вплоть до последнего гвоздя.

Одним из немногих не прикрытых революций учебных заведений были екатеринославские курсы «Полиглот». Поблажка вышла из-за того, что курсы образовались буквально за несколько дней до Октябрьской революции. Фотография из юбилейного издания от 1927 г.

Разумеется, счёты использовали не только в учебном процессе, но и в практической деятельности.
Рисунок из бухгалтерского журнала (какого, уже не упомнить, конец 1920-х). Вообще, если художник хотел нарисовать бухгалтера, он рисовал человека со счётами, и все становилось ясно.

А это счетный кабинет Ленинградского областного промышленно-экономического техникума, 1928 г. Бухгалтеры обучаются.

Упомянутые выше курсы «Полиглот», но несколькими годами позже и переименованные в Азово-Черноморский учебный комбинат. По правую руку будущих бухгалтеров – русские счёты, а по левую – арифмометры. Конкуренция между гаджетами в самом разгаре, и исход ее совершенно не ясен.

Картинка из книжки от 1929 г. Книжка называлась «Какая польза в хозяйстве от записей и расчетов» и рассказывала о том, как умный мужик записывал в тетрадочку свои операции и у него сложилось тип-топ, а недальновидный сосед смеялся да подтрунивал, пока не остался у разбитого корыта.

Следующие рисунки середины 1930-х, на тему сельскохозяйственной бухгалтерии, но уже не единоличной, а колхозной. Тренд, сами понимаете. Из журнала «Учет в социалистическом земледелии».

В 1935 г. журнал «Учет в социалистическом земледелии» был переименован в «Учет и финансы в колхозах». Новая вычислительная техника наступала на пятки, но фотографии бухгалтеров со счётами продолжали исправно публиковаться. Вот их сколько, и это только из моей коллекции, мизер от общего числа, нащелканного неугомонными советскими фотокорами.

Ну и в заключение фотография из журнала «Спутник счетовода» от 1932 г., тоже на сельскохозяйственную тематику. Колхозный бригадир подсчитывает трудодни.

Собственно это все. Через несколько десятилетий появились контрабандные персоналки из Китая, и бухгалтеры зажили как белые люди, в свое удовольствие.

Как появились счеты — HintFox

Люди издавна старались облегчить себе счет с помощью различных средств и приборов. Первой, самой древней «счетной машиной» были пальцы рук и ног. На них человек научился отсчитывать довольно большие числа. Различными загибами пальцев рук изображали не только единицы и десятки, но и сотни и тысячи. Изображение чисел с помощью жестов рук продолжали до миллионов.

В древности торговцы производили расчеты при помощи зерен, камешков и раковин, которые впоследствии стали выкладывать на специальной доске, названной затем абаком. Абак у греков и римлян подвергся дальнейшему усовершенствованию и стал счетной доской, счетным прибором, вроде наших нынешних счетов.

Русский народ изобрел идеальный прибор – счеты — для облегчения счисления по десятичной системе. Эти счеты по справедливости называются русскими. В книгах можно встретить указание, что счеты были изобретены китайцами, что они от китайцев перешли к сибирским народам и что известные в русской истории купцы Строгановы привезли их в Россию. Указывается и время, когда якобы появились счеты в России: по одним источникам – при Дмитрии Донском (XIV век), по другим – при Петре Первом (на рубеже XVII и XVIII веков). Эти рассказы лишены основания, к сожалению, рассказы о восточном происхождении попали в «Историю государства Российского» Н. М. Карамзина и отсюда в большинство учебников.

Китайцы, правда, имеют счетный прибор, соответствующий нашим счетам, но он основан на другой идее. Он носит название «суан-пан» и представляет неглубокий ящик удлиненной формы, разделенный по длине на неравные части перегородкой. Поперек ящика, от одной более длинной стенки к противоположной, идут укрепленные концами в стенках прутики. На всех прутьях в более широком отделении ящика, ближе стоящем к считающему, имеется по пяти шариков; в верхнем, более узком отделении ящика, на каждом прутике по два шарика. Шарики нижней части суан-пана служат для счета до пяти, из двух шариков верхней части суан-пана каждый соответствует пятерке.

В XVI веке китайский суан-пан был усвоен японцами, лишь с тем отличием, что в верхнем отделении прибора японцы ставили на каждый прутик по одному шарику. Прибор этот в Японии называется «сорубан».

Изменение, внесенное японцами в устройство прибора, правильно, так как второй шарик является излишним: каждый раз, когда в верхней части прутика надо придвинуть к перегородке второй шарик, получается десяток, и, очутившись у перегородки, два шарика нужно откинуть и заменить одним шариком в нижней части следующего слева прутика. Таким же образом следовало бы удалить с нижнего отделения суан-пана и сорубана пятые шарики, а у русских счетов – с каждой проволоки десятые шарики.

Надо отметить, что одно из самых ранних описаний русских счетов, сделанное датским математиком-богословом Петером Ван Хавеном в 1743 году, как и некоторые другие старые источники, совершенно отчетливо указывает на то, что у счетов на каждой проволоке имеется по девяти шариков. Таким образом, можно утверждать, что этот русский народный счетный прибор самим народом был доведен до совершенства. Лишний десятый шарик появился позднее и сохранился до сих пор, хотя авторы XIX столетия неоднократно указывали, что он является лишним и мешающим.

Из этого описания видно, что в китайских и японских «счетах» число 5 занимает особое место среди остальных чисел, чего нет в русских счетах. Русские счеты основаны в чистом виде на десятичном счислении, в то время как в китайском суан-пане сохранились пережитки пятеричного счисления, – счета при помощи пальцев одной руки. Следы пятеричного счисления сохранились и в римской нумерации, в которой имеем:

Шесть — VI — пять да один,

Семь — VII — пять да два,

Восемь — VIII — пять да три,

Четыре — IV — пять без одного.

До XVI века включительно западноевропейские народы пользовались способом счета, соответствующим конструкции суан-пана. Назывался этот способ «счетом на линиях». Аналогичный способ счета был и у русского народа, но он был рано совершенно вытеснен изобретением десятичных счетов, в то время как у китайцев и японцев сохранился до сих пор. Поэтому мы никак не можем считать наши десятичные счеты заимствованными от восточных народов, а должны признать их русским изобретением, а сами счеты по справедливости называть «русскими счетами»

Многие обороты нашей речи свидетельствуют о том, что счеты русским народом употребляются с очень давних пор. «Сбрасывать со счета», «прикидывать», «накидка», «скидка», «сводить счеты, «скостить» и много аналогичных выражений в народном языке появилось в результате пользования счетами в течение долгого времени.

Чаще всего на счетах приходится считать деньги. Широкое распространение русских десятичных счетов находится в связи с тем, что в России раньше, чем в других странах, возникла десятичная денежная система: рубль равен 10 гривенникам, гривенник – 10 копейкам, червонец – 10 рублям. Историки западных стран приписывают приоритет введения десятичной денежной системы Соединенным Штатам Америки. Однако там деление доллара на 100 центов установилось только к концу XVIII века. В России же переход к десятичному делению денежных единиц был закончен в 1704 году, следовательно, на 100 лет ранее Соединенных Штатов Америки.

К русским счетам мы не должны относиться с пренебрежением, как примитивному счетному аппарату. Этот прибор так долго и с такой честью служил русскому народу, что заслуживает нашей благодарности и уважения.

зачем учиться арифметике, когда считать в уме уже не надо

Проект Alma Mater

В Томске открылась школа ментальной арифметики – это педагогическая новинка, которой на самом деле уже несколько тысяч лет. Главный инструмент для обучения ментальной арифметике – счеты. Как с их помощью умножать трехзначные числа за несколько секунд и почему этот навык полезен не для учебы, а для жизни, читайте в материале.

За столом в учебной комнате сидит первоклассник Егор и перебирает костяшки маленьких счетов. Перед ним – папка толщиной в несколько сантиметров, на каждой странице –арифметические примеры. Включен секундомер.

– 152 минус 37. 92 плюс 13, – диктует преподаватель.

Егор отвечает с задержкой в несколько секунд и почти не ошибается. А если и дает неправильный ответ, то скорей от усталости. Занятие подходит к концу. А час арифметики, когда тебе всего восемь и больше всего нравятся не примеры, а хоккей, – не шутки. Когда Егор считает, он ничего не записывает. Тому, кто привык решать «в столбик», это может со стороны показаться почти чудом.

Егор не вундеркинд, не «человек дождя» и даже не отличник. Он занимается ментальной арифметикой.

Суаньпань, соробан и абак

13 коротких вертикальных спиц, на каждую нанизано по пять костяшек. Верхняя костяшка на спице отделена от нижних рамкой. Каждая нижняя костяшка называется «земной» и обозначает единицу. Верхняя – «небесная» – равняется пяти «земным». Так выглядит соробан – японский вариант китайских счетов – суаньпань. Их более древний прародитель – греческий абак.

В 2005 году журнал Forbes назвал абак вторым самым важным открытием всех времен, который больше всего повлиял на развитие цивилизации за всю историю человечества. А ЮНЕСКО признало нематериальным достоянием человечества. На счетах учат считать детей в 52 странах мира. В Японии, Китае и ряде азиатских стран счеты включены в обязательную программу начальной школы.

В чем разница?

Как мы учимся считать? Сначала складываем яблоки, кубики – этот этап называется наглядно-действенным мышлением. Потом переходим на счетные палочки, счеты. Потом нам рассказывают, что закорючки в тетради – это цифры и два яблока на письме обозначаются символом «2». Это уже абстрактное мышление.

– Проблема в том, что, когда в 4-6 лет ребенок начинает учить математику, абстрактное не является ведущей формой мышления и имеет гораздо меньшее значение для него, чем образное или даже предметно-действенное. Математическое образование должно согласовываться с периодами развития ребенка. Также, например, в художественной школе ребенка до 10 лет не учат изображать перспективу, потому что ничего из этого не выйдет, – поясняет кандидат психологических наук Дмитрий Баланев.

Зачем арифметика, когда есть калькулятор?

В обучении на счетах все начинается с передвигания костяшек пальцами обеих рук. Единицы, десятки, сотни – ребенок считает слева направо. Это для него естественно: мы так же пишем, читаем. А вот в столбик считаем справа налево, и многих это путает. Когда ребенок хорошо осваивает навык с помощью счетов, может считать в уме, поэтому методика называется ментальной. В исследовании Джеймса Стиглера, который изучал опыт применения счетов в обучении тайваньских детей арифметике, было установлено, что учащиеся пятого класса способны складывать в уме пять трехзначных чисел примерно за три секунды.

В томской школе самые старательные ученики решают около 800 примеров за месяц. Отрабатывая навык, ребята считают на скорость.

– Преподаватель, которая обучала нас, говорила, что после ментальной арифметики ей мир стал казаться более медленным. Я тоже замечаю, что отношение ко времени меняется, – говорит педагог томской школы ментальной арифметики «Пифагорка» Екатерина Абакумова. – Минута – это ужасно долго. У нас есть несколько учеников, которые любят «покопаться», довольно рассеянные, а здесь они учатся собранности.

– Некоторые школьники, научившись мгновенно считать в уме, успевают делать и классную, и домашнюю работу по математике в столбик, – рассказывает Екатерина.

Счет не в счет

Но важно понимать, что быстрый счет в уме – это только побочный эффект от занятий. Поэтому родители ошибутся, если отправят ребенка на занятия с помощью счетов, чтобы устранить пробелы по математике в школе.

– Нужно правильно ставить цель: мы учим считать не для того, чтобы научить считать, – поясняет Дмитрий Баланев. – Да, повзрослев, ребенок не будет этого делать постоянно, но этот навык находится в основе многих других действий, даже нематематических. Это нужно при оперировании информацией, при оценке – эти процессы происходят неосознанно, но, тем не менее, человек, который умеет быстро считать, умеет быстро оценивать.

Выходит, что каждый раз, когда мы, «жалея» ребенка, разрешаем ему воспользоваться калькулятором при решении примеров, мы не даем ему сформировать навык оценивания.

Чем реальней, тем лучше

Если ребенок научился считать на счетах, он переходит на так называемые «интеллектуальные счеты», то есть, считая в уме, представляет при этом не цифры, а те же костяшки счетов. В это время работает правое полушарие, отвечающее за образное мышление.

Проверить это можно легко. Ребята, которые хорошо научились считать с помощью соробана, могут параллельно считать в уме (работает правое полушарие) и переводить с английского (активизируется левое) или делать физические упражнения.

– Развитое правое полушарие помогает нам принимать решение: когда для этого используется левое полушарие, человек, действуя логически, может зайти в тупик, и именно образное мышление помогает нам найти выход из ситуации, – говорит Екатерина Абакумова.

– Математике нужны и «логики», и «образники». Проблема в другом: у нас в пользу логики произошел перекос, – поясняет Дмитрий Баланев. – Да, можно в 3-4-5 лет научить ребенка читать, писать, но смысла в этом особого нет, и, более того, никаких реальных потребностей ребенка эта деятельность не обслуживает.

По словам эксперта, куда логичнее и полезнее для развития ребенка обращать его внимание на то, что его окружает в реальном мире: вещи, явления, бытовые дела.

– Сейчас ребенок находится в обедненной среде благодаря различным цифровым устройствам. Их использование опасно тем, что вместо реального мира он имеет дело с абстракциями, о происхождении которых ничего не знает. И я вас уверяю, что, если возьмем счеты на экране планшета, какими бы реалистичными они ни были, они дают совсем не то, что реальные счеты. Я бы даже предложил делать эти костяшки разных размеров, цветов, из разных материалов, разной фактуры. Тогда счеты превращаются в отличный инструмент по изучению не абстрактного, а реального мира, – считает Дмитрий Баланев.

Галина Сахаревич

История возникновения счет, или Как хорошо уметь считать!

Ученые полагают, что человек научился считать более 100 тыс. лет назад. Вычислительные операции применялись во время обмена продуктами питания и орудиями труда с другими племенами, для составления календарей миграции животных, на которых охотились древние люди, и для определения времени посадки растений.

Естественными «счетными устройствами» были пальцы рук и ног, которых древним людям вполне хватало для нехитрых расчетов. Результаты счета фиксировались с помощью узелков на веревках или зарубок на ветках деревьев и костях животных.

Со временем стали появляться более сложные приборы для вычислений. Первым из них считается абак, придуманный в Вавилоне в III тыс. до н. э. Абак представлял собой дощечку с углублениями, по которым передвигали косточки или ракушки, имевшие определенное числовое значение. Такие счеты служили главным образом для выполнения действий сложения и вычитания. В V в. до н. э. египтяне усовершенствовали конструкцию, начав использовать вместо линий и углублений проволоку с нанизанными камешками.

Абак завоевал популярность во всем мире, а в ходе продолжительной эволюции сформировались три основных вида абака — китайские, японские и русские счеты. Все они сохранили свое назначение и с успехом применяются до сих пор, к примеру, на занятиях по программе «Ментальная арифметика».

Суаньпань — деревянная рамка с рядами натянутых проволочек, на каждой из которых по 7 косточек, — появилась в Китае в XII в. Китайцы разработали сложную технику работы на суаньпань, позволяющую складывать, вычитать, умножать, делить числа и даже вычислять квадратные и кубические корни.

В Японии на основе суаньпань сконструировали соробан. Прямоугольная рамка, поделенная по горизонтали планкой, содержит от 23 до 27 вертикальных палочек, на каждую из которых нанизано по 5 косточек: одна, равная пяти, в верхней части и четыре для обозначения единиц в нижней. Благодаря такой разбивке сумма косточек на каждой палочке может составлять все числа от 0 до 9. Соробан признан самым оптимальным и быстрым механическим счетным устройством, поскольку позволяет отображать каждое число только одним способом, что исключает путаницу при вычислениях. В Японии соробан не только активно используется в качестве учебного пособия в школах, но и популярен как вид спорта и развлечения.

Русским счетам, появившимся в допетровские времена, потребовалось 200 лет, чтобы обрести привычный нам внешний вид. Сначала русская модификация римского абака состояла из четырех полей, которые умещались в два складных ящичка. Русские счеты, основанные на десятичной системе счисления, позволяют оперировать не только целыми числами, но и четвертями, десятыми и сотыми дробными долями. Это простейшее счетное устройство использовалось российскими продавцами вплоть до конца XX века.

Сегодня научно доказано, что счеты способствуют освоению десятичной системы счисления, пониманию азов математики и совершенствованию навыков устного счета. На изучении принципов работы абака основана уникальная методика развития интеллектуальных способностей детей — ментальная арифметика, которая набирает популярность во всем мире.

Как вы рассчитываете на счетах? | блог @ CACM

Герберт Брудерер
12 ноября, 2020
Комментарии

На блошиных рынках вездесущи счеты (см. Рис. 1). Тем не менее, вряд ли кто-то из западных европейцев знает, как устроен бусовый каркас. Десятилетия назад такие устройства часто использовались в наших школах. Их использовали, чтобы учить детей считать.

В Венском техническом музее (Вена) хранится практическая модель. Наблюдения показывают, что у посетителей возникают проблемы, если для расчета доступно слишком мало бус в ряду.Подобные опыты также происходят во время живых демонстраций.

Бисерная рамка тысячелетней давности бывает разных форм, например, китайские, японские или русские счеты. В Китае эти вспомогательные средства все еще можно найти время от времени, однако их в значительной степени заменили смартфоны. Из российской системы счета были разработаны школьные счеты. Он основан на десятичной системе счисления. Эти арифметические фреймы представляют собой цифровые устройства.

Рис. 1: Три бортовых рамки, каждая в нулевом положении.

Кредит: Bruderer Informatik, CH-9401 Rorschach, Switzerland

Счеты подходят для всех четырех основных арифметических операций

С помощью вычислительной доски можно выполнять все четыре основных арифметических операции — сложение, вычитание, умножение и деление. Умножение — это повторное сложение; деление, последовательное вычитание. С бусинками обученные люди могут очень быстро решать арифметические задачи. Это показано на видео из Немецкого музея в Мюнхене.

В нулевом положении все валики находятся либо с левой, либо с правой стороны. При расчетах предпочтительно начинать с единиц, десятков и сотен.

Единицы: десятки, сотни, тысячи.

На нижнем стержне указаны единицы, на втором нижнем стержне — десятки, на третьем нижнем стержне — сотни и т. Д. Каждый стержень содержит 10 бусинок. Для удобства работы по пять бисеринок в каждом ряду разного цвета.

Представление номера

В следующем примере все буртики находятся на левой стороне в основном положении.Значения 12 345 (см. Рис. 2) и 98 765 (см. Рис. 3) отображаются следующим образом:

Рис. 2 : Счетная рамка показывает число 12 345. На нижнем стержне десятичного калькулятора указаны единицы, над ними — десятки и т. Д.

Кредит: Bruderer Informatik, CH-9401 Rorschach, Switzerland

Рис. 3: Значение 98 765 отображается на счетной рамке.

На этом цифровом калькуляторе 10-значные числа, т.е.е. могут отображаться значения до 9 миллиардов (9 999 999 999).

Кредит: Bruderer Informatik, CH-9401 Rorschach, Switzerland

Несколько простых примеров объяснят эту процедуру. Есть разные способы.

Сложение: 37 + 8 =?

Все борта находятся на левой стороне . Сначала вы перемещаете вправо 3 десятка бусинок и 7 единиц бисера. Но для добавления значения 8 доступны только 3 единицы бисера. Таким образом, вы перемещаете 1 десятку бусинки вправо и удаляете 2 единицы бисерины: 37 + 8 = 37 + (10-2) = 45.

или:

Все борта находятся на правой стороне . Сначала влево перемещаются 3 десятка бусинок и 7 единиц бисера. Но для добавления значения 8 доступны только 3 единицы бисера. Следовательно, перемещаем на 1 десятку бусинки влево и удаляем 2 единицы бусины: 37 + 8 = 37 + (10-2) = 45.

Вычитание: 456-78 =?

Все бусинки на левой стороне. Вы перемещаете 6 единиц бусинок, 5 десятков бусинок и 4 сотни бусинок в правую сторону. Чтобы вычесть число 8, переместите 1 десятку бусинки влево и прибавьте 2 единицы бисерины (-8 = -10 + 2).Счетная рамка показывает значение 448. Чтобы вычесть значение 70, переместите 1 сотню шариков влево и 3 десятка шариков вправо (-70 = -100 + 30). Это дает число 378.

или:

Все бусинки на левой стороне. Вы перемещаете 6 единиц бусинок, 5 десятков бусинок и 4 сотни бусинок в правую сторону. Чтобы вычесть число 70, вы переместите 1 сотню бусинок влево и прибавите 3 десятка бусинок (-70 = -100 + 30). Счетная рамка показывает значение 386. Чтобы вычесть значение 8, переместите шарик на 1 десяток влево и на 2 единицы вправо (-8 = -10 + 2).Это дает число 378.

Умножение: 4 x 57 =?

Все бусинки на левой стороне. Сначала устанавливается значение 57. Число 57 складывается 3 раза: прибавляется 1 десятка бусинок, и удаляются 3 единицы бисерины (+ 10-3 = + 7). Теперь 1 сотня бусинок перемещается вправо, 5 десятков бусинок уходят влево (+ 100-50 = + 50). Счетная рамка показывает значение 114. Одна десятка шариков перемещается вправо, 3 единицы шарика удаляются (+ 10-3 = + 7). Добавлены пять десятков бусин (+50). На счетах отображается значение 171.Семь бусинок и 1 сотня бусинок перемещаются вправо, 5 десятков бусинок перемещаются влево (+ 7 + 100-50 = 57). По счетной рамке результат 228.

Дивизион: 1,737: 579 =?

Все бусинки на левой стороне. Число 579 вычитается как можно чаще. Сначала устанавливается число 1,737 (дивиденд). Теперь 5 сотен бусин сдвинуты влево (-500). Поскольку доступно всего 3 десятка бусинок, 1 сотня бусинок идет влево, 3 десятка бусинок перемещаются вправо (-100 + 30 = -70).Одна десятка бусинок идет влево, одна бусина — вправо (-10 + 1 = -9). Устройство показывает значение 1158.

Теперь 1 тысяча бусинок уходит влево, 5 сотен бусинок вправо (-1000 + 500 = -500). Одна сотня бусинок перемещается влево, 3 десятка бусинок перемещаются вправо (-100 + 30 = -70). Теперь отнимается 1 десятка бусинки, добавляется 1 бусинка (-10 + 1 = -9). В рамке теперь отображается число 579.

Наконец, 5 сотен шариков, 7 десятков шариков и 9 единиц шариков перемещаются в левую сторону (-500-70-9 = -579), и в рамке отображается значение 0.Нам пришлось 3 раза вычесть число 579 (делитель), поэтому результат (частное) равен 3.

Как рассчитывали римляне?

Работать с римской системой счисления сложно. Великие здания показывают, что римляне, тем не менее, были хорошими калькуляторами, потому что вычисления производились на счетах. Римские цифры использовались только для обозначения чисел (начальные значения, промежуточные и окончательные результаты). Сохранилось лишь несколько римских ручных абаков. Они расположены в Аосте, Париже и Риме.В них используются не бусинки, а пуговицы, которые перемещаются в вертикальных пазах. Для этого устройства кладут на стол. Цифры от 0 до 9 представлены 4 кнопками единиц и 1 кнопкой пятерки, числа от 10 до 100 — 4 кнопками десятков и 1 кнопкой пятидесятых и т. Д. Римляне могли, таким образом, представлять число 0, но не имели числа . 0.

Заключительные замечания
По сути, вам не нужно рассчитывать с бортовой рамкой, вам просто нужно посчитать.Поэтому говорят также о счетной рамке.
Список литературы
Барнард, Фрэнсис Пьерпон: счетчик забросов и счетная доска. Глава в истории нумизматики и ранней арифметики, Oxford University Press, Oxford 1916, 358 страниц, 63 пластины, https://amzn.to/35qEddC
Bruderer, Herbert: Meilensteine der Rechentechnik, De Gruyter Oldenbourg, Берлин / Бостон, 3-е издание 2020 г., том 1, 971 страница, 577 иллюстраций, 114 таблиц, https: // www.degruyter.com/view/title/567028?rskey=xoRERF&result=7
Bruderer, Herbert: Meilensteine der Rechentechnik, De Gruyter Oldenbourg, Берлин / Бостон, 3-е издание 2020 г., том 2, 1055 страниц, 138 иллюстраций, 37 таблиц, https://www.degruyter.com/view/title/567221?rskey = A8Y4Gb & результат = 4
Bruderer, Herbert: Milestones in Analog and Digital Computing, Springer Nature Switzerland AG, Cham, 3-е издание 2020 г., 2 тома, 2075 страниц, 715 иллюстраций, 151 таблица, https: //www.springer.com / de / book / 9783030409739
Дилсон, Джесси: Счеты. Карманный компьютер, St.Martin’s Press, Нью-Йорк, 1968, 143 страницы, https://amzn.to/35mVPHy
Кодзима, Такаши: японские счеты. Его использование и теория, Charles E. Tuttle Company, Ратленд, Вермонт, Токио, 1969, 102 страницы
.
Луна, парирование: счеты. Его история; его дизайн; его возможности в современном мире, Gordon and Breach Science Publishers, Inc., Нью-Йорк, 1971, 186 страниц.
Пуллан, Дж. М .: История абака, Hutchinson & Co (Publishers) Ltd, Лондон, Мельбурн и т. Д.1968 г., 140 с.
Йошино, Ю.: Объяснение японских счётов, Dover Publications, Inc., Нью-Йорк, 1963, 253 страницы.
Герберт Брудерер — бывший преподаватель дидактики информатики в ETH Zurich. Совсем недавно он стал историком технологий. [email protected], herbert.bruderer@bluewin.
Записей не найдено
Abacus, самый старый калькулятор — ALOHA Mind Math
11 Apr Abacus, самый старый калькулятор
Отправлено в 08:06 в без категории по alohamindmath Использование инструментов для выполнения математических расчетов и транзакций используется примерно с 2700 г. до н.э. в регионе Месопатамии.Abacus, также называемый счетной рамкой, является старейшим из существующих калькуляторов. В нашей сегодняшней статье мы поговорим о различных типах абачи и о том, почему мы выбрали именно тот, который мы используем в ALOHA.
Абак, самый старый калькулятор
One использует счеты для сложения, вычитания, умножения и деления. Он используется для ручного скольжения счетчиков по стержням, связанным рамкой, отсюда и название — счетная рамка. Прелесть такого устройства в том, что оно помогает студентам изучать основную систему счисления, заимствовать и переносить числа, комбинации пяти и десяти, а также визуализировать математические и мысленные вычисления.Одним из дополнительных преимуществ абака является то, что они могут использоваться людьми с ослабленным зрением.
Шумерские счеты —
, созданный в период 2700-2300 гг. До н.э. в районе Месапотамии. Это самая старая форма счетного устройства. Изображение справа представляет этот тип счётов в виде часов. Ее также называют шестнадцатеричной системой, которая имеет платформу на 60 отсчетов. Возможно, поэтому он так хорошо работает с нашими текущими методами учета времени.Вы можете представить себе это на запястье?
Реконструкция римских абаков — музей RGZ в Майнце, 1977 г. Бронзовый оригинал находится в Национальной библиотеке Франции в Париже. (Фото: Википедия)
Римские счеты —
На самом деле
был больше похож на стол с тремя различными типами, которые назывались пылевыми счётами, линейными счётами и рифлеными счётами. Представьте, что вы пытаетесь выполнить деление римскими цифрами. Например, число 1943 будет MCMXLIII.Теперь разделите это на LXVII, и вы получите что? XXVIIII. Мне нужно много подумать!
Суанпан —
Это версия Abacus, используемая китайцами. Он используется со 2 века до нашей эры. Внешний вид представляет собой каркасную конструкцию с двумя бисеринками в каждом ряду над разделительной перемычкой и пятью бисеринами снизу. Suanpan позволяет выполнять основные арифметические функции, а также функции извлечения квадратного и кубического корня.
Русский Abacus —
Шоты — это то, что русские называют своими счетами.На каждом стержне 10 бусинок. Расчеты производятся перемещением всех бусинок с правой стороны на левую. Каждая проволока имеет по 10 бусинок на изогнутой проволоке. Ряд из 4-х бисеринок — четвертинки «копейки» или «рубля». Эти абаки регулярно использовались в России до 1990-х годов. Есть версия, которая используется во многих западных странах, похожая на русскую Schoty.
Soroban Abacus —
На фото справа пример японских счётов. Он имеет одну бусину вверху и 4 или 5 бусинок внизу.Японские счеты называются Соробан. Соробан имеет нечетное количество столбцов. Обычно существует минимум 9 столбцов, обозначенных точкой через каждые три столбца. Используя визуальные образы соробана, можно прийти к ответу за то же время, или даже быстрее, чем это возможно с физическим инструментом. Есть большая корреляция с мысленными образами этих счётов. Мы используем Soroban Abacus в наших программах ALOHA.
Различные типы Abacus и их использование
Abacus — одно из самых замечательных нововведений в сфере образования, которых когда-либо достигал человечество.Он следует интерактивному подходу, чтобы тренировать свой ум с основами математики на совершенно новом уровне. Абакус используется во всем мире как один из важных инструментов для развития умственных математических способностей.
Для всех вас, кто до сих пор не понимает, о чем мы говорим, Abacus — это ручное средство расчета, состоящее из бусинок или дисков, которые можно перемещать вверх и вниз на серии палочек или ниток внутри. обычно деревянный каркас. Это один из лучших способов развить чувство числа.Числа физически конструируются и обрабатываются в Abacus. Практика по 10-15 минут в день может эффективно развить ваши навыки математических расчетов.
Типы счётов
Счеты не новое изобретение, они относятся к 2700–2300 гг. До н.э. в месопотамский период как форма шумерских счётов . Он претерпел ряд модификаций в разное время в разных частях света, что привело к тому, что мы называем «школьными счетами», которые мы используем сегодня. Чтобы понять счеты, очень важно узнать о их начале и о том, как они достигли своего текущего состояния.Итак, этот пост посвящен различным типам счётов и их использованию.
Roman Abacus
Вместо рядов и строк древние римляне использовали для перемещения камней в качестве счетчиков вверх и вниз на гладком столе для вычислений. Римские счеты были разработаны для работы менял и банкиров, бизнесменов и инженеров. Счеты изготовлены из металлической пластины, где большая часть углубляется в пазы. Помимо этого, римляне также изобрели три различных типа счётов.
The Dust Abacus
The Line Abacus и
Grooved Abacus
Suanpan или китайские Abacus
Китайские счеты, известные как suanpan , обычно содержат более семи стержней с двумя стержнями. на каждом стержне верхней палубы и по пять бусинок в нижней. Каждая из двух бусинок верхней деки имеет значение 5, в то время как каждая бусинка нижней деки имеет значение 1. Проволока представляет собой степень десяти.
Изготовлен из твердой древесины. Счеты suanpan впервые были упомянуты в книге 190 г. н.э. династии Восточная Хань, а именно в Дополнительных заметках по искусству фигур, написанных Сюй Юэ. Сходство римских счётов с Suanpan проливает свет на то, что послужило источником вдохновения для их разработки.
Японские счеты соробана
Произведенный от китайского суанпан, соробан был разработан в Японии в 14 веке. Бусы в соробане изготавливаются из дерева с металлическими стержнями из ротанга или бамбука, которые скользят вверх и вниз.Японские счеты все еще используются сегодня, однако их наследие затмевается широко используемыми современными электронными калькуляторами.
Каждый столбец или стержень японских абак может представлять число от 0 до 9. Когда счет установлен на 0, все грани нижней деки выровнены по низу, а бусинки верхней деки выровнены по верху. По соответствующей стоимости каждого удилища каждая бусина нижней деки стоит 1, а верхняя дека — 5.
Абакус Ли
Абакус Ли в основном описывается как улучшенная версия абакус суанпан и соробан.Он был изобретен в 1950 году Ли Кай Ченом на Тайване. Он в основном включает в себя особенности как китайских, так и японских счётов. Одним из достоинств улучшенных счётов Ли было то, что с ними действительно легко работать и учиться для новичков.
PC: idirect.com/
Система обозначений, согласно которой каждый стержень представляет собой определенную цифру, а каждый счетчик бусинок — конкретное число, не оставляет никаких сомнений даже в уме даже самого новичка. Таким образом, на этих счетах легко выполнять различные арифметические операции быстрее и эффективнее, чем на старых счетах.
Русский Abacus
Основное отличие российских Abacus от китайских — это положение стержней. Стержни в российских абаках располагаются горизонтально. Бусинки сдвигаются справа налево. Типичные шотландские счеты имеют ширину 28 см и высоту 46 см.
Необходимо положить счеты на стол под таким углом, чтобы направление движения правой руки совпадало с проводниками счеты. Это похоже на направление книги, в которой вы пишете.Кроме того, стержни слегка изогнуты, чтобы предотвратить обратное скольжение счетных шариков.
Арифметика Рекенрек

Рекенрек или арифметическая стойка — это не просто еще один тип счётов, но его функциональность очень похожа на счеты в обучении арифметике. Итак, это версия абака, и мы должны поместить ее в список. Это средство обучения, разработанное Адрианом Трефферсом, исследователем учебной программы математики в Институте Фройденталя в Голландии, которое обеспечивает визуальную перспективу числовых отношений и различных математических операций. Он состоит из двух рядов по 10 бусин.Также доступны более крупные версии с десятью рядами по десять бусин. Каждый ряд состоит из пяти красных и пяти белых бусинок. Установка позволяет студентам подготовить мысленный образ чисел и использовать его (5 или 10) в качестве якоря для счета, сложения и вычитания.
Двоичные счеты
Последние разработки показали, что счеты больше не ограничиваются выполнением арифметических операций. Его также можно использовать для объяснения того, как компьютеры манипулируют числами. Двоичные счеты выполняет одну из таких функций, обучая преобразованию десятичных знаков в двоичные.Ряд бусинок в параллельных проволоках расположены в трех отдельных рядах, причем каждая бусина представляет счетчик как «включено» и «выключено», или «1» или «0».
Cranmer Abacus
Cranmer Abacus на самом деле является модификацией существующих абакусов для поддержки учащихся с нарушениями зрения. Эти счеты были разработаны Тимом Кранмером. Счеты позволяют учащимся манипулировать бусинками, что приведет к более глубокому пониманию чисел, чем использование калькуляторов. Это можно использовать при вычислении чисел, которые включают арифметические процессы, такие как сложение, вычитание, умножение, деление, а также для вычисления квадратных корней и кубических корней.

Идея состоит в том, чтобы использовать кусок мягкой ткани или резины позади бусинок, чтобы предотвратить любые случайные движения. Возможности еще больше расширяются, если использовать шрифт Брайля для отработки вычислений. Типичные счеты кранмера имеют размеры 6 1/8 на 3 ¼ на 7/16 дюймов. У большинства из них 13 стержней, но у некоторых есть 15. В каждом стержне содержится одна бусина, которая расположена над перекладиной, а другие четыре борта расположены ниже.
Поделитесь словом
Если вы найдете этот пост полезным, пожалуйста, помогите нам распространить информацию.Поделитесь публикацией с друзьями, семьей и коллегами. Не забывайте подписываться на наши обновления. Любые предложения и рекомендации настоятельно рекомендуются. Вы можете связаться с нами через контактную форму, и мы свяжемся с вами в ближайшее время.

До того, как появились калькуляторы — Справочник по Abacus
Счеты — это устройство, состоящее из бусинок, которые скользят по стержням, которые помещаются в раму. В древности счеты использовались как калькулятор; он помогал выполнять математические процессы, такие как счет, сложение, вычитание и умножение.Калькуляторы и компьютеры — относительно новые изобретения, в результате чего использование счётов немного устарело. Тем не менее, счеты по-прежнему являются важным средством обучения и могут упростить сложные вычисления.
Использовать перед калькуляторами
До изобретения современных калькуляторов люди могли рассчитывать, используя различные счетные устройства. Ранние люди могли использовать пальцы рук и ног для решения некоторых проблем. По мере роста самых ранних цивилизаций торговцы могли использовать камни или семена, чтобы помочь им с уравнениями.Бусы абака в конечном итоге стали жизненно важными для торговли товарами и услугами. Другие устройства, использовавшиеся до калькуляторов, включают логарифмическую линейку, кости Напьера и ранние машины, такие как аналитическая машина Бэббиджа.
Изобретение
Предшественником современных абаков была счетная доска, на которой были углубления или линии, между которыми перемещались камешки или бусинки. С другой стороны, счеты имели стержни и могли быть сделаны из камня, металла или дерева. Некоторые историки предполагают, что оригинальные счеты были изобретены в Китае тысячи лет назад, около 500 г. до н.э.C.E. Это устройство имеет как верхнюю, так и нижнюю дека с стержнями и бусинами, и называлось «суанпан».
Как это работает
То, как вы используете счеты для вычислений, зависит от стиля и дизайна инструмента. Стандартные китайские счеты имеют шесть стержней: верхняя дека с двумя бусинками на каждом стержне и нижняя дека с пятью бусинами на каждой стержне. Каждый стержень представляет собой числовое значение: сотни тысяч слева, десять тысяч следующие, тысячи, сотни, десятки и единицы справа.Все бусинки начинаются в самом нижнем положении, уложенном в нижней части счет. Вы можете считать числа, подталкивая бусинки в крайнее верхнее положение. Например, чтобы сосчитать один, вы должны переместить одну бусину на нижнюю стойку на дальнем правом стержне до упора вверх. Чтобы сложить числа, вы должны переместить бусинки вверх по стойке, которая соответствует разряду каждого числа. Количество бусинок в верхнем положении покажет сумму.
Вариации в разных культурах
Существует несколько дизайнов счётов; разные культуры и страны использовали разные инструменты.Китайские счеты — классический инструмент с пятью бусинками внизу и двумя бусинками сверху. Русский и римский дизайн также являются вариациями абака. Японские счеты, называемые соробан, до сих пор используются в современных культурах, чтобы помогать людям выполнять в уме математические вычисления.
Использование в современном обществе
Некоторые люди до сих пор используют счеты для расчета сумм. Слепые люди часто находят абачи полезными, потому что эти инструменты позволяют им манипулировать бусинками и чувствовать их, чтобы находить ответы на математические задачи.Учителя могут использовать абачи с молодыми учениками, чтобы помочь им изучить числовую ценность и другие фундаментальные математические концепции. Архитекторы, работающие в некоторых частях мира, используют abaci для измерения размеров и планирования проектов. Некоторые опытные пользователи счётов могут манипулировать бусинками быстрее, чем кто-то вводит числа в калькулятор.
Японский Анзан
Японские счеты — это обычный инструмент для математических процессов. Опытные пользователи счётов могут достичь впечатляющих скоростей вычислений, просто представив изменение положения бусинок вместо их фактического перемещения.Эта мысленная математика известна как «анзан», что означает «мысленный расчет». Некоторые ученики тратят много времени на выполнение задач по математике, чтобы помочь им повысить скорость и точность вычислений. Регулярно выполняя математические задачи на счетах, учащиеся могут расширить свои математические навыки. Освоение анзана может позволить учащимся овладеть математикой и другими академическими предметами.
Русский
Русские счеты
Abacus — первое простейшее устройство для подсчет.Они прошли долгий путь эволюции, который можно разделить на четыре этапа. Первый предвосхищает создание входа, он считает с помощью шариков, очень близко к западноевропейскому счету по линиям. Второй этап — подсчет досок. Он начинается в конце 16 века и завершается в начале 18 века. На этом этапе изобретаются русские счеты, сильно отличающиеся от современных. один.
Счеты с четырьмя полями (середина 17 века)
Он имел сначала четыре, а затем два счетных поля и был универсальный счетный инструмент.Начинают использоваться только что начатые десятичные позиционные обозначения в России, и практически все расчеты производились на счетах.
Следующий, третий этап включает 18-е и начало 19-го век. В начале этого этапа счеты приобрели классическую форму, а в дальнейшем — улучшилось только внешне, с точки зрения удобства использования. Однако на на этом этапе счеты больше не являются универсальным счетным инструментом, они превратиться во вспомогательный инструмент, расчеты на бумаге принимают ведущее место.
Четвертый этап развития русских счет включает начало 19-е 20-е века. Растущая потребность в механизации расчетов вызвала многочисленные попытки модернизировать счеты и снова придать им характер универсальный счетный инструмент. Однако эта идея была в корне противоречивой: счеты как сугубо ручной инструмент не мог конкурировать в выполнении умножения и подразделение с усовершенствованными конструкциями механических счетных машин.Русские счеты, имеющие классическая форма, оставалась самым популярным вспомогательным вычислительным инструментом до 70-е годы 20 века. С 70 лет успешно конкурируют с ними карманные электронные калькуляторы, хотя счеты все еще широко используются в настоящее время.
Литература: Апокин И., Майстров Л.Е. История компьютера удобства. М .: «Наука», 1990, с. 36–37
Типы абаков [Обновлено в 2020 г.]
Это первоначальная статья «Типы счётов».
Мы заметили, что результаты поиска Google показали две статьи по названию «Типы счётов» .Другой скопирован у нас. Мы попросили их дать обратную ссылку, но они отказались.
В соревновании Flash Anzan на Всеяпонском чемпионате по соробану чемпион Такео Сасано сумел сложить пятнадцать трехзначных чисел всего за 1,7 секунды.
Введение
Разве это не интересно? Простая рамка со скользящими биконическими бусинами решает математические задачи !! Вау, это больше, чем просто благо для человечества, не так ли? несомненно, математика всегда была и остается горьким тыквенным супом для масс.Но, как назло, математика — это часть нашей повседневной жизни, и мы вынуждены заниматься ею.
Не волнуйтесь, лучший способ выйти из этой ситуации — стать проницательным человеком. Вам интересно, как? Конечно, продолжайте читать !!. Если вы хотите изучить другие наши курсы, вы можете или если вы заинтересованы в том, чтобы зарегистрировать своего ребенка на онлайн-конкурсе Abacus, вы тоже можете 🙂
Присоединяйтесь ко мне, ребята, пока я проведу вас через всю подробную книгу воплощения человеческого изобретения в математике — The Abacus!
Abacus
Abacus — самый старый из эффективных вычислительных инструментов, используемых на сегодняшний день.Следующее можно сделать с помощью счеты.
Сложение-Вычитание
Умножение — деление
Подсчет десятичных знаков — извлечение квадратных и кубических корней
Вычисление отрицательных чисел
Поразительно, не правда ли? Мы слышим от вас. Итак, читайте дальше, чтобы получить ответы.
ABACUS — Второе лучшее древнее человеческое изобретение после ножа и карандаша
Начнем с истории..
Во-первых, люди раннего возраста сыграли важную роль в создании почти половины современных изобретений. Счеты — одно из таких эволюционных изобретений. Торговля была неотъемлемой частью древних времен, торговцы использовали для учета своих товаров гальку и ветки.
Это были времена, когда не существовало даже письменной формы чисел. В конце концов, с увеличением количества этим методом было довольно сложно управлять запасами и вести учет.
Во-вторых, математика существовала с первых дней развития бизнеса и торговли в истории эволюции человека. Вот почему счеты стали всемирно признанным инструментом. Набор Abacus действительно производит революцию в сфере образования.
Что означает слово Abacus?
ABACUS — это аббревиатура, в которой
A означает изобилие
B обозначает Beads
A означает дополнение
.
C означает Расчет
U — это Utility
.
S означает System
.
Греческое слово Abax или Abacon дало начало слову Abacus.Эти слова означают стол, планшет или плоскую поверхность. С другой стороны, семитское слово Abq, обозначающее песок, говорит об истории. Таким образом, эти описания дали начало слову Abacus.
Типы абак
Abacus — это искусственное счетное устройство, изобретенное 5000 лет назад. Кроме того, он претерпел определенную эволюцию с точки зрения дизайна и использования.
Историки считают, что китайские умы изобрели счеты около 500 г. до н.э. Тем временем слава об успехе абака начала распространяться.Такие страны, как Тайвань, Корея, Малайзия и Япония, были поражены абаковой лихорадкой. Со временем дизайн набора для счётов сильно изменился по стилю, размеру и материалу. Время, люди и технологии улучшили счеты.
Наборы для счеты по-прежнему представляют собой комбинацию стержней и гальки. Однако нет никаких фактов, подтверждающих подтвержденное утверждение об изобретении счётов. Его истинное происхождение остается неизвестным.
Древнейшая форма и этимология
Самой ранней формой счётов был счетный стол, покрытый песком или мелкой пылью, на котором пальцы рисовались стилусом и при необходимости стирались им.Это описание привело к появлению греческого слова «ABAX» , из которого счеты и получили его этимологию.
Пришествие римлян в Abacus
Со временем числа и расчеты стали важной частью торговли и коммерции. Римляне разработали более простой способ использования счётов, названный «римскими ручными счётами». Это был каменный стол с подвижными камнями, скользящими вверх и вниз.
Типы румынских счётов
Также римляне изобрели три различных типа счётов.
The Dust Abacus
The Line Abacus и
Рифленые счеты
Строки соответственно представляли разряды чисел.
Римские цифры и счеты
Римляне использовали Abacus для вычислений с использованием римских цифр. Еще они назвали счетную доску Calculi. Это означает маленькие камни. Их набор Abacus состоял из семи длинных и более коротких канавок. В верхних бороздках имелась одна бортика.Зато у нижних было по четыре бусинки. Последние два столбца использовались для римской математики со смешанным основанием.
Бисер в верхнем пазу обозначил разрядную пятерку. Нижние бороздки отмечали разрядные значения от десятков до миллионов. Шло время, с появлением современных технологий римляне перешли на микрокалькуляторы в 1974 году.
Китайские счеты Suanpan
Древние китайские счеты, называемые СУАНПАН, были разработаны в двенадцатом веке и не получили известности до четырнадцатого века.
Однако это изобретение было довольно сложным для расчетов, поскольку оно имело две бусинки на верхней палубе. В конечном итоге он потерпел неудачу из-за своей конструкции.
Китайская шариковая арифметика
Современная система нумерации основана на индуистско-арабской математике. Несомненно, широкое распространение он получил к концу XVI века. Именно тогда китайцы назвали счеты «шариковой арифметикой». С тех пор они стали использовать его в качестве основного режима расчетов.
Обычно счеты Suanpan изготавливались из твердой древесины, их длина составляла 20 см. Китайцы называют это счетом 2: 5, исходя из его структуры. Он был разработан таким образом, чтобы вычислять с безграничной точностью
Китайцы ссылались на Abacus, используя различные имена, такие как Supan, Jusan и Jupan. Римские счеты повлияли на дизайн китайских счеты.
Сорта Суанпан
Китайцы использовали суанпан для десятичных чисел. Потому что у него был пустой стержень, показывающий ноль.Современная и наиболее совершенная версия Suanpan состояла из бусинок 4 + 1, индикатора положения и кнопки сброса всех значений для обнуления.
Suanpan Abacus 5: 2 все еще используется в школах Гонконга как часть сохранения культурного наследия.
Японские счеты соробана
Японцы получили форму Abacus из Китая через Корею примерно в шестнадцатом веке. В японском способе строительства методы работы с счетами претерпели некоторые усовершенствования.К девятнадцатому веку он был упрощен и приобрел свою нынешнюю форму примерно в 1920-х годах. Несомненно, нынешняя форма Соробана выглядит намного элегантнее и привлекательнее.
Изучение анатомии
Go-dama-Верхняя бусина номинала пять. Ичи-дама — нижняя четка, стоимость которой равна единице. Тем не менее, длина этих наборов для счётов варьируется от 13 до 31 стержня, в зависимости от требований.
В каждом третьем ряду этого набора для счетов есть точка, обозначающая завершение целого числа.Помимо сложения и вычитания, эти счеты позволяют использовать дополнительное число.
«Анзан» — это название соробанских абаков. На сегодняшний день это активная часть японской школьной программы.
Восточноазиатские Stschoty Abacus
На сегодняшний день Щоты являются счетным устройством в России на протяжении веков. Его ширина 28 см, высота 46 см. В частности, для учащихся доступны маленькие Stschotys размером 13 x 18.Кроме того, у него был толстый деревянный каркас с прикрепленными к нему горизонтальными стержнями.
Железные стержни располагались горизонтально. Не говоря уже о том, что бусинки перемещались слева, чтобы управлять числами. Кроме того, в Stschoty почти от 10 до 14 рядов без разделительной полосы между ними.
Один ряд во всем Stschoty снабжен 4-мя бисеринами для вычисления дробей. При весе до 175 граммов эта модель редко использовалась для основных расчетов. Кроме того, он не соответствовал стандартам японских и китайских Abacus.
Вьетнамские счеты
Эти счеты из Вьетнама имеют по 5 бусин на верхней и нижней палубах. Его размеры 160 мм X90 мм.
Каждый столбец представляет степень до 10.
Горизонтальная балка, разделяющая конструкцию, не имеет особого назначения, и эта сложная конструкция остается под вопросом
Вьетнамцы не использовали счеты активно, как другие страны.Они либо наняли бухгалтера, либо использовали калькулятор. Более того, запутанная структура их набора Abacus и отсутствие интереса вьетнамцев к его использованию приводят к постепенному прекращению его существования.
Улучшенные счеты Ли
Ли Кай Чен изобрел улучшенные счеты Ли в 1950 году на Тайване. Его размеры 33 см на 20 см. Это комбинация структуры китайского суанпан (5 + 2) и японского соробона (4 + 1). Несомненно, это изобретение было наиболее эффективной формой абака.Потому что он использовался при извлечении квадратных корней.
Улучшенные счеты Ли известны своей безошибочной манипуляцией. Несмотря на сложную структуру, новичкам легко научиться. Однако такие вычисления, как сложение и вычитание, в основном выполняются на двух нижних частях абака. Наконец, в двух верхних рядах были произведены умножение и деление.
Счеты Ли Кай Чена известны своей универсальностью, позволяющей без особых усилий извлекать квадратные и кубические корни.
Как пользоваться Abacus
Указательный и большой пальцы используются для перемещения бусинок по стержням.
Каждая бусина на верхней колоде оценивается в 5 баллов. Напротив, каждая бусина в нижней колоде оценивается как 1.
Как бы просто это ни звучало, есть только два шага для выполнения вычислений с использованием абак. Толкайте бусинки вверх и вниз в наборе абак, чтобы манипулировать числами.
Мы узнали достаточно истории о Abacus.
Шаг 1. Обнуление
Начнем с того, что это подготовительный этап к запуску любого вида вычислений с использованием счётов. Установка устройства на столе осуществляется путем скольжения большого и указательного пальцев вдоль балки. Это этап обнуления или «Установка нуля».
Во-вторых, удаление всех бусинок от центрального луча обеспечивает ясность расчетов. Это также знаменует начало новой арифметической задачи. Следовательно, это делается для того, чтобы значение числа в наборе счётов было равно нулю.
Шаг 2: Подсчет
Бусинки считаются засчитанными, когда они перемещаются к планке, разделяющей колоды. Бусы в верхней колоде называются Бусами Небесными. Бусы земные — это бусы в нижней палубе.
Осторожно переместите бусинку из нижней части первой колонки к панели ответа, это значение считается до единицы. После подсчета 4 в нижней колоде результат засчитывается как 5 для верхней. После использования бусинки в верхней части результат переносится в следующий столбец как 10.
Да, бусинки в нижней деке имеют значение 1, а бусинки в верхней деке имеют значение 5. Это увеличивается влево с разрядами соответственно. Это продолжается в левой части набора счётов с увеличивающимися разрядами. Понять набор счеты намного проще, чем вы можете себе представить.
Эта подсчетная рамка способна творить чудеса, помимо своей скромной внешности!
Зная местную стоимость
Знание числового значения — самая важная часть обучения счетам.Каждый столбец имеет собственное разрядное значение. Каждая бусинка, добавленная в этот столбец, соответствует разряду.
В типичном наборе для счётов значение разряда увеличивается влево, например единицы, десятки, сотни и т. Д. Самый правый столбец — это столбец единиц, следующий соседний слева — столбец десятков. Следующий слева столбец — это столбец сотен и так далее.
Земная бусина, добавленная в столбец единицы, означает, что значение равно единице. Точно так же земная бусина, добавленная в столбец сотен, представляет собой число сотня.Вы разбираетесь в этом, дети?
Добавьте к этому вычисления с плавающей запятой, обозначив пространство между двумя столбцами как десятичную точку. Здесь все строки справа от этого места представляют дробную часть. Все строки слева представляют собой целое число.
Техника
Как бы просто это ни звучало, выполнение вычислений с использованием набора для счётов требует использования всего 3 пальцев. Их
Большой палец
Указательный палец и
Средний палец
Обычная техника пальцев — это мантра абака.Большой, указательный палец вдоль среднего пальца перемещает бусинки. Большой палец поднимает бусинки с нижней деки. Указательный палец используется для перемещения бусинки вниз с верхней деки. В некоторых расчетах средний палец перемещает бусинки в верхней деке.
Требуется немного практики, чтобы научиться манипулировать числами разными пальцами. Однако этот метод составляет основу умственной математики исключительно посредством визуализации.
У меня не было компьютера до 19 лет, но у меня были счеты
Счеты для детей
Знаете ли вы, что человеческий мозг способен хранить данные размером до 1000 терабайт?
Удивительная сила памяти человека проявляется в полной мере в детстве.Поэтому все, что выучено, практиковалось и освоено с детства, остается в нашей памяти навсегда.
От оттачивания навыков детей до неограниченного использования мозга — счеты играют важную роль в развитии у детей способности к бесконечности. Кроме того, это повышает их общую успеваемость в учебе. Вот почему уроки Abacus для детей — несказанная необходимость в современном мире.
ABD в Академии Thej
Мысленные вычисления на основе абак (ABD) — это разновидность тренировки на счетах.Это когнитивный навык высокого уровня для выполнения вычислений с использованием эффективного алгоритма. Несомненно, он эффективно доказал, что улучшает работу мозга у детей. Мы в Thej Academy обеспечиваем долгосрочное воздействие азбуки на детей. Кроме того, это приводит к более эффективному соединению нервных путей.
Abacus и Mental Focus Results
Кто из нас страдает из-за недостатка внимания? Кроме того, многие ли из нас обладают фотогеничной памятью? В наши дни есть своевременная замена и альтернатива всему и вся.Мы не заботимся о повышении уровня нашей концентрации. Как ни странно, такое нежелание может привести к снижению производительности. Abacus позволяет детям значительно повысить уровень своего внимания. Чтобы решить любую математическую задачу, все, что нужно запомнить, — это конечное положение бусинок.
Любую проблему можно решить, визуализировав доску для счетов вместе с положением последней бусинки. Таким образом можно быстро решать сложные проблемы.
Преимущества занятий с абакусом для детей
Самые известные мировые институты доказывают, что счеты развивают у человека следующие аспекты.
Ребенок работает на счетах обеими руками. Эта координация приводит к стимуляции правого и левого полушарий одновременно. В результате работает весь мозг. Это одновременное функционирование левого и правого полушарий мозга наблюдается, когда они заняты очень немногими видами деятельности, такими как плавание и борьба на мечах.
Повышенная концентрация
В этом конкурентном мире любой квалифицированный человек с целеустремленностью достигает успеха. Abacus поможет вам улучшить вашу психическую стабильность и навыки памяти.
Представление счётов в уме для манипулирования числами в течение длительных периодов практики приводит к значительному повышению уровня внимания детей.
Логическое рассуждение
Было обнаружено, что по сравнению с учениками, не учащимися на счетах, у детей, которые занимаются счетами, больше логических рассуждений.
Исследователи утверждают, что у ребенка, который занимается счетами, когнитивные способности на 70% выше, чем у ребенка, который не занимается счетами.Излишне говорить, что активный когнитивный ум помогает вам работать лучше и сохраняет ум острым и активным. Это относится не только ко всем основным математическим вычислениям, но и к дробям, в которых быстрое мышление играет важную роль.
Фотогеничная память
Повышенная мощность памяти — всегда несказанное преимущество. Сила памяти — это умственная сила человека. Он сочетает в себе своевременное сосредоточение внимания и способность хватать. Дети, занимающиеся счетами, демонстрируют необычайный диапазон уровней памяти.Кроме того, это помогает мозгу легко вспоминать вещи.
Некоторые специалисты по счетам используют свою способность для запоминания целых страниц своих учебников, заполненных годами
.
Abacus в Академии Thej
С математикой так весело работать! Thej Academy имеет практический опыт коучинга Abacus с 2007 года. Мы проводим различные курсы для детей и выпускников.
В Академии Thej у нас немного другой подход к обучению всех, кто интересуется счетами.Мы понимаем способности вашего ребенка и работаем с индивидуальным вниманием, чтобы развить его навыки работы со счетами. Мы улучшаем навыки слушания и творческие способности ребенка, используя Abacus в качестве основного инструмента. Это помогло нам получить обильные результаты и ошеломляющие отклики.
Подход Академии Thej
Мы обучаем детей таким образом, чтобы облегчить работу всего мозга. Мы помогаем им обрести интеллект, улучшая «Вундеркинды в области математики». Мы верим в маленькие шажки, потому что счеты — это ступенька на пути к блестящему будущему вашего ребенка.
В наши дни каждый ребенок очень боится математики. Мы в Thej Academy меняем подход вашего ребенка к математике с помощью нашего исключительно острого обучения. Мы обеспечиваем высокие результаты на академических и других конкурсных экзаменах.
И, что самое главное, мы делаем обучение увлекательным!
Изучи счеты в Академии Тей, оставайся гением на всю жизнь
Помимо академического роста, обучение счетам также увеличивает силу концентрации и скорость реакции.У нас в Thej Academy есть опытные наставники. Они направляют детей в правильном направлении для повышения умственной силы и успеваемости. Звучит огромно, но простой курс под названием Abacus справится со всем. Мы также проводим обучение, чтобы стать профессиональным сертифицированным учителем счётов.
Обеспокоены, если ваш ребенок несовершеннолетний, чтобы присоединиться к классу счетчиков? Хотите знать, может ли Thej Academy помочь начинающему предпринимателю? Дышите, ребята, у нас есть ответы на все ваши вопросы!
Основная идея обучения Abacus в Академии Thej состоит в том, чтобы улучшить чьи-либо умственные арифметические способности.Все, что вам нужно сделать, это запомнить последнее число, которым вы управляли, и его разрядное значение. Наши преподаватели помогут вам с нуля довести вас до нужного уровня. Так просто!!
Заключение
Вы школьник и хотите изучать Abacus? Вы начинающий предприниматель, желающий самостоятельно изучать и преподавать счеты? Мы в Thej Academy верим в совместное обучение и рост. Подлинность наших услуг сделала нас лучшим центром Abacus в Несапаккам, Ченнаи.
Итак, ребята, присоединяйтесь к Академии Thej — универсальной программе для изучения счетов без возрастных ограничений!
Пережить технологические ураганы и при этом остаться частью развивающегося мира — непростая задача. Несмотря на то, что это простой инструмент, на сегодняшний день Abacus производит революцию в массах. Все, что вам нужно, — это правильный наставник, адекватный контроль и качественная передача практических знаний. Изучение Abacus может творить чудеса с детьми этого поколения.
Это не только поможет вашему ребенку преуспеть в учебе, но также повысит его общую самооценку и обнаружит свою внутреннюю силу.
Не стесняйтесь позвонить нам или позвонить, чтобы стать частью этого удивительного мира счётов. Хотите принять участие в онлайн-соревновании? Запишитесь сюда
Abacus — Энциклопедия Нового Света
Счеты (множественное число счеты или счеты ), также называемая счетной рамкой , представляет собой вычислительный инструмент для выполнения арифметических процессов, часто сконструированный в виде деревянной рамы с бусинами, скользящими по проволоке. Пользователь, называемый абакистом , перемещает счетчики вручную на стержнях или в канавках.Он использовался за столетия до принятия письменной индуистско-арабской системы счисления и до сих пор широко используется купцами и клерками в Китае, Японии, Африке и других странах.
Счетная таблица Грегора Райша: «Философская маргарита», 1508 г.
Счеты — это простой, недорогой, но мощный инструмент для расчетов. Хотя электронные калькуляторы заменяют его по практическим причинам, пользоваться счетами по-прежнему преподается в технологически развитых странах, таких как Япония. Как и в случае с популярными настольными играми, такими как шахматы, сёги и го, для учащихся проводятся местные, региональные и национальные соревнования по использованию счётов.
Истоки
Первые счеты, скорее всего, были основаны на плоском камне, покрытом песком или пылью. Слова и буквы были нарисованы на песке; в конце концов были добавлены числа и использовались камешки для облегчения расчетов. Вавилоняне использовали эти пылевые счеты еще в 2400– годах до н. Э. ^[1] Происхождение счетных счетчиков со строками неясно, но Индия, Месопотамия или Египет считаются вероятными точками их происхождения. ^[2] Китай сыграл важную роль в развитии и эволюции абака.
Из этого были разработаны различные абаки; самые популярные были основаны на бипятичной системе с использованием комбинации двух оснований (основание-2 и основание-5) для представления десятичных чисел. Но самые ранние абаки, использовавшиеся сначала в Месопотамии, а затем писцами в Египте и Греции, использовали шестидесятеричные числа, представленные с множителями 5, 2, 3 и 2 для каждой цифры.
Использование слова abacus датируется до 1387 года, когда в среднеанглийской работе это слово было заимствовано из латыни для описания счётов песчаной доски.Латинское слово произошло от abakos, — от греческого родительного падежа abax («счетная таблица»). Поскольку abax также имел смысл «стол, посыпанный песком или пылью, используемый для рисования геометрических фигур», некоторые лингвисты предполагают, что греческое слово может быть образовано от семитского корня, ābāq (произносится как «а-вак») , еврейское слово, означающее «пыль». Хотя подробности передачи неясны, это также может происходить от финикийского слова abak, означающего «песок».»Предпочтительное множественное число abacus является предметом разногласий, но используются оба abacus ^[3] и abaci ^[4].
Вавилонские счеты
Вавилоняне могли использовать счеты для сложения и вычитания. Однако это примитивное устройство оказалось трудным в использовании для более сложных вычислений. ^[5] Некоторые ученые указывают на персонаж из вавилонской клинописи, который, возможно, произошел от изображения абака.^[6]
Египетские счеты
Использование абака в Древнем Египте упоминается греческим историком Геродотом, который пишет, что способ их использования египтянами был противоположным по направлению по сравнению с греческим методом. Археологи нашли древние диски различных размеров, которые, как считается, использовались в качестве счетчиков. Однако настенные изображения этого инструмента не были обнаружены, что ставит под сомнение степень использования этого инструмента.^[2]
Греческие счеты
Табличка, найденная на греческом острове Саламин в 1846 году, датируется 300 годом до н. Э. , что делает ее самой старой из обнаруженных до сих пор счетных досок. Это плита из белого мрамора длиной 149 см, шириной 75 см и толщиной 4,5 см, на которой нанесено 5 групп отметок. В центре планшета находится набор из 5 параллельных линий, поровну разделенных вертикальной линией, завершенной полукругом на пересечении самой нижней горизонтальной линии и единственной вертикальной линии.Под этими линиями — широкое пространство с разделяющей его горизонтальной трещиной. Ниже этой трещины находится еще одна группа из одиннадцати параллельных линий, снова разделенных на две части линией, перпендикулярной им, но с полукругом в верхней части пересечения; третья, шестая и девятая из этих линий отмечены крестиком в месте пересечения с вертикальной линией.
Римские счеты
Реконструированные римские счеты
Обычный метод расчета в Древнем Риме, как и в Греции, заключался в перемещении счетчиков на гладком столе.Первоначально использовались камешки, камни. Позже, в средневековой Европе, жетоны стали производить. Отмеченные линии обозначают единицы, пятерки, десятки и т. Д., Как в римской системе счисления. Эта система «встречного литья» продолжалась в поздней Римской империи и в средневековой Европе и сохранялась в ограниченном использовании до девятнадцатого века. ^[7]
В дополнение к более распространенному методу, использующему свободные счетчики, было найдено несколько образцов римских счётов, показанных здесь в реконструкции.Он имеет восемь длинных канавок, содержащих до пяти бусинок в каждой, и восемь более коротких бороздок, в каждой из которых либо по одной бусинке, либо нет.
Канавка с маркировкой I указывает единицы, X десятков и так далее до миллионов. Бусинки в более коротких канавках обозначают пятерки — пять единиц, пять десятков и т. Д., По существу, в десятичной системе с двоичным кодированием, очевидно связанной с римскими цифрами. Короткие бороздки справа могли использоваться для маркировки римских унций.
Индийские счеты
Источники первого века, такие как Abhidharmakosa , описывают знание и использование счётов в Индии.^[8] Примерно в пятом веке индийские клерки уже находили новые способы записи содержания Абаков. ^[9] индуистские тексты использовали термин шунья (означает ноль) для обозначения пустого столбца на счетах. ^[10]
Китайские счеты
Суанпан (число, представленное на картинке — 6 302 715 408)
Самое раннее упоминание о суаньпане находится в книге первого века династии Восточная Хань, а именно дополнительных заметках по искусству фигурок , написанных Сюй Юэ.^[11] Однако точная конструкция этого люстра неизвестна.
Обычно suanpan имеет высоту около 20 см и бывает разной ширины в зависимости от оператора. Обычно в нем более семи стержней. На каждом стержне верхней колоды по две бусинки, а в нижней — по пять бусинок для десятичных и шестнадцатеричных вычислений. Бусины обычно имеют округлую форму и изготавливают из твердых пород дерева. Подсчет бусинок осуществляется перемещением их вверх или вниз по направлению к лучу. Suanpan можно мгновенно вернуть в исходное положение быстрым рывком вдоль горизонтальной оси, чтобы повернуть все бусинки от горизонтального луча в центре.
Suanpans можно использовать для других функций, кроме подсчета. В отличие от простой счетной доски, используемой в начальной школе, были разработаны очень эффективные методы suanpan для выполнения операций умножения, деления, сложения, вычитания, извлечения квадратного и кубического корня с высокой скоростью.
В знаменитом длинном свитке Riverside Scenes на фестивале Qingming , написанном Чжан Цзэдуанем (1085-1145) во времена династии Сун (960-1297), отчетливо виден suanpan , лежащий рядом с бухгалтерской книгой и рецептами врача. прилавок аптекарский (Фейбао).
Сходство римских счётов с китайскими предполагает, что одни могли вдохновить других, поскольку есть некоторые свидетельства торговых отношений между Римской империей и Китаем. Однако прямая связь не может быть продемонстрирована, и сходство абачей может быть случайным, в конечном итоге и то, и другое связано со счетом пятью пальцами на руке. В то время как римская модель (как и большинство современных японских) имеет 4 плюс 1 бусину на десятичный разряд, стандартная suanpan имеет 5 плюс 2 для менее сложных арифметических алгоритмов в шестнадцатеричной системе счисления.Вместо того, чтобы бегать по проводам, как в китайской и японской моделях, бусинки римской модели бегут по канавкам, что, по-видимому, значительно замедляет арифметические вычисления.
Другой возможный источник suanpan — китайские счетные стержни, которые работали с десятичной системой, но не имели понятия нуля как заполнителя. Ноль, вероятно, был представлен китайцам во времена династии Тан (618-907 гг.), Когда путешествие по Индийскому океану и Ближнему Востоку обеспечило бы прямой контакт с Индией и исламом, позволив им перенять понятие нуля и десятичной точки из Индии. и исламские купцы и математики.
Корейские и японские счеты
Счеты мигрировали из Китая в Корею около 1400 года, а позже из Японии — около 1600 года. ^[12] Корейская версия счётов называется jupan (주판) или supan (수판) или jusan (주산).
Китайский суаньпан назывался в Японии соробан (算盤, そろばん, букв. «Счетный лоток»). ^[13] Как и suanpan , , соробан все еще используется в Японии сегодня, даже несмотря на распространение, практичность и доступность карманных электронных калькуляторов.
Счеты коренных американцев
Изображение кипу инков
В некоторых источниках упоминается использование счётов под названием nepohualtzintzin в древней ацтекской культуре. В этих мезоамериканских счетах использовалась пятизначная система с основанием 20.
Кипу инков представлял собой систему узловатых шнуров, которые использовались для записи числовых данных, как продвинутые счетные палочки, но не использовались для выполнения вычислений. Расчеты проводились с использованием юпаны (кечуа, что означает «инструмент для счета»; см. Рисунок), которая все еще использовалась после завоевания Перу.Принцип работы юпаны неизвестен, но в 2001 году было предложено объяснение математической основы этих инструментов. Сравнивая форму нескольких юпан, исследователей обнаружили, что вычисления были основаны на использовании последовательности Фибоначчи 1, 1, 2, 3, 5 и степеней 10, 20 и 40 в качестве значений разряда для различных полей в инструменте. Использование последовательности Фибоначчи позволит свести к минимуму количество зерен внутри любого поля.
Русские счеты
Русские счеты schoty (счёты) обычно имеют одну наклонную деку с десятью бусинами на каждой проволоке (кроме одной проволоки с четырьмя бусинами для дробей в четверть рубля).Этот провод обычно находится рядом с пользователем. (В более старых моделях есть еще одна 4-бусная проволока для четверти копеек, которая чеканилась до 1916 года.) Русские счеты часто используют вертикально, с проволокой слева направо, как книжку. Проволока обычно изогнута, чтобы выступать вверх в центре, чтобы бусины были прикреплены к любой из двух сторон. Он очищается, когда все бусинки сдвигаются вправо. Во время манипуляции бусинки перемещают влево. Для удобства просмотра две средние бусинки на каждой проволоке (5-я и 6-я бусинки) обычно имеют цвет, отличный от остальных 8 бусинок.Точно так же левая полоса проволоки тысяч (и проволоки миллиона, если она есть) может иметь другой цвет.
Русские счеты до сих пор используются в магазинах и на рынках по всему бывшему Советскому Союзу, хотя в большинстве школ им больше не преподают.
Школьные счеты
Школьные счеты, используемые в датской начальной школе. Начало двадцатого века.
Во всем мире абачи использовались в дошкольных и начальных школах в качестве вспомогательного средства при обучении системе счисления и арифметике.В западных странах широко распространена бусная рамка , похожая на российские счеты, но с прямыми проволоками и вертикальной рамкой (см. Изображение). Его до сих пор часто рассматривают как пластиковую или деревянную игрушку.
Показанные здесь счеты часто используются для представления чисел без использования разряда. Каждая бусина и каждая проволока имеют одинаковое значение и могут представлять числа до 100.
Наиболее значительным образовательным преимуществом использования счётов, а не бусинок или счетчиков при отработке счета и простого сложения, является то, что это дает учащемуся представление о группировках по 10, которые являются основой нашей системы счисления.Хотя взрослые воспринимают эту структуру с основанием 10 как должное, на самом деле ей сложно научиться. Многие шестилетние дети могут сосчитать до 100 наизусть, лишь слегка осознавая задействованные закономерности.
Использование слепыми
Адаптированные счеты, называемые счеты Кранмера, до сих пор широко используются слепыми людьми. За бусинами кладут кусок мягкой ткани или резины, чтобы они случайно не сдвинулись с места. Это удерживает бусинки на месте, пока пользователи их ощущают или манипулируют.Они используют счеты для выполнения математических функций умножения, деления, сложения, вычитания, квадратного корня и кубического корня.
Несмотря на то, что слепые учащиеся пользуются говорящими калькуляторами, счеты по-прежнему очень часто преподают этим учащимся в младших классах как в государственных школах, так и в государственных школах для слепых. Счеты обучают математическим навыкам, которые невозможно заменить говорящими калькуляторами, и являются важным инструментом обучения слепых учеников. Слепые ученики также выполняют задания по математике, используя шрифт Брайля и код Немета (тип кода Брайля для математики), но задачи с большим умножением и делением в столбик могут быть длинными и трудными.Счеты дают слепым и слабовидящим ученикам инструмент для решения математических задач, который соответствует скорости и математическим знаниям, необходимым их зрячим сверстникам, использующим карандаш и бумагу. Многие слепые люди считают эту числовую машину очень полезным инструментом на протяжении всей жизни.
Счеты в средневековых изображениях
Банкноты
↑ Эдвин Д. Рейли и Уильям Леонард Лангер, Краткая энциклопедия компьютерных наук (Нью-Йорк: Джон Вили и сыновья, 2004), 825.
↑ ^2,0 ^2,1 Дэвид Юджин Смит, История математики (том 2) (Courier Dover Publications, 1958, ISBN 0486204308), 159-160.
↑ Oxford English Dictionary, 1989.
↑ Merriam-Webster’s 2003.
↑ Этторе Карруччо, Математика и логика в истории и современной мысли (Aldine Transaction, 2006, ISBN 0202308502), 14.
↑ Томас Крамп, Японская игра в числа: использование и понимание чисел в современной Японии (Нью-Йорк: Рутледж, 1992), 188.
Перейти ↑ J. M. Pullan, The History of the Abacus (London: Books That Matter, 1968), 18.
↑ Питер Н. Стернс и Уильям Леонард Лангер, Энциклопедия всемирной истории: древняя, средневековая и современная, в хронологическом порядке (Нью-Йорк: Houghton Mifflin Books, 2001), 44.
↑ Томас Уильям Кёрнер и Уильям Леонард Лангер, Удовольствия от счета (Нью-Йорк: Houghton Mifflin Books, 1996), 232.
↑ Ричард Энтони Моллин, Фундаментальная теория чисел с приложениями (CRC Press, 1998), 3.
↑ Пэн Йоке Хо, Ли, Ци и Шу: Введение в науку и цивилизацию в Китае (Courier Dover Publications, 2000), 71.
↑ abacus Получено 21 декабря 2017 г.
↑ Счеты: Краткая история. Проверено 21 декабря 2017 года.
Список литературы
Карруччо, Этторе. Математика и логика в истории и современной мысли. Aldine Transaction, 2006. ISBN 0202308502.
Крамп, Томас. Японская игра в числа: использование и понимание чисел в современной Японии. Рутледж, 1992. ISBN 0415056098.
Доменичи, Вивиано и Давиде Доменичи. «Говорящие узлы инков» Археология 49 (6) (ноябрь / декабрь 1996)
Кодзима, Такаши. Японские счеты: его использование и теория. Токио; Нью-Йорк: Чарльз Э. Таттл, 1954. ISBN 0804802785.
Кёрнер, Томас Уильям и Уильям Леонард Лангер. Удовольствие от счета. Houghton Mifflin Books, 1996. ISBN 0521568234.
Меннингер, Карл В. Числовые слова и числовые символы: культурная история чисел. MIT Press, 1969. ISBN 0262130408.
Моллин, Ричард Энтони. Фундаментальная теория чисел с приложениями. CRC Press, 1998. ISBN 0849339871.
Peng Yoke Ho. Ли, Ци и Шу: Введение в науку и цивилизацию в Китае. Courier Dover Publications, 2000. ISBN 0486414450.
Пуллан, Дж.М. История абака. Лондон: книги, которые имеют значение, 1968. ISBN 00
103.
Рейли, Эдвин Д. и Уильям Леонард Лангер. Краткая энциклопедия компьютерных наук. John Wiley and Sons, 2004. ISBN 04700
.
Смит, Дэвид Юджин. История математики. (Том 2). Courier Dover Publications, 1958. ISBN 0486204308.
Стернс, Питер Н. и Уильям Леонард Лангер. Энциклопедия всемирной истории: древняя, средневековая и современная, в хронологическом порядке. Houghton Mifflin Books, 2001. ISBN 0395652375.
Внешние ссылки
Все ссылки получены 8 апреля 2021 г.
Кредиты
New World Encyclopedia писателей и редакторов переписали и завершили статью Wikipedia в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства.Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования.