ЛЕКЦИЯ 6. ДИСКОНТИРОВАНИЕ ДЕНЕЖНЫХ ПОТОКОВ
ЛЕКЦИЯ 6. ДИСКОНТИРОВАНИЕ ДЕНЕЖНЫХ ПОТОКОВ
Дисконтирование денежных потоков.
Проценты и будущая стоимость
Текущая стоимость
Аннуитеты
В некоторых стандартах бухгалтерского учета используются понятия дисконтированной стоимости, например, при оценке операций по аренде или финансовых вложений на длительный период времени.
Дисконтирование денежных потоков
Взаимосвязь времени и денег:
— деньги тратятся с целью получения прибыли;
— финансовые вложения должны давать дополнительную прибыль или экономию, чтобы оправдать эти траты. Однако мы должны отметить, что величина прибыли или дохода должна быть достаточно высокой для того, чтобы окупить вложения;
— финансовые вложения можно считать эффективными в том случае, если они дают как минимум такую прибыль или такой доход, уровень которого компенсирует инвестору продолжительность отрезка времени, в течение которого он должен ждать его получения.
Таким образом, при оценке программ финансовых вложений необходимо установить, дадут ли финансовые вложения достаточную прибыль с учетом их разновременности. Метод дисконтирования денежных потоков- это метод оценки, который принимает в расчет изменение стоимости денег во времени.
Важно понять, что применение дисконтированной стоимости денег не зависит от инфляции. Другими словами, даже если инфляция равняется нулю, деньги все равно имеют стоимость с учетом будущих доходов, которые они могут принести при инвестировании (теория вмененных издержек или упущенной выгоды).
Проценты и будущая стоимость
Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т.д.), либо от инвестиций производственного и финансового характера.
Проценты, которые применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления, называется простыми.
Пример:
Ссуда в размере 500,000 выдана на 3 года по простой ставке процента 30% годовых. Проценты за 3 года составят:
500,000*30%*3=450,000
Сложные проценты- проценты полученные на реинвестированные проценты, т.е процент, выплачиваемый по ссуде или финансовому вложению, присоединяется к основной сумме, в результате чего проценты выплачиваются на основную сумму, и на полученные проценты.
Вычисление сложных процентов- процесс обратный дисконтированию, так как при помощи сложных процентов определяются будущая стоимость имеющейся в настоящее время денежной наличности.
Пример:
Если бы сейчас нам предстояло вложить 1,000 в банк под 10% годовых с расчетом выплат процентов раз в год (в конце года) то мы рассчитывали бы на следующие показатели доходности:
А) через год стоимости инвестиции увеличилась бы до следующей величины:
1,000+10% от 1,000 = 1,000*(1+10%) =1,000*(1,10)=1,100
Выплаты по процентам составили бы 100
Б) Если бы мы держали свои деньги на этом банковском счете, то через 2 года стоимость инвестиции составила бы 1,210(1,100*1,1).
Выплаты по процентам за второй год составили бы 110 (1,210-1,100).
Это можно записать по-другому – показав как величину первоначальной инвестиции были бы начислены проценты за два года, т.е.:
1,000*(1,1)*(1,1)=1,000*(1,1)²=1,210
В) Аналогичным образом, если бы мы продолжали держать деньги в банке и в следующее году, то стоимость инвестиции возросла бы в конце третьего года до:
1,000*(1,1)*(1,1)*(1,1)=1,000*(1,1)³=1,331
Проценты за третий год составили бы (1,331-1,210)=121
Этот пример показывает методику определения стоимости инвестиций при использовании сложных процентов
Принципы сложных процентов используются при расчете будущей и текущей (дисконтированной) стоимости денежных потоков.
Будущая стоимость- стоимость в будущем инвестированных сейчас денежных средств.
Для определения стоимости, которую будет иметь инвестиция через несколько лет при использовании процедуры сложных процентов- будущей стоимости, применяется следующая формула:
FV=PV *(1+r)ⁿ, где
А)5 лет
Б)6 лет
Будущая стоимость 1 доллара через n лет при ставке 10% приведена в таблице С-3.
А) 5 лет FV= 2,000*1,611=3,222
Б)6 лет FV=2,000*1,772=3,544
Аннуитеты
В большинстве современных коммерческих операций подразумевается не разовые платежи, а последовательность денежных поступлений (или, наоборот выплат) в течение определенного периода. Это может быть серия доходов и расходов некоторого предприятия, регулярные или нерегулярные взносы, создание разного рода фондов. Такая последовательность называется потоком платежей.
Аннуитет (финансовая рента)- поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет.
Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг в инвестиционном анализе. Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам, выплата по регрессным искам.
Аннуитеты различаются между собой следующими основными характеристиками:
— величиной каждого отдельного платежа
— интервалом времени между последовательными платежами (периодом аннуитета)
— сроком от начала аннуитета до конца его последнего периода
— процентной ставкой, применяемой при нарушении или дисконтировании платежей
Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо, если платежи осуществляются в конце интервалов, мы получаем аннуитет постумерандо (обыкновенный аннуитет) самый распространенный случай.
Наибольший интерес с практической точки зрения представляют аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью. Именно такие аннуитеты мы и изучим.
Будущая стоимость аннуитета
Будущая стоимость аннуитета- сумма будущих стоимостей каждой отдельной выплаты или поступления, включенных в аннуитет. Например, мы можем инвестировать в течение 3 лет 250 по ставке 10% годовых с начислением процентов каждый год. Какова будущая стоимость аннуитета в 250?
Для расчета применяется формула будущей стоимости FV=PV *(1+r)ⁿ для каждого периода отдельно.
Будущая стоимость 250, инвестируемых в конце каждого года в течение 3 лет:
1-ый год 250*(1+0,1)²=250*1,21=302,50
2-ой год 250*(1+1,01)=250*1,10=275,00
3-ий год 250*1 =250*1,00 =250,00
3,31 827,50
для облегчения расчетов применяется специальная таблица С-4 будущей стоимости аннуитетов в 1 доллар, выплачиваемого в конце года, пользуясь которой мы получим: 250*3,31=827,50.
Текущая стоимость аннуитета
671,72
Этого же самого результата можно достичь более простым путем с применением таблицы текущей (дисконтированной) стоимости аннуитета в 1 доллар, выплачиваемого в конце периода таблица С-2: 250*2,4869=621,72.
Во всех случаях когда в произвольном потоке платежей встречаются серии, которые могут быть описаны как постоянные или изменяющиеся по некоторому закону аннуитеты, следует обращать внимание на начальный момент и срок этих аннуитетов, не совпадающие с начальным моментом и сроком полного потока платежей.
ЛЕКЦИЯ 6. ДИСКОНТИРОВАНИЕ ДЕНЕЖНЫХ ПОТОКОВ
infopedia.su
Наращение и дисконтирование денежных потоков
Поскольку процесс инвестирования, как правило, имеет большую продолжительность в практике анализа эффективности капитальных вложений, обычно приходится иметь дело не с единичными денежными суммами, а с потоками денежных средств.
Вычисление наращенной и дисконтированной оценок сумм денежных средств в этом случае осуществляется путем использования соответствующих формул для каждого элемента денежного потока.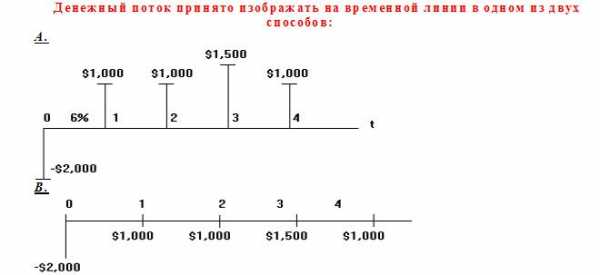
Представленный на рисунке денежный поток состоит в следующем: в настоящее время выплачивается (знак “минус”) $2,000, в первый и второй годы получено $1,000, в третий — $1,500, в четвертый — снова $1,000.
Используя формулу, для всех элементов денежного потока от 0 до n получим будущее значение денежного потока:
Пример 1. После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия? Решим задачу с использованием временной линии.
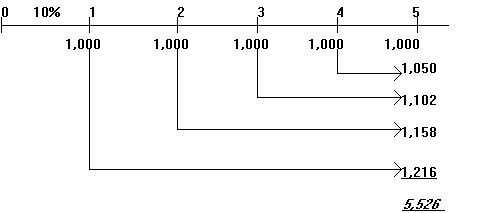
Таким образом через 5 лет предприятие накопит $5,526, которые сможет инвестировать.
В данном случае денежный поток состоит из одинаковых денежных сумм ежегодно. Такой поток называется аннуитетом. Для вычисления будущего значения аннуитета используется формула:
которая следует из предыдущей при CFk = const и CF0 = 0.
Расчет будущего значения аннуитета может производиться с помощью специальных финансовых таблиц. В частности, с помощью таблицы 2 при r = 5% и n = 5 получаем множитель 5,526, который соответствует результату расчета примера.
Дисконтирование денежных потоков осуществляется путем многократного использования формулы, что в конечном итоге приводит к следующему выражению:
Пример 2. Рассмотрим денежный поток с неодинаковыми элементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для которого необходимо определить современное значение (при показателе дисконта 6%). Решение проводим с помощью временной линии:
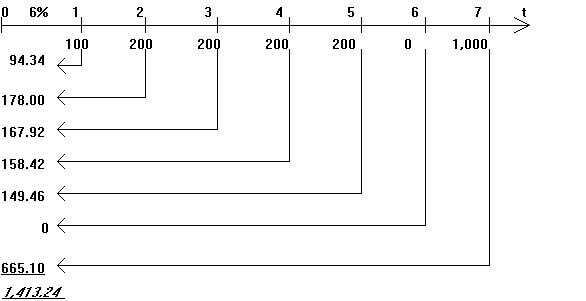
Дисконтирование аннуитета (CFj = const) осуществляется по формуле:
Пример 3. Предприятие приобрело облигации муниципального займа, которые приносят ему доход $15,000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования получаемых каждый год $15,000 в 12 %. Необходимо определить настоящее значение этого денежного потока.
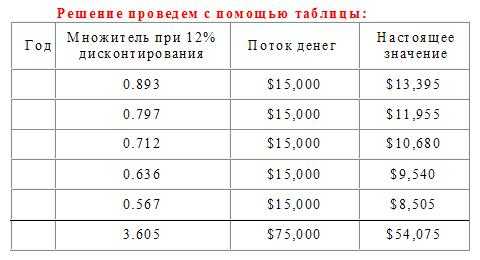
По результатам расчетов мы видим, что:
— дисконтированное значение денежного потока существенно меньше арифметической суммы элементов денежного потока,
— чем дальше мы заходим во времени, тем меньше настоящее значение денег: $15,000 через год стоят сейчас $13,395; $15,000 через 5 лет стоят сейчас $8,505.
Современное значение бесконечного (по времени) потока денежных средств определяется по формуле:
которая получается путем суммирования бесконечного ряда, определяемого формулой при n стремящемуся к бесконечности.
Понравился данный материал?
Не стесняйся, поставь лайк, расскажи о нас своим друзьям, однокурсникам, короче, всем, кому был бы полезнен наш сайт! Тебе ничего не стоит, а нам приятно, что не зря стараемся 😉
managment-study.ru
Метод дисконтирования денежного потока (ДДП)
- Метод дисконтирования денежного потока (ДДП)
Метод дисконтирования денежного потока (ДДП) (discounted cash flow method — DСF method) — метод оценки бизнеса путем расчета дисконтированной стоимости денежных потоков, ожидаемых от объекта оценки в будущем. Это наиболее распространенный способ оценки (определения стоимости) бизнеса в рамках доходного подхода к оценке. Основан на расчете текущей (приведенной) стоимости компании (предприятия) путем дисконтирования ожидаемых будущих экономических выгод (часто — будущей прибыли), которые она принесет своим владельцам. В методе ДДП используется ставка дисконтирования, равная ставке доходности (отдачи), которая, по расчетам оценщика, требуется для привлечения инвестиций в данный объект.
Общая модель метода ДДП такова:
Где :
PV – (present value) – современная (приведенная) стоимость
n – последний период, для которого прогнозируется экономический доход; n может быть равен бесконечности.
Ei– ожидаемая экономическая выгода в i-том периоде (например, прибыль, выплачиваемая в конце этого периода)
k — ставка дисконтирования (стоимость капитала, то есть ожидаемая норма рентабельности, доступная на рынке для других инвестиций, сравнимых по риску и другим инвестиционным характеристикам).
i -будущий период (обычно определяемый как некоторое число лет) , за который ожидается получить прогнозируемые экономические доходы.
То же: Метод анализа дисконтированных денежных потоков. См. также: Анализ дисконтированного денежного потока; Двухстадийная модель дисконтирования денежного потока. Метод дисконтирования будущих чистых доходов (будущей прибыли)
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- Метод дисконтирования будущих чистых доходов (будущей прибыли)
- Метод дискреционного денежного потока продавца
Смотреть что такое «Метод дисконтирования денежного потока (ДДП)» в других словарях:
Метод дисконтирования денежного потока — ДДП Метод оценки бизнеса путем расчета дисконтированной стоимости денежных потоков, ожидаемых от объекта оценки в будущем. Это наиболее распространенный способ оценки (определения стоимости) бизнеса в рамках доходного подхода к оценке. Основан на … Справочник технического переводчика
МЕТОД ДИСКОНТИРОВАННОГО ДЕНЕЖНОГО ПОТОКА — (англ. discounted cash flow approach) – метод определения стоимости собственности при доходном подходе к оценке. Заключается в прогнозировании будущих доходов, которые, как ожидается, собственность принесет в течение ряда лет, и приведении этих… … Финансово-кредитный энциклопедический словарь
Метод анализа дисконтированных денежных потоков — (discounted cash flow method — DСF method) – См.: Метод дисконтирования денежного потока (ДДП) … Экономико-математический словарь
Дисконтированный денежный поток (ДДП) — (Discounted Cash Flow DCF) будущие величины денежного потока, рассчитанные в текущих денежных единицах исходя из ожидаемого значения ставки дисконтирования. Метод ДДП (DCF) один из основных в практике оценки бизнеса … Экономико-математический словарь
М — Магистраль [turnpike] Мажоритарный акционер (Majority shareholder) Мажоритарная доля собственности (majority interest) Мажоритарный контроль (majority control) … Экономико-математический словарь
Доходный подход к оценке бизнеса — (income estimation approach) – Совокупность методов оценки стоимости объекта оценки, основанных на определении ожидаемых доходов от объекта оценки. Это – одно из трех главных направлений в определении оценочной стоимости бизнеса, доли участия… … Экономико-математический словарь
доходный подход к оценке бизнеса — Совокупность методов оценки стоимости объекта оценки, основанных на определении ожидаемых доходов от объекта оценки. Это – одно из трех главных направлений в определении оценочной стоимости бизнеса, доли участия собственников в акционерном… … Справочник технического переводчика
Оценка недвижимости — Оценка стоимости недвижимости процесс определения рыночной стоимости объекта или отдельных прав в отношении оцениваемого объекта недвижимости. Оценка стоимости недвижимости включает: определение стоимости права собственности или иных прав,… … Википедия
дисконтирование — Приведение экономических показателей к сопоставимому по времени виду путем умножения их на коэффициент дисконтирования. В частности, дисконтированием денежных потоков называют приведение их разновременных (относящихся к разным этапам оценки… … Справочник технического переводчика
Дисконтирование — [discounting] приведение экономических показателей разных лет к сопоставимому по времени виду. Применение дисконтирования объясняется тем, что человеку свойственно более высоко ценить сегодняшние блага (стоимости) по сравнению с будущими, и … … Экономико-математический словарь
economic_mathematics.academic.ru
Дисконтирование денежных потоков
Понятие «дисконтирование» относится к числу ключевых в теории инвестиционного анализа. Буквальный перевод этого слова с английского («discounting») означает «снижение стоимости, уценка».
Дисконтированием называется операция расчёта современной ценности денежных сумм, относящихся к будущим периодам времени.
Иначе говоря, дисконтирование денежных потоков — это приведение их разновременных (относящихся к разным шагам расчёта) значений к их ценности на определенный момент времени, который называется моментом приведения (t). Момент приведения может не совпадать с базовым моментом (t0). Дисконтирование применяется к денежным потокам, выраженным в текущих или дефлированных ценах и в единой валюте.
Основным экономическим нормативом, используемым при дисконтировании, является норма дисконта (Е), выражаемая в долях единицы или в процентах в год. Различаются следующие нормы дисконта: коммерческая, участника проекта, социальная и бюджетная.
— коммерческая норма дисконта используется при оценке коммерческой эффективности проекта; она определяется с учетом альтернативной (т.е. связанной с другими проектами) эффективности использования капитала;
— норма дисконта участника проекта отражает эффективность участия в проекте предприятий (или иных участников). Она выбирается самими участниками. При отсутствии чётких предпочтений в качестве неё можно использовать коммерческую норму дисконта;
— социальная (общественная) норма дисконта используется при расчётах показателей общественной эффективности и характеризует минимальные требования общества к общественной эффективности проектов;
— бюджетная
норма дисконта используется при расчётах показателей бюджетной эффективности и отражает альтернативную стоимость бюджетных средств.
Дисконтирование денежного потока на m-м шаге осуществляется путём умножения его значения на коэффициент дисконтирования Кm, рассчитываемый по формуле:
где Кm — коэффициент дисконтирования;
Е – норма дисконта;
tm — момент начала шага;
t0 — момент приведения.
finekon.ru
